Dynamics of Thermodynamically Stable, Kinetically Trapped, and Inhibitor-Bound States of Pepsin

Abstract

The pepsin folding mechanism involves a prosegment (PS) domain that catalyzes folding, which is then removed, resulting in a kinetically trapped native state. Although native pepsin (Np) is kinetically stable, it is irreversibly denatured due to a large folding barrier, and in the absence of the PS it folds to a more thermodynamically stable denatured state, termed refolded pepsin (Rp). This system serves as a model to understand the nature of kinetic barriers and folding transitions between compact states. Quasielastic neutron scattering (QENS) was used to characterize and compare the flexibility of Np, as a kinetically trapped state, with that of Rp, as a thermodynamically stable fold. Additionally, the dynamics of Np were compared with those of a partially unfolded form and a thermally stabilized, inhibitor-bound form. QENS revealed length-scale-dependent differences between Np and Rp on a picosecond timescale and indicated greater flexibility in Np, leading to the conclusion that kinetic stabilization likely does not correspond to reduced internal dynamics. Furthermore, large differences were observed upon inhibition, indicating that QENS of proteins in solution may prove useful for examining the role of conformational entropy changes in ligand binding.

Introduction

Kinetic stability is an important factor in the functional lifetime of a protein (1,2), misfolding diseases (3), and biotechnology applications (4); however, a mechanistic understanding of the determinants of this stability is currently lacking. A number of zymogen-derived peptidases require the prosegment (PS) domain to facilitate folding, and once the PS is removed, the native enzyme conformations exist as kinetically trapped states in which both unfolding and refolding are hindered by large activation barriers (5,6). Such proteins may serve as useful models to understand the nature of kinetic folding and unfolding barriers, particularly those that separate compact folded states.

As described previously (7), native pepsin (Np) also exists as a kinetically trapped conformation and has a folding mechanism similar to that of the serine peptidases typified by α-lytic peptidase (αLP) (8). Pepsin is derived from its zymogen form, pepsinogen, which consists of a 44-residue N-terminal PS domain and a 326-residue mature domain. Upon zymogen folding, the PS is autocatalytically removed at acidic pH to yield mature pepsin. Although Np is kinetically stable at pH 5.3 due to a 24.5 kcal/mol unfolding barrier, it is irreversibly denatured due to a comparable folding barrier of 24.6 kcal/mol (7). Pepsin partially unfolds at pH 8, forming an extended intermediate state (i.e., intermediate pepsin (Ip)), and upon its return to pH 5.3 forms a thermodynamically stable, yet inactive, refolded state (i.e., refolded pepsin (Rp)) (9). Rp was found to have a native-like compactness (R_g ≈ 20 Å for both Np and Rp), but with ∼9% less β-strand secondary structure and a 5°C higher T_m (9). The PS facilitates folding from Rp to Np by lowering the folding activation barrier by 6 kcal/mol (increasing the folding rate 85,000-fold), and by thermodynamically stabilizing the native conformation, thus driving the equilibrium from PS-Rp toward PS-Np (7). Once the PS is removed, the folding and unfolding activation barriers increase and Np is destabilized such that it exists as a kinetically trapped, thermodynamically metastable state relative to Rp (7).

It has been proposed that certain peptidases may have developed kinetically trapped native states to enhance resistance to proteolysis, with the resistance due to increased rigidity (10,11). Specifically, hydrogen/deuterium (H/D)-exchange NMR measurements of αLP revealed large exchange protection factors throughout the structure, indicating a high level of conformational rigidity (11). However, studies on the dynamics of other kinetically trapped proteins are lacking.

In addition to the stability-dynamics relationship, the role of dynamics in protein-ligand interactions is not well understood, although this area is directly relevant to drug design and calculations of ligand-binding affinity (12,13). The affinity of the ligand-protein interaction is determined by enthalpic and entropic terms, given as (14,15):

$$\Delta G_{\text{bind}}=\Delta H_{\text{bind}}-\text{T}\Delta S_{\text{bind}}=\Delta H_{\text{bind}}-\text{T}\left(\Delta S_{\text{solvent}}+\Delta S_{\text{protien}}+\Delta S_{\text{ligand}}\right).$$ (1)

The total binding entropy, ΔS_bind, is further broken down into changes in solvent entropy, ΔS_solvent, and conformational entropies of the protein, ΔS_protein, and ligand, ΔS_ligand. The change in protein conformational entropy is typically neglected in ligand-binding studies because of the difficulty of measuring (15) or calculating (13) this contribution. However, recent experimental and theoretical evidence suggests that changes in conformational entropy play a major role in defining binding affinity (13,14).

Most aspartic proteases are potently inhibited by pepstatin A, a naturally occurring hexapeptide with the sequence Iva-Val-Sta-Ala-Sta-Ala-Sta, where statine (Sta) is an uncommon amino acid and the N-terminus of Val is modified with isovaleric acid (Iva) (16). Pepstatin binds pepsin with an inhibition constant, K_i, of 46 pM (17), which is one of the highest affinity levels found for natural inhibitors. Pepstatin binding occurs within the active site cleft between the N- and C-terminal domains, and results in very little change in the crystal structure, with a root mean-square deviation (RMSD) of 0.33 Å between the bound and unbound forms (see Fig. S1 in the Supporting Material).

Investigators have used quasielastic neutron scattering (QENS) to study the role of dynamics in protein folding and stability for a number of globular proteins in solution, primarily comparing the picosecond dynamics of native and partially or completely unfolded states. Examples of such proteins include Staphylococcal nuclease (18), neocarzinostatin (19), yeast phosphoglycerate kinase (20), bovine α-lactalbumin (21,22), calmodulin (23), and α-amylase (24–26). Relatively few QENS studies have examined ligand-binding and protein dynamics. Early examples include inelastic neutron scattering studies on lysozyme bound with an inhibitor (27) and hexokinase bound with its substrate, glucose (28), which were able to show that changes in dynamics of proteins in solution could be measured with neutron scattering. More recently, inelastic neutron scattering was used to study dihydrofolate reductase in the presence of the substrate methotrexate (29), which revealed that ligand binding actually increased the quasielastic broadening of the elastic peak, suggesting increased flexibility. However, because the samples were prepared as hydrated powders and measurements were made at 120 K, the interpretation of the results for physiological conditions was not clear.

In this study, we used QENS to compare the picosecond-to-nanosecond dynamics of pepsin under various folded states (Np, Ip, and Rp) and when bound with pepstatin (NpP) to examine the relationships between stability and conformational flexibility. In D₂O solution and at 298 K, dynamical motions on these timescales correspond to diffusive side chain motions when labile H atoms are replaced via H/D exchange. Specifically, we compared the picosecond internal dynamics of Np and Rp to examine the hypothesis that a kinetically trapped native state is dynamically constricted relative to the thermodynamically stable state. These data also help us understand the nature of the large pepsin folding/unfolding barrier, because it is necessary to characterize the structure and dynamics of the states separated by this barrier, i.e., Np and Rp. In addition, we measured the changes in pepsin dynamics upon binding of pepstatin to quantify the effects of ligand binding on protein flexibility and conformational entropy. A limited number of QENS studies have investigated protein dynamics in response to ligand binding, and the well-characterized pepsin system, bound with a high-affinity inhibitor, provides a unique opportunity to investigate this feature.

Materials and Methods

Materials

Pepstatin A and porcine pepsin (EC 3.4.23.1) of the highest purity available were purchased from Sigma-Aldrich (St. Louis, MO). D₂O (99.9%), NaOD (40% in 99.9% D₂O), and deuterated acetic acid-D4 were purchased from ACP Chemicals (Montreal, QC). Trace metal grade ammonium hydroxide from Fisher Scientific (Fair Lawn, NJ) was used. All other reagents were of ACS grade.

QENS sample preparation

The commercial porcine pepsin was further purified and samples were prepared as described in the Supporting Material.

QENS measurements

Refer to the Supporting Material for a brief introduction to QENS. Neutron scattering experiments were performed with the use of the NG4 time-of-flight (TOF) disk chopper spectrometer (DCS) (30) and the NG2 high-flux backscattering spectrometer (HFBS) (31) located at the National Institute of Standards and Technology Center for Neutron Research (NCNR, Gaithersburg, MD).

The DCS instrument was operated in low-resolution mode with a neutron wavelength of 6 Å. The momentum transfer range was 0.2 ≤ Q ≤ 2.0 Å⁻¹ with an energy resolution of 57 μeV, as determined by measuring the elastic scattering from vanadium. Each sample and the buffer were measured for 24 h and the sample temperature was maintained at 298 K.

The HFBS instrument was operated with an energy transfer range of ± 17 μeV, a momentum transfer range of 0.25 ≤ Q ≤ 1.75 Å⁻¹, and an energy resolution of 1 μeV, as determined by measuring the scattering from vanadium. Each sample and the buffer were measured for ∼22–30 h and the temperature was maintained at 298 K.

Samples were diluted to a concentration of 50 mg/ml (Np, Rp, and Ip) or 100 mg/ml (Np and NpP) in D₂O buffer consisting of 100 mM acetic acid-D4/NaOD with a final pD of 5.55 (Np, Rp, and NpP) or 8 (Ip) and loaded into annular aluminum cans for measurements, as described in the Supporting Material.

The transmission of neutrons through the sample without scattering, T = exp(− t × n × σ_s), was calculated from the sample thickness (t), the total scattering and absorption cross-section of the sample (σ_s), and the number of scattering units per unit volume (n). For the 50 and 100 mg/ml samples, ∼8% and 9% of the incident neutrons were scattered, indicating that multiple scattering effects were negligible.

QENS data reduction and analysis

The data were normalized for background scattering, detector efficiency, and corrected using the detailed balance factor. The TOF data were combined from an initial 913 spectra into 19 spectra with an energy step of 0.02 meV over the range of −1 to +1 meV, and a Q step of 0.1 Å⁻¹. The scattering from the solvent was subtracted from that of the protein solutions, taking into account the protein-excluded volume. Considering a partial specific volume for pepsin of 0.783 cm³/g (9) gives a final solvent fraction, f_solvent, of 0.96 for a protein concentration of 50 mg/ml and 0.93 for a protein concentration of 100 mg/ml, which was included in the solvent subtraction procedure:

$$S_{\text{protein}}\left(Q,\omega \right)=S_{\text{solution}}\left(Q,\omega \right)-\left(f_{\text{solvent}}\right)·S_{\text{solvent}}\left(Q,\omega \right).$$ (2)

where S_protein(Q, ω) is the scattering function corresponding to scattering solely from the protein, obtained by subtracting the scattering from the buffer solvent alone from that of the protein solution. The reduced and subtracted scattering data were analyzed according to:

$$S_{\text{protein}}\left(Q,\omega \right)=e^{-Q^2\langle u^2\rangle /3}·\left[A_0\left(Q\right)·R\left(Q,\omega \right)+A_i\left(Q\right)·L_1\left({\Gamma }_1,\omega \right)\otimes R\left(Q,\omega \right)\right]+Bo+B\omega .$$ (3)

A Gaussian, R(Q, ω), was used to represent the elastic scattering, and a single Lorentzian, L₁(Γ₁, ω), was used to represent the quasielastic scattering, where Γ₁ is the halfwidth at half-maximum (HWHM) of the Lorentzian peak.

An inelastic term, $e^{-Q^2\langle u^2\rangle /3}$ (the Debye-Waller factor), corresponds to high-frequency vibrational motions. However, energy transfers due to the inelastic term generally contribute only to the flat background, and energy transfers for proteins in solution are primarily quasielastic, which causes a slight broadening of the elastic band centered around ℏω = 0 (32). The terms A₀(Q) and A_i(Q) represent the elastic incoherent structure factor (EISF) and the quasielastic incoherent structure factor, respectively, which are related because they sum to unity. A linear background (Bo + Bω) was included in the TOF fits but not in the HFBS fitting. In this analysis, the QENS is assumed to be due solely to internal rather than whole-particle diffusive motions, because although the latter are likely negligible on a picosecond timescale, they may become substantial on the nanosecond–microsecond timescale (refer to the Supporting Material for further discussion). The TOF data were reduced with the use of the program MSlice, the HFBS data were reduced with the HFBS reduction tool, and curve fitting was performed with the program PAN. All programs were accessed from within the DAVE suite available from the National Institute of Standards and Technology (33).

Differential scanning calorimetry

Differential scanning colorimetry (DSC) experiments were performed with the use of a MicroCal VP-DSC (MicroCal, Northampton, MA) as described in the Supporting Material.

Results

The following sections describe QENS data obtained by directly comparing Np, Ip, and Rp at a protein concentration of 50 mg/ml, and additional experiments in which Np and NpP were compared at 100 mg/ml.

Picosecond dynamics measured with TOF-QENS

We used TOF-QENS to measure changes in the flexibility of pepsin, essentially focusing on the diffusive dynamics of side chains occurring on a picosecond timescale. We determined the limit of the experimental resolution by measuring the scattering from vanadium, which scatters neutrons isotropically and elastically. The full width at half-maximum (FWHM) of the vanadium peak was ∼57 μeV, which corresponds to a time limit of ≈145 ps. Thus, motions occurring on a timescale slower than 145 ps could not be detected and could only contribute to the elastic scattering.

The data of interest are the difference spectra, S_protein(Q, ω), obtained by subtracting the buffer spectra from the protein solution spectra using Eq. 2. A major caveat is that the D₂O solvent makes a substantial contribution to scattering (∼80% of the total scattering (34)), and it can be difficult to measure changes in protein dynamics in solution against such a large solvent scattering background. The subtraction process increases the noise of the data, and thus the buffer spectra must be measured to the best counting statistics possible. For example, in this study, each sample and buffer solution was measured for 24 h. However, by using high protein concentrations (i.e., ≥50 mg/ml), one can often perform comparative studies using QENS of proteins in solution (18–26), although the solvent subtraction procedure necessarily assumes that the contribution of the bulk D₂O in the buffer sample is identical to that in the protein solution. The difference spectra for Np at 50 and 100 mg/ml are shown in Fig. 1, and the additional elastic scattering and quasielastic broadening of the elastic peak due to pepsin dynamics can be seen before and after subtraction of the solvent contribution.

Figure 1.

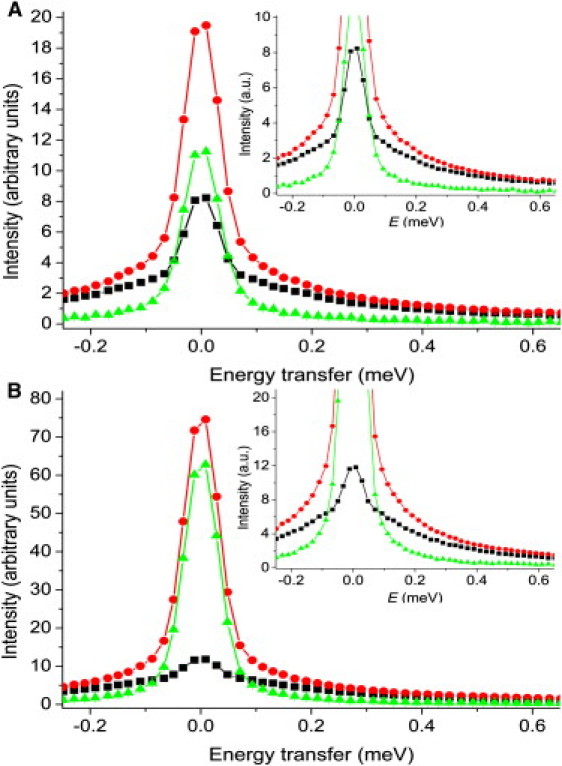
TOF-QENS solvent subtraction results. Difference spectra were obtained by subtracting the buffer sample scattering (black squares) from that of the protein solution (red circles) using Eq. 2 to obtain the protein-only spectra, S_protein(Q, ω) (green triangles). (A) Np, 50 mg/ml at Q = 1.2 Å⁻¹. (B) Np, 100 mg/ml, Q = 1.2 Å⁻¹. Error bars are smaller than the data point symbols.

The reduced and corrected difference spectra were fit according to Eq. 3 (see Fig. S3). For the data collected from samples of 50 mg/ml (Np, Ip, and Rp), minimal restrictions on the fitting parameters were used. Conversely, the Lorentzian FWHM was fixed at 0.2 meV for the 100 mg/ml data (Np and NpP) because, after the first series of nonrestricted fitting, it became evident that the FWHM of the Lorentzian was essentially constant except at low Q, where the FWHM decreased as a function of Q (data not shown). Because fitting in the low-Q region suffered from low quasielastic broadening, this indicated that the Lorentzian FWHM should be fixed to the average value obtained over the mid-range Q (∼0.8 to ∼1.6 Å⁻¹), which was ∼0.2 meV for both Np and NpP. This protocol is not uncommon (25), because the FWHM of the Lorentzian component either increases with Q (22,35,36) or remains constant with Q (19,20,23,24), but does not decrease with larger Q.

Correlation time of motions: FWHM analysis

Given the finite resolution and counting statistics, a single Lorentzian is generally sufficient to fit QENS data from protein samples. Thus, the multitude of diffusive modes of internal motion is represented as one averaged mode with a characteristic frequency proportional to the FWHM of the Lorentzian function. Examining the FWHM as a function of Q gives insight into the length-scale dependence of the timescale of motion.

As shown in Fig. 2 A, the trend in the FWHM with Q was similar for Np and Ip, and the magnitudes were much larger than for Rp at higher Q-values, although they were quite similar toward low Q. This indicates that at longer length scales, Q < 0.8 Å⁻¹ and d > 7.9 Å, the motions in Np, Ip, and Rp were of similar frequency, whereas on shorter length scales, Q > 1.3 Å⁻¹ and d < 4.8 Å, the frequency of motion continued to increase for Np and Ip, and became more Q-independent for Rp. That is, the FWHM began to plateau at Q > 1.3 Å⁻¹ in the case of Rp, but did not quite reach the plateau for Np and Ip within the measured range. The observation that the correlation times are independent of the length scale indicates that the same type of motion (i.e., a correlated motion) is observed (22). Jump motions are believed to dominate toward smaller length scales and give rise to the plateau in the FWHM trend (22,36), as seen for Rp (Fig. 2 A). Assuming that the same behavior exists in Np and Ip, we extrapolated the plateau values using a jump diffusion model (36,37):

$$\left(Q\right)=\left(D{Q}^2\right)/\left(1+D{Q}^2\tau \right),$$ (4)

where D is a diffusion constant and τ is the dwell time between jumps. In fitting the data, 1/FWHM_α was used in place of τ, where in this case,

$$\tau =2h/\text{FWH}{\text{M}}_{\alpha },$$ (5)

as follows from

$$E=h\omega =\left(h/2\pi \right)\left(2\pi /\tau \right)=h/\tau ,$$ (6)

where E is the HWHM. The activation barriers to jump motions can be compared for different samples from the relative dwell time:

$$\Delta E_{\text{a}}=k_{\text{B}}T\text{ln}\left({\tau }_1/{\tau }_2\right).$$ (7)

Figure 2.

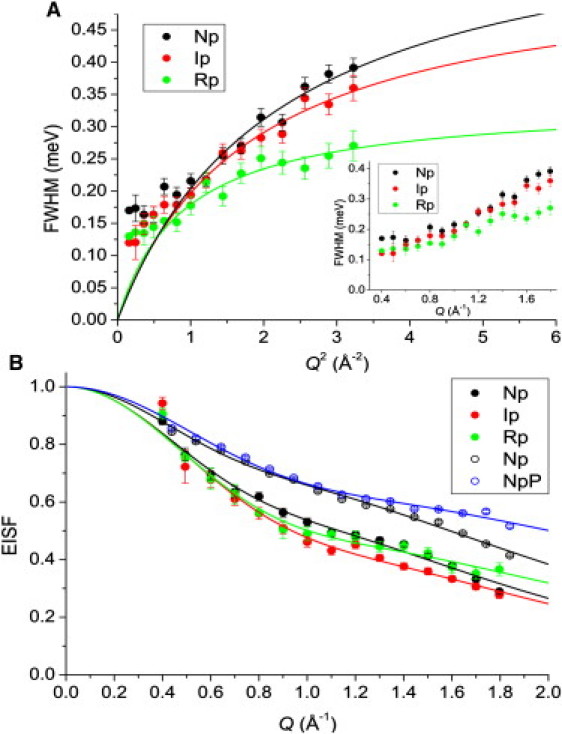
Fitting results from TOF-QENS data. (A) Neutron energy transfers, FWHM, versus Q² fit with a jump diffusion model (Eq. 4) for Np, Ip, and Rp at 50 mg/ml. Inset shows FWHM versus Q without fitting. (B) EISF for Np, Ip, and Rp at 50 mg/ml (solid points), and for Np and NpP at 100 mg/ml (open points). Lines indicate fits according to Eq. 9. Error bars indicate fitting errors. Error bars that are not visible are smaller than the data point symbols.

Furthermore, the jump distance (L) is given by (36):

$$L={\left(D\tau \right)}^{1/2}$$ (8)

Interpreting the higher, Q-dependent FWHM values with a jump diffusion model gave similar jump distances for Np (0.67 ± 0.08 Å), Ip (0.74 ± 0.08 Å), and Rp (1.06 ± 0.17 Å), but with a longer residence time between jumps for Rp (24 ps) than in Np and Ip (13–15 ps), and correspondingly a 1.6 kJ/mol larger activation barrier to motions in Rp. The similar amplitudes but different frequencies of jump diffusion suggest that rotational motions were dominant at high Q.

In fitting the FWHM data according to the jump diffusion model, we included only the higher Q-value data, from 0.9 ≤ Q ≤ 1.8 Å⁻¹, because the data from 0.4 ≤ Q ≤ 0.8 Å⁻¹ were relatively Q-independent. Thus, another plateau was observed in the FWHM toward low Q-values, which is indicative of another type of correlated diffusive motion. Furthermore, the FWHM of Np, Ip, and Rp tended toward finite values as Q → 0, indicating that constrained diffusion was observed (37). The fact that the FWHM for Np, Ip, and Rp tended toward similar values as Q → 0 suggests that all three states were undergoing constrained diffusive motions with similar correlation times. We characterized the amplitude of this motion by analyzing the EISF (see below). The frequency for unconstrained, continuous diffusional motion varies linearly with Q according to DQ² (37), as was observed above Q ∼0.8 Å⁻¹ for Np, Ip, and Rp (Fig. 2 A). Together, the plateau in the FWHM at low Q and the DQ² behavior at intermediate Q are in accord with the continuous diffusion in a spherical volume model developed by Volino and Dianoux (38). Thus, three dynamic regimes were observed, with plateaus at both low and high Q-values, and a linear increase in FWHM over the mid-range Q. Similar trends in the FWHM with Q² have been observed for bovine α-lactalbumin (22) and dihydrofolate reductase (36).

Amplitude of motions, EISF analysis

The internal motions of the nonexchanged H atoms were described by fitting an analytical model to the EISF. Initially, a continuous diffusion model, diffusion within a spherical volume (DSV) (38), was applied alone, but it could not be used to adequately fit the EISF above Q ≈ 1.4 Å⁻¹ due to the appearance of a shoulder (such a feature has been observed for other proteins; see Supporting Material for discussion). Thus, the DSV model was combined with a three-site jump (3SJ) diffusion model, giving:

$$\text{EISF}=\text{DSV}·3\text{SJ}$$ (9)

The DSV model, parameterized by the radius of the hard-walled sphere, r, is given as (22):

$$\text{DSV}=f_{\text{nd}}+\left(1-f_{\text{nd}}\right)·9/{\left(Qr\right)}^6·{\left[\text{sin}\left(Qr\right)-Qr\text{cos}\left(Qr\right)\right]}^2.$$ (10)

The 3SJ model, parameterized by the jump distance, d, is given as (32):

$$3\text{SJ}=\left(1/3\right)·\left[1+2·\left(\text{sin}\left(Qd{3}^{1/2}\right)·1/\left(Qd{3}^{1/2}\right)\right)\right].$$ (11)

In this form, the fraction of nondiffusing (f_nd) scattering groups accounts for the H atoms that do not undergo DSV motions on the measured timescale, and undergo only 3SJ motions.

The use of the jump diffusion model here should not be taken to solely represent the rotational motions of methyl protons. Rather, they should be considered as representative of local diffusive motions of a different character compared with those represented by the DSV model. For example, surface-exposed residues could be expected to diffuse more freely than internal residues, which may undergo limited jump diffusion (37). Generally, the use of any analytical model is an oversimplification of the true dynamic behavior, but is suitable to interpret QENS data, which represent a global average of all H atom motions occurring in the relevant space-time scale of the experiment.

The results of the EISF fits with Eq. 9 are given in Table 1. The EISF data indicate relatively similar amplitudes of motions for Np and Rp (Fig. 2 B), although the fraction of mobile H groups was slightly lower in Np, as judged from the fits and also from the larger amplitude of the data. Ip clearly showed a greater amount of diffusive H than Np (smaller f_nd and lower EISF values), although the amplitude of motion was slightly lower.

Table 1.

Amplitudes of picosecond and nanosecond diffusive motions from TOF^∗ and HFBS^† data

	Concentration (mg/ml)	Picosecond			Nanosecond
		r (Å)	d (Å)	fnd	r (Å)	fnd
Np	50	3.92 ± 0.29	0.83 ± 0.04	0.67 ± 0.03	5.82 ± 0.46	0.11 ± 0.03
Ip	50	3.39 ± 0.35	0.78 ± 0.11	0.56 ± 0.07	6.63 ± 0.25	0.13 ± 0.01
Rp	50	3.53 ± 0.24	0.64 ± 0.08	0.56 ± 0.04	n/a	n/a
Np	100	4.21 ± 0.25	0.73 ± 0.02	0.79 ± 0.01	5.04 ± 0.24	0.16 ± 0.02
NpP	100	3.32 ± 0.16	0.50 ± 0.03	0.70 ± 0.02	4.98 ± 0.25	0.15 ± 0.02

Uncertainties indicate fitting errors.

^∗EISF fitting parameters were obtained according to Eq. 9.

^†EISF fitting parameters were obtained according to the DSV model, Eq. 10.

Differences in the EISFs of Np versus NpP (Fig. 2 B) were observed only at Q > 1.2 Å⁻¹. The EISF values for Np dropped sharply above 1.2 Å⁻¹ due to an increased intensity of the Lorentzian quasielastic component toward higher Q, indicating a stronger presence of diffusive motions in Np versus NpP. Increased motion in Np was represented by larger amplitudes of both free diffusion and jump diffusion than found for NpP (Table 1).

A comparison of the data in Fig. 2 B reveals a possible concentration effect, because the EISF values for Np and NpP at 100 mg/ml are larger across the entire Q-range, which is represented by the larger f_nd-values of the 100 mg/ml data (Table 1). This result indicates that although the geometry and amplitude of motion were similar at the two concentrations, the fraction of H that underwent motions in the time window of the experiment was reduced at 100 mg/ml.

Change in conformational entropy upon binding of pepstatin

Because scattering from side-chain Hs dominate the data, and we assume that the side chains move as a single group, we can use the change in conformational space explored by each group to estimate the ΔS_conf, using the relation determined by Fitter (24)

$$\Delta S_{\text{conf}}^{DSV}=3\text{R}\text{ln}{r}_{\text{a}}/r_{\text{b}},$$ (12)

to describe spherical diffusive motions, and using

$$\Delta S_{\text{conf}}^{3SJ}=\text{R}\text{ln}{d}_{\text{a}}/d_{\text{b}},$$ (13)

to describe jump diffusion. The conformational space explored is defined by the DSV and 3SJ models and the radius of diffusion, r, and jump distance, d, respectively. Using the values for Np and NpP (100 mg/ml) from the fits to Eq. 9, we found the $\Delta S_{\text{conf}}^{DSV}$ and $\Delta S_{\text{conf}}^{3SJ}$ of pepsin upon binding of pepstatin to be −1.4 cal/mol/K/residue and −0.7 cal/mol/K/residue, respectively. Assuming that all pepsin residue side chains participated in the observed dynamics, the sum total conformational entropy change, $\Delta S_{\text{conf}}^{tot}$ (−0.63 kcal/mol/K) was nearly double the total entropy change, ΔS_bind (−0.33 kcal/mol/K), determined from the DSC measurements, which are described below. These results suggest that desolvation and the increase in solvent entropy are not enough to compensate for ΔS_conf, and thus binding is driven primarily by a large reduction in enthalpy.

Qualitatively, these data show that a substantial change in conformational entropy occurs upon pepstatin binding. However, it is difficult to perform a quantitative comparison of ΔS_conf and ΔS_bind, for two reasons. First, the dynamics data from QENS were obtained at 298 K, whereas the thermodynamic data from DSC were obtained at 355 K, and the temperature dependence of ΔS_conf may be significant. Second, the conversion of the dynamics data into an estimate of ΔS_conf is not a straightforward process, and the use of simplified models, such as Eqs. 12 and 13, likely introduces error. For example, a recent study of calmodulin-ligand binding using NMR found that a large empirical scaling factor was required to calibrate the determination of ΔS_conf from dynamics measurements (15). The scaling factor was determined by comparing the difference between the total and solvent binding entropy changes (ΔS_bind − ΔS_solvent) with the apparent ΔS_conf determined from the NMR data.

Nanosecond dynamics measured with the HFBS

To complement the TOF data, which reported on diffusive motions faster than 145 ps, we made QENS measurements using a backscattering instrument, which has a much higher energy resolution and can detect motions occurring on a nanosecond timescale. The resolution of the HFBS experiments, determined by measuring the FWHM of the scattering from a vanadium sample, was 1 μeV. Thus, atoms with motions with correlation times slower than ≈8 ns appeared immobile and contributed only to the elastic scattering centered at zero energy transfer, whereas motions faster than this could be studied as quasielastic scattering. However, in comparison with the TOF studies, the HFBS measurements suffered from a reduced signal/noise ratio and a limited Q-range of ∼0.4 to 1.3 Å⁻¹, due to severely reduced counting statistics at higher Q-values. HFBS data were collected for Np and Ip at 50 mg/ml, and for Np and NpP at 100 mg/ml.

Amplitude and correlation times of motions

The reduced, buffer-subtracted HFBS spectra were fit according to a modified form of Eq. 3, which included only a Gaussian and a Lorentzian without the linear background term, Bo + Bω, and the EISF and the FWHM of the Lorentzian were obtained for further analysis. The EISF variation with Q was adequately fit using Eq. 10, according to the DSV model (Fig. 3 A), and the results of the fits are given in Table 1. In the case of Np versus Ip (50 mg/ml), the EISF trends were similar, although the amplitude of diffusive motions may have been slightly larger for Ip. A large difference in the FWHM was observed (Fig. 3 B), with Ip tending toward much higher frequencies at larger Q. For both Np and Ip, the FWHM tended toward nonzero values as Q → 0, supporting the notion that both states were characterized by confined diffusion of similar length scale. In the case of Np versus NpP (100 mg/ml), no apparent differences were observed between these states in terms of the EISF (Fig. 3 A) and FWHM (Fig. 3 B) Q dependencies, although the FWHM was overall slightly broader for Np than for NpP. The FWHM versus Q trend for all the samples showed only the DQ² behavior, yet the FWHM did not approach zero toward low Q, supporting the use of the constrained DSV model (Fig. 3 B).

Figure 3.

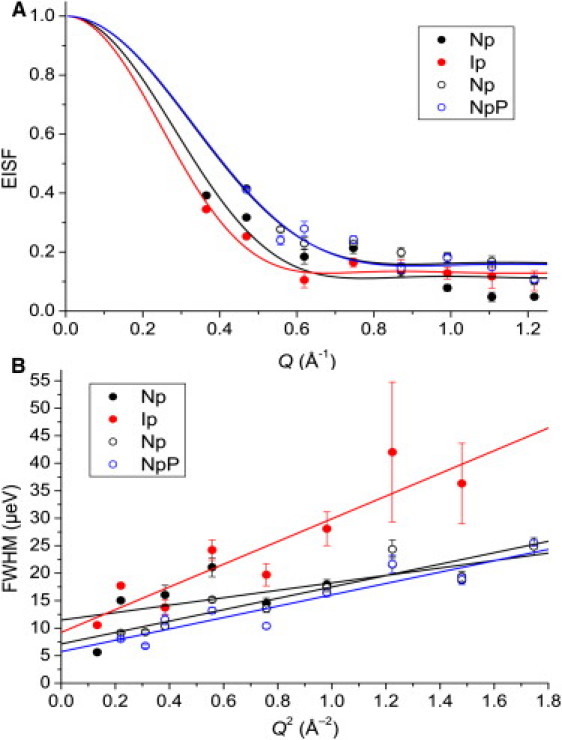
Fitting results from HFBS data for Np and Ip at 50 mg/ml (solid points) and Np and NpP at 100 mg/ml (open points). (A) EISF. Lines indicate fits according to the DSV model given in Eq. 10. (B) Neutron energy transfers, FWHM. Lines indicate linear fits to the data. Error bars indicate fitting errors. Error bars that are not visible are smaller than the data point symbols.

A comparison of the data obtained at 50 mg/ml and 100 mg/ml indicates that pepsin at a higher concentration was characterized by a smaller radius of diffusive motion and a slightly greater fraction of nondiffusing H (Table 1), in agreement with observations from the TOF data. Furthermore, the FWHM of the Lorentzian component for pepsin at 100 mg/ml tended toward lower values as Q → 0. From the DSV model (38), the diffusion coefficient, D, within the confined spherical volume of radius, r, was obtained from the extrapolated, nonzero FWHM value at Q = 0 Å⁻¹ by means of the following equation (22,36):

$$\text{FWHM}/2=4.333D/r^2.$$ (14)

In this case, the FWHM was converted from meV to Hz with the use of Eq. 6. The coefficients at 50 mg/ml ((1.08 ± 0.29) × 10⁻⁶ cm²/s (Np) and (1.13 ± 0.40) × 10⁻⁶ cm²/s (Ip)) were larger than those at 100 mg/ml ((0.51 ± 0.08)×10⁻⁶ cm²/s (Np) and (0.40 ± 0.08)×10⁻⁶ cm²/s (NpP)). These findings suggest that by increasing the protein concentration from 50 mg/ml to 100 mg/ml, we were able to reduce the diffusive side-chain motions within the observed space-time windows (∼20–3 Å⁻¹ and 100–20 ps for TOF, and ∼20–4 Å⁻¹ and 8–0.3 ns for HFBS).

Changes in pepsin stability upon pepstatin binding

We measured the increase in pepsin stability upon binding of pepstatin using DSC (see Fig. S4). Pepstatin binding increased both the T_m and unfolding enthalpy, ΔH_unf, from 61.46 ± 0.01°C and 190 ± 4 kcal/mol for Np to 81.90 ± 0.65°C and 330 ± 21 kcal/mol for NpP. These values are in agreement with DSC results previously reported for the binding of pepsin with acetyl-pepstatin at pH 3.0, where unbound pepsin gave a ΔH_unf of 184 kcal/mol and pepstatin binding increased the T_m by at least 17°C (39). The change in heat capacity upon unfolding, ΔC_p, was estimated from the pre- and post-transition baselines and was found to be similar for both samples, with a ΔC_p of 4.26 ± 0.08 kcal/mol/°C for Np and 3.92 ± 0.26 kcal/mol/°C for NpP. These values are similar to that previously determined for Np in 20 mM acetic acid/NaOH buffer, pH 5.3, with a ΔC_p of 5.17 ± 0.20 kcal/mol/°C (9). Using the ΔH_unf, T_m, and ΔC_p values for Np and the T_m for NpP, we determined the binding constant of pepstatin for pepsin using the approach developed by Brandts and Lin (40). This method yielded a K_i of 27 fM at 81.90°C, which is a few orders of magnitude less than the K_i of 45.7 pM at 25°C previously determined using an enzyme activity assay (17). The complete binding thermodynamics were obtained with the following equation:

$$\Delta G_{\text{bind}}=\text{RT}\text{ln}{K}_{\text{i}},$$ (15)

where ΔG_bind is the free energy of binding. Combining ΔG_bind with the binding enthalpy, ΔH_bind, which can be taken as the difference between the unfolding enthalpies of the free and bound forms (41), we determined the entropy change upon binding using Eq. 1. The thermodynamic parameters, at 355 K, were ΔG_bind = −22 kcal/mol, ΔH_bind = −140 kcal/mol, and TΔS_bind = −118 kcal/mol (ΔS_bind = −0.33 kcal/mol/K). Thus, pepstatin binding was characterized by a large entropy penalty that was compensated for by a larger enthalpy of binding.

The stability of Np and NpP were also compared in D₂O buffer as used in the QENS experiments. The DSC scans in D₂O buffer appeared similar to the scans in H₂O buffer but with the T_m values increased by 9°C for both Np and NpP, indicating that D₂O had a similar effect on each sample (data not shown).

Discussion

Stability and dynamics

The enhanced picosecond fluctuations measured by QENS indicated that Np was more flexible than Rp. Furthermore, Np was characterized by picosecond diffusive motions similar to those observed for the Ip state, which can be assumed to be highly flexible as a partially unfolded structure. Additionally, Np underwent a greater extent of H/D exchange than either Rp or NpP, as determined by Fourier transform infrared spectroscopy, indicating a higher degree of flexibility at longer timescales (see Fig. S5). From crystal structure data, pepsin is known to have a flexible C-terminal domain, with higher B-factors (42) and a flexible flap motif that closes over the active site upon ligand binding (43).

Considering that Rp is more stable than Np, both thermodynamically (larger ΔG_unf) and thermally (higher T_m) (9), these findings fit with the trend that stability and flexibility are inversely related features. For example, such a relationship has been shown for lysozyme and RNase A (44), and in comparisons between homologous thermophilic and mesophilic dehydrogenases (45,46). However, the relationship between stability and flexibility remains complicated. QENS studies of thermophilic versus mesophilic α-amylase (25,26) indicated that the more stable protein was more flexible on a picosecond timescale. It was suggested that a lower unfolding ΔS_conf was an adaptive mechanism to increase stability while maintaining the flexibility of the thermophilic enzyme (25,26). Similarly, a comparison of thermophilic and mesophilic dihydrofolate reductase by elastic incoherent scattering showed larger fluctuations in the thermophilic protein (47).

Different mechanisms may be employed to balance enthalpy and entropy to favor the native state, and the flexibility-stability relationship may vary among different proteins. In the same way, the relationship between kinetic stability and flexibility likely varies from protein to protein. Furthermore, although a distinction has been made between native states at equilibrium and kinetically trapped native states, such as αLP (8) and pepsin (7), thermodynamically stable native states may also be kinetically stable. For example, the unfolding rate for trypsin (k_unf = 0.84 × 10⁻⁸ s⁻¹ at 273 K), a thermodynamically stable serine peptidase homologous to αLP, was slower than that for αLP (k_unf = 2.1 × 10⁻⁸ s⁻¹ at 273 K) (10). A number of thermodynamically stable proteins have been characterized as having slow unfolding kinetics, with k_unf < 1 × 10⁻⁸ s⁻¹, and thus as having large unfolding barriers (2,48).

A cooperative unfolding transition, a rigid native state, kinetic stability, and enhanced protease resistance have all been linked as defining features of αLP as a kinetically trapped state (10,11). Conversely, Np is characterized by a noncooperative unfolding transition (9) and a flexible structure; nonetheless, Np is also a kinetically trapped native state. Although pepsin and αLP are both kinetically stable, zymogen-derived peptidases, their physiological environments are quite different, with αLP being secreted by bacteria into soil (11) and pepsin being secreted into the stomach of mammals (49). With respect to proteolysis resistance, these two enzymes have quite different needs and thus likely evolved different mechanisms of resistance. Whereas enhanced kinetic stability and rigidity are hypothesized to increase the proteolytic stability of αLP in the soil (10,11), pepsin has developed a tolerance to low pH, so it needs to be sufficiently resistant only to autoproteolysis, as most other peptidases would be unfolded in the stomach at pH < 3. Although increased rigidity was related with enhanced resistance to proteolysis in αLP (10,11), this alone does not support the notion that increased rigidity is related to kinetic stability. The finding that αLP was rigid may be a specific rather than a general feature of kinetically stable proteins; however, further studies of the stability and flexibility of more proteins are needed to determine whether such general relationships exist.

Concentration effect on dynamics

Due to the low counting statistics and large solvent contribution involved in QENS experiments with protein solutions, concentrations of at least 50–100 mg/ml are generally required (34). Although increasing the pepsin concentration from 50 mg/ml to 100 mg/ml improved the counting statistics, this may have also resulted in a reduction in protein flexibility at the higher concentration. Np and NpP at 100 mg/ml were characterized by EISFs qualitatively similar in shape to those obtained for Np, Ip, and Rp at 50 mg/ml; however, the magnitudes were higher for the 100 mg/ml data, indicating a lower fraction of H participating in the observed motions (Figs. 2 B and 3 A; Table 1). The fact that these features were observed in both the TOF and HFBS data further supports the notion that there was a systematic reduction in pepsin flexibility due to the increased concentration.

It is known that protein concentration can affect structure, stability, and dynamics, although the exact relationship is not yet clearly known. For example, an examination of the thermal stability of various proteins at low (<1 mg/ml) and high (>50 mg/ml) concentrations (50) revealed that at high concentrations, fibrinogen and hemoglobin were stabilized (ΔT_m ≈ +2°C to +10°C), whereas BSA and lysozyme were destabilized (ΔT_m ≈ −2°C to −10°C). Few QENS studies have examined the effect of protein concentration on internal flexibility. A study on myoglobin that examined the dynamics of both the solvent and the protein in various H₂O/glycerol and D₂O/glycerol mixtures indicated that the protein became more rigid with either a decrease in water content or an increase in solvent viscosity (51). Another study compared the dynamics of myoglobin and lysozyme in the form of hydrated powders and in solution (60 mg/ml), and the results showed that the proteins were much more flexible in solution (35). It is possible that an increased protein concentration could also increase the solution viscosity and reduce both the hydration water dynamics and internal protein dynamics.

Ligand binding and conformational entropy changes

This study shows that QENS can be used to measure changes in protein dynamics upon ligand binding, in solution, and that these changes can be used to examine the role of conformational entropy in ligand-binding mechanisms. However, the exact role of conformational entropy change in pepsin inhibition was beyond the scope of this work and will require further careful measurements of the total entropy change, ΔS_bind, and the conformational entropy change, ΔS_conf, at the same temperature. The difference between the two should give the entropy change of the solvent.

An accurate determination of ΔS_conf will require a determination of the change in dynamics across many orders of magnitude of timescale, including vibrational (femtosecond), diffusive (picosecond–nanosecond) and large-scale conformational (microsecond–millisecond) motions. It is important to note that conformational entropy is not measured directly; instead, dynamical parameters, such as the radius of spherical diffusion by QENS (24) or a relaxation order parameter by NMR (15), are measured. These parameters are then converted into an estimate of entropy on the basis of a model, and this process also requires verification. Finally, it would be most useful to determine the ΔS_conf for different inhibitors covering a range of affinities, from fM < K_i < μM, to identify possible trends. Information on how to predict and minimize ΔS_conf penalties could be useful for designing rational inhibitors (12,13). QENS could be an important technique for investigating dynamics and ligand binding, particularly given that protein size is not a limitation and different timescales can be studied.

Conclusions

Considering the correlation times, length scales of motion, and fraction of atoms that participate in the measured space-time window, the internal flexibility increased in the order Rp < Np < Ip. These results indicate that kinetic stabilization does not correspond to a reduction in picosecond diffusive motions, at least in the case of pepsin.

It is possible that kinetic stability may have no particular correlation to conformational dynamics, but instead may be related to local features that give rise to instability in the unfolding transition state, such as strained structural motifs (52), electrostatic interactions (4), and solvation (53). Many thermodynamically stable proteins are also kinetically stable, some even more so than pepsin and αLP, such that a large barrier to unfolding should not be expected to correspond to increased rigidity in a kinetically trapped versus a thermodynamically stable fold. This point leads to a fundamental question: What is the biological significance of the PS-catalyzed folding mechanism?

The most striking and unique feature that αLP and pepsin have in common is a kinetically trapped native conformation that would otherwise not exist without the action of the PS. An alternative hypothesis is proposed, according to which PS-catalyzed folding enhances protein evolvability by allowing more destabilizing mutations to accumulate in the mature domain. As directed-evolution studies have found, the evolution of enzyme function is eventually limited by the loss of conformational stability, because mutations that result in a new function are generally destabilizing (54,55). Therefore, the development of a new function requires the occurrence of other, functionally neutral yet stabilizing mutations (55), thus compensating for the functional mutations. Previous studies demonstrated experimentally that the chaperonins GroEL/ES provide a buffering capacity for protein evolvability (54,56). In the absence of GroEL/ES, it was found that destabilizing mutations set a lower limit to evolution of function and expression, whereas the presence of the chaperonins increased the tolerance for destabilizing mutations and allowed for a greater evolution of specificity and activity (54,56). PS domains must also provide a similar buffering capacity, allowing for a greater search of evolutionary space. Pepsin and αLP are evidence that this statement is true, as PS-catalyzed folding has enabled the evolution of metastable and unstable folds, respectively.