The computer program STRUCTURE does not reliably identify the main genetic clusters within species: simulations and implications for human population structure

Abstract

One of the primary goals of population genetics is to succinctly describe genetic relationships among populations, and the computer program STRUCTURE is one of the most frequently used tools for doing so. The mathematical model used by STRUCTURE was designed to sort individuals into Hardy–Weinberg populations, but the program is also frequently used to group individuals from a large number of populations into a small number of clusters that are supposed to represent the main genetic divisions within species. In this study, I used computer simulations to examine how well STRUCTURE accomplishes this latter task. Simulations of populations that had a simple hierarchical history of fragmentation showed that when there were relatively long divergence times within evolutionary lineages, the clusters created by STRUCTURE were frequently not consistent with the evolutionary history of the populations. These difficulties can be attributed to forcing STRUCTURE to place individuals into too few clusters. Simulations also showed that the clusters produced by STRUCTURE can be strongly influenced by variation in sample size. In some circumstances, STRUCTURE simply put all of the individuals from the largest sample in the same cluster. A reanalysis of human population structure suggests that the problems I identified with STRUCTURE in simulations may have obscured relationships among human populations—particularly genetic similarity between Europeans and some African populations.

One of the principal goals of population genetics is to describe the genetic structure of populations. In essence, this means summarizing the genetic similarities and differences among populations in as simple of a manner as possible. For some taxa, this is easy. For example, the range-wide population structure of Atlantic salmon has two salient features: Atlantic salmon in Europe and North America are very different from each other, and within each continent, genetic differentiation between populations is proportional to geographic distance (King et al., 2001). The population structure of other species can be difficult to summarize. For example, human population structure is quite complex, and there has been recent debate on the extent to which human genetic diversity is distributed in clusters or along clines (for example, Manica et al., 2005; Rosenberg et al., 2005).

No matter how simple or complex genetic relationships among populations may be, geneticists need to be careful that the statistical methods they use to summarize relationships do not distort the actual relationships among populations. Imposing inappropriate statistical models upon genetic data is all too easy. For example, if populations have an isolation-by-distance population structure, an unweighted pair group method with arithmetic mean tree could easily provide a misleading depiction of the genetic structure (Kalinowski, 2009). This happens because an unweighted pair group method with arithmetic mean tree cannot show a population structure that is not hierarchical.

The computer program STRUCTURE (Pritchard et al., 2000; Falush et al., 2003; Hubisz et al., 2009) is currently one of the most frequently used statistical tools for describing population structure. The program does this by sorting individuals into Hardy–Weinberg/linkage equilibrium populations, which creates clusters of individuals that have distinctive allele frequencies. An important step in this analysis is deciding how many clusters to sort individuals into. This number, K, is selected by the user. If K is equal to the actual number of Hardy–Weinberg populations that the individuals belong to, STRUCTURE will attempt to sort individuals into the populations they came from. This can be very useful when the origin of individuals is unknown. However, STRUCTURE is also frequently used to identify the main genetic clusters within species. In this second type of analysis, individuals are assigned to clusters in the same manner as above, but K is deliberately set to be smaller than the actual number of populations. Rosenberg et al. (2001) argued that such clustering is useful for ‘identification of population relationships, history, and within-species genetic units for conservation', last sentence of paper).

In the 10 years since STRUCTURE was created, over 3000 papers have cited the program, and many users of STRUCTURE have used the program to describe genetic relationships among populations. For example, in a landmark study of human population structure, Rosenberg et al. (2002; 2005) used STRUCTURE to sort people from 52 ethnic groups into five clusters. This analysis clustered individuals by continent, and this result has been influential in subsequent discussions of human population structure. However, this result—and other analyses of population-level relationships made by STRUCTURE—may need to be reevaluated. The mathematical model used by STRUCTURE was designed for clustering individuals into Hardy–Weinberg/linkage equilibrium populations. It was not designed for clustering individuals into groups of populations, and may not work as its users intend when this is done.

A few investigators have evaluated how well STRUCTURE works in different applications, but this testing has shed little light on how well STRUCTURE summarizes relationship among populations. For example, Rosenberg et al. (2001) showed that STRUCTURE could accurately sort individual chickens by breed, but this empirical test did not evaluate how well STRUCTURE could cluster individuals into groups of related populations. Evanno et al. (2005) addressed this later question using simulated data and showed that STRUCTURE was able to do this successfully. However, Evanno et al. (2005) used a hierarchical island model of gene flow which made the biologically simplistic assumption that all groups of populations were equally different from each other. Real populations are expected to show more complex relationships, and this may affect the manner in which STRUCTURE assigns individual to clusters. Lastly, Schwartz and McKelvey (2008) showed that when individuals were distributed continuously on a two-dimensional landscape, and mated preferentially with neighboring individuals, STRUCTURE sometimes clustered individuals in unpredictable ways. This clearly showed that STRUCTURE does not work well when individuals do not belong to distinct Hardy–Weinberg populations, but does not offer much insight to how well STRUCTURE works for taxa whose individuals belong to distinct populations—as is often the case.

The goals of this paper are twofold. First, I will use computer simulation to examine whether STRUCTURE can correctly group individuals into clusters when populations have had a history of fragmentation and isolation. This is one of the simplest types of histories that a set of populations might have, and one of the most commonly used models to describe genetic relationships among natural populations. Second, I will explore two previously published data sets of human genetic diversity to determine whether problems identified in the simulations have influenced depictions of human population structure.

Simulations

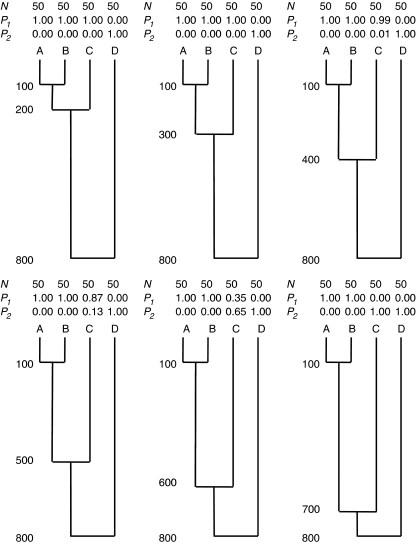
The first goal of this investigation is to examine how well STRUCTURE can summarize population structure for a simple model of population fragmentation. To do this, I simulated microsatellite genotypes in a four-population model of divergence, in which an ancestral population was repeatedly and instantaneously split into descendant populations that thereafter did not exchange members (Figure 1). In this evolutionary model, populations A and B are closely related to each other, population C is less closely related to A and B (but still more closely related to A and B than to D) and population D is the most genetically divergent population. If STRUCTURE was told to partition individuals from these populations into two clusters, and STRUCTURE works as its users expect, individuals from populations A, B and C should be placed into one cluster, and individuals from population D should be placed into the other cluster.

Figure 1.

The effect of evolutionary history on clustering. The numbers to the left of the six phylogenies are divergence times measured in generations before present (for example, populations A and B diverged 100 generations ago). Above each phylogeny are the sample sizes taken from each population (N), and the proportion of ancestry from those samples attributed to K=2 clusters (P₁ and P₂) by the program STRUCTURE 2.2.

Coalescent methods were used to simulate microsatellite genotypes for the evolutionary history shown in Figure 1. While doing this, I assumed that the effective population size of all populations (including ancestral populations) was 2000 individuals. I used a single-stepwise model of mutation, with a mutation rate of 2 × 10⁻⁴. Given these parameters, the expected heterozygosity within populations is 0.51, and expected pairwise F_ST (Weir and Cockerham, 1984) between populations ranges from 0.02 to 0.14 (Table 1). Data sets were simulated for 50 diploid individuals per population with 1000 unlinked loci per individual. I used a large number of loci because I wanted to test whether STRUCTURE has an inherent tendency to cluster individuals in an inappropriate manner, not whether sampling error affects clustering. Selected results were checked by simulating data with the publically available computer program SimCoal2 (http://cmpg.unibe.ch/software/simcoal2/) using the same evolutionary parameters. STRUCTURE version 2.2 was used to group individuals from these four populations into two clusters. (A beta version of new release of STRUCTURE (version 2.3) has recently become available, but the authors recommend that the methods implemented in version 2.2 be used when data sets are ‘highly informative' so these are the results that I present here. I obtained similar results using STRUCTURE 2.3 using sampling locations as priors (LOCPRIOR option)). Default parameters values were used while running STRUCTURE, including assuming that allele frequencies were correlated and that individuals could be classified as hybrids. A burn in period of at least 10 000 Markov-chain Monte-Carlo steps was used, followed by at least 20 000 steps for the actual clustering. Four to eight data sets were simulated for each of the evolutionary histories shown in Figure 1, and results were averaged across data sets.

Table 1. Expected values of pairwise F_ST (Weir and Cockerham, 1984) for the evolutionary histories examined in this study.

	100/200/800				100/300/800				100/400/800
	A	B	C		A	B	C		A	B	C
A	—			A	—			A	—
B	0.024	—		B	0.024	—		B	0.024	—
C	0.045	0.045	—	C	0.065	0.065	—	C	0.083	0.083	—
D	0.141	0.141	0.141	D	0.141	0.141	0.141	D	0.141	0.141	0.141
	100/500/800				100/600/800				100/700/800
	A	B	C		A	B	C		A	B	C
A	—			A	—			A	—
B	0.024	—		B	0.024	—		B	0.024	—
C	0.099	0.099	—	C	0.114	0.114	—	C	0.128	0.128	—
D	0.141	0.141	0.141	D	0.141	0.141	0.141	D	0.141	0.141	0.141

The numbers in bold (e.g., 100/200/800) are the population divergence times for the evolutionary histories examined (Figure 1) F_ST values were estimated from one million simulated loci. The data sets used in the simulations described in this paper had 1000 loci, so F_ST values for these data varied slightly.

Two specific questions were addressed in the simulations. First, I investigated whether the relative amount of divergence among the populations affected the ability of STRUCTURE to correctly identity which populations were most similar. I tested this by varying the relationship of population C to populations A and B (Figure 1). Second, I investigated whether variability in sample size affected clustering. I did this by varying the number of individuals sampled from populations C and D (N=25, 50, 100 diploid individuals), while keeping the sample sizes for populations A and B constant (N=50 diploid individuals).

Results from the simulations showed that the clustering arrangements produced by STRUCTURE were affected by the relative amount of differentiation among the populations, and that in some circumstances, STRUCTURE produced clusters that were not consistent with the main evolutionary divisions within the populations. For example, Figure 1 shows that STRUCTURE created evolutionarily accurate clusters when populations A, B and C were closely related to each other (for example, divergence times: 100/200/800). However, when population C was less closely related to populations A and B—but still more related to A and B than to D—STRUCTURE clustered individuals from population C with population D (Figure 1, evolutionary history 100/700/800).

I selected three evolutionary histories to explore how variation in sample size affected clustering: 100/400/800, 100/600/800 and 100/700/800. These specific evolutionary histories were chosen because they spanned the range of evolutionary histories for which STRUCTURE produced evolutionarily appropriate and inappropriate results. Results from these simulations showed that the clustering arrangements produced by STRUCTURE were strongly affected by variation in sample size (Table 2). This is best illustrated for the evolutionary history with population divergence times 100/600/800 (Table 2). Depending on the sample sizes for populations C and D, STRUCTURE produced very different clustering arrangements. These included clustering all individuals from population C with population D, clustering all individuals from population C with populations A and B (the appropriate solution), and putting all the individuals from population C into their own cluster. Intermediate results were also obtained.

Table 2. The effects of sample size upon clustering by STRUCTURE for three different evolutionary histories: 100/400/800, 100/600/800 and 100/700/800 (Figure).

	ND
		25	50	100
100/400/800
	25	1.00, 1.00, 0.66, 0.00	1.00, 1.00, 0.82, 0.00	1.00, 1.00, 0.85, 0.00
NC	50	1.00, 1.00, 0.33, 0.00	1.00, 1.00, 0.99, 0.00	1.00, 1.00, 0.98, 0.00
	100	1.00, 1.00, 0.00, 0.93	1.00, 1.00, 1.00, 0.00	1.00, 1.00, 1.00, 0.00
100/600/800
	25	1.00, 1.00, 0.24, 0.00	1.00, 1.00, 0.56, 0.00	1.00, 1.00, 0.72, 0.00
NC	50	1.00, 1.00, 0.00, 0.01	1.00, 1.00, 0.35, 0.00	1.00, 1.00, 0.85, 0.00
	100	1.00, 1.00, 0.00, 0.64	1.00, 1.00, 0.00, 0.99	1.00, 1.00, 1.00, 0.00
100/700/800
	25	1.00, 1.00, 0.00, 0.00	1.00, 1.00, 0.39, 0.00	1.00, 1.00, 0.65, 0.00
NC	50	1.00, 1.00, 0.00, 0.21	1.00, 1.00, 0.00, 0.00	1.00, 1.00, 0.80, 0.00
	100	1.00, 1.00, 0.00, 0.65	1.00, 1.00, 0.00, 0.83	1.00, 1.00, 1.00, 0.00

N_C and N_D are the samples sizes for populations C and D, respectively. Populations A and B had a sample size of 50 individuals for all of simulations. The data within the table shows the proportions of genetic ancestry within samples from populations A, B, C and D that was assigned to each of two clusters. The evolutionarily appropriate clustering arrangement is 1.00, 1.00, 1.00, 0.00, which indicates that all the genes from populations A, B and C were assigned to one cluster, and all the genes from population D were assigned to the second cluster.

A potential explanation for STRUCTURE's inappropriate results is that some of the population structures that I examined were intrinsically difficult to analyze. Other methods for describing population structure might have the same problems. I tested this hypothesis by re-analyzing the phylogenies that STRUCTURE did not describe well using traditional methods for describing population structure. Specifically, I calculated pairwise F_ST (Weir and Cockerham, 1984) and checked the matrix of genetic distances to see if it contained the same error as STRUCTURE (having population C be more similar to population D than to A or B). I did this 1000 times for the phylogeny in Figure 1 with divergence times 100/700/800. With this phylogeny, the F_ST matrix showed population C to be more similar to population A and B than to D approximately 99% of the time (992 out of 1000 simulations). This shows that this genetic data for these populations are not intrinsically difficult to work with. The problem seems to be with how STRUCTURE analyzes the data.

The results above show that if the value of K used to run STRUCTURE is less than the actual number of populations, STRUCTURE will sometimes place individuals from unrelated populations into the same cluster. The fact that STRUCTURE does this should not be surprising, for, as mentioned above, the mathematical model used by STRUCTURE was designed to place individuals into Hardy–Weinberg/linkage equilibrium populations—not to identify relationships among groups of populations. Therefore, we would expect that STRUCTURE would create better clusters if more realistic values of K were used. I tested this hypothesis, by reanalyzing the most challenging data sets identified above using a range of values for K (K=2, 3, 4 and 5). In every case, STRUCTURE easily identified that a value of K=2 was too low, and that individuals from populations C and D belonged in their own cluster. This shows that the evolutionarily inappropriate clustering observed was caused by using a value of K that is too small.

STRUCTURE uses a mathematically sophisticated algorithm to assign individuals to clusters, and I am not able to provide a definitive explanation of what is causing the pathological results described above. However, I suspect that the problem is that the probability of the genotypic data is maximized by placing as many individuals as possible into genetically homogeneous clusters—with little regard to how the remaining individuals are clustered. Consider the sample size experiment depicted in Table 2. When the samples size of population C was large relative to the samples from the other populations (that is, N_C=100), STRUCTURE had a tendency to place all the individuals from population C into a cluster of their own, and to place all of the individuals from the other populations into a second cluster. For STRUCTURE to do this, the probability of the data for this clustering arrangement must be higher than the probability of the data for a clustering arrangement that places individuals from population C into a cluster with individuals from populations A and B. This is plausible. If 100 individuals from population C are placed into their own cluster, loosely speaking, there will be a close match between the allele frequencies in the cluster and the genotypes of the individuals in the cluster. More formally, a homogenous cluster composed of individuals from population C will maximize the probability of observing the genotypes of these individuals from the allele frequencies in the cluster. Placing individuals from additional populations into the same cluster as C will change the allele frequencies in the cluster so that they less closely match any of the genotypes in the cluster (or more formally, will decrease the probability of observing the genotypes of the individuals assigned to the cluster given the allele frequencies in the cluster). STRUCTURE seeks an arrangement of individuals that maximizes the global likelihood, so it is easy to envision how creating one homogenous cluster could more than compensate for placing all of the other individuals into a heterogeneous wastebasket cluster.

Reanalysis of human population structure

The hallmark of the problems described above is that individuals from genetically divergent populations are clustered together—even though they are genetically more similar to individuals in other clusters. It is difficult to estimate how often this may have happened in empirical studies. Here, I will look at two landmark human data sets (Rosenberg et al., 2005; Tishkoff et al., 2009) to see whether STRUCTURE has obscured genetic similarities and differences among populations.

The evolutionary history of Europeans and Africans is probably similar to the phylogenies that I used to test STRUCTURE (Figure 1). There is a consensus that modern humans originated in Africa 100 000–200 000 years ago, and that the rest of the world was colonized by a modest number of Africans that left Africa some time later (Weaver and Roseman, 2008). The source of the migration out of Africa is not known, but microsatellite data suggests Europeans are more closely related to present-day African farmers than to African hunter gatherers (Zhivotovsky et al., 2003). Given this evolutionary history, populations A and B in the simulations that I performed (Figure 1) may represent European populations, population C may represent African farmers from whose ancestors Europeans are descended, and population D may represent African hunter gatherers. If this scenario is correct, and there has been a long term separation between contemporary farmers and hunter gatherers in Africa (as suggested by Zhivotovsky et al., 2003), we would predict that contemporary African farmers would be genetically more similar to Europeans than to African hunter gathers. This is exactly what a reanalysis of the microsatellite data of Rosenberg et al. (2005) shows. I calculated the average degree of allele sharing between all individuals in each pair of populations examined by Rosenberg et al. (2005), and found several African populations (Kenyan Bantu, Mandenka, Yoruba) shared more alleles with Europeans than with the San or Mbuti hunter gatherers (Table 3). I obtained the same result using J_xy (Nei, 1978) and F_ST (Weir and Cockerham, 1984).

Table 3. Two measures of genetic similarity for Europeans and Africans calculated from the microsatellite data of Rosenberg et al. (2005).

	Russian	Basque	French	Italian	Bantu South Africa	Bantu Kenya	Mandenka	Yoruba	Biaka Pygmy	Mbuti Pygmy	San
Russian	—	0.3781	0.3795	0.3788	0.3064	0.3182	0.3144	0.3109	0.3024	0.2964	0.2902
Basque	0.0126	—	0.3839	0.3828	0.3043	0.3187	0.3118	0.3088	0.2994	0.2936	0.2926
French	0.0050	0.0062	—	0.3825	0.3071	0.3209	0.3154	0.3115	0.3018	0.2936	0.2925
Italian	0.0059	0.0070	0.0012	—	0.3085	0.3208	0.3164	0.3128	0.3015	0.2937	0.2923
Bantu (S. Africa)	0.0561	0.0636	0.0546	0.0516	—	0.3373	0.3373	0.3378	0.3206	0.3115	0.3094
Bantu (Kenya)	0.0485	0.0544	0.0463	0.0450	0.0090	—	0.3417	0.3418	0.3242	0.3141	0.3053
Mandenka	0.0539	0.0620	0.0534	0.0510	0.0117	0.0123	—	0.3454	0.3246	0.3100	0.3038
Yoruba	0.0549	0.0625	0.0545	0.0520	0.0095	0.0095	0.0087	—	0.3234	0.3105	0.3019
Biaka pygmy	0.0625	0.0709	0.0631	0.0619	0.0251	0.0257	0.0283	0.0268	—	0.3102	0.3006
Mbuti pygmy	0.0728	0.0811	0.0749	0.0743	0.0380	0.0406	0.0464	0.0437	0.0441	—	0.2977
San	0.0819	0.0872	0.0802	0.0800	0.0422	0.0506	0.0547	0.0532	0.0542	0.0632	—

The average degree of allele sharing between individuals is shown above the diagonal. Weir and Cockerham's version of F_ST (1984) is shown below the diagonal. The Biaka, Mbuti and San are hunter gathers.

The genetic similarities between Europeans and some Africans that I found are not evident in the output of STRUCTURE (Rosenberg et al., 2005). STRUCTURE clustered all sub-Saharan Africans into a single cluster and all Europeans into another cluster (Rosenberg et al., 2005)—which suggests that the peoples of each of these continents are genetically more similar to each other than to peoples on other continents. Previous analyses of genetic diversity in humans do not seem to have noted the genomic similarity of Europeans and present-day African farmers. It has been shown for mitochondrial DNA (Ingman et al., 2000) and for Y-chromosomes (for example, Underhill and Kivisild, 2007), but apparently has not been recognized for autosomal loci which make up the majority of human genome.

Tishkoff et al. (2009) recently presented a comprehensive analysis of genetic diversity in Africa. Their data included 121 African populations genotyped at 848 microsatellite loci. Tishkoff et al. relied heavily on STRUCTURE to analyze their data, and this may have influenced their results. For example, when I repeated the allele sharing analysis that I performed for the data of Rosenberg et al. (2005), I found many sub-Saharan African populations were more similar to European populations (as measured by allele sharing, J_XY, or F_ST) than to African hunter gatherers. In addition, I compared genetic differences between populations measured by F_ST with STRUCTURE results, and this suggested that clustering artifacts could have influenced the conclusion of Tishkoff et al. (2009) that the San of South Africa and the Mbuti pygmies of Central African have shared ancestry. The strongest evidence for this conclusion was that STRUCTURE clustered these populations together. However, as measured by pairwise F_ST (Weir and Cockerham, 1984) the San and Mbuti are two of the most genetically different populations within Africa (Table 3). It is possible, therefore, that the similarity of the San and Mbuti indicated by STRUCTURE is a clustering artifact and not due to recent common ancestry. Further work on this question is warranted.

Discussion

The simulations presented above show that in some simple evolutionary models of population fragmentation, the computer program STRUCTURE does not cluster the most genetically similar individuals into the same cluster. The problem seems to be caused by forcing the program to cluster individuals into an inappropriately small number of clusters. Reanalysis of two microsatellite data sets in humans suggest that this may have affected depictions of human population structure.

In my discussion of human genetic diversity above, I argued that the evolutionary history of Europeans and Africans could be represented by simple bifurcating phylogeny (Figure 1) in which present-day African farmers and African hunter gathers diverged from each other a long time ago and remained reproductively isolated since then. I believe this is a reasonable model for the evolutionary history of Africans, but realize this question is the focus of ongoing research and do not intend to take a strong stance on this question. I will admit, for example, the possibility of recent gene flow between African farmers (or their ancestors) and African hunter gatherers as suggested by Quintana-Murci et al. (2008). Uncertainty regarding the evolutionary history of humans does not affect my main conclusion regarding human genetic diversity. The most important point that I made concerning human genetic diversity is that there are genetic similarities between Europeans and Africans (and genetic differences among Africans) that are not evident in the output of STRUCTURE. This is an empirical observation that does not depend on knowing the actual evolutionary history of humans. If humans have had an evolutionary history different from the model that I used in my simulations, it means that there is at least one other evolutionary history for which STRUCTURE produces misleading results.

I hope the results presented here motivate additional research on how STRUCTURE and other individual clustering algorithms (for example, Corander et al., 2008; Santafé et al., 2008; Zhang, 2008) behave in a wide range of evolutionary scenarios. Users of these clustering algorithms might also reconsider whether individual-based clustering is the best way to describe genetic relationships among populations. STRUCTURE is invaluable for studying individuals whose population of origin is not known, but the program is ill suited for describing relationships among populations. The standard output of STRUCTURE—a color-coded plot of the ancestry of each individual (Rosenberg, 2004)—contains only a limited amount of information regarding population structure. These plots are often not effective for showing the amount of genetic similarity or difference within clusters; nor do they indicate genetic relationships among clusters. Both of these issues are evident in the papers describing human population structure that I have discussed above (Rosenberg et al., 2005; Tishkoff et al., 2009). For example, the ancestry plots produced by STRUCTURE do not show that there are much larger genetic differences between many sub-Saharan African populations than between Western European populations (Rosenberg et al., 2005, Figure 2), or that native Americans are more similar to Asians than to Europeans.

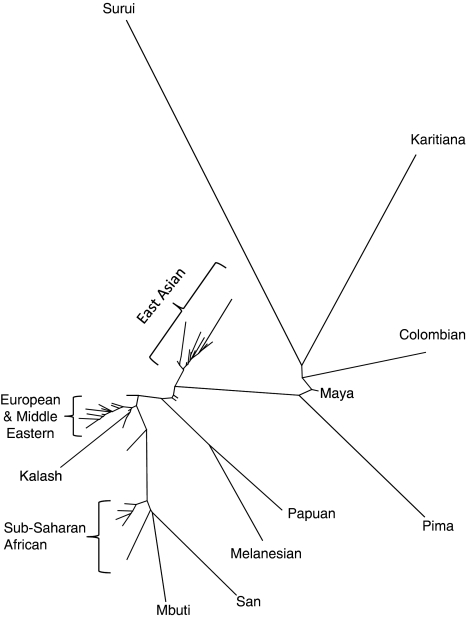
Figure 2.

Unrooted neighbor-joining tree of the microsatellite data of Rosenberg et al. (2005). Weir and Cockerham's (1984) F_ST was used as a genetic distance. Most of the unlabeled populations in the center of the tree are populations in Pakistan, India and surrounding areas. The San and Mbuti are hunter gatherers of sub-Saharan Africa. The Surui, Karitiana, Columbian, Maya and Pima are Native Americans.

In STRUCTURE's defense, no single analysis is appropriate for all data, nor can a single analytic method be expected to reveal all patterns in data. Furthermore, the simulations presented here show that in many circumstances, STRUCTURE will produce evolutionarily appropriate clusters. If this wasn't true, STRUCTURE probably wouldn't be as widely used as it is. However, when the goal of a genetic study is to summarize genetic similarities and differences among populations, and the individuals sampled come from discrete populations, traditional methods for describing population structure may often be more useful. For example, an unrooted, neighbor-joining tree (Saitou and Nei, 1987) constructed from an unbiased genetic distance (for example, Nei, 1978; Weir and Cockerham, 1984) can be very effective for displaying population structure, even when populations have not had a hierarchical history of population fragmentation (Kalinowski, 2009). Such a tree (Figure 2) contains much more information about population structure in humans than results from STRUCTURE. For example, it clearly shows the genetic uniqueness of hunter-gatherer populations in Africa (Mbuti and San, Figure 2), the large amount of genetic differentiation among native American populations, and the genetic similarity of peoples living on adjacent continents. Furthermore, the R² value for the tree (Kalinowski, 2009) is 0.98, which indicates that the tree provides a good fit to the data used to construct it. However, even a tree with a R² of 0.98 does not accurately depict all of the relationships between populations. A close look at the branch lengths in the neighbor-joining tree of humans (Figure 2) shows that it depicts all sub-Saharan African populations as being more similar to each other than to European populations. Thus, the genetic similarities noted above between some African and European populations are not evident.

Figure 2 might easily be interpreted as showing human population structure consists of five evolutionary units, each roughly corresponding to a continent (as identified by Rosenberg et al. (2002) using STRUCTURE). However, what cannot be seen from Figure 2, is that the populations sampled are geographically clustered. On a global scale, genetic diversity in humans is largely clinal (Manica et al., 2005; Lawson Handley et al., 2007), so populations that are close to each are usually genetically similar. The five primary clusters on the tree are largely a byproduct of isolation-by-distance and geographic clustering. A tree made from the geographic distance between these populations looks very similar (results not shown).

Evolutionary trees, of course, are not the only alternative methods for describing population structure. Space does not permit a review of all the methods available, but principle component analysis, multidimensional scaling, and related methods (for example, Patterson et al., 2006) deserve mention. Such analyses can describe relationships among individuals that do not belong to discrete populations (for example, Novembre et al., 2008) and for populations that have an isolation-by-distance structure (for example, King et al., 2001). Whatever methods are used to describe population structure, care must be taken that they provide a fair representation of population structure.

The author declares no conflict of interest.