Conserved and differential gene interactions in dynamical biological systems

Abstract

Motivation: While biological systems operated from a common genome can be conserved in various ways, they can also manifest highly diverse dynamics and functions. This is because the same set of genes can interact differentially across specific molecular contexts. For example, differential gene interactions give rise to various stages of morphogenesis during cerebellar development. However, after over a decade of efforts toward reverse engineering biological networks from high-throughput omic data, gene networks of most organisms remain sketchy. This hindrance has motivated us to develop comparative modeling to highlight conserved and differential gene interactions across experimental conditions, without reconstructing complete gene networks first.

Results: We established a comparative dynamical system modeling (CDSM) approach to identify conserved and differential interactions across molecular contexts. In CDSM, interactions are represented by ordinary differential equations and compared across conditions through statistical heterogeneity and homogeneity tests. CDSM demonstrated a consistent superiority over differential correlation and reconstruct-then-compare in simulation studies. We exploited CDSM to elucidate gene interactions important for cellular processes poorly understood during mouse cerebellar development. We generated hypotheses on 66 differential genetic interactions involved in expansion of the external granule layer. These interactions are implicated in cell cycle, differentiation, apoptosis and morphogenesis. Additional 1639 differential interactions among gene clusters were also identified when we compared gene interactions during the presence of Rhombic lip versus the presence of distinct internal granule layer. Moreover, compared with differential correlation and reconstruct-then-compare, CDSM makes fewer assumptions on data and thus is applicable to a wider range of biological assays.

Availability: Source code in C++ and R is available for non-commercial organizations upon request from the corresponding author. The cerebellum gene expression dataset used in this article is available upon request from the Goldowitz lab (dang@cmmt.ubc.ca, http://grits.dglab.org/).

Contact: joemsong@cs.nmsu.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

Biological systems encoded by a common genome can manifest highly diverse dynamics, because the same set of genes can interact differentially across specific molecular contexts (Califano, 2011). Such differential gene interactions give rise to cell differentiation in development, divergent cellular types and differences between normal and pathological cells. Hence, it is of pivotal importance to compare gene interactions across biological systems so as to delineate context-dependent molecular mechanisms. Automated omic technologies for gene expression, protein activity and metabolic profiling have enabled genome-wide studies of molecular interaction patterns. Although numerous biological system modeling methods have been developed (Chou and Voit, 2009), reverse engineering of biological networks is still challenging due to insufficient sampling or perturbation in practical biological experiments (Bonneau, 2008; Marbach et al., 2010). This has motivated us to compare interactions across conditions in two biological systems directly from data profiles, overriding independent network reconstruction for each system.

Previous work, mostly employing reconstruct-then-compare or differential correlation, has met limited success in exploring differential interactions, due to restricting assumptions. Reconstruct-then-compare methods (Gholami and Fellenberg, 2010; Sharan et al., 2005; Tischler et al., 2008) ignore uncertainty in the estimated model parameters and can wrongfully announce a conserved interaction as differential due to random noise. And differential correlation approaches (Hu et al., 2009; Leonardson et al., 2010; Mentzen et al., 2009), also known as differential coexpression, utilize difference in correlation coefficients between a pair of variables across two conditions to detect differential interactions. Although uncertainty is accounted for, several assumptions hamper the usefulness of this strategy. The most limiting requirement is equality of data and noise variance under the two conditions (See discussion on their limitations in Supplementary Material). Such requirements are often not met in biological experiments.

To overcome the limitations of differential correlation or reconstruct-then-compare, we introduce and validate a novel statistical framework for comparing interactions in dynamical system models (DSMs). We call the framework comparative DSM (CDSM). We use homogeneity to refer to the similarity of an interaction across conditions (Gholami and Fellenberg, 2010; Shiraishi et al., 2010), and heterogeneity for the difference of an interaction across conditions (Ouyang and Song, 2009). Zhao and colleagues developed an expected conditional F (ECF) statistic to evaluate heterogeneity across conditions, but the asymptotic distribution of ECF is open (Lai et al., 2004; Ma et al., 2011). We used two F-statistics to evaluate heterogeneity and homogeneity of interactions as illustrated in Figure 1, providing a basis to detect conserved and differential interactions in biological networks across conditions (Fig. 2). We demonstrated (in Supplementary Material) that our framework reduces to differential correlation if one adds four restricting assumptions: equality of sample sizes, zero data mean, equality of data variance and equality of noise variance across conditions. With a fifth assumption on equality of variance between data and noise, our framework becomes equivalent to reconstruct-then-compare which we will refer to as numerical comparison (Ouyang and Song, 2009). By overcoming these unpractical assumptions on experiments, the CDSM framework is more general for differential interactions than other known methods.

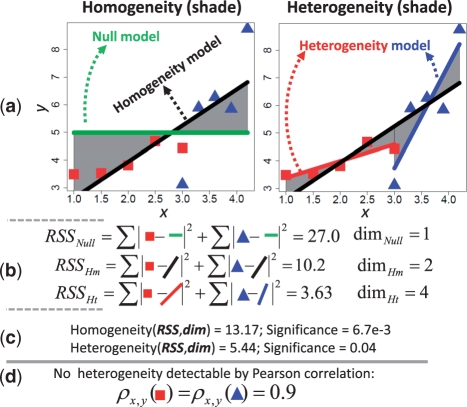
Fig. 1.

Computing heterogeneity and homogeneity of interactions across two conditions. Here, we use a linear interaction as an example. (a) In each condition, five independent noisy observations of random variables X and Y are provided. Condition 1 (red squares): (1.0,3.49), (1.5,3.53), (2.0,3.80), (2.5,4.68), (3.0,4.43); Condition 2 (blue triangles): (3.0,3.11), (3.3,5.89), (3.6,6.27), (3.9,5.85), (4.2,8.74). A null model is first obtained: y=4.98 (the green line). By pooling all 10 points, a homogeneity model (Hm) is obtain: y=0.9x + 2.27 (the black line). Then we obtain the heterogeneity model (Ht) which contains y=0.61x + 2.77 (the red line) and y=3.74x − 7.49 (the blue line), estimated from each group of 5 points, respectively. (b) The three models are evaluated by residual sum of squares (RSS) and model complexities via parameter dimensions (dim). (c) Finally, we compute the homogeneity and heterogeneity of the interaction between X and Y across conditions. They are related to the shaded area in the left and right panel in (a). The significant homogeneity indicates a common interaction trend; the significant heterogeneity suggests a difference between the two lines in the heterogeneity model, evidenced by a difference in slope. (d) In contrast, the difference in slope between the two models is undetectable by differential correlation, as difference between the Pearson's correlation coefficients across the two conditions is zero.

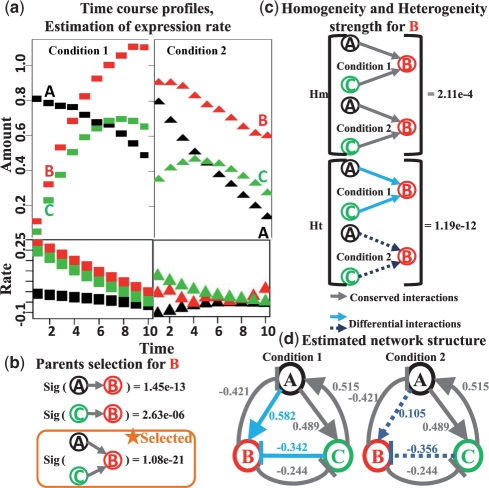
Fig. 2.

Overview of the comparative dynamical system modeling (CDSM) framework. Variables A, B and C represent three interacting molecules. (a) The input to CDSM is time courses of the three molecules under two conditions. Each series of time course data contains 10 time points. The expression rate for each variable is estimated from the time courses by pspline. (b) With variable B as an example, its parents are selected to be A and C, which represent the most significant total regulation strength among all possible interactions. (c) Homogeneity and heterogeneity across two conditions are calculated for the selected parent combination. The interaction for B showed significant heterogeneity of P-value 1.19e-12. Thus, we considered the interaction for B differential across the two conditions. (d) After applying CDSM on all three variables, we identified two conserved interactions targeting A and C and one differential interaction targeting B.

The CDSM framework was evaluated by simulation studies and then applied to detect differential and conserved interactions during mouse cerebellar development. Our method outperformed numerical comparison (Shiraishi et al., 2010) and differential correlation (Hu et al., 2009) in two simulation studies, using a cdc2-cyclin cell division cycle model with known regulation kinetics and a realistic network of unknown architecture with 1000 nodes, respectively. We then applied our method to compare gene interactions during development of the mouse cerebellum, an excellent biological model system for studying nervous system development. Although morphological events are well documented during cerebellar development (Goldowitz and Hamre, 1998; Sotelo, 2004), the molecular mechanisms are nebulous and it is hypothesized that diverse gene interactions occur sequentially and in a tightly controlled manner (Larouche and Goldowitz, 2012). Therefore, we attempted two studies using our method to identify conserved and differential interactions on genome-wide microarray time course data obtained during cerebellar development. For the first study of screening genetic interactions from other organisms in BioGRID (Stark et al., 2006, 2011), we generated hypotheses on 58 and 52 significant genetic interactions involved in external granule layer (EGL) expansion for the DBA and BL6 mouse strains, respectively. These putative interactions are implicated in cell cycle, apoptosis and morphogenesis, and to a lesser extent differentiation. In a second study, 1639 differential interactions among gene clusters were identified when comparing cerebellar gene expression in two developmental events. Specifically, gene expression in a prenatal period in cerebellar development, characterized by the presence of the glutamatergic cell germinal zone known as the Rhombic lip, was compared with gene expression during a late embryonic to post-natal period, characterized by the presence of distinct internal granule layer (IGL). This second study also revealed novel gene interactions as new testable biological hypotheses, and we highlighted those that are involved with the WNT pathway.

2 A COMPARATIVE DYNAMICAL SYSTEM MODELING FRAMEWORK

Our objective has been to develop methods to compare interactions across experimental conditions, using observed time course trajectories from dynamical systems. The data acquired in today's biological experiments hardly allow complete network reconstruction of all molecular interactions. This is due to a low sample size (rarely >1000) in a high-dimensional space of tens of thousands of genes. We attempt to alleviate such data insufficiency by a comparative framework to identify those consistently conserved or differential interactions across conditions. We define an interaction as direct influence from some parent variables to a child variable. A pair of interactions across experimental conditions is conserved if and only if the same child variable has the same relationship with the same set of parent variables; otherwise, it is differential. In the DSM representation of a gene network, a relationship is denoted by an ordinary differential equation (ODE). We propose a CDSM framework for two purposes. The first is to determine from comparative data whether a pair of interactions, given parents and child, is conserved or differential across experimental conditions. The second is to identify novel interactions, based on consistency in potential conserved or differential interactions, by comparing data from two networks of unknown architecture. We describe the CDSM framework in three parts. First, we define the DSM. Then we describe the CDSM framework through statistical testing of homogeneity, heterogeneity and total strength of given interactions. A strategy of learning biology networks of unknown architecture will also be discussed. Figure 2 provides an overview of the CDSM framework using a concrete example.

2.1 The dynamical system model

In biomolecular networks, dynamics of interacting molecules are often described by DSMs, such as those in the BioModels Database (Le Novère et al., 2006). Based on the DSM, we will build our CDSM framework to identify conserved and differential interactions. Variables in the DSM denote the concentrations of molecules (mRNA, protein or metabolite). A DSM represents a system of interacting variables by a set of ODEs, each defined as a many-to-one interaction by

(1)

where x_i is the i-th variable in a DSM, x(t)=(x₀(t), x₁(t),…, x_N−1(t))^⊤ is a vector of all N variables in the DSM at time t, f_i is a function that determines the rate of change, dx_i(t)/dt, β_i is the interaction coefficient vector for x(t) in the function f_i and β_i0 is a constant coefficient. The functional form of f_i depends on prior knowledge about a system, and we use a linear combination of linear or non-linear terms (Ellner and Guckenheimer, 2006). Examples of these terms are linear in x_j, quadratic x_j² or x_jx_k and sigmoidal 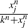(n and k are constants). Here, we call the dependent variable x_i the child and its parents are all the independent variables in β_i that have an effect on x_i. Details of reconstruction of DSMs are given in Supplementary Material.

2.2 The comparative DSM framework

In the DSM context, we established a CDSM framework to compare interactions in biological networks from time course observations across experimental conditions. Although the CDSM can be applied on more than two conditions, we use two conditions to illustrate our approach. A pair of interactions is differential if any coefficient in Equation (1) is different across two conditions; otherwise, it is conserved. Let matrices X⁽¹⁾ and X⁽²⁾ be two sets of time course observations under two conditions, each column represents concentrations of all molecules at a certain time point. Let T₁ and T₂ be the total number of observed time points. Let y⁽¹⁾ and y⁽²⁾ be two vectors of expression rates of a molecule of interest under two conditions, respectively. Here we ignore the subscript i from Equation (1), as the method is all discussed for variable i as a child. The expression rates are estimated as derivatives of smoothing splines using the R package pspline (Heckman and Ramsay, 1996).

Homogeneity is the extent an interaction is similar across two conditions, which we represent using a homogeneous interaction model. Preservation in the form and strength of gene interactions can maintain essential biological functions, such as those conserved in animal development across species and environments. To detect a conserved interaction, we use a single interaction model to explain data observed under both conditions. Therefore, we create this model from the pooled datasets and call it the homogeneous model, represented by y=f(x(t), β_c)+β₀. Based on the pooled dataset, the interaction coefficient vector β_c and constant coefficient β₀ are estimated by least squares. The model complexity is df_c=dim(β_c)+1. Let 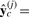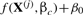be the prediction made for condition j by the estimated homogeneous model.

The homogeneity test determines whether a homogeneous model is supported by the pooled dataset through goodness-of-fit. In this statistical test, the alternative hypothesis is that the homogeneous model has some non-zero interaction coefficients, β_c≠0; the null hypothesis is that the interaction coefficients are all zero β_c=0, the null model, with complexity df_n=1. The residual sum of squares (RSS) of the distances between the observations and the model predictions are, respectively, 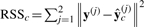and 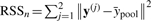, where 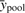is the mean value over time across both conditions. RSS measures the goodness-of-fit of a model to the data. In the context of gene expression, the null model serves as a control when fluctuation in gene expression over time is due to noise only. Then we perform homogeneity test through the F-statistic computed through multiple linear regression. Because the homogeneous model degrades to a null model when β_c=0, the null model is nested within the homogeneous model. This gives rise to an F-statistic defined as

(2)

Such defined F_c strikes a balance between goodness-of-fit (RSS_c,RSS_n) and model complexity (df_c and df_n). Under the null hypothesis of no interaction, F_c asymptotically follows an F-distribution with (df_c−df_n) numerator and (T₁+T₂−df_c) denominator degrees of freedom, if the noise follows a normal distribution (Zar, 2009). The P-value p_c, the upper-tail probability of F_c, gives the statistical significance of the homogeneous model and thus indicates the strength of homogeneity. Strong homogeneity is a necessary condition for conserved interactions. However, differential interactions can also have substantial homogeneity. For example, a parent gene can enhance the expression of its child in both conditions but with different strengths (coefficients). To tell differential interactions apart from conserved ones, one must examine the heterogeneity of an interaction across two conditions to be defined next.

Heterogeneity is the extent an interaction differs across two conditions, which we represent by a set of heterogeneous models. Heterogeneity of gene interactions may arise as a consequence of molecular evolution, manifesting in biological diversity. We test heterogeneity between interactions by checking whether two individual models are necessary to explain the two datasets beyond what a homogeneous model can do. We consider two models, y^(j)=f^(j)(x^(j),β_d^(j))+β₀^(j), where j=1, 2, each for a condition, together as a set of heterogeneous models. Let (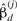,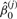) be the best model estimator under condition j obtained by least squares. If the heterogeneous models are considerably different from the homogeneous model defined earlier, heterogeneity of the interaction across two conditions is justified.

The heterogeneity test determines whether the set of heterogeneous models is different from the homogeneous one. In this test, the alternative hypothesis is that the individual models of interactions are different from each other: β_d⁽¹⁾≠β_d⁽²⁾ or β₀⁽¹⁾≠β₀⁽²⁾. The null hypothesis is β_d⁽¹⁾=β_d⁽²⁾ and β₀⁽¹⁾=β₀⁽²⁾, equivalent to the homogeneous model. The overall goodness-of-fit for the heterogeneous model is measured by 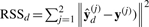, where 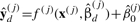is a vector of predictions from the heterogeneous model under condition j. The complexity of the set of heterogeneous model is the number of its free parameters, df_d=∑_j=1²(dim(β_d^(j))+1). When a set of heterogeneous models contains equal coefficients, they degrade to a homogeneous model. Thus, the homogeneous model is nested within the heterogeneous models. This suggests an F-test to measure the relative improvement of the heterogeneous models over the homogeneous one by

(3)

where df₁=df_d−df_c and df₂=T₁+T₂−df_d. RSS_c and the complexity df_c of the homogeneous model are defined earlier. This ratio considers improvement (RSS_c−RSS_d) in goodness-of-fit relative to the cost of increased complexities (df_d−df_c). Under the null hypothesis, the test statistic F_d asymptotically follows an F-distribution with df₁ numerator and df₂ denominator degrees of freedom if the additive noise is normally distributed (Zar, 2009). The P-value, p_d, the upper−tail probability of F_d, gives the statistical significance of the heterogeneous models over the homogeneous model. Given test size α, we can determine if heterogeneity of an interaction exists between two conditions. A conserved interaction must have homogeneity by a large F_c without heterogeneity (small F_d); but a differential interaction must exhibit heterogeneity by a large F_d with or without homogeneity. However, F_d or F_c alone only assesses partial information of a given interaction under two conditions. They must be combined to evaluate the total strength of an interaction.

The total strength refers to overall activity of an interaction in two conditions, regardless of homogeneity or heterogeneity. A gene interaction may be inactive under both conditions. It is thus of interest to test for such scenarios. The principle here is to compare how two interaction models for each condition statistically explain the data better than no interaction at all. This reduces to testing the heterogeneous models versus the null model. A statistical test can thus be formulated to examine the total strength of an interaction across two conditions. The alternative hypothesis is β_d⁽¹⁾≠0, β_d⁽²⁾≠0, or β₀⁽¹⁾≠β₀⁽²⁾; the null hypothesis is β_d⁽¹⁾=β_d⁽²⁾=0 and β₀⁽¹⁾=β₀⁽²⁾. The heterogeneous model and the null one, as estimated previously, have goodness-of-fit RSS_d and RSS_n, respectively. Because the heterogeneous models degrade to the null one when β_d⁽¹⁾=β_d⁽²⁾=0, the null model is nested within the heterogeneous models. Then one can use the following F-statistic to assess the total strength of the interaction

(4)

Under the null hypothesis of no interaction, F_t also asymptotically follows an F-distribution with (df_d−df_n) numerator and (T₁+T₂−df_d) denominator degrees of freedom when the noise is normally distributed (Zar, 2009). The P-value, p_t, the upper-tail probability of F_t, gives the statistical significance of the total interaction.

Not surprisingly, homogeneity, heterogeneity and total strength are not independent to each other. The three corresponding statistical tests are summarized in Table 1. The total strength is a relative measure of the heterogeneous models against the null model; heterogeneity is a relative measure of the heterogeneous models against the homogeneous model; and homogeneity is a relative measure of the homogeneous model against the null model. They are connected through the goodness-of-fit and the complexity of models. From Equations (2), (3) and (4), we obtain a rule that decomposes F_t to F_c and F_d in the log form

(5)

where 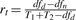, 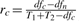and 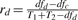are the ratios of degrees of freedom. By decomposing the total interaction strength to homogeneity and heterogeneity, it suggests that any F-statistic can be determined mathematically given the other two. Thus, with homogeneity and heterogeneity, one can learn in further detail whether the difference or the commonality of an interaction contributes to its activity across conditions. Therefore, the decomposition rule underpins the CDSM framework and has profound implications.

Table 1.

Three hypothesis tests for homogeneity, heterogeneity and total strength of an interaction across two experimental conditions

Test on an interaction across two conditions	Null hypothesis	Alternative hypothesis	Test statistic	Significance
Heterogeneity test	β(1)d=β(2)d and β0(1)=β0(2)	β(1)d≠β(2)d or β0(1)≠β0(2)	Fd	pd
Homogeneity test	βc=0	βc≠0	Fc	pc
Total strength test	β(1)d=β(2)d=0 and β0(1)=β0(2)	β(1)d≠β(2)d or β0(1)≠β0(2)	Ft	pt

By the decomposition rule, a given interaction can be studied for being conserved or differential across two conditions. After computing p_c, p_d and p_t, one can compare them with given test size α to make one of four decisions regarding the interaction between two conditions: inactive if and only if p_t>α, differential if and only if p_t≤α and p_d≤α, conserved if and only if p_t≤α, p_d>α and p_c≤α, and active (but neither differential nor conserved) if and only if p_t≤α, p_d>α and p_c>α.

The CDSM framework also provides an alternative to learn two systems of unknown network architecture by comparison, as our second objective. We can learn the network architecture by inspecting simultaneously the parents of a child. There are three strategies depending on the emphasis on conservation, differentiation or overall strength of interactions. First, when system conservation is the emphasis of network learning, one may reasonably assume that mechanisms for two systems are the same, and select best parents of a child to maximize homogeneity according to p_c. Second, if system differentiation is the primary emphasis, best parents of each child can be selected to maximize heterogeneity according to p_d. A caveat is that neither strategy guarantees the best goodness-of-fit to the data. Third, when one is equally concerned with conservation and differentiation of a system, the total interaction strength provides a comprehensive measure to select the best parents for each child via p_t. By the decomposition rule, strong total interaction strength (F_t) can be attributed to various combinations of homogeneity (F_c) and heterogeneity (F_d). Based on p_c and p_d, one can further determine whether each interaction is conserved or differential.

Since the three test statistics, F_c, F_d and F_t, may not follow F-distributions in case of small sample sizes and are subject to multiple testing for parent selection, we correct the three P-values of CDSM by permutation tests (see details in Supplementary Material).

3 SIMULATION STUDIES

We demonstrate the effectiveness of CDSM by two simulation studies. We applied CDSM on simulated datasets, to be contrasted with two other alternative methods: numerical comparison (Shiraishi et al., 2010) and differential correlation (Hu et al., 2009). The first simulation study evaluated the performance of differential interaction detection on a given network, cdc2-cyclin cell division cycle model (Tyson, 1991). The performance based on F_d of the CDSM is consistently better than numerical comparison. A preliminary result appeared in Ouyang and Song (2009) and the complete detail is included in Supplementary Material.

The second simulation study further showed an advantage of CDSM over numerical comparison and differential correlation on comparing large realistic networks of unknown architecture. As the groundtruth, the architecture of a 1000-gene network is extracted from GeneNetWeaver (GNW) (Marbach et al., 2009) based on known transcription regulation in the yeast. Two DSMs, each including 1000 ODEs, are generated according to the extracted architecture, where each ODE expresses a parent–child regulatory relationship with a sigmoidal form

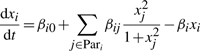(6)

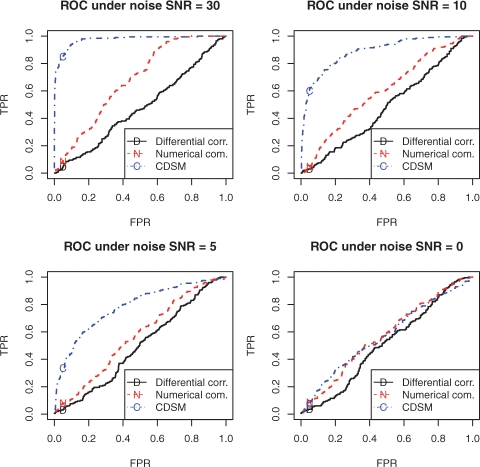
where x_i represents the expression level of gene i, Par_i the parents of gene i and βs the model coefficients. Coefficients in 800 pairs of interactions are made the same in the two DSMs, while those for the other 200 pairs are made different. They constitute the groundtruth for the conserved and differential interactions, respectively. The goal is to detect them on time course data generated by the two DSMs, under various noise levels. The time course data contained three trajectories with different initial conditions, and each of them included 20 time points with equal time lapses. All three methods are blind to the architecture. Because both conserved and differential interactions are expected, we choose parents according to the total interaction strength using p_t in CDSM. The performance of the three methods on identifying differential interactions across the two systems is shown by receiver operating characteristic (ROC) curves in Figure 3. Our CDSM achieved the best performance across all noise levels. Except at the extremely high noise level of a zero signal-to-noise ratio (SNR) when all methods failed, the advantage of CDSM is substantial: its true positive rate (TPR) can be 35–90%, at a false positive rate (FPR) of 0.05, while the other two approaches had almost no statistical power, i.e. TPR, at the same FPR. Advantage of CDSM over numerical comparison is expected because the former properly accounted for uncertainty in model coefficients. The highly pronounced disadvantage of differential correlation is due to its invalid assumptions on linearity of interactions and on noise variances as discussed in Section 1 and Supplementary Material.

Fig. 3.

The advantage of CDSM on detecting conserved and differential interactions when network architecture is not given, in contrast to numerical comparison and differential correlation. In the figures, TPR, the true positive rate, is the ratio of detected true differential interactions to total true differential ones; and FPR, the false positive rate, stands for the ratio of falsely detected differential interactions to total true conserved ones. The closer to the top-left corner an ROC is, the better the performance. The diagonal line stands for the performance of random guessing. For all noise levels, CDSM achieved the best performance among the three methods.

4 CONSERVED AND DIFFERENTIAL GENE INTERACTIONS DURING MOUSE CEREBELLAR DEVELOPMENT

We applied the CDSM to identify conserved and differential interactions during mouse cerebellum development using gene expression time course data. The cerebellum is an excellent model system for studying nervous system development, because it is a relatively homogeneous system—90% is composed of granule cells. Various developmental events, such as expansion of the EGL (Wallace, 1999), occur sequentially in a tightly controlled manner (Goldowitz and Hamre, 1998; Wang and Zoghbi, 2001). These events are well-documented morphologically, but the transcription regulation network responsible for the chain of events remains poorly understood. Cerebellar samples from BL6 and DBA mouse strains were obtained from embryos each day from E12 to E19 and every 3 days post-natally, from P0 to P9 and consisted of two or three biological replicates at each day. Relative abundance of mRNA from the samples was measured using the Illumina microarray platform (Oliphant et al., 2002) covering over 46 000 transcripts. By the CDSM, we examined known gene interactions (identified in other biological systems) in a first study and proposed novel hypothetical gene interactions that play non-uniform roles during cerebellar development in a second study.

In the first study, we screened known genetic interactions—validated in other biological systems—for their involvement in the biological event of EGL expansion in cerebellar development. Between E12 and E15, granule cell progenitors arise from a germinal zone known as the Rhombic lip and migrate over the surface of the cerebellum to form the EGL. Mainly driven by Shh signaling from Purkinje cells, the EGL expands and gives rise to cells that migrate inward to form internal granule layer (IGL). This process continues until at least 3 weeks post-natal (Solecki et al., 2001; Wallace, 1999). The EGL expansion phase begins as early as E16 and extends to P9 and beyond. In contrast, we call the days preceding the formation of the EGL—E12 to E15—the pre-EGL stage. We focused on 1435 transcripts of known transcription factor (TF) genes reported in a mouse TF database (Fulton et al., 2009). We used BioGRID (Stark et al., 2006, 2011) to further narrow our focus to previously identified interactions yielding a list of 104 pairs of known genetic interactions reported in various organisms (BioGRID version 3.1.74; updated in February, 2011). We tested each given genetic interaction by CDSM to query whether it is active during the pre-EGL or EGL expansion, and if so, whether this interaction is conserved or differential when comparing the gene expression pattern in the two temporal periods. The result, summarized in Table 2, suggests distinct involvement of transcription regulation in three of four cellular processes across the two stages. Listed in Supplementary Tables S2 and S3 are 58 significant (p_t≤0.05) genetic interactions detected in the DBA strain, and 52 in the BL6 strain. There are 36 differential (p_d≤0.05) and 21 conserved interactions in the DBA strain, and 21 conserved and 30 differential interactions in the BL6 strain. Genes in these interactions are involved in cell cycle regulation, cell differentiation and cell apoptosis, all collectively contributing to morphogenesis. Among these interactions, 22 are involved in brain/neuron development for DBA and BL6, respectively, and 11 are differential for the DBA or BL6 strain when comparing the pre-EGL stage with the EGL expansion phase. Overall, the distributions of conserved and differential interactions in the four biological processes are consistent between the two strains. In Supplementary Material, we visualized differential and conserved interaction patterns through phase diagrams for two pairs: Meis1.1400575-Scx.130066 in the DBA strain and Six3.3830402-Pax6.101660253 in the BL6 strain, respectively.

Table 2.

Summary of conserved and differential genetic interactions between pre-EGL stage and EGL expansion in biological processes, in DBA and BL6, respectively

Biological process	DBA strain		BL6 strain
	Conserved	Differential	Conserved	Differential
Cell cycle	18	29	19	26
Differentiation	9	14	12	12
Apoptosis	8	22	10	19
Morphogenesis	4	15	6	12
Total	21	36	21	30

An interaction might be involved in more than one biological process. Across the two developmental stages and consistently in both strains, more differential than conserved interactions are detected for cell cycle, morphogenesis and apoptosis, but not for differentiation.

Many of the differential interaction gene ontology categories identified by the analysis (cell cycle regulation, morphogenesis, and even apoptosis) can be reasonably explained based on events occurring in the development of the granule layer. For example, differential interactions involving genes known to regulate cell proliferation are expected during EGL expansion since this phase of cerebellar development is prominently characterized by extensive cell proliferation and production of billions of cells that constitute this population in the mature cerebellum. Moreover, the morphogenetic phase of granule cell development occurs when cell division ceases. Thus, the morphogenesis-related genes expressed during EGL expansion should be expressed at much higher levels than when compared with the pre-EGL period. Finally, apoptosis in granule cells has been noted to occur in these cells during and after migration; and it would therefore be expected that genes involved in this process would be expressed at much higher levels in the EGL-expansion phase when compared with the pre-EGL period. As granule neurons are the most abundant population of neurons in the cerebellum, our analyses are likely biased toward granule cell events. From a differentiation perspective, the majority of granule cells probably differentiate after P9 and this could explain why fewer differential gene interactions involved are detected in the data.

Although these interactions are based on expression data from whole cerebellar tissue samples, they are most likely to explain the population behavior of granule cells, because billions of these cells are produced during the EGL expansion phase. Notably, many of the putative interactions are associated with brain disabilities that involve abnormal cerebellar development. For instance, Pax6, as identified in our study, is involved in regulating neuronal migration, morphology and proliferation in several neuronal subtypes including cerebellar granule cells (Duparc et al., 2006; Swanson et al., 2005). Pax6 mutations in humans are associated with small eyes and cerebella. Also the identified Scx is associated with several nervous system diseases in humans, and has been implicated in neurodegeneration (Yeghiazaryan et al., 1999). (See Supplementary Material for a complete discussion on the relevance of the detected genetic interactions in this study to cerebellar development.) Therefore, we expect that the detected gene interactions provide testable hypotheses regarding cerebellar development for further biological experiments.

In the second study, we searched for novel gene interactions in the mostly architecture-unknown transcriptional networks required for mouse cerebellar development, using the same dataset as in the first study. We predicted putative network architecture by analyzing two developmental events: presence of Rhombic lip spanning E12 to E17 and presence of distinct IGL spanning E18, E19, P0, P3, P6, P9. These two events present an opportunity to compare gene interactions across embryonic and post-natal stages, since they approximate developmental milestones for the cerebellar granule neuron. We began by filtering the expression data to remove transcripts either without expression change across time or that were inconsistent between the DBA and BL6 mouse strains. We also grouped linearly correlated transcripts into 1823 clusters, as transcripts with linearly correlated time courses are mathematically equivalent for DSM modeling. A representative is selected for each cluster that is most linearly correlated to the other transcripts in the same cluster. Details are given in Supplementary Material. Finally, we applied CDSM to detect conserved and differential interactions across the two developmental events. In CDSM, we utilized a sigmoidal regulation model [Equation (6)] with a maximum number of two parents and self-regulation allowed. The most significant parent combination for each transcript measured by its p_t was selected to form an estimated topology. Then F_c and F_d of each transcript cluster representative were used to determine conserved and differential interactions.

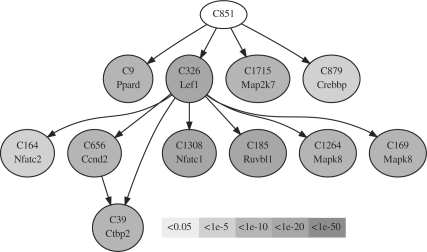
This study yielded three findings on mouse cerebellar development based on the putative network architecture generated by CDSM. First, more differential interactions (1639) than conserved ones (184) between the presence of Rhombic lip and distinct IGL were identified. We used an α=0.05 test size cutoff after multiple testing adjustment. Based on the composition of cell type in the cerebellum, the interactions revealed by our analysis are expected to be heavily biased toward gene expression events associated with the granule cell population (≃90% of cells in the mature cerebellum). Major developmental events of this cell type (expansion and migration of the progenitor population in the presence-of-the-rhombic-lip period versus proliferation, migration, and morphogenesis during the presence-of-distinct-EGL period) are approximately coincident with the birth of a mouse. Thus, more differential interactions explain the change in activity in the granule cell population. Second, a TF named Lef1, whose downstream genes are more heavily involved in the WNT pathway than other TFs, was influenced differently between the presence of Rhombic lip and presence of distinct IGL. Detected interactions among some TFs and their target genes involved in the WNT pathway are shown in Figure 4, and a table of statistical significances of involved clusters is given in Supplementary Material. Third, genes in cluster C851 are highly active in influencing four genes (Ppard, Lef1, Crebbp, Map2k7) in the WNT pathway. They are as follows: Rsc1a1, Zfp367, Rnf26, Gli2, Impa2, Rfc1, Polb, Fen1, B830045N13Rik, BC062185, Uros, Prr14, Bik, Zkscan17, Pmf1, Mybl2, Tk1, Tbl2 and Plec1. Although most of these interactions have not been reported in the literature, recent research suggests evidence of a relationship between Mybl2 and Crebbp (Rønneberg et al., 2011) or Mybl2 and Fosl1 (Pennanen et al., 2009), which are associated with aberrant cell proliferation in cancer. As the WNT pathway is known to be involved in cerebellar development, these gene interactions that influence the WNT pathway are most promising for future biological investigation.

Fig. 4.

Significant differential interactions detected between transcripts involving the WNT pathway by CDSM in the presence of Rhombic lip versus distinct IGL. The gray scale defined in the boxes represents the significance (p_d) of a differential interaction targeting a gene cluster. The darker the node is, the more differential is an interaction. Each node is labeled with its cluster name and a gene of interest. An interaction, between representatives of C326, containing Lef1, and C656 containing Ccnd2, shifted across the two developmental events. The statistical significance of each differential interaction is given in the Supplemental Material.

5 DISCUSSION

We have proposed and validated the CDSM framework to detect conserved and differential gene interactions across molecular contexts from time course observations. Instead of focusing on the reconstruction of interactions, often limited by data insufficiency, we use CDSM to compare interactions across conditions. We achieved the comparison by decomposing the total interaction strength, F_t, across conditions into strengths of homogeneity F_c and heterogeneity F_d, and therefore established a decomposition rule. The CDSM framework was validated by two simulation studies, in which it outperformed two alternative methods: numerical comparison and differential correlation. Numerical comparison ignored uncertainty and did not perform well. Differential correlation did not do well either, due to its limitations in dealing with non-linearity, combinatory effects and unequal variance of the variables and noise. The CDSM overcomes these issues and can be particularly effective for comparing gene regulatory networks to detect inherent systematic changes in terms of differential interactions, beyond system state changes via differential gene expression analysis.

Applying CDSM to the time course microarray data for cerebellar development revealed conserved and differential interactions across various events. The gene regulatory network underlying cerebellar development is poorly understood. Our rationale is to find gene interactions that were either consistently conserved or differential in two setups through CDSM on genome-wide time course observations. In our first and more conservative setup, we studied how genetic interactions known in other organisms may participate in mouse cerebellar development. We found 58 and 52 significant interactions putatively involved in EGL expansion, for the DBA and BL6 mouse strains, respectively. These efforts identified promising candidates for further biological validation. For instance, E2f1, E2f2, Pax6, Pitx2 and Scx are now hypothesized to be involved in cerebellar granule cell development. In the second and more explorative setup, we detected, at the genome scale, many de novo differential interactions between the presence of Rhombic lip and presence of distinct IGL. Among these interactions, the most promising ones are those that are found to influence general developmental pathways such as the WNT pathway. An example is the novel gene interactions involved in a TF named Lef1—an essential output of the WNT pathway—whose downstream gene interactions are strongly differential when comparing the two developmental events. Overall, these identified gene interactions have generated testable hypotheses that merit further biological investigation.

Three conditions are important to make CDSM fruitful, based on our simulation studies. First, our framework works better on a cascaded network architecture, often the case for biological systems, than on random networks. That is, an upstream differential interaction can be reliably detected, without announcing downstream interactions differential even if the expression levels of downstream genes may have changed. Second, the DSM is based on the estimation of the derivative of each variable to time, and is thus effective to deal with systems with smooth dynamics, but not discrete non-smooth observations. Third, the DSM heavily relies on the correct mathematical form for interactions, and the comparative results will be reliable only when a sufficiently good approximation of the interaction form is used in the modeling.

Several future directions are possible for comparative modeling of interactions. The CDSM is readily applicable to data obtained by experiments using combinatorial gene perturbation, such as data from high-throughput quantitative genetic interaction assays (Costanzo et al., 2010). Also, a wider range of mathematical forms for interactions can be included beyond our proposed models of additive non-linear terms, without changing the underlying statistical framework. This will be feasible with an increasing supercomputing power. Furthermore, prior biological knowledge obtained from alternative means can be incorporated to limit the search space for potential interactions.