Abstract
We present a simple, and physically motivated, coarse-grained model of a lipid bilayer, suited for micron scale computer simulations. Each ≈25 nm2 patch of bilayer is represented by a spherical particle. Mimicking forces of hydrophobic association, multiparticle interactions suppress the exposure of each sphere’s equator to its implicit solvent surroundings. The requirement of high equatorial density stabilizes two-dimensional structures without necessitating crystalline order, allowing us to match both the elasticity and fluidity of natural lipid membranes. We illustrate the model’s versatility and realism by characterizing a membrane’s response to a prodding nanorod.
INTRODUCTION
Lipid bilayers form the basis of biological membranes. Integral membrane proteins and a variety of small molecules are embedded in this two-dimensional fluid, which is stabilized by hydrophobic interactions: the bilayer structure effectively shields the lipid’s hydrophobic alkane chains from exposure to the aqueous solvent. Despite this complexity on the molecular level, biological membranes at large length scales are well characterized by surprisingly few material properties. In particular, their behavior on large length scales is consistent with that of crude elastic models, which take as input only a bending rigidity, i.e., the membrane’s resistance to smooth shape deformations. It is unclear below what scale such representations become inappropriate, in part due to computational difficulties of incorporating thermal fluctuations, which invariably gain importance as the scale of observation is reduced from the macroscopic. At the opposite extreme computer simulations of lipid bilayers at atomistic resolution provide detailed access to the spectrum of thermal fluctuations. They are limited, however, to length and time scales of tens of nanometers and hundreds of nanoseconds, respectively.1, 2
Many important biological phenomena involve membrane deformations over several micrometers and span seconds or even minutes. They thus occur on length scales intermediate between those natural to elastic continuum models and to atomistic representations. In attempts to bridge this gap, a large variety of simplified models for interactions between lipid molecules have been proposed in the literature. These range from systematically coarse-grained systems at near-atomistic3, 4 or molecular5, 6 resolution to solvent-free heuristic models;7, 8 a recent review can be found in Ref. 9. Common to these models is an attempt to mimic the amphipathic character of individual lipid molecules. While considerably less expensive than atomistic simulations in their computational demands, these approaches are still limited in the scope of fluctuations and response they can feasibly capture.
Extending computer simulations to examine large scale behaviors such as aggregation of membrane-associated proteins or deformations induced by growth of an actin network would appear to require coarse-graining beyond the scale of individual lipid molecules. Several such approaches have been proposed.10, 11, 12, 13, 14, 15 Most represent in a discrete way the fluctuations implied by Helfrich’s continuum model of an elastic sheet.16, 17 Because these methods use the relevant elastic constants such as the bending rigidity and the surface tension as input parameters, they are guaranteed by construction to reproduce the correct large scale behavior. Such mesoscopically coarse-grained models have been successfully applied in the study of processes involving significant membrane deformations, for example, liposome remodeling due to N-BAR domain interactions.18, 19
When the continuum limit is used as a starting point for mesoscopic model building, one loses the ability to predict the macroscopic material properties from the underlying physical interactions. In this work we present an alternative approach that follows transparently from the statistical mechanics of hydrophobicity and the underlying membrane thermodynamics. This is not only aesthetically pleasing, it also results in a model of surprising simplicity and computational efficiency. Whereas discretized expressions for the bending energy can be numerically unstable and prone to intricate topological dependencies,20 our method employs only simple functions that can be evaluated quickly. Despite its simplicity, our model successfully captures several important properties of lipid bilayer physics, such as intrinsic fluidity and the ability to spontaneously assemble into two-dimensional sheets. It is furthermore sufficiently versatile to reproduce a wide range of biologically relevant elastic properties.
In our model, we envision the lipid bilayer as a collection of small membrane patches of size d≈5 nm, roughly the thickness of a typical bilayer,21 each comprising ∼100 phospholipid molecules. For geometric simplicity, we represent each patch as a volume-excluding sphere with an axis of rotational symmetry pointing from one polar head group region to the other. Cohesion of such patches is due of course to the presence of water: Exposing the hydrophobic portion (i.e., the equatorial region of our model spheres) to solvent incurs a free energetic cost, while exposing the hydrophilic portion (i.e., the polar caps of our model spheres) is thermodynamically advantageous. At length scales ≳1 nm both of these contributions should be proportional to the exposed area.22 Remarkably, these considerations alone are sufficient to successfully mimic the flexibility and fluidity of natural bilayers.
The model we have developed from these simple physical notions resembles in some respects one reported long ago by Drouffe and co-workers.10 They similarly considered association of spherical units each representing a bilayer patch comparable in size to the membrane’s thickness. The anisotropic interactions acting among their particles, however, were devised not to reflect pertinent thermodynamic driving forces at this length scale, but instead to foster formation of fluid elastic sheets. In our view the potential energy function used in that work would be difficult to motivate on microscopic grounds, and no attempt was made in Ref. 10 to do so. For this reason we expect that our approach will generalize more naturally to describe scenarios that involve membrane properties beyond long-wavelength fluidity and elasticity.
As a more immediate and practical justification for our new approach, we found that the original model by Drouffe et al., as described in Ref. 10, does not yield stable two-dimensional structures. In the Appendix0, we detail a revised version of that model which is consistent with previously reported properties. But even in this case the model membrane’s bending rigidity is atypically small for biophysical systems.
MODEL
For a collection of N particles, each representing a patch of lipid bilayer, we adopt the energy function
| (1) |
where the hard-core potential UHC enforces the constraint that the separation between any two particles is at least d. The quantities and characterize, respectively, the equatorial and polar coordination numbers of particle i. The functions Aeq(n) and Apol(n) determine solvent exposure of these two regions based on their coordination. The positive constant ϵ sets the scale of these solvent-mediated interactions. Based on the surface tension between water and oil, γ≈50 mJ∕m2, and the hydrophobic surface area of a membrane patch, A≈60 nm2, we expect γA≈740 kBT to be an appropriate value for ϵ.
In detail, we define the fluctuating density of a particle’s equatorial and polar neighbors as
| (2) |
| (3) |
The contributions of particle j to the coordination densities of particle i are thus determined both by the distance rij=|rij| between their centers, and by the normalized projection of their separation vector rij onto the axis of particle i (which points along the unit vector ). They are attenuated by the functions
| (4) |
and
| (5) |
over scales determined by parameters ra, rb, za, and zb. In this way, particle j counts toward the equatorial (polar) coverage of particle i only if it lies near its center and not too far off the equatorial plane (polar axis).
For a partially occluded object, such as our idealized membrane particles when surrounded by neighbors, calculating the area accessible to solvent molecules of finite size is a nontrivial operation. Furthermore, this task is not sensible to carry out in detail for the reduced representation we have chosen. Essential features of the functions Aeq(n) and Apol(n) are nonetheless straightforward to ascertain: As n increases, exposed area at first declines steadily. At some value lower than the maximum permitted by steric constraints, it should nearly vanish, since perfect close-packing is not needed to thoroughly exclude solvent from the bilayer’s interior (or from the polar exterior). For , variation in exposed area should be very weak. We caricature this dependence with computationally inexpensive, piecewise linear functions:
| (6) |
| (7) |
Appropriate values of and will depend on the relative thicknesses of hydrophobic and polar regions, specified in our model by za and zb.
The membrane free energy we have described is markedly multibody in character, but in a way that is both physically meaningful and simple to understand. Its parameters correspond intuitively to the geometry and chemistry of constituent molecules. Below we present results of Monte Carlo computer simulations for this model, which employed single particle translations and rotations as trial moves, as well as shape deformations of the periodically replicated simulation box when an external tension was imposed. For these calculations, we selected and , which yield a rigidity typical of biological membranes. By varying these values, it is possible to tune the elasticity of the assembled bilayer, as well as more subtle properties such as internal viscosity or rupture tension.
RESULTS
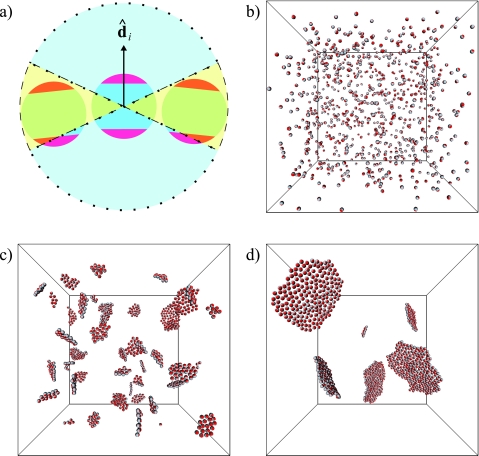
We first demonstrate that a sheetlike configuration is indeed the equilibrium state of our model at finite temperature. Figure 1 shows snapshots from a Monte Carlo trajectory in which an initially disperse collection of membrane particles spontaneously organizes into two-dimensional structures that then diffuse and coalesce.23 This coarsening process is expected to proceed until only a single membrane sheet remains in the simulation box. A free boundary in the resulting structure can be avoided either by forming a membrane sheet that spans the periodically replicated simulation box, or by adopting a boundary-free geometry such as a spherical vesicle.
Figure 1.
(a) Illustration of our model. Each particle corresponds to a fragment of lipid bilayer, comprised of a central hydrophobic core and two surrounding hydrophilic layers. The unit vector specifies the orientation of particle i. Also shown are the spatial regions used to compute the numbers of equatorial (enclosed by dashed line) and polar (enclosed by dotted line) neighbors of particle i. (b) Random initial configuration for a trajectory of N=864 particles. As time progresses, particles quickly form two-dimensional patches that continue to coarsen. Shown are snapshots after (c) 100 and (d) 1000 Monte Carlo sweeps.
We next provide evidence that the elastic properties of our model match quantitatively those of natural lipid bilayers. Specifically, on length scales well beyond a particle radius d (corresponding to the bilayer’s thickness), its shape fluctuations are well described by the Helfrich model of incompressible fluid elastic sheets,16, 17 with macroscopic material properties in accord with experimental measurements. In Helfrich’s model, a nearly flat segment of membrane exhibits a fluctuation spectrum
| (8) |
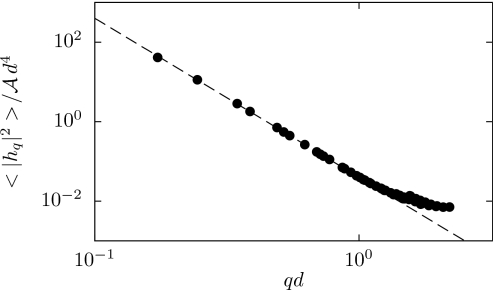
Here, is the Fourier transform of the membrane height h(x), q is a two-dimensional wavevector conjugate to the Cartesian position x on a flat reference membrane with area A, and ⟨.⟩ denotes the equilibrium average. For lipid mixtures common in cell membranes, the bending rigidity κ ranges from 10 to 30 kBT.24 To the extent that the membrane’s area per molecule is constant, the surface tension σ plays the role of minus chemical potential and increases linearly with applied lateral tension τ.25
For the purpose of estimating the normal mode fluctuations of Eq. 8 from simulation, we wish to avoid imposing lateral tension (requiring τ=0). As a practical matter, however, it is convenient in this calculation to prescribe a fixed box geometry (and thus a fixed set of wavevectors). We began by performing simulations in which the box size was allowed to fluctuate at zero lateral tension. The resulting average box size was then adopted as a constraint for a second set of simulations, in which we computed the distribution of height fluctuations.26 At large length scales we indeed observe the characteristic behavior predicted by the Helfrich model, as shown in Fig. 2. The computed proportionality coefficient indicates a bending rigidity of κ≈25 kBT, well within the range of measured values.24 By manipulating the parameters and , we are able to reproduce the elastic behavior of membrane sheets over a wide range of bending rigidities (Table 1).
Figure 2.
Spectrum of height fluctuations around a flat reference state, equilibrated at zero lateral tension. The dashed line is a fit to the expected behavior 8 with σ=0, yielding a bending rigidity κ=25.2 kBT.
Table 1.
Computed bending rigidities for different values of the model parameters and .
| κ∕kBT | ||
|---|---|---|
| 0.01 | 0.2 | 126.8±0.8 |
| 0.02 | 0.2 | 63.4±0.5 |
| 0.05 | 0.2 | 25.2±0.1 |
| 0.1 | 0.2 | 12.1±0.1 |
| 0.4 | 0.6 | 2.1±0.03 |
The advantage of our model lies in a facile ability to address mesoscale response without sacrificing the microscopic basis of corresponding fluctuations. As a representative biophysical example that calls for these capabilities, we considered the resistance of a fluctuating membrane to impingement of a nanorod oriented perpendicular to the lipid bilayer. Experimental realizations of this situation include extension of polymerizing actin filaments close to a cell membrane27 and external forcing of a carbon nanotube against a cell wall.28
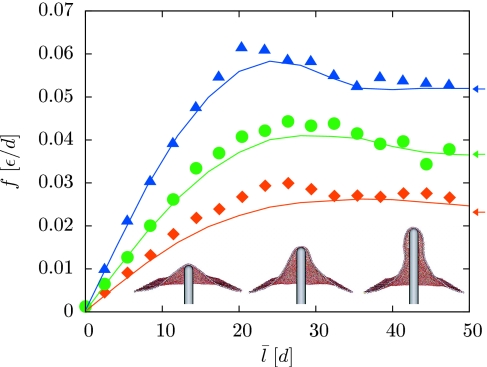
Insets of Fig. 3 depict the reversible membrane deformations we have studied in this context. The prodding nanorod is modeled here as a volume-excluding, rigid spherocylinder of radius R=3d, which defines a region in space inaccessible to the membrane particles. Its vertical displacement l determines the size of the membrane deformation. We set l=0 for a nanorod that would contact the membrane, in a completely flat configuration, at a single point. To prevent global translation of the membrane when l>0, we constrain the vertical positions of a small number of membrane particles. This pinning could be viewed as a mimicry of cytoskeletal attachments that would suppress overall translations in a living cell.21
Figure 3.
Restoring force as a function of protrusion length for three different values of the lateral tension τ: 0.0002ϵ∕d2 (squares), 0.0005ϵ∕d2 (circles), and 0.001ϵ∕d2 (triangles). For each value of τ and l0 we performed computer simulations at two values of K (0.2 and 1 in units of ϵ∕d2). The force was evaluated using Eq. 11 at a length corresponding to the arithmetic mean of the two average lengths ⟨l⟩. Solid lines show the results of the corresponding continuum calculations with σ=τ (Ref. 36). Arrows indicate the constant plateau force for long cylindrical protrusions in the continuum limit (Refs. 29, 30, 31). The inset shows cutaway views of typical configurations at τ=0.0005ϵ∕d2 and l0=17.5, 29.5, 41.5 (left to right), illustrating the transition from a global deformation to a localized, tubular protrusion. In our calculations the nanorod is placed at the center of the periodically replicated simulation box, and a small number of membrane particles are immobilized at the boundary to avoid overall membrane translation.
To calculate membrane-induced forces on the nanorod, we treat the rod height l as a dynamical variable subject to an external potential, V(l)=(1∕2)K(l−l0)2. The free energy of this degree of freedom can then be written as the sum W(l)+V(l), where W(l) originates from the fluctuating constraints imposed by membrane particles. Expanding the latter to quadratic order around a fixed length l1, W(l)=W(l1)+W′(l1)(l−l1)+(1∕2)W″(l1)(l−l1)2, one finds that the average value and variance of l can be expressed in terms of the derivatives of W as
| (9) |
| (10) |
Using these relationships, we can compute the (negative) membrane-induced force f(l)=W′(l)=W′(l1)+W″(l1)(l−l1) as
| (11) |
This equation contains the well-known expression for the force on a particle in a harmonic potential under linear perturbations as the special case W″(l1)=0.
Force-extension curves for this extrusion process are plotted in Fig. 3 for three different values of τ. The restoring force initially increases in proportion to filament length, and ultimately reaches a plateau value at large l. This limiting force is in good agreement with the constant force predicted by the Helfrich model for the stretching deformation of an elastic cylinder,29, 30, 31 provided that σ is dominated by lateral tension. Similar agreement is found for the diameter of the membrane tubule (data not shown). At intermediate extensions, f exhibits a local maximum, signaling a mechanical instability associated with the transformation between two different classes of membrane configurations. This observation is consistent with recent experiments on the formation of membrane tethers from giant vesicles32 and conclusions drawn from continuum calculations.29, 30
OUTLOOK
In addition to mechanical responses exemplified here by nanorod protrusion, several other biologically relevant membrane processes could be addressed through straightforward extensions of our model. For example, lateral demixing of multicomponent lipid bilayers could be studied by endowing each membrane particle with a degree of freedom representing the local composition. The organization of embedded proteins could be simulated using a description of the macromolecule that is compatible with our membrane model. Studying time-dependent behavior would require, in addition, a set of dynamical rules for updating particle arrangements. Most simply, the Monte Carlo trajectories we have used here to sample equilibrium configurations could be interpreted as an approximation of physical time evolution. Integrating equations of motion that involve derivatives of potential energy would require smoothed versions of the interactions we have described. Already, the mesoscale realism and computational economy of our approach recommends its use for examining a wide range of lipid bilayer fluctuation phenomena beyond the reach of molecular models.
ACKNOWLEDGMENTS
We thank Anthony Maggs for helpful discussions of the work presented in Ref. 10. This work was supported by the Director, Office of Science, Office of Basic Energy Sciences, of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231. A.P. and L.M. contributed equally to this work.
APPENDIX: MEMBRANE MODEL BY DROUFFE AND CO-WORKERS
The model proposed by Drouffe and co-workers in Ref. 10 operates on the same lengthscale and focuses on the same degrees of freedom as the model presented in this work. It employs an energy functional of the form
| (A1) |
The first term is a pairwise repulsive energy that penalizes overlap of different particles, which we treat as hard spheres. The second term is a pairwise anisotropic interaction energy,
| (A2) |
where B(rij) is a positive weight function that limits the range of the interaction to ≈2d, η=1 in Ref. 10, α∊{1,2} depending whether the particles are symmetric, and
| (A3) |
is a monotonically increasing function over the range of its argument x∊[0,1].
The last term in Eq. A1 is a multibody potential that favors configurations in which each particle is surrounded by 6 nearest neighbors,
| (A4) |
where C(ρi)=(ρi−6)2, ρi=∑j≠ih(rij), and h(rij) is a weight function with unit value for small particle separations.
To implement this model one must specify the dependence of B(r) and h(r) on interparticle distance, which was done only graphically in Ref. 10. We assign these quantities simple functional forms that are piecewise linear in r2,
| (A5) |
| (A6) |
Values of B and h resulting from this choice closely resemble those plotted in Ref. 10.
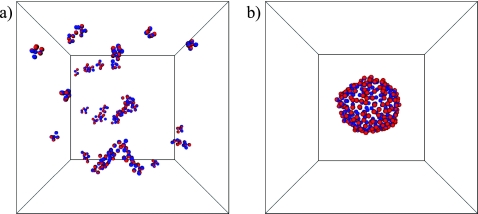
We performed Monte Carlo computer simulations of the model defined by Eqs. A1, A2, A3, A4, A5, A6 for α=1 at a temperature T=1.6ϵ. For these conditions, Drouffe and co-workers report the spontaneous assembly of randomly distributed and oriented particles into a two-dimensional sheet, in which the orientation vectors of neighboring particles are nearly parallel. However, in our simulations we find that for these parameter values the system forms many small clusters of particles without apparent internal order. Similar configurations are obtained when a completely ordered sheet is used as the initial condition [Fig. 4a], which indicates that the inability to form stable membranes is thermodynamic in origin, and not due to dynamical artifacts caused by the Monte Carlo method.
Figure 4.
(a) Typical configuration of the membrane model developed by Drouffe and co-workers (α=η=1, T=1.6ϵ). A flat sheet of 256 particles with parallel orientation vectors was used as the initial configuration. This structure dissolves quickly into a disordered collection of small clusters. (b) Final configuration of a trajectory starting from the same initial state, but employing an alternative parameter set (α=1, η=−1, and T=0.5ϵ). The initially flat sheet remains stable, and closes to form a vesicle.
The lack of stable membranelike structure in this published version of the model is straightforward both to understand and to remedy. When η=1, the first term in the brackets of Eq. A2 actually disfavors parallel alignment of neighboring particles’ orientational vectors; this energy contribution is minimum when axes of adjacent particles are antiparallel (in the case α=1) or perpendicular (α=2). Suspecting a typographical error in Ref. 10, we set η=−1 in order to instead favor the desired alignment. Equilibrium states resulting from this modification, however, still feature a collection of many small aggregates of particles at the temperature T=1.6 reported in Ref. 10. In this case the adhesive interaction A4 is insufficient to overcome the loss in entropy associated with forming a single membrane sheet. Only after reducing the temperature to T=0.5ϵ were we able to observe stable sheetlike structures and vesicles in our simulations [Fig. 4b]. This modified set of model parameters results in membrane sheets with a bending rigidity κ=4.9±0.1 kBT, which is smaller than values measured for biophysical phospholipid bilayers.24
References
- Brannigan G., Lin L. C.-L., and Brown F. L. H., Eur. Biophys. J. 35, 104 (2006). 10.1007/s00249-005-0013-y [DOI] [PubMed] [Google Scholar]
- Edholm O., in Computational Modeling of Membrane Bilayers, edited by Feller S. E. (Academic, New York, 2008). [Google Scholar]
- Shelley J. C., Shelley M. Y., Reeder R. C., Bandyopadhyay S., and Klein M. L., J. Phys. Chem. B 105, 4464 (2001). 10.1021/jp010238p [DOI] [Google Scholar]
- Marrink S. J., de Vries A. H., and Mark A. E., J. Phys. Chem. B 108, 750 (2004). 10.1021/jp036508g [DOI] [Google Scholar]
- Ayton G. S. and Voth G. A., J. Phys. Chem. B 113, 4413 (2009). 10.1021/jp8087868 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ayton G. S., Lyman E., and Voth G. A., Faraday Discuss. 144, 347 (2010). 10.1039/b901996k [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cooke I. R., Kremer K., and Deserno M., Phys. Rev. E 72, 011506 (2005). 10.1103/PhysRevE.72.011506 [DOI] [PubMed] [Google Scholar]
- Brannigan G., Philips P. F., and Brown F. L. H., Phys. Rev. E 72, 011915 (2005). 10.1103/PhysRevE.72.011915 [DOI] [PubMed] [Google Scholar]
- Venturoli M., Sperotto M. M., Kranenburg M., and Smit B., Phys. Rep. 437, 1 (2006). 10.1016/j.physrep.2006.07.006 [DOI] [Google Scholar]
- Drouffe J. -M., Maggs A. C., and Leibler S., Science 254, 1353 (1991). 10.1126/science.1962193 [DOI] [PubMed] [Google Scholar]
- Gompper G. and Kroll D. M., J. Phys.: Condens. Matter 12, A29 (2000). 10.1088/0953-8984/12/8A/304 [DOI] [Google Scholar]
- Ayton G. and Voth G. A., Biophys. J. 83, 3357 (2002). 10.1016/S0006-3495(02)75336-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Noguchi H. and Gompper G., Phys. Rev. E 73, 021903 (2006). 10.1103/PhysRevE.73.021903 [DOI] [PubMed] [Google Scholar]
- Ayton G. S., Izvekov S., Noid W. G., and Voth G. A., Curr. Top. Membr. 60, 181 (2008). 10.1016/S1063-5823(08)00007-0 [DOI] [Google Scholar]
- Kohyama T., Physica A 388, 3334 (2009). 10.1016/j.physa.2009.05.011 [DOI] [Google Scholar]
- Helfrich W., Z. Naturforsch. C 28, 693 (1973). [DOI] [PubMed] [Google Scholar]
- Safran S. A., Statistical Thermodynamics of Surfaces, Interfaces and Membranes (Addison-Wesley, Reading, MA, 1994). [Google Scholar]
- Ayton G. S., Blood P. D., and Voth G. A., Biophys. J. 92, 3595 (2007). 10.1529/biophysj.106.101709 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ayton G. S., Lyman E., Krishna V., Swenson R. D., Mim C., Unger V. M., and Voth G. A., Biophys. J. 97, 1616 (2009). 10.1016/j.bpj.2009.06.036 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gompper G. and Kroll D. M., J. Phys. (France) 6, 1305 (1996). 10.1051/jp1:1996246 [DOI] [Google Scholar]
- Alberts B., Johnson A., Lewis J., Raff M., Roberts K., and Walter P., Molecular Biology of the Cell, 4th ed. (Garland Science, New York, 2002). [Google Scholar]
- Chandler D., Nature (London) 437, 640 (2005). 10.1038/nature04162 [DOI] [PubMed] [Google Scholar]
- The elastic behavior of the model membrane is dominated by entropic effects, yielding a nearly temperature-independent reduced bending rigidity κ∕kBT. Translation and rotation of finite membrane patches, on the other hand, proceed by displacements of individual particles, which are suppressed at low temperatures. To accelerate the self-assembly process the trajectory shown in Fig. was generated at a higher temperature ϵ=25 kBT.
- Rawicz W., Olbrich K. C., McIntosh T., Needham D., and Evans E., Biophys. J. 79, 328 (2000). 10.1016/S0006-3495(00)76295-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fournier J. -B. and Barbetta C., Phys. Rev. Lett. 100, 078103 (2008). 10.1103/PhysRevLett.100.078103 [DOI] [PubMed] [Google Scholar]
- To compute the fluctuation spectrum of a membrane that spans the simulation box in the xy-plane we define the height function h(x,y)=∑i=1NziΘ(xi−x)Θ(yi−y)∕∑i=1NΘ(xi−x)Θ(yi−y) where Θ(x)=1 if |x|≤Δ∕2 and zero otherwise. Evaluating this function for points (x,y) that form a square grid of resolution Δ and taking the two-dimensional discrete Fourier transform, we obtain the Fourier amplitude ĥq. This procedure generates a systematic bias at large wavevectors (Ref. ). Taking this bias into account does not change the value of κ for our model.
- Liu A. P., Richmond D. L., Maibaum L., Pronk S., Geissler P. L., and Fletcher D. A., Nat. Phys. 4, 789 (2008). 10.1038/nphys1071 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen X., Kis A., Zettl A., and Bertozzi C. R., Proc. Natl. Acad. Sci. U.S.A. 104, 8218 (2007). 10.1073/pnas.0700567104 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Derényi I., Jülicher F., and Prost J., Phys. Rev. Lett. 88, 238101 (2002). 10.1103/PhysRevLett.88.238101 [DOI] [PubMed] [Google Scholar]
- Powers T. R., Huber G., and Goldstein R. E., Phys. Rev. E 65, 041901 (2002). 10.1103/PhysRevE.65.041901 [DOI] [PubMed] [Google Scholar]
- Atilgan E., Wirtz D., and Sun S. X., Biophys. J. 90, 65 (2006). 10.1529/biophysj.105.071480 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koster G., Cacciuto A., Derenyi I., Frenkel D., and Dogterom M., Phys. Rev. Lett. 94, 068101 (2005). 10.1103/PhysRevLett.94.068101 [DOI] [PubMed] [Google Scholar]
- Cooke I. R. and Deserno M., J. Chem. Phys. 123, 224710 (2005). 10.1063/1.2135785 [DOI] [PubMed] [Google Scholar]
- Brakke K. A., Exp. Math. 1, 141 (1992). [Google Scholar]
- Brakke K. A., Surface Evolver 2.30c. http://www.susqu.edu/brakke/evolver. [DOI] [PMC free article] [PubMed]
- Continuum calculations were performed by finding the ground state energy of a membrane under the Helfrich energy functional, given by the surface integral ∫SdS(σ+2κH2), where H is the local mean curvature. Calculation were performed using the Surface Evolver software package (Refs. ), which employs discretized approximations for both the membrane shape and the operators in the energy functional. To mimic the geometry of our particle simulation as closely as possible, we constrained the membrane height to zero on a square frame of side length 60d, and set the Cartesian coordinates of a single vertex to (0,0,l). The force f(l) was computed as the derivative of the ground state energy with respect to l.