Investigating the electrophysiological basis of resting state networks using magnetoencephalography

Abstract

In recent years the study of resting state brain networks (RSNs) has become an important area of neuroimaging. The majority of studies have used functional magnetic resonance imaging (fMRI) to measure temporal correlation between blood-oxygenation-level–dependent (BOLD) signals from different brain areas. However, BOLD is an indirect measure related to hemodynamics, and the electrophysiological basis of connectivity between spatially separate network nodes cannot be comprehensively assessed using this technique. In this paper we describe a means to characterize resting state brain networks independently using magnetoencephalography (MEG), a neuroimaging modality that bypasses the hemodynamic response and measures the magnetic fields associated with electrophysiological brain activity. The MEG data are analyzed using a unique combination of beamformer spatial filtering and independent component analysis (ICA) and require no prior assumptions about the spatial locations or patterns of the networks. This method results in RSNs with significant similarity in their spatial structure compared with RSNs derived independently using fMRI. This outcome confirms the neural basis of hemodynamic networks and demonstrates the potential of MEG as a tool for understanding the mechanisms that underlie RSNs and the nature of connectivity that binds network nodes.

In recent years interest has grown in the study of connectivity between spatially separate functionally specific brain regions. The way in which separate areas synchronize to form networks is integral to information processing (1, 2). Abnormal communication between regions is thought to be the basis for a number of neurological pathologies (e.g., schizophrenia) (3). It follows that if we are to generate a complete understanding of brain function (and dysfunction), then elucidation of the role of brain networks will be critical. The majority of research in this area has been conducted using functional magnetic resonance imaging (fMRI). During the “resting state”, blood-oxygenation-level–dependent (BOLD) fMRI signals originating in spatially separate brain regions are correlated in time (4–6). This correlation implies connectivity between those areas, even in the absence of a task. Temporally correlated BOLD signals have led to the discovery of a number of resting state networks (RSNs) that are consistent across time and subjects. These networks are known to have functional relevance and clinical significance (7, 8). Whereas RSNs have also been investigated using noninvasive measures of electrophysiology [electroencephalography (EEG) (9) and magnetoencephalography (MEG) (10–12)], this investigation has been limited to analysis in sensor space or has relied on prior assumptions about spatial locations or patterns of the networks. To date, it has not been shown that MEG (or EEG) can independently measure the spatial pattern of RSNs in the manner that has been demonstrated in fMRI (13). This result would confirm a neural basis for the spatial patterns of RSNs and the utility of MEG as a tool for understanding the mechanisms that underlie network formation. Here, we use a unique methodology to independently discover RSNs in MEG data and to test the hypothesis that RSNs, derived from MEG data, match closely an equivalent set derived from fMRI data.

MEG involves measurement of magnetic fields that are induced by synchronized current flow in neuronal assemblies (14). Unlike their electrical equivalent (EEG), magnetic fields are not distorted by inhomogeneous conductivity in the head. This difference, coupled with higher sensor density and complex source reconstruction algorithms (15–18), gives MEG improved spatial resolution compared with EEG. The direct nature of MEG, its high spatial resolution, and its excellent temporal resolution make it the most attractive noninvasive technique for measurement of electrodynamic connectivity. The utility of MEG as a means to investigate RSNs has been shown in recent papers: de Pasquale et al. (11) showed correlation between resting state temporal MEG signals originating in nodes of the default mode network (DMN) and the “task positive” or dorsal attention network (DAN). Liu et al. (12) examined correlations between oscillatory power envelopes at the sensor level showing that significant envelope correlation could be measured across hemispheres. Brookes et al. (10) used seed-based envelope correlation in conjunction with beamformer spatial filtering methods to show interhemispheric motor cortex connectivity in source space. These reports showed that RSNs measured using fMRI are mirrored in MEG data. However, the ill-posed inverse problem (projecting sensor space data into the brain) means that separating real from spurious connectivity in MEG remains difficult (19). Following source-space projection, MEG signals from spatially separate voxels are not necessarily independent. This outcome is a result of source-space blurring (caused by lead field geometry) and misattribution of sources due to errors in inverse modeling. These effects combine to cause “signal leakage” across voxels, which can result in artifactually high correlation values that do not reflect genuine connectivity. This problem is limiting MEG research into RSN formation.

In this paper we show networks derived from 5-min resting state MEG measurements in 10 individuals. Following artifact rejection our MEG data are frequency filtered into bands of interest (δ, θ, α, β, and γ) and projected into source space using a beamformer spatial filter (16). The amplitude envelope (Hilbert envelope) of source-space neural oscillatory signals is computed and temporally down-sampled. These envelope signals are used to investigate statistical interdependencies between brain regions. High temporal correlation between envelopes is taken to imply connectivity and thus network behavior. To elucidate temporal interdependencies, MEG envelope data are processed using both temporal independent component analysis (ICA) and seed-based correlation analysis.

ICA is a powerful multivariate method for finding the underlying processes that make up multidimensional (e.g., spatiotemporal) data and has been successfully applied to resting state fMRI data to measure the spatial structure of RSNs (13). ICA has been used extensively for artifact rejection in MEG, but not to investigate RSN structure. A recent paper (20) has, however, shown that ICA applied to short time Fourier-transformed MEG data allows investigation of the sources of rhythmic activity. Here we apply ICA to temporally smoothed source-space–projected Hilbert envelope data to elucidate the spatiotemporal signatures of electrodynamic RSNs. We compare MEG (temporal) ICA results to seed-based correlation approaches and to previously published work (21) showing RSNs identified using spatial ICA in fMRI. We use temporal ICA in MEG in contradistinction to spatial ICA in fMRI, as the temporal and spatial dimensions offer the most information in MEG and fMRI, respectively. Results show significant similarity between the two modalities and suggest some advantages of ICA over seed-driven approaches.

Results

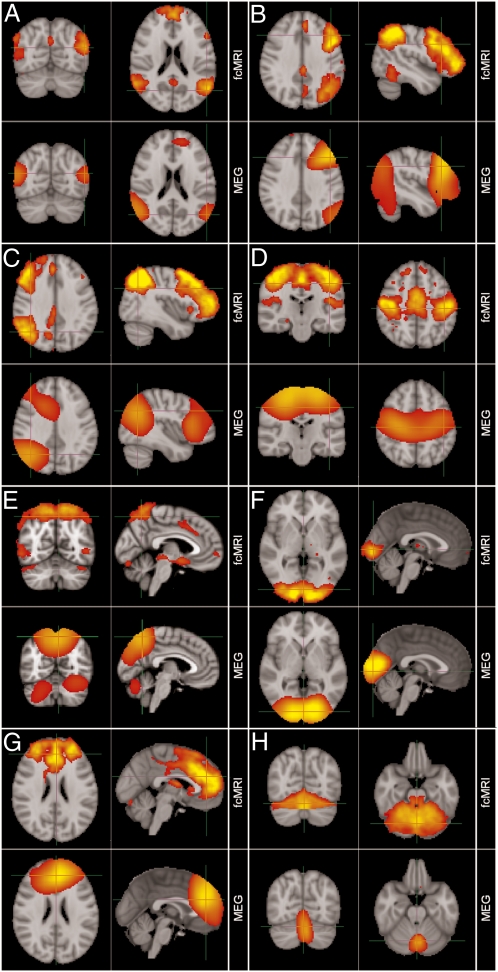
The spatial maps representing temporally independent time signals (tICs), extracted from MEG Hilbert envelope data via temporal ICA, were generated (Materials and Methods). Of the 25 tICs generated, 8 RSNs’ spatial maps were unambiguously paired with RSNs derived from application of spatial ICA to resting state fMRI data (21) and these are shown in Fig. 1 A–H (Upper, fMRI; Lower, MEG). Fig. 1A shows the DMN identified independently using fMRI and MEG data filtered into the α-band. Separate network nodes were observed in medial frontal cortex and the left/right inferior parietal lobules as expected (22). Fig. 1B shows a left lateralized frontoparietal (FP) network and Fig. 1C shows a right lateralized mirror image. These task-positive networks have been reported in fMRI studies (21, 23) and show compelling similarity across modalities with a similar left–right split. Fig. 1 D–H shows MEG-based tICs originating in the sensorimotor network (Fig. 1D), the medial parietal region (Fig. 1E), the visual cortex (Fig. 1F), the medial frontal cortex (Fig. 1G), and the cerebellum (Fig. 1H). In all cases a single fMRI-independent component can be found that matches the MEG. Note the difference in spatial resolution of the two modalities, with fMRI exhibiting improved spatial resolution compared with MEG. This difference is particularly noticeable in medial frontal cortex where several spatially separate peaks/nodes are observed in fMRI, but these are merged in MEG.

Fig. 1.

Comparison of brain networks obtained using ICA independently on MEG and fMRI data. (A) DMN (α); (B) left lateral frontoparietal network (β); (C) right lateral frontoparietal network (β); (D) sensorimotor network (β); (E) medial parietal regions (β); (F) visual network (β); (G) frontal lobes including anterior cingulate cortex (β); (H) cerebellum (β). (A–H) Upper, fMRI (thresholded at Z = 3); Lower, MEG [thresholded at a correlation coefficient of 0.3, apart from the left lateralized frontoparietal network (B) in which the threshold was reduced to 0.16 for visualization].

Spatial matching of components across modalities was achieved using a quantitative spatial Pearson correlation metric, with statistical significance measured using Monte Carlo simulations (SI Materials and Methods). Significant cross-modal spatial agreement was observed in all networks shown in Fig. 1 apart from the cerebellum. The Hilbert envelope signals on which the MEG ICAs were based represent the amplitude envelope of neural oscillations. This observation thus supports work showing that neural oscillations mediate functional connectivity between network nodes. We failed to obtain unambiguous spatial correlates of 2 of the 10 networks reported previously (21).

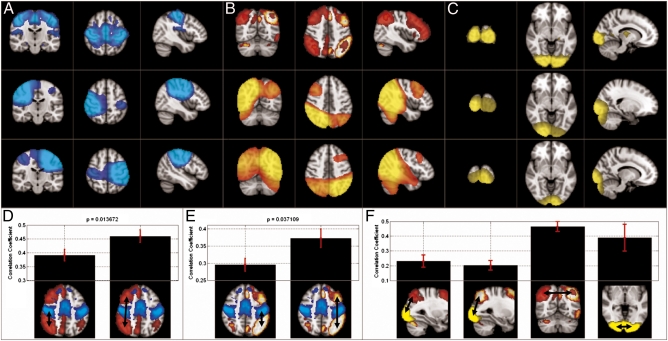
To further confirm the results shown in Fig. 1, a seed-based correlation analysis was also undertaken. Fig. 2 shows results in four networks: left FP, right FP, motor, and visual. In all cases the seed locations were derived on the basis of fMRI. Correlation maps show Pearson correlation measured between temporally down-sampled Hilbert envelopes from the seed location and all other locations. As for ICA, time courses were concatenated across subjects to create the maps. Fig. 2A shows results for the motor network: Top, fMRI; Middle, MEG with a seed in right primary motor cortex; and Bottom, MEG with a seed in left primary motor cortex. Fig. 2B shows equivalent results for the FP networks: Top, fMRI; Middle, MEG (seed in right parietal); and Bottom, MEG (seed in left parietal). Fig. 2C shows the visual network: Top, fMRI; Middle, MEG (seed in right primary visual); and Bottom, MEG (seed in left primary visual). In all cases note reasonable similarity across modalities.

Fig. 2.

MEG seed-based correlation analysis in the β-band. (A) Motor network: Top, fMRI (ICA result); Middle, MEG, right motor seed; Bottom, MEG, left motor seed. (B) FP network: Top, fMRI; Middle, MEG, right parietal seed; Bottom, MEG, left parietal seed. (C) Visual network: Top, fMRI; Middle, MEG, left visual seed; Bottom, MEG, right visual seed. (D and E) Correlation between the parietal and motor areas compared with correlation between parietal and frontal areas in the right (D) and left (E) hemispheres. (F) Comparison between correlation measured between left visual and left parietal, right visual and right parietal, and left/right parietal and left/right visual. In D–F, colored overlays represent the network nodes and are based on fMRI data.

Fig. 2D shows correlation between the posterior node of the right FP network and the right motor cortex compared with correlation between the posterior and anterior nodes of the right FP network. Here, Pearson correlation is computed within subjects and SE across subjects is shown (to show that the effect is not driven by just a few subjects). Fig. 2E shows the equivalent result for the left hemisphere. In both cases, despite the motor area being anatomically closer to the parietal region than the frontal lobe, correlation within the FP network was significantly (P < 0.05) higher than correlation between networks. Fig. 2F shows similar results comparing within- and across-network correlation in the FP and visual networks. Taken together, results shown in Fig. 2 support those given in Fig. 1 and show that, even without ICA, networks observed in fMRI are mirrored in MEG data. However, MEG results are spatially less well defined using correlation analysis compared with ICA. Specifically, a large region around the seed location is highlighted and is due to signal leakage between voxels in close proximity to the seed. This leakage is usually referred to as “seed blur” and is less apparent in our MEG ICA. Note also that unlike ICA, correlation images in the FP network yield regions of high correlation in the opposite hemisphere.

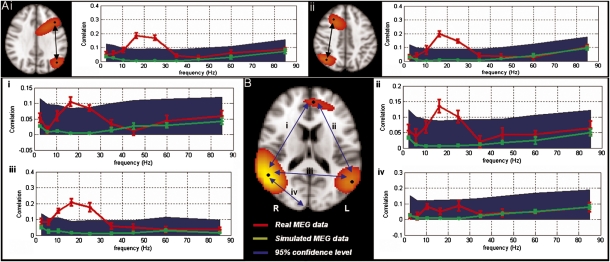
Although compelling, the results presented above could be driven by individual temporal components existing at multiple brain locations as a result of signal leakage. To investigate this further, and to also assess the contribution of different frequencies to the observed connectivity, we carried out a further seed-based correlation analysis. This time pairs of locations of interest were identified (using seed locations from the MEG ICA maps to ensure maximal sensitivity to MEG effects). Temporal correlation between down-sampled Hilbert envelopes from these location pairs was measured as a function of carrier frequency (i.e., δ, θ, α, β, and γ). Further, to obtain a statistical null distribution, and to test that the observed correlations were not artifacts of spatial filtering, we used multiple simulations similar to those previously described (10) (Materials and Methods). Fig. 3A shows results in the FP networks whereas Fig. 3B shows results in the DMN (motor and visual networks are given in SI Materials and Methods). Inset images in Fig. 3 show seed locations projected onto a single slice in Montreal Neurological Institute (MNI) space: The red line shows correlation measured using real data, the green line shows correlation measured using simulated data, and the blue area shows the correlation required for statistical significance (P < 0.05), derived from the null distribution. Note that in all cases significant connectivity is observed and also that a frequency profile is apparent with correlations peaking in the β-band. In Fig. 3B, iv we examine correlation between the right inferior parietal lobule and the primary visual cortex. Note that primary visual cortex is anatomically closer to the right posterior parietal lobule and yet no significant correlation is observed.

Fig. 3.

MEG seed-based correlation analysis across frequencies. (A) The FP network. (A, i) Left lateral parietal [MNI (−48, −70, 20) mm] and prefrontal [MNI (−34, 20, 44) mm] cortices. (A, ii) Right lateral parietal [MNI (42, −70, 24) mm] and prefrontal [MNI (18, 20, 40) mm] cortices. (B) DMN. (B, i) Anterior cingulate [MNI (−4, 50, 14) mm] and right inferior parietal lobule [MNI (56, −54, 16) mm]. (B, ii) Anterior cingulate and left inferior parietal lobule [MNI (−56, −62, 16) mm]. (B, iii) Left and right inferior parietal lobules. (B, iv) Connectivity between right inferior parietal lobule and the right primary visual cortex.

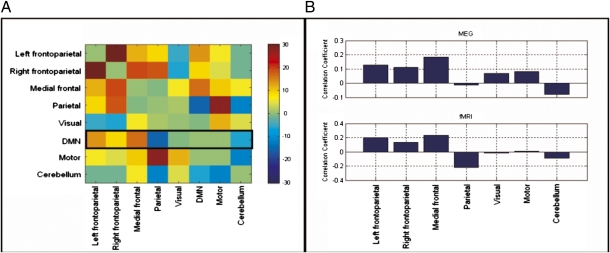
Finally, we return to results of the MEG and fMRI ICA. Fig. 4 A and B shows results of cross-correlation analysis between tICs representing each of the eight networks shown in Fig. 1. Fig. 4A shows an fMRI-derived matrix depicting temporal correlation between BOLD time courses extracted from each of the networks. Because temporal ICA was used in MEG, a direct comparison between such matrices is not possible because MEG-ICA forces orthogonality between tICs for each network. However, the DMN was identified using α-band data whereas all other networks were identified in β-band data. Because ICA was applied independently to each frequency band, orthogonality is not imposed between the α-band DMN time course and the other β-band–derived networks, and so a comparison of the temporal correlation between the DMN and the other networks is possible. This comparison is shown in Fig. 4B alongside the fMRI equivalent and shows that fMRI and MEG have similar patterns of temporal correlation between the DMN and the other RSNs.

Fig. 4.

(A) fMRI-derived temporal correlation matrix (%). (B) Comparison of temporal correlation between MEG and fMRI: Upper, correlation between the DMN tIC (α-band) and tICs for all other networks (β-band); Lower, equivalent temporal correlation derived using fMRI.

Discussion

We used source-space–projected MEG data to derive fluctuations in the amplitude envelope of neural oscillatory activity across frequency bands to investigate the electrophysiological basis of eight RSNs robustly observed in fMRI. We then used ICA to identify temporally independent envelope signals originating from the brain. These analyses have shown that a number of tICs originate from spatially separate networks of brain regions. The spatial signature of those networks is correlated with RSN spatial maps identified using fMRI. These observations confirm the electrophysiological basis of hemodynamic connectivity in these networks. Furthermore, unlike previous publications (10–12) in this area, no a priori spatial information was required to extract the MEG RSNs, making this a unique independent verification of RSN spatial structure using electrophysiological metrics.

The demonstration that the RSNs have electrophysiological underpinnings is consistent with evidence from fMRI data that RSNs are functionally meaningful. However, beyond this confirmation, we have been able to elucidate the electrophysiological mechanisms underlying RSN behavior. Our Hilbert envelopes represent the instantaneous amplitude of neural oscillatory activity, and thus our results confirm that neural oscillations play a key role in synchronizing electrical brain activity across spatially separate brain regions. Furthermore our results show some frequency dependence; correlation between nodes of the FP, default mode, and motor networks was observed across the 10- to 30-Hz range, but was strongest in the β-band. This finding agrees with work by Mantini et al. (9) who used concurrent EEG/fMRI to show that the envelope of band-limited EEG signals correlates with BOLD signals from separate network nodes. Finally we note that resting state correlations occur on a relatively slow timescale (>1 s), implying that fluctuations in network activity occur slowly (at least in resting state measurements). This timescale is similar to that accessible to BOLD fMRI and this may allow insight into why fMRI has been successful in investigating RSNs.

The beamformer methodology used to project MEG data into source space has previously been shown to represent a promising technique for connectivity measurement (10, 15, 19, 24). Beamforming is an adaptive source localization algorithm, meaning that source-space projection depends on the data. This outcome means that signals whose spatial topography cannot be explained by a dipolar source in the brain are suppressed, giving beamforming high spatial resolution and interference rejection properties. However, in beamforming, spatially separate but temporally correlated sources are suppressed. At first sight this suppression appears to be a major confound for network measurements; indeed using externally driven phase-locked responses (e.g., induced in the bilateral auditory cortices by binaural stimuli) (17) it is possible to show failure of beamformer localization. Most importantly, in this work we compute temporal correlation, not between raw source-space–projected time series, but between temporally down-sampled Hilbert envelopes. That is, it is possible for two signal envelopes to be perfectly correlated without any correlation between their respective time series. Also, the resting state data acquired are dominated by neural oscillations; we know from invasive studies that these oscillations have stationary coherence domains of typically <1 cm (25); and evidence suggests that coherence between distant brain regions is likely to be transient coherence (24, 26–28). Even if this transient coherence were zero phase lag, previous simulation work has shown that it must persist for a significant portion of the time window (300 s) of interest to affect beamformer estimates of connectivity (24).

The fact that beamforming can successfully elucidate RSNs and that this process relies on envelope correlation is an important neurobiological finding. In fMRI, connectivity is implied by BOLD signal correlation between regions, but the precise physiology and the exact causal network structures underlying these correlations in general remain unknown. Here we have measured significant correlation between the envelopes of electrophysiological signals from distal cortical regions, implying a neural oscillatory basis to BOLD functional connectivity. However, as with fMRI, correlated signals are not necessarily indicative of direct/causal functional connections. For example, power/amplitude correlation could be driven by a third brain region and could be caused by changes in attention or arousal. Alternatively, correlated envelope modulations could be driven by transient bursts of coherent activity within networks. A limitation of the work shown here is that we assess only within-frequency connectivity and there is a growing amount of literature (e.g., ref. 29) suggesting power at high frequency is modulated by the phase of lower-frequency signals; this result could also offer an explanation of the envelope correlations observed. Whereas the answer to these questions is inaccessible to fMRI, MEG offers an exciting means to probe the underlying nature of such covariations with a variety of metrics and models available.

ICA has been used previously and extensively for artifact rejection in MEG; however, its use in identification of oscillatory signals has remained limited. This limitation is likely due to its susceptibility to interference and the fact that amplitude-modulated oscillatory signals exhibit a largely Gaussian statistical distribution (and ICA relies on non-Gaussianity in recovered sources) (20). Here, a combination of Hilbert envelope computation and temporal down-sampling acts to increase the signal to noise ratio of MEG data and allow for identification of meaningful tICs. An important methodological finding here is the improvement in delineation of RSNs in ICA compared with seed-based correlation. In the correlation results presented in Fig. 2, a high degree of seed blur is observed, which reflects signal leakage, a problem that is less apparent in ICA. The nonindependence of MEG voxels means that any one MEG time course contains a mix of activity originating at that location and its surrounding regions. Via assessment of independence, ICA is able to extract the components of a voxel time course that relate to activity in one particular network while ignoring other components, which are attributed to other tICs (and possibly other networks).

Finally, ICA does not necessarily eliminate all spurious MEG connectivity. It remains conceivable that a single temporal component could exist at multiple brain locations as a result of misattribution of sources brought about by inverse modeling error. Specifically, previous results (10) show correlation between beamformer weights from separate voxels is distributed anisotropically around a seed location and thus a single temporal component can be spread across the equivalent anisotropic volume. Such confounds must be taken into account. Although this study does not present a method for dealing with this problem directly within the ICA, we have investigated it in simulations. This approach generates a null distribution that accounts for spurious connectivity arising from (i) correlated beamformer weights, (ii) field spread between the two sources of interest, and (iii) correlated interference across MEG sensors. Through this approach we have shown that correlations between nodes of the default mode, frontoparietal, and motor networks genuinely represent connectivity and not artifacts of poor source-space reconstruction. This approach is more conservative than other approaches testing for spurious connectivity (10). Although interference from nonneuronal physiology (i.e., the cardiac/respiratory cycles) or other brain sources is not explicitly accounted for in simulation, it is reasonable to assume that it will be suppressed (10, 30).

Conclusion

In this paper we have described a means to characterize resting state brain networks using MEG data. MEG offers a useful way to measure connectivity between brain regions because it bypasses the hemodynamic response and measures the electrophysiological basis of brain activity. Here, we assess connectivity in source space by a unique combination of beamformer spatial filtering and ICA. We have shown that ICA offers some advantages compared with seed-correlation–based approaches; however, ICA cannot eliminate all spurious connectivity from MEG measurements and so should be used in conjunction with other methods to test for nonindependent projected MEG signals. Most importantly, we have shown significant similarity between RSNs derived from MEG and fMRI data, confirming a neural basis of hemodynamic networks. MEG offers the potential to gain a better understanding of RSNs and the nature of connectivity that binds network nodes. Finally, RSNs are of considerable clinical relevance; the work presented here offers exciting possibilities to probe the electrophysiological pathology that underlies neuropathological conditions.

Materials and Methods

Data Acquisition.

MEG data were acquired using the third-order synthetic gradiometer configuration of a 275-channel whole-head CTF system. Subjects were asked to lie in the scanner and view a centrally presented fixation cross while 300 s of data were recorded. During data acquisition the location of the subject's head within the scanner was measured by energizing coils placed at three fiducial points on the head (nasion, left preauricular, and right preauricular). If any subject moved >5 mm during the experiment, data from that subject were discarded. Following acquisition, the positions of the coils were measured relative to the subject's head shape using a 3D digitizer (Polhemus isotrack). An MPRAGE structural MR image was acquired (Philips Achieva 3T; 1 mm³ resolution, 256 × 256 × 160 matrix, TR = 8.3 ms, TR = 3.9 ms, TI = 960 ms, shot interval = 3 s, FA = 8°, and SENSE factor = 3). The locations of the fiducial markers and MEG sensors with respect to the brain anatomy were determined by matching the digitized head surface to the head surface extracted from the anatomical MRI. MEG data artifacts were removed via visual inspection.

Beamforming and Hilbert Envelope Computation.

MEG data were frequency filtered into the 1- to 4-Hz (δ), 4- to 8-Hz (θ), 8- to 13-Hz (α), 13- to 30-Hz (β), and 30- to 50-Hz (γ) bands and projected into source space using a scalar beamformer (16). Covariance matrices were generated independently for each frequency band, using all 300 s of recorded data on a subject-by-subject basis. All covariance matrices were regularized using a regularization value of 4× the minimum singular value of the unregularized matrix. Voxels were placed on a regular 5-mm grid spanning the entire brain and source orientation at each voxel was based on a nonlinear search for maximum projected signal-to-noise ratio. The forward solution was based on a dipolar model (31). Following beamformer projection, source-space signals were normalized by an estimate of projected noise and a Hilbert transform was applied to each voxel time course to derive the “analytic signal”. The absolute value of the analytic signal was computed to yield an amplitude envelope of oscillatory power, termed the “Hilbert envelope”. The Hilbert envelope at each voxel was down-sampled to an effective sampling rate of 1 Hz. Source-space envelope data were smoothed spatially (FWHM 5 mm) and transformed to standard (MNI) space using FLIRT in FSL, and the voxel size was resampled to an 8-mm grid. Datasets from all subjects were concatenated in the time dimension across subjects.

ICA.

Temporal ICA was applied to the concatenated dataset using the fastICA (research.ics.tkk.fi/ica/fastica) algorithm. Prewhitening was applied before ICA to reduce the dataset to 30 principal components. Twenty-five independent components were derived. The spatial signature of each tIC (i.e., the maps shown in Fig. 1) was measured by Pearson correlation between the tIC and the time course of each voxel in the concatenated dataset. This process was implemented independently for each frequency band of interest. Quantitative comparison between RSN maps derived using MEG ICA and RSN maps from spatial ICA in fMRI (21) was undertaken using a spatial Pearson correlation coefficient metric and statistical significance of spatial correlation was measured using a Monte Carlo simulation approach. For full details see SI Materials and Methods.

Seed-Based Correlation Analysis.

Seed-based correlation analysis was undertaken to support our MEG ICA in showing that independent temporal signals arise from spatially orthogonal networks. Seed locations in the motor, FP, and visual networks were derived in MNI space on the basis of fMRI data. Down-sampled Hilbert envelopes were extracted for each of these seed locations. To generate seed-based correlation maps (Fig. 2 A–C), data were concatenated across subjects and Pearson correlation between seed time course and down-sampled Hilbert envelopes for all other brain voxels was computed. To compute correlation between seeds (Fig. 2 E and F), Pearson correlation between seed time courses was measured within each subject, and mean and SE across subjects were computed. Where connectivity values between seed pairs were compared, a Wilcoxon sign-rank test was used to assess statistical significance.

Cross-Frequency Analysis and Simulations.

To compute connectivity spectra (Fig. 3) seed and test locations were defined on the basis of the MEG ICA maps. [This definition was chosen instead of MR seed locations (used above) to account for slight differences in localization in MEG compared with fMRI.] The Hilbert envelopes for the seed and test locations were derived and temporally down-sampled to a 0.5-s time resolution. Pearson correlation between down-sampled envelopes was computed for each subject individually. Results were averaged across subjects and SE across the group was computed.

The validity of correlation measurements made between seed and test locations was tested using a simulation approach (10). On each iteration of the simulation, two dipolar sources were simulated at the seed and test locations. The time courses for these two sources comprised Gaussian random noise colored by frequency filtering to the band of interest. No significant correlation existed between simulated seed and test time courses. The source orientations and the variance of the source time courses were equivalent to those derived by application of the beamformer to real MEG data for the same subject, location, and frequency band. The simulated time courses were multiplied by lead fields for the two locations/orientations and 300 s of simulated MEG data were constructed. Three hundred seconds of MEG data were recorded (using the third-order gradiometer configuration of the 275-channel system; sampling rate, 600 Hz) with no subject in the scanner. These noise data were added to the simulated data, resulting in a simulated MEG dataset. These simulated data were used repeatedly to assess statistical significance of measured functional connectivity (FC) values. On each repetition of the simulation, different seed and test time courses were used. Simulated MEG data were projected into the brain using the same beamformer weights derived from and applied to the real MEG data. Because our simulated data were designed to be similar to the real resting state data, beamformer reconstruction of the simulated source time courses was successful. However, no correlation between simulated sources was introduced, meaning that following beamformer projection, if FC analysis of simulated data generated high correlation, this result was spurious and due to weights correlation, field spread, or correlated noise across sensors. One hundred iterations of the simulation were run per subject. These values were mean corrected, concatenated across subjects, and used to derive a statistical null distribution with which to test the significance of cross-frequency correlation.