Patient-Specific Modeling of Dyssynchronous Heart Failure: A Case Study

Abstract

The development and clinical use of patient-specific models of the heart is now a feasible goal. Models have the potential to aid in diagnosis and support decision-making in clinical cardiology. Several groups are now working on developing multi-scale models of the heart for understanding therapeutic mechanisms and better predicting clinical outcomes of interventions such as cardiac resynchronization therapy. Here we describe the methodology for generating a patient-specific model of the failing heart with a myocardial infarct and left ventricular bundle branch block. We discuss some of the remaining challenges in developing reliable patient-specific models of cardiac electromechanical activity, and identify some of the main areas for focusing future research efforts. Key challenges include: efficiently generating accurate patient-specific geometric meshes and mapping regional myofiber architecture to them; modeling electrical activation patterns based on cellular alterations in human heart failure, and estimating regional tissue conductivities based on clinically available electrocardiographic recordings; estimating unloaded ventricular reference geometry and material properties for biomechanical simulations; and parameterizing systemic models of circulatory dynamics from available hemodynamic measurements.

1. Introduction

Mathematical theories and computational models have led to improved integrative understanding of the cardiovascular system. As a result, there is an increased appreciation that distinct “normal” phenotypes can have a strong influence on disease risk and therapeutic responses. As clinical information becomes more abundant, new approaches to personalized medicine will be needed. In the complex multi-genic syndrome of heart failure, patients are typically classified based on the particular etiologic pathology, the type and severity of their symptoms, and the degree to which normal physical activity is impaired. Despite these classifications, cardiologists still find themselves facing the question: Which patient is likely to respond best to a particular therapeutic intervention and how can we refine the diagnosis and personalize heart failure therapies? In the case of cardiac resynchronization therapy (CRT), for example, non-response rates are typically reported to be around 30% (McAlister et al., 2007), suggesting that there is a significant opportunity to improve the indications by which patients are selected for this procedure.

Multi-scale models of the heart have reached the level of detail and experimental validation at which they are showing promise for clinical application (Neal and Kerckhoffs, 2010; Niederer et al., 2011; Trayanova, 2011). For example, recent coupled models of ventricular electromechanics provided insights into the mechanisms by which electrical dyssynchrony can exacerbate mechanical pump dysfunction in dyssynchronous heart failure (Kerckhoffs et al., 2009; Kerckhoffs et al., 2010; Niederer et al., 2011). To achieve the predictive power required for clinical applications, multi-scale patient-specific models should ideally combine available measurements of individual cardiac anatomy, electrical activation patterns, ventricular wall mechanics and hemodynamics with prior knowledge of regional human myocardial fiber architecture, material properties and myocyte physiological and biophysical properties from failing human hearts. The extent to which the utility of patient-specific models will rely on specific clinical information remains to be determined, but will depend on the particular clinical application. If possible, model results should also be validated with independent measurements from the same patient, though this will require carefully designed clinical trials with statistical methodologies (Neal and Kerckhoffs, 2010).

Thus patient-specific modeling presents many new challenges, particularly those associated with: (1) the lack of detail regarding physical and biological properties of the human heart compared with animal models; (2) the need for subject-specific parameter estimation from limited, noisy data typically obtained using non-invasive measurements; (3) the need to account for intrinsic sources of variability in models and their effects on the reliability of results; (4) the need to perform large numbers of simulations to estimate parameters and test outcomes of various treatment options; (5) the need to perform numerous large-scale computations in a clinically useful time-frame, while keeping patient data secure; and (6) the need to archive and share models and model metadata in their entirety in a way that permits validation and re-use without compromising patient confidentiality.

Here we briefly discuss these specific issues in the context of patient-specific modeling of dyssynchronous heart failure, and illustrate the approaches taken to tackle modeling challenges that generate clinically useful personalized models of cardiac electromechanical function.

2. Methods

2.1 Clinical study

To illustrate the patient-specific modeling process, we consider a single 65-year old male patient at the Veteran’s Administration Medical Center in San Diego, California who signed an informed consent after approval of the human subjects protocol by the Institutional Review Board. Selection criteria were limited to patients with heart failure complicated by electrical dyssynchrony due to a conduction abnormality such as left bundle branch block (LBBB), and who were classified as candidates for CRT. The selected patient had ischemic cardiomyopathy with congestive heart failure symptoms, LBBB and mild mitral regurgitation. The presence of a transmural myocardial infarct at the posterio-septal wall of the LV, extending 64% of the apico-basal length of the ventricular wall was documented using (99)Tc-(m)-MIBI exercise stress single photon emission computed tomography myocardial perfusion imaging..

Both, the pre- and post-implantation survey included electrocardiogram, transthoracic two-dimensional (2D) and continuous-wave Doppler echocardiography (Sonos, Philips Medical IE33, Bothell, WA) to acquire ventricular dimensions and hemodynamic data, and intracardiac pressure measurements obtained during catheter-based electroanatomic mapping. Activation times were measured in the left ventricle (LV) and right ventricle (RV) with the pacemaker switched on and off. An electroanatomic mapping system (NavX, St. Jude Medical) was used to obtain a spatial map (Lo and Chen, 2009) of the LV and RV endocardial activation patterns. Table 1 summarizes the patient characteristics and hemodynamics.

Table 1.

Patient characteristics and measurements. NHYA is the New York Heart Association functional classification; QRSd is the QRS complex duration; CO, cardiac output; EF, ejection fraction; HR, heart rate; SV, stroke volume; MRV is the mitral valve regurgitation volume; MV E/A, mitral valve E/A wave ratio; RVEDP, end-diastolic right ventricular pressure; RVESP, end-systolic right ventricular pressure; LVEDP, end-diastolic left ventricular pressure; LVESP, end-systolic left ventricular pressure; LVEDV, end-diastolic left ventricular volume; LVESV, end-systolic

NHYA 3	SV (ml) 54.5	LVEDP (mmHg) 23
QRSd (ms) 148	MRV (ml) 26.5	LVESP (mmHg) 114
CO (L/min) 3.07	MV E/A 1.87	LVEDV (ml) 189
EF% 34	RVEDP (mmHg) 15	LVESV (ml) 108
HR (bpm) 56	RVESP (mmHg) 40

2.2 Computational reconstruction of the heart

The problems associated with developing patient-specific multi-scale models of ventricular electromechanics are summarized here in four sections: anatomic reconstruction, electrical activity, biomechanics and hemodynamics.

2.2.1 Anatomic Model Reconstruction

The first challenge of multi-scale cardiac modeling is to obtain the patient-specific geometric model of the heart. Non-invasive clinical imaging techniques have become standard procedures for the diagnosis of patients with heart failure. These imaging techniques include cardiac ultrasound (echocardiography), computed tomography (CT), and magnetic resonance imaging (MRI). The accuracy of the model reconstruction depends on the type of imaging technique used. While MRI and CT are higher resolution and frequently used in research studies, they are expensive and exceptional for heart failure patients. The current analysis focuses on model reconstruction from ultrasound images, since echocardiography is routinely performed in heart failure patients to assess ventricular morphology and measure quantitative hemodynamic and ventricular pump function. Owing to the lower resolution of ultrasound images, the resulting geometric model can be fitted using fewer degrees of freedom (DOF), although there is a corresponding loss of anatomic detail.

The approach developed by Nielsen and colleagues was used to reconstruct the finite element model (LeGrice et al., 1997; Nielsen et al., 1991). The method uses prolate-spheroidal coordinates (λ,μ,θ) to model the ventricular geometry, and fits surface measurements using least squares optimization of only the transmural λ-coordinate interpolated with high-order bicubic-Hermite elements. This mesh fitting strategy reduces the required number of geometric degrees of freedom compared with low-order interpolation of Cartesian coordinates (Nielsen et al., 1991).

When the boundary contours are noisy or sparse (for example in the case of echocardiography), the fits can be regularized with smoothing penalty functions to prevent unrealistic oscillations or rapid changes in curvature in the fitted surfaces (Nielsen et al., 1991). Using least-squares finite element methods and initializing the prolate spheroidal model with a small number of manually identified landmarks at the base and apex, the biventricular mesh shown in Fig. 1 was fitted to 2D echocardiographic recordings of the patient with an RMS error of 0.35 mm using only 192 geometric degrees of freedom. By comparison, a model with the same degrees of freedom fitted to higher resolution data from 64-slice CT had an RMS error of 2.4 mm. Refining this mesh from 40 to 108 elements decreased the error to 0.24 mm, comparable to the error in the lower resolution mesh fitted to the echocardiographic contours.

Figure 1.

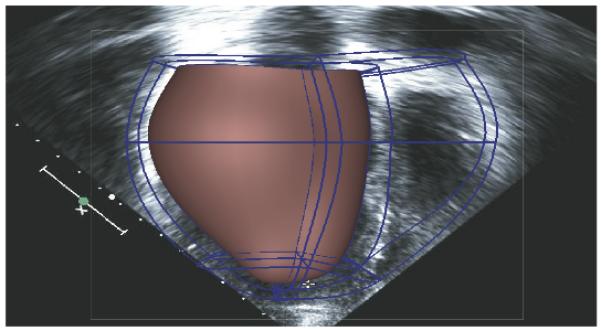
Compact high-order cubic Hermite finite element mesh fitted to echocardiographic recordings of left and right ventricular shape in a patient with congestive heart failure.

Myofiber and laminar sheet orientations are also required to model the anisotropic electromechanical properties of the myocardium (Costa et al., 2001; Hooks et al., 2002). Diffusion tensor magnetic resonance imaging (DTMRI) can provide regional information on myofiber architecture throughout the ventricular walls. Histological measurements in animal hearts have provided evidence to support the assumption that the major primary axis of water diffusion in myocardium tends to coincide with the mean myofiber direction (Costa et al., 2001), thus validating the utility of DTMRI for fiber orientation. The question of the alignment of the secondary and tertiary axes with the sheet and sheet-normal directions, respectively, has also been quantitatively investigated (Helm et al., 2005; Neal and Kerckhoffs, 2010; Tseng et al., 2003). Recently, some studies have also suggested that DTMRI might also be successfully obtained in patients in vivo (Toussaint et al., 2010). Studies suggest that fiber orientations are remarkably conserved between individuals when geometric variations are taken into account (Helm et al., 2006). Therefore, the task of including myocyte orientations in patient-specific models is focused on mapping fiber architecture from ex-vivo studies into the patient-specific ventricular geometry (Sermesant et al., 2009; Vadakkumpadan et al., 2010).

While DTMRI is an attractive method for non-destructively imaging myocardial fiber architecture, the use of diffusion tensor measurements to interpolate vector fields describing myofiber and sheet orientations in finite element models is complicated by several factors, most notably the fact that correct interpolation of tensor components requires an affine invariant Riemannian framework; Euclidean averaging of diffusion tensor components produces a tensor swelling artifact (Chefd’hotel et al., 2004). Regularization techniques are also used for noise reduction in the raw data (Fillard et al., 2007b). The Log-Euclidean metric proposed by Arsigny (Arsigny et al., 2006) can overcome these artifacts, and preserves the major and minor axes of the diffusion tensor derived from human heart DTMRI when the Log-Euclidean transformed components are interpolated in three-dimensions using high-order cubic Hermite finite elements (Fig. 2). While DTMRI methods are promising, the current model used the fiber orientations reported by Nielsen (Nielsen et al., 1991) obtained from standard histological methods in fixed canine hearts.

Figure 2.

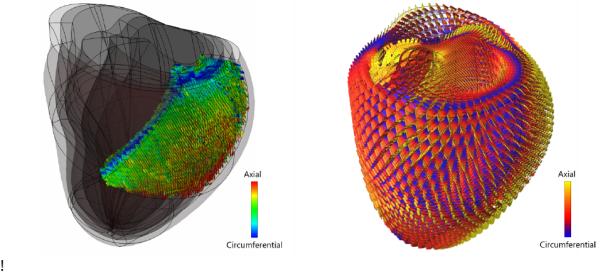
Left: Partial reconstruction of an ex vivo human DTMRI scan. The data has been aligned to a cubic Hermite finite element mesh that has been fitted to the anatomy of the same ex vivo heart. Right: Glyph representation of a trilinear interpolation of the complete ex vivo DTMRI dataset throughout the entire heart using the Log-Euclidian tensor metric (Fillard et al., 2007a) that allows for fast computations and interpolation without tensor distortion or swelling.

The infarct location was identified by an expert using a MIBI stress test to assess regional coronary blood flow, indicating that the patient suffered from a right coronary artery transmural infarct, with myocardial scarring involving the distal portion of the septal wall. A tri-linear field was fitted to the mesh in the diastolic state using the blood flow color map, with data ranging from 1 to 100% perfusion. This field was further used to set up the regional conductivities and material properties in the finite element mesh.

2.2.2 Electrical Activity

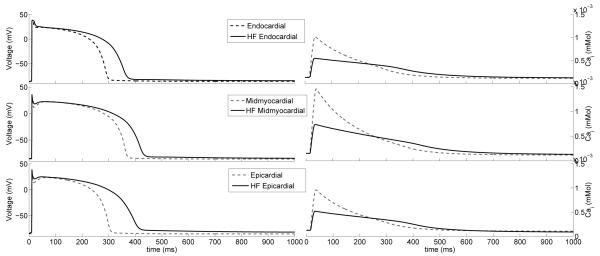
To include the effects of heterogeneous action potential morphology and excitation-contraction coupling without the added computational cost of bidomain simulations (Potse et al., 2006), a mono-domain formulation (Rogers and McCulloch, 1994) was employed. A human ventricular myocyte model was included with sufficient detail to account for transmural heterogeneities in action potential morphology (ten Tusscher et al., 2004). Parameters were modified to account for the major electrophysiological alterations that occur in human congestive heart failure (Priebe and Beuckelmann, 1998) (Table 2). Transmural heterogeneities in myocyte electrophysiologic properties were included by modeling portions of the wall with different cellular properties: endocardial (inner 25%), midmyocardial (middle 50%) and epicardial (outer 25%). In the septum, the inner 50% of cells were endocardial and outer 50% were midmyocardial (Fig. 3).

Table 2.

Parameters modified from the model by Ten Tusscher (ten Tusscher et al., 2004)

Model parameters	Heart Failure
GIto	↓65%
KNaCa exchange	↑200%
VSR Ca pump	↓60.14%
Kleak	↑32.27%
GKs	↓40%
GK1	↓50%

Figure 3.

Endocardial, midmyocardial and epicardial myocytes action potentials (left) and calcium transients (right) of the normal (dotted line) (ten Tusscher et al., 2004) and failing (solid line) single cell.

The NavX system displays the geometric position of the recording electrode tip in real-time. A cloud of 3D points crudely approximating the endocardial surface geometry is obtained by sweeping the cavity with the mapping catheter as it records endocardial electrograms. In order to represent the activation pattern, it was necessary to map the electrical recordings to their appropriate locations in the computational model of the failing heart geometry. To align the recorded data with the model, the entire data set was rotated into the coordinate frame of the computational mesh. Each recording position was then projected onto the closest point on the endocardial surfaces of the LV and RV (Fig. 4). The patient-specific mesh obtained from echocardiography was refined to yield 5120 tri-cubic Hermite elements (51,456 DOF). In order to compute a realistic activation pattern for the patient with LBBB, it was necessary to position stimulus sites consistent with the electroanatomic maps. A stimulus was applied for 5 ms at 50,000 μA/cm³. Conductivity throughout the myocardium was assumed to be anisotropic with respect to the fiber structure, and was also set to be ten times larger at the endocardial surface to represent the faster activation of the Purkinje system of both the RV and LV. To set the myocardial conductivities in the model, we first generated a simulation using the observed pacing site and the myocardial conductivity in the fiber direction as I₁₁=0.133417 S/m and I₂₂=0.0176061 S/m in the sheet and transverse directions. The infarct region was modeled as a decrease in the conductivity, and followed the infarct and border regions as determined by the MIBI scan. A set of simulations was performed iteratively to obtain an adequate activation sequence at the endocardium, and total activation time equal to the known QRS duration. To test the convergence of the electrophysiology model, we performed a simulation using the model with four times as many elements (200,192 DOF) solved with the same PDE step size and the same conductivity. Results show the total activation time and QRS duration were 16% shorter. However, since the conductivity parameters had originally been chosen to match the observed QRS duration, when we rescale the conductivities in the refined model to match the QRS duration, the RMS difference between activation times in the coarse and refined models was 1.2%. Hence for the current model, the activation time solutions were converged satisfactorily. The patient-specific electrophysiologic model was solved for a 600 ms interval on a desktop PC with an nVidia GTX-295 GPU in 3 hours, 24 minutes.

Figure 4.

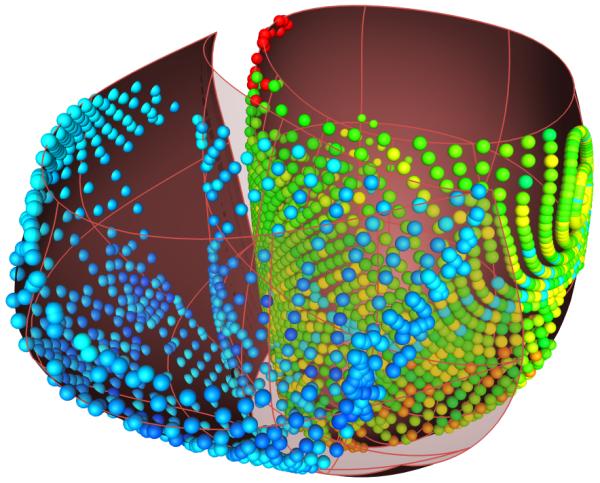
Electroanatomic map measurements of LBBB (left) projected to the end-diastolic mesh and resulting activation times (right) from the computational model [ms]. Red indicates the latest activated region, coinciding with the basal location of a scar.

Normal (ten Tusscher et al., 2004) vs. heart failure tissue model simulations (not shown) were also analyzed. Parameters like conductivity had to be set differently at the tissue scale for each of the myocyte cell models. It was found that the failing myocyte model resulted in more rapid conduction than the normal cell model, and action potential duration was longer. For example, using the same conductivities, we computed a total activation time in the normal cell model of 148 ms, and total repolarization of 490 ms; however, the failing cell model exhibited a 148 ms total activation time and total repolarization time of 560 ms. Lengthening of the action potential duration in heart failure has been well described as a consequence of myocyte electrical remodeling.

2.3 Ventricular Wall Mechanics

2.3.1 Unloaded Geometry

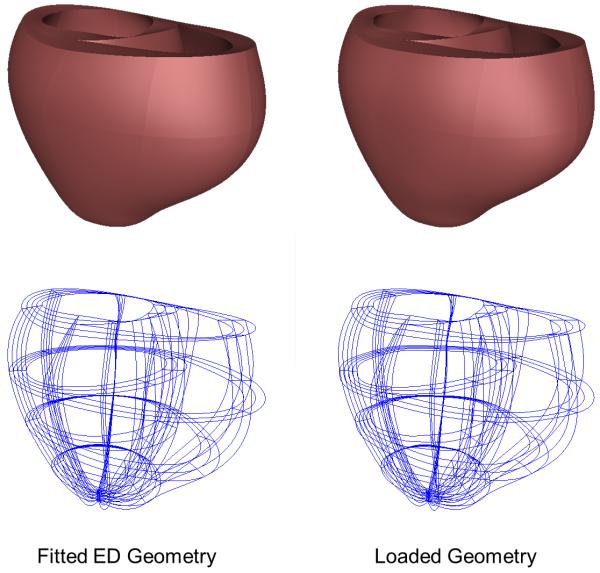
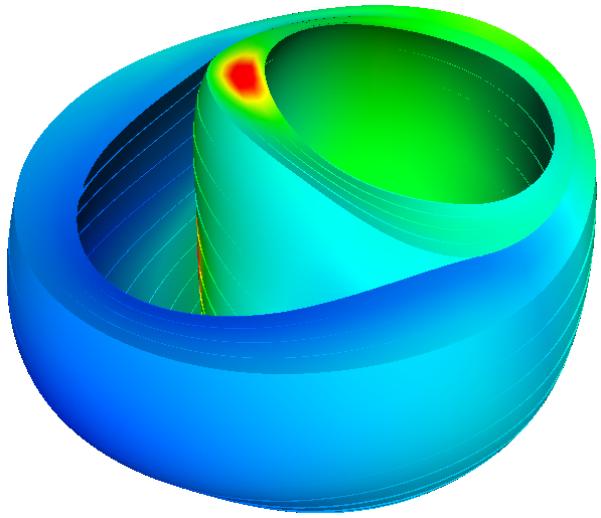
An essential requirement of the mechanical model is an unloaded reference geometric mesh, however the heart is continually loaded in vivo (Alastrué et al., 2008; de Putter et al., 2007). While end-diastole is the closest state in the cardiac cycle to fully resting, end-diastolic pressures are not zero, especially in heart failure. Some investigators have used the end-systolic (Walker et al., 2005) or mid-diastolic (Sermesant and Razavi, 2010) configuration as the unloaded reference geometry, because the ventricular volumes are closer to the expected unloaded diastolic volume, but stresses during systole are even higher than at end-diastole, which casts doubt on the validity of this assumption. Rajagopal (Rajagopal et al., 2006) developed a method to directly estimate the unloaded geometry of human breasts that has been applied to heart modeling by Nordsletten (Nordsletten et al., 2010). That ventricular model used an empirical formula for unloaded ventricular volume proposed by Klotz (Klotz et al., 2006) to estimate the unloaded geometry. Our method for estimating the unloaded geometry is based on the multiplicative decomposition of the deformation gradient tensor, as described in modeling of growth (Rodriguez et al., 1994). The objective of the iterative estimation scheme is to find the unloaded reference geometry that minimizes the difference between the measured end-diastolic geometry and the computed geometry when the unloaded model is inflated to the measured end-diastolic pressures assuming nonlinear myocardial material properties. In the first step, the fitted end-diastolic model is treated as an unloaded reference state and inflated to the measured end-diastolic LV and RV pressures. The inverse of the resulting deformation tensor is then applied to the measured end-diastolic mesh to compute a set of nodal residuals that are then incrementally decreased to zero to obtain an estimate of the unloaded geometry. This sequence is then iterated to minimize the distance between the coordinates of the measured and loaded end-diastolic geometries. This procedure converged to within 1.5% of the measured end-diastolic geometry and within less than 1% of the measured volumes in four iterations (Fig. 5). The maximum displacement between the computed and measured end-diastolic geometries was 2 mm.

Figure 5.

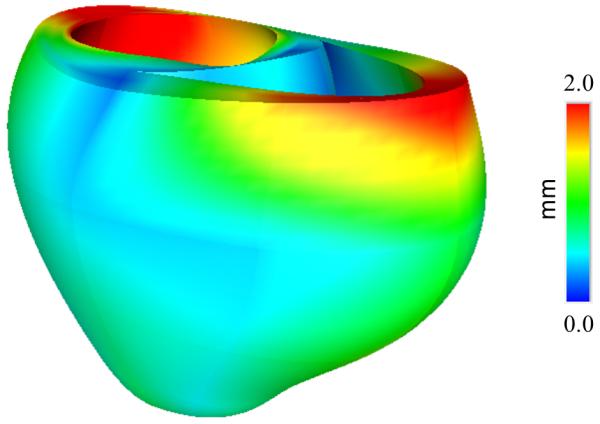
(A) End-diastolic geometry fitted from imaging data and unloaded geometry inflated to end-diastolic LV and RV pressures. (B) Displacement between the two meshes.

Furthermore, for all mechanical simulations, displacements were constrained as follows: longitudinal displacements were prevented at all nodes on the basal plane, rotation about the long axis was prevented at basal epicardial nodes, and symmetry constraints were applied to derivative degrees of freedom at the apex. Details are given in the online supplement.

2.3.2 Resting Material Properties

Researchers have proposed many forms of constitutive equation to model the passive heart tissue. Passive myocardium has been proposed to be orthotropic (Costa et al., 2001; Holzapfel and Ogden, 2009; Hunter et al., 1998; Schmid et al., 2006) with respect to mutually orthogonal fiber-sheet-normal local material coordinate axes (Dokos et al., 2000). However, the myocardium is also commonly modeled as transversely isotropic (Costa et al., 1996; Guccione et al., 1991; Humphrey et al., 1990; Humphrey and Yin, 1987) to reduce the number of material constants that need to be determined. Typically, these three-dimensional material laws and parameters are based on ex-vivo measurements in animal tissues that include the effects of anisotropy due to the fiber and sometimes sheet structure. However, we are unaware of any multi-axial testing of the human myocardium, though some investigators have measured one-dimensional stress-strain curves in isolated cardiac muscle strips (Meyer et al., 1998). Therefore, investigators have used three-dimensional constitutive models proposed for animal tissues and have solved semi-inverse problems to identify material properties for human myocardium based on non-invasive imaging of strain (Nash and Hunter, 2000; Young and Frangi, 2009) using MRI. Since MRI strain measurements are not available from routine clinical exams, the current model makes use of pressure-volume (PV) relations to estimate material parameters.

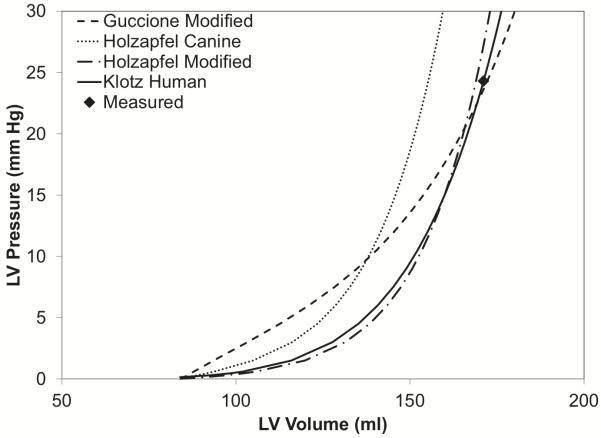
Klotz and co-workers (Klotz et al., 2006) suggested a standardized volume normalization of the end-diastolic pressure-volume relation (EDPVR) that eliminates most of the variation between individuals (including heart disease patients) and across species. They showed that the volume-normalized EDPVR can be approximated by the power law expression: EDP=A_n(EDV)^B_n where A_n = 28.2 mmHg and B_n = 2.79 for normal subjects and a wide range of pathologies including dilated cardiomyopathy. We tested the ability of two popularly used exponential anisotropic strain-energy functions with parameters derived from canine studies (Costa et al., 2001; Guccione et al., 1995; Holzapfel and Ogden, 2010) to reproduce Klotz’s EDPVR in the patient. The solid tracing in Figure 6 shows the EDPVR predicted when Klotz’s normalized curve was rescaled to the measured end-diastolic pressure and volume in the patient (23 mmHg, 161 ml) making use of the unloaded ventricular volume computed from the finite element mesh derived from the end-diastolic geometric model. Interestingly, the volume of the estimated unloaded geometric model (84 ml) is only 5 ml larger than that predicted by a separate empirical relation proposed by Klotz and colleagues. However, using the published parameters for normal dog myocardium, the constitutive models predicted significantly lower end-diastolic volumes than those measured in the patient (dotted curve). This may reflect a loss of myocardial stiffness associated with matrix metalloproteinase activity in heart failure (Spinale et al., 2000). It may also reflect the fact that experimentally isolating ventricular myocardium for tissue testing tends to increase tissue stiffness by the effects of rigor, edema and cutting injury. When we linearly scaled the strain energy functions to match the measured end-diastolic pressure and volume, we noted that the constitutive model by Holzapfel (Holzapfel and Ogden, 2010) (long-dash dot curve) is quite similar in shape to the power-law EDPVR, whereas the transversely isotropic model proposed by Guccione (Guccione et al., 1991) (dashed curve) is noticeably less nonlinear. Since there is no patient-specific information with which to estimate the anisotropy or non-linearity of the myocardial material properties, the exponent parameters or anisotropy of the original canine model were not adjusted here. In order to model the infarct in the patient, the infarct region was identified using the MIBI scan, and the isotropic term of the model (Holzapfel and Ogden, 2009) was set ten times stiffer as observed by Walker (Walker et al., 2005)

Figure 6.

Illustration of the E DPVR (end-diastolic pressure volume relationship) from the patient-specific model and the Klotz curve. The end-diastolic volume (EDV, 161 ml) and end-diastolic pressure (EDP, 23 mmHg) were measured in the patient.

2.3.3 Contractile Material Properties

With measurements of cardiac deformation (by MR tagging) and ventricular pressures, contractile properties can be estimated – even allowing for regional variation (Sermesant and Razavi, 2010; Walker et al., 2005). MRI however is expensive and MR tagging is not part of routine clinical evaluation. With cardiac ultrasound and ventricular pressure measurements, estimations of globally homogeneous contractile properties can still be obtained. Echocardiography and blood pressure measurements provide an estimation for end-systolic left ventricular volume and pressure, respectively (Arts et al., 2010).

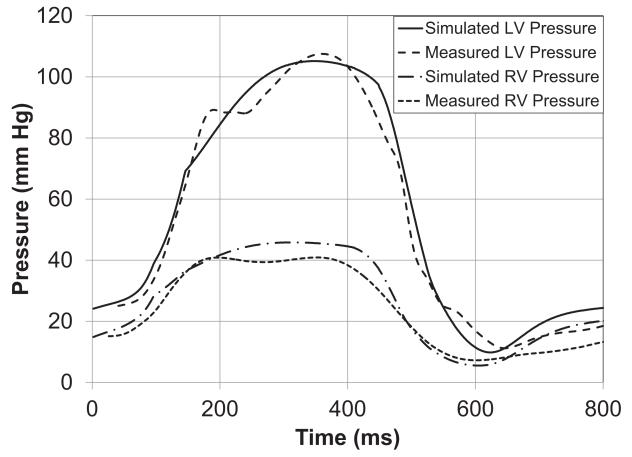
The contractile model proposed by Lumens (Lumens et al., 2009) was used here. Having determined an unloaded ventricular finite element mesh and passive material properties, the ventricular model was first passively inflated to the measured end-systolic left ventricular volume. From this point, the model was activated isovolumically and the active myofiber stress scaling parameter, contraction rise time and relaxation time were adjusted until systolic pressure, dp/dt_max and dp/dt_min, from the model matched those measured from the patient (Fig. 7). In a healthier subject with an end-systolic volume lower than the unloaded volume, the model can first be activated from the unloaded state. The contractility parameter can then be adjusted simultaneously with decreasing the cavity volume, such that the measured end-systolic volume and pressure are reached.

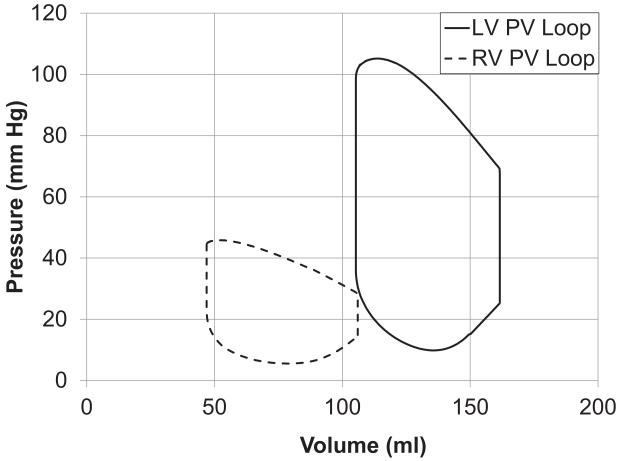
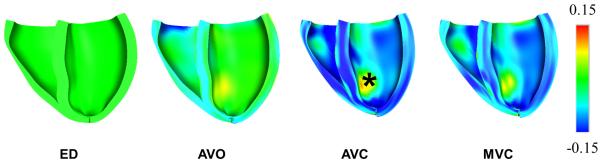
Figure 7.

(A) Left and Right ventricular pressure tracings computed by the model and measured. (B) Model-predicted left and right ventricular pressure-volume loops. (C) Long-axis sectional view of bi-ventricular model at 4 cardiac phases: end-diastole (ED), aortic valve opening (AVO), aortic valve closure (AVC), mitral valve opening (MVO). Fiber strain with respect to end-diastole is rendered in color from −0.15 (blue) to +0.15 (red). Note end-systolic bulging in region of inferior infarct labeled with *.

2.4 Hemodynamics

The venous and arterial vasculatures link the heart with the rest of the organs. Blood flow and pressure constitute the major feedback regulation to heart function, other than neuronal and humoral control. Therefore, circulatory models are part of the input, parameter estimation and output validation of patient-specific models. Various circulatory parameters can be measured non-invasively using echocardiography (LV and RV volume, valve diameter estimations, fractional shortening, aortic blood velocity, ejection fraction and ratio of early to late diastolic filling.) Furthermore, non-invasive estimates of vessel diameter changes can also be used to estimate pressure waveforms using transform functions when measurements cannot be obtained invasively.

Lumped parameter models have been commonly used as boundary conditions for 3D finite element models of the heart (Frank, 1899; Golden et al., 1973; Guccione and McCulloch, 1993; Gurev et al., 2010; Kerckhoffs et al., 2007a). The first models of the circulation viewed the cardiovascular system as a two-element Windkessel (Frank, 1899). In the Windkessel model the circulatory system is a large compliant compartment (representing the major arteries) and a peripheral resistance (representing the capillaries) that opposes the blood flow. The arterial walls are considered rigid, and two parameters are not sufficient to account for high-frequency components of the pressure-volume relationship in non-rigid, compliant, wave propagating medium (Lumens et al., 2010; Stergiopulos et al., 1999). Therefore this model lacks the detail to generate realistic waveforms of the human circulatory system. The three-element Windkessel (Boemser and Ranke, 1930; Rice et al., 2008; Westerhof et al., 1973) was developed to account for a characteristic impedance of the aorta, and therefore, an enhanced frequency response. The third element is related to the local inertia in the proximal aorta. Waveforms are more realistic, but parameters fitted and estimated seem to differ from measurements. A fourth parameter was then added to generate a four-element Windkessel model, accounting for the inertia of the entire arterial system, which partially resolves this problem (Stergiopulos et al., 1999).

Here, we initially inflated the ventricular finite element model to the measured end-diastolic pressures (LVEDP=23 mmHg and RVEDP = 14 mmHg). Next, the ventricular finite element model was coupled to an afterload model, consisting of isovolumic phases when ventricular pressures are lower than arterial pressures and two three-element Windkessel models (one for the left and one for the right ventricle) during ejection (Kerckhoffs et al., 2007b). Contraction was started with the computed LBBB activation sequence. The parameters for the LV three-element Windkessel model were determined such that stroke volume and end-systolic pressure matched between model and experiment. The RV Windkessel parameters were adjusted in the same way as for the LV, but using the measured RV pressure. In the last step, we coupled the three-element Windkessel models to compliant venous compartments that return the blood back to the ventricles, thus closing the blood circulation. Parameter values for these compartments were determined such that measured end-diastolic pressures were obtained in the model. For all circulation parameter values the reader is referred to the online supplement.

LV end-systolic pressure in the model was 106 mmHg, which is approximately the same as the patient’s LV end-systolic pressure of 114 mmHg. Figure 7(A) compares the simulated LV pressure during an ejecting beat with the clinically measured pressures. It can be seen that the peak pressure as well as the rate of rise and fall of the pressure in the cavity (dp/dt_max and dp/dt_min) were well captured by the model. Forward stroke volume and ejection fraction in the patient were 54.5 ml and 34%, respectively, not including the mitral regurgitant volume of 26.5 ml. In the model, mitral regurgitation was not included; hence all stroke volume was ejected to the aorta. Figure 7(B) shows the PV-loop for the same ejecting beat with a stroke volume of 56 ml and ejection fraction of 35%. Figure 7(C) shows the fiber strain in the model with respect to end-diastole at 4 cardiac phases. Fiber shortening does not occur in the infarct region during systole and is visible at aortic valve closure in Fig. 7(C).

We performed a validation of regional function by comparing fractional changes in model dimensions from end-diastole to end-systole with corresponding values in a geometric model fitted directly to echocardiographic images at end-systole and end-diastole. The fractional change in LV lateroseptal internal diameter was 14% in the model compared with 10% in the echocardiogram. LV anteroposterior internal diameter shortened 18% in both the model and echo measurements. Base-apex shortening was 9% in the model compared with 7% measured during echo. The anterior-posterior outer dimension decreased 6% during systole in the model compared with 9% in the echo measurements. Posterior wall thickening was 16% in the model compared with 20% by echo. However, anterior wall thickening was only 3% in the model compared with 18% measured. From these relative changes, it can be seen that the model was generally but not entirely consistent with these gross measurements of systolic wall motion, but clearly more extensive validation and investigation will be required.

2.4.1. Future considerations

The circulatory system can be represented in greater detail by adding more individual components to the lumped parameter model including baroreceptor feedback (Lumens et al., 2009), airway mechanics (de Putter et al., 2007; Kerckhoffs et al., 2010), and blood gas handling (Dash and Bassingthwaighte, 2004; Liu et al., 1998). Therefore, some specific pathologies, surgical interventions or trauma can be simulated (Lu et al., 2001; Sun et al., 1997). With such models, it is possible to obtain descriptions of blood flows, pressures and volumes in a more integrated manner. However, these models generally require the estimation of a large number of parameters that often cannot be measured in humans, so parameters from different species must be used.

One approach to this problem is to include adaptation rules so that the model can compute the required parameters. The CircAdapt model (Arts et al., 2005) has been developed using this approach. It includes an inertia component, more realistic valve behavior and the nonlinear properties of the vessel wall. CircAdapt also includes mechanisms to control arterial pressure by total blood volume, while peripheral resistance controls cardiac output. This model applies adaptation rules to peripheral blood vessels to estimate compliance and resistance, which can also reduce the number of parameters to be determined and can be setup using patient’s measurements [26]. A number of parameter values can be obtained from imaging data and arterial pressure measurements without having CircAdapt estimate them. Some of the parameters that can be estimated using CircAdapt are the valve dimensions, estimation of valve regurgitation, cardiac output and – depending on image quality – atrial dimensions.

3. Computational Requirements

One of the major impediments to the use of computational models in the clinic is the time-consuming process of model assembly and solution. With the advent of Graphic Processor Units (GPUs), large-scale computations can be accelerated, optimized and solved on small-scale computational platforms.

For some electrophysiology simulations, over 98% of the time is spent solving systems of ordinary differential equations (ODEs). We have been able to accelerate the ODE computation times, obtaining up to a 97x speedup on an nVidia GTX-295 GPU compared with a 4-core Intel i7 workstation (Lionetti, 2010). This has been done using a source-to-source translator that converts a python description of the cellular model into optimized CUDA source code, which is then compiled and executed on the nVidia GPU. This reduces the need for large, specialized clusters in the clinical environment. Storage and large memory systems are continually increasing their capacity and performance. These advances will be critical for routine model simulations that will be useful for the cardiologist.

4. Conclusion

Patient-specific models of the cardiovascular system are a promising approach to personalized cardiovascular medicine. For patient-specific models of the heart, key inputs derived from clinical measurements include unloaded cardiac reference geometry and electrical activation patterns. Cell behavior differs between health and disease, and it is important to model the heart in its diseased state. Hemodynamic measurements are necessary to estimate contractile parameters and model circulatory boundary conditions. The clinical value of the present model can be further assessed by testing its ability to predict cardiac functional alterations during cardiac resynchronization therapy and ultimately to help optimize the therapeutic protocol. Here we have made a first step towards this goal by defining the baseline model of a patient with dyssynchronous heart failure.