Full field digital mammography and breast density: comparison of calibrated and non- calibrated measurements

Abstract

Background

Mammographic breast density is an important and widely accepted risk factor for breast cancer. A statement about breast density in the mammographic report is becoming a requirement in many States. However, there is significant inter-observer variation between radiologists in their interpretation of breast density. A properly designed automated system could provide benefits in maintaining consistency and reproducibility. We have developed a new automated and calibrated measure of breast density using full field digital mammography (FFDM). This new measure assesses spatial variation within a mammogram and produced significant associations with breast cancer in a small study. The costs of this automation are delays from advanced image and data analyses before the study can be processed.

Objectives

We evaluated this new calibrated variation measure using a larger dataset than previously. We also explored the possibility of developing an automated measure from unprocessed (raw data) mammograms as an approximation for this calibrated breast density measure.

Methods

A case-control study comprised of 160 cases and 160 controls matched by age, screening history, and hormone replacement therapy was used to compare the calibrated variation measure of breast density with three variants of a non-calibrated measure of spatial variation. The operator-assisted percentage of breast density measure (PD) was used as a standard reference for comparison. Odds ratio (OR) quartile analysis was used to compare these measures. Linear regression analysis was applied to assess the calibration’s impact on the raw pixel distribution.

Results

All breast density measures showed significant breast cancer associations. The calibrated spatial variation measure produced the strongest associations [OR: 1.0 (ref.), 4.6, 4.3, 7.4]. The associations for PD were diminished in comparison [OR: 1.0 (ref.), 2.7, 2.9, 5.2]. Two additional non-calibrated measures restricted in region size also showed significant associations [OR: 1.0 (ref.), 2.9, 4.4, 5.4], and [OR: 1.0 (ref.), 3.5, 3.1, 4.9]. Regression analyses indicated the raw image mean is influenced by the calibration more so than its standard deviation.

Conclusion

Breast density measures can be automated. The associated calibration produced risk information not retrievable from the raw data representation. Although the calibrated measure produced the stronger association, the non-calibrated measures may offer an alternative to PD and other operator based methods after further evaluation, because they can be implemented automatically with a simple processing algorithm.

1. Introduction

Mammographic breast density is a significant factor for breast cancer risk that has been studied for many years (1, 2). A statement about breast density is a part of the radiological report according to the 4^th edition of the Breast Imaging Reporting and Data System (BI-RADS) (3). BI-RADS breaks down the estimate of breast density into quartiles: from almost entirely fat (0–25% glandular tissue) to extremely dense (75–100% glandular tissue). The breast density part of this report is meant to guide referring physicians to the risk of a cancer being obscured by the background tissue. The downside is that there is significant variation in the way breast density is reported from the 2D examination read by the radiologist (4). BI-RADS breast density is also used as a measure of risk in research (2) as a coarse approximation for the percentage of breast density measure. Breast density as a breast cancer risk factor is not currently used in clinical practice due to the lack of standardization and automation of its measurement (5).The attributes of an automated breast density measure for clinical applications should have a high degree of replication and translate across imaging platforms without extensive modification.

There are various methods used to assess breast density, as reviewed previously (6). For the most part, the breast density and breast cancer associations have been developed with measurements that did not consider the inter-image acquisition technique differences. In particular, the operator-assisted percentage of breast density approach (or PD) has shown repeatedly to correlate well with breast cancer (2) without considering the acquisition technique. Methods for automating PD are not widely used (6). An alternative method of assessing breast density is to calibrate, or adjust, for the acquisition technique differences (7–11).

Calibration should reduce unwanted measurement variation and produce a measure of mammographic density that shows stronger associations with breast cancer than non-calibrated methods such as PD. However, measurements based on calibration with digitized film mammography have produced mixed findings. Some work shows that calibration does not produce anything beyond PD (12, 13). Other researchers found that calibration strengthens the breast density associations with film mammography (14). Using full field digital mammography (FFDM), we have shown that calibration can be used to both describe PD (15) and to develop a new measure of breast density (16). This new measure is calculated as the standard deviation (SD) of the calibrated pixels within the breast area, which captures spatial variation. This measure provided stronger associations with breast cancer than PD in a small study (16).

Our calibration methodology was described in detail previously (17–20) and is briefly discussed here to put the various measurements in context. The calibration produces image data normalized for the inter-image acquisition technique differences at the pixel level (or more coarse scales) referred to as the percent glandular representation, which is a normalized effective x-ray attenuation coefficient metric. Differences in the compressed breast thickness, target-filter combination, x-ray tube voltage, and exposure are rectified by the calibration process. There are many technical problems (15, 18) that if not addressed will introduce considerable error into the calibration output.

The calibration may not influence the moments of the raw pixel distribution uniformly. If the calibration primarily operates on the central (or mean) value of the pixel distribution for a given image, the standard deviation of the raw pixel values (derived from non-calibrated images) may also be a measure of breast cancer risk. The objectives of this work were (a) evaluate the new calibrated standard deviation measure (or PG_SD) with a larger dataset than used previously, (b) explore the possibility of developing a breast density measure without calibration that shows a similar association with breast cancer as PG_SD, and (c) characterize the calibration influence on the raw pixel distributions. To meet these objectives, we performed a case-control study to evaluate PG_SD and explored the standard deviation from the raw FFDM images as the breast density metric. For one measure, the standard division was calculated from the raw data using the same region as for PG_SD. Two additional standard deviation measures were considered from the raw data by restricting the region sizes. These non-calibrated measures were compared with PG_SD using their association with breast cancer as the endpoint. PD was applied to raw mammograms and used as a common reference for comparison. Regression analysis was used to compare calibrated and non-calibration pixel distribution characteristics to understand the quantities most influenced by calibration. Our previous work was performed at a more coarse calibration scale (15, 16). In contrast, the calibration was performed at the pixel-level for this report.

2. Methods

2.1 Study Population

The patient accrual was part of an ongoing case-control study. The study population, selection methods, and matching particulars have been discussed previously (15) and are not discussed here in detail. In brief, the study accrual has been updated in this report to include more participants. In this IRB approved study, women diagnosed with a primary breast cancer (September 2007-March 2011) were included as cases (n=160) identified from those attending the breast clinics at the H. Lee Moffitt Cancer Center. For the controls, three groups of cases were considered based on their screening history. Group 1 was comprised of women that had a negative screening mammogram within 30 months prior to their breast cancer diagnosis (n₁ = 141). Group 2 was comprised of women who had a negative screening history that fell outside of the group 1 parameters, such as a woman who had a screening in 2007 but not again until 2010 at which time she was diagnosed with cancer (n₂ = 14). Group 3 was comprised of women who were just starting screening and were diagnosed at their baseline mammogram (n₃ = 5). Case data and images were either located by retrospective records review (n = 52) for those women with images archived on the study FFDM unit or recruited, consented, and imaged for the study (n = 108). Controls (n=160) were identified retrospectively from the pool of women undergoing breast cancer screening mammography at the H. Lee Moffitt Cancer Center with archived images acquired with the study FFDM unit and were individual matched to their cases by age (±2 years) and hormone replacement therapy usage and duration (± 1year).

2.2 Spatial Variation Breast Density

Various breast density measures and their association with breast cancer were compared using a matched case-control design. To reduce anomalous spatial variation, the analysis was contained to the portion of the image that was in contact with the compression paddle during imaging. Using methods described previously (15, 19), the breast image area was eroded by 25% along a radial direction. This area defined the effective breast area. The degree of breast area reduction is an approximation that eliminates anomalous region where the compressed breast thickness is not well defined. Both PG_SD and the standard deviation calculated from the raw data (or R_SD ) were derived from this modified breast area. The measures R_SDL and R_SDX were derived from reducing the effective breast area further and calculating the standard deviation. R_SDL was derived with 35% erosion. Because mammograms have a fractal characteristic (21–23), R_SDX was considered by restricting the measure to a 3 × 3 cm² box within each image. The box was located by first segmenting the breast region from the background and forming a binary mask, where the breast region pixels equal 1 and the other pixels were set to zero. Parallel to the chest wall, the box was centered on the centroid (determined with the binary segmented image) and extended from the detector edge to 3 cm along the direction perpendicular to the chest. Examples of the box location-size are shown in Figure 1. This measure was used to investigate (or control for) two possible influences. First, in fractal noise fields such as mammograms, the variance is a function of the region-size from which it is measured, where the larger the area, the larger the variance. Secondly, PG_SD is a decreasing function of increasing breast area (16). All measures of breast density were compared with PD as means of standardized control.

Figure 1.

Image examples. From left to right, this shows images with the largest box area / breast area ratio, image with the medium ratio, and the image with the smallest ratio (right). The image areas from left to right in pixel units are 2426894, 1324519 and 386023. The outlined box in 3 × 3 cm² (300 ×300 pixels) and is vertically centered on the segmented image vertical centroid coordinate. R_SDX breast density was derived from this region. These images are processed clinical display images. We use these as raw image surrogates for display purposes because the raw images are not useful for display illustrations without manipulation.

2.3 Percentage of Breast Density (PD)

The dataset consisting of all cases-control images (left and right CC view images) were first de-identified and randomized. PD was generated with the Cumulus3 (CM) software (University of Toronto) using the batch file procedure to process the raw (non-processed images) FFDM images. The CM operator was blinded to the case-control status and original image identifiers. To avoid operator fatigue, a single operator performed the PD labeling in multiple reading sessions.

2.4 Breast Cancer Association Comparisons

To assess the breast density measure association with breast cancer, the non-cancer breast of each case was matched with the ipsilateral breast of its control. All mammograms were performed with a General Electric (Milwaukee, WI) Senographe 2000D FFDM mammography unit (i.e. one unit) that is used for routine screening at our center. The cranio-caudal (CC) views were used for all our analyses. A standard quartile analysis was used for the odds ratio (OR) comparisons, where the control breast density distribution was used to determine the cutoff values for each measure using conditional logistic regression. The first quartile of breast density for each measure served as the reference group for the second-fourth quartiles, providing a means for comparing the inter-measure OR distributions. Body mass index (BMI) measured in kg/m² and breast area (pixel units) were used as continuous variable adjustments in the analyses, while menopausal status was adjusted as a binary variable. The area under the receiver operating characteristic curve (or Az) was also used for predictive capability comparisons. This analysis, (including the Az estimations) was performed with the SAS software package (SAS Institute Inc., NC).

2.5 Calibration Assessment

One objective of this work was to investigate the nature of the calibration without considering the case-control status as the endpoint comparison. Similar pixel distribution measures were derived from calibrated and non-calibrated mammograms and compared. The average (or PG) and standard deviation of the calibrated pixels values (i.e. PG_SD) were used as the two calibrated measures. The mean (R_M) and standard deviation (i.e. R_SD) of the raw pixel values were used as two non-calibrated measures. The respective means and standard deviations were investigated with linear regression analysis. For this analysis, we used the combined image dataset (i.e. 320 study images derived from both cases and controls).

3. Results

3.1 Breast Density Measurement Association

Demographic and risk factor distributions are presented for both breast cancer cases and controls in Table 1. The two groups are similar in most measures. However, the cases have a few more menopausal women and the majority of women overall all postmenopausal. Associations between the five breast density measurements and breast cancer are summarized in Table 2. In this table, the ORs and Az quantities were adjusted for BMI, simultaneous adjustments for BMI and breast area, and the simultaneous adjustments for all three factors. When controlling for all factors, PG_SD provided the largest OR associations with breast cancer [OR: 1.0 (ref.), 4.6, 4.3, 7.4; Az = 0.651] among the measures. In comparison, the PD associations [OR: 1.0 (ref.), 2.7, 2.9, 5.2; Az=0.643] were somewhat diminished. The R_SDL associations [OR: 1.0 (ref.), 2.9, 4.4, 5.4; Az = 0.654 ] were slightly greater than PD, and the R_SDX associations [OR: 1.0 (ref.), 3.5, 3.1, 4.9; Az =0.650] were similar to PD. In comparison with the other measures, R_SD provided the weakest association [OR: 1.0 (ref), 2.2, 2.9, 3.8; Az = 0.634]. The estimated standard error (SE) for all Az quantities was SE_Az ≈ 0.03 indicating the inter-measure Az differences are marginal for most comparisons. To help explain the R_SD and R_SDL relative association, we also investigated the calibrated standard deviation calculated from the 35% eroded breast region (or PG_SDL). In contrast, the PG_SDL associations weakened when using the reduced breast area but were similar to that of PD (data not shown).

Table 1.

Patient characteristics

Characteristic	Case n	Case mean / SD or %	Control n	Control mean / SD or %
Age	160	58.5 / 10.6	160	58.5 / 10.5
HRT
Never used	84	52.5%	88	55.0%
1–5 yrs	26	16.3%	23	14.4%
6–10 years	17	10.6%	17	10.6%
11 – 15 yrs	12	7.5%	10	6.3%
> 15 yrs	21	13.1%	22	13.8%
BMI (kg/m2)	1591	26.4 / 4.5	160	25.3 / 4.3
Breast area (pixels)	160	1392643 / 478251	160	1318957 / 407717
Menopausal (post)	123	76.9%	115	71.9%

This table provides the number (n) of cases and controls in the hormone replacement therapy (HRT) stratifications by years (yrs) and for the other measures. The mean and standard deviation (SD) for the age, body mass index (BMI), and breast area distributions, and menopausal status (postmenopausal or not) breakdown by case - control group are also provided.

¹BMI was missing for one case observation.

Table 2.

Breast density measurement associations

Quartile OR (95% CI)	First (n1)	Second (n2)	Third (n3)	Fourth (n4)	Az
PD n=160	23	41	39	57
BMI adjusted	1.00 (Ref.)	2.50 (1.12, 5.56)	2.85 (1.26, 6.45)	4.94 (2.10, 11.62)	0.630
BMI, area adjusted	1.00 (Ref.)	2.57 (1.15, 5.75)	2.87 (1.26, 6.53)	5.17 (2.17, 12.33)	0.637
BMI, area, menopausal adjusted	1.00 (Ref.)	2.70 (1.19, 6.14)	2.94 (1.27, 6.80)	5.24 (2.18, 12.59)	0.643
PGSD n=160	22	53	38	47
BMI adjusted	1.00 (Ref.)	3.36 (1.58, 7.13)	2.89 (1.24, 6.74)	4.84 (1.95, 12.02)	0.637
BMI, area adjusted	1.00 (Ref.)	3.80 (1.75, 8.24)	3.56 (1.46, 8.69)	6.18 (2.34, 16.28)	0.639
BMI, area menopausal adjusted	1.00 (Ref.)	4.63 (2.05, 10.47)	4.26 (1.69, 10.76)	7.43 (2.72, 20.28)	0.651
RSD n=160	26	42	41	51
BMI adjusted	1.00 (Ref.)	1.81 (0.89, 3.67)	2.11 (0.97, 4.61)	2.78 (1.29, 5.97)	0.617
BMI, area adjusted	1.00 (Ref.)	2.07 (0.99, 4.30)	2.59 (1.13, 5.94)	3.48 (1.52, 7.93)	0.625
BMI, area menopausal adjusted	1.00 (Ref.)	2.17 (1.03, 4.57)	2.86 (1.22, 6.72)	3.76 (1.62, 8.70)	0.634
RSDL n=160	21	39	44	56
BMI adjusted	1.00 (Ref.)	2.41 (1.15, 5.08)	3.39 (1.52, 7.58)	4.37 (1.94, 9.85)	0.636
BMI, area adjusted	1.00 (Ref.)	2.66 (1.24, 5.68)	3.82 (1.67, 8.76)	4.95 (2.14, 11.46)	0.646
BMI, area, menopausal adjusted	1.00 (Ref.)	2.89 (1.34, 6.27)	4.44 (1.88, 10.49)	5.38 (2.29, 12.63)	0.654
RSDX n=160	24	55	36	45
BMI adjusted	1.00 (Ref.)	2.96 (1.44. 6.10)	2.29 (1.06, 4.95)	3.57 (1.48, 8.59)	0.639
BMI, area adjusted	1.00 (Ref.)	3.35 (1.58, 7.09)	2.89 (1.26, 6.64)	4.74 (1.81, 12.40)	0.639
BMI, area, menopausal adjusted	1.00 (Ref.)	3.50 (1.64, 7.47)	3.11 (1.34, 7.23)	4.87 (1.85, 12.84)	0.650

This table gives the quartile odds ratio (OR) stratifications and area under the receiver operating characteristic curve (Az) quantities for each of the five breast density measures: (1) operator-assisted percentage of breast density (PD), (2) calibrated standard deviation (PG_SD), (3) raw image standard deviation (R_SD), (4) raw image standard deviation from the reduced breast area (R_SDL), and (5) raw image standard deviation from the fixed box (R_SDX). The number of cases in each stratification (n₁–n₄) is listed in the top row. The 95% confidence interval (CI) is provided parenthetically beneath each OR.

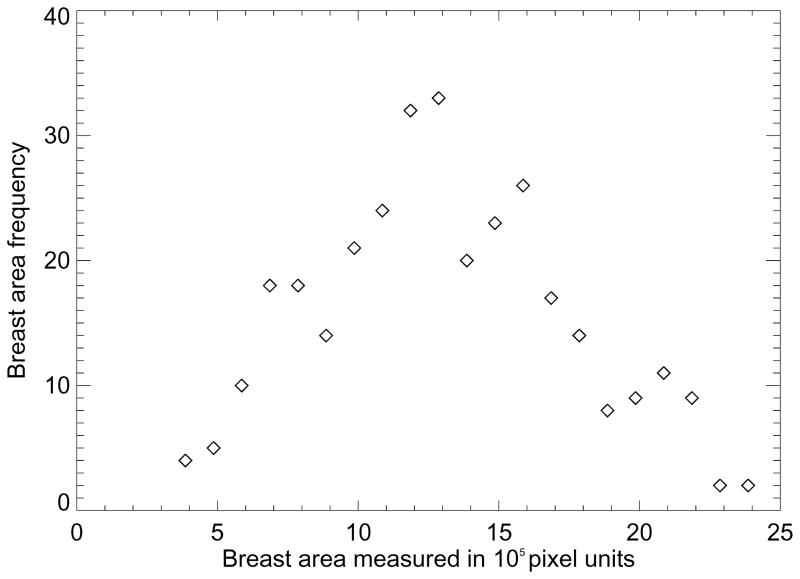
To estimate the area loss due to the erosion process, we used a coarse approximation that applies to CC views. If we assume the breast area (A) geometry is a half hemisphere, A~ r² , where r is the radius. The differential area change approximation with respect to the erosion is given by dA ~ 2R×ΔR, with ΔR = 0.25×R or 0.35×R for the 25% and 35% erosion, respectively. The percentage area reduction is then ≈ 100% ×dA/A, which gives 50% and 70%, for the 25% and 35% erosion. Thus, the R_SDL measure included roughly 30% of the available pixels within the breast region, whereas R_SD included 50% of the pixels. To put the R_SDX measurement in context, the box relative to various breast sizes is shown in Figure 1. From left to right we show the box relative to the larger breast, medium size breast, and smallest breast in the dataset. The breast area histogram is shown in Figure 2. The symmetric behavior (and central tendency) shown in Figure 2 indicates that many of the images have breast areas similar to the medium size breast shown in Figure 1 (middle illustration). For all measures, the ORs and Az quantities increased (increased magnitude of association) when controlling for (a) BMI, (b) BMI and breast area, and (c) BMI, breast area and menopausal status. However, the four variation measures were more strongly influenced by the breast area than PD when considering the respective ORs. The ORs for the box-restricted measure were also influenced by breast area. These findings also indicate that menopausal status is captured by the breast density measures to varying degrees. For example, we let x₀ = the 4^th quartile OR without controlling for menopausal status and x₁= 4^th quartile OR when controlling for menopausal status for a given measure. The percent change (PC) is then given by PC = (x₁-x₀)/x₀ × 100%. For the calibrated PG_SD, PC = 20.2%, and for the R_SDL, PC = 8.7%. In contrast for PD, PC=1.4% and for R_SDX, PC = 2.7%. Because the calibrated measure was influenced the most by menopausal status, we assessed its relationship further. PG_SD was used to predict pre-menopausal status with logistic regression, which gave OR = 1.9 (1.5–2.5) per standard deviation change in PG_SD and Az = 0.690.

Figure 2.

The breast area frequency histogram. This shows the frequency histogram for the breast area measured in 10⁵ pixel units (i.e. the bin-width used for the horizontal axis). The symmetric behavior indicates most images are similar to the middle image in Figure 1.

3.2 Correlation Comparisons

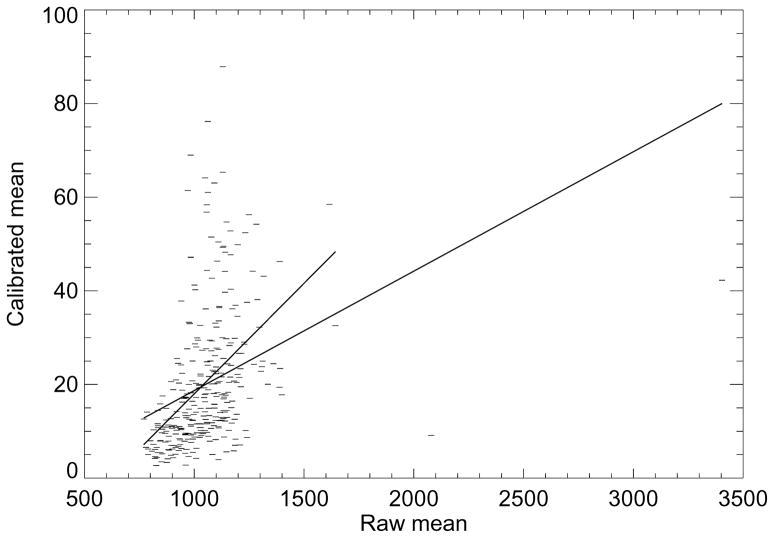
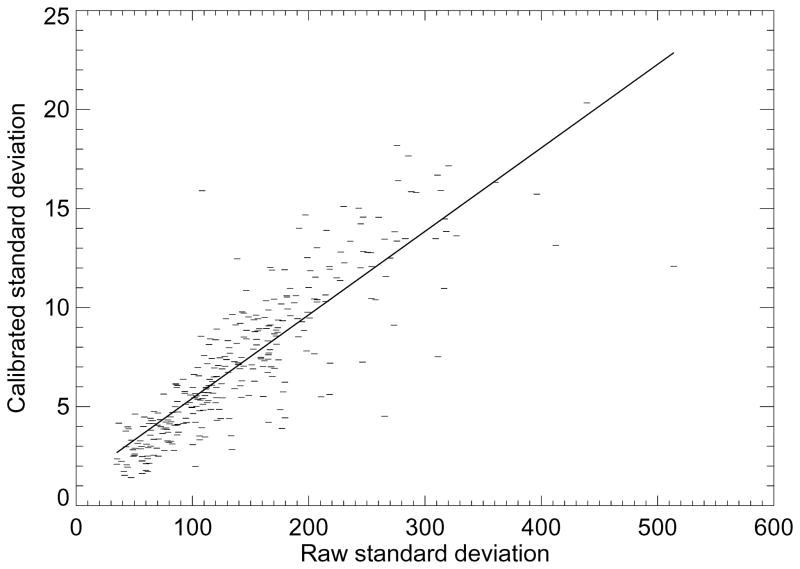
To show the influence that the calibration has on the raw image mean (or R_M ), the calibrated mean (or PG) was modeled as a linear function of R_M as shown in Figure 3. In this plot, we used both the entire dataset (the line with greater length) and a restricted dataset determined by removing three outliers located to the right (the line with shorter length). The respective slopes for each line were m = 0.026 (SE=0.004) and 0.047 (SE=0.005). In both cases, the slopes were significantly different from zero (P <0.0001). However, the respective coefficients of determination were R² = 0.12 and 0.19, indicating the linear model does not explain the relationships well. As shown in Figure 4, PG_SD (calibrated standard deviation) was modeled as a linear function of R_SD (the raw image standard deviation), which gave m = 0.042 (SE=0.002 and P <0.0001) with R² = 0.73. Because of the R_SDL significant OR associations, we performed a similar regression with PG_SD, which gave m = 0.048 (SE=0.001, P<0.0001) and R² = 0.77 (plot not shown). Thus, the standard deviation measures derived from the two different data representations are collinear.

Figure 3.

Mean regression. This plot shows the calibrated mean values modeled as a linear function of the raw image mean values (dashes). The regression fitted lines (solid) indicates the two measures are not described well by this relationship, indicating the calibration has a strong influence. The data was modeled with all the points (line with the longer length) and with three outlines removed (line with the shorter length) from the right. The respective slope (m) and standard errors for each plot were m = 0.026 ± 0.004 and 0. 047 ± 0.005 with R² = 0.12 and 0.19.

Figure 4.

Standard deviation regression. This plot shows the calibrated standard deviation modeled as a linear function of the raw image standard devotion (dashes). The slope and standard error were m= 0.042 ± 0.002. The regression fitted line (solid) shows the two measures are highly correlated (R² = 0.73) indicating that the calibration re-scales the standard deviation quantities while approximately maintains the internal distances between the samples.

4. Discussion

Our study investigated various automated methods of measuring breast density and made comparisons with PD. All measures of breast density showed a significant association with breast cancer to varying degrees. Among the measures, PG_SD showed the strongest OR associations with breast cancer, indicating calibration produced information not retrievable or available from the raw data representation. Furthermore, the relationship between PG and R_M was not described well by a linear model. In contrast, the linear model reasonably explained the relationship between the PG_SD and R_SD measures. This provided supporting evidence for the significant association produced by the raw image breast density measures. These findings suggest that much of the data within the breast area confounds the standard deviation measures from the raw data. R_SDL was based on the analysis of roughly 30% of the breast area, while producing significant associations. Eliminating a significant portion of the breast region improved the raw image standard deviation associations, whereas further erosion diminished the PG_SD associations. The R_SDX findings are more difficult to interpret. This measure produced significant association while considering a relatively small section of the image in many situations. Moreover, the OR relationships were influenced by controlling for breast area. Possible reasons for the elevated associations may be that this box-region is likely to include the focal spot and the distance between the compression paddle and detector is relatively more uniform in comparison with larger regions. Our work also showed that standard deviation measures were more heavily influenced by both menopausal status and breast area in comparison with PD. The relationships with menopausal status, breast area, and the new breast density measures will require further analyses to fully understand the underlying mechanisms. There are several limitations with our study. The work was preformed with a relatively limited dataset. Cases were recruited and selected retrospectively, whereas all controls were located retrospectively. We used both 25% and 35% erosion as static parameters to eliminate the portion the breast that may interfere with the spatial variation measures. Further investigation is required to determine the appropriate portion of the breast for the variation measures in both the raw and calibration representations. A better approximation may be to let the amount of erosion adjust according to image size. There is also uncertainty in the calibration due to the tissue equivalent phantoms (15) used to develop the calibration system and the warp/tilt of the compression paddle (19, 24, 25). We have developed approximate solutions addressing these uncertainties, which will require further analyses with larger datasets. The PD associations were within (upper range) the expected range found in the literature (2) . For the new measures of variation breast density, we are unaware of other findings in the literature at this time, precluding independent comparisons. The PG_SD findings are in agreement with our earlier related work (16). We might expect associations found from the new measures to vary when analyzing other study populations and images acquired with different detector technologies. However, the inter- measure comparisons in this report are internally valid.

5. Conclusions

The calibrated measure provided the strongest OR associations among the measures considered. The standard deviation measures from the raw mammograms also provided significant associations with similar predictive capability as the calibrated measure (i.e. the Az findings). Both the calibrated and non-calibrated variation measures are automated. We note, the gains due to calibration result from considerable phantom imaging and data analyses (18–20), required to maintain calibration accuracy. In contrast, R_SDL results from a relatively simple algorithm.

The lack of automated quantitative breast density measurements has so far limited the clinical use of breast density for patient management (5). Understanding the best method for estimating of breast density is still an unresolved problem. It may be too early to assess whether calibration is useful or if it can be applied broadly across institutions, because it is a newer approach that will require further investigation.

Both standardization and automation of breast density reporting would assist the radiologist in providing a further measure of risk to the referring clinician and provide a means for developing personalized screening frequency strategies. Realization of this potential is based on an algorithm to accurately and reliably quantify breast density independent of a subjective reader and in a manner that does not disrupt clinic throughput or patient management. These new measures evaluated in this report may provide automated solutions for the measurement of breast density after undergoing rigorous evaluations with different datasets