Abstract
Evaporative demand and soil water deficit equally contribute to water stress and to its effect on plant growth. We have compared the genetic architectures of the sensitivities of maize (Zea mays) leaf elongation rate with evaporative demand and soil water deficit. The former was measured via the response to leaf-to-air vapor pressure deficit in well-watered plants, the latter via the response to soil water potential in the absence of evaporative demand. Genetic analyses of each sensitivity were performed over 21 independent experiments with (1) three mapping populations, with temperate or tropical materials, (2) one population resulting from the introgression of a tropical drought-tolerant line in a temperate line, and (3) two introgression libraries genetically independent from mapping populations. A very large genetic variability was observed for both sensitivities. Some lines maintained leaf elongation at very high evaporative demand or water deficit, while others stopped elongation in mild conditions. A complex architecture arose from analyses of mapping populations, with 19 major meta-quantitative trait loci involving strong effects and/or more than one mapping population. A total of 68% of those quantitative trait loci affected sensitivities to both evaporative demand and soil water deficit. In introgressed lines, 73% of the tested genomic regions affected both sensitivities. To our knowledge, this study is the first genetic demonstration that hydraulic processes, which drive the response to evaporative demand, also have a large contribution to the genetic variability of plant growth under water deficit in a large range of genetic material.
Water deficit results from an insufficient offer of soil water compared with evaporative demand. It is essential to take into account both components of water deficit in the search for drought tolerance, in a context in which evaporative demand is likely to increase (Jung et al., 2010). High evaporative demand has large effects on growth and gas exchanges even in well-watered plants (Ben Haj Salah and Tardieu, 1996; Sadok and Sinclair, 2009), but it is rarely considered in genetic analyses of responses to water deficit. Therefore, a genetic analysis of the effects of both soil water depletion and evaporative demand is a necessary step for identifying sources of drought tolerance.
Reduction in leaf expansion with water deficit is an adaptive process that reduces transpiration rate via a decreased leaf area. It saves water during vegetative stages in favor of reproductive stages and avoids deleteriously low leaf water potentials at a given soil water status (Tardieu et al., 2010). This process is safer than drought-induced stomatal closure, which is accompanied by an increase in leaf temperature that may cause heat stress. However, it also provokes an irreversible reduction in whole-plant photosynthesis via a decreased leaf area (Monteith, 1977). Recently, the effects on yield of quantitative trait loci (QTLs) of sensitivity of leaf elongation to water deficit have been analyzed by simulation in hundreds of drought scenarios (Chenu et al., 2009). An allele conferring a high sensitivity of leaf elongation to water deficit results in an either positive or negative effect on yield depending on the drought scenario, including soil type and plant management. As a consequence, we have proposed (Tardieu and Tuberosa, 2010) that sensitivity should be genetically analyzed per se in phenotyping platforms, while its consequence on yield is analyzed in a further step with a combination of field experiments and crop models that explore a large range of scenarios, current or future.
Evaporative demand affects negatively the rate of expansive growth in leaves, even in well-watered plants, with half times of minutes (Shackel et al., 1987; Sadok et al., 2007). This response involves leaf turgor (Shackel et al., 1987; Bouchabké et al., 2006), and its effects can be alleviated by pressurizing the root system (Munns et al., 2000). Root hydraulic conductivity has a large role because blocking the aquaporin activity affects leaf elongation rate with an effect that increases with evaporative demand and is suppressed by pressurization of the root system (Ehlert et al., 2009). The role of abscisic acid (ABA) on this response is controversial (Kholová et al., 2010; Tardieu et al., 2010). These facts strongly suggest that the negative effect of evaporative demand on leaf growth is mainly linked to hydraulic processes. Conversely, the effect of soil water deficit is often considered to be largely nonhydraulic, because the turgor of growing cells is often maintained under water deficit (Tang and Boyer, 2002). Several mechanisms have been proposed for this nonhydraulic effect, in particular changes in cell wall plasticity involving expansin activity (Wu and Cosgrove, 2000; Muller et al., 2007) or cell division rate (Granier et al., 2000), with the possible involvement of long-distance chemical signaling with ABA, pH, or reactive oxygen species (Yamaguchi and Sharp, 2010). However, the time constants are similar and very short for both evaporative demand and soil water deficit, thereby ruling out a direct effect of several above-mentioned mechanisms (Tardieu et al., 2011). Exposure of roots to low water potential causes almost immediate cessation of growth (Chazen and Neumann, 1994; Fricke, 2004), and plants that have stopped growth recover full elongation in less than 1 h after rewatering (Parent et al., 2009). ABA, which was understood to be a major contributor to nonhydraulic effects, has a clear effect on root hydraulic properties via aquaporin contents and activity (Parent et al., 2009), while its nonhydraulic effect on growth is debated (Tardieu et al., 2010). Responses of leaf growth to soil water deficit and to evaporative demand, therefore, involve physiological processes and time constants that are more similar than believed some years ago.
A way to further test this similarity of mechanisms is to perform a genetic analysis of both sensitivities and to test to what extent they are controlled by common regions of the genome. Sensitivity to evaporative demand can be analyzed independently from soil water deficit in experiments with well-watered plants, which relate leaf elongation rate to leaf-to-air difference in water vapor pressure (VPDla; Supplemental Fig. S1). We have shown earlier that the negative effect of light on leaf elongation rate is accounted for by its effect on VPDla (Ben Haj Salah and Tardieu, 1996) and that maize (Zea mays) does not show a clear diurnal rhythm, so changes in leaf elongation rate during a day can be interpreted as an effect of VPDla (Poiré et al., 2010). Sensitivity to soil water potential can be analyzed independently from evaporative demand if one considers night periods, after which soil and plant water potentials have reequilibrated (Supplemental Fig. S2). Responses are linear, so the sensitivities of a given plant to soil water deficit or to VPDla can be estimated by the slopes or x intercepts of these linear relationships (Reymond et al., 2003; Welcker et al., 2007). These parameters are conserved for a given genotype across environments (growth chambers, greenhouse, and field) and years. Therefore, they can be considered as stable characteristics of a genotype usable in genetic analyses (Tardieu and Tuberosa, 2010).
The objective of this study was to identify genomic regions involved in sensitivities to evaporative demand or to soil water deficit (QTLs) across several genetic backgrounds and to test to what extent common QTLs influence both sensitivities. We tested this hypothesis with different genetic material involving (1) three mapping populations with either tropical (population P) or temperate (populations D and E) origins, (2) one mapping population resulting from the introgression of a tropical drought-tolerant line in a temperate line, and (3) two introgression libraries involving four lines with either dent or flint origins. We first performed a meta-analysis of QTL results and then analyzed the most interesting genomic regions with introgression lines whose backgrounds and donors were genetically independent of those used for QTL analyses.
RESULTS
A Large Genetic Variability of Sensitivities to Soil Water Deficit and Evaporative Demand That Correlated Phenotypically
Response curves to soil water potential and to evaporative demand were established for each of the 443 studied recombinant inbred lines (RILs) of the three mapping populations (for details, see Supplemental Figs. S1 and S2). Soil water deficit caused a large range of responses over the whole set of RILs in the three mapping populations (Table I; Fig. 1, D–F). Most sensitive RILs stopped leaf elongation at –0.4 MPa, while the less sensitive grew in a soil as dry as –1.3 MPa. This range of soil water potential represents 60% of that classically considered as available to plants (0 to −1.5 MPa). Hence, the combination of only five sources of alleles generated a considerable genetic variability of sensitivity to soil water deficit. The most resilient RILs belonged to the tropical population P, and the most sensitive belonged to the temperate population D. Evaporative demand was also associated with a large variation of responses (Fig. 1, A–C). Most sensitive RILs stopped leaf elongation at a VPDla of 3.5 kPa, while others still grew at 75% of their maximum rate at the same VPDla. The most sensitive mapping population was the tropical population P, and the least sensitive was the temperate population E.
Table I. Overview of the considered genetic material and experiments.
ABL, Advanced backcrossed lines; BCxSy, backcross population of x generations of backcross followed by y generations of selfing; P1 and P2, CIMMYT lines Ac7643 and Ac7729/TZSRW.
| Name of Population | Parents | Background | Type of Population | Size of Populationa | Tested Environmental Conditionsb | No. Exp.c | Data Origin |
| Mapping populations | |||||||
| D | F2 × Io | European Flint × Iodent | RIL | 110 | VPD, Ψ | 5 | Reymond et al. (2003, 2004); new data |
| E | F2 × F252 | European Flint × U.S. Dent | RIL | 98 | VPD, Ψ | 5 | New data |
| P | P1 × P2 | Tropical | RIL | 200 | VPD, Ψ | 6 | Welcker et al. (2007); new data |
| Introgression lines | |||||||
| NILG | Gaspé × B73 | Northern Flint × U.S. Dent | BC5S4 | 18 | VPD, Ψ | 4 | New data |
| NILF,D | eDent × eFlint | Elite Dent × Elite Flint | BC4S4 | 16 | VPD, Ψ | 4 | New data |
| NILD | eDent × eFlint | Elite Dent × Elite Flint | BC5S3, short introgressions | 23 | VPD | 1 | New data |
| ABLT | CML444 × F252 | Tropical × U.S. Dent | Pools of BC2S5 | 4 × 10 | VPD, Ψ | 4 | New data |
Number of lines considered in this work.
Environmental conditions in experiments. Ψ, Soil water potential.
Number of independent experiments. Plants were transferred between the growth chamber and the greenhouse; therefore, each experiment comprises two experimental conditions.
Figure 1.
Genetic variability of the sensitivity of leaf elongation rate to evaporative demand (A–C) or to soil water deficit (D–F) in three mapping populations. For each maize line, elongation rate is normalized by its maximum value, observed during the night. Solid lines show mean values for each considered population; dotted lines show decile recombinant inbred lines (i.e. the interval between the two dotted lines in each panel represents 95% of the population). Gray areas in A to C show extrapolated response curves out of the experimental range.
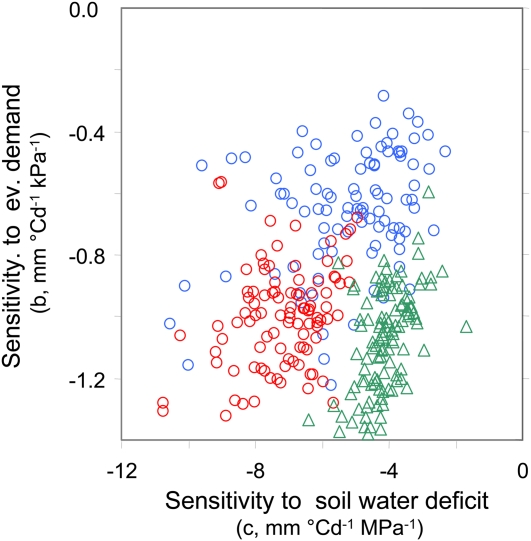
The two sensitivities were phenotypically related (Fig. 2). Two distinct clouds of points were observed, one corresponding to the tropical population P (r = 0.57) and one common to the temperate populations D and E (r = 56). At a given level of sensitivity to soil water deficit, RILs of the tropical population P were more sensitive to evaporative demand than those of the temperate populations D and E. This suggests that sensitivities were not linked via a simple functional cause (e.g. plant size) but more likely shared a partly common genetic determinism in each mapping population.
Figure 2.
Relationship between the sensitivities to evaporative demand and to soil water deficit in the three mapping populations. Each symbol represents one recombinant inbred line. Green triangles, Population P; red circles, population D; blue circles, population E.
A Large Number of Relatively Small-Effect QTLs Can Be Reduced to a Smaller Number of Meta-QTLs across Experiments and Populations, Covering 9% to 19% of the Maize Genome
QTLs were calculated independently for each population and each sensitivity characterized by two indicators (slope or x intercept). In order to avoid an overrepresentation of some QTLs in the analysis, only one QTL per genomic position was retained for each sensitivity (Supplemental Table S1).
Sensitivity to soil water deficit was associated with 23 QTLs with log of the odds (LOD) scores usually higher than 3 (2.1–5.5) and r2 of 0.08 to 0.27 (Table II; Supplemental Table S1). As expected from the genetic variability observed in Figure 1, fewer QTLs were observed in population D compared with the other two populations. The higher number of QTLs detected in population P was probably linked to the higher number of tested RILs. For each individual trait and population, detected QTLs jointly accounted for 29% to 45% of the total phenotypic variance, compared with heritabilities of 0.42 to 0.69 (Reymond et al., 2003; Welcker et al., 2007). Sensitivity to evaporative demand for well-watered plants was associated with 32 QTLs with LOD scores ranging from 2.4 to 6.4 and r2 from 0.07 to 0.29. More QTLs were detected in populations D and P than in population E, probably because of the lower number of RILs in the latter population. For each sensitivity and population, detected QTLs accounted for 35% to 53% of the total phenotypic variance, for heritabilities of 0.47 to 0.71.
Table II.
Meta-QTLs identified in this study
| No.a | Chromosome Binb | No. of QTLsc | Individual QTL Refs.d | Populatione | Parameterf | Percentage of Genome Meta-QTLsg | Markerh | Position in C Map (cM)i | IC C Map (cM)i | Position in IBM (cM)j | IC IBM (cM)j |
| 1 | 1.05 | 1 | 52 | E | c | 1.03 | umc229 | 132 (132) | 28 | 397 (397) | 64 |
| 2 | 1.06 | 2 | 1, 2 | P | b | 0.99 | umc276c | 168 (168) | 27 | 544 (544) | 49.8 |
| 3* | 1.09–10 | 2 | 28, 43 | D | b, c | 0.75 | tb1 | 287 (287) | 20 | 882 (882) | 40 |
| 4* | 1.10–11 | 1 | 3 | P | b | 0.44 | bnlg1347a | 308 (308) | 12 | 958 (958) | 36 |
| 5 | 1.11 | 1 | 12 | P | c | 0.02 | umc1538a | 337 (337) | 1 | 1,047 (1,047) | 7 |
| 6* | 2.03 | 3 | 13, 29, 44 | P, D | b, c | 0.41 | umc1422 | 53 (412) | 11 | 157 (1,297) | 17.6 |
| 7* | 2.07–08 | 3 | 4, 14, 46 | E, P | b, c | 0.18 | bnlg1721 | 186 (545) | 5 | 498 (1,638) | 28 |
| 8 | 3.04 | 3 | 5, 15, 30 | P, D | b, c | 0.28 | AY111333 | 97 (722) | 8 | 253 (2,120) | 40.5 |
| 9 | 3.06 | 1 | 31 | D | b | 0.51 | gpm753d | 154 (779) | 14 | 466 (2,334) | 29 |
| 10 | 3.09 | 1 | 16 | P | c | 1.88 | IDP7549 | 281 (906) | 51 | 744 (2,612) | 94.7 |
| 11 | 4.03 | 1 | 32 | D | b | 0.50 | gpm861b | 86 (1,033) | 14 | 143 (2,861) | 46.2 |
| 12 | 4.06–07 | 1 | 33 | D | b | 1.10 | IDP2466 | 174 (1,121) | 30 | 371 (3,089) | 60.8 |
| 13 | 4.09 | 1 | 17 | P | c | 0.07 | IDP7548 | 255 (1,201) | 2 | 646 (3,364) | 7 |
| 14* | 5.03 | 2 | 6, 18 | P | b, c | 0.81 | pza02792 | 98 (1,335) | 22 | 225 (3,694) | 26.2 |
| 15* | 5.03 | 1 | 34 | D | b | 0.73 | umc1315 | 124 (13,61) | 20 | 260 (3,729) | 26.3 |
| 16* | 5.04 | 2 | 19, 35 | P, D | b, c | 0.87 | pza00270 | 157 (1,394) | 24 | 328 (3,797) | 63.9 |
| 17* | 5.06 | 2 | 7, 20 | P | b, c | 0.31 | pip1b | 214 (1,451) | 8 | 484 (3,953) | 18.3 |
| 18 | 6.02–03 | 1 | 45 | D | c | 0.99 | csu146a | 92 (1,626) | 27 | 121 (4,286) | 50.5 |
| 19* | 6.04 | 2 | 21, 53 | E, P | c | 0.54 | umc1857 | 132 (1,666) | 15 | 203 (4,368) | 29.7 |
| 20* | 7.01–02 | 2 | 36, 47 | D, E | b | 0.53 | gpm913a | 102 (1,936) | 14 | 115 (4,860) | 49.3 |
| 21* | 7.02–03 | 2 | 37, 54 | D, E | b, c | 0.56 | umc98b | 139 (1,973) | 15 | 259 (5,004) | 41 |
| 22* | 7.04–05 | 2 | 37, 48 | D, E | b | 0.16 | TIDP2793 | 205 (2,039) | 4 | 530 (5,275) | 11.6 |
| 23* | 8.03 | 2 | 8, 22 | P | b, c | 0.35 | gpm583 | 84 (2,199) | 10 | 213 (5,594) | 35.9 |
| 24* | 8.05 | 2 | 9, 38 | P, D | b | 0.54 | bnlg2181 | 121 (2,236) | 15 | 367 (5,748) | 18.7 |
| 25* | 8.06 | 3 | 49, 50, 39 | D,E | b | 0.77 | gpm702b | 160 (2,275) | 21 | 430 (5,811) | 24.8 |
| 26* | 8.07–08 | 3 | 23, 39, 51 | E, P, D | b, c | 0.38 | uaz128 | 219 (2,334) | 10 | 474 (5,855) | 13.1 |
| 27 | 9.02–03 | 1 | 24 | P | c | 0.55 | gpm78b | 65 (2,429) | 15 | 164 (6,185) | 51.6 |
| 28* | 9.06 | 2 | 40, 55 | E, D | b, c | 0.47 | csu634 | 139 (2,503) | 13 | 383 (6,404) | 61.3 |
| 29* | 9.07 | 2 | 25, 41 | P, D | b, c | 0.40 | IDP7215 | 184 (2,548) | 11 | 561 (6,582) | 36 |
| 30* | 10 | 3 | 10, 26, 42 | P, D | b, c | 0.10 | psr119c | 1 (2,559) | 3 | 28 (6,704) | 2.6 |
| 31 | 10.02–03 | 1 | 27 | P | c | 0.88 | umc2069 | 46 (2,605) | 24 | 156 (6,832) | 92.3 |
| 32 | 10.07 | 1 | 11 | P | b | 0.47 | gpm101d | 161 (2,719) | 13 | 524 (7,200) | 21 |
| Total | 55 | 18.6 |
Meta-QTLs identified with asterisks are of particular importance, harboring QTLs with a LOD score greater than 3, identified in at least two populations or in two traits in a population.
Position of the meta-QTL in the genome. The entire figure is chromosome number, and the decimal is relative chromosomal position (bin) according to the IBM2 2008 Neighbors Map used as a reference map (www.maizegbd.org).
Number of QTLs harbored by this genomic region (see Supplemental Table S1). The number in the last line of the table is the total number of QTLs.
References of QTLs as in Supplemental Table S1. Numbers in boldface are for QTLs with LOD scores larger than 3.6 and effects larger than 15%. Numbers in italics are for QTLs with LOD scores ranging from 2.3 to 3 (effect between 9% and 14%).
Mapping populations in which a QTL has been detected in the corresponding genomic region.
Sensitivity to either evaporative demand (b) or soil water deficit (c).
Proportion of the genome covered by the corresponding meta-QTL.
Left flanking public marker closest to the meta-QTL position.
Position of the meta-QTL in the consensus map (in parentheses, cumulative cM counted from the top of chromosome 1) and confidence interval.
Position of the meta-QTL and confidence interval in the IBM2 2008 Neighbors Map (www.maizegdb.org).
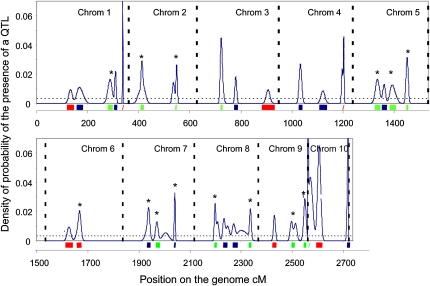
The 55 QTLs detected in the three populations on any of the two sensitivities were reduced to 32 meta-QTLs covering 19% of the genome (Fig. 3; Table II). Fourteen of those involved at least two populations (three populations in one case). The 19 most reliable meta-QTLs covered 9% of the genome (Fig. 3; Table II).
Figure 3.
Overview of meta-QTLs affecting the response of leaf growth to water deficit or evaporative demand. Blue curves show the density of probability of the presence of a QTL in the considered interval of 0.5 cM. The dotted horizontal line is the threshold defined as five times the average value for the uniform probability. Meta-QTLs are projected on the consensus map as thick bars: red, meta-QTL for sensitivity to soil water deficit; blue, meta-QTL for sensitivity to evaporative demand; green, meta-QTL for both sensitivities. Meta-QTLs annotated with asterisks are the most promising because they harbored QTLs with high LOD scores and/or were detected in at least two mapping populations or for two sensitivities in a population.
One-Third to One-Half of Meta-QTLs Colocalized between Both Sensitivities
In each population, an appreciable proportion of QTLs were common to both sensitivities. This was the case for seven out of 21 QTLs in population P (Supplemental Table S1). This proportion increased to seven out of 15 if the analysis was restricted to QTLs with LOD scores greater than 3. Hence, from one-third to one-half of QTLs were common to the two sensitivities in population P. Fewer colocalizations were observed in the other two populations, possibly because of the lower power of the QTL detection.
The meta-QTL analysis confirmed a high proportion of colocations, with 13 meta-QTLs out of 32 (41%) common to both sensitivities. In addition, four meta-QTLs of sensitivities to either evaporative demand or soil water deficit were very close to a complementary meta-QTL, suggesting that the same QTL may affect both sensitivities in these regions. The proportion of common QTLs raised to 50% in this case (meta-QTLs 1, 2, and 3–5 on chromosome 1 and meta-QTLs 14 and 15 on chromosome 5) and corresponded to a genomic region covering 6% of the maize genome.
Introgressions of Genomic Regions in Different Genetic Backgrounds Confirmed Meta-QTLs and Commonality of Sensitivities to Evaporative Demand and Soil Water Deficit
Three populations of introgression lines were used to test the meta-QTLs presented above, with backgrounds and donors independent of the genetic material used for QTL identification (Table I; Fig. 4A). They confirmed 11 genomic regions, among which six were confirmed in two populations of lines (one in three populations; Table III). Those with the strongest effects were meta-QTLs 6, 17, 23, and 28 (Supplemental Table S2). A methodological check was performed with genomic regions carrying no QTL in the Gaspé × B73 population. As expected, these regions had nonsignificant effects (Supplemental Table S2). It is noteworthy that tested genomic regions that had nonsignificant effects were not necessarily invalidated. This can reflect an absence of functional effect of the allelic difference at the tested site or experimental errors in the considered comparison.
Figure 4.
Effects of introgressed genomic regions at meta-QTL positions on the sensitivities of leaf growth to evaporative demand and soil water deficit. A, Positions of introgressed genomic regions in the genome. Each NIL is represented horizontally, and chromosome positions are indicated vertically. Green and gray lines indicate confirmed and putative positions, respectively, of introgressions into the recipient parent (orange lines). NILs introgressed into targeted meta-QTLs (MQTL; mapped on IBM2 2008 Neighbors Map [www.maizegdb.org]; for details, see Fig. 3) were selected within three independent populations: NILG, NILD,F, and ABLT (Table I). B, Differences in sensitivity between NILs and their respective recipient lines, expressed as the proportion of the sensitivity of the recurrent parent, for sensitivity to evaporative demand (parameter b) and to soil water deficit (parameter c). Black bars indicate significant differences (P < 0.05); gray bars indicate nonsignificant differences; and hatched bars are used when the effects of the introgression on sensitivities to evaporative demand and soil water deficit were apparently opposite because of a low effect on the latter.
Table III.
Effects of introgressed genomic regions at meta-QTL positions on the sensitivities of leaf elongation rate to soil water deficit and evaporative demand
| MQTL No.a | Chromosome Binb | Expected Effectc | Observed Effectd | ||
| NILG | NILF,D | ABLT | |||
| 3*, 4* | 1.09–10 | b | bc | bc | – |
| 5 | 1.11 | c | ns | – | – |
| 6* | 2.03 | bc | bc | – | – |
| 7* | 2.07 | bc | b | – | nse |
| 11 | 4.03 | b | bc | b | – |
| 12 | 4.06–07 | b | ns | – | – |
| 14* | 5.03 | bc | ns | – | – |
| 16* | 5.04 | bc | bc | c | c |
| 17* | 5.06 | bc | bc | c | – |
| 21* | 7.02–03 | bc | – | b | – |
| 23* | 8.03 | bc | b | ns | – |
| 24* | 8.05 | b | c | c | – |
| 25* | 8.06 | b | – | b | c |
| 26* | 8.07–08 | bc | ns | – | – |
| 28* | 9.06 | bc | bc | – | – |
Meta-QTL identification as in Table II. Asterisks indicate meta-QTLs considered as most promising.
Position of the meta-QTL in the genome. The first digit is chromosome number, and the decimal is the relative chromosomal position (bin) according to the IBM2 2008 Neighbors Map used as a reference map (www.maizegbd.org).
Expected effect of the introgression according to the QTL analysis: b, effect on the sensitivity to evaporative demand; c, sensitivity to soil water deficit; bc, sensitivity to both.
Observed effect in experiments with introgressed lines of populations of NILs Gaspé × B73 (NILG), Elite Flint × Elite Dent materials (NILF,D), and in pools of 10 lines of an advanced backcross with different alleles at meta-QTL positions (ABLT).
ns, Nonsignificant.
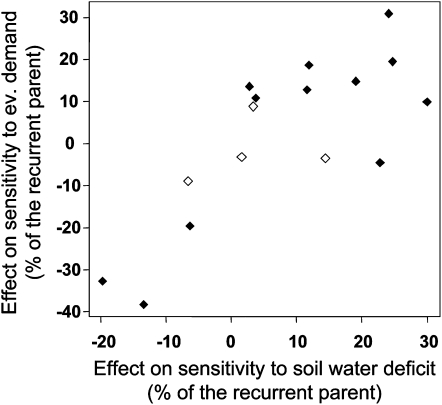
Most introgressed genomic regions affected both sensitivities (72%), even when the corresponding meta-QTL was associated with one sensitivity only. For example, among the five genomic regions tested for their effect on sensitivity to evaporative demand, three resulted in effects on both sensitivities and one resulted in an effect on the sensitivity to soil water deficit (Table III). The signs of the allelic effects on both sensitivities were identical in all lines, with significant effects for both sensitivities (Fig. 4). These allelic effects were related quantitatively in the population Gaspé × B73, with a correlation of 0.78, so introgressed lines that were the most resilient to evaporative demand were also the most resilient to soil water deficit (Fig. 5).
Figure 5.
Relationships between the effects of introgression lines on the sensitivities of leaf elongation rate to evaporative demand and to soil water deficit in the NILG population of near isogenic lines, normalized by the sensitivity of the recurrent parent. Each symbol represents one recombinant inbred line: black symbols, significant effect (P < 0.05); white symbols, nonsignificant effect.
The Precise Analysis of One Genomic Region Confirms the Validity of Close Meta-QTLs
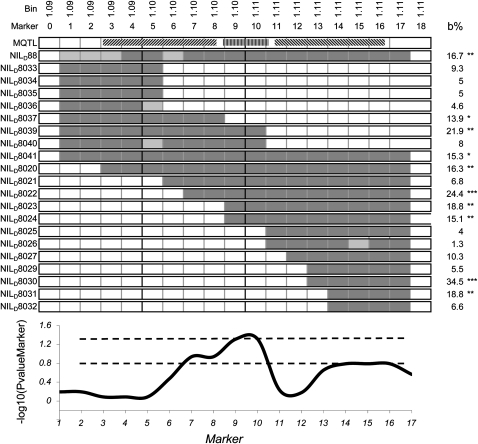
Some of the meta-QTLs presented in Figure 3 are located at close positions. We have tested whether such situations reflect the presence of two or more QTLs or reveal limitations of the meta-analysis approach. For that, we have analyzed close meta-QTLs (meta-QTLs 3–5 located in bins 1.09–1.11; Table II) with 21 lines of the NILF,D (for nearly isogenic line) population sequentially introgressed in this region (Fig. 6). Lines with dent alleles at markers 7 to 10 had a significantly altered sensitivity compared with the recurrent parent in seven cases out of eight, with a mean phenotypic effect of 16% for markers 9 and 10, while those introgressed at markers 1 to 5 had not. Consistently, a variance analysis performed on individual markers of all lines considered jointly showed a significant effect in the region composed between markers 9 and 10 (11 centimorgan [cM] on the IBM2 2008 Neighbors Map, bin 1.10; www.maizegdb.org). However, two lines not introgressed in this region but with dent alleles at markers 14 to 17 also resulted in an altered sensitivity (26% effect), thereby suggesting that another causal polymorphism was present in bin 1.11 (50 cM on the IBM2 2008 Neighbors Map). Overall, the three very close meta-QTLs observed in the considered region may correspond to at least two different causal polymorphisms, one for meta-QTLs 3 and 4 and one for meta-QTL 5.
Figure 6.
Effect of 21 sequential introgressions into bins 1.09 to 1.11 on the sensitivity of growth to evaporative demand in the population of NILD, F. A, Positions of introgressed regions (dark segments, dent allele) and recurrent genome (white segments, flint allele). Positions of meta-QTLs 3, 4, and 5 are also represented on the top. B, Effect of the introgression lines on the sensitivity of leaf elongation rate to evaporative demand expressed in proportion to the sensitivity of the recurrent parent. * P < 0.1, ** P < 0.05, *** P < 0.01. C, Profile of log10 of the P value in the test of the difference in sensitivity between the introgressed and nonintrogressed alleles at individual markers.
DISCUSSION
A Large Number of QTLs with Relatively Small Effects Suggests a Complex Genetic Architecture
Based on the sum of intervals of confidence of QTLs identified in any of the three studied mapping populations, the proportion of the genome covered by QTLs of sensitivity of leaf elongation to water deficit was 33%. It was reduced to 19% based on the intervals of confidence of meta-QTLs and to 9% for the most promising and tested meta-QTLs. These proportions are relatively small compared with the proportion of the genome involved in tolerance to water deficit, which covers more than half of the genome in several studies (Tuberosa et al., 2002; Sawkins et al., 2006; Ribaut et al., 2008). A first explanation for this smaller proportion is that the sensitivity of leaf elongation to water deficit is less complex than that of yield, thereby generating a minor number of QTLs. A second possibility is that the genotype × environment interaction usually generates a large number of QTLs in one environment only, thereby resulting in a large number of QTLs (Tuberosa et al., 2002; Malosetti et al., 2007; Maccaferri et al., 2008). This was not the case here, because QTLs involve sensitivities calculated over the whole range of environments, thereby encapsulating the genotype × environment interaction (Tardieu and Tuberosa, 2010).
It remains that the genetic variation studied here is determined by the allelic segregation at at least nine genomic regions corresponding to strong QTLs confirmed in different genetic backgrounds, involving public material but also the introgression of tropical material into a dent line and introgressions of elite material into elite lines. Effects were relatively small compared with those identified in studies with Arabidopsis (Arabidopsis thaliana), which displays typical r2 of 0.1 to 0.5 (Tisné et al., 2010). A large number of relatively small-effect QTLs is consistent with that observed for maize flowering time (Buckler et al., 2009), a simpler trait than sensitivity to water deficit. Therefore, this could be a characteristic of maize rather than an indication of a very complex trait per se. The detailed analysis of one genomic region suggests that close genomic regions may harbor different causal polymorphisms, so at least part of very close meta-QTLs in our analysis are not artifactual.
To What Extent Are the Genetic Determinisms Common between the Sensitivities of Leaf Elongation to Evaporative Demand and Soil Water Deficit?
While the QTL analysis suggests that one-third to one-half of QTLs are common to both sensitivities, the analysis of introgressed lines suggests a larger degree of colocalization (72%). Indeed, genomic regions harboring a QTL for the sensitivities to either evaporative demand or soil water deficit most often affected both sensitivities in introgressed lines. The low proportion of genetic variance explained by QTLs suggests that several QTLs remain undetected, which could lead to an underestimation of the number of QTLs contributing to both sensitivities. Therefore, it can be proposed that at least three-fourths of their genetic determinism is common to both sensitivities.
This commonality of QTLs challenges the view that sensitivities to soil water deficit and evaporative demand depend on different mechanisms. Sensitivity to evaporative demand is considered to depend on hydraulic signals and effectors, while sensitivity to soil water deficit is often considered to depend on cell wall properties, themselves under the control of chemical signals. Cell walls of leaf tissues become less extensible when plants are exposed to soil water deficit, thereby reducing tissue expansion rate, with the involvement of several gene families (Cosgrove, 2005). The expression of several expansin genes in growing regions of leaves is appreciably affected by water deficit, with correlations between local expansin expression and local elongation rate (Wu and Cosgrove, 2000; Muller et al., 2007). However, it is very difficult to disentangle experimentally the changes in cell turgor, hydraulic conductivity, and cell wall plasticity (Tang and Boyer, 2002; Bouchabké et al., 2006; Ehlert et al., 2009), suggesting a tight coordination between processes. This coordination could involve orchestrating genes such as DELLA (Achard et al., 2006). An alternative could be that cell wall stiffening in growing zones of leaves is triggered by a hydraulic signal between roots and shoots. Indeed, stiffening occurs in leaves a few minutes after exposure of roots to polyethylene glycol, even when roots are killed by freezing and thawing (Chazen and Neumann, 1994; Chazen et al., 1995). Any of these cases would generate common QTLs for both processes, located at a polymorphism that affects the signaling pathway, even if effectors differ between the two processes.
Combined with the results highlighted in the introduction, namely the commonality of time courses for the effects of evaporative demand and soil water deficit (Chazen and Neumann, 1994; Fricke, 2004) and the effect of ABA on elongation via hydraulic processes (Parent et al., 2009; Tardieu et al., 2010), this genetic analysis contributes to the view that hydraulic processes may play an essential role in the reduction in leaf elongation with soil water deficit in addition to their contribution to the response of evaporative demand.
Breeding Programs Have Probably Contributed to a Reduced Sensitivity to Both Evaporative Demand and Soil Water Deficit
QTLs for important traits related to yield formation (i.e. anthesis-silking interval [ASI]) colocalize with QTLs of the two sensitivities identified here, suggesting that breeders have indirectly selected for a reduced sensitivity to both evaporative demand and soil water deficit. In particular, six QTLs of ASI detected in five experiments with population P colocalized with meta-QTLs presented here with consistent allelic effects (Welcker et al., 2007). Because silk elongation rate has an essential contribution to ASI (Fuad-Hassan et al., 2008), this suggests an effect of QTLs on both silk and leaf elongation rate. In the same way, meta-QTL 7 identified here on chromosome 2 (bin 2.08) harbored QTLs of ASI, silk elongation, ear growth, and yield in four mapping populations with diverse tropical parents (Sawkins et al., 2004). The same meta-QTL harbored QTLs of root growth and yield in a meta-analysis of Tuberosa et al. (2002). These results suggest that the genetic architecture of leaf expansive growth, presented here, also affects several traits involved in reproductive development (silk growth, ear growth) or architecture of the root system. Breeding for these traits, therefore, has tended to reduce the sensitivities of all traits to water deficit.
However, QTLs for low sensitivity of growth to evaporative demand or soil water deficit have different effects on yield depending on the climatic scenario (Chenu et al., 2009). Hence, a selection based on yield and indirect traits may select for low sensitivity some years and high sensitivity in subsequent years, leading to oscillations of the alleles, which are fixed in the breeding populations (Chapman et al., 2003; Hammer et al., 2006). A phase of allele identification in phenotyping platforms, such as that presented here, is probably necessary to focus the breeding strategy (Tardieu and Tuberosa, 2010).
MATERIALS AND METHODS
Genetic Material
Three populations of maize (Zea mays) RILs were analyzed (Table I). Population D originated from a cross between F2, an early European flint inbred line, and Io, an Iodent inbred line, after six cycles of selfing. It consisted of 145 RILs mapped with 152 RFLP probes (Causse et al., 1996). Population E derived from a cross between F2 and F252, an early dent line developed in France from North American materials, after six cycles of selfing. It consisted of 98 RILs mapped with 173 RFLP probes (A Charcosset, unpublished data). Population P was developed by the International Maize and Wheat Improvement Center (CIMMYT) from a cross between two tropical lines with contrasting sensitivities to water deficit (Ac7643 and Ac7729/TZSRW; referred to as P1 and P2) after six generations of selfing. It consisted of 200 RILs mapped with 132 RFLP probes (Ribaut et al., 2004; Sawkins et al., 2004).
The test of the effect of individual genomic regions was performed by using two populations of NILs with unique introgressions targeting 17 genomic regions (covering 0.4%–3.6% of the genome; Table I). The first population included 16 NILs selected in the introgression library resulting from the cross of a northern flint line (Gaspé Flint) and an Iowa Stiff Stalk line (B73; Salvi et al., 2011). It resulted from five generations of marker-assisted backcross followed by three selfings (referred to as NILG hereafter). The lengths of introgressed regions ranged from 51 to 261 cM on the IBM2 2008 Neighbors Map (www.maizegdb.org), which is about four times longer than previous maps (Fig. 4; Supplemental Table S2). The second population consisted of 14 NILs selected in an introgression library resulting from the reciprocal crosses between two Limagrain elite lines, with four generations of backcross and four cycles of selfing (BC4S4; referred to as NILF and NILD). The lengths of introgressed regions ranged from 31 to 247 cM on the IBM2 2008 Neighbors Map (Fig. 4; Supplemental Table S2). For deeper analysis of one genomic region on chromosome 1 (247 cM in the IBM2 2008 Neighbors Map; bins 1.09–1.11), we have used 21 NILs derived from two initial NILs (NILD88 and NILD8041) that covered the whole region, resulting in a series of lines with sequential introgressed chromosome segments ranging from 50 to 150 cM (Fig. 6).
Finally, we have used four pools of 10 BC2S5 lines derived from a backcross of CML444, a tropical drought-tolerant line developed by CIMMYT, into the dent line F252 (referred to as ABLT hereafter). These pools differed at targeted loci (mapped with three to five simple sequence repeat markers) but also at other loci randomly distributed along the genome. Analysis was based on comparison of a pair of pools carrying either the allele CML444 or the allele F252 in the targeted genomic region.
Growing Conditions and Measured Traits
The responses of leaf elongation rate to evaporative demand and soil water deficit were studied in a series of experiments in a greenhouse and growth chamber (Table I), with protocols reported in previous papers (Sadok et al., 2007; Welcker et al., 2007). Briefly, the elongation rate of leaf 6 was monitored with a 15-min temporal definition in 200 to 400 plants (depending on experiments) for 7 to 16 d using the phenotyping platform Phenodyn (http://bioweb.supagro.inra.fr/phenodyn/). Meristem temperature, air relative humidity, air temperature, and light intensity were measured every 15 min as described by Sadok et al. (2007). Soil water potential was estimated from data of soil water content, itself derived from pot weight as described by Welcker et al. (2007). Plants were grown in the greenhouse with naturally fluctuating light (200–1,100 μmol m−2 s−1 at noon) or in the growth chamber (400–500 μmol m−2 s−1). In a first set of experiments, well-watered plants were subjected to changes in evaporative demand, which was naturally fluctuating in the greenhouse (from 0.8 to 3.2 kPa) and imposed sequentially at three successive target values (from 1 to 3 kPa), each 5-h-long step in the growth chamber. The same plants commuted between the two growing conditions in each experiment. In another set of experiments, plants were subjected to a range of soil water potentials, from –0.02 to –1.4 MPa, in the greenhouse. Watering was withheld when the fifth leaf appeared, so the measured sixth leaf grew while soil water status declined. Plants were rewatered when leaf elongation rate reached a low value, and a second cycle of soil drying was considered in the analysis. We checked that leaf elongation rate recovered to its initial value after rewatering.
Experiments and Data Analysis
Genetic analyses were carried out on data obtained from 2000 to 2005, based on five independent experiments for population D, five for population E, and six for population P (Table I). Experiments with introgressed lines were carried out from 2007 to 2009, with the same protocol as above. Four independent experiments were performed in the greenhouse and growth chamber, in which all NILs were studied simultaneously. One experiment was carried out with the family of NILs with small introgressed chromosome segments in bins 1.09 to 1.11 (Table I).
Time courses of leaf elongation rates were first corrected for temperature by expressing them per unit of thermal time. We showed (Parent et al., 2010) that this method is acceptable in the range 12°C to 30°C, which was experienced by plants in the experiments presented here. Using appropriate R scripts (R_Development_Core_Team, 2005), the resulting values were related to variations in evaporative demand or soil water potential. For well-watered plants, values of leaf elongation rates were related to evaporative demand for periods of 3 h during the day, either in the greenhouse or the growth chamber. For plants subjected to soil water deficit, leaf elongation rate was related to soil water potential for periods of 4 h at the end of the night. The sensitivity of leaf elongation rate to evaporative demand was then assessed by the slope of the linear relationship between rate and VPDla, corrected for the effect of light as described by Reymond et al. (2003; parameter b). The main effect of this correction was to set evaporative demand to zero during the night (Supplemental Fig. S1) and to reduce it when PPFD was lower than 500 μmol m−2 s−1, a rare event in this study. The sensitivity to soil water status was assessed by the slope of the linear relationship between leaf elongation rate and soil water potential (parameter c; Welcker et al., 2007). The x intercepts of relationships were also considered and represent the evaporative demands or soil water potentials that cause the cessation of leaf growth (parameters b0 and c0, respectively). Those slopes and x intercepts were computed individually for each RIL using R scripts available at http://bioweb.supagro.inra.fr/phenodyn/. For a given line, the regressions were computed on the basis of the cloud of data points originating from different experiments, years, and locations.
The four studied parameters (b, b0, c, and c0) used as phenotypic variables were then subjected to a QTL analysis by composite interval mapping using the PlabQTL package (Utz and Melchinger, 2000). QTLs were detected independently for each trait and population and for two different years (in the case of population P). To avoid overrepresentation of some genomic regions, QTLs were then grouped when related parameters colocalized (b and b0 on the one hand, c and c0 on the other hand) or for QTLs observed in two different years (Supplemental Table S1). The QTL with the highest contribution to the phenotypic variance (r2) was retained in further meta-analyses. Individual QTL data have been partly published previously for populations D and P (Reymond et al., 2003; Welcker et al., 2007), while data corresponding to population E are reported here for the first time (Table I).
For introgression lines, leaf elongation rates to VPD or soil water potential corresponding to NILs and recurrent parents were analyzed by covariance analysis (R procedure lm [R Development Core Team, 2009]). The effect of the introgression was assessed via the P value of the covariance analysis test and by the difference between the values of parameters for the NIL and the recurrent parent, expressed in percentage of the value of the recurrent parent. We additionally tested the effect of the same alleles shared by several lines at a given position by using a two-sided t test implemented in R. Pools of BC2S5 lines were analyzed in the same way as pairs of NILs, with one cloud of points for each pool of lines that differed at QTL positions.
Meta-Analysis of QTL
A consensus map was built by merging the three different genetic maps, which included 649 markers common to the IBM2 2008 Neighbors Map or mapped on it, thereby allowing projection on this reference map. Briefly, we first established correspondences between marker loci in individual maps based on synonymous names provided in maizeGDB and chose sets of markers with unambiguous locus order. In addition, we integrated two highly recombinant maps for populations D and E (Falque et al., 2005) for the generation of the consensus map in order to increase connections between maps. Forty-four markers had inconsistent positions in different maps and were removed. The consensus map was then built using the weighted least-squares method for calculation of the goodness-of-fit parameter, which takes into account the distance between the markers in each individual map, calculated as:
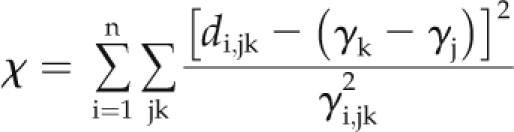 |
where n is the number of mapping populations (3), di,jk is the estimate in the ith map of the distance between the adjacent markers j and k, γ2i,jk is the corresponding expected variance, and γj and γk are the positions of the markers j and k, respectively, on the consensus map (Veyrieras et al., 2007; http:/bioinformatics.org/mqtl). We then projected the studied QTLs on the consensus map using a scaling rule between the original QTL flanking markers and the corresponding markers on the consensus map. For a given QTL location, the new confidence interval on the consensus chromosome was computed by taking into account the average scaling between the original and the consensus chromosome (Veyrieras et al., 2007).
To quantify the contribution of a chromosome region to trait variation, we calculated a parameter called “overview,” which estimates the probability that a given genome segment comprises a QTL in one of the considered experiments/populations (Chardon et al., 2004). It was assumed that the true position of QTLi was normally distributed around the most likely location, qi, of the QTL, with a variance of S2i: N(pi, S2i) (Visscher et al., 1996), where S2i can be estimated as (Lynch and Walsh, 1998):
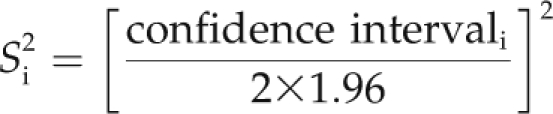 |
For each QTL detected on a given chromosome, we then calculated step by step (every 0.5 cM) the probability that its true position lies in this 0.5-cM interval. The overview parameter is the sum of the probabilities that the 0.5-cM interval comprises a QTL across experiments/mapping populations as:
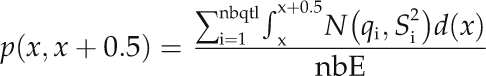 |
where nbqtl is the number of detected QTLs and nbE is the number of mapping populations (Chardon et al., 2004). This parameter was plotted along the consensus map. To highlight regions where the density shows a notable peak, we plotted on the same graph the average value of the parameter that is equivalent to the uniform probability that a 0.5-cM-long segment comprises a QTL, knowing the average number of QTLs per mapping population (nbQTL/nbE) but without information on QTL positions:
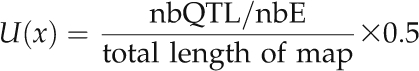 |
The number of meta-QTLs for each chromosome and their positions with the corresponding confidence interval were then determined using the MetaQTL software. Penalized likelihood criteria were computed to choose the most likely number of meta-QTLs, namely Akaike Information Criterion, Bayesian Information Criterion, and Average Weight of Evidence. Each value of the criteria was associated with its weight of evidence, ωk:
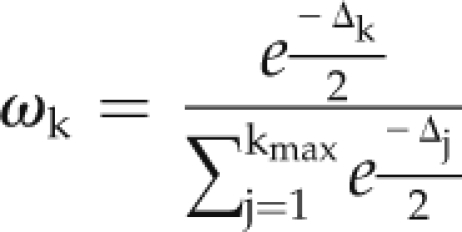 |
where ωk is the difference between the criterion value for the model with k meta-QTLs and the value for the model with the best criterion value. After determining the number of meta-QTLs for each group of traits and chromosomes, we estimated the position of each meta-QTL and its confidence interval.
Supplemental Data
The following materials are available in the online version of this article.
Supplemental Figure S1. Building the response curve of leaf elongation rate to leaf to air vapor pressure deficit.
Supplemental Figure S2. Building the response curve of leaf elongation rate to soil water potential.
Supplemental Table S1. QTLs detected in individual mapping populations.
Supplemental Table S2. Effects of introgressed genomic regions at meta-QTL positions.
Acknowledgments
We thank J.M. Ribaut (Generation Challenge Programme) and the CIMMYT maize program for providing the genetic material for the mapping population P and for making possible the development of the AB-QTL population from the introgression of an elite drought-tolerant line into temperate germplasm; B. Gouesnard (INRA) for the generation of the BC2S5 of the latter (ABLT) and C. Tollon (INRA) for its genotyping; P. Lessard (Biogemma) for giving access to the introgression library generated from elite germplasm (NILF,D); J. Joet (INRA) for training in MetaQTL analysis; and M. Falques (INRA) for development of the genetic map of population E. We are grateful to B. Suard and S. Berthezene (INRA, LEPSE) for help in experiments on the Phenodyn platform and to Cecilio Frois (INRA) for the data in Supplemental Figure S1. We also thank Dr. R. Tuberosa (University of Bologna), L. Moreau (INRA), and J.M. Ribaut (Generation Challenge Programme) for critical review of the work.
References
- Achard P, Cheng H, De Grauwe L, Decat J, Schoutteten H, Moritz T, Van Der Straeten D, Peng JR, Harberd NP. (2006) Integration of plant responses to environmentally activated phytohormonal signals. Science 311: 91–94 [DOI] [PubMed] [Google Scholar]
- Ben Haj Salah H, Tardieu F. (1996) Quantitative analysis of the combined effects of temperature, evaporative demand and light on leaf elongation rate in well-watered field and laboratory-grown maize plants. J Exp Bot 47: 1689–1698 [Google Scholar]
- Bouchabké O, Tardieu F, Simonneau T. (2006) Leaf growth and turgor in growing cells of maize (Zea mays L.) respond to evaporative demand under moderate irrigation but not in water-saturated soil. Plant Cell Environ 29: 1138–1148 [DOI] [PubMed] [Google Scholar]
- Buckler ES, Holland JB, Bradbury PJ, Acharya CB, Brown PJ, Browne C, Ersoz E, Flint-Garcia S, Garcia A, Glaubitz JC, et al. (2009) The genetic architecture of maize flowering time. Science 325: 714–718 [DOI] [PubMed] [Google Scholar]
- Causse M, Santoni S, Damerval C, Maurice A, Charcosset A, Deatrick J, Vienne D. (1996) A composite map of expressed sequences in maize. Genome 39: 418–432 [DOI] [PubMed] [Google Scholar]
- Chapman S, Cooper M, Podlich D, Hammer G. (2003) Evaluating plant breeding strategies by simulating gene action and dryland environment effects. Agron J 95: 99–113 [Google Scholar]
- Chardon F, Virlon B, Moreau L, Falque M, Joets J, Decousset L, Murigneux A, Charcosset A. (2004) Genetic architecture of flowering time in maize as inferred from quantitative trait loci meta-analysis and synteny conservation with the rice genome. Genetics 168: 2169–2185 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chazen O, Hartung W, Neumann PM. (1995) The different effects of PEG 6000 and NaCl on leaf development are associated with differential inhibition of root water transport. Plant Cell Environ 18: 727–735 [Google Scholar]
- Chazen O, Neumann PM. (1994) Hydraulic signals from the roots and rapid cell-wall hardening in growing maize (Zea mays L.) leaves are primary responses to polyethylene glycol-induced water deficits. Plant Physiol 104: 1385–1392 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chenu K, Chapman SC, Tardieu F, McLean G, Welcker C, Hammer GL. (2009) Simulating the yield impacts of organ-level quantitative trait loci associated with drought response in maize: a “gene-to-phenotype” modeling approach. Genetics 183: 1507–1523 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cosgrove DJ. (2005) Growth of the plant cell wall. Nat Rev Mol Cell Biol 6: 850–861 [DOI] [PubMed] [Google Scholar]
- Ehlert C, Maurel C, Tardieu F, Simonneau T. (2009) Aquaporin-mediated reduction in maize root hydraulic conductivity impacts cell turgor and leaf elongation even without changing transpiration. Plant Physiol 150: 1093–1104 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Falque M, Décousset L, Dervins D, Jacob AM, Joets J, Martinant JP, Raffoux X, Ribière N, Ridel C, Samson D, et al. (2005) Linkage mapping of 1454 new maize candidate gene loci. Genetics 170: 1957–1966 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fricke W. (2004) Rapid and tissue-specific accumulation of solutes in the growth zone of barley leaves in response to salinity. Planta 219: 515–525 [DOI] [PubMed] [Google Scholar]
- Fuad-Hassan A, Tardieu F, Turc O. (2008) Drought-induced changes in anthesis-silking interval are related to silk expansion: a spatio-temporal growth analysis in maize plants subjected to soil water deficit. Plant Cell Environ 31: 1349–1360 [DOI] [PubMed] [Google Scholar]
- Granier C, Inzé D, Tardieu F. (2000) Spatial distribution of cell division rate can be deduced from that of p34(cdc2) kinase activity in maize leaves grown at contrasting temperatures and soil water conditions. Plant Physiol 124: 1393–1402 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hammer G, Cooper M, Tardieu F, Welch S, Walsh B, van Eeuwijk F, Chapman S, Podlich D. (2006) Models for navigating biological complexity in breeding improved crop plants. Trends Plant Sci 11: 587–593 [DOI] [PubMed] [Google Scholar]
- Jung M, Reichstein M, Ciais P, Seneviratne SI, Sheffield J, Goulden ML, Bonan G, Cescatti A, Chen JQ, de Jeu R, et al. (2010) Recent decline in the global land evapotranspiration trend due to limited moisture supply. Nature 467: 951–954 [DOI] [PubMed] [Google Scholar]
- Kholová J, Hash CT, Kumar PL, Yadav RS, Kocová M, Vadez V. (2010) Terminal drought-tolerant pearl millet [Pennisetum glaucum (L.) R. Br.] have high leaf ABA and limit transpiration at high vapour pressure deficit. J Exp Bot 61: 1431–1440 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lynch M, Walsh B. (1998) Genetics and analysis of quantitative traits. Sinauer Associates, Sunderland, MA [Google Scholar]
- Maccaferri M, Sanguineti MC, Corneti S, Ortega JLA, Salem MB, Bort J, DeAmbrogio E, del Moral LFG, Demontis A, El-Ahmed A, et al. (2008) Quantitative trait loci for grain yield and adaptation of durum wheat (Triticum durum Desf.) across a wide range of water availability. Genetics 178: 489–511 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Malosetti M, Ribaut JM, Vargas M, Crossa J, Boer MP, Eeuwijk FAV. (2007) Multi-trait multi-environment QTL modelling for drought-stress adaptation in maize. Spiertz JHJ, Struik PC, van Laar HH, , Scale and Complexity in Plant Systems Research: Gene-Plant-Crop Relations, Vol 21. Springer, Dordrecht, The Netherlands, pp 23–34 [Google Scholar]
- Monteith JL. (1977) Climate and the efficiency of crop production in Britain. Philos Trans R Soc Lond B Biol Sci 281: 277–294 [Google Scholar]
- Muller B, Bourdais G, Reidy B, Bencivenni C, Massonneau A, Condamine P, Rolland G, Conéjéro G, Rogowsky P, Tardieu F. (2007) Association of specific expansins with growth in maize leaves is maintained under environmental, genetic, and developmental sources of variation. Plant Physiol 143: 278–290 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Munns R, Passioura JB, Guo J, Chazen O, Cramer GR. (2000) Water relations and leaf expansion: importance of time scale. J Exp Bot 51: 1495–1504 [DOI] [PubMed] [Google Scholar]
- Parent B, Hachez C, Redondo E, Simonneau T, Chaumont F, Tardieu F. (2009) Drought and abscisic acid effects on aquaporin content translate into changes in hydraulic conductivity and leaf growth rate: a trans-scale approach. Plant Physiol 149: 2000–2012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parent B, Turc O, Gibon Y, Stitt M, Tardieu F. (2010) Modelling temperature-compensated physiological rates, based on the co-ordination of responses to temperature of developmental processes. J Exp Bot 61: 2057–2069 [DOI] [PubMed] [Google Scholar]
- Poiré R, Wiese-Klinkenberg A, Parent B, Mielewczik M, Schurr U, Tardieu F, Walter A. (2010) Diel time-courses of leaf growth in monocot and dicot species: endogenous rhythms and temperature effects. J Exp Bot 61: 1751–1759 [DOI] [PMC free article] [PubMed] [Google Scholar]
- R_Development_Core_Team (2009) R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna [Google Scholar]
- Reymond M, Muller B, Leonardi A, Charcosset A, Tardieu F. (2003) Combining quantitative trait loci analysis and an ecophysiological model to analyze the genetic variability of the responses of maize leaf growth to temperature and water deficit. Plant Physiol 131: 664–675 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ribaut J, Betrán J, Monneveux P, Setter TL. (2008) Drought tolerance in maize. Bennetzen JL, Hake SC, , Handbook of Maize: Its Biology. Springer, Berlin, pp 311–344 [Google Scholar]
- Ribaut JM, Bänziger M, Setter T, Edmeades GO, Hoisington DA. (2004) Genetic dissection of drought tolerance in maize: a case study. Nguyen H, Blum A, , Physiology and Biotechnology Integration for Plant Breeding. Marcel Dekker, New York, pp 571–611 [Google Scholar]
- Sadok W, Naudin P, Boussuge B, Muller B, Welcker C, Tardieu F. (2007) Leaf growth rate per unit thermal time follows QTL-dependent daily patterns in hundreds of maize lines under naturally fluctuating conditions. Plant Cell Environ 30: 135–146 [DOI] [PubMed] [Google Scholar]
- Sadok W, Sinclair TR. (2009) Genetic variability of transpiration response to vapor pressure deficit among soybean (Glycine max [L.] Merr.) genotypes selected from a recombinant inbred line population. Field Crops Res 113: 156–160 [Google Scholar]
- Salvi SCS, Corneti S, Bellotti M, Carraro N, Sanguineti MC, Castelletti S, Tuberosa R. (2011) Genetic dissection of maize phenology using an intraspecific introgression library. BMC Plant Biol 11: 4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sawkins MC, DeMeyer J, Ribaut JM. (2006) Drought adaptation in maize. Ribaut JM, , Drought Adaptation in Cereals. Haworth Press, New York, pp 259–299 [Google Scholar]
- Sawkins MC, Farmer AD, Hoisington D, Sullivan J, Tolopko A, Jiang Z, Ribaut JM. (2004) Comparative map and trait viewer (CMTV): an integrated bioinformatic tool to construct consensus maps and compare QTL and functional genomics data across genomes and experiments. Plant Mol Biol 56: 465–480 [DOI] [PubMed] [Google Scholar]
- Shackel KA, Matthews MA, Morrison JC. (1987) Dynamic relation between expansion and cellular turgor in growing grape (Vitis vinifera L.) leaves. Plant Physiol 84: 1166–1171 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang AC, Boyer JS. (2002) Growth-induced water potentials and the growth of maize leaves. J Exp Bot 53: 489–503 [DOI] [PubMed] [Google Scholar]
- Tardieu F, Granier C, Muller B. (2011) Water deficit and growth: co-ordinating processes without an orchestrator? Curr Opin Plant Biol 14: 283–289 [DOI] [PubMed] [Google Scholar]
- Tardieu F, Parent B, Simonneau T. (2010) Control of leaf growth by abscisic acid: hydraulic or non-hydraulic processes? Plant Cell Environ 33: 636–647 [DOI] [PubMed] [Google Scholar]
- Tardieu F, Tuberosa R. (2010) Dissection and modelling of abiotic stress tolerance in plants. Curr Opin Plant Biol 13: 206–212 [DOI] [PubMed] [Google Scholar]
- Tisné S, Schmalenbach I, Reymond M, Dauzat M, Pervent M, Vile D, Granier C. (2010) Keep on growing under drought: genetic and developmental bases of the response of rosette area using a recombinant inbred line population. Plant Cell Environ 33: 1875–1887 [DOI] [PubMed] [Google Scholar]
- Tuberosa R, Salvi S, Sanguineti MC, Landi P, Maccaferri M, Conti S. (2002) Mapping QTLs regulating morpho-physiological traits and yield: case studies, shortcomings and perspectives in drought-stressed maize. Ann Bot (Lond) 89: 941–963 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Utz HF, Melchinger AE. (2000) A Computer Program to Map QTL. Institute of Plant Breeding, Seed Science, and Population Genetics, University of Hohenheim, Stuttgart, Germany [Google Scholar]
- Veyrieras JB, Goffinet B, Charcosset A. (2007) MetaQTL: a package of new computational methods for the meta-analysis of QTL mapping experiments. BMC Bioinformatics 8: 49. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Visscher PM, Haley CS, Thompson R. (1996) Marker-assisted introgression in backcross breeding programs. Genetics 144: 1923–1932 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Welcker C, Boussuge B, Bencivenni C, Ribaut JM, Tardieu F. (2007) Are source and sink strengths genetically linked in maize plants subjected to water deficit? A QTL study of the responses of leaf growth and of anthesis-silking interval to water deficit. J Exp Bot 58: 339–349 [DOI] [PubMed] [Google Scholar]
- Wu YJ, Cosgrove DJ. (2000) Adaptation of roots to low water potentials by changes in cell wall extensibility and cell wall proteins. J Exp Bot 51: 1543–1553 [DOI] [PubMed] [Google Scholar]
- Yamaguchi M, Sharp RE. (2010) Complexity and coordination of root growth at low water potentials: recent advances from transcriptomic and proteomic analyses. Plant Cell Environ 33: 590–603 [DOI] [PubMed] [Google Scholar]