Ultrahigh resolution protein structures using NMR chemical shift tensors

Abstract

NMR chemical shift tensors (CSTs) in proteins, as well as their orientations, represent an important new restraint class for protein structure refinement and determination. Here, we present the first determination of both CST magnitudes and orientations for ¹³Cα and ¹⁵N (peptide backbone) groups in a protein, the β1 IgG binding domain of protein G from Streptococcus spp., GB1. Site-specific ¹³Cα and ¹⁵N CSTs were measured using synchronously evolved recoupling experiments in which ¹³C and ¹⁵N tensors were projected onto the ¹H-¹³C and ¹H-¹⁵N vectors, respectively, and onto the ¹⁵N-¹³C vector in the case of ¹³Cα. The orientations of the ¹³Cα CSTs to the ¹H-¹³C and ¹³C-¹⁵N vectors agreed well with the results of ab initio calculations, with an rmsd of approximately 8°. In addition, the measured ¹⁵N tensors exhibited larger reduced anisotropies in α-helical versus β-sheet regions, with very limited variation (18 ± 4°) in the orientation of the z-axis of the ¹⁵N CST with respect to the ¹H-¹⁵N vector. Incorporation of the ¹³Cα CST restraints into structure calculations, in combination with isotropic chemical shifts, transferred echo double resonance ¹³C-¹⁵N distances and vector angle restraints, improved the backbone rmsd to 0.16 Å (PDB ID code 2LGI) and is consistent with existing X-ray structures (0.51 Å agreement with PDB ID code 2QMT). These results demonstrate that chemical shift tensors have considerable utility in protein structure refinement, with the best structures comparable to 1.0-Å crystal structures, based upon empirical metrics such as Ramachandran geometries and χ¹/χ² distributions, providing solid-state NMR with a powerful tool for de novo structure determination.

The chemical shift is an exquisite and powerful probe of molecular structure, deriving from the interaction of molecular orbitals with an external magnetic field, B₀. Understanding the relationships between chemical shifts and protein structure has substantial implications for modern nuclear magnetic resonance (NMR) spectroscopy, chemistry, and structural biology (1–12). The chemical shift tensor (CST) is rich with information, even when two-thirds of it is averaged to zero by molecular tumbling in solution or magic-angle spinning (MAS) of solid samples. The remaining isotopic chemical shifts remain an excellent resource for structure determination and validation, and higher-order interactions of the CST have substantial contributions to NMR relaxation (13–19). Therefore, detailed knowledge of CSTs permits a precise analysis of motion (20–22). Solid-state NMR (SSNMR) of fully aligned samples exploits amide ¹⁵N tensor information to determine the orientations of helices relative to the bilayer (23, 24). We have previously shown that use of a force field in which experimental ¹³Cα CSTs are compared with ab initio CSTs [generated as a function of backbone conformation (ϕ, ψ)] significantly improves the precision and accuracy of SSNMR-computed protein structures (10). In addition to determination of NMR-based structures and dynamics, CST datasets are invaluable for the continued development of quantum chemical techniques to compute isotropic and anisotropic chemical shifts, furthering our understanding of appropriate basis sets and functions for accurate MO theory of proteins (4, 6, 11, 25–27).

Over the past decade, protein structure determination by SSNMR has progressed substantially in terms of the rate of data collection and analysis, as well as in the resolution and complexity of the resulting structures (10, 28–36). In most cases, structures have been determined by using a combination of semiquantitative distance restraints (comparable to solution NOEs) together with semiempirical dihedral angle restraints, obtained from isotropic chemical shifts and chemical shift databases. More recently, we have demonstrated that tensor recoupling is also a powerful route to structure refinement since incorporating relative dipolar tensor orientations (36), CSTs (10), and precise z-filtered transferred echo double resonance (zf-TEDOR) distances (35) as restraint classes in annealing algorithms substantially enhances the precision and accuracy of the resulting protein structures. The next logical, yet technically challenging and heretofore unprecedented, step is to extend this approach by incorporating both tensor magnitudes as well as orientations into simulated annealing calculations. This approach promises further enhancement of structure quality and provides key internal controls for both backbone and side-chain conformations.

Here we present such results, first by determining the relative site-specific orientations of ¹H-¹⁵N (and ¹H-¹³C) dipolar tensors relative to the axis system of the ¹⁵N (and ¹³C) CST, building upon prior MAS studies of proteins (37) and static peptide samples (38–40). These NMR tensorial parameters are obtained using a set of three-dimensional (3D) synchronous recoupling pulse sequences. These datasets enable the accurate determination of CST orientations relative to the molecular frame for the majority of the backbone ¹⁵N and ¹³Cα sites in a crystalline protein, GB1 (41). The ¹³Cα tensors’ orientations are then incorporated, along with other restraint classes, into simulated annealing calculations, resulting in structures exhibiting especially high precision [defined by the backbone rmsd (bbrmsd)] and accuracy (defined by the agreement with crystal structures and structure validation metrics).

Results and Discussion

Determination of ¹⁵N and ¹³Cα CST Magnitudes, Orientations and Order Parameters.

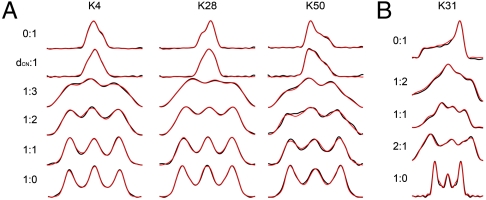
We first carried out a series of 3D [Rec]-¹⁵N-¹³C correlation experiments each consisting of a 2D NCA plane with a tensor recoupling period in the third dimension. The resulting lineshapes depend upon the CST as well as its relative orientation to the dipole vector (Fig. 1), consistent with conventions of prior studies (37). Further details regarding the tensor notation (Fig. S1) and pulse sequence (Fig. S2) are provided in Materials and Methods and SI Text. The key elements of the data collection are ROCSA recoupling of the CST (42) and 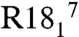heteronuclear dipolar recoupling (43). Using a 2-¹³C-glycerol,U-¹⁵N GB1 sample (28, 36, 44) all 53 observable ¹⁵N and ¹³C resonances were resolved in the NCA isotropic 2D plane (Leu Cα is unlabeled). Four of the experiments measured tensor magnitudes for the ¹⁵N and ¹³C CSTs and the ¹H-¹⁵N and ¹H-¹³C vectors. The seven remaining experiments correlated the CST with these vectors using ROCSA and 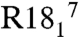periods, evolved synchronously with different ratios of evolution time. To orient the ¹³Cα tensor, ¹H-¹³C:CST ratios of 1∶1, 1∶2, and 1∶3 were utilized, with an additional ¹³C CST: ¹⁵N-¹³C ratio of 1∶1 to break mirror-plane degeneracies; to orient the ¹⁵N CST, ratios of ¹H - ¹⁵N:CST of 1∶1, 2∶1, and 1∶2 were acquired. Together these experiments yielded 563 lineshapes (> 10 per residue), reporting uniquely upon each tensor magnitude and the orientation with respect to the molecular frame. Order parameters for < 100 microsecond motions, derived directly from analysis of the ¹H-¹³Cα and ¹H-¹⁵N dipolar couplings (Fig. S3), indicate a rigid backbone. Aside from G41, we anticipate minimal motional averaging (approximately 1.5%) of CST magnitudes, based upon path integral calculations of Tang et al. (26). Further examples of fitted lineshapes are provided in SI Text (Figs. S4–S6), along with the full compilation of orientations (Tables S1 and S2).

Fig. 1.

Dipolar:CST correlation spectra for both ¹³Cα and ¹⁵N sites. Experimental spectrum is presented in black, with simulations in red. Ratios provided are the ratio of dipolar to CST evolution. Row two of A indicates ratio of ¹⁵N-¹³Cα dipolar:CST evolution. (A) Fit lineshapes for [¹H-¹³C]∶[¹³C CST] correlation spectra for lysines with different secondary structures are presented. K4 is located in a β-sheet, K28 in the α-helix, and K50 in a β-turn with an unusual positive value of ϕ. (b) Fit ensemble of [¹H-¹⁵N]∶[¹⁵N CST] correlation spectra. Fit is representative of limited variations of ¹⁵N tensors throughout GB1.

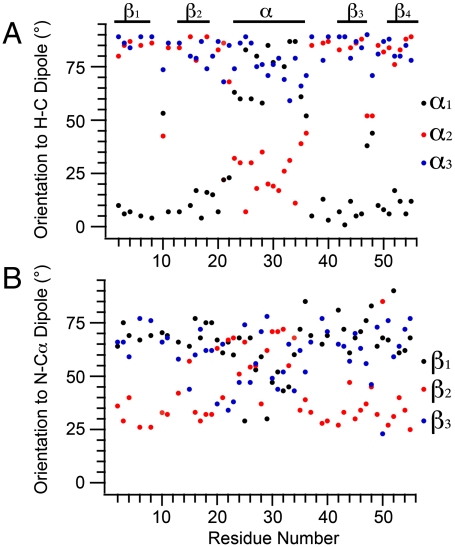
These datasets together report upon the ¹³Cα CST orientation with respect to the ¹H-¹³Cα (α₁, α₂, α₃) and ¹⁵N-¹³Cα (β₁, β₂, β₃) bond vectors. Tensor magnitudes were reported in our previous study (10); the results we report here, to restrain orientations, were acquired under identical experimental conditions. The ¹³Cα exhibits a broad range of total magnitude and rhombicity, depending upon residue type and secondary structure. Beyond the changes in tensor anisotropy (δ) and asymmetry (η) discussed previously (7, 10), the orientation of each element to the molecular frame varies greatly (Fig. 2 and Fig. S7). For example, in a typical β-sheet conformation the δ₁₁ element is oriented from 0 to 25° of the ¹H-¹³C bond vector, and closer to perpendicular to this vector in α-helical conformations. The orientation of the ¹³C CST to the ¹⁵N-¹³C bond is also a strong reporter of backbone torsion, in most cases a transposition of the β₁ and β₂ angles, often accompanied by a conversion to the complement of the angle. All angles fitted are provided in Table S1.

Fig. 2.

Analysis of [¹H-¹³C] dipolar:¹³C CST correlation spectra. (A) Fit α angles, defining orientation of each tensor element to the HC dipole, as a function of residue number. All angles over 180° were converted to their < 90° complement for clarity. Clear trends are observed where δ₁₁ is oriented within 20° of the dipole in β-strands but moves within 30° of the bond normal in the α-helix. δ₂₂ and δ₃₃ are near perpendicular to the HC bond in the β-sheet, while δ₁₁ and δ₂₂ reorient up to 80° in the α-helix. (B) Fit β angles defining the orientation of each tensor element to the NC bond vector. While overall variation of orientation is not as pronounced, there is a strong shift in the β₂ angle between helical and sheet conformations with a concerted, smaller adjustment of β₁ and β₃.

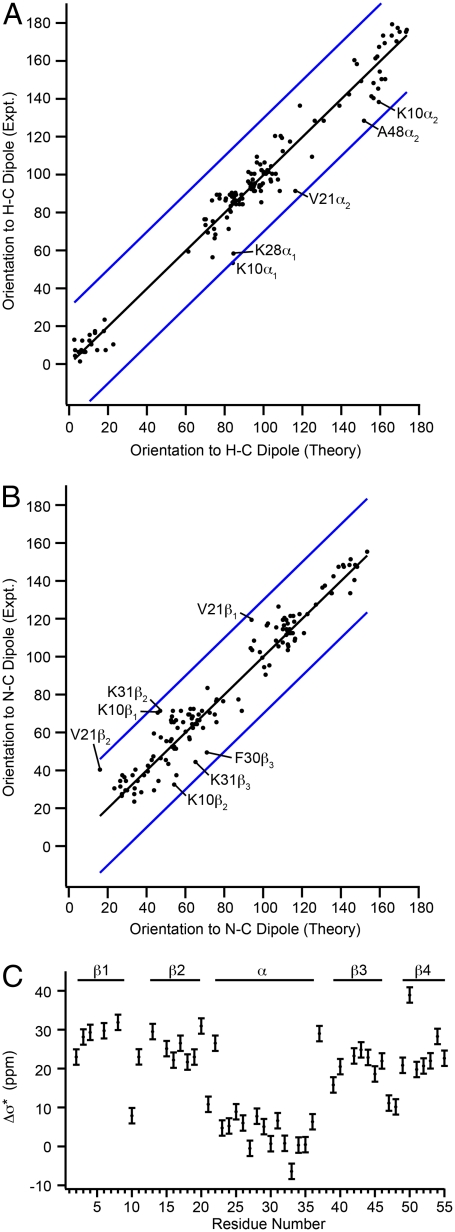
We investigated the trends and consistency of the ¹³Cα orientations in two ways. First, we compared our measurements with ab initio chemical shielding surfaces that are available for all 20 common amino acids (http://feh.scs.uiuc.edu/amino_acid.php), (4, 6, 11) where we find excellent overall agreement. The theory-versus-experimental correlations are presented in Fig. 3 A and B, where it can be seen that all experimental values are within 30° (depicted in blue) of the predicted values. The overall agreement for each dataset is very good with an rmsd for (α₁, α₂, α₃) of 8.0° and an R² = 0.97 (Fig. 3A). In the case of (β₁, β₂, β₃), the rmsd and R² values are 8.5° and 0.95 (Fig. 3B), comparable to previously reported results for small peptides (6). Second, we computed the values for Δσ^∗, defined as the difference between the shielding parallel to the ¹H-¹³C dipole and the shielding perpendicular to the dipole; this parameter was previously measured in solution for ubiquitin and calmodulin (15).

Fig. 3.

Agreement of fit ¹³Cα CST orientations with ab initio predictions and reconstructed Δσ^∗ values as a function of residue number. For most sites, fits are within 30° of the predicted orientation, within the maximum experimental error. (A) Experimental ¹³C CST orientations α₁, α₂, and α₃ (black dots) and (B) experimental orientations β₁, β₂, and β₃ (black dots) plotted against theoretical angles predicted by ab initio surfaces of Sun et al. assuming 2QMT crystal structure geometries. Blue lines indicate a deviation of ± 30°. (c) Reconstructed Δσ^∗ magnitudes. β-sheets sites range from 20–33 ppm and α-helical from -6–8 ppm, largely consistent with values reported by Tjandra and Bax.

Observed outliers, highlighted in Fig. 3, are K10, K28, K31, and V21. In the case of K10 and V21, the agreement is actually quite good when the dihedral angles from the 2GI9 crystal structure are used, suggesting these deviations might represent a real, small difference between the microcrystal formulation used and that from the 2QMT crystal structure. In the case of the helical lysines, the measured values fit regions of the ab initio surface that are within 15° of those found in the 2QMT structure. Overall, the greatest deviations between theory and experiment are for angles near 90°, a known weak region for tensor correlation experiments, and a disproportionate number of these angles are in the α-helix. It is possible that some effects not included in the ab initio calculations, such as the helix dipole, might make a contribution to the ¹³Cα shielding in this region, and such effects are indeed important in computing helical ¹⁵N shifts (45). This issue might be addressed in the future by implementing even stronger ¹³C (CST)-(¹⁵N-¹³C) correlations, by using ROCSA-REDOR type correlations.

The tensor magnitudes and orientations were used to reconstruct Δσ^∗ values, as measured in solution (Fig. 3C), reproducing the observed trends (14). Here, β-sheet Δσ^∗ values range from 20 to 33 ppm. The largest Δσ^∗ value is for K50, which has a positive value of ϕ in all available crystal structures, which is unusual for a nonglycine residue. Δσ^∗ values in the α-helix (residues 23 to 36) range from -6 to 8 ppm. Turns with near α-helical conformation exhibit near-helical values of Δσ^∗ but are slightly larger (by 2 to 3 ppm) as compared to those in the α-helix. Previously, it was observed that most Thr and Ser residues exhibited large negative values of Δσ^∗. This is not observed in the present dataset; however, only one Thr is in the α-helix (T25), making this finding inconclusive. The chemical shift of the Cβ of T25 is nearly identical to the Cα resonance frequency, so it is possible that there is some leakage to the Cβ resonance, which is partially labeled in the 2-¹³C-glycerol preparation, accounting for this effect.

GB1 Structure Refined with ¹³C Tensor Orientations.

A series of structures were generated using ¹³C CST tensor magnitudes and orientations as structural constraints in an Xplor-NIH calculation, following the protocol described previously (10). These structures were solved using combinations of seven different restraint force fields, each abbreviated using a single initial for simplicity; all calculations are summarized in Table 1. They include distances from spin diffusion or ¹H-¹H couplings (N) (34, 36), TEDOR distances (T) (35), TALOS dihedral angles (D), CST magnitudes (C) (10), CST orientations (O), vector angles (VEAN, V) (36), and semiempirical database potentials (SE) (46–48). When compared with structures without CST or VEAN information, the tensor-refined structures possessed higher precision and better agreement with the crystal structures than those computed without these restraints. In addition to better precision and accuracy of the lowest energy structures, all 200 structures refined with CST restraints had an overall bbrmsd of 0.23–0.5 Å, and agreement with the 2QMT crystal structure of 0.51 to 1.1 Å, depending upon the distance restraints used. In all cases, the 10 lowest energy structures (of 200 total structures generated) composed the structural ensemble.

Table 1.

Structural ensemble statistical agreement internally and against the closest related crystal structure

Restraints Used*								rmsd
Structure	N	T	D	C	O	V	SE	Backbone	vs. 2QMT	All Heavy Atom
1	X				X			0.40 ± 0.07	1.06 ± 0.05	1.07 ± 0.08
2	X		X	X	X			0.19 ± 0.04	1.02 ± 0.02	0.98 ± 0.04
3	X	X	X					0.19 ± 0.06	0.69 ± 0.03	0.68 ± 0.04
4	X	X		X	X			0.18 ± 0.03	0.60 ± 0.02	0.72 ± 0.03
5	X	X	X	X	X			0.15 ± 0.03	0.59 ± 0.02	0.71 ± 0.04
6	X	X	X	X	X	X		0.14 ± 0.03	0.57 ± 0.02	0.68 ± 0.03
7	X	X	X			X	X	0.19 ± 0.03	0.55 ± 0.01	0.71 ± 0.04
8	X	X		X	X	X	X	0.22 ± 0.03	0.57 ± 0.04	0.75 ± 0.04
9	X	X		X	X		X	0.18 ± 0.03	0.55 ± 0.02	0.71 ± 0.04
10	X	X	X	X	X		X	0.17 ± 0.06	0.54 ± 0.03	0.73 ± 0.03
11	X	X	X	X	X	X	X	0.16 ± 0.03	0.51 ± 0.02	0.72 ± 0.03

^*Abbreviations for restraints used: ¹H-¹H couplings/¹³C-¹³C DARR distances (N); TEDOR distances (T), TALOS dihedral angles (D), CST magnitudes (C), CST orientations (O), vector angles (V), semiempirical database potentials (SE).

To improve continuity of the spline function used to create the CST potential from the ab initio surfaces, and to eliminate any ambiguity from mirror symmetries of the CST orientations measurements, all angles were converted to the complement < 90°. This greatly improved the continuity of the constructed energy surface and thus the convergence of the annealing algorithm. In the first two calculations, distance tables from our previous CST structure refinement were used. In the first, only CST orientations and distances were used (NO) and in the second, CST magnitudes and TALOS dihedrals were added (NDCO). The bbrmsd for the NO structures was 0.4 Å, with an rmsd agreement of 1.06 Å with the 2QMT crystal structure. This is comparable in precision but a significant improvement in accuracy relative to the previously published NC structure (10). The inclusion of TALOS dihedral angles and CST magnitudes and orientations improved the resolution of the structure to 0.19 Å with comparable accuracy (1.02-Å agreement with 2QMT). If the CST magnitudes are removed (i.e., distances and CST orientations only) there was a negligible difference in the results; however, the comparable calculation lacking orientations (structure 4 of ref. 10) yields less precise structures. The major advantage of using orientations in this case is that they are independent of the tensor scaling and offset effects observed in the comparison of theoretical and experimental CST magnitudes; thus they are immune to common errors from—e.g., motional averaging and/or pulse sequence imperfections. In all cases, the structures with CST information improved upon structures solved with only distance information.

After these control structures were refined, to confirm the effectiveness of these restraints, more structures were generated using all of the restraint types defined above. These include highly precise distances from TEDOR (T) (49, 50), a technique already shown to greatly improve protein structures and described in detail elsewhere (35). A calculation including TALOS restraints and all available distances (NTD) produced a structure with a bbrmsd of 0.19 Å and an agreement with the 2QMT crystal structure of 0.69 Å. Once the CST magnitudes and orientations were added to the calculations (NTDCO), the bbrmsd improved to 0.15 Å, and the agreement with the 2QMT structure improved to 0.59 Å. Inclusion of VEAN restraints (NTDCOV) resulted in a slightly better structure (0.14-Å bbrmsd, 0.57 vs. 2QMT). A structure with all available distances and CST restraints (NTCO) showed a slight deterioration in statistical quality (0.18-Å bbrmsd, 0.60 vs. 2QMT) compared to the NTDCOV structure but still an improvement upon the NTD ensemble. We also found that allowing the calibration factors for the CST surface to vary during annealing gave slightly better results than using the previously calibrated conversion factors (though by at most 0.04 Å).

At this point, semiempirical Ramachandran database (46, 47) and hydrogen bonding energy database (SE) (48) potentials were included. This further improved the overall structural quality (0.16-Å bbrmsd, 0.51 Å vs. 2QMT) for the ensemble with all currently available restraints (NTDCOV-SE, Fig. 4). Removal of the vector angles (NTDCO-SE) or the CST restraints (NTDV-SE) yielded similar structures (0.17 Å/0.54 Å and to 0.19 Å/0.55 Å) in which the structure retaining CST information has slightly better agreement with the crystal structure, but the vector-angle structure has higher precision. Removal of TALOS and VEAN restraints (NTCO-SE) yielded a structure with 0.18-Å bbrmsd and 0.55-Å rmsd with 2QMT. Unlike TALOS (which relies upon a database of highly resolved X-ray structures), there is no explicit or implicit biasing toward favorable regions of Ramachandran space in the CST restraints presented here. Thus, it appears that employing the RAMA potential with CST restraints yields the closest accord with the X-ray results. This could of course indicate bias toward the X-ray results through the use of semiempirical database potentials; however, since the results of these calculations also exhibit the best overall agreement with all experimental restraints, this possibility seems remote. The structures (4, 8 and 9) with CST restraints, but without TALOS, exhibit improved accuracy over the structure (3) solved using only TALOS to restrain dihedral geometry. The TALOS restraints improve the convergence properties of calculations but are not required in the final stages of refinement.

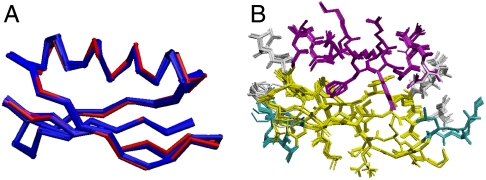
Fig. 4.

GB1 structure calculated using all CST information, vector angles, TALOS dihedrals, and all distances. (A) The 10 lowest energy structures (out of 200) are presented in blue with 2QMT crystal structure represented in red; bbrmsd = 0.16 Å and agreement with 2QMT is 0.51 Å. (B) The lowest 10 energy structures are presented in CPK to illustrate the overall heavy atom order. The all heavy atom rmsd is 0.72 Å.

The quality of each structure was evaluated using several metrics. First, the internal consistency defined by the backbone and all heavy atom rmsds, followed by the agreement of each ensemble mean to the most relevant crystal structure (Table 1) were determined. Second, each structural ensemble was evaluated with PROCHECK_NMR (51). We report four metrics: regions of Ramachandran space populated by percentage, the average χ¹ and χ² deviations, and hydrogen bonding energy (Table S3). The χ¹ and χ² deviations present further evidence of overall improvements in structure quality, serving as a cross validation to illustrate that improvements in backbone geometry lead to tighter overall folds and improved geometries. Third, we determined the overall agreement of each ensemble with both CST (Table S4) and vector angle (Table S5) restraints. Finally, shifts were generated for each structure using the chemical shift prediction program SPARTA (52) and compared to the experimentally measured chemical shifts (Table S6). In all cases, these analyses indicated that all structures were highly consistent with one another having backbone resolution comparable to X-ray structures of 1.0–2.0-Å resolution. Not only do these SSNMR structures exhibit excellent structure validation metrics, the agreement of our highest-resolved structure with the 2QMT crystal structure is on the order of agreement among the four deposited crystal structures of GB1 (Table S7).

During these calculations, violations in several previously published distance, TEDOR, and TALOS dihedral restraints were identified and relaxed. In total, 20 TALOS error bars were doubled at some point during the calculations (though only 10 of the original restraints would have violated in the best final structures, within the originally published uncertainties), and the error estimates for 11 spin diffusion, 2 ¹H-¹H, and 26 TEDOR distances were increased. The TEDOR distances that violated had predicted error bars of 0.5 Å or less, and were lengthened by 1 Å. Most often, these restraints violated in the direction of geometries in agreement with the 2QMT crystal structure. These altered restraints are given in Tables S8 and S9.

¹⁵N CST Magnitudes and Orientations.

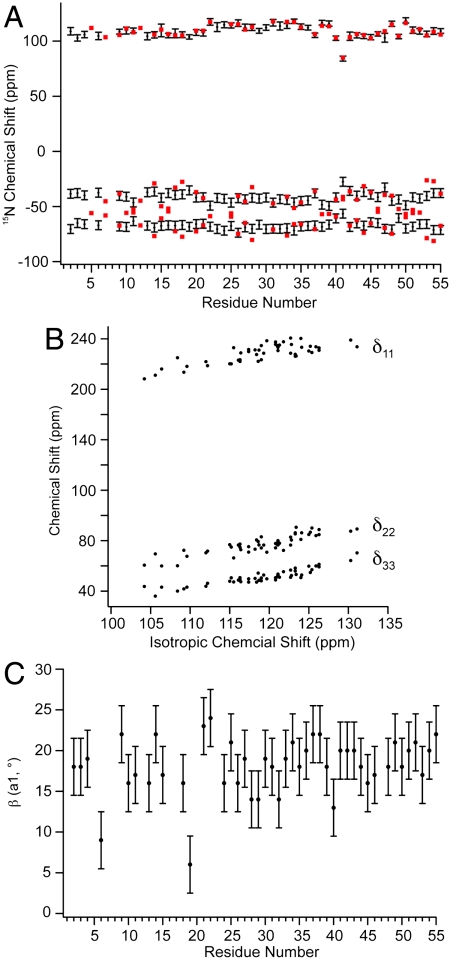
The magnitudes of the principal elements of the ¹⁵N tensors are presented in Fig. 5A (and Table S2). Agreement between these measured values of δ₁₁ (δ₁₁ = δ + δ_iso in this instance) and our previous slow-MAS study (depicted in red in Fig. 5A) showed an rmsd between the two datasets of 1.6 ppm and an R² of 0.95. The tensor anisotropy was larger for the α-helical residues than for the β-sheet residues, as found also in thioredoxin (53). Similarly, the measured values of η (the tensor anisotropy) were slightly smaller in α-helical (η = 0.23) than in β-sheet residues (η = 0.27). Plotting each tensor element (in the “full” representation) vs. the isotropic chemical shift reveals that, unlike C′ tensors, ¹⁵N isotropic chemical shift perturbations result from concerted shifts of all tensor elements rather than large shifts of a single element (Fig. 5B). The most deshielded ¹⁵N shift tensor element, δ₁₁, is oriented 9–24° from the ¹H-¹⁵N bond (Fig. 5C), δ₂₂ is approximately 97° ± 12° from the ¹H-¹⁵N vector and δ₃₃ is oriented near the N-Cα bond, in or within 10° of the peptide plane (approximately 75° ± 12° from the ¹H-¹⁵N bond). All CST orientations are shown in Table S2 and are in good accord with recent ab initio studies (45). Of particular interest is the observation that our tensor measurements indicate the ¹⁵N tensor deviates from ideal prolate symmetry, with η ranging from 0.15 to 0.32. Our original hypothesis was that this discrepancy between our data and other studies might result from the high covariance between relaxation and η when η <  ∼ 0.5. However, recent density functional theory calculations of ¹⁵N CSTs in the α-helix of GB3 by Cai et al. (45) agree well with all of our tensor elements (Fig. S8A), (R² = 0.99 and rmsd of 6.5 ppm) and a recent solution NMR study presents even larger tensor asymmetry (54). It should be noted that δ₂₂ and δ₃₃ are significantly smaller in magnitude than δ₁₁ in the traceless representation, leading to greater uncertainty in the fitted orientation. The smaller magnitudes of δ₂₂ and δ₃₃ in the traceless representation, and their near perpendicular orientation to the ¹H-¹⁵N vector, suggest that uncertainties in the magnitude of these elements might be inconsequential for most solution NMR relaxation studies but might be more important in the interpretation of PISEMA spectra, making a better understanding of these tensors (especially in α-helical conformations) of interest. Recent solution NMR work also reveals strong statistical agreement with our results (Fig. S8B) for the full tensor, albeit with some outliers.

Fig. 5.

Amide chemical shift tensor analysis for protein GB1. (A) Principal elements of ¹⁵N tensor in the traceless representation compared to previously published slow-MAS data. Principal elements are presented in black with error bars corresponding to one standard deviation. Tensor values from previous work are presented in red. The rmsd between δ₁₁ elements from both datasets is 1.6 ppm, and 6 ppm for δ₂₂ and δ₃₃ values corresponding to a deviation of η of 0.13. (B) Chemical shift tensor elements plotted against isotropic chemical shift. The correlation reveals that the changes in the isotropic chemical shift result from largely correlated shifts of all three principal elements. R² for each element (δ₁₁, δ₂₂, δ₃₃) are 0.82, 0.75, and 0.62, respectively. (C) The angle β (a1) as a function of residue number. The angle β defines the orientation of the δ₁₁/δ_zz tensor element to the HN bond dipole.

Conclusions

The chemical shift tensors of all ¹⁵N and ¹³C sites in a protein report upon a vast range of molecular properties, including electronic structure, backbone conformation, steric clashes, electrostatics, side-chain packing, and dynamics. Specifically, a detailed knowledge of backbone amide and Cα tensors is relevant to an increasing range of structural and dynamics work throughout NMR and structural biology in general. In this paper, we have provided a unique example of the determination of ¹³Cα and ¹⁵N chemical shift tensor magnitudes and orientations throughout a protein, using SSNMR tensor correlation techniques. As a first example of their utility, ¹³Cα CST information was used to refine the structure of a 6-kDa protein. The ¹³Cα shift tensor orientations are in good accord with ab initio quantum chemical prediction and provide an important parameter with which to refine SSNMR structures not currently available from experimental databases. These methods complement already established tensor refinement methods in SSNMR and further the pursuit of atomic-resolution structure determination by SSNMR. Validation of these structures reveals a quality on par with 1-Å X-ray structures. The experimental backbone amide tensors are in accordance with recent density functional theory predictions of tensor orientations in the helical residues of GB1, illustrating the importance of such measurements to macromolecular electronic structure calculations.

The methodology and information described here lays the groundwork for future CST studies determining both the structure and dynamics of a range of systems. Overall, we have established that SSNMR is a powerful tool for readily measuring important tensor quantities with site-resolution without the need for conservative mutagenesis and multiple molecular alignments. These results were achieved by using three-dimensional spectroscopy and, in principle, can be implemented on much larger systems given that spectrometers operating at twice the field used in this work are now available. Now that precise orientations and magnitudes have been determined for a range of residue types and secondary structural motifs, future structural work might include static ¹³Cα spectra of oriented samples as a complement to the well-established PISEMA experiment. In addition, now that more tensor orientation information is known, the chemical shift can be incorporated into an even wider array of relaxation/dynamics measurements in solution NMR.

Materials and Methods

Sample Preparation.

Samples of GB1 were prepared using 2-¹³C-glycerol as the ¹³C source in the minimal growth media. Protein was precipitated as described previously and packed wet into the central 80% of a limited-speed (thin wall) 3.2-mm Varian rotor (Varian, Inc.).

NMR Spectroscopy.

All spectra were acquired using a 500-MHz Varian InfinityPlus spectrometer and 3.2-mm T3 Balun™ ¹H-¹³C-¹⁵N probe. Pulse widths (π/2) for ¹H, ¹³C, and ¹⁵N were 1.9 μs, 2.5 μs, and 5.0 μs, respectively. Spinning was maintained at 11.111 ± 0.002 kHz. Periods recoupling ¹H-¹⁵N/¹³C dipoles and ¹⁵N/¹³C CST line shapes were inserted into a 3D experiment using an NCA plane for site resolution, following the model used in our previous studies. Dipolar recoupling was achieved using the recoupling element and CST interactions were recoupled using ROCSA. Optimal resolution and sensitivity of the ¹⁵N-¹³C planes were achieved using SPECIFIC CP and TPPM decoupling during acquisition with approximately 75 kHz B₁ on ¹H. Eleven total spectra were acquired: one each for the ¹⁵N and ¹³C CST, the ¹H-¹⁵N and ¹H-¹³C dipoles, and seven dipole-CST correlated spectra. In these spectra ROCSA and dipolar dimensions were evolved synchronously in the same dimension, with different ratios of evolution time, in units of rotor periods. [¹H-¹⁵N]∶[¹⁵N CST] ratios included 1∶1, 2∶1 and 1∶2. [¹H-¹³C]∶[¹³C CST] ratios included 1∶1, 1∶2, and 1∶3. In addition a ¹³C CST recoupling experiment was performed where ¹⁵N was not decoupled, providing coevolution of the ¹³C CST and ¹³C-¹⁵N dipolar Hamiltonians.

Data Analysis.

All eleven spectra were processed using NMRPipe. Lorentzian-to-Gaussian apodization functions were applied in the two isotropic chemical shift dimensions, with a net line broadening of 30 Hz for ¹³C and 15 Hz for ¹⁵N. Peak intensities in each ¹⁵N-¹³C (F1–F3) plane were determined and trajectories of each correlation spectrum (t₂) extracted using the autoFit.tcl package in NMRPipe. All trajectories for each site were fit to exact spin simulations assuming a 2 spin basis. A subset of each experimental set were tested using a basis with all ¹H within 2.5 Å; however, this only impacted the relaxation matrix and had little to no impact upon the fit angles and dipolar magnitudes. The fitting procedure was facilitated by in-house FORTRAN-77 code that called both external MINUIT minimization libraries (55), and the SPINEVOLUTION (56) simulation package.