Abstract
Clinical analysis of acute viral infection in blood requires the separation of viral particles from blood cells, since the cytoplasmic enzyme inhibits the subsequent viral detection. To facilitate this procedure in settings without access to a centrifuge, we present a microfluidic device to continuously purify bionanoparticles from cells based on their different intrinsic movements on the microscale. In this device, a biological sample is layered on top of a physiological buffer, and both fluids are transported horizontally at the same flow rate in a straight channel under laminar flow. While the micron sized particles such as cells sediment to the bottom layer with a predictable terminal velocity, the nanoparticles move vertically by diffusion. As their vertical travel distances have a different dependence on time, the micro- and nanoparticles can preferentially reside in the bottom and top layers respectively after certain residence time, yielding purified viruses. We first performed numerical analysis to predicate the particle separation and then tested the theory using suspensions of synthetic particles and biological samples. The experimental results using dilute synthetic particles closely matched the numerical analysis of a two layer flow system containing different sized particles. Similar purification was achieved using diluted blood spiked with human immunodeficiency virus. However, viral purification in whole blood is compromised due to extensive bioparticle collisions. With the parallelization and automation potential offered by microfluidics, this device has the potential to function as an upstream sample preparation module to continuously provide cell depleted bio-nanoparticles for downstream analysis.
INTRODUCTION
Clinical diagnosis of acute viral infection in blood requires purifying viral particles from blood cells, considering the inhibitory effect of the cytoplasmic content to the subsequent nucleic acid amplification reactions. In clinical laboratories, this task is routinely handled by centrifugation, while diagnosis at the point of care demands simple assays without access to bulky instruments. Although manual1 or CD format2, 3, 4 centrifuges have been recently reported, it is still non-trivial to integrate them into micro total analysis systems.
Alternatively, microfluidic plasma or viral extractors based on non-centrifugal mechanisms have been actively explored in research laboratories. Passive filtration devices, including micro-fabricated planar filter5, 6, 7, 8, 9 or embedded membranes,10 purify plasma components from blood cell through size exclusion. However, they have a limited throughput and are prone to clogging or red blood cell (RBC) lysis. Biomimedic devices with bifurcation structures11, 12 or expanding channels13, 14 exploit the plasma skimming effect to separate cells from plasma, but only a small fraction of plasma can be extracted since the cell free plasma layer is usually very thin. Other hydrodynamic devices such as deterministic arrays,15 inertial focusing channels,16, 17 and microgroove structures18, 19 have been created to sort cells, but very few of them have been optimized to purify nanoparticles in blood. In addition, external electromagnetic fields have been implemented in microchips to induce bulk electrohydrodynamic flow,20 move RBC in a magnetic gradient,21 or physically immobilize blood cells through dielectrophoresis,22 but the extensive accessories to generate high fields and∕or the requirement to pre-treat blood samples limit their applications. Magnetic activated particle sorting23, 24 after tagging the target species with magnetic beads purify and concentrate viral particles effectively, while it still faces the challenge of extensive manual handling and low throughput for point of care uses.
In this paper, we present a simple, two-layer microfluidic device to continuously purify viruses from blood cells with a high yield of the target virus. This device takes advantage of the different intrinsic movements of micron- and submicron-sized bioparticles on the microscale. While blood cells sediment in a physiological solution with a predictable terminal velocity, submicron-sized viral particles move around by diffusion. Since the two movements have different dependence on time, when a biological sample is layered on top of a buffer solution, the two species can preferentially separate in the vertical direction. Continuous sample processing is achievable in a microfluidic environment when both the biological sample and the supporting buffer are convected in a laminar flow that does not interfere with the intrinsic particle transport. We first performed numerical analysis to predicate the separation effect for different sized particles and then validated the model using suspensions of synthetic particles and diluted blood containing HIV viruses. The continuous operation mode and the parallelization capability offered by microfluidics make this design compatible with high throughput applications. Another advantage of the device is the high yield of the target nanoparticles, always greater than 50% determined by the nature of diffusion. These properties make this device appealing to purify circulating viral particles existing in a low concentration or in a small sample volume. With the automation potential of lab-on-a-chip type of devices, this viral separation design can function as an upstream sample preparation module to continuously provide cell depleted bionanoparticles at the point of care for downstream analysis.
MATERIALS AND METHODS
Materials
Ethanol (200 proof), glass coverslips, hemacytometer, and microslide fieldfinder were obtained from Fisher Scientific (Fair Lawn, NJ). For microfluidic chip fabrication, SU-8 photoresist and developer were purchased from MicroChem (Newton, MA). Silicone elastomer and curing agent were from Dow Corning (Midland, MI). Phosphate buffered saline (PBS) was obtained from Mediatech (Herndon, VA). Lyophilized bovine serum albumin (BSA) and sodium dodecyl sulfate (SDS) were from Aldrich Chemical Co. (Milwaukee, WI). Polystyrene spheres 5 μm in diameter internally dyed with Firefli™ Fluorescent Green (Ex 468∕Em 508 nm) and 100 nm in diameter internally dyed with Firefli™ Fluorescent Red (Ex 542∕Em 612 nm) were purchased from Thermo Scientific (Fremont, CA). HEK 293T∕17 cells were obtained from ATCC (Manassas, VA). The four plasmids used to produce HIV viral particles were generously provided by three laboratories: the pJR-FL plasmid encoding HIV envelope (R5 stain) was from Dr. Dan Littman at New York University; the pGag-eGFP plasmid to produce the viral capsid protein was from Dr. Marilyn Resh of Memorial Sloan-Kettering Cancer Center; the pcRev (originally constructed by Dr. Bryan Cullen of Duke University) and HIV-1 based packaging vector pR8ΔEnv lacking the env gene (originally constructed by Dr. Didier Trono of the École Polytechnique Fédérale de Lausanne) were from Dr. Gregory Melikian at the Institute of Human Virology in the University of Maryland. The HIV p24 enzyme-linked immunosorbent assay (ELISA) kit from Perkin Elmer (Waltham, MA) was used to determine the viral concentration. Fresh human blood from healthy donors was obtained from Lehigh Valley Health Network (Allentown, PA) following an IRB protocol approved by Lehigh University.
Chamber design and fabrication
PDMS microfluidic devices were fabricated (Fig. 1) using the standard soft lithography technique. First, SU-8 photoresist was patterned on a silicon wafer by photolithography to form a negative mold. Next, a 10:1 mixture of poly(dimethylsiloxane) (PDMS) prepolymer and curing agent was poured onto the mold and baked at 70 °C until cured. After cutting and removing the PDMS channels from the SU-8 mold, a top channel was carefully aligned with a bottom channel and the two were bonded permanently through oxygen plasma at a forward power of 50 W and pressure 100 mT above the base pressure for 30 s. The channels were then blocked with 1% BSA in PBS to reduce nonspecific binding on the channel walls before further experiments.
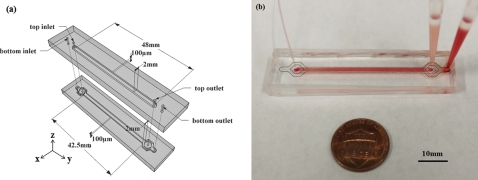
Figure 1.
Schematic illustration of the device structure with labeled dimensions (a) and a photograph showing the device in action (b). The device contains two layers of microchannels: the biological sample is injected into the top layer and a carrier buffer is injected into the bottom to allow the separation of the cells versus viral particles by their intrinsic movements. In the photograph, the dark dash line outlines the bottom layer channel and the light dash line outlines the top layer channel.
The overlapping channel of the two layers has a dimension of 2 mm × 42.5 mm × 100 μm (width × length × height) (Fig. 1). The inlet of the bottom channel branches so that the islands in between support the top layer sample flow before it is layered on the bottom cushion buffer. The same branch at the bottom layer outlet allows separate collection of the outflow from two different vertical layers. The flow resistance at the branch region is low compared to that of the main channel, so similar amount of fluid exits from the two layers, as observed in our experiments. COMSOL simulations revealed similar distribution of particle concentration in channels of various dimensions but comparable convection velocity, while the throughput is proportional to the channel width. The width to height ratio was selected here to provide a reasonable throughput while avoiding significant PDMS sagging.
Production of HIV particles
The HIV particles were produced by transfecting HEK293T∕17 cells with four plasmids as described before.25 Briefly, HEK 293T cells on a 6 cm dish were transfected with 7.2 μg pGag-eGFP, 48 μg pJR-FL, 12 μg pcRev, and 24 μg pR8ΔEnv using the calcium phosphate protocol. Transfected cells were kept in a CO2 incubator for 48 h, and the supernatant medium was collected, briefly centrifuged to remove cell debris, and passed through a 0.45 mm filter. The viral suspension was then aliquoted and stored at −80 °C. The infectivity of the HIV viruses was also determined using the β-Gal assay, as described before, to confirm the transfection success.25
Particle separation using synthetic beads
To demonstrate the principle of particle separation based on their intrinsic movements in the vertical direction, single particle suspensions containing either 5 μm polystyrene microbeads or 100 nm polystyrene nanobeads were introduced into the top inlet at different flow rates (3, 6, 10, 15, 20 μl∕min) using a syringe pump (Chemyx Inc. Fusion 400, Stafford, TX). The particles were diluted in PBS∕0.3% SDS to a final particle concentration of 0.2% (v∕v). This concentration of SDS was found to maintain a dispersed state of the nanoparticles through light scattering analyses (data not shown). Particle free PBS∕0.3% SDS was injected into the bottom inlet at the same flow rate. The outflow was collected from the top and bottom outlets individually. The particle concentration was determined by optical absorbance at 470 nm for the microbeads and 545 nm for the nanobeads, respectively, using a UV-Vis spectrometer. These two wavelengths matched the excitation wavelengths of the fluorophores embedded in the particles and the absorbance was found to correlate linearly with the particle concentration in the suspension (data not shown). Since the flow resistances in the two layers are comparable, similar outflow volumes were expected from the two outlets. When the outflow volumes from the two outlets differed by over 20%, the samples were discarded since obstruction inside the device could lead to chaotic flow and significant sample mixing that compromised the separation.
Separation experiments using biological samples
To mimic a blood sample from a subject of viral infection, lab stocks of HIV viruses were spiked into whole blood or 10 times diluted blood by PBS. We also diluted the HIV stock in bare PBS containing 1% BSA. The final viral concentration was ∼105 HIV virions∕mL in all cases. The biological sample was injected into the top inlet of the device at a flow rate of 3 or 6 μl∕min, which correlated to sufficient residence time to deplete red blood cells from the top layer. The supporting layer injected from the bottom inlet was PBS for experiments involving blood or PBS∕1%BSA for experiments with bare HIV. After collecting the outflow from the top and bottom outlets individually, cells were counted manually under an optical microscope using a hemocytometer and HIV viral concentration was determined using a commercial p24 ELISA kit. The p24 protein comprises the viral capsid and its concentration directly relates to the viral concentration.26
Numerical analysis
COMSOL Multiphysics software (COMSOL Inc., Burlington, MA) was utilized to simulate the concentration change of a source containing a diffusive solute in contact with a solute-free drain. A “Transport of Diluted Species” model was used. The model was set up where both layers were 100 μm thick and 2 mm wide. The top and bottom faces (z = 0 and z = 200 μm) of composite structure were considered no-slip boundaries. The density and viscosity of both layers were set to be 1 g∕cm3 and 0.001 Pa · s. The diffusion coefficients of the solute were calculated using the Stokes-Einstein relation for nano-species of different sizes (Eq. 2). To observe the concentration evolution with time, both layers were set to move in the y direction at an average velocity of 0.45 mm∕s. Fluid flow was assumed to be steady state, and incompressible, and inertia was neglected. The flow was laminar and fluid velocity in the y direction was not expected to interfere with the intrinsic diffusion of a diluted solute in the z direction. A triangulated mesh of roughly 3.6 × 106 elements was used to ensure solver accuracy.
Statistics and data analysis
All experiments were repeated in at least 3 different devices. The averages were shown in the figures, and each error bar represented the standard deviation of the mean.
RESULTS AND DISCUSSION
Numerical analysis of intrinsic micro- and nanoparticle transport
Bioparticles in a static suspension undergo two intrinsic movements, sedimentation from gravity and diffusive random walk. When the gravitational force, buoyant force, and drag force are balanced in the z direction, sedimentation of a spherical object moving with a low Reynolds number is characterized by the terminal velocity
| (1) |
where g is acceleration of gravity, d is diameter of the sphere, μ is fluid viscosity, ρm is density of the sphere, and ρ is density of the fluid. The settling distance of a sphere in the stead state is Vtt. The diffusion coefficient of a spherical particle through a liquid of low Reynolds number is characterized by the Stokes-Einstein relation
| (2) |
where kB is Boltzmann’s constant, T is temperature, μ is fluid viscosity, and r is particle radius. Using the random walk theory, the diffusion length of a sphere is estimated as .
To determine which intrinsic transport process dominates for a suspended particle of a particular size, Péclet number, Pe, is calculated
| (3) |
where U is terminal velocity, L is a characteristic length, and DAB is the particle diffusion coefficient. Using a characteristic dimension of 100 μm (thickness of the biological sample layer tested in the experiments below), solution density of 1 g∕cm3, particle density of 1.05 g∕cm3 (lower limit for biological particles), and solution viscosity of 0.001 Pa · s, Pe for different sized bioparticles under intrinsic movements of sedimentation and diffusion were calculated and shown in Table TABLE I..
Table 1.
Calculated Péclet numbers for typical biological particles of different sizes under intrinsic movements of sedimentation and diffusion. The terminal velocity and diffusion coefficient were calculated using Eqs. 1, 2 in the text. The parameters used for the calculations are as follows: characteristic length = 100 μm (thickness of the biological sample layer tested in the experiments below), solution density = 1 g∕cm3, bioparticle density = 1.05 g∕cm3 (lower limit for cells and viruses), solution viscosity = 0.001 Pa · s, and temperature = 296 K.
| Species | Cells | Cells | Platelets | Viruses and exosomes | Proteins | ||
|---|---|---|---|---|---|---|---|
| Diameter of beads | 10 μm | 5 μm | 1 μm | 100 nm | 50 nm | 20 nm | 5 nm |
| Terminal velocity (nm∕s) | 2722.2 | 680.6 | 27.2 | 0.3 | 7.5 × 10−2 | 1.2 × 10−2 | 7.5 × 10−4 |
| Diffusion coefficient (m2∕s) | 4.39 × 10−14 | 8.78 × 10−14 | 4.39 × 10−13 | 4.39 × 10−12 | 8.78 × 10−12 | 2.20 × 10−11 | 8.78 × 10−11 |
| Péclet number | 1033.4 | 129.1 | 1.0 | 1.1 × 10−3 | 1.4 × 10−4 | 9.1 × 10−6 | 1.4 × 10−7 |
The distinct Péclet numbers for cells and bionanoparticles indicate that their intrinsic movements are dominated by different transport processes. Specifically, the Péclet number is much greater than 1 for blood cells a few micrometers in diameter, i.e., their movements are dominated by sedimentation in a medium with density and viscosity comparable to water. For typical blood cells 6–9 μm in diameter and having a density of 1.05–1.1 g∕cm3 suspended in PBS, the terminal velocity is found to be in the range of 0.98–4.41 μm∕s. While it takes ∼10−4 second for blood cells to reach the terminal velocity,27 this duration is very short compared to the sample residence time in our experiments and is neglected in the following analyses. Thus, when a diluted suspension of cells is layered on top of a buffer cushion, the cell concentration will decrease linearly with time in the original sample (Fig. 2d).
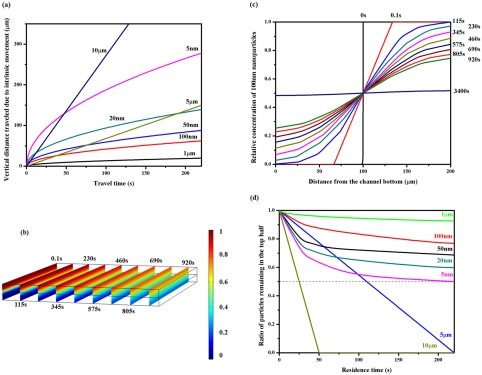
Figure 2.
Numerical analysis of the concentration change for different sized particles in a two layer structure. (a) Vertical distance traveled by bioparticles of various sizes in water due to intrinsic movements. The travel distances were calculated using the sedimentation or diffusion equations presented in the text. (b) COMSOL simulation showing the concentration evolution for a two layer structure where a suspension containing a diffusive solute was layered on a carrier fluid. The solute diffusion coefficient was set to be 4.39 × 10−12 m2/s, corresponding to that of the 100 nm particles in water. The density and viscosity of the medium was set to be 1 g/cm3 and 0.001 Pa · s. The convection velocity in the y direction was set to be 46 μm/s so the concentration profiles after different contact time could be plotted. The color indicates the relative concentration and the slices correspond to various time points post initiation of diffusion. The diffusion times were labeled next to the slices. (c) The concentration profile along the z direction dissected from (b) with the diffusion time labeled on the right. It takes over 3400 s for 100 nm particles to reach the concentration equilibrium in the simulated geometry. (d) COMSOL simulation showing expected particle concentration remaining in the top layer at different time points. A ratio of 0.5 (dashed line) indicates no preferential particle residence. The numerical analysis suggests that bioparticles with diameters of 5–10 μm sediment to the bottom layer in ∼200 s while over 50% of the nanoparticles remain in the top layer. The relative nanoparticle concentration remaining in the top layer depends on its size or diffusion coefficient.
On the other hand, nanoparticles on the order of 100 nanometers in diameter or smaller have a Péclet number much smaller than 1, suggesting their intrinsic movements in a physiological solution is mostly diffusive. We calculated the diffusion coefficients of a few nanoparticles with biologically relevant sizes (Table TABLE I.) using the Stokes-Einstein relation. Next, we set up a COMSOL model in which a source suspension containing a diffusive solute was layered on top of a drain free of solute, both fluid layers being 100 μm thick. The concentration evolution in the two layer structure was then simulated as a function of time. Fig. 2b demonstrates the cross-sectional concentration maps in the composite structure at various time points post the initiation of contact using the diffusion coefficient calculated for 100 nm particles in water. Fig. 2c shows the vertical concentration change for 100 nm spheres extracted from the middle plane along the flow direction in Fig. 2b. It is clearly observed that equilibrium is not reached before 3400 s for 100 nm spheres to diffuse through a 100 μm thick drain. The nanoparticles preferentially locate in the source region before they homogenize in both layers. The concentration curves were then used to calculate the ratio of nanoparticles remaining in the source layer. Similar operation was performed using diffusion coefficients corresponding to different sized nanoparticles, and Fig. 2d summarizes their concentration drop from the source layer with time. For comparison, the concentration changes for cell sized particles in the top half are included in the same figure.
Comparing their concentration behavior in the two layer geometry, it was observed that the concentration of cell sized particles drops faster in the top layer than nanoparticles, as long as the residence time is beyond the cross point (Fig. 2d). For 100 nm particles, the cross point is about 1 s. For a residence time of ∼200 s, >90% of 5 μm spheres settle to the bottom layer, while the concentration of 100 nm particles in the top 100 μm layer only dropped by 20%. Thus, bionanoparticles around 100 nm in diameter can be purified from cells with a significant yield using the simulated geometry based on intrinsic particle transport. It should be pointed out that the above analysis is over-simplified since particle interactions were neglected; thus, it is only applicable to dilute suspensions. Nonetheless, it provides useful insight into intrinsic particle movement on the microscale. We next implemented a microfluidic chip to test the theoretical analysis using synthetic and biological particles.
Experimental results
Separation of synthetic nanospheres from microspheres
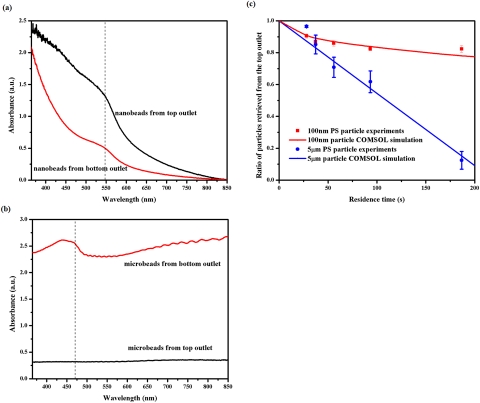
To test the numerical analysis described above, we constructed a microfluidic chip in which a biological sample was layered on top of a support fluid to purify viral particles from cells based on their intrinsic movements in the vertical direction. The purpose of the support fluid was to carry away cells but kept most of the viral particles in the top layer sample. Both layers were 100 μm thick, similar to the simulated structure. The two layer sample was also horizontally transported in a laminar flow to allow continuous sample processing. The Reynolds number was <0.045 for all the flow rates tested in our work; thus, the convection was not expected to significantly influence the intrinsic vertical movement of the particles in a dilute suspension. We first used suspensions containing polystyrene spheres either 5 μm or 100 nm in diameter diluted in PBS∕0.3% SDS at a particle concentration of 0.2% (v∕v). The particle sizes were selected to mimic blood cells and HIV viral particles, respectively. The density of the polystyrene beads, 1.05 g∕cm3, is on the low end of the cell density range (1.05–1.1 g∕cm3), so they represent the population with a slow sedimentation rate. The suspension was injected into the top inlet, while an identical buffer containing no sphere was used as a carrier solution in the bottom layer. The flow rates for both layers were the same at 20, 15, 10, 6, or 3 μl∕min, and the corresponding sample residence times in the device were 28, 37, 56, 93, or 187 s. The outflows from the top and bottom halves were collected, and the particle concentration was determined by suspension absorbance at 470 nm for the microspheres and 545 nm for the nanospheres (Fig. 3a, 3b). The ratio of particles remaining in the top layer at various residence time points was plotted in Fig. 3c. It was observed that the concentration of 5 μm microspheres decreased nearly linearly in the original sample (circles in Fig. 3c), while the concentration of 100 nm nanospheres decreased gradually, following a diffusive behavior (squares in Fig. 3c). In both cases, the change of particle concentration in the top layer closely matched the prediction from COMSOL simulation (lines in Fig. 3c). At a residence time of 187 s, the concentration of microspheres dropped to <10% in the top outflow, but >80% of the nanospheres was retrieved from the same outlet. When microbeads and nanobeads were mixed together at a total particle concentration of 0.2% and introduced from the top outlet, comparable separation result was observed visually, while it was difficult to quantify the two species independently due to their overlapping UV-Vis absorption spectra. Another limitation of the analyses using synthetic particles was the adhesion of polystyrene spheres to the PDMS floor at a flow rate lower than 3 μl∕min, despite the use of SDS. Thus, no residence longer than 187 s, which corresponds to the flow rate of 3 μl∕min, was tested, although longer residence time was expected to further improve the nanosphere purity with only a slight drop in the yield.
Figure 3.
Representative UV-Vis absorption spectra of (a) nanoparticle and (b) microparticle suspensions retrieved from the microchip at a flow rate of 3 μl/min. The 100 nm polystyrene nanoparticles were labeled with Firefli™ Fluorescent Red (Ex 542/Em 612 nm) and 5 μm polystyrene microparticles were labeled by Firefli™ Fluorescent Green (Ex 468/Em 508 nm). Suspensions containing a single type of synthetic particles were injected into the top inlet of at 3 μl/min. The outflow from the top and bottom outlets were analyzed by UV-Vis spectroscopy and repetitive spectra are presented. The absorbance at 545 nm for nanoparticles and 470 nm for microparticles were used to quantify their concentrations since they correlated linearly with the particle concentration. Similar spectra were acquired for other flow conditions. (c) Experimental data (solid dots and solid squares) showing the ratio of particles retrieved from the top outlet at different residence time points. PBS/SDS solutions containing either 5 μm or 100 nm polystyrene particles were injected into the top inlet and particle free PBS/SDS solution was injected into the bottom inlet. The two layers had identical flow rates of 20, 15, 10, 6, and 3 μl/min, and the particle residence time in the devices were calculated for the plot. Each data point was repeated in at least 3 devices, and error bars represent standard deviations from these repeats. The experimental measurements closely matched results from COMSOL simulation (blue and red lines).
Separation of HIV viral particles from blood cells
Following the success in synthetic particle separation, we then spiked HIV viruses into healthy donor’s blood to mimic a blood sample from an HIV infected subject. Red blood cells (RBCs), the most abundant cell species in blood, have a density of ∼1.09–1.1 g∕cm3 and a terminal velocity of ∼2.45 μm∕s in PBS buffer. The sedimentation rate of RBCs in plasma is slowed down to 1.63 μm∕s due to higher viscosity (1.2 Pa · s) and density (1.025 g∕cm3) of plasma.28 Even so, it should only take RBCs ∼60 s to settle 100 μm. Thus, the two flow rates of 6 and 3 μl∕min, corresponding to residence times of 93 and 187 s, were selected to separate blood cells from HIV viral particles.
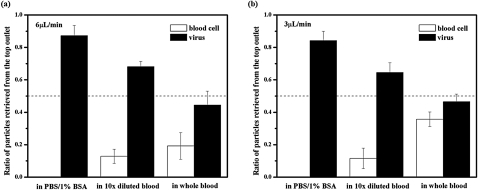
First, we spiked HIV particles in blood diluted ten times in PBS and injected it into the top inlet of the device. The carrier buffer in the bottom layer was PBS. As shown in Fig. 4, when both layers were flowed at 6 μl∕min (residence time 93 s), nearly 90% of the blood cells moved out of the top layer, while nearly 70% of HIV particles remained in this layer. At a slower flow rate of 3 μl∕min or a residence time of 187 s, both the blood cell and viral concentration in the top layer dropped slightly. As a control, we also diluted the HIV stock using PBS∕1% BSA and injected it into the top inlet of the device. In this case, the carrier buffer was PBS∕1% BSA. In the absence of blood cells, 87.3 ± 6.3% and 84.2 ± 5.8% of viral particles remained in the top layer under a flow rate of 6 μl∕min and 3 μl∕min, respectively. The compromised viral yield in 10× diluted blood is likely a result of collisions with cells, which accelerates nanoparticle mixing in the vertical direction. In addition, collisions between cells also hamper their unidirectional settling.29 As a result, cell contamination was found in the top layer despite sufficient residence time for red blood cells to completely settle out of this layer in theory. Switching the biosample to the bottom layer while flowing the buffer from the top inlet may improve the purity of virus retrieved from the top outlet, but the maximum yield is expected to drop to 50% accordingly.
Figure 4.
Relative ratios of blood cells and HIV viral particles retrieved from the top outlet. The biological samples were injected into the top inlet and PBS (for experiments containing blood) or PBS/1% BSA (for blood free experiments) was injected into the bottom. Both layers had identical flow rates of either 6 μl/min (a) or 3 μl/min (b). (a) At a flow rate of 6 μl/min, 87.3 ± 6.3% of HIV viral particles were retrieved from the top outlet in the absence of blood cells. When HIV particles were spiked in blood diluted ten times by PBS, 68.2 ± 3.3% of viruses and 12.8 ± 4.4% of blood cells were retrieved from the top outlet. In whole blood, 44.4 ± 8.7% of viruses and 19.2 ± 8.2% of blood cells were retrieved from the top outlet. (b) When the flow rate was 3 μl/min for both layers, 84.2 ± 5.8% of HIV viral particles were retrieved from the top outlet in the absence of blood cells. When HIV particles were spiked in blood diluted ten times by PBS, 64.5 ± 6.0% of viruses and 11.6 ± 6.3% of blood cells were retrieved from the top outlet. In whole blood, 46.5 ± 4.7% of viruses and 35.7 ± 4.5% of blood cells were retrieved from the top outlet.
Accelerated nanoparticle mixing and disturbed cell sedimentation was further exaggerated in whole blood. When the top layer contained HIV spiked in whole blood, about 50% viral particles and 19% blood cells were retrieved from the top outlet for a residence time of 93 s. At a longer residence time of 187 s, the blood cell contamination from the top outflow increased to 30%. The even worse separation at slower flow rate was caused by unsteady convection. At 3 μl∕min, blood cell movement was often observed pulsatile in the device. This was likely a result of a significant increase of blood viscosity at low shear rates,30 which led to high flow resistance in the cell-rich region and unpredictable flow patterns. Besides particle collisions, another factor that may contribute to the poor separation in whole blood is the unmatched density between plasma and the bottom carrier fluid, which could cause the blood layer to collapse. Increasing both the bottom layer density and the residence time may alleviate this problem. Unfortunately, it was hard to test this hypothesis with the current design given the unsteady flow at the low flow rate. Future designs that allow longer residence time but still maintain a high shear rate will be evaluated with different carrier fluid compositions for whole blood processing.
The device presented here purifies bionanopaticles from blood cells in a diluted suspension where particle collisions are insignificant. Using HIV particles for demonstration here, we envision that the principle can be applied to the purification of other submicron species in blood. It should be noted that the nanoparticle yields decrease with their diameters in a device of a fixed dimension (Fig. 2d). For example, in the current microdevice of a 100 μm thick channel in each layer, the theory predicts retrieval of >80% of 100 nm particles from the top outlet after 187 s, but homogenized presence of 5 nm particles throughout the thickness. Nonetheless, since the diffusion and sedimentation distances always cross regardless of the nanoparticle size (Fig. 2a), it will be possible to separate them using the described principle. At least 50% of the nanoparticle target could be retrieved from the nature of diffusion and the yield can be improved by optimizing the device dimension for a specific target size.
CONCLUSION
In conclusion, we take advantage of the intrinsic differences in their movements to purify viral particles from a blood sample in a microfluidic chip. The two layer flow design allows continuous sample processing and extraction of a high proportion of the target particles. The mechanism can be easily applied to effectively purify other submicron species from blood cells. The capability of continuous separation and >50% yield without significant instrument requirement makes the design suitable for processing small volume and low concentration targets at resource limited settings.
ACKNOWLEDGMENTS
We are grateful for the helpful discussions with Professor James Gilchrist. The HIV viral stock was kindly prepared by Yi Hu. Funding for the research was provided by National Institute of Health under Grant No. NIAID-1R21AI081638.
References
- Wong A. P., Gupta M., Shevkoplyas S. S., and Whitesides G. M., Lab Chip 8, 2032 (2008). 10.1039/b809830c [DOI] [PubMed] [Google Scholar]
- Cho Y., Lee J., Park J., Lee B., Lee Y., and Ko C., Lab Chip 7, 565 (2007). 10.1039/b616115d [DOI] [PubMed] [Google Scholar]
- Zhang J., Guo Q., Liu M., and Yang J., J. Micromech. Microeng. 18, 125025 (2008). 10.1088/0960-1317/18/12/125025 [DOI] [Google Scholar]
- Lee B., Lee J., Park J., Lee J., Kim S., Cho Y., and Ko C., Lab Chip 9, 1548 (2009). 10.1039/b820321k [DOI] [PubMed] [Google Scholar]
- Crowley T. and Pizziconi V., Lab Chip 5, 922 (2005). 10.1039/b502930a [DOI] [PubMed] [Google Scholar]
- VanDelinder V. and Groisman A., Anal. Chem. 78, 3765 (2006). 10.1021/ac060042r [DOI] [PubMed] [Google Scholar]
- Jaggi R. D., Sandoz R., and Effenhauser C. S., Microfluid. Nanofluid. 3, 47 (2007). 10.1007/s10404-006-0104-9 [DOI] [Google Scholar]
- Tachi T., Kaji N., Tokeshi M., and Baba Y., Anal. Chem. 81, 3194 (2009). 10.1021/ac802434z [DOI] [PubMed] [Google Scholar]
- Chen X., Cui D. F., and Chen J., Electrophoresis 30, 3168 (2009). 10.1002/elps.200900068 [DOI] [PubMed] [Google Scholar]
- Thorslund S., Klett O., Nikolajeff F., Markides K., and Bergquist J., Biomed. Microdevices 8, 73 (2006). 10.1007/s10544-006-6385-7 [DOI] [PubMed] [Google Scholar]
- Kersaudy-Kerhoas M., Kavanagh D., Dhariwal R.. Campbell C., and Desmulliez M., Lab Chip 10, 1587 (2010). 10.1039/b926834k [DOI] [PubMed] [Google Scholar]
- Yang S., Undar A., and Zahn J., Lab Chip 6, 871 (2006). 10.1039/b516401j [DOI] [PubMed] [Google Scholar]
- Rodriguez-Villarreal A. I., Arundell M., Carmona M., and Samitier J., Lab Chip 10, 211 (2010). 10.1039/b904531g [DOI] [PubMed] [Google Scholar]
- Sollier E., Rostaing H., Pouteau P., Fouillet Y., and Achard J. L., Sens. Actuators B 141, 617 (2009). 10.1016/j.snb.2009.05.023 [DOI] [Google Scholar]
- Davis J., Inglis D., Morton K., Lawrence D., Huang L., Chou S., Strum J., and Austin R., Proc. Natl. Acad. Sci. USA 103, 14779 (2006). 10.1073/pnas.0605967103 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Di Carlo D., Irimia D., Tompkins R. G., and Toner M., Proc. Natl. Acad. Sci. USA 104, 18892 (2007). 10.1073/pnas.0704958104 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Russom A., Gupta A. K., Nagrath S., Di Carlo D., Edd J. F., and Toner M., New J. Phys. 11, 075025 (2009). 10.1088/1367-2630/11/7/075025 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hsu C. H., Di Carlo D., Chen C. C., Irimia D., and Toner M., Lab Chip 8, 2128 (2008). 10.1039/b813434k [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen H. H. and Gao D., Appl. Phys. Lett. 92, 173502 (2008). 10.1063/1.2917794 [DOI] [Google Scholar]
- Arifin D., Yeo L., and Friend J., Biomicrofluidics 1, 014103 (2007). 10.1063/1.2409629 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qu B., Wu Z., Fang F., Bai Z., Yang D., and Xu S., Anal. Bioanal. Chem. 392, 1317 (2008). 10.1007/s00216-008-2382-4 [DOI] [PubMed] [Google Scholar]
- Nakashima Y., Hata S., and Yasuda T., Sens. Actuators B 145, 561 (2009). 10.1016/j.snb.2009.11.070 [DOI] [Google Scholar]
- Lien K., Lin J., Liu C., Lei H., and Lee G., Lab Chip 7, 868 (2007). 10.1039/b700516d [DOI] [PubMed] [Google Scholar]
- Chen G., Alberts C., Rodriguez W., and Toner M., Anal. Chem. 82, 723 (2010). 10.1021/ac9024522 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miyauchi K., Kim Y., Latinovic O., Morozov V., and Melikyan G., Cell 137, 433 (2009). 10.1016/j.cell.2009.02.046 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blumel J., Burger R., Gerlich W., Gurtler L., Heiden M., Hitzler W., Jansen B., Klamm H., Lefevre H., Lower J., Ludwig W., Montag- Lessing T., Offergeld R., Paessens A., Pauli G., Seitz R., Schlenkrich U., Werner E., and Willkommen H., Transfus. Med. Hemother. 32, 196 (2005). 10.1159/000087620 [DOI] [Google Scholar]
- Truskey G. A., Yuan F., Katz D. F., Transport Phenomena in Biological Systems (Prentice Hall, NJ, 2009). [Google Scholar]
- Cabrales P., Tsai A., Winslow R., and Intaglietta M., Am. J. Physiol. Heart Circ. Physiol. 289, H2392 (2005). 10.1152/ajpheart.00225.2005 [DOI] [PubMed] [Google Scholar]
- Zhang X. and Davis R., J. Fluid Mech. 230, 479 (1991). 10.1017/S0022112091000861 [DOI] [Google Scholar]
- Chien S., Science 168, 977 (1970). 10.1126/science.168.3934.977 [DOI] [PubMed] [Google Scholar]