Adaptively and Spatially Estimating the Hemodynamic Response Functions in fMRI

Abstract

In an event-related functional MRI data analysis, an accurate and robust extraction of the hemodynamic response function (HRF) and its associated statistics (e.g., magnitude, width, and time to peak) is critical to infer quantitative information about the relative timing of the neuronal events in different brain regions. The aim of this paper is to develop a multiscale adaptive smoothing model (MASM) to accurately estimate HRFs pertaining to each stimulus sequence across all voxels. MASM explicitly accounts for both spatial and temporal smoothness information, while incorporating such information to adaptively estimate HRFs in the frequency domain. One simulation study and a real data set are used to demonstrate the methodology and examine its finite sample performance in HRF estimation, which confirms that MASM significantly outperforms the existing methods including the smooth finite impulse response model, the inverse logit model and the canonical HRF.

1 Introduction

The functional MRI (fMRI) study commonly uses blood oxygenation level-dependent (BOLD) contrast to measure the hemodynamic response (HR) related to neural activity in the brain or spinal cord of humans or animals. Most fMRI research correlates the BOLD signal elicited by a specific cognitive process with the underlying unobserved neuronal activation. Therefore, it is critical to accurately model the evoked HR to a neural event in the analysis of fMRI data. See [6] for an overview of different methods to estimate HRF in fMRI. A linear time invariant (LTI) system is commonly implemented to model the relationship between the stimulus sequence and BOLD signal where the signal at time t and voxel d, Y (t, d), is the convolution of a stimulus function X(t, d) and the HR function (HRF) h(t, d) plus an error process ε(t, d). While nonlinearities in the BOLD signal are predominant for stimuli with short separations, it has been shown that LTI is a reasonable assumption in a wide range of situations [6].

Almost all HRF models estimate HRF on a voxel-wise basis which ignores the fact that fMRIs are spatially dependent in nature. Particularly, as the case in many fMRI studies, we observe spatially contiguous effect regions with rather sharp edges. There are several attempts to address the issue of spatial dependence in fMRI. A possible approach is to apply a smoothing step before individually estimating HRF in each voxel of fMRI data. Most smoothing methods, however, are independent of the imaging data and apply the same amount of smoothness throughout the whole image [7]. These smoothing methods can blur the information near the edges of the effect regions and thus dramatically increase the number of false positives and false negatives. An alternative approach is to model spatial dependence among spatially connected voxels by using conditional autoregressive (CAR), Markov random field (MRF) or other spatial correlation priors [9,11]. However, calculating the normalizing factor of MRF and estimating spatial correlation for a large number of voxels in the 3D volume are computationally intensive [2]. Moreover, it can be restrictive to assume a specific type of correlation structure for the whole 3D volume (or 2D surface).

The goal of this paper is to develop a multiscale adaptive smoothing model (MASM) to construct an accurate nonparametric estimate of HRF across all voxels pertaining to a specific cognitive process in the frequency domain. Compared with all existing methods, we make several major contributions. (i) To temporally smooth HRF, MASM incorporates an effective method for carrying out locally adaptive bandwidth selection across different frequencies; (ii) To spatially smooth HRFs, MASM builds hierarchically nested spheres by increasing the radius of a spherical neighborhood around each voxel and utilizes information in each of the nested spheres across all voxels to adaptively and simultaneously smooth HRFs; (iii) MASM integrates both spatial and frequency smoothing methods together; (iv) MASM uses a backfitting method [3] to adaptively estimate HRFs for multiple stimulus sequences across all voxels. The group-level inference like testing the significant regions based on estimated HRFs will be further studied in the future.

2 Model Formulation

2.1 Multiscale Adaptive Smoothing Model

Suppose that we acquire a fMRI data set in a three dimensional (3D) volume, denoted by 𝒟 ⊂ R³, from a single subject. In real fMRI studies, it is common that multiple stimuli are present [11]. Under the assumption of the LTI system, the BOLD signal is the individual response to the sum of all stimuli convoluted with their associated HRFs. Let X(t) = (X₁(t),…, X_m(t))^T be the sequence vector of m different stimuli and its associated HRF vector H(t, d) = (H₁(t, d),…, H_m(t, d))^T. Specifically, in the time domain, most statistical models to estimate HRF under the presence of m different stimuli assume that

$$Y(t,\mathbf{d})=\mathbf{H}(·,\mathbf{d})\otimes \mathbf{X}(t)+\epsilon (t,\mathbf{d})={\displaystyle \int }<\mathbf{H}(\mathbf{d},t-u),\mathbf{X}(u)>\mathit{\text{du}}+\epsilon (t,\mathbf{d}),$$ (1)

where ε(t, d) is a spatial and frequent error process.

Instead of directly using model (1), our MASM focuses on the discrete Fourier coefficients of Y (t, d), H(t, d), X(t), and ε(t, d), which are, respectively, denoted by ϕ_Y(f_k, d), ϕ_H(f_k, d), ϕ_X(f_k), and ϕ_ε(f_k, d) at the fundamental frequencies f_k = k/T for k = 0,⋯, T − 1. Specifically, in the frequency domain, MASM assumes that

$${\varphi }_Y(f,\mathbf{d})=<{\varphi }_{\mathbf{H}}(f,\mathbf{d}),{\varphi }_{\mathbf{X}}(f)>+{\varphi }_{\epsilon }(f,\mathbf{d}),$$ (2)

where ϕ_H(f, d) = (ϕ_H1 (f, d),…, ϕ_Hm(f, d))^T, ϕ_X(f) = (ϕ_X1 (f),…, ϕ_Xm (f))^T. An advantage of MASM in (2) is that the temporal correlation structure can be reduced since the Fourier coefficients are approximately asymptotically uncorrelated across frequencies under some regularity conditions [8,1]. Moreover, ϕ_ε(f, d) is assumed to be a complex process with the zero mean function and a finite spatial covariance structure. MASM assumes that for each stimuli j and each voxel d, ϕ_Hj (f, d) is close to ϕ_Hj (f′, d′) for some neighboring voxels d′ and frequencies f′. This is essentially a spatial and frequent smoothness condition, which allows us to borrow information from neighboring voxels and frequencies. Equation (2) and different shape neighborhoods at different voxels are the two key novelties compared to the existing literatures [6].

2.2 Weighted Least Square Estimate

Our goal is to estimate the unknown functions {ϕ_H(f, d) : d ∈ 𝒟, f ∈ [0, 1]} based on MASM and the Fourier transformed fMRI data ℱ(Y) = {ϕ_Y (f_k, d) : k = 0,⋯, T −1, d ∈ 𝒟}. To estimate ϕ_H(f, d), we may combine all information at fundamental frequencies f_k ∈ η_f (r) = (f−r, f+r)∩{k/T : k = 0, 1,…, T−1} with r > 0 and voxels d′ ∈ B(d, s), where B(d, s) is a spherical neighborhood of voxel d with radius s ≥ 0 to construct an approximation equation as follows:

$${\varphi }_Y(f_k,\mathbf{d}\prime )\approx <{\varphi }_{\mathbf{H}}(f,\mathbf{d}),{\varphi }_{\mathbf{X}}(f_k)>+{\varphi }_{\epsilon }(f_k,\mathbf{d}\prime ).$$ (3)

Then to estimate ϕ_Hj (f, d) for j = 1,⋯,m, respectively, we construct m local weighted functions L_[−j](ϕ_Hj (f, d); r, s) as

$${\displaystyle \sum _{f_k\in {\eta }_f(r)}{\displaystyle \sum _{\mathbf{d}\prime \in B(\mathbf{d},s)}}{|{\varphi }_{Y[-j]}(f_k,\mathbf{d}\prime )-{\varphi }_{H_j}(f,\mathbf{d}){\varphi }_{X_j}(f_k)|}^2{\tilde{\omega }}_j(\mathbf{d},\mathbf{d}\prime ,f,f_k;r,s)}$$ (4)

for j = 1,⋯,m, where ϕ_{Y [−j]} (f_k, d′) = ϕ_Y (f_k, d′) −Σ_l≠j ϕ_Hl (f_k, d′)ϕ_Xj (f_k). Moreover, weight ω̃_j(d, d′, f, f_k; r, s) characterizes the physical distance between (f, d) and (f_k, d′) and the similarity between ϕ_Hj (f, d) and ϕ_Hj (f_k, d′). The procedure for determining all weights ω̃_j(d, d′, f, f_k; r, s) will be given later. We derive a recursive formula to update the estimates ϕ̂_Hj (f, d) and Var(ϕ̂_Hj (f, d)) for j = 1,…, m based on any fixed weights {ω̃_j(d, d′, f, f_k; r, s) : d′ ∈ B(d, s), f_k ∈ η_f (r)}. We obtain ϕ̂_Hj (f, d) by differentiating L_[−j](ϕ_Hj (f, d); r, s) as follows:

$$\frac{{\displaystyle {\sum }_{f_k\in {\eta }_f(r)}{\displaystyle {\sum }_{{\mathbf{d}}^T\in B(d,s)}}{\tilde{\omega }}_j(\mathbf{d},\mathbf{d}\prime ,f,f_k;r,s)\overline{{\varphi }_{X_j}(f_k)}{\varphi }_{Y[-j]}(f_k,\mathbf{d}\prime )}}{{\displaystyle {\sum }_{f_k\in {\eta }_f(r)}{\displaystyle {\sum }_{\mathbf{d}\prime \in B(\mathbf{d},s)}}{\tilde{\omega }}_j(\mathbf{d},\mathbf{d}\prime ,f,f_k;r,s){\varphi }_{X_j}(f_k)\overline{{\varphi }_{X_j}(f_k)}}}$$ (5)

where $\overline{{\varphi }_{X_j}(f_k)}$ is the conjugate of ϕ_Xj (f_k). We approximate Var(ϕ̂_Hj (f, d)) as

$$\frac{\{{\displaystyle {\sum }_{f_k\in {\eta }_f(r)}|{\displaystyle {\sum }_{\mathbf{d}\prime \in B(\mathbf{d},s)}}{\tilde{\omega }}_j(\mathbf{d},\mathbf{d}\prime ,f,f_k;r,s)\overline{{\varphi }_X(f_k)}{\widehat{\varphi }}_{j\epsilon }(f_k,\mathbf{d}\prime ){|}^2}\}}{{\{{\displaystyle {\sum }_{f_k\in {\eta }_f(r)}{\displaystyle {\sum }_{\mathbf{d}\prime \in B(\mathbf{d},s)}}{\tilde{\omega }}_j(\mathbf{d},\mathbf{d}\prime ,f,f_k;r,s){\varphi }_X(f_k)\overline{{\varphi }_X(f_k)}}\}}^2},$$ (6)

where ϕ̂_jε(f_k, d′) = ϕ_Y (f_k, d′) − Σ_l≠j ϕ̂_Hl (f_k, d′)ϕ_Xj (f_k). Based on ϕ̂_Hj (f, d) for j = 1,⋯,m, we can get

$${\tilde{H}}_j(t,\mathbf{d})=\frac{1}{T}{\displaystyle \sum _{k=0}^{T-1}}{\widehat{\varphi }}_{H_j}(f_k,\mathbf{d})\text{ exp }(i2\pi {\mathit{\text{tf}}}_k)\text{ for any }\mathbf{d}\in 𝒟\text{ and }t.$$ (7)

2.3 Mutliscale Adaptive Estimation Procedure

We use a multiscale adaptive estimation (MAE) procedure to determine {ω̃_j(·) : j = 1,⋯,m} and then estimate {ϕ_H(f, d) : d ∈ 𝒟, f ∈ [0, 1]}. MAE borrows the multiscale adaptive strategy from the well-known Propagation-Separation (PS) approach [10,5]. MAE starts with building two sequences of nested spheres with spatial radii s₀ = 0 < s₁ < ⋯ < s_S and frequent radii 0 < r₀ < r₁ <…< r_S. The key idea of MAE for multiple stimuli is to sequentially and recursively compute ϕ̂_Hj (f, d) from j = 1 increasing to m. Generally, MAE consists of four key steps: initialization, weight adaption, recursive estimation and stopping check. In the initialization step, we set s₀ = 0, r₀ > 0, say r₀ = 5/T, and the weighting scheme ω̃_j(d, d, f, f_k; r₀, s₀) = K_loc(|f − f_k|/r₀). We also set up another series {r_s = r_s−1+b_r : s = 1,⋯, S} as the frequent radii with a constant value b_r, say, b_r = 2/T. Then we apply the backfitting algorithm to iteratively update ${\widehat{\varphi }}_{H_j}^{(0)}(f,\mathbf{d})$ and obtain an estimate of $\text{Var}({\widehat{\varphi }}_{H_j}^{(0)}(f,\mathbf{d}))$ for j = 1,⋯,m until convergence.

In the weight adaptation step, for s > 0, we set ${\tilde{\omega }}_j^{(i)}(\mathbf{d},\mathbf{d}\prime ,f,f_k;r_s,s_s)$ as

$$K_{\mathit{\text{loc}}}({\Vert \mathbf{d}-\mathbf{d}\prime \Vert }_2/s_s)K_{\mathit{\text{loc}}}(|f-f_k|/r_s)K_{\mathit{\text{st}}}(\frac{\Vert {\widehat{\varphi }}_{H_j}^{(i-1)}(f,\mathbf{d})-{\widehat{\varphi }}_{H_j}^{(i-1)}(f_k,\mathbf{d}\prime )\Vert }{\sqrt{\Vert \text{Var}({\widehat{\varphi }}_{H_j}^{(i-1)}(f,\mathbf{d}))\Vert }}),$$ (8)

where ‖·‖ is the norm operator and ‖·‖₂ is the L₂ norm. The functions K_loc(x) and K_st(x) are two kernel functions such as the Epanechnikov kernel [10,5].

In the recursive estimation step, at the i^th iteration, we compute ${\widehat{\varphi }}_{j\epsilon }^{(i)}(f,\mathbf{d})={\varphi }_Y(f,\mathbf{d})-{\displaystyle {\sum }_{l\ne j}}{\widehat{\varphi }}_{H_l}^{(i-1)}(f,\mathbf{d}){\varphi }_{X_l}(f)$ . Then based on weights ${\tilde{\omega }}_j^{(i)}(\mathbf{d},\mathbf{d}\prime ,f,f_k;r_s,s_s)$ , we sequentially calculate ${\widehat{\varphi }}_{H_j}^{(i)}(f,\mathbf{d})$ and approximate $\text{Var}({\widehat{\varphi }}_{H_j}^{(i)}(f,\mathbf{d}))$ according to (5) and (6).

In the stop checking step, after the i₀-th iteration, we calculate the adaptive Neyman test statistic, denoted by $W_j^{(i)}(\mathbf{d};s_s,r_u)$ , for the j-th stimulus to test difference between ${\widehat{\varphi }}_{H_j}^{(i)}(\mathbf{d})=\{{\widehat{\varphi }}_{H_j}^{(i)}(f_0,\mathbf{d}),\dots ,{\widehat{\varphi }}_{H_j}^{(i)}(f_{T-1},\mathbf{d})\}\text{ and }{\widehat{\varphi }}_{H_j}^{(i-1)}(\mathbf{d})=\{{\widehat{\varphi }}_{H_j}^{(i-1)}(f_0,\mathbf{d}),\dots ,{\widehat{\varphi }}_{H_j}^{(i-1)}(f_{T-1},\mathbf{d})\}$ . If $W_j^{(i)}(\mathbf{d};s_s,r_s)$ is significant, then we set ${\widehat{\varphi }}_{H_j}^{(s)}(f,\mathbf{d})={\widehat{\varphi }}_{H_j}^{(i-1)}(f,\mathbf{d})$ for all s ≥ i at voxel d.

Finally, when s = S, we report the final ${\widehat{\varphi }}_{H_j}^{(S)}(f,\mathbf{d})$ at all fundamental frequencies and substitute them into (7) to calculate ${\widehat{H}}_j^{(S)}(t,\mathbf{d})$ across voxels d ∈ 𝒟 for all j = 1,⋯,m. After obtaining HRFs for all stimuli, we may calculate their summary statistics including amplitude/height (H), time-to-peak (T), and full-width at half-max (W) and then carry out group-level statistical inference, say to test whether H significantly differs from 0, on the images of these estimated summary statistics [6].

3 Results

Simulation

We conducted a set of Monte Carlo simulations to examine the finite sample performance of MASM and MAE and compared them with several existing HRF models. We simulated the data at 200 time points (i.e., t = 1, 2,⋯, 200) with a 40×40 phanton image containing 9 regions of activation-circles with varying radius at each time point. These 9 regions were also grouped into three different BOLD patterns with each group consisting of three circles, which have the same true signal series. The three true HRFs were set as zeros for t > 15 and otherwise for t > 0 according to

$$h_j(t)=A_j·{(t/d_{j1})}^{a_{j1}}\text{ exp }(-(t-d_{j1})/b_{j1})-c{(t/d_{j2})}^{a_{j2}}\text{ exp }(-(t-d_{j2})/b_{j2})$$

with (A₁,A₂,A₃) = (1, 5, 3), c = 0.35, (a₁₁, a₁₂) = (6, 12), (a₂₁, a₂₂) = (4, 8), (a₃₁, a₃₂) = (5, 10), (b_j1, b_j2) = (0.9, 0.9) and (d_j1, d_j2) = (a_j1 * b_j1, a_j2 * b_j2) for j = 1, 2, 3. The boxcars consisting of either zeros or ones were independently generated from a Bernoulli random generator with the successful rate=0.15, denoted by X_j(t), j = 1, 2, 3. So the true BOLD signals were simulated as $Y(t)={\displaystyle {\sum }_{j=1}^3}{H}_j\otimes X_j(t)$ . The signals in each group of the activation-circles were scaled to be Y₁(t) = Y (t)/6, Y₂(t) = Y (t)/4 and Y₃(t) = Y (t)/2, respectively. The noise ε(t) were generated from a Gaussian distribution with mean zero and standard deviation σ = 0.2. Note that it is straightforward to embed AR noise to simulate the serial autocorrelation. Finally, the simulated BOLD signal was set as Y_j(t) + ε(t) for j = 1, 2, 3. In this simulation, the smallest signal-to-noise rate (SNR) is around 0.6.

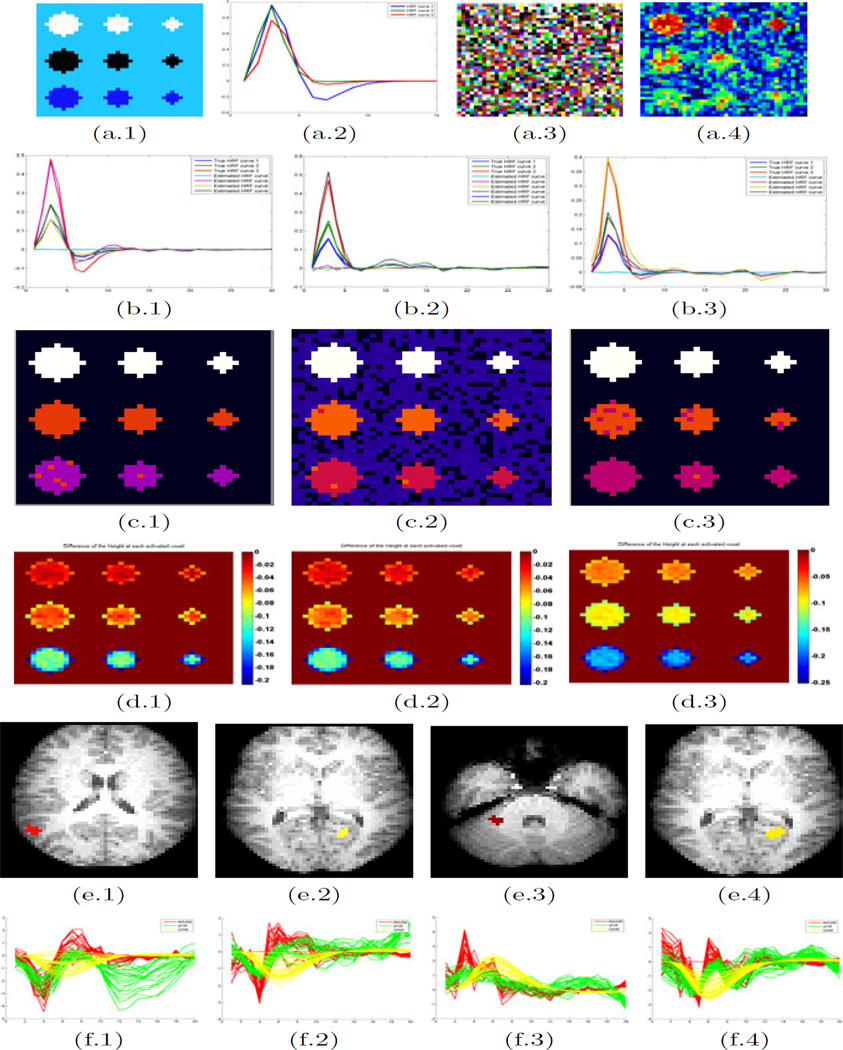
In order to determine the signal patterns, we implemented some EM-based clustering method with ignoring the details for the sake of space and then computed the average of the estimates in each cluster. The estimates of the clustered HRFs are displayed in Fig. 1 (b.1–3 and c.1–3). It seems that our algorithm can simultaneously recover the correct HRFs in all active regions.

Fig. 1.

Set-up of Simulation: (a.1) a temporal cut of the true images; (a.2) the true curves of HRF: h₁(t), h₂(t) and h₃(t); (a.3) a temporal cut of the simulated images; (a.4) the Gaussian smooth result. The estimated results: estimates of HRF for the (b.1 and c.1) 1st; (b.2 and c.2) 2nd; (b.3 and c.3) 3rd sequence of events. The row (b.1–3) is the average estimated HRF in each cluster. The row (c.1–3) is the recovered pattern relative to each sequence of events. The comparison statistics D_j with sFIR: (d.1–3) the difference of estimated Height(H) at each voxel for the three stimulus sequences. The color bar denotes the value of D_j for the j^th voxel. Data analysis results: (e.1)–(e.4) the slices containing ROIs (colored ones) of the F maps for the 1st–4th stimulus sequences, respectively; (f.1)–(f.4) estimated HRFs at the significant ROIs corresponding each condition from MASM (red), sFIR (green) and GAM(yellow).

To evaluate our method, we compared MASM with some state-of-art methods in [6], which include (i) SPMs canonical HRF (denoted as GAM); (ii) the semi-parametric smooth finite impulse response (FIR) model (sFIR); and (iii) the inverse logit model (IL). Subsequently, we evaluated the HRF estimates by computing H, T, and W as the potential measure of response magnitude, latency and duration of neuronal activity. It has been reported in [6] that IL is one of the best methods in accurately estimating H, T, and W.

Let $D={\displaystyle {\sum }_{i=1}^N{\displaystyle {\sum }_{j=1}^M}}(|{\widehat{x}}_{\mathit{\text{ij}}}-x_0|-|{\widehat{y}}_{\mathit{\text{ij}}}-x_0|)/(\mathit{\text{NM}})$ , where x̂_ij and ŷ_ij, respectively, denote the statistics H, T, or W, calculated from MASM and from the other three methods, and x₀ represents the true value of H (or T, W) in the different active regions corresponding to the different event sequences. Moreover, N and M, respectively, represent the numbers of replications and voxels in active regions with N = 100. We computed the average absolute error differences between our method and the other three methods. Generally, the negative value of D indicates that our method outperforms other methods. Table 1 reveals that MASM can provide more accurate estimates of the HRF summary statistics than the other three methods.

Table 1.

Comparisons of the differences of the absolute errors between our method with sFIR, IL and GAM, respectively. C1, C2 and C3 denote the 1st, 2nd and 3rd sequences of events, respectively. A1, A2 and A3 denote the 1st, 2nd and 3rd active regions. Values in the parentheses are the standard errors. H=Height, W=Width, T=Time-to-Peak.

Param	sFIR				IR				GAM
H		A1	A2	A3		A1	A2	A3		A1	A2	A3
	C1	−0.02 (0.045)	−0.04 (0.045)	−0.09 (0.060)	C1	−0.11 (0.0819)	−0.16 (0.115)	−0.32 (0.218)	C1	−0.13 (0.039)	−0.20 (0.044)	−0.42 (0.059)
	C2	−0.02 (0.041)	−0.04 (0.043)	−0.10 (0.057)	C2	−0.09 (0.0699)	−0.14 (0.096)	−0.27 (0.175)	C2	−0.11 (0.041)	−0.17 (0.045)	−0.36 (0.057)
	C3	−0.01 (0.046)	−0.02 (0.047)	−0.07 (0.064)	C3	−0.07 (0.0673)	−0.10 (0.089)	−0.21 (0.161)	C3	−0.07 (0.038)	−0.11 (0.045)	−0.25 (0.066)
T		A1	A2	A3		A1	A2	A3		A1	A2	A3
	C1	−0.08 (0.722)	0.05 (0.326)	0.01 (0.073)	C1	−3.74 (3.313)	−3.49 (3.309)	−3.19 (3.292)	C1	−2.50 (0.425)	−2.66 (0.298)	−2.84 (0.070)
	C2	−0.55 (0.685)	0.07 (0.292)	0.01 (0.069)	C2	−3.50 (3.440)	−3.34 (3.475)	−2.88 (3.419)	C2	−2.57 (0.452)	−2.75 (0.287)	−2.91 (0.069)
	C3	−0.55 (1.159)	−0.10 (0.513)	−0.10 (0.513)	C3	−3.54 (3.404)	−3.26 (3.430)	−3.03 (3.415)	C3	−2.46 (0.577)	−2.66 (0.427)	−2.87 (0.254)
W		A1	A2	A3		A1	A2	A3		A1	A2	A3
	C1	−0.20 (0.671)	−0.28 (0.596)	−0.42 (0.518)	C1	−1.70 (2.1222)	−1.73 (2.127)	−1.66 (2.094)	C1	−3.33 (0.623)	−3.41 (0.576)	−3.46 (0.515)
	C2	−0.38 (0.760)	−0.41 (0.597)	−0.49 (0.513)	C2	−1.78 (2.143)	−1.80 (2.099)	−1.79 (2.018)	C2	−3.35 (0.634)	−3.41 (0.575)	−3.49 (0.512)
	C3	−0.32 (0.870)	−0.33 (0.741)	−0.48 (0.658)	C3	−1.79 (2.179)	−1.85 (2.123)	−2.08 (2.221)	C3	−3.30 (0.713)	−3.42 (0.677)	−3.63 (0.550)

From Table 1, amongst the tested HRF estimation alternatives, the sFIR seems to provide the closest results. Thus we pick sFIR to make another comparison. We applied the Gaussian smoothing with FWHM equal 4mm to the original simulated data before running sFIR and compared them to MASM without using the Gaussian smoothing. An evaluation statistics for the j^th voxel is given by $D_j=\frac{1}{100}{\displaystyle {\sum }_{i=1}^{100}}(|{\widehat{x}}_{\mathit{\text{ij}}}-x_0|-|{\widehat{y}}_{\mathit{\text{ij}}}-x_0|)$ . The comparison results for the parameter H given in Fig. 1 (d.1–3) as a representative reveals that MASM outperforms sFIR, especially on the boundary voxels as Gaussian smoothing blurred them.

Real Data

We used a subject from a study designed for the investigation of the memory relationship with four different stimulus sequences. We used Statistical Parametric Mapping (SPM) [4] to preprocess the fMRI and MRI images and apply a global signal regression method to detrend the fMRI time series. The F-statistics maps were generated by SPM to test the activation regions triggered by four sequences of stimulus events. For each stimulus, we set a threshold with p value less than 0.01 and the extension K = 20 to find significant regions of interest (ROIs). We plotted the estimated HRFs by using MASM, sFIR and GAM in these ROIs and chose one of them in each brain mapping as a demonstration to compare MASM with sFIR and GAM (Fig. 1 (e.1–4)). Based on the SPM findings with GAM, we found the deactive ROIs in Figures (e.1), (e.2) and (e.4) and the active ROIs in Figure (e.3). They are consistent with those ROIs obtained from the other two methods. HRFs calculated from MASM and sFIR have similar H, W, and T, which are different with those statistics obtained from HRFs based on GAM(Fig. 1 (f.1–4)). This result is consistent with our simulation result (see Table 1). Furthermore, we found that HRFs calculated from sFIR had big variation at their tails compared to those calculated from MASM. It may indicate that MASM is an accurate estimation method for reconstructing HRFs in fMRI.