Time-Resolved NMR: Extracting the Topology of Complex Enzyme Networks

Abstract

The use of nondestructive NMR spectroscopy for enzymatic studies offers unique opportunities to identify nearly all enzymatic byproducts and detect unstable short-lived products or intermediates at the molecular level; however, numerous challenges must be overcome before it can become a widely used tool. The biosynthesis of acetyl-coenzyme A (acetyl-CoA) by acetyl-CoA synthetase is used here as a case study for the development of an analytical NMR-based time-course assay platform. We describe an algorithm to deconvolve superimposed spectra into spectra for individual molecules, and further develop a model to simulate the acetyl-CoA synthetase enzyme reaction network using the data derived from time-course NMR. Simulation shows indirectly that synthesis of acetyl-CoA is mediated via an enzyme-bound intermediate (possibly acetyl-AMP) and is accompanied by a nonproductive loss from an intermediate. The ability to predict enzyme function based on partial knowledge of the enzymatic pathway topology is also discussed.

Introduction

Biological systems are inherently dynamic systems that evolve, or sometimes exist at near steady-state conditions, at the expense of pools of energy-supplying substrates. Understanding these systems at the metabolic level is a fundamental problem in kinetic analysis. Although the study of the reaction kinetics of a single enzyme is a well-established field, application to biological systems is not, and appropriate methodologies for studying these more-complex systems are still evolving. Such methodologies should work at single-enzyme, multienzyme, and (eventually) whole-cell levels. The difficulties of capturing a process without interfering in it (e.g., stopping the enzymatic reaction by tissue maceration) and finding a reasonably sensitive method to monitor the system present additional challenges. Real-time NMR offers a possible means of meeting these challenges. NMR is a quantitative, nondestructive diagnostic tool that is commonly used to determine molecular structure with minute structural detail. The ability to obtain quantitative information on concentrations and identify a wide range of compounds is important for metabolic applications. The ubiquitous occurrence of protons in metabolites and the direct correlation of their signal intensity with concentration makes proton NMR especially useful. Although it is inherently a less sensitive method than mass spectrometry, advances in field strength, cryoprobe technology, and more efficient acquisition methods have reduced the sensitivity limitations of this methodology. Proton-NMR is currently capable of monitoring small (10 μM) metabolites on the timescale of a few minutes. However, taking advantage of the wealth of data that can be obtained requires parallel improvements in data-reduction and kinetic-modeling methods.

Of course, NMR has numerous applications for monitoring enzymatic reactions at various levels of complexity (1–3). Although a few recent studies have examined profiling changes in whole cellular systems (4–6), most studies have focused on enzyme systems with small numbers of well-defined substrates and products. In these cases, most peaks corresponding to the molecular species of interest are well resolved and can be individually integrated to obtain time courses for variations in substrate and product concentrations. However, as systems become more complex, the NMR spectra become more complicated, with hundreds of crowded peaks. Often NMR peaks belonging to structurally similar molecules overlap, and it is a major challenge to deconvolve spectra into sets of peaks representing individual molecular species. We recently explored the use of real-time ¹H-NMR-based assays and found it to be a powerful method for diagnosing enzyme reactions, especially when intermediates in enzyme reactions have a short lifespan (2). However, before such a method can routinely be used with many enzymes (and ultimately whole cells), two other major challenges must be overcome: 1), we must be able to deconvolve superimposed spectra into spectra for individual molecular species and monitor the time course of concentrations of each molecular species; and 2), we must be able to simulate enzymatic network topologies in such a way that encompasses the correct pathway and allows identification of that pathway.

The successful use of quantitative ¹H NMR usually depends on the identification of one or several well-isolated peak(s) from superimposed spectra for each component and the selection of proper NMR acquisition and processing parameters (e.g., sufficiently long relaxation times to achieve equilibrium of magnetization) (7,8). Before quantitative ¹H NMR can be applied to more-complicated systems with fewer isolated peaks, a better approach that can deal with overlapping peaks and remain quantitative even when optimal data acquisition parameters cannot be used must be developed.

Chemical reaction networks provide a natural language for describing the mechanistic details of an enzymatic pathway and the interactions between multiple pathways in complex multienzyme systems. The time evolution of metabolite concentrations in such systems profoundly depends on, and is therefore informative about, the underlying network topology. It is straightforward to predict the time evolution, given the network topology and its kinetic reaction rate coefficients, by solving the network's kinetic rate equations. However, the inverse problem of reconstructing the network, and hence the mechanistic details of the pathway from time-series data, presents major challenges even if the data are complete, dense, and free of noise. In real metabolic time-series experiments, the mechanistic network information is obscured further by the incompleteness, sparsity, and noise of the data. Relevant network models, even for fairly simple single-enzyme systems, are rich in unknown model parameters, such as rate coefficients and initial conditions, which are poorly constrained by the incomplete, sparse, and noisy data. The ensemble network simulation (ENS) method (9–11) was developed to deal with this ubiquitous problem of incomplete, poorly constrained biological circuit models, and it is uniquely suited for the task of kinetics-based network topology reconstruction and discrimination. The ENS method rests on the realization that a great deal can be known about a network's observable kinetics, even if many of its rate coefficients are poorly constrained or not known. The central idea of ENS is then to forego reconstruction of one unique model parameterization and to generate instead a statistical sample of all such parameterizations that are consistent with the data. ENS thus produces probabilistic predictions of the network's time evolution that enable us to discriminate between competing hypothesized network topologies.

As a case study, we tested the methodologies described above with the enzyme acetyl-coenzyme A (acetyl-CoA) synthetase (ACS). ACS is a well-studied enzyme in bacteria (12) and humans (13), and is required for the synthesis of acetyl-CoA (AcCoA), a major cell metabolite. ACS has been proposed to convert ATP and acetate to an enzyme-bound intermediate (ACS/acetyl-AMP), and upon addition of CoA to transfer the acetate to CoA to yield pyrophosphate (PPi), AMP, and AcCoA (14). The enzyme has been characterized to a lesser extent in plants. Using this enzyme as a test system, we describe what to our knowledge is a new procedure for investigating its activity by real-time NMR analysis. A computational procedure is used to extract NMR spectra of individual enzymatic compounds from the complex, time-evolving, superimposed spectra. A simulation procedure based on kinetic networks is then used to discriminate among several hypothesized enzymatic networks. It is hoped that this procedure will provide a novel tool to identify interactions and control points in other complex metabolic systems.

Experimental Procedures

Preparation of Arabidopsis ACS samples

The methods used for gene cloning, protein expression, purification, and characterization of enzymatic properties are described in the Supporting Material. All other reagents were obtained from commercial sources.

Real-time ¹H-NMR analysis of ACS

ACS reactions (180 μL final volume) were performed in a final mixture of D₂O/H₂O (9:1 v/v) in 50 mM sodium phosphate, pH/pD 7.6, 5 mM MgCl₂, 1.2 mM ATP, 2.0 mM CoA, 1.0 mM acetate, and 12.5 μg recombinant ACS. The enzyme was not exchanged with D₂O, but was added in a small volume of a similar protonated sodium phosphate buffer just before NMR monitoring of the reaction. Real-time ¹H NMR spectra were obtained on a Varian (Palo Alto, CA) direct-drive spectrometer system with a 3 mm cryogenic probe operating at 600 MHz. Immediately upon addition of enzyme, the reaction mixture was transferred to a 3 mm NMR tube and monitored continuously by ¹H-NMR spectroscopy at 37°C. The first spectrum was acquired beginning 2 min after the addition of enzyme to the reaction mixture, due to spectrometer setup requirements. Then 300 sequential 1D proton spectra with water presaturated were acquired over a 90 min time period under the following experimental conditions: 90° pulse, 2 s acquisition time, and 2 ms relaxation time. Each spectrum consisted of four transients. For kinetic monitoring, all spectra were processed by Fourier transformation after exponential weighting with 1 Hz line-broadening and zero-filling to 64 k points. Spectra were referenced to the water resonance at 4.765 ppm. Data were also processed using MATLAB code (The MathWorks, Natick, MA) for deconvolution of superimposed peaks. Details of this procedure are described in the Supporting Material.

Standards for compounds involved in the ACS reaction were prepared at 1 mM in a final mixture of D₂O/H₂O (9:1 v/v) in 50 mM sodium phosphate, pH/pD 7.6, 5 mM MgCl_2. The NMR spectra were acquired as described above, except that each spectrum consisted of 16 transients instead of four to achieve a better signal/noise (S/N) ratio.

Deconvolution of superimposed peaks

The mathematical details involved in deconvolution of the superimposed peaks are described in the Supporting Material.

Extracting time-course variations of reactant concentrations

Two methods were employed to calculate the time course of concentrations of reactants for ENS: 1), conventional NMR resonance peak integration of well-resolved diagnostic peaks with background subtraction (PIBS); and 2), multiple peak spectral fitting (MPSF, described below). In the PIBS approach, diagnostic peaks of interest were manually selected for each metabolite from the time-series spectra, and the peak integration was performed using procedures in Vnmrj (Palo Alto, CA). The concentrations of each reactant were then calculated by normalizing the peak integral values to the known initial concentrations of the starting materials.

In the MPSF approach, least-squares methods are used to fit the experimental time-series data by a linear superposition of the aligned spectral standards, obtained from the nonnegative matrix factorization (NMF) alignment method described in the Supporting Material, with time-dependent superposition amplitudes that are directly proportional to the desired concentration time courses. The MPSF inputs are the time-series experimental data matrix E, of dimension P × T, and the corresponding aligned spectral standards S, represented as a matrix of dimension P × N. Here, the time-series spectral data are restricted to spectral windows containing peaks from the metabolites of interest, P denotes the total number of NMR spectral frequency bins from all selected windows; T is the number of observation times; and N is the number of aligned standards (i.e., the number of individually observed metabolites), included in the linear superposition. E and S are used to find the best-fitting metabolite concentration time courses, T, represented as a nonsquare N × T matrix. That is, the spectral time-series data are represented as E = ST, and the matrix T of the best-fitting concentration time courses is obtained as:

$$\text{T}={({\text{E}}^{\text{T}}\text{S}{({\text{S}}^{\text{T}}\text{S})}^{-1})}^{\text{T}}$$ (1)

ENS of the metabolic network

The technical details are described in the Supporting Material, but in brief, a statistical sample of parameterizations for a model (denoted as θ) that is consistent with the data is generated. Then probabilistic predictions of the network's time evolution are produced. The generation of large statistical θ-samples is achieved computationally by means of a Monte Carlo (MC) random walk procedure in θ-space. This random walk is guided by an ensemble probability distribution Q(θ) that favors θ-choices that yield model predictions consistent with (and disfavors θ-choices inconsistent with) the metabolic time-series data, as quantified by χ²(θ). The MC-averaged converged χ²-values are used to rank the models.

Results

AcCoA synthetase from Arabidopsis

A truncated construct of the ACS from Arabidopsis was cloned and expressed locally. A detailed characterization of the enzyme is included in the Supporting Material. Based on this characterization, the components to consider in building network models are acetate, CoA, AcCoA, ATP, AMP, ADP, PPi, phosphate (Pi), and any potential intermediates.

Real-time NMR of the AtACS-catalyzed reaction

We first established that ACS activity can be monitored by ¹H-NMR. The time course for ACS production of AcCoA is presented in Fig. 1 A. It clearly shows that certain peaks between 2 and 4 ppm are increased in size, whereas others are reduced. The fact that the enzyme forms AcCoA is evidenced by the three diagnostic peaks belonging to protons on the acetate-cysteamine-pantothenate (ACP) moiety of AcCoA, the triplet signal at 3.04 ppm corresponding to the two protons of AcCoA-ACP-H10″, the triplet signal at 2.5 ppm corresponding to the two protons of AcCoA-ACP-H7″), and the singlet signal at 2.4 ppm corresponding to the three protons of the methyl group (AcCoA-ACP-H12″), which rise as a function of time (Fig. 1 A). Peaks corresponding to the acetate methyl protons (acetate-H1 at 2.0 ppm) and the two peaks diagnostic of the cysteamine-pantothenate (CP) part of CoA (CoA-CP-H10″ at 2.72 and CoA-CP-H7″ at 2.55 ppm) are reduced simultaneously during the enzymatic reaction. Selected portions of the ¹H-NMR spectra corresponding to protons belonging to the purine bases of ATP, AMP, CoA, and AcCoA provide additional information related to the progression of the reaction. One of the diagnostic peaks for the adenosine base of AMP (AMP-Ade-H8 at 8.66 ppm) increases, whereas the adenosine peak for ATP (ATP-Ade-H8 at 8.58 ppm) decreases as the enzyme converts more ATP, acetate, and CoA to AMP and AcCoA (Fig. 1, B and C). Manual peak assignment also shows a decrease in a peak belonging to the ribose of ATP (ATP-Rib-H5′ at 4.47 ppm). The time-course behavior for other peaks from AcCoA (Rib-H1′ at 6.23 ppm), CoA (Rib-H1′ at 6.23 ppm), ATP (Rib-H1′ at 6.23 ppm), and AMP (Rib-H1′ at 6.23 ppm) in this region is not immediately clear due to peak overlap (Fig. 1 D). Although manual identification of select peaks is possible, our purpose is to analyze NMR spectra using methods that are less dependent on manual inspection, and to identify additional peaks belonging to the same molecule so that variations in the intensities of these peaks can improve the precision of kinetic monitoring.

Figure 1.

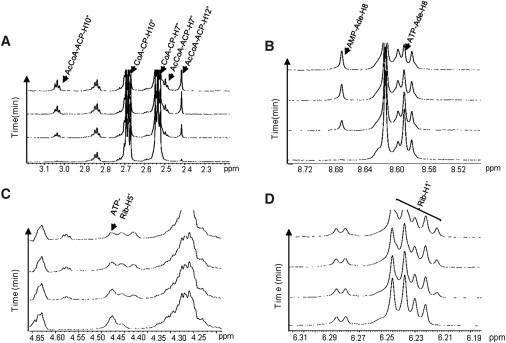
Real-time monitoring of ACS forward reaction by ¹H NMR. The NMR-based assays, consisting of ATP (1.2 mM), acetate (1.0 mM), CoA (2.0 mM), and ACS (12.5 μg), were carried out at 37°C in a 600 mHz spectrometer. The first spectrum was obtained ∼2 min after the addition of enzyme, and subsequently 299 spectra were collected over a 70 min period. Representative spectra in the time course are shown. Labeled abbreviations: Ade (adenosine), Rib (ribose), ACP (acetate-cysteamine-pantothenate). (A) A portion of the ¹H-observed, time-resolved spectra showing ACS conversion of CoA to AcCoA (diagnostic peaks of the protons belonging to the carbons of ACP regions at 2.2–3.2 ppm). (B) A portion of the spectra showing ACS conversion of ATP to AMP as AcCoA is synthesized (diagnostic peaks of the protons belonging to the carbons of the adenosine base of AMP or ATP at 8.4–8.7 ppm). (C) A portion of the spectra showing ACS conversion of ATP to AMP as AcCoA is synthesized (diagnostic peaks of the protons belonging to the carbons of the ribose region of ATP at 4.2–4.6 ppm). (D) A portion of the spectra showing the ribose regions (6.19–6.32 ppm) where peaks were not resolvable due to overlapping signals from different molecular species.

Mathematical deconvolution of superimposed peaks

To deconvolve superimposed peaks from experimental NMR data, the NMR spectra of individual metabolites expected to occur in the time-series assay were acquired at 1 mM. Compared with NMR-based enzyme reaction assays, these individual-metabolite standard spectra are usually of better quality (i.e., with a higher S/N ratio) because nontime-varying data can be averaged over longer periods of time to reduce noise. As explained in Experimental Procedures, the standard spectral peaks must first be aligned by NMF to match the locations of corresponding spectral peaks in the metabolic time-series spectra before they can be used to deconvolve the time-series spectra into concentration time courses.

Fig. 2 illustrates the simplest variant of this NMF alignment, in which we use only one well-resolved, isolated diagnostic peak that arises from only one single metabolite (CoA in this case) and does not overlap with spectral weight from any other metabolites. Fig. 2 A shows representative time-series data for a target diagnostic peak of CoA (CoA-CP-H10″). The asymmetric pattern of this peak is due to the second-order distortion, which was also observed in the CoA standard spectrum. Fig. 2 B shows a subset of the shifted diagnostic peaks that we generated from the observed CoA standard spectrum by applying small successive shifts in peak location. A rank-one variant of the NMF optimization method (described in Experimental Procedures) was used to find the best-fit amplitude vector a, which represents the time-series diagnostic peak as a superposition of the shifted diagnostic peaks generated from the standard. This results in a sharp maximum in the amplitudes plotted versus the diagnostic peak shift (Fig. 2 C), and identifies the best alignment location (marked with an X in Fig. 2 C). The corresponding shifted diagnostic peak of maximum amplitude is best aligned with the target diagnostic peak (Fig. 2 A) of the time series and it can be used as (part of) the aligned spectral standard to represent CoA in an MPSF deconvolution analysis of the spectral time series. We assessed errors in the MPSF alignment procedure by running the alignment algorithm 100 times and plotting the alignment probability distribution. The distribution widths (full width at half-maximum) averaged ∼4 × 10⁻⁴.

Figure 2.

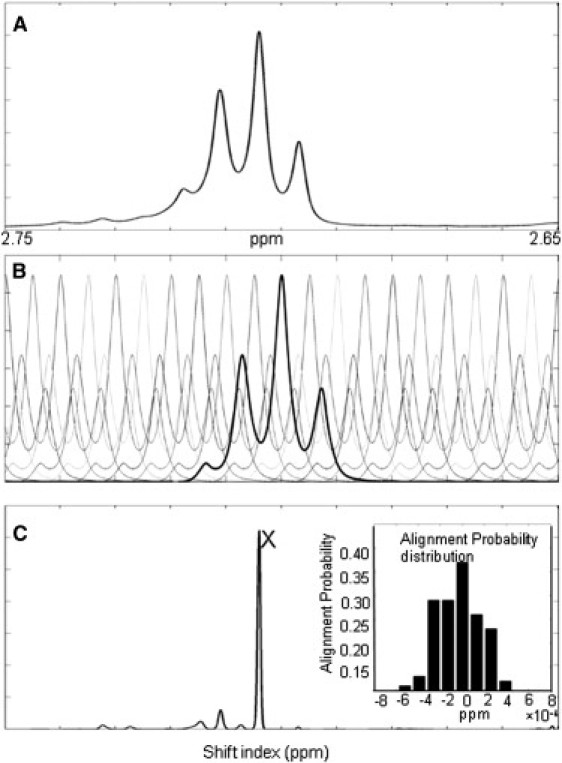
Determination of peak location. (A) A diagnostic peak (CoA-CP-H10″) from the time-series spectrum of the ACS forward reaction. The peak was used to find the best fit between the standard and the NMR time-resolved diagnostic peak. (B) A library of representative shifted diagnostic peaks (CoA-CP-H10″) from a premeasured CoA standard. For clarity, in this panel only a subset of the full library of shifted peaks is presented. The full library contains one shifted peak per grid point. (C) Estimation of peak location using NMD. A single large spike (denoted with an X) was picked out as the best fit of the location of the diagnostic peak. This optimization procedure was then repeated 100 times using random initial conditions to determine the probability distribution of alignment locations (C, inset).

By using this alignment procedure in the MPSF analysis, we were able to incorporate a much larger number of spectral peaks into the analysis, including nondiagnostic frequency regions in which multiple metabolite standards may have overlapped. We used the time-averaged spectrum of the NMR time-series data to determine which frequency windows to include in the fit by superposition of aligned spectral standards, because this spectrum contained the most abundant information. Some regions were excised because they had no relevant peaks and contributed only noise to MPSF fits. Other regions, such as the peak due to H₂O were also excluded. In Fig. 3, we plot two sets of spectral windows used for data fitting. In Fig. 3 B a set of windows surrounding only the easier-to-fit diagnostic peaks is depicted. Fig. 3 C depicts a set of spectral windows surrounding more peaks, including windows that are unusable for standard peak integration methods because peaks in these windows overlap significantly. Fig. 3, A and D, show details of the spectral information in panels B and C. The S/N ratio of fits increased as the number of peaks per aligned standard increased. We will now describe this MPSF method of first aligning the standards and then fitting multiple peaks to the data in more detail.

Figure 3.

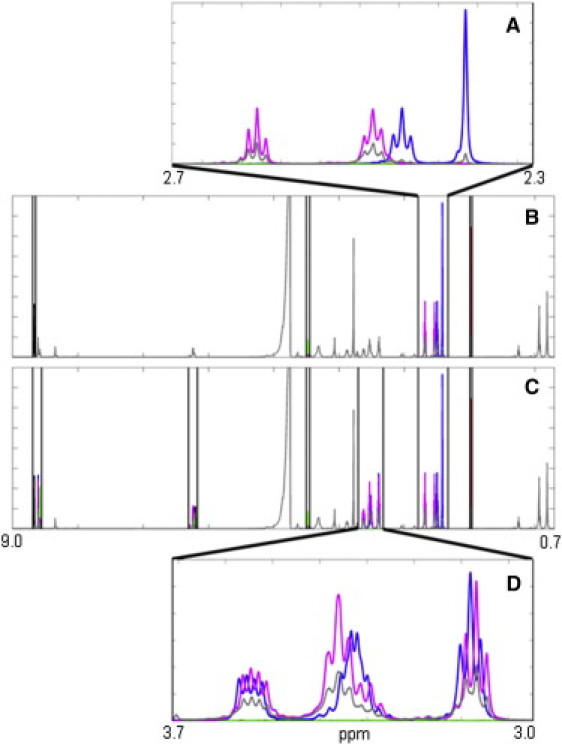
Choosing a location to perform peak fitting. (A) Detail of one of the diagnostic windows. (B) Diagnostic peak (i.e., relatively isolated peaks that are easy to distinguish from preacquired spectral standards) windows (indicated by vertical bars) used for peak location determination (using NMD) and an initial peak fitting analysis. Blue, AcCoA; red, acetate; black, AMP; green, ATP; magenta, CoA; dotted blue line, time-averaged spectrum from experiment. (C) A larger set of windows used for MPSF. Vertical bars demarcate the spectral windows used. (D) Detail of a window in which multiple peaks overlap. Once the exact location of the spectral standards has been determined, the overlapping spectra in this window are used to perform MPSF.

First, all known initial reactants (CoA, acetate, and ATP) were used to fit to the experimental data (Fig. 4, B and C). When we compare the best fit with experimental data, it is clear that a number of peaks (indicated by arrows) are unaccounted for. AMP is expected to be a product of the reaction; therefore, the initial reactants plus AMP were included to obtain a new, better fit (Fig. 4, C and D). Because the obvious remaining peak in the acetyl group is likely to be the product AcCoA, this standard is also used in the fit. The AcCoA standard also has a CP group and spectral contributions from this group. Including these signals allows for a better fit in both regions, further reducing the residual (Fig. 4, D and E).

Figure 4.

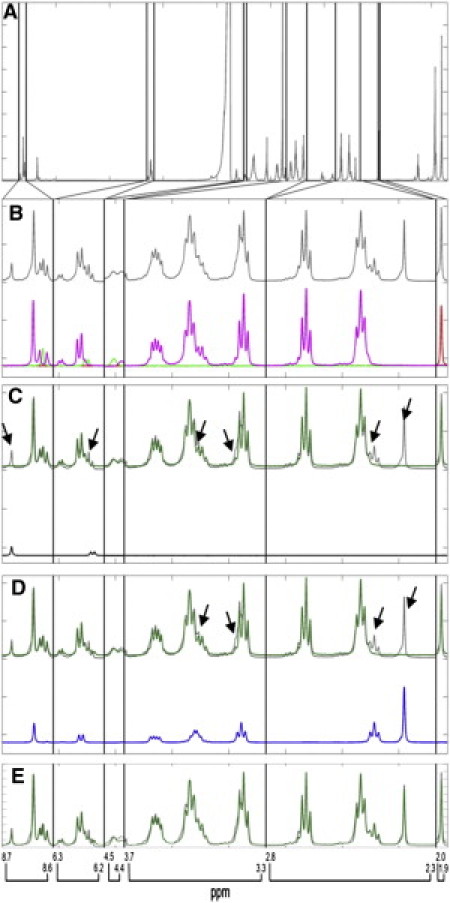
MPSF. (A) Average spectrum from experimental data. Spectral windows used in data fitting are denoted by vertical black lines. (B) Experimental data fit with spectral standards for the initial reactants. The top traces in this panel are experimental data (gray). The bottom traces show the actual standards at the fit amplitudes (red, acetate; green, ATP; and magenta, CoA). (C) Experimental data fit with the product AMP (black). The upper part shows the experimental data (gray) and the combined fit of ATP, acetate, and CoA standards (dark green). Arrows point to the peaks that are unaccounted for when spectra of ATP, acetate, and CoA are used to fit the experimental data. The lower part shows the actual AMP standard at the fit amplitude. (D) Experimental data fit with another product AcCoA (blue). The upper part shows the experimental data (gray) and the combined fit of ATP, acetate, CoA, and AMP standards (dark green). Arrows point to the peaks that were left when spectra of ATP, acetate, AMP, and CoA were used to fit the experimental data. The lower part shows the actual AcCoA standard at the fit amplitude. (E) Experimental data (gray) fit with AcCoA, acetate, AMP, ATP, and CoA standards (dark green).

To demonstrate the improvement in S/N ratio from MPSF, in Fig. 5 we compare the metabolite concentration estimates of ATP and AMP for the two data-processing methods (diagnostic NMR resonance PIBS and MPSF) using all of the peaks in the windows shown in Fig. 3 C. Error bars for the MPSF fit were generated as described in Experimental Procedures. Note that the S/N ratio is improved by an order of magnitude when the MPSF used the largest set of spectral windows. With this method, the concentrations of substrates and products were determined as a function of time and the results were used as input to reconstruct the metabolic network of the ACS-catalyzed reaction.

Figure 5.

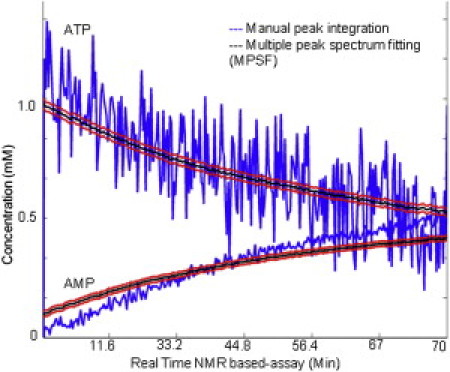
Improved S/N ratio of concentrations of metabolites obtained by least-squares peak fitting. (Blue line) time course generated by PIBS using NMR operation software Vnmrj (Palo Alto, CA). (Red/black lines) MPSF using selected windows (Fig. 3C). The black line denotes the mean, and red lines denote 2-σ error bars (see Experimental Procedures for the error bar determination method). Fitting peaks in multiple windows by MPSF gives an order of magnitude improvement in concentration estimation.

Network reconstruction of the AtACS-catalyzed reaction

Previous studies have examined the activity of ACS in detail in both bacteria and vertebrate animals (14), and argued for the existence of an enzyme-bound intermediate, acetyl-AMP. Here we wanted to simulate a metabolic network for plant ACS based on NMR data without a preconceived requirement for this intermediate. The ACS enzyme network must at a minimum accommodate three substrates (ATP, acetate, CoA), an enzyme (E), and three products (PPi, AMP, and AcCoA), based on the assay derived by NMR and high-performance liquid chromatography data. In addition, any number of enzyme-bound intermediates or side products (E/substrates, E/intermediates, E/products, intermediate, Pi, and ADP) that cannot be observed or distinguished from other metabolites in NMR analysis due to the limitations of detection, are postulated and included into the network. In the four model network diagrams shown in Fig. 6 A, each compound is represented as a rectangular node, and each forward-backward reaction step pair is represented as a circular node. For clarity, the substrate and product flux directions are indicated by arrows for forward reaction steps only; for corresponding backward reaction steps, the arrow directions are reversed.

Figure 6.

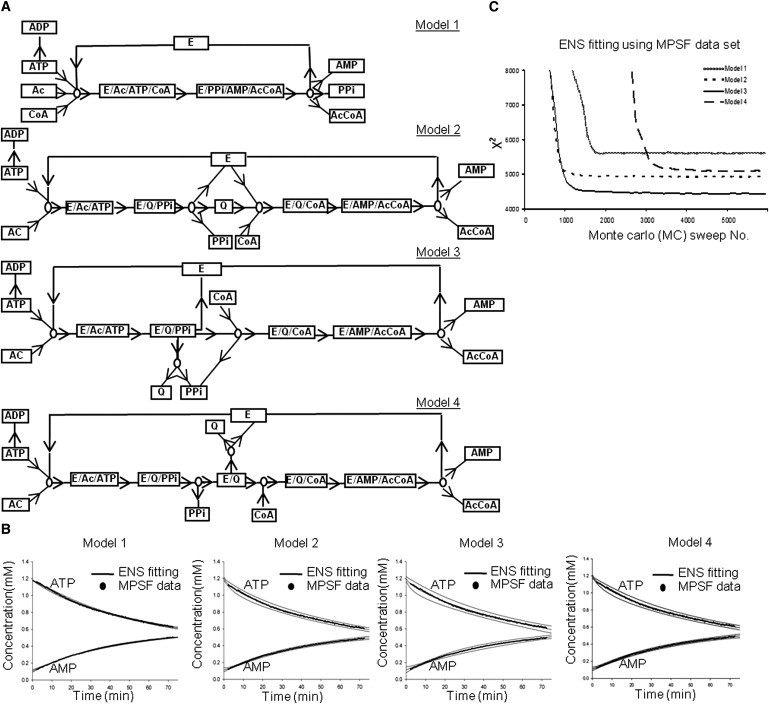
Network reconstruction of the ACS-catalyzed reaction using the MPSF-processed data set. (A) Schematic representation of models 1–4 for the ACS-catalyzed reaction. For clarity, only forward reaction steps are shown, but all corresponding backward reaction steps (with arrow directions reversed) are included in each model, except for the backward step of ATP→ADP, which is treated as irreversible. E, enzyme; Q, acetyl-AMP. (B) Time course of concentrations of AMP and ATP show how the ENS results fit the MPSF-processed experimental data for different models. Dots represents the MPSF experimental data, and solid lines represent ENS results by the ensemble mean (middle line) and uncertainty bands with two ensemble standard deviations around the mean (upper and lower lines). (C) The χ²-values of ENS MC random walk process versus the MC sweep number for the MPSF-processed data set with 6000 MC sweeps, starting from a random rate coefficient (random θ) MC initialization. One of 20 repetitions (restarts) of this MC process is shown in C.

Model 1 (Fig. 6 A) constitutes the simplest possible mechanism for the conversion of ATP, acetate, and CoA into AcCoA and PPi. It has just one single intermediate E/substrate complex and one E/product complex. In contrast to other possible models, model 1 neither allows nor requires the production of additional intermediates in either an enzyme-bound form or as a free molecule. In the other three models (models 2–4), an acetyl-AMP intermediate (denoted by Q) was introduced into the reaction network based on previous studies of ACS from bovine, which suggested that animal ACS-catalyzed reactions are carried out through an enzyme-bound acetyl-AMP (15). It is possible that plant ACS also follows the same reaction network. As shown in Fig. 6 A, model 2 suggests that the release of acetyl-AMP from the enzyme is required for reaction. In model 3, acetyl-AMP is functional as an enzyme-bound intermediate for the entire reaction. The release of acetyl-AMP is not required, but is allowed as a nonessential side product. Such side products could in fact hinder the enzymatic conversion if they were endowed with a substantial rate coefficient. Model 4, which was derived from model 3, required an enzyme-bound intermediate for the reaction. The difference between models 3 and 4 is that the substrates and products are incorporated or released at different points along the pathway.

Each model was used to perform an ENS and predict the time courses of concentrations of substrates and products for comparison with each of the two sets of concentration time-series data (one data set derived by the NMR software integration program (PIBS), and the other by the MPSF method as described in Experimental Procedures). Fig. 6 B and Fig. S2 A show how the ENS means for each model fit the MPSF-processed time-series data for all metabolites. To further demonstrate which model fits the experimental data better, we calculated the residuals of each reactant and enzymatic product by subtracting the ENS means from the experimental data. As an example, the residuals of AMP are plotted against time in Fig. S3. At most of the time points, the residuals acquired from models 1 and 4 are larger than the ones obtained from models 2 and 3. This result suggests that models 2 and 3 might give a better fit to the experimental data than models 1 and 4. Fig. 6 C and Fig. S2 B show the corresponding variations in the χ²-function as the model parameter space is searched by the ENS MC random walk process. As explained in the Supporting Material, the χ² function measures the deviation between model and data, and guides the random walk toward an improved quality of fit. This random walk process is started and restarted 20 times, each time with a new random model parameter initialization. Convergence to similar χ²-values after most (re)starts supports the adequacy of the search time. As explained in the Supporting Material, only (re)starts that converged with an average χ² < χ_max² = 6000 are included in the ENS grand averages shown in Fig. 6 B and Fig. S2 A. Model 1 provides a significantly worse fit to the data than any of the other models, and model 3 provides a substantially better fit than all other models, for both data sets. The fits by model 4 are worse than those of model 2. The ENS χ² results thus clearly discriminate between the four models in terms of quality of fit, and suggest that model 3 is the most compatible with the data. This indicates that the ACS-catalyzed reaction is carried out through an enzyme-bound intermediate while allowing for nonproductive release of the intermediate before CoA addition. Further conceptual and technical details of the ENS fitting and model discrimination procedure are discussed in the Supporting Material, including assessments of statistical significance, and uncertainties in the underlying model parameterizations, as listed in Table S2.

Overall, the χ²-values for the PIBS-processed data set, as shown in Fig. S2 B, are about a factor of 4 larger than those of the MPSF-processed data for all four models, but the rank ordering of the four models in terms of the best χ²-values is basically the same for both data sets. In an acceptable fit, χ² should be on the order of the number of experimental input data points J, i.e., of order J = 3878 and 2995 for PIBS and MPSF, respectively. As shown in Fig. 6 C, only model 3 and (just barely) model 2 meet the acceptable-fit criterion, and they do so only for the MPSF data set. This suggests that the PIBS procedure may in fact introduce substantial additional systematic errors, possibly associated with poor baseline representation in the commercial fitting and peak integration software.

Discussion

Because of its nondestructive properties, quantitative ¹H NMR is an ideal approach for monitoring real-time metabolic reactions in vitro or in vivo. Most previous studies relied on the integration of well-defined peaks and ignored overlapping peaks (7). It is well known that the accuracy of conventional peak integration depends on how well the peaks are isolated and how well the baseline has been corrected (8). However, in most metabolic reactions, the overlapping peaks contain critical information, and by ignoring them we sacrifice important opportunities to improve the precision of the concentration measurements and identification of underlying compounds. The approach we developed here allowed us to deconvolve overlapping peaks. By fitting a larger number of peaks, we were able to achieve a much better S/N ratio than we could have using traditional integration of only well-resolved peaks. Furthermore, we were able to uncover peaks from underlying previously unidentified metabolites.

The ENS method was developed to reconstruct kinetic network systems from partial information. In this study, using the time-course concentration variations of substrates and products, we found that ENS favored a model in which the plant ACS-catalyzed reaction was carried out through an enzyme-bound intermediate. This result is in line with the enzymatic mechanisms suggested for ACS enzymes from other species (14).

It is important to note that selection among models does not mean that the selected model represents a unique solution. Given the distinction among models 1–3, however, it is appropriate to discuss how the data provided made this distinction, especially in the absence of data regarding the product PPi and the released intermediate product Q. In model 1, the rate of product production will always depend on the product of all three reactants (CoA, acetate, and ATP). In model 2 or 3, there can be regimes in which acetate and ATP saturate the enzyme and the rate of production will depend only on the enzyme and CoA concentrations. It is harder to see how models 2–4 are distinguished. However, a possible explanation is that there is a disconnection in the stoichiometry for production of the products AMP and AcCoA from ATP and acetate in the actual experiment. The difference is then accounted for by the release of Q as a side-product in model 3. Since Q is not observed, it can remain as Q at a level under the limit of the instrumental detection, or it can be further degraded into unobservable products whose signals might be obscured by those of products produced in other steps. For example, if acetyl-AMP is the intermediate, it might dissociate in the actual experiment into AMP and acetate (one of the starting materials and one of the products of the overall reaction) without the production of AcCoA. This dissociation process is not included in either model, but model 3 has greater flexibility to reproduce the net effect of this process on the stoichiometry by releasing Q as a side-product without unduly constraining the rate coefficients for the main ACS conversion pathway.

Conclusions

The procedures described above are broadly applicable to a variety of metabolic processes. Although the proton NMR methodology described is a nearly universal means of monitoring participants in enzyme-catalyzed reactions, it is not completely universal, in that we did not detect nonprotonated participants such as PPi. However, it is possible to carry out ³¹P observation, and recent instrumental advances have provided the means of doing this simultaneously with ¹H observation (16). There are also obvious improvements that can be made to our method, one of which is the development of a more integrated data-reduction, network-analysis procedure. The data-reduction procedure will also benefit from the development of metabolite databases. Studies to that end are already under way in other laboratories (17,18). Network analysis is also not limited to single enzymes, and modeling of coupled enzyme systems is certainly possible. Extensions of the NMF and ENS methods can deal effectively with incomplete data sets in which time series have been observed only for a subset of metabolites (9–11,19). The ENS approach presented here assumes that a candidate set of fixed model network topologies is provided as a known input into the simulation. The method can be extended to deal with and extract topological information for systems of partially unknown network topology. The limitations and possible extensions of both NMF and ENS are discussed further in the Supporting Material. Future applications even to whole-cell systems can be anticipated.