Probing Single-Molecule Enzyme Active-Site Conformational State Intermittent Coherence

Abstract

The relationship between protein conformational dynamics and enzymatic reactions has been a fundamental focus in modern enzymology. Using single-molecule Fluorescence Resonance Energy Transfer (FRET) with a combined statistical data analysis approach, we have identified the intermittently appearing coherence of the enzymatic conformational state from the recorded single molecule intensity-time trajectories of enzyme 6-Hydroxymethyl-7,8-dihydropterin pyrophosphokinase (HPPK) in catalytic reaction. The coherent conformational state dynamics suggests that the enzymatic catalysis involves a multi-step conformational motion along the coordinates of substrate-enzyme complex formation and product releasing, presenting as an extreme dynamic behavior intrinsically related to the time bunching effect that we have reported previously. The coherence frequency, identified by statistical results of the correlation function analysis from single-molecule FRET trajectories, increases with the increasing substrate concentrations. The intermittent coherence in conformational state changes at the enzymatic reaction active site is likely to be common and exist in other conformation regulated enzymatic reactions. Our results of HPPK interaction with substrate support a multiple-conformational state model, being consistent with a complementary conformation selection and induced-fit enzymatic loop-gated conformational change mechanism in substrate-enzyme active complex formation.

Introduction

Enzymatic reactions involving complex dynamics of substrate-enzyme binding, substrate-enzyme complex formation, catalytic reaction, and product releasing, typically show temporal and spatial inhomogenieties.^1–4 Single-molecule enzymology approaches are powerful in characterizing such complex dynamics by probing one enzyme molecule at a time, recording single-molecule time trajectories of specific conformational changes and catalytic turnover cycles.^5–11 The conformational dynamics of the enzymatic active-site motions and the mechanism between enzyme conformational changes and substrate turnover are under intensive studies, and the relationship between enzyme conformational dynamics and enzymatic reaction turnovers has been a fundamental focus in modern enzymology.^{4, 12–22} Here we report an observation of coherent active-site conformational dynamics of the enzyme 6-hydroxymethyl-7,8-dihydropterin pyrophosphokinase (HPPK) in catalyzing pyrophosphorylation reaction.

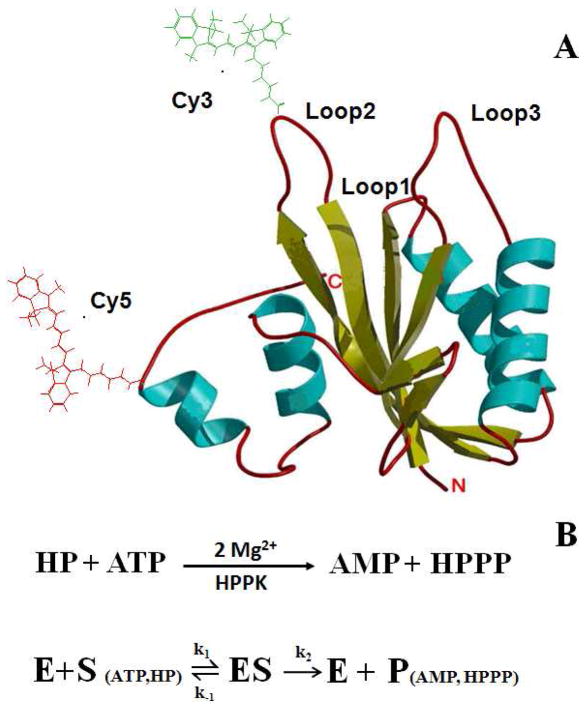
HPPK, an 18 kDa 158-residue monomeric protein (Figure 1A), catalyzes the pyrophosphorylation reaction for the formation of 6-hydroxymethyl-7,8-dihydropterin pyrophosphate (HPPP) from 6-hydroxymethyl-7,8-dihydropterin (HP) reacting with adenosine-5′-triphosphate (ATP) (Figure 1B), and leads to the biosynthesis of folates, a vitamin essential for life.^{23, 24} HPPK consists of three flexible catalytic loops that are critical to the enzymatic reaction activity.^{23, 24} Among the three catalytic loops, loop 2 and loop 3 undergo significant open-close conformational changes in each catalytic cycle, correlating with substrate (HP and ATP) binding and product (HPPP and AMP) releasing. It has been shown that the residues in loop 2 bind with one of the substrates, HP, while the residues in loop 3 interact with the substrate, ATP. ^{23, 24}

Figure 1.

(A) Crystal Structure of the Apo HPPK. The cyan spirals represent the α helices and the yellow arrows are the β strands. The loops are shown in red pipes. Amino acid residue 48 and 151 are labeled with FRET dye pair Cy3 and Cy5, respectively. The drawing is derived from the Protein Data Bank (1HKA). (B) Enzymatic reaction of HPPK-catalyzed pyrophosphoryl transfer. The dynamic processes involve (1) the binding of two substrates (ATP and HP) to the enzyme (E) to form the enzyme-substrate complex (ES); (2) the enzymatic turnover of the enzyme-substrate complex and the release of products (P).

Materials and Methods

Sample preparation and characterization

The HPPK was mutated with residues 48 on loop 2 and residue 151 near the C-terminal helix both replaced by cysteine. A fluorescent dye pair Cy3/Cy5 was attached to the mutated enzyme with thiolation. The two mutations were designed to monitor the conformational dynamics of loop 2 as the distance of the two residues changes most significantly through the catalytic cycles of HPPK. In our experiments, the samples for single-molecule enzymatic reaction measurements were made by mixing 10μl enzyme-substrates solution with 10μl 1% agarose gel in between two clean glass cover slips to form a sandwich. All the solutions and agarose gel are prepared with 100 mM Tris-HCl buffer and 10 mM MgCl₂ at pH 8.3. In addition, the oxygen scavenger solution containing a mixed 0.8% D-glucose, 1mg/ml glucose oxidase, 0.04mg/ml catalase, and about 1mM of 6-hydroxy-2,5,7,8-tetramethylchroman-2-carboxylic acid (Trolox) were added to protect the FRET dye molecules from possible photobleaching or blinking due to triplet state formation.^{25, 26} (see supporting information, Supplementary 1 for details)

Single-molecule imaging and FRET measurement

We have used the single-molecule photon stamping approach^{3, 27, 28} to record the single-molecule FRET fluctuation time trajectories photon-by-photon for both the donor and acceptor simultaneously. A detailed description of the experimental setup has been published elsewhere.^{27, 28} (see supporting information, Supplementary 2 for details)

Correlation function analyses

We have used a multiple approach of correlation function analysis, including 2^nd order autocorrelation function and cross-correlation function calculated from two-band fluctuation trajectories ({I_A(t)} and {I_D(t)}) to analyze the single-molecule FRET fluctuation dynamics. The time-dependent strength between the two fluctuating variables of I_A(t) and I_D(t) is evaluated by the cross correlation (C_cross(t)) functions.^29–34 The cross-correlation (C_cross(t)) functions are defined by Eq 1 and Eq 2.

$$C_{\mathit{cross}}(t)=\langle \mathrm{\Delta }{I}_A(0)\mathrm{\Delta }{I}_D(t)\rangle /\langle \mathrm{\Delta }{I}_A(0)\mathrm{\Delta }{I}_D(0)\rangle =\langle (I_A(0)-\langle I_A\rangle )(I_D(t)-\langle I_D\rangle )\rangle /\langle (I_A(0)-\langle I_A\rangle )(I_D(0)-\langle I_D\rangle )\rangle$$ (1)

When I_A= I_D, we have autocorrelation function,

$$C_{\mathit{auto}}(t)=\langle \mathrm{\Delta }{I}_A(0)\mathrm{\Delta }{I}_A(t)\rangle /\langle \mathrm{\Delta }{I}_A{(0)}^2\rangle =\langle (I_A(0)-\langle I_A\rangle )(I_A(t)-\langle I_A\rangle )\rangle /\langle {(I_A(0)-\langle I_A\rangle )}^2\rangle$$ (2)

where I_A(t) and I_D(t) represent the signal variables measured in time trajectories {I_A(t)} and {I_D(t)}. < I_A > and < I_D > are the means of the fluctuation trajectories of {I_A(t)} and {I_D(t)}, respectively. In our analyses, {I_A(t)} and {I_D(t)} are the time trajectories of fluorescence photon counts or intensities.

2D regional correlation mapping analysis

The primary analytical approach of the 2D regional correlation analysis is to calculate a two-dimensional cross-correlation function amplitude distribution (TCAD). In this analysis, a start time and a stop time, t_start and t_stop, are scanned to chose the calculation of cross-correlation function from a pair of signal intensity time trajectories, {I_A(t)} and {I_D(t)}. The two scanning parameters, t_start and t_stop, define the start time (t_start) and the time lapse (from t_start to t_stop) of a cross-correlation function calculation window along a two-band fluctuation signal trajectory. This 2D calculation gives a cross-correlation for defined segments from t_start to t_stop as:

$$C_{\mathit{cross}}(\tau ,t_{\text{start},}:t_{\text{stop}})=\underset{t_{\mathit{start}}}{\overset{t_{\mathit{stop}}}{\int }}{I}_A(t)I_D(t-\tau )dt=\sum _{t_{\mathit{start}}}^{t_{\mathit{stop}}}{I}_A(t)I_D(t-\tau )$$ (3)

The initial amplitude of C(τ, t_start: t_stop ) was presented by the difference between the first n points and the next n + m points from τ = 0:

$$\zeta =\{<\text{C}(1:\text{n})>\}-\{<\text{C}(\text{n}+1:\text{n}+\text{m})>\}$$ (4)

The index n and m defines the precision of calculated initial amplitude, ζ, of the correlation function. In our analysis, we chose n = m = 5, which is sufficient to obtain a reliable value of ζ from the calculated cross-correlation function. As a function of t_start and t_stop, the value of ζ is plotted as a 2D map of t_start to t_stop. A hot color represents positive amplitude of C(τ) and a cold color represents negative amplitude of C(τ). Positive amplitude indicates correlation, and negative amplitude indicates anti-correlation.

Results and Discussion

Coherence of enzymatic conformational state in catalysis reaction

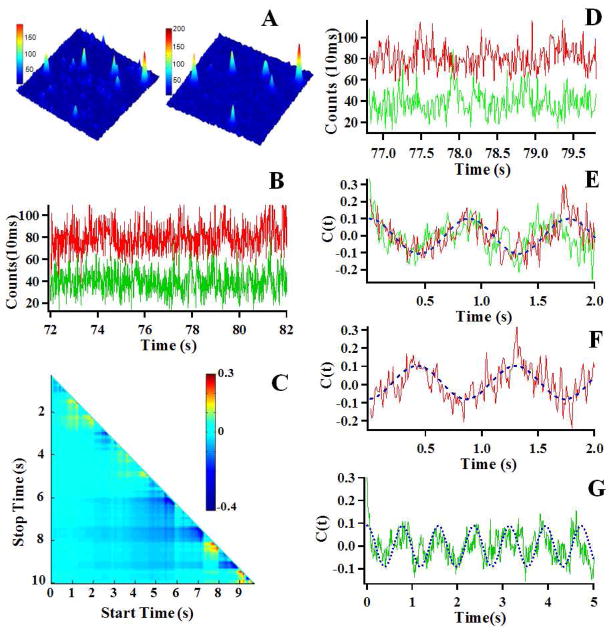
Figure 2A shows FRET donor-acceptor (D-A) two-channel fluorescence images of single HPPK molecules labeled with Cy3 and Cy5 in the presence of 100 μM ATP and 100 μM HP. Each individual peak in the images is attributed to a single HPPK molecule. FRET D-A distance varies with protein conformational changes thereby resulting in both donor and acceptor fluorescence intensity fluctuations. Figure 2B shows a portion of the intensity-time trajectories of the donor ({I_D(t)}, green) and acceptor ({I_A(t)}, red) labeled HPPK in the presence of substrates. Typically, single-molecule D-A fluorescence intensity fluctuations recorded from a single protein molecule involve anti-correlated fluctuations resulting from FRET, thermal-driven correlated or non-correlated fluctuations, and inherent measurement noise. Applying two-dimensional cross-correlation function amplitude distribution (TCAD) to analyze the D-A fluorescence time trajectories^{35, 36} (Figure 2C), we are able to identify the segments that show dominated anti-correlated fluctuations from FRET, therefore, exclusively analyzing the single-molecule conformational dynamics from a rather complex fluctuation background.

Figure 2.

(A) Single molecule fluorescence images (10μm×10μm) of Cy3 and Cy5 labeled HPPK in the presence of 100 μM ATP and 100 μM HP. The emission is from the Cy3 (Left) and Cy5 (Right) dyes attached to the HPPK enzyme. (B) A part of the single-molecule intensity-time trajectories of the donor (Cy3, Green) and acceptor (Cy5, Red) labeled on HPPK in the presence of 100 μM ATP and 100 μM HP. (C) The result of TCAD analysis on the single-molecule donor-acceptor fluorescence intensity trajectories shown in 2B. The cold color represents that the D-A is anti-correlated, whereas the warm color represents that the D-A is correlated. (D) A part of the single-molecule intensity-time trajectories of the donor and acceptor from the long trajectories shown in 2B, the anti-correlated fluctuation features are evident. (E) Autocorrelation functions (C(t)_AA and C(t)_DD) of the donor (Green) and the acceptor (Red) from the single-molecule intensity-time trajectories shown in 2D, the fitted (blue) oscillatory frequency is 1.2±0.1 s⁻¹ (F) Cross-correlation function (C(t)_AD) from the single-molecule intensity-time trajectories shown in 2D, the fitted (blue) coherence frequency is 1.2±0.1 s⁻¹, the same as C(t)_AA and C(t)_DD. The result of the same decay rates of the three correlation functions calculated from the single-molecule D-A single time trajectories indicates that the fluctuation dynamics is originated from the same origin, i.e., single-molecule FRET fluctuations associated with conformational change fluctuations of HPPK. (G) Autocorrelation C(t)_DD) of the donor (Green) from the single molecule intensity-time trajectories shown in 2B, dephasing appears in ~4.5 seconds.

We have observed the coherence of active-site conformational changes involved in HPPK enzymatic reaction cycles. A significant portion of D-A intensity-time trajectories (Figure 2D) shows intermittent temporal coherence in enzymatic conformational state changes, evidenced by the coherence features in both the autocorrelation functions (Figure 2E) and cross-correlation functions (Figure 2F) calculated from the single-molecule D-A intensity time trajectories (Figure 2D). Specifically, an initial rising from a negative amplitude to zero shown in the cross-correlation function (Figure 2F) indicates a typical anti-correlated dynamic behavior of fluctuations, followed by a coherence pattern at a time scale of sub-seconds. Both autocorrelation function and cross-correlation function show the same coherence frequencies, which indicates that the coherence is originated from the same process, i.e., conformational changes probed by single-molecule FRET. We attribute the coherence to the reoccurrence of enzymatic conformational state in the enzymatic reaction cycles. The coherence stays for as long as ~4.5 seconds (Figure 2G), corresponding to a narrow distribution of the open-close conformational state dwelling times. Here we emphasize that what we have observed is the conformational active-site state change coherence, i.e., the active-site open-close event occurrence shows coherence. The coherence only intermittently appears in the correlation function calculated from a single-molecule conformational fluctuation trajectory.

Substrate concentration dependence of the conformational state changes

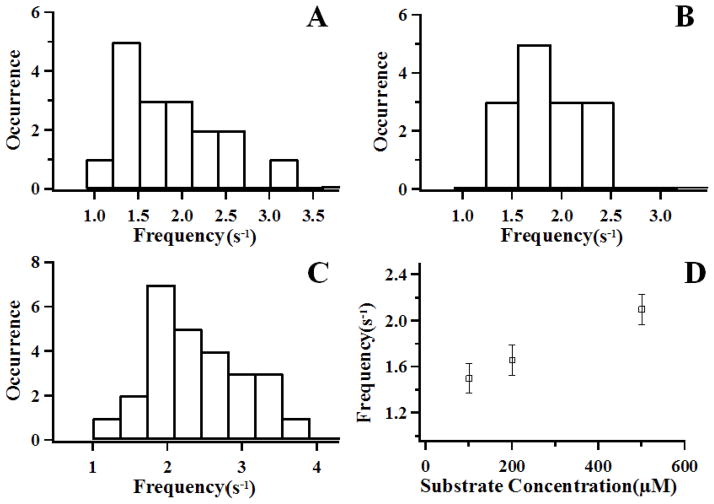
Figure 3A–3C show distributions of coherence frequency of ~1 to 4 s⁻¹ calculated from the correlation functions of the single-molecule trajectories measured under three different substrate concentrations of 100, 200, and 500 μM for both HP and ATP. Our results indicate that the coherence frequency is concentration dependent (Figure 3D), increasing from 1.5±0.1 to 2.1±0.1 s⁻¹ as the substrate concentration increase from 100μM to 500μM. We have conducted a further control experiment to verify that the coherence is not laser-driven (see supporting information, Supplementary 3 for details). Our results strongly suggest that the conformational state changes are induced by the substrate-enzyme interactions in forming the reactive complex. Furthermore, the frequency of the open-close conformational changes can be higher than the enzymatic reaction turnovers rate ~ 0.7 s⁻¹ at the saturating concentration of ~200 μM from ensemble-averaged measurements.³⁷ The observation of substrate-dependent conformational open-close change rates beyond the enzymatic reaction turnover rate (Figure 3) suggests that the open-close conformational state changes involve both productive and non-productive substrate-enzyme complex formations, and both the dissociation of active complex and the releasing of product regulate the opening motion of loop 2 at the active site of HPPK enzyme.

Figure 3.

The distributions of coherence frequency of the conformational change fluctuations under enzymatic reactions with various substrate concentrations. (A) 100μM ATP + 100μM HP; (B) 200μM ATP + 200μM HP; (C) 500μM ATP + 500μM HP; (D) Statistical results of coherence frequency distribution in enzymatic reaction under various substrate concentrations.

We have developed a two-dimensional correlation analysis approach to reveal the anti-correlated FRET donor-acceptor (D-A) fluorescence fluctuations from a noise and thermal fluctuation background.^{35, 36} In a single-molecule FRET measurement of protein conformational dynamics, the measured D-A fluorescence intensity trajectories should show the anti-correlated D-A intensity fluctuations associated with the D-A distance fluctuations. On the other hand, local-environment thermal fluctuations typically give correlated or non-correlated D-A florescence intensity fluctuations. Specifically, measurement noise, fluctuations beyond the measurement time resolution, and the thermal fluctuations of the local environment often intermittently dominate segments of a trajectory to show correlated or non-correlated fluctuations.^{35, 36} Practically, an overall calculation of time-correlation function may not reveal the intermittently-appearing anti-correlated FRET fluctuation, or even show correlated thermal fluctuations.³⁸ Our 2D regional correlation analysis method is capable of identifying the FRET D-A anti-correlated fluorescence intensity fluctuations at any segments of an experimental fluctuation time trajectory, which is not possible for a conventional correlation analysis to average over across the whole time trajectory. Using the 2D regional correlation analysis, by scanning the start point and end point along a fluctuation trajectory or a pair of fluctuation trajectories, we are able to identify whether a fluctuation in a specific segment is correlated, anti-correlated, or non-correlated. For each segment selected by 2D regional correlation analysis, a conventional correlation analysis can be applied to each specific segment to obtain detailed fluctuation dynamics.

Enzyme-substrate interactions regulate enzymatic conformational fluctuation

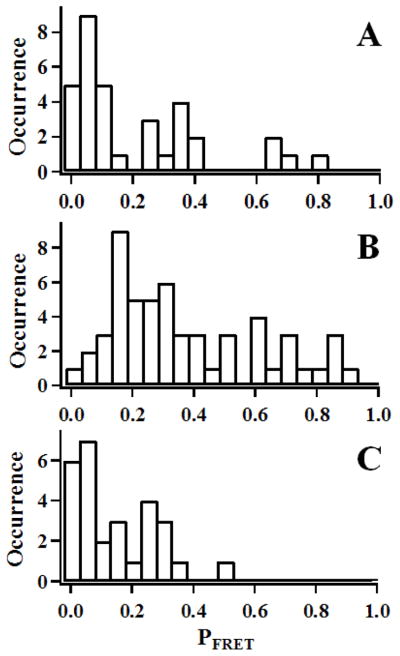
By using the TCAD,^{35, 36} we have analyzed single-molecule time trajectories of HPPK under different reaction conditions, including apo-HPPK, HPPK with substrate ATP+HP, and HPPK with inhibitor. The appearances of the anti-correlated FRET fluctuations are intermittent in nature. The appearance probability (P_FRET) presents the fraction that D-A signals are anti-correlated and resolved from the TCAD analysis. Figure 4 shows the histograms of the P_FRET distributions measured under different conditions. It is apparent that the P_FRET is significantly higher when the enzyme is under an enzymatic reaction condition with substrates (Figure 4B) than that when the enzyme is under the condition without substrates (Figure 4A), or with the inhibitor AMPCPP (Figure 4C). These results suggest that: (1) the conformational change fluctuations exist under the conditions of both with and without substrates; (2) for the fluctuation periods without apparent anti-correlation, the FRET fluctuations most likely exist but are buried in the background of correlated and non-correlated thermal fluctuations. It is highly possible that the real FRET fluctuation P_FRET is much higher than what we have detected in experiments; and (3) our results suggest that both the conformational selection mechanism and the induced fit mechanism are likely complementary for the HPPK enzyme-substrate conformational dynamics. Conformational selection mechanism dominates the protein conformational fluctuation at non-specific binding between the substrate and enzyme. This is evidenced by the P_FRET distributions (Figure 4): The distribution of the P_FRET is broad for the apo HPPK but much narrower in the presence of the substrates or inhibitor. Ligand binding to the apo HPPK active site changes the HPPK conformational state distributions to a much selected narrow subset; whereas the induced fit mechanism dominates the specific binding between the substrate and active site of the enzyme in forming active substrate-enzyme complex ready to react, which results in the appearance of the coherence in conformational dynamics. Our attribution is also consistent with recent reported works on the effects of enzyme-substrate interactions on conformational transitions of other enzymes.^39–42 In the absence of substrates, the enzyme explores a wide range of conformational space and consequently undergoes accessible conformational changes at broad time scale; and when substrates present, the conformational changes are regulated by the interactions between the enzyme and the substrate, so the time scale of these conformational changes is bunched up to a narrow scale. Through hydrogen bonding, electrostatic interactions, and solvent fluctuations, the substrates play an induced-fit role in regulating conformational change fluctuation patterns and rates under a thermal fluctuation local environment at the enzyme active site. For example, the inhibitor, AMPCPP, locks loop3 and leads to a non-functional motion of loop 3 and loop2. Comparing the loop motions of the apo-HPPK and HPPK-AMPCPP-HP complex states, it seems that non-functional conformational changes are similar, but functional conformational changes are selected and regulated by the enzymatic reaction conditions. We attribute the observed active-site conformational state change coherence to the enzyme-substrate interactions that associate with static electric field interactions, and covalent and non-covalent chemical interactions.

Figure 4.

The anti-correlated FRET signal appearance probability (P_FRET) from 2D regional correlation function analysis of single-molecule time trajectory. The P_FRET presents the ratio of the cumulated time duration of detected FRET anti-correlated signal fluctuations versus the total time length of the single-molecule signal time trajectories. The histograms show the statistical distributions of detected FRET with anti-correlated D-A intensity fluctuations when HPPK enzyme under different conditions: (A) apo HPPK, (B) under an enzymatic reaction condition with the presence of 100 μM ATP and 100 μM HP, (C) in the presence of an enzyme inhibitor, 100 μM AMPCPP (α,β-Methylene adenosine 5′-triphosphate) and 100 μM HP.

We rule out the possibility that the measured conformational dynamics is due to dye (Cy3 and Cy5)-protein interactions on the experimental time scale based on the following evidence: (1) the dynamics of measured enzymatic conformation and the dynamics of labeled dye molecules on protein are in different time scales from that of the protein active-site open-close conformational fluctuations. The measured enzymatic conformational dynamics here are on the millisecond to second time scale; whereas the hydrodynamic motions of the labeled dyes are on the nanosecond time scale,⁴³ which has been experimental proved by our previous³ and the present single-molecule anisotropy results (Figure S2); (2) the intermittent coherence in enzymatic conformational state dynamics are observed only when the HPPK enzyme is under the catalytic reaction condition in the presence of substrate ATP and HP, and the coherence frequency is substrate concentration dependent as shown in Figure 3. We did not observe the intermittent coherence in the conformational state dynamics in the absence of substrates, although apo-HPPK conformational fluctuations are observable.

We have recently reported a time bunching effect on the hinge-bending conformational motion dynamics of T4 lysozyme under enzymatic reaction conditions.^{27, 44} The two domains of the T4 lysozyme involved in the open-close hinge-bending motions in open up for forming non-specific enzyme-substrate (polyssaciride) and close down to form enzyme-substrate active complex, resulting in chemical reaction followed by product release. The bunching effect indicates that the hinge-bending open-close motion time is narrowly distributed or bunched in a Gaussian-like distribution with a defined second moment. We have attributed the bunching effect to consecutive multiple-step conformational motions, i.e., the Gaussian distribution is a result of the convolution of multiple and consecutive Poisson rate processes. Apparently, the coherence in the enzyme conformational state changes of the HPPK loop 2 conformational dynamics observed in this work is a specific rate process of the bunched conformational motion dynamics.

Recording the conformational state fluctuation trajectories provides a real-time observation of single-molecule protein conformational dynamics under non-equilibrium conditions in enzymatic reactions. The coherent conformational time-trajectory indicates a recurrence of the protein conformations at the active site under the enzymatic reaction that involves substrate binding, enzyme-substrate complex forming, and product releasing.^{45, 46} It is the substrate-enzyme binding and the substrate-enzyme complex formation that serve as a driving force and negative entropy source for the coherent dynamics at the single-molecule level. Accordingly, the conformational recurrence is driven by recurrence of the local environment, such as electrostatic field, electrostatic interactions, and hydrophilicity at the active site of enzyme.^{13, 47–49} Damping on a time scale of dephasing due to local environment fluctuations and multiple nuclear coordinate fluctuations dictate the resolved conformational coherence, resulting in the observation of intermittent characteristics of the conformational state coherence. Due to the transition between different conformation states of the enzyme or intermittently dominating environmental thermal fluctuations, the conformational dynamics do not always show the resolvable coherent behaviors under the enzymatic reaction conditions.

The role of protein conformational changes in regulating the overall enzymatic activities has been extensively debated in recent years.^15–21 These debates focus mainly on a few significant aspects: (1) There are two essentially orthogonal nuclear coordinates, one chemical reaction coordinate involving enzymatic conversion of substrate to product (ES→EP), and one conformational coordinate involving in substrate-enzyme complex formation and dissociation (E+S← →ES), and product releasing (EP→E+P).²⁰ Typically, along the chemical coordinates, the chemical reaction is a fast process on the femtoseconds to submicroseconds time scales, involving only minimum protein conformational changes.^18,23 In contrast, along the conformational coordinates, the formation of substrate-enzyme complex and the dissociation of product-enzyme complex are significantly slower on the microseconds to seconds time scales, usually involving large conformational motions that are observable by single-molecule FRET measurements.^{18, 23} (2) Enzymatic reaction dynamics in the chemical coordinates shows Markovian or non-Markovian, or even power-law dynamics,^{1, 20, 50–63} whereas enzymatic dynamics along the conformational coordinates typically involve with multiple-step conformational motions, such as, bunching^{27, 44} and even oscillatory conformational changes^{64, 65} (3) The rate-limiting step can be along either conformational or chemical reaction nuclear coordinates. In the measurements of single-molecule conformational dynamics and enzymatic turnovers of HPPK, what we have probed is the dynamics in the conformational coordinate that is essential for forming the active complex for a pyrophosphoryl transfer reaction. Due to the limited time resolution and signal-to-noise sensitivity, we are only able to probe the conformational dynamics along the conformational coordinates in substrate-enzyme complex formation and dissociation, and product releasing, but not the dynamics along the chemical reaction coordinates. Presumably, the rate for chemical reaction step (ES→EP) is significantly higher than the conformational motion rates.^{18, 21} According to the literature, product releasing is the rate limiting step in the HPPK enzymatic catalytic reaction.³⁷ The observation that conformational state change coherence rate increases beyond the saturating substrate concentrations also indicates that conformational changes are regulated by complex formation and dissociation processes, and the catalytic loops conformational changes can be at higher rates than product releasing rates, which suggest that (1) it is the product releasing process that controls the rate limiting dynamics; (2) the conformational motions in forming substrate-enzyme complex states can be both productive and non-productive, being at a higher rate than that of the enzymatic reaction turnovers. There are potentially biological implications of the intrinsic bunched and even coherent conformational dynamics; for example, the formation of spatial and/or temporal biological complexity, structures, and function fluctuations in living cells.

The coherence, intrinsically a result of the time bunched effect,^{27, 44} for enzymatic conformational dynamics reported here is related but significantly different from the previously reported memory effect. ^{1, 3} The typical characteristics of a memory effect in dynamics is that a long turnover time is likely to be followed by a long one, and a short turnover time is likely to be followed by a short one in an enzymatic reaction.^{1, 3} For a typical memory effect in enzyme conformational motions under an enzymatic reaction, the conformational motion times may cover a broad time scale of many folds along the diagonal direction in a two dimensional joint probability distributions,^{1, 3} and the second moment of the time distribution is not necessarily finite as the time distribution is non-Gaussian and often Lévy or Lorenzin.^{33, 34, 66} However, in a bunching effect including the coherence reported here associated conformational dynamics, the conformational motion times distribute in a relatively narrow range. The second moment of the time distribution is finite and the time distribution is Gaussian or Gaussian-like. ^{27, 44}

Conclusions

We have observed coherent enzymatic active-site conformational state changes of HPPK under enzymatic reaction conditions, revealing an intermittent coherence, a specific time bunching effect, in dynamics at defined frequencies under enzymatic reaction conditions. The coherence in conformational dynamics comes from the disordered and stochastic conformational changes under enzymatic reaction conditions. This unique disorder to order dynamic behaviors is not observable in conventional ensemble-averaged measurements. According to our single-molecule measurements, the open and close conformational changes of the active-site of HPPK are induced by substrate binding and product releasing associated with spontaneous thermal fluctuations. The interplay between the protein disorder-ordered structures and structure-function inter-relationships result in the coherent conformational dynamics under enzymatic reactions.^{67, 68} We suggest the intermittent conformational state coherence, as a specific bunching effect and typical dynamic behaviors of non-equilibrium enzymatic reaction dynamics, generally exists in the enzymatic conformational dynamics, especially for conformational regulated enzymatic reactions. Their occurrence possibilities are determined by the nature of the conformational motions, which is regulated by the interaction between enzyme and substrate, such as geometrical constraints, solvent perturbation, electrostatic interaction, hydrophobicity, and binding modes.