Advances in Resistive Pulse Sensors: Devices bridging the void between molecular and microscopic detection

Abstract

Since the first reported use of a biological ion channel to detect differences in single stranded genomic base pairs in 1996, a renaissance in nanoscale resistive pulse sensors has ensued. This resurgence of a technique originally outlined and commercialized over fifty years ago has largely been driven by advances in nanoscaled fabrication, and ultimately, the prospect of a rapid and inexpensive means for genomic sequencing as well as other macromolecular characterization. In this pursuit, the potential application of these devices to characterize additional properties such as the size, shape, charge, and concentration of nanoscaled materials (10 – 900 nm) has been largely overlooked. Advances in nanotechnology and biotechnology are driving the need for simple yet sensitive individual object readout devices such as resistive pulse sensors. This review will examine the recent progress in pore-based sensing in the nanoscale range. A detailed analysis of three new types of pore sensors – in-series, parallel, and size-tunable pores – has been included. These pores offer improved measurement sensitivity over a wider particle size range. The fundamental physical chemistry of these techniques, which is still evolving, will be reviewed.

Introduction

In 1996, Kasianowicz et al. [1] initiated a revival in Coulter based resistive pulse sensing with the demonstration of single stranded DNA detection using a biological α-hemolysin pore. The ability to discriminate slight differences in the size of the four DNA base pairs [2] has since generated considerable interest in using nanopores for DNA sequencing [3–5]. The simplicity, measurement sensitivity, and individual single-object readout capabilities of resistive pulse sensors makes them attractive devices for characterization. This, in addition to advances in nanofabrication techniques, has driven the development of a myriad of synthetic (solid state) nanopore sensors for a broad range of single molecule, DNA, and particulate sample measurement applications. This review will highlight how the Coulter Principle and advances in resistive pulse sensor designs are improving the detectable size range and throughput of particulate samples. Of particular interest are recent innovative device designs, including microfluidic and elastic pore devices that utilize in-series, parallel, and size-tunable resistive pulse sensors to enhance nanoscale object characterization.

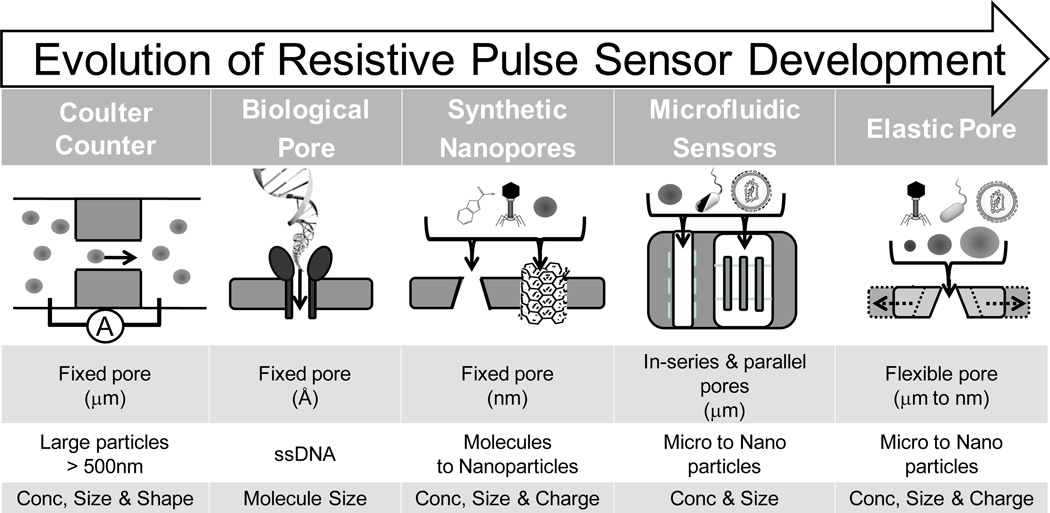
As shown in Figure 1, advances in synthetic biology and nanofabrication techniques have given rise to a multitude of resistive pulse sensor materials, structures and designs. These devices can be roughly categorized into biological, synthetic, and microfluidic based sensors. A central aim of these devices has been the ‘miniaturization’ of the Coulter counter for submicron to single molecule detection. Deblois and Bean [6] first demonstrated the use of a submicron resistive pulse sensor for the detection and characterization of nanoscaled objects, including nanoparticles and viruses [7]. Recent advances in nanofabrication has enabled the manufacture and use of much smaller pore sensors such as a 5 nm synthetic pore, created by ion-beam sculpting a silicon nitride membrane, to observe single DNA molecule translocations [8]. Synthetic nanopores have since been used to measure DNA hybridization [9, 10], folding [11], length (Mw) and concentration [12, 13], as well as detection of single molecules [14]. An advantage of synthetic pores is that the material and fabrication technique can be used to tailor and create an array of different pore types.

Figure 1.

From microparticle to single molecule detection: the miniaturization and modification of the Coulter counter. Coulter Counter – a fixed micropore for measuring the concentration and size of large particles. Biological Nanopore– α-hemolysin is a natural biological ion channel that has been used for molecular detection of single stranded DNA. Nanofabricated Synthetic Nanopores – fixed pores with a size and shape specific to manufacture. Microfluidic Sensors – offer multichannel, hydrodynamic focusing and new electrical readouts. Elastic Pore – a size-tunable pore sensor that can, by stretching, change the pore size to suit analysis conditions.

To date, numerous synthetic nanopore and microfluidic sensors have been reported. As pore fabrication is not a primary focus of this review, we direct readers toward a number of excellent recent review articles which provide greater detail about pore materials and fabrication techniques [14–17]. The breadth of the field however, can be inferred by the utilization of numerous pore materials including carbon nanotubes [18–21], micropipettes [22], silicon nitride [23], polymers [24], and polydimethylsiloxane [25], as well as the application of diverse fabrication techniques to make pore sensors, such as ion beam sculpting, track etching and laser melting, electron beam, and soft lithography. Nanofabrication of pore sensors is attractive, as it provides the ability to precisely control and tailor the pore properties, i.e. dimension, surface chemistry and mechanical stability either through the choice of pore material or by post manufacture modification of the pore. For example, the ability to chemically modify the surface of pores has been used to tailor the size of the pore opening [26] and to impart desired membrane surface charge [27] or reactive coupling groups within the pore. Biologically modified pore surfaces with biological capture probes have been used for the molecular capture detection of ricin [28–30], a potential bio-terrorism agent, in addition to studying DNA-protein binding [31–33]. Furthermore, and as detailed in the Background and section entitled ‘Sizetunable pores’ in this review, tailoring the size and shape of a pore influences both the detectable size range and measurement sensitivity. This tailoring of the size and shape of a pore also enables a wider range of applications for resistive pulse sensors beyond single molecule detection and DNA characterization. In this respect, there is a strong interest for using sensitive single event techniques, such as resistive pulse sensors, for the detection and characterization of nanoscale objects.

Nanoscale particulates (objects between 20 – 1,000 nm) are ubiquitous as well as scientifically and commercially important. They exist naturally as proteins, viruses, exosomes, and liposomes, and are widely used in everyday commercial products such as paints, cosmetics, and pharmaceuticals, as well as being an important part of industrial processes including food processing, oil recovery, and mineral tailing separation. The properties and behavior of these materials are fundamentally dependent on their size, shape, concentration, and charge [34]. For example, dispersion stability is dependent on particle size and charge as well as concentration. In addition to stability, measuring particulate concentration is emerging as an important detection parameter in biology. Changes in exosomal concentrations in blood and urine have been proposed as potential diagnostic markers for lung cancer [35] and renal injury [36], respectively. Also generating considerable interest is characterizing small changes in the size, shape, and charge of individual synthetic and biological nanoparticles.

The presence of small particulate populations with properties different to the larger population have been shown to give rise to colloidal instability or initiation of a biological pathway [37]. For example, slight changes in the amino acid composition or post-translational modification of proteins (biological particles) can affect their size, shape, and charge, which subsequently affects their function in solution. Post-translational phosphorylation of the p53 protein, which has been linked to tumor suppression in cancer, results in the favorable stability and accumulation of the protein in the tumor [38]. Therefore, characterizing dispersion properties on a particle-by-particle basis represents a comprehensive approach for investigating and understanding the fundamental behavior of all particulate suspensions.

Particulate properties are commonly analyzed using ensemble (bulk analysis) techniques such as light scattering. These techniques allow particle characterization in most solvents and over a wide particle size range, i.e. from a few nanometers to several microns. However, ensemble techniques often give rise to erroneous results, as they can be biased by small populations within a complex dispersion. For example, Mie and dynamic light scattering techniques are inherently biased by larger particles in a suspension due to the proportional relationship between light scattering intensity and particle size (i.e. I∝d⁶) [34]. Furthermore, characterizing particle shape is typically not possible due to theoretical modeling constraints of all particles as spheres. Particle shape can be measured by imaging techniques such as light and electron microscopy, however, these devices are sample size limited and therefore typically labor intensive to process. This limits not only measurement accuracy, but also elucidation of the role that these properties and their distribution play in the overall behavior of particulate suspensions.

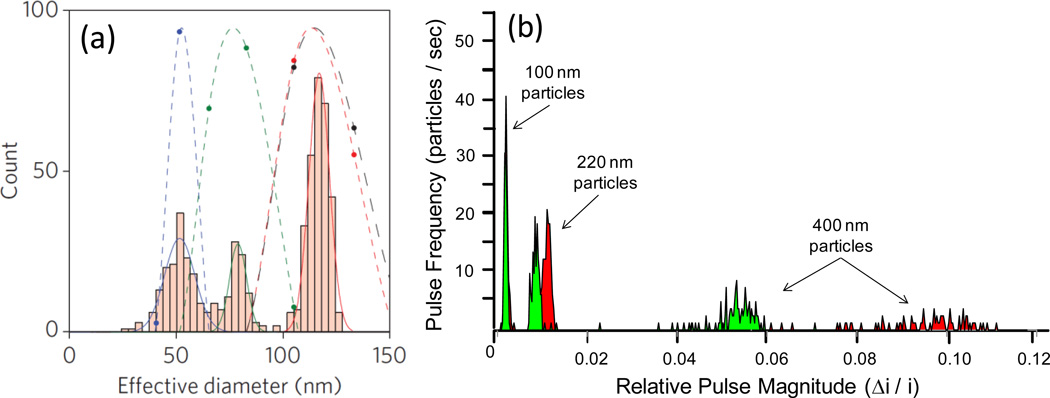
Thus, a key reason for the current interest in resistive pulse sensors is the individual particle-by-particle readout, measurement sensitivity, and the wealth of information, i.e. size, shape, charge, and concentration, which can be characterized about individual particles within a suspension. The collective measurement of hundreds to thousands of events via resistive pulse sensing can be accumulated to examine the distribution properties of the entire colloidal particle suspension. Measurements acquired by resistive pulse sensors are advantageous in that they are typically more accurate due to higher sensitivity than ensemble (Mie and dynamic light scattering) techniques [7, 39, 40]. Previous resistive pulse sensor studies have demonstrated the ability to discriminate between nanoparticles exhibiting a mere 10% difference in diameter. Recently, Fraikin et al. [41] were able to discriminate between a mixed suspension of 51, 75, and 117 nm particles using a conically shaped nanopore, which dynamic light scattering reported as a single peak corresponding to the largest 117nm particle size, as shown in Figure 2(a). Advances in pore design, i.e. size-tunable pores, have recently demonstrated the ability to improve the measurement sensitivity of pore sensors by changing the pore size. As shown in Figure 2(b), using an elastic pore sensor, Roberts et al. [42] demonstrated the ability to discriminate between populations in a mixed suspension of 100, 220, and 400 nm particles, in addition to an increase in the signal magnitude as a result of pore size reduction. This measurement sensitivity, as well as their individual particle readout, makes resistive pulse sensors appealing characterization devices.

Figure 2.

Improved size measurement sensitivity and discrimination of resistive pulse sensors (a) Conical nanopore vs dynamic light scattering of a trimodal suspension of 50, 75 and 117 nm polystyrene particles. Nanopore (bar histograms) are able to distinguish between the three particle sizes in contrast dynamic light scattering gives rise to a single peak at 117 nm. Reprinted with permission from reference [41]. (b) Tuning pore size of a new elastic pore sensor improves particle sizing sensitivity of a trimodal suspension of 100, 220 and 400 nm particles by increasing the magnitude of the resistive pulse signal via reducing the particle-to-pore volume. Adapted from reference [42].

The validity of using resistive pulse sensors, such as commercial Coulter Counters, to measure the size and concentration of micro particulates in suspension is well-established. With pore sizes typically hundreds of microns in size Coulter counters continue to be successful instruments for counting and sizing micro-bodies such as cells in hematology. They have also been used to measure marine particulate diversity [40], potentially immunogenic ‘subvisible’ (micron sized) pharmacological protein therapeutics [39], counting and sizing sperm [43] as well as being used as quality control devices in industrial processes. Reducing the size of the pore to submicron dimensions has enabled resistive pulse sensing of nanoscale objects including polymeric and biological particulates [39, 40, 44], adenovirus [45], bacteriophage T7 [41, 46], and individual protein-antibody complexes [47, 48]. Although not often exploited, resistive pulse sensing offers much more information than just particle size and concentration.

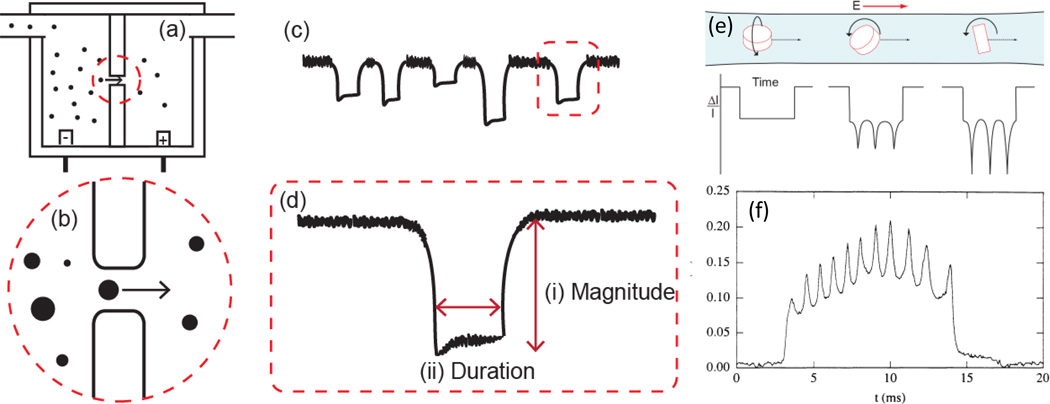
The resistive pulse signal generated by objects passing through a pore, as described in greater detail below, can also be used to elucidate the shape, charge, and conductivity of particles. Although there have been a number of theoretical models to describe the pulse signal generated due to particle shape [49] and surface charge [50–53] under varying pore dimensions, membrane charge, and electrolyte concentrations few studies to date have taken advantage of using pulse sensors for experimentally measuring these properties. Of these, the findings of Golibersuch [54], Berge et al. [44, 55], Ito et al. [18, 19], and Holden et al. [56] stand out in their use and extension of resistive pulse sensing for characterizing particulate samples. Golibersuch [54] and Berge et al. [44, 55] both modeled and experimentally measured the difference in pulse signal arising from oblate (disc) and prolate (ellipsoid) particles traversing a long cylindrical pore sensor. Interestingly they also observed the rotational tumbling of oblate red blood cells and Rochelle salt particles in the pore via fluctuations in the pulse signal magnitude, as shown in Figure 3 (e) and (f). Ito et al. [18, 19] were able to measure the electrophoretic mobility of single particles using a carbon nanotube sensor. Quantitative single particle charge measurements, comparable to commonly employed light scattering techniques, were possible as particle translocation was due only to particle electrophoretic mobility, i.e. no external pressure or electoosmotic forces were present in the carbon nanotube sensor. Holden et al. [56] recently demonstrated the ability to measure the effective conductivity, i.e. salt concentration, of ‘soft’ materials such as proteins, via the pulse signal generated for a polyelectrolyte microgel particle with increasing electrolyte media concentration. Measuring these properties on an individual object basis presents a new methodology for characterizing their distribution and role in suspension, which is not possible by other techniques.

Figure 3.

Coulter principle for sensing colloidal particle dispersions: (a) A typical setup for a Coulter-type device, two fluid cells separated by an insulating membrane containing a single pore. (b) As particles pass through the pore a resistive pulse (blockade event) proportional to the excluded volume of the particle is measured. (c) The current profile of particle blockade events. The frequency of these events is a function of the pressure and electrokinetic effects in the system as well as the concentration of particles. (d) A detailed blockade profile of a singled blockade event from (c) showing (i) pulse magnitude and (ii) pulse duration. (e) Theoretical pulse current profile of a single oblate ellipsoid (disc-shaped) particle undergoing rotation in line with, at a 45 degree angle, and perpendicular to the electric field in a cylindrical pore. (f) experimental signal trace of an oblate ellipsoid undergoing 5 complete rotations, as shown by the ten oscillations in the single pulse trace, reprinted with permission from reference [44].

The increasing interest in developing techniques that can rapidly, cheaply, and above all accurately characterize the concentration, size, shape, and surface charge of objects in suspension has invoked considerable interest in devices that utilize resistive pulse sensing [30, 57–59].

Background

Originally conceived in 1953, the fundamental theories behind resistive pulse sensing, also known as the Coulter Principle, remain the cornerstone of pore based sensors [60]. Due in part to the interest in using the Coulter Principle for characterizing nanoscale objects, a number of recent articles have begun re-evaluating the resistive pulse signal [61, 62]. Through analyzing the origins of the generated resistive pulse signal of pore sensors, greater and more accurate information about the properties of particles passing through pores can be extracted. A summation of common theoretical equations and corresponding references used for calculating particle size, shape, charge, and concentration from the resistive pulse signal are given in Table 1.

Table 1.

Using the resistive pulse signal, common equations for calculating particle size, shape, charge, and concentration from the resistive pulse frequency, magnitude, and duration.

Nomenclature
A	Cross sectional area of a pore	f⊥	Shape factor for spheroid with longest dimension perpendicular to pore wall	ve	Electrosmotic velocity
C	Particle concentration	fΠ	Shape factor for spheroid with longest dimension parallel to pore wall	vp	Fluid velocity
				vs	Object velocity through pore
D	Pore diameter	R	Resistance	vμ	Electrophoretic velocity
Ds	Small pore opening diameter in a conical pore	ΔR	Change in resistance	μ	Electrophoretic mobility
Dl	Large pore opening diameter in a conical pore	L	Pore length	Δt	Pulse duration, translocation time
d	particle diameter	Lc	Effective resistive pore length	V	Pore volume
EM	Electric potential	J	Event frequency	v	Particle volume
f	Shape factor	ρ	Solution resistivity	z	Direction along pore length axis

Measured variable		Equation Conditions/References
	Eq. 1	$R=\rho {\displaystyle \underset{L}{\overset{0}{\int }}\frac{\mathit{\text{dz}}}{A(z)}}$
		Resistance in a pore [65]
Resistance R	Eq. 2	$R=\frac{4L_c\rho }{\pi D^2}$
		For a cylindrical pore [6] Lc = L + 0.8Di
	Eq. 3	$R=\frac{4L_c\rho }{\pi D_s{D}_L}$
		Total resistance in a conical pore. Replacing DL and L with Dz and z, the diameter of the pore at a distance z from the small opening can be used to calculate the resistance gradient profile [76].
	Eq. 4	$\frac{\mathrm{\Delta }R}{R}=f\frac{v}{V}S(d/D)$
		A general expression resistance change to particle and pore volume fraction [6, 65, 68]. For spherical particle (f =3/2) and d << D (S = 1) this becomes Maxwell’s theory.
	Eq. 5	$\frac{\mathrm{\Delta }R}{R}=\frac{d^3}{D^2{L}_c}S(d/D)$
		The general expression in terms of a cylindrical pore containing a spherical particle. Combining (1) and (4).
Pulse Magnitude $\frac{\mathbf{\Delta }R}{R}$	Eq. 6	f is particle shape factor [49, 54, 68]   f = 3/ 2   For spherical particles [65]   f = f⊥ + (fΠ − f⊥)cos2 α
		For non-spherical oblate and prolate spheroids as they tumble through a pore [49, 54, 68].
	Eq. 7	$S(d/D)={\left[1-0.8{(d/D)}^3\right]}^{-1}$
		An empirical correction factor developed to describe the non-linear trend between v and V [69, 70, 77].
Pulse Frequency	Eq. 8	$J=\frac{\pi v_s{D}^2}{4}C$
		Nernst-Planck equation relating event frequency to dispersion concentration in a cylindrical pore [20]. The formula includes velocity contributions from electrophoretic and electroosmotic flow, diffusion and external pressure.
Pulse Duration Δt	Eq. 9	$\frac{1}{\mathrm{\Delta }t}\propto f(v_{\mu })+f(v_p)+f(v_e)$
		Particle velocity through a cylindrical pore is a combination of electrokinetic and fluid flow forces [52, 78]. Diffusion velocity is considered negligible in a pore. The combined velocities are inversely proportion to the pulse duration.
	Eq. 10	$\mu =\frac{L_c^2}{E_M\mathrm{\Delta }t}$
		Particle Charge (electrophoretic mobility) measurements can be made when vp and ve are negligible [50, 78].

ⁱL_c = L+0.8D in all following formulas (with exception of conical pore, Eq. 3). This takes into account the residual electric field outside the pore openings.

A typical resistive pulse sensor is composed of two fluid reservoirs filled with a conductive electrolyte media and connected by a small aperture or pore, as shown in Figure 3(a). When a voltage is applied across the pore the resistance to the resulting ionic current is typically proportional to the pore length and inversely proportional to the cross sectional area of the pore, as shown in Table 1 for a generic (Eq 1) and cylindrical (Eq2) pore. Changing the size and shape of the pore alters the total resistance across a pore but can also give rise to a resistance gradient profile through the pore, as is the case for conically shaped pores (Eq3). The effects of conical pore shape affect the resistance, and hence the electric field, which is focused at the small pore opening [63]. This focusing of the resistance to a small detection region, also known as the sensing zone, makes conical pores attractive for sensitive measurements and hence their extensive application for DNA detection.

Regardless of pore shape, objects are detected in pore sensors as a change in the resistance across the pore. This resistance change can also be measured as a change in voltage or ionic current, as these readout signals are related to each other according to Ohms law. As the general principles in resistive pulse sensing are similar for all pores, this review will focus on the general theories and how these have been applied for characterizing objects in cylindrical pores. A few studies have investigated quantification using non-cylindrical pores. However, quantitative characterization in these pores becomes a nontrivial matter due to the non-uniform resistance profile [64].

Sensing particles by the Coulter Principle is based on Maxwell’s theory [65] that the presence of non-conducting particulate objects in a conductive media gives rise to an increased resistance proportional to the particle-excluded volume. As shown in Figure 3(b) and (c), a resistance ‘pulse’ in time is generated for individual particles passing through a pore. The resistive pulse profile generated by non-conducting particles is dependent on the both the particle and pore properties [44]. For example, cylindrical pores typically generate a ‘square’ signal profile whereas conical pores generally produce a peak shaped signal due to the resistance gradient in these pores (see Eq 2 & 3 in Table 1) [66]. In general, the frequency, magnitude, duration, and shape of individual particle resistive pulses (Figure 3(d)) can be used to elucidate the size, shape, charge, and concentration of particles. Table 1 outlines some of the key equations to derive particle characteristics from the resistive pulse signal. In general, particle size is proportional to the magnitude of the change in resistance in the pore by Equation 4, i.e. the generated pulse magnitude is dependent on the particle-to-pore volume ratio (v/V). Therefore, altering the pore size changes the measurement sensitivity. This equation also takes into account the effect of particle shape, through a shape factor f (Eq 6), and non-ideal effects of electric field line ‘bulging’ due to the particle-to-pore size ratio (d/D), via a size factor S (Eq 7). The magnitude of f is dependent on both the shape and orientation of the particle in the pore, as shown in Figure 3(e). For spherical particles f is constant and equal to 3/2 in accordance to Maxwell’s theory [65]. In contrast non-spherical particles give rise to non-uniform blocking of the electric field through the pore. The effects of oblate and prolate spheroids with aspect ratios (diameter-to-length ratio) from 0.1 to 10 have been empirically modeled (Eq 6) and experimentally observed, as shown in Figure 3(f) [44, 49, 54, 67, 68]. The size factor S accounts for the deviation from the linear relationship between particle volume and pulse magnitude due to bulging of the electric field as the particle diameter approaches the pore diameter. Typically for small particles in large pores, i.e. when d/D << 0.5, S is negligible. As d/D ≥ 0.5 S becomes increasing important to ensure particle size is not over estimated due to field bulging effects. A number of empirical equations have been developed to account for the non-linear relationship between particle volume and pulse magnitude arising from small, intermediate and large particles in pores with varying shapes [62, 66, 69, 70].

The frequency of the pulse events with time (Figure 3(c)) is related to the particle dispersion concentration by the Nernst-Planck equation (Eq 8) and includes velocity contributions from electrophoretic and electroosmotic flow, diffusion and external pressure forces [52]. Pulse duration is also a combination of these forces as outlined by Equation 9. Under ideal conditions where electroosmotic and pressure are negligible, Equation 10 can be used to calculate the electrophoretic mobility, and therefore particle charge if the electric field through the pore is known. As demonstrated by the breadth of fundamental research outlined in Table 1, resistive pulse sensors have been shown to offer a plethora of information about individual particles in suspension.

It is important to note that the Coulter Principle only applies to non-conducting particles and particles with small electric double layers. Conductive or highly charged macromolecules or particulates such as DNA [71], DNA coated particles [42, 72], metallic [73], and highly porous particles [74] have been shown to reduce rather than increase the resistance across the pore. In the case of porous particles or particles with a large double layer this is due to the associated ion concentration with these particles. This gives rise to a smaller than theoretically predicted or even an inverse (positive) pulse signal. For highly charged particles the double layer effect can be enhanced by reducing the electrolyte concentration [34]. The resulting change in pulse signal, i.e. going from negative to positive, has been used to infer information on particle surface charge [75] and the conductivity of ‘soft’ particulates [56].

Current detection limitations

Despite the interest and considerable potential as analytical devices, most pore sensors are currently limited by detection speed and size range as well as the need for highly conductive dispersion media. The detection size range and measurement sensitivity is dependent on the particle-to-pore size and signal-to-noise ratios in addition to off-axial translocation of particles through the pore. Thus there has been considerable focus on understanding and building new devices that address these limitations. We will highlight the current understanding of these limitations and some of the ways they are being addressed here before going into greater detail about how advances in pore designs, i.e. in-series, parallel, and size tunable pores, are overcoming the current key limitations in pore based detection.

Detection speed and size range

Pore sensor sensitivity is dependent on the electrical instrumental bandwidth resolution (i.e. kHz or MHz recording speed) as well as the speed that objects traverse the pore. Increasing the translocation speed typically decreases the measurement sensitivity due to a ‘truncation’ of the resistive pulse signal as a result of fewer data points being collected. By reducing the measurement bandwidth from 40kHz to 1 kHz, thereby reducing the recoding speed, Uram et al. [79] observed up to a 50% decrease in the pulse magnitude generated by 190 nm viruses passing through a pore. This decrease in pulse magnitude corresponds to a 12.5 % under estimation in virus particle size. In addition to under sizing particles the current limitation in electrical instrumental bandwidth resolution and corresponding fast translocation speeds of DNA has so far restricted the use of nanopores for single base sequencing of DNA. The typical translocation time for an individual DNA base pair is less than a microsecond which is below the current bandwidth resolution required for single base pair differentiation [79]. Although not directly applicable to nanoparticle characterization a few innovative devices and methodologies have been explored to reduce the translocation time of DNA. These include chemically [80, 81] and biologically [82] modifying α-hemolysin pores, changing instrumental conditions e.g. pore size [83], applied voltage, temperature, as well as the salt concentration and viscosity of the solution [84], repeated ‘flossing’ of DNA back and forth through the pore [23, 85], and the synthesis of ‘kinked’ pores [86].

As resistive pulse particle sizing is dependent on the particle-to-pore volume ratio, as shown in Table 1, reducing the pore size, as shown in Figure 2(b), can also be used to improve the measurement sensitivity. Fixed size pore sensors are therefore typically limited to a detectible particle-to-pore ratio size range of ~1.5 to 80% [6, 70, 87]. The upper detection limit is dependent on the physical size of the pore whereas the lower limit depends on the electrical readout signal-to-noise ratio. This becomes a fundamental issue for the analysis of real-world polydisperse particle suspensions such as marine particulate diversity [40] and ‘sub-visible’ pharmacological protein therapeutics [39] as it requires the manufacture and use of multiple sized pores. Alternatively, size-tunable pore devices overcome this issue by tuning the pore size in real-time to the sample size at hand, as discussed in greater detail later in this review.

Signal-to-noise

Ion current fluctuations (noise) in nanopore based resistive pulse sensors are further limiting the sensitivity of these devices. There are two major noise sources, one stemming from the external electrical power system (low frequency), the other from intrinsic noise of electronic circuit components (several hundred Hz to several MHz) [88]. Smeets et al. [89] discuss in detail the role and sources of high and low frequency intrinsic noise of solid state nanopores. While the high frequency component is shown to be due to Johnson noise of electrical circuits, the low frequency component is shown to be related to the number of free charge carriers and nanobubbles.

Recently Xu et al. [90] and Sridhar et al. [91] developed a new readout methodology to improve the signal-to-noise ratio of pulse sensors based on metal oxide semiconductor field effect transistors (MOSFET). Using this readout they were able to detect a particle-to-pore ratio down to 0.006%, which is ten times smaller than the minimum achieved by DeBlois and Bean [6, 7, 70]. Advances in this readout technique, i.e. the addition of symmetric mirror channels, have further reduced the minimum particle-to-pore detection ratio [88, 92]. Using a two-stage differential amplification method, Wu et al. [88] detected a minimum volume ratio of 0.0004%, which is claimed to be ten times smaller than the current commercial Coulter Counters (0.0037%). Although promising new device designs such as multi and size-tunable pores alter the pore size to overcome issues in detection sensitivity and size range limitations.

Off-axial translocation

Particle sizing accuracy is dependent on the path particles take through a pore sensor. Particles not traveling through center of the pore, known as off-axial particle translocation, will result in a higher than expected pulse magnitude and therefore a larger calculated particle size. Interestingly the orientation of non-spherical particles can also influence the pulse magnitude. This difference is due to the inhomogeneous electric field present in pores with higher electric field near the pore wall in addition to positional differences in the cross sectional area of non-spherical particles ‘blocking’ different ratios of the electric filed. Scaled-up models investigating particle position in a pore have shown that up to 15% deviation in the pulse magnitude can be attributed to off axial translocation [93, 94]. This error increases as the particles-to-pore ratio decreases [44, 62, 93]. However, off axial effects can be addressed by hydrodynamic focusing of particles into the center of the channel. Thom et al. [94] first introduced hydrodynamic focusing and recently a number of new devices have used this in microfluidic devices to improve measurement accuracy [92, 95] and sensitivity [96], as described later in this review.

Conductivity of media

Resistive pulse sensors operate using highly conductive electrolytes, because resistance changes due to particle translocations are difficult to measure in poorly conductive media. Microfluidic capacitance sensors which measure the AC capacitance instead of the traditional DC resistance allows for the use of poorly conductive media to detect nano and micron particles [59, 97]. These devices have been shown to be useful for the detection of cells [98, 99] and blood borne microparticles [100], as well as biomolecules such as DNA [101], and in engineering applications for monitoring particles in low conductance hydrophobic media [102].

Advances in pore design: in-series, parallel and size-tunable pores

Multipore analysis was originally conceived in 1976 to improve particle concentration measurements [103]. However, shortcomings in electronics as well as apparatus size and design, made multipore devices impractical at the time. Recent advances and greater control in nanofabrication (i.e. photolithography and microfluidics) has heralded the ability to create new multipore resistive pulse sensor devices. For example, Carbonaro and Sohn [104] were able to simultaneously perform two independent sandwich immunoassays by placing two pore sensors on a single microfluidic device. Since then numerous lithographic-based pore sensors have been described [59]. These pulse sensors have been used to count and size objects as small as nanoparticles and as large as cells [97, 105] depending on the fabricated channel size. Recently, two unique and promising designs were conceived, specifically in-series and parallel microfluidic pores. In addition to these devices our group has been working with an elastic pore device commercialized by Izon Science Ltd. (NZ) that allows real-time tuning of the pore size by applying a macroscopic stretch to the pore membrane. These devices offer the potential of improved measurement sensitivity based on detection of a wider range of particle sizes and higher sample throughput as compared to common single fixed pore devices.

Pores in-series

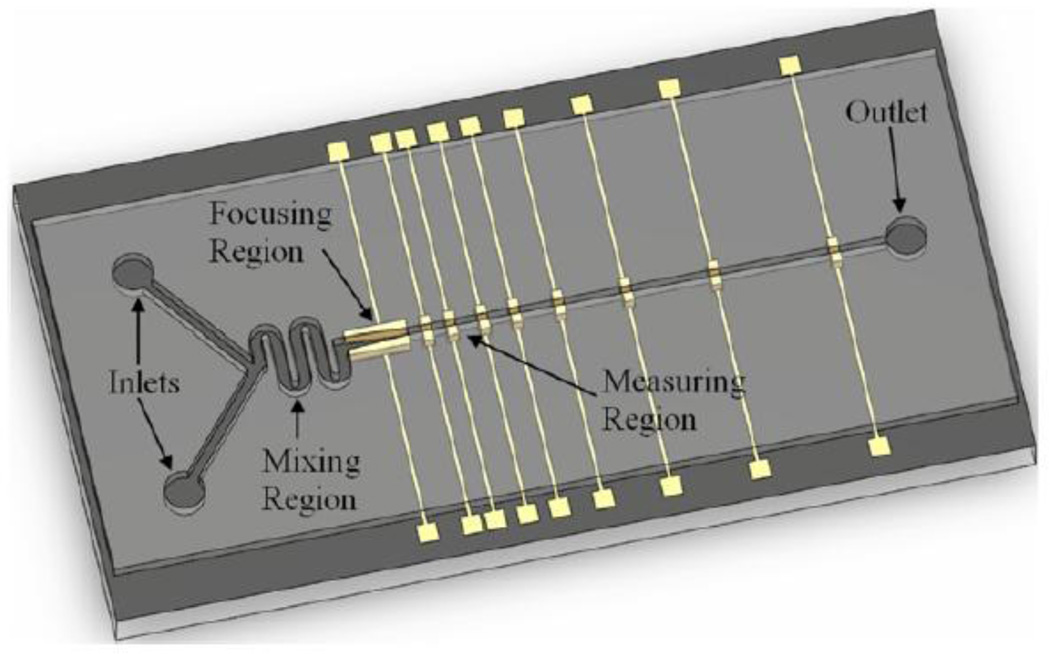
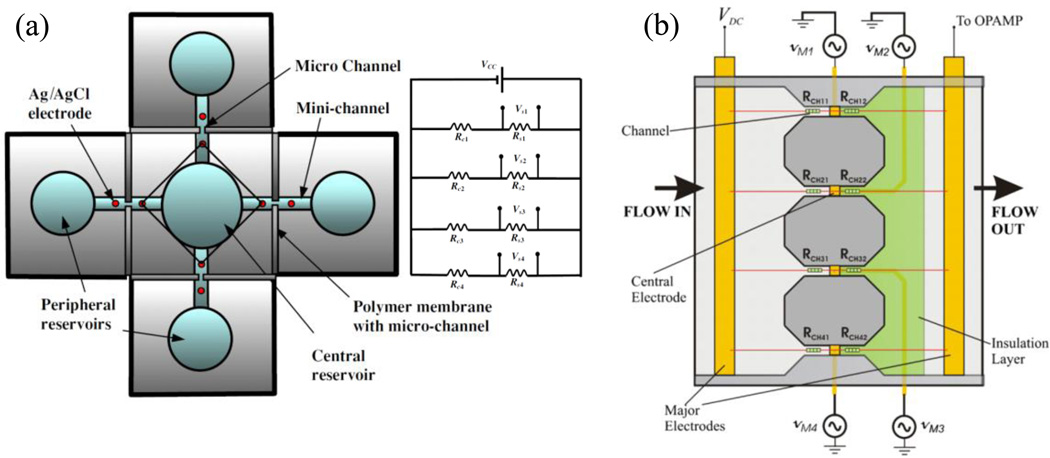
In-series pulse sensor devices offer the ability to monitor changes in object properties with time. Previously, monitoring has been accomplished by cycling an object repeatedly through the same sensor. Such monitoring requires several experimental controls, i.e. devices must provided precision feedback [55], unique particle constructs are necessary [85], and that analysis was limited to a single object within a suspension. Recently, Wu et al. [92] created the first in-series resistive pulse sensor. A series of electrodes were placed perpendicular along a microfluidic channel fabricated in polydimethylsiloxane (Figure 4). This enabled size measurements of microparticles and fibroblasts size to be taken at precise time points as they flowed past each consecutive electrode sensor. Therefore, increasing the flow rate decreases the time between successive measurements. Furthermore, effects of osmotic changes on cell size were probed by varying the solution conditions (i.e. salt concentration) which was incorporated into the design by adding a second solution port and mixing channel prior to the sensing channel. Although the experiment and testing apparatus were well-designed, probing the cell size change of a 19µm-diameter fibroblast was beyond the detection sensitivity of the device, as only a 1% increase in the pulse signal was observed.

Figure 4.

In-series coulter device. Objects flow past a series of electrode sensors perpendicular to the channel that give rise to voltage pulse measurements similar to particles passing through an aperture. Changes in the object volume with time can be determined via changing the flow rate. Reprinted with permission from reference [92].

Parallel pore sensors

To date, two ‘truly’ parallel pore devices have been described. These devices utilize multiple pores connected by a common sample inlet and/or outlet, which increases sample throughput. For example, Jagtiani et al. [106] demonstrated a 4 channel pore sensor (Figure 5 (a)) that could increase the throughput of a single sample by 300% or analyze 4 independent samples simultaneously, depending upon sample insertion direction. By injecting the sample separately into the 4 ports and using the common reservoir as an outlet, they were able to simultaneously measure the size and concentration of 20 and 40 µm polymer particles, as well as Cottonwood and Juniper Scopulorum tree pollens. Although the design is promising for increasing particle throughput, the inlet, pore, channel and electrode size severely limit the number of parallel pores possible.

Figure 5.

Parallel Coulter devices (a) multi-reservoir multi channel device with the ability to measure up to 4 analytes simultaneously and corresponding electrical diagram, from reference [106]. (b) Single reservoir multi-pore device that incorporates AC field encoding of each channel, from reference [108]. Reprinted with permission.

In contrast, another parallel pore design, as shown in Figure 5 (b). fabricated by the same group utilized photolithography to create a microfluidic device with a common sample inlet and outlet stream to pass the sample through parallel pore detectors [107]. This device was also able to measure the size and concentration of 40 µm polymer and Juniper Scopulorum tree pollen particles. Recently, they were able to ‘encode’ each of the pore channels by modifying the electrode layout to generate an AC field in each channel, i.e. 25, 40, 55 and 70 kHz [108]. Pulse magnitudes for each of the channels signal, which was recorded at a sampling rate of 2.5 MHz via electronic band pass filtering corresponding to the AC field encoding. The key advantage of this encoding strategy is that it reduces the detection electronics by creating a single ‘combined’ yet decodable electrical readout for all the channels. However, encoding in this fashion presents the limitation that increasing the number of encoding channels, and therefore the corresponding encoding frequency decreases the sampling rate. This can give rise to ‘truncation’ of the pulse signal due to the reduction of data points for each pulse, ultimately resulting in the under-sizing of particles [79].

A key limitation of these and many other microfluidic devices is the limited selection of electrode materials and planer placement to the pore openings. Polarization of the gold electrodes and the non-uniform height dependent electric field gives rise to a reduced resistance pulse signal that decreases with increasing particle height from the electrode surface. A promising new microfluidic ‘floating’ electrode set-up may help reduce this variation in signal, as it places the electrodes across rather than along the channel wall [106]. This electrode set up has been shown to be less sensitive to the particle position within the channel, which can be focused into the center by increasing the parabolic flow profile [95]. An obvious problem for these and all fixed pore devices however is the need to size-fractionate polydisperse samples prior to analysis to prevent blocking of the pore. This can potentially be achieved in microfluidic devices by incorporating a filtering component into the device [104]. However, sample filtering introduces user defined boundaries that limit true sample distribution analysis. Therefore, new size tunable pore devices offer many advantages over fixed pore systems.

Size-tunable pore sensors

As particle size detection limits and measurement sensitivity are dependent on the pore dimensions, changing the pore sensor size in real-time is advantageous for a numerous reasons. To date, two approaches of pore size tuning have been described in the literature, one utilizes hydrodynamic focusing in a microfluidic sensor, and the second utilizes a pore fabricated in an elastic membrane by mechanical puncturing with a microscopic tip. These sensors are outlined in this section.

Hydrodynamic focusing aperture size on a microfluidic sensor

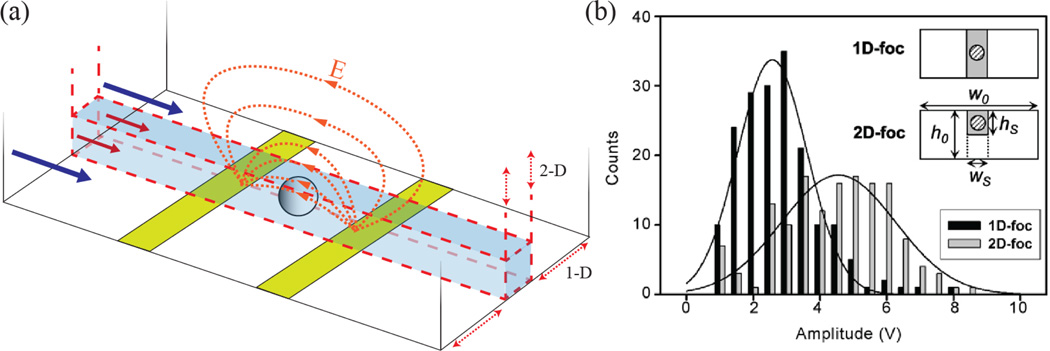
Rodriguez-Trujillo et al. [96] demonstrated the ability to increase the pulse signal of 20 µm particles 1.6 times by hydrodynamicly focusing the sample stream near the electrode sensors in a microfluidic device, shown in Figure 6. The effective aperture was reduced from 65 (H) × 180 µm (W) to 64 × 25 µm in 1-D and to 32 × 25 µm in 2-D by hydrodynamically focusing the particle and electrolyte sample stream with low conductive deionized water streams. Although promising for improving the single-to-noise ratio when characterizing polydisperse particulate samples, the planar electrode layout gives rise to particle sizing error due to the height dependent variance in the generated pulse signal magnitude.

Figure 6.

(a) 1-D and 2-D hydrodynamic focusing of the sample stream (red arrows) by non-conductive deionized water (blue arrows). (b) Increase in particle pulse magnitude via hydrodynamically focusing the electrolyte solution containing the particles near the electrodes, effectively reducing the sensing zone aperture size. Reprinted with permission from reference [96].

Elastic, size-tunable, pore sensors

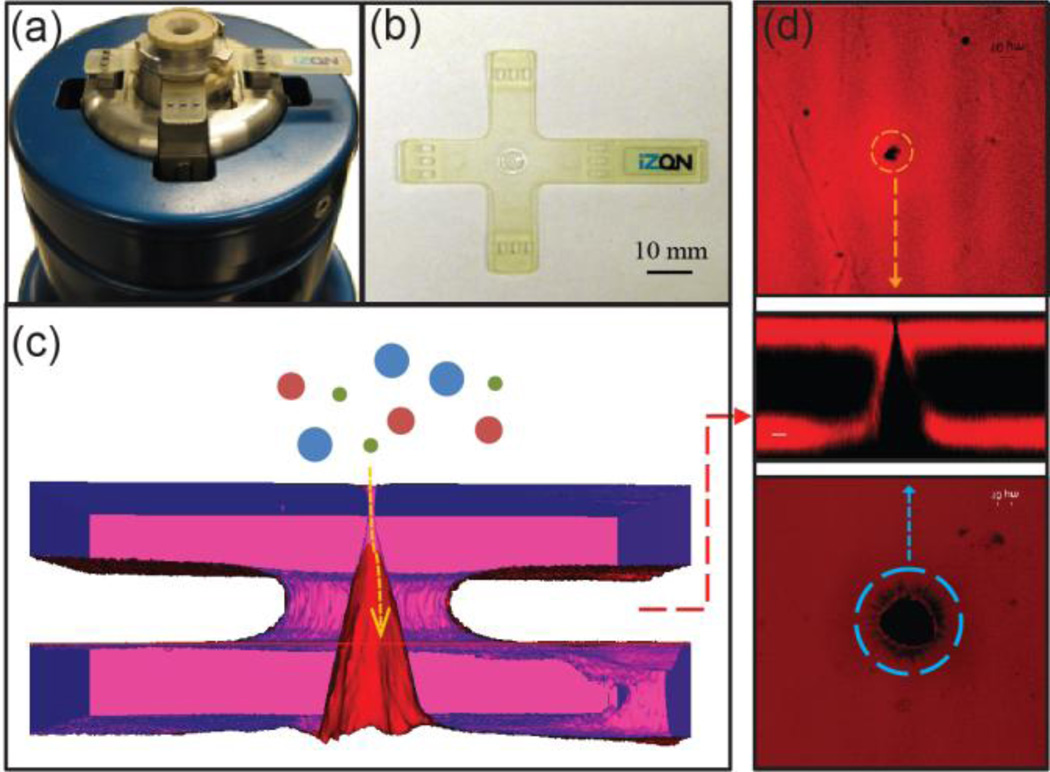
Elastic size-tunable pores are relatively new devices in the field of pore based sensing devices. Fabricated by puncturing an elastic polyurethane ‘cruciform’ membrane with a micronsized tungsten needle Sowerby et al. [109–111] were the first to describe and patent an elastic pore sensor (Figure 7). The produced pores are dependent on the puncturing process with shape and dimensions similar to the puncturing needle. As shown in Figure 7, these pores are typically conically shaped with a large and small pore opening of ~20 µm and ~500 nm, respectively [112]. However, smaller or larger pore opening ratios as well as different pore geometries are an obvious possibility via modification of the puncturing needle. The pore size is manipulated by applying a macroscopic axial stretching force to the elastic ‘cruciform’ membrane. In this way the pore diameter can be rapidly changed, or ‘tuned’, to suit the size of the colloidal dispersion being interrogated. Applying 10 mm of membrane stretch has been shown to decrease the membrane thickness by ~15%, while increasing the pore openings by 54%. Interestingly, the pore opening undergoes a Mullins effect, i.e. stress-softening when initially stretched, which requires several 0–7 mm stretching cycles before reaching equilibrium.

Figure 7.

The elastic nanopore and qNano system (a) A qNano fluid cell with an elastic pore membrane mounted on adjustable ‘stretching’ jaws. (b) An elastic nanopore membrane, the pore is located in the inner septum ring at the centre of the cruciform. (c) 3-D image developed from confocal microscopy of an elastic pore membrane showing a schematic representation of a nanoparticle entering the pore. (d) Confocal image of the small and large opening as well as membrane cross section illustrating the conically shaped pore.

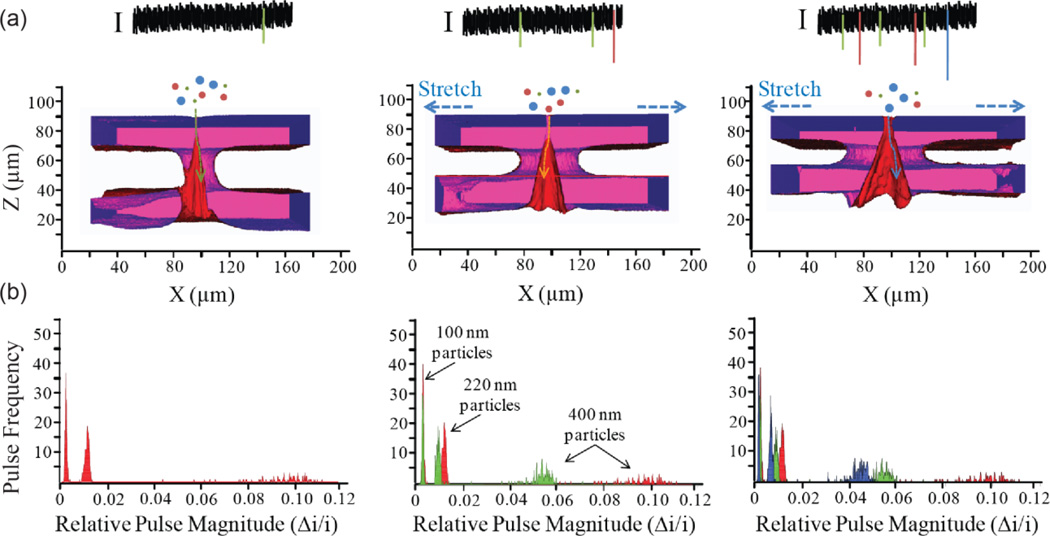
Tuning the pore size enables a wider size range of particles to be detected by a single pore while also improving measurement sensitivity [42, 45]. This pore tuning for optimal sample detection, also known as scanning ion occlusion sensing (SIOS), has been shown to improve discrimination between particles in a mixed ‘polydisperse’ suspension of 100, 220 and 400 nm particles, as well as give rise to a two-fold increase in the signal magnitude for each particle set compared to the largest pore sized analyzed (Figure 8).

Figure 8.

Elastically tuning pore size changes measurement sensitivity (a) 3-D confocal images of the pore opening (red) and membrane (blue, purple). White space between membrane surfaces is an artifact due to limited penetration of the Rhodamine dye into the membrane. Macroscopic stretch values were 2, 7 and 12 mm (from left to right), giving small pore opening diameters of 4.90, 6.12, and 6.43 µm, respectively, large pore opening diameters of 15.92, 32.24 and 44.90 µm, respectively, and membrane thickness values of 95.70, 77.60, 52.00 µm, respectively. A schematic representation of measured ionic current signal I for a trimodal particle suspension passing through an elastic membrane at three increasing stretches is included. (b) Pulse magnitude signal of a trimodal suspension composed 100, 220 and 400 nm particles. Increasing the pore size by stretching decreases the pulse magnitude for the trimodal suspension as shown by the red, green and blue histograms.

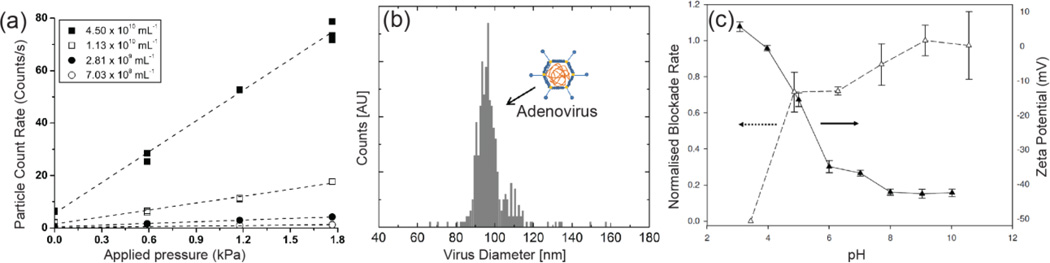
As quantitative sizing requires accurate prior knowledge of the pore dimensions, which change for elastic pores, we recently described a simple calibration method based on the linear relationship between particle volume and pulse signal magnitude (Table 1). Calibrating the pore using monodisperse particles overcomes the challenge of characterizing the complex and changing pore dimensions. It was shown that particles between 100 and 780 nm exhibit a good linear correlation [45]. Please note that this calibration method is not limited to this size range but also can be applied to micron particles and nanoparticles smaller than 100 nm. Decreasing the pore size by reducing the membrane stretch by 1 mm resulted in a 60% increase in the slope of the linear correlation between pulse signal magnitude and particle volume. This corresponds to a 60% increase in the sizing sensitivity. This calibration methodology has been used to quantitatively size a range of particle materials as well as a 96.5 ± 15 nm adenoviruses sample, as shown in Figure 9 (b) [45].

Figure 9.

Elastic pore characterization of (a) particle count rate, pulse frequency, of 100 nm polystyrene particles at 4 different concentrations as a function of applied pressure, reprinted from reference [114]. (b) Size distribution of a recombinant adenovirus, reprinted from reference [45]. (c) The relative electrophoretic mobility and corresponding zeta potential measurements of 500 nm carboxylic acid modified silica particles, reprinted from reference [114]. Reprinted with permission.

Selective gating

Purification of macromolecules and particles based on size and charge is of considerable scientific and commercial interest. Although not a primary focus of resistive pulse sensors, selective gating and detection of objects through pores offers a number of advantages over common employed dialysis and chromatography separation techniques. Porous ultrathin silicon membranes with nanofabricated controlled pore sizes between 5 and 25 nm in diameter have been shown to effectively separate small molecules based on their charge and even selectively separate two proteins of similar size (BSA and IgG), which is not possible by conventional dialysis techniques due to the wider pore size distribution [113]. More recently Prabhu et al. [27] were able to achieve 99% purity when separating 22 and 58 nm particles through a single silicon pore sensor based on the particle surface charge. By using a single pore Prabhu et al. [27] were able to monitor the selective passage of the higher charged smaller particles through the pore via the Coulter Principle. Particle separation was accentuated by modulating the elctroosmotic flow in the pore via changing the surface charge of the pore membrane. In this way only particles with an electrokinetic force greater than the viscous drag due to electroosmosis in the pore translocated the pore.

Elastic pore sensors have also been shown to selectively gate larger objects from analysis by reducing the pore size. Sowerby et al. [111] demonstrated the ability to effectively ‘close’ their elastic pore at no applied stretch preventing the translocation of DNA through the pore. Likewise, Roberts et al. [42] were able to selectively gate the passage of the largest 400 nm particles by 67 % through reducing the pore size. Presumably this methodology could be used to size a ‘fractionate’ and accurately measure a polydisperse sample.

Measuring concentration

A main feature attraction of Coulter counters and nanopores is their ability to accurately and easily measure dispersion concentration. Elastic pores extend this ability to measuring the concentration of a wide particle size distribution which is too small to detect by alternative techniques such as flow cytometry and microscopy. Willmott et al. [114] demonstrated that particle blockade pulse frequency scaled linearly with applied pressure for a range of particle concentrations of 100 nm carboxylated polystyrene particles, as shown in (a). Recently, Roberts et al. [115] reported a methodology for quantitatively measuring particle concentrations form the change in blockade pulse frequency with applied pressure. The device was calibrated by comparing the blockade pulse frequency of a known concentration standard to the blockade pulse frequency of the unknown sample. It was shown that in a model system of 210 – 710 nm diameter polystyrene particles with concentrations from ~1×10¹⁰ to 2×10⁸ particles/mL that the event frequency scales linearly with applied pressure and concentration. These measurements were shown to be independent of both particle size and charge. This calibration methodology was used to measure the concentration of ~1 um baculovirus occlusion bodies and the ~600 nm marine cyanobacteria Prochloroccus. Results obtained were in excellent agreement to cytometry (within 6%) and optical microscopy (within 17%) based concentration measurements.

Alternatively a calibration-free method can be applied, provided the pore-geometry is well characterized, allowing the estimation of fluid flow rates to enable concentration measurements via the Hagen-Poiseuille equation [116]. In the calibration-free case the error is introduced by the pore characterization methods, such as optical and electron microscopy. In a first attempt to achieve calibration-free concentration analysis, limitations and associated errors in our recent microscopy analyses of the pore geometry resulted in an 86% difference to the actual concentration of the measured standard [115].

Measuring charge

To date, few nanopore studies other than Ito et al. [18, 19] have used resistive pulse sensors to characterize the electrophoretic mobility (surface charge, ζ-potential) of individual objects using resistive pulse sensing. This is due in part to the complexity of forces acting on particles within a pore, i.e. external pressure and electoosmosis through the pore. Ito et al. [18, 19] were able to eliminate these additional forces by using an uncharged carbon nanotube sensor and no applied pressure. Willmott et al. [114] recently demonstrated the use of blockade pulse frequency measurements to elucidate the relative electrophoritic mobility of particle dispersions using an elastic nanopore. Removing the external applied pressure to drive particles through the pore, thereby increasing the effect of electrophoretic forces on particle translocation, gave rise to pulse frequency measurements that correlated to the particle surface charge. The relative blockade pulse frequency increased as the magnitude of the particle ζ- potential (Figure 9 (c)), as measured by phase analysis light scattering (PALS), increased above or below zero charge. This was observed for a range of particle materials and sizes over a pH range of 3 to 10.

Conclusions

Advances in nanofabrication and the increasing need for techniques in nano and biotechnology that can characterize individual particles have driven a revival in resistive pulse sensors. This renewed interest in a technique originally described over fifty years ago is due to new fabrication techniques and approaches that have improved measurement sensitivity, as well as interest in the wealth of information about individual particles contained in the resistive pulse signal, i.e. the size, shape, surface charge and concentration of objects in dispersion. Recently, a number of innovative devices have extended the capabilities of the original Coutler device. These include in-series, parallel, and size-tunable pore sensors. Such devices enable greater sample throughput and a wider size detection range. This new class of resistive pulse sensors also offers an alternative method for characterizing particulate dispersions on an event-by-event basis, and with greater sensitivity as compared to other common ensemble characterization techniques.

Biographies

Darby Kozak is a Senior Research Fellow within the Australian Institute for Bioengineering and Nanotechnology (AIBN) at the University of Queensland. His current research interests include resistive pulse sensors for particle characterization and developing particle based molecular diagnostics for the high throughput screening of polymer-biomolecule interactions. Prior to joining the AIBN he gained his BSc in Chemical Engineering from the University of Washington, USA in 2001 and his PhD in 2005 from the University of Bristol, UK where he studied non-ionic surfactants for stabilizing non-aqueous colloidal dispersions

Will Anderson is a PhD student at the Australian Institute for Bioengineering and Nanotechnology (AIBN) at the University of Queensland currently working on developing new nano/micro resistive pulse sensor devices for the characterization of nanoscale objects. Prior to undertaking his PhD at the AIBN, Will gained his BSc in Biotechnology (Hons) from the University of Queensland in 2010 and was a visiting scientist at the New Zealand nanotechnology company, Izon Science Ltd.

Robert Vogel is a Materials Scientist / Physicist interested in the design of advanced nanomaterials for optoelectronic, photovoltaic and biotechnology applications. Robert is currently a senior researcher at IZON Science, a New Zealand nanotechnology company specialising in the fabrication of nanoparticle counters. He gained his Diploma in Biophysics at the Technical University Munich in 1997 and his PhD in Chemistry at the University of Queensland (2003), studying ‘Dye-Doped Mesostructured Materials for Optical Device Applications’. In 2007 he co-founded a technology start-up, specialising in the fabrication of nanostructured semiconductor thin films for renewable energy applications.

Matt Trau is a Physical Chemist interested in biological and medical applications of nanotechnology. Matt is currently a Professor of Chemistry at the University of Queensland (UQ) and is also deputy director and co-founder of the Australian Institute for Bioengineering and Nanotechnology. Since graduating from the University of Sydney (BSc Hons I, University Medal) and the University of Melbourne (PhD in Physical Chemistry, 1993), he has held positions within industry and academia across the globe. These include a Fulbright Research Fellowship at Princeton University, USA, a research scientist at Dow Chemical and ICI Pty Ltd, as well as Lecturer, Senior Lecturer, Assoc Prof and Professor at UQ.