A new likelihood estimator and its comparison with moment estimators of individual genome-wide diversity

Abstract

The inbreeding coefficient of an individual, F, is one of the central parameters in population genetics theory. It has found important applications in evolutionary biology, conservation and ecology, such as the study of inbreeding depression. In the absence of detailed and reliable pedigree records, researchers have developed quite a few estimators to estimate F or the genome-wide homozygosity from genetic marker data. The statistical properties and comparative performances of these metrics are rarely known, however, which impedes an informed choice of the most appropriate one in practical applications. In this investigation, I propose a new likelihood F estimator that makes efficient use of marker information and takes into account of allelic dropouts, null alleles and prior knowledge of inbreeding. I compare the likelihood estimator with three moment estimators of F and three metrics of genomic homozygosity (or heterozygosity) by analysing both simulated and empirical datasets. It is shown that the likelihood estimator invariably outperforms the other estimators and metrics across all datasets analysed. For a typical dataset in heterozygosity-fitness correlation studies involving 10–20 microsatellites and 50 individuals, the correlation between the likelihood estimator and F (the simulated true inbreeding coefficient) is about 8∼35% higher than that between the moment estimators and F. A frequently applied metric, multilocus heterozygosity (MLH), and an F estimator based on the consideration of the proportion of alleles in homozygous conditions, F̂_R, are shown to have particularly poor performances. The low correlation between MLH and fitness traits, which is widely observed in numerous empirical studies, might be partially caused by the adoption of this inefficient estimator of genomic inbreeding.

Introduction

Individuals in natural populations vary in their genealogy and thus have different genome-wide diversity. Those having more or/and more recent common ancestors between their maternal and paternal lineages are expected to harbour less genetic diversity and show more genome-wide homozygosity. Individuals with the same genealogy also differ in genome-wide diversity because of the high stochasticity in Mendelian inheritance (Stam, 1980; Hill, 1993). The relative level of an individual's genome-wide diversity can be measured and assessed by its inbreeding coefficient, a concept developed by Wright (1922). He defined the inbreeding coefficient of an individual, F, as the correlation between the gametes combining to form the individual. Later F was redefined as the probability that two genes at any locus in the individual are identical by descent (Haldane and Moshinsky, 1939; Malecot, 1948). If the inbreeding coefficient of an individual is F, then the heterozygosity at any locus of the individual is expected to be reduced to 1−F of that of an outbred individual (F=0). A completely inbred individual (F=1), therefore, will have no variation at any locus of its genome (that is, homozygous for the whole genome).

The inbreeding coefficient of an individual can be easily calculated from its pedigree (Wright, 1951). Unfortunately, however, pedigree records are frequently lacking, incomplete or inaccurate in most natural populations. Alternatively, various genetic markers can be used to measure individual genome-wide diversity. Several metrics have been proposed and applied for such purposes, such as multilocus heterozygosity (MLH), internal relatedness (IR) and d² (Coltman and Slate, 2003; Balloux et al., 2004; Chapman et al., 2009; Szulkin et al., 2010). In particular, as surrogates for inbreeding coefficients, these metrics are applied widely to study the heterozygosity-fitness correlations (HFC) in natural populations, and significant correlations are usually interpreted as evidence of inbreeding depression (Szulkin et al., 2010).

It now becomes clear from numerous empirical studies on HFC (reviewed recently by Coltman and Slate, 2003; Chapman et al., 2009; Szulkin et al., 2010) that the correlations are generally weak (r<0.1 in average) and inconsistent among populations. The low HFCs are partially explained by the low correlation between MLH measured at a few marker loci and inbreeding (that is, genome-wide homozygosity) in large random mating populations, in which both the mean and the variance of individual inbreeding coefficients are expected to be low (for example, Balloux et al., 2004; Slate et al., 2004). Indeed, in the absence of identity disequilibrium (the correlation in homozygosity among loci within an individual) due to non-uniform inbreeding or linkage (Crow and Kimura, 1970), the allelic states (that is, either heterozygous or homozygous) become independent of each other among loci within individuals, and the MLH at a set of markers will reflect the diversity of these particular markers only and will be uncorrelated with the heterozygosity elsewhere in the genome (Chakraborty, 1981; Szulkin et al., 2010). Both theoretical (for example, Slate et al., 2004) and simulation (Balloux et al., 2004) studies suggested that MLH and fitness are unlikely to be correlated unless inbreeding events are frequent and severe, and unless a large number of markers are used (∼200).

ID should be ubiquitous in natural populations because of the widespread occurrences of non-random mating (for example, partial selfing and mating between close relatives), population structure (for example, social structure and subdivision), population bottlenecks and migration. Additionally, linked markers will gain extra ID caused by their physical linkage. In the presence of ID, the diversity assessed at a set of marker loci will be correlated with that of the entire genome and thus could act as a proxy of F of an individual. However, simple proxies of F such as MLH fail to capture and use marker information fully and are thus expected to be inferior to a direct estimate of F from the same marker data.

First, metrics like MLH are expected to vary among loci due to locus-specific properties such as mutation rates. For the same individual, a different set of markers will lead to a different MLH value, and the MLH of highly polymorphic markers like microsatellites will be larger than that of lowly polymorphic markers such as single-nucleotide polymorphisms (SNPs). In contrast, an estimator of F should be marker independent. Second, because of the inherent difference in heterozygosity among loci due to locus rather than individual properties, it is difficult to interpret MLH as a proxy for F. For example, two individuals cannot be compared impartially in inbreeding levels when their MLH is assessed for two different sets of loci (for example, SNPs and microsatellites). So long as the two sets of markers assayed for two individuals are not completely overlapping (due to, for example, missing data for one or both individuals), the MLH of the two individuals may differ because of the difference not in inbreeding, but in markers. In contrast, estimates of F from different loci are expected to be the same for a given individual and can thus be optimally combined (weighted) using allele frequency and other information to yield an overall estimate of F. Third, genotype data are imperfect (Bonin et al., 2004; Pompanon et al., 2005). Microsatellites, for example, may suffer from allelic dropouts and null alleles, which may bias inbreeding and MLH estimates. Because F estimators are model-based, it is possible to avoid or reduce the bias by incorporating genotyping errors in the model, as shown below. Due to these reasons, therefore, the low HFC observed in empirical studies (Coltman and Slate, 2003; Chapman et al., 2009; Szulkin et al., 2010) and supported by theoretical considerations (Balloux et al., 2004; Slate et al., 2004) may be partially caused by the inefficiency of MLH as a surrogate for F, rather than the absence or weakness of identity disequilibrium or inbreeding depression.

It is challenging to estimate individual inbreeding coefficient accurately from a small number of markers. Most marker-based inbreeding estimators are developed for estimating the average F of individuals, or population level inbreeding (for example, Li and Horvitz, 1953; Robertson and Hill, 1984; Hill et al., 1995; Ayres and Balding, 1998). A few estimators are proposed to use unlinked codominant markers (Ritland, 1996; Ritland and Travis, 2004; Carothers et al., 2006; Wang, 2007), unlinked dominant markers (Dasmahapatra et al., 2008) or linked genomic markers (Leutenegger et al., 2003) to estimate individual inbreeding coefficients. Some of the estimators were compared with MLH in estimating individual inbreeding coefficients using empirical and simulated genomic marker data (Polašek et al., 2010). More systematic comparative studies of these F estimators and the widely used surrogates are needed to understand their behaviours and to facilitate the choice and use of the most appropriate estimator in molecular ecology, conservation biology and human genetics studies.

In this investigation, I will derive a new likelihood estimator of individual inbreeding coefficient from its marker genotype data, and compare it with other F estimators and surrogates in accuracy using both simulated and empirical data. I also improve a moment F estimator by using its symmetric form and by applying locus-specific weights. The analysis results from simulated and empirical datasets are helpful in understanding the behaviours and relative performances of different estimators, and in choosing the appropriate estimator in practical applications. They are also useful in the experimental design of and the interpretations of the results in studies involving individual inbreeding coefficients or surrogates, such as HFC studies.

Methods

In this section, I derive a new likelihood estimator that accommodates allelic dropouts and null alleles, and briefly describe a number of moment estimators of F and a few widely used metrics for individual genomic diversity or homozygosity. I then describe the simulations and some empirical datasets that are used to investigate the behaviours and to compare the accuracies of different estimators.

Likelihood estimator

Consider a locus with k +1 alleles, denoted by A_i with index i=0, 1, 2, . . . k. The first allele, A₀, is undetectable (null) and its frequency in the population is q. The remaining k alleles, A_i (i>0), are detectable codominant alleles, and their frequencies in the population are p_i. Obviously, q+Σ_i=1^kp_i=1 and q=0 for a null allele free locus. I assume allelic dropouts affect heterozygous genotypes only, and when a single dropout occurs (at a rate d) to a heterozygote, it leads to one of the two possible homozygous phenotypes at an equal probability (Wang, 2004). Double dropouts at the same locus of the same individual are ignored, because they rarely occur and, if they do, can be easily detected and thus rectified by regenotyping. Allelic dropouts and null alleles are assumed to occur independently to a genotype, and the probability of both occurring to the same genotype is negligibly small. Under these assumptions, the probability of the observed phenotype (A_iA_i or A_iA_j), or the likelihood of F, of an individual is

where P_N=(1−F)q²+Fq is the expected frequency of null allele homozygotes. For a set of L loci under linkage equilibrium, the likelihood function is

where the likelihood at locus l, Q_l, is calculated by (1) using locus specific values of p_i, d and q.

In natural populations, the inbreeding coefficients of most individuals are small. To incorporate this prior information and to reduce the overestimation of F due to the imposed constraint of F⩾0 in the likelihood function, I apply a prior probability of e^−F to the likelihood function

Maximising (3) gives the maximum likelihood estimate of F. As it is intractable to solve (3) analytically, I use Brent's method (Press et al., 1996) to obtain numerical solutions of (3) with F̂ constrained to the legitimate range of [0, 1]. Tests using numerous simulated and empirical datasets with a large number of initial F̂ values indicate that the method is fast and converges reliably irrespective of the initial F̂ values. For simplicity, estimator (3) is denoted as F̂_L hereafter.

Moment F estimators

Ritland (1996) derived an estimator of the inbreeding coefficient of an individual from its multilocus genotype data,

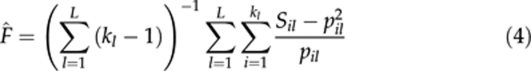where p_il is the frequency of allele i (=1, 2, … k_l) at locus l (=1, 2, …, L), and S_il is an indicator variable taking a value of 1, if the individual is homozygous for allele i at locus l or 0, if otherwise. For a single locus (L=1), this estimator is the same as that derived by Li and Horvitz (1953), based on the consideration of the proportion of alleles in homozygous conditions. In the single locus estimator, an equal weight is given to each allele irrespective of its frequency (Ritland, 1996). The multilocus estimate of (4) was obtained by (Ritland, 1996) by weighting single locus estimates. The weight for a locus is the inverse of the variance of the estimate from the locus, obtained assuming F=0. For simplicity, estimator (4) is denoted as F̂_R hereafter.

In the case of a single k-allele locus, (4) yields an estimate of F̂_ii=(1/p_i−1)/(k−1) for an A_iA_i homozygote and F̂_ij=−1/(k−1) for any A_iA_j heterozygote (i≠j). For a homozygote, F̂_ii>0 and the magnitude of F̂_ii decreases with an increasing p_i (the frequency of the allele in the genotype) and k (number of alleles). In other words, (4) gives a higher positive F estimate for an individual who is homozygous for a more rare allele at a locus with fewer alleles. F̂_ii is larger than, equal to and smaller than 1, when p_i <1/ k, p_i=1/k and p_i>1/k, respectively. Extremely large estimates occur to homozygotes of very rare alleles. If p_i=1/k², for example, F̂_ii=k+1. This suggests that (4) is very sensitive to allele frequencies and may be affected by misspecification of allele frequencies, mutations and genotyping errors. For a heterozygote, F̂_ij<0 and the magnitude of F̂_ij decreases with k, irrespective of the frequencies of the alleles in the heterozygote. Overall, (4) is lower bounded by −1 (which occurs to a heterozygote at a biallelic locus), but has no upper bound. The distribution of (4) is rightward skewed.

Carothers et al. (2006) obtained a single-locus F estimator

where h is the expected heterozygosity and S is an indicator variable taking a value of either 1, if the individual is a homozygote or 0, if otherwise, at the locus. (5) is the same as that derived by Li and Horvitz (1953), based on the consideration of the total proportion of heterozygotes. Carothers et al. (2006) showed that (5) is an unbiased estimator of F and its variance is (1−F)(1/h−1+F), which reduces to 1/h−1 approximately for low inbreeding. Using the inverse of the variance as the locus weight, a multilocus estimator is obtained

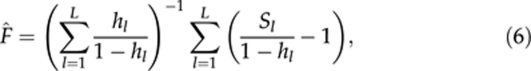where h_l is the expected heterozygosity and S_l is the indicator variable for homozygosity as defined in (5), at locus l (=1, 2, …, L). For simplicity, estimator (6) is denoted as F̂_C hereafter.

In the case of a single locus, (5) yields an estimate of F̂_ii=1 for any homozygote and F̂_ii=1−1/h for any heterozygote (i≠j). Theoretically (5) is upper bounded by 1 and has no lower bound, as F̂_ij decreases with a decreasing heterozygosity. In contrast to F̂_R, therefore, F̂_C is leftward skewed. However, F̂_C is less skewed than F̂_R, and is less sensitive to rare alleles, mutations and genotyping errors.

Ritland and Travis (2004) derived, following Lynch and Ritland's (1999) approach to pairwise relatedness estimation, an estimator for the inbreeding coefficient of an individual with a single locus genotype A_iA_j (i,j=1, 2, …, k)

where allele i is arbitrarily chosen as the reference allele and the indicator variable S=1 if i=j and S=0 if i≠j. A better estimator is to use both alleles as reference and take the average of the two resulting estimates as the overall estimate

Estimator (8) is the same as (7) when the individual is a homozygote (i=j), but is more accurate than (7) when the individual is a heterozygote (i≠j). It is shown in Appendix A that (8) is an unbiased estimator of F. Using the inverse of the variance of (8) (see A1) as a weight, I obtain a multilocus estimator

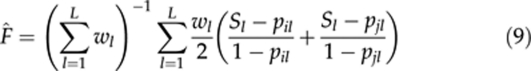where, for locus l,

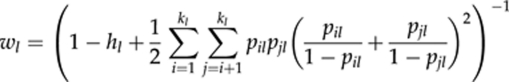is the weight, S_l is the indicator variable for homozygosity (=1/0 if the individual is a homozygote/heterozygote), h_l is the expected heterozygosity and p_il is the frequency of allele i. For simplicity, estimator (9) is denoted as F̂_LR hereafter.

In the case of a single locus, (8) yields an estimate of F̂_ii=1 for any homozygote and 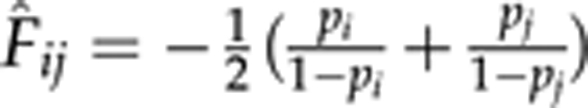for a heterozygote A_iA_j (i≠j). F̂_ij is always negative and its magnitude (absolute value) decreases with the frequencies of the two alleles in the heterozygote. F̂_ij → 0 when both p_i → 0 and p_j → 0, and F̂_ij → −1 when both p_i → 0.5 and p_j → 0.5. Therefore, (8) falls in the range of [−1, 1]. In general, F̂_LR is less skewed than both F̂_R and F̂_C. It is less sensitive than F̂_R and more sensitive than F̂_C to rare alleles, mutations and genotyping errors.

In the case of multiple biallelic loci, w_l reduces to h_l/(1−h_l), and (8) reduces to (5). Irrespective of the number and allele frequency distribution of loci, (9) and (6) are identical. In the case of an equal allele frequency, the three estimators (F̂_LR, F̂_R and F̂_C) are identical and reduce to 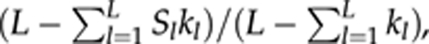where k_l is the number of alleles at locus l (=1, 2, …, L).

Surrogate metrics

Quite a few metrics have been proposed and applied to measure and assess individual homozygosity or heterozygosity. They are widely applied to HFC studies as surrogates for inbreeding coefficients (Chapman et al., 2009; Szulkin et al., 2010). Here I focus on three of them.

The MLH of an individual is the proportion of loci that are heterozygous. It is a diversity measurement, and its complement gives the proportion of loci that are homozygous and acts as a proxy of inbreeding coefficient. If there is inbreeding depression, therefore, one should observe a negative correlation between MLH and a fitness component among individuals. There are quite a few variants to MLH (Chapman et al., 2009; Szulkin et al., 2010). MLH ignores locus specific properties (for example, number and frequencies of alleles), and thus is simple to calculate and is robust to misspecifications of allele frequencies, scoring errors and mutations. It is criticised, however, for wasting information, which may lead to reduced accuracy. For example, a homozygote for a rare allele should indicate a higher level or/and a greater chance of inbreeding than a homozygote for a common allele. Similarly, a homozygote at a locus with many alleles in an even frequency distribution should indicate a higher level or/and a greater chance of inbreeding than a homozygote at a locus with few alleles in a skewed frequency distribution. MLH fails to incorporate allele frequency information within a locus and between loci and may be inappropriate when markers differ in number and frequency of alleles, or when not all individuals are typed with the same panel of markers (Aparicio et al., 2006).

Aparicio et al. (2006) proposed a homozygosity index that weighs the contribution of loci by their expected heterozygosity. The index, called homozygosity by locus (HL), is defined as

where, at locus l, S_l is an indicator variable that takes values of 1 and 0 when the individual is a homozygote and heterozygote, respectively, and h_l is the expected heterozygosity. HL varies between 0, when all loci are heterozygous and 1, when all loci are homozygous. For two individuals having the same number of homozygous loci, the one whose homozygous loci are more informative (that is, with higher h_l values) has a higher HL. No distinctions are made, however, among genotypes within a locus in calculating HL. Individuals having the same set of homozygous loci will have the same value of HL, although they may be homozygous for different alleles of different frequencies.

Adapting Queller and Goodnight's (1989) measure of relatedness between individuals, Amos et al. (2001) proposed a metric, called IR, to measure the relatedness between paternal and maternal alleles at a locus in an individual. It is defined as

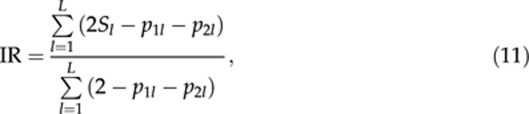where S_l is as defined in (10) and p_1l and p_2l are the frequencies of the two alleles in the individual genotype at locus l (=1, 2, …, L). IR varies between 1, when all loci are homozygous, and −1, when all loci are biallelic and heterozygous.

It can be shown that, while 1−MLH, HL and IR are all positively correlated with inbreeding coefficients (F), they are biased estimators of F. However, the degree of bias is irrelevant when the absolute values of F are insignificant as in correlation analyses (such as HFC).

Evaluation of estimators using simulated data

The performances of F estimators and surrogate metrics are measured by their correlation coefficients with the true F values in simulations. The true F value of an individual is drawn from a beta distribution with parameters α and β, so that the mean and variance of F are α/(α+β) and αβ/((α+β)²(α+β+1)), respectively. For a given F, the individual genotype is generated from a given allele frequency distribution at a locus, and genotypes at multiple loci are generated independently assuming linkage equilibrium. Where allelic dropouts or null alleles are considered, individual genotypes are changed at random, following the models and at the rates of these events before being analysed for inbreeding. Allele frequencies at a locus are drawn from a uniform Dirichlet distribution and are used in generating simulated genotypes, and in calculating F estimators and surrogate metrics.

To investigate the impact of the variance in actual F on the performances of different estimators, values of parameters α and β are chosen in simulations to yield a fixed mean (0.05, which is close to those in empirical studies) and a variable variance (0.0001–0.0256) of F. To understand the relative performances of different F estimators when different numbers of markers with variable polymorphisms are used, genotype data at a variable number of loci with a variable number of alleles per locus were simulated and analysed by the estimators. To investigate the sensitivity of different estimators and metrics to the misspecification of allele frequencies, a sample of individuals is drawn from the population to estimate allele frequencies. The estimated frequencies are then used in calculating F estimators and surrogate metrics. To investigate the effect of allelic dropouts on the performances of the estimators, genotype data with a variable allelic dropout rate were generated and analysed by different estimators. For the likelihood estimator, the data were analysed with dropouts both accounted for and ignored. For a given set of parameters, 100 000 replicated datasets are simulated and analysed to produce a correlation coefficient between each F estimator (surrogate metric) and the simulated true F value.

All estimators and metrics should be positively correlated with F, except for MLH, which is negatively correlated with F. To facilitate comparison with other estimators and metrics, the absolute values of correlation for MLH are drawn in all graphs.

Evaluation of estimators using two empirical datasets of human populations

To compare the performances of the F estimators and surrogate metrics in practical situations, they are applied to the analysis of two empirical datasets. One dataset is from Rosenberg et al. (2005), which contains the genotype data at 783 autosomal microsatellite loci and 210 insertion/deletion polymorphisms of 1048 individuals from 53 populations. The other dataset is from Pemberton et al. (2008), which contains the genotype data at 2810 SNPs of 957 individuals. Both datasets are available online from http://rosenberglab.bioinformatics.med.umich.edu/diversity.html. As individual inbreeding coefficients are unknown, it is impossible to use the correlation coefficient as adopted in simulations to measure accuracy. However, to be a good estimator of F or genomic diversity, it should yield estimates, from two independent sets of markers that are correlated (Balloux et al., 2004). For each dataset, a number of L markers are selected at random without replacement from the original set of loci to form one subset, and another subset of L markers is selected similarly. The two non-overlapping subsets are then used to calculate an F estimator or metric of each individual, and the correlation coefficient between the two sets of estimates is calculated. This process is repeated 1000 times for each value of L.

Results

Variance of actual F

At a given low mean value (0.05) of actual F, the correlations between different metrics and F values as a function of the variance of F are compared in Figure 1. As can be seen, all metrics become more correlated with F with an increasing variance in F, as expected. When the variance of F is small, all individuals tend to have the same or very similar levels of inbreeding. In such a case, no matter which metric is used and how informative the markers are, the correlation is always small. This is understandable because the covariance and thus correlation between two random variables becomes zero when either variable tends to become constant. A more appropriate measurement of the accuracy of a metric is its mean squared error, which incorporates both the variance and bias of the metric and is valid, regardless of the variance of F. Unfortunately, however, mean squared error is not suitable for comparing F estimators and other metrics, as the latter can be highly biased whereas the former are unbiased. This caveat of correlation coefficient as an accuracy measurement should be born in mind and a low correlation does not necessarily mean that F is not accurately estimated by the unbiased estimators (F̂_L, F̂_LR, F̂_R and F̂_C).

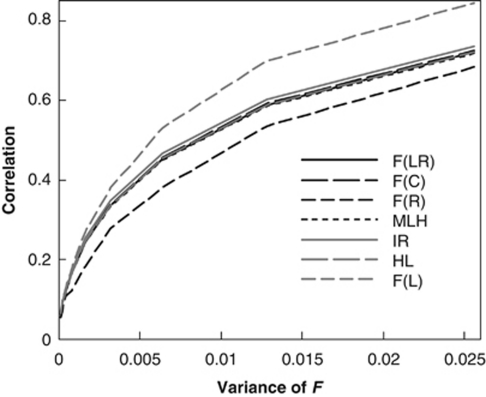
Figure 1.

Correlation coefficient between each estimator (metric) and true F as a function of the variance of F. A total of 10 markers, each having 10 alleles with frequencies drawn from a uniform Dirichlet distribution, are used in calculating the F estimators (metrics). In the simulations, an individual F value was drawn from a beta distribution with a fixed mean of 0.05, and with a variance increasing from 0.0001 to 0.0256 on the x axis.

Among the estimators and metrics, F̂_L is the best, F̂_R is the worst, whereas the rest have the same intermediate performance in the whole range of the variances of F. F̂_R gives unbiased estimates of F, but the estimates are highly variable and thus have a low correlation with F. In (4), weighting is applied to alleles within a locus and to different loci, based on the assumption of F=0. Although this is probably the best weighting scheme when inbreeding is low, it does cause a loss of precision for individuals with a substantial level of inbreeding. The other two moment estimators, F̂_LR and F̂_C, use a similar weighting scheme, but the scheme is applied to loci only. Furthermore, F̂_R is highly sensitive to the presence of rare alleles and could lead to extremely large estimates for a homozygote of very rare alleles.

In Figure 1, a fixed low level of inbreeding, 0.05, is simulated to mimic real populations. A review reveals that the mean and variance of individual inbreeding in 12 vertebrate populations are on average 0.042 (range 0.007–0.103) and 0.0047 (range 0.0007–0.0192) (Slate et al., 2004). Using a variable number of microsatellites (13–138), the correlation between MLH and F is observed to be −0.26 on average, with a range of −0.03∼−0.54 (Slate et al., 2004). These results are qualitatively consistent with the simulation results shown in Figure 1. At other levels of mean inbreeding, results similar to those shown in Figure 1 were also obtained in simulations.

Number of markers

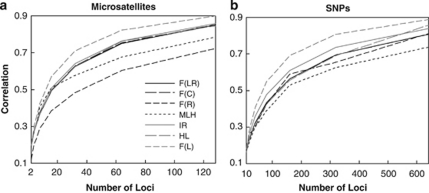
Figure 2 shows the correlations between different metrics and F values as a function of the number of markers used in analyses. The mean and variance of F were fixed at 0.05 and 0.005 in simulations to match the observed values in empirical studies (Slate et al., 2004). For the case of microsatellites (each having 10 alleles, Figure 2a), F̂_L outperforms the other metrics no matter how many markers are used. The worst metric is F̂_R, in agreement with Figure 1. MLH becomes the second worst metric with an increasing number of loci, probably because it discards allele frequency information. In contrast, the two improved metrics, IR and HL, have a performance, which is much better than that of MLH and is similar to that of F̂_LR and F̂_C. The correlations between F̂_L and F are 0.57 and 0.71, respectively, when L=16 and 32, respectively. For MLH to attain the same levels of correlations with F, however, L=32 and 120 markers must be used, respectively.

Figure 2.

Correlation coefficient between each estimator (metric) and true F as a function of the number of loci. The simulated individual F value was drawn from a beta distribution with a mean and variance of 0.05 and 0.005, respectively. For the cases of microsatellites (a) and SNPs (b), each locus has 10 and 2 alleles, respectively, with frequencies in a uniform Dirichlet distribution.

Similar results are obtained for SNPs (each having two alleles), as shown in Figure 2b. The differences are, MLH performs the worst and F̂_LR becomes identical to F̂_C. The performance of F̂_R is improved to become the second worst, because of the much-reduced chances of rare alleles and much-fewer weightings within a locus.

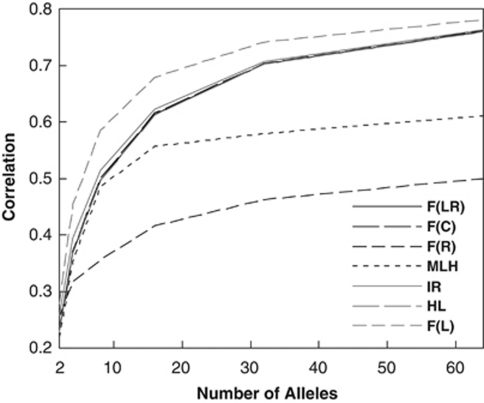
Number of alleles

Figure 3 compares the correlations between different metrics and F values as a function of the number of alleles per locus (k). Although all metrics are increasingly correlated with F with an increasing value of k, MLH and F̂_R become almost attenuated when roughly k=16. This is because MLH makes no use of allele frequency information, which becomes more important with an increasing value of k under the uniform Dirichlet distribution. F̂_R is sensitive to rare alleles and could yield extremely large estimates for homozygotes of rare alleles. Furthermore, there are k equal weightings about the k alleles at a locus, the weightings being optimal only when F=0 (Ritland, 1996). Because of these two causes, F̂_R becomes more and more inferior to other metrics in performance with an increasing k. In practice, this estimator has some value only when k is small, such as the case of SNPs.

Figure 3.

Correlation coefficient between each estimator (metric) and true F as a function of the number of alleles per locus. The number of loci is fixed at 20, and individual F values were drawn from a beta distribution with a mean and variance of 0.05 and 0.005, respectively.

Except for MLH, all metrics use allele frequency information and their performances (excluding that of F̂_R) improve with an increasing number of alleles. Again, the likelihood estimator outperforms the others, regardless the value of k, whereas F̂_LR, F̂_C, IR and HL are almost indistinguishable in performances.

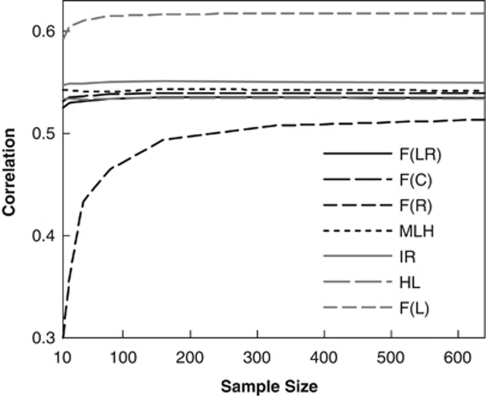
Sample size

In the above, allele frequencies are assumed known in calculating each metric. In reality, however, allele frequencies are estimated from a sample of individuals and how robust the metrics are to misspecifications of allele frequencies is of practical interest. Figure 4 plots the correlations between different metrics and F values as a function of the size of the sample used in estimating allele frequencies. All metrics, except for F̂_R, are fairly robust to sampling errors of allele frequencies. There is no substantial loss of performance even when only 10 individuals are used to estimate allele frequencies. In contrast, F̂_R is extremely susceptible to sampling errors of allele frequencies. Its correlation with F stabilizes only when sample size reaches about 300 (Figure 4).

Figure 4.

Correlation coefficient between each estimator (metric) and true F as a function of the size (number of individuals) of the sample used for estimating allele frequencies. The number of loci was fixed at 20, each locus had 10 alleles with frequencies drawn from a uniform Dirichlet distribution, and individual F values were drawn from a beta distribution with a mean and variance of 0.05 and 0.005, respectively.

Allelic dropouts

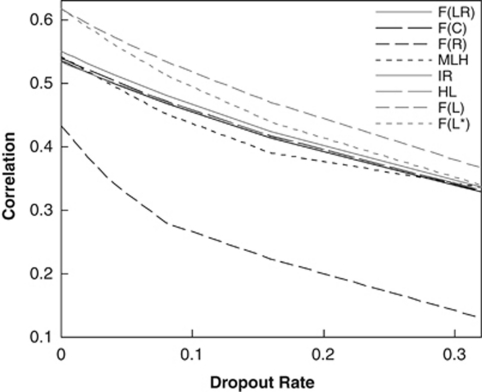
Allelic dropouts lead to an excess of homozygotes and thus an overestimation of F if they are ignored. Figure 5 compares the correlations between different metrics and F values as a function of the dropout rate (d) at each of 20 loci. The likelihood estimator was implemented with allelic dropouts either ignored (that is, assuming d=0) or taken into account. As can be seen, all metrics become less correlated with F with an increasing value of d. This is true even with the likelihood estimator in which allelic dropouts are accommodated. As expected, the likelihood estimator is more sensitive to dropouts. Its performance drops faster than that of other metrics with an increasing d value, when dropouts are ignored. In contrast, when dropouts are accounted for, the likelihood estimator is always substantially better than other estimators, regardless of the value of d. Similar results were obtained for the cases of null alleles, and both null alleles and dropouts.

Figure 5.

Correlation coefficient between each estimator (metric) and true F as a function of the dropout rate at each locus. The number of loci was fixed at 20, each locus had 10 alleles with frequencies drawn from a uniform Dirichlet distribution, and individual F values were drawn from a beta distribution with a mean and variance of 0.05 and 0.005, respectively. The dotted grey line (denoted as F(L^*)) shows the correlation between F values and likelihood estimates obtained by ignoring allelic dropouts (d=0).

Analysis of empirical datasets

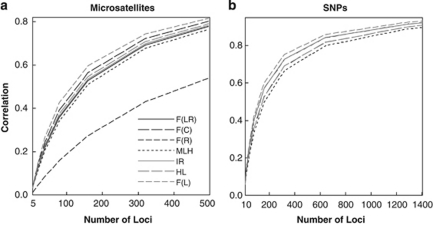
The correlations between estimates from two subsets of markers as a function of the number of markers included in a subset (L) are shown in Figure 6. For microsatellites, F̂_R has the lowest correlation, regardless of the value of L, confirming the simulation results for markers with multiple alleles. F̂_L has the highest correlation, whereas MLH has the second lowest correlation throughout the range of L (5–496). For SNPs, F̂_L has the highest and MLH has the lowest correlation. F̂_LR and F̂_C are identical and are indistinguishable from HL in correlation. IR and F̂_R have very similar correlations that are slightly smaller than those of F̂_L.

Figure 6.

Correlation coefficients between estimates from two non-overlapping subsets of markers for each estimator (metric) as a function of the number of markers in a subset. Two empirical datasets were analysed. The first (a) has genotypes of 1048 individuals from 53 human populations at 993 microsatellite loci (Rosenberg et al., 2005), and the second (b) has genotypes of 957 human individuals at 2810 SNPs (Pemberton et al., 2008). For SNPs, F̂_C, F̂_LR and IR are indistinguishable.

For both datasets, the highest correlation obtained with F̂_L is larger than 0.8, suggesting a high level of identity disequilibrium. This is not surprising considering that the datasets of microsatellites and SNPs come from 53 and 54 worldwide populations, respectively. These populations are genetically differentiated (for example, Rosenberg et al., 2005) and are different in size, and thus in levels of inbreeding. Furthermore, consanguineous marriages are customary in some populations (Bittles and Neel, 1994), which leads to a further increase in identity disequilibrium.

Discussion

In this investigation, I proposed a likelihood estimator of individual inbreeding coefficient (F) that makes efficient use of marker information (allele frequencies) and takes into account of allelic dropouts, null alleles and prior knowledge of inbreeding. The estimator is compared with three moment estimators of F and three metrics of homozygosity (or heterozygosity) by analysing both simulated and empirical datasets. It is shown that the likelihood estimator invariably outperforms the other estimators and metrics across all situations considered.

The performance differences among the estimators and metrics come mainly from the schemes used to weigh the information among alleles within a locus and among loci. The optimal weighting is built into the likelihood estimator naturally, whereas the weighting scheme for each moment estimator of F is derived assuming F=0. For inbred individuals (F>0), the weighting is obviously suboptimal and thus leads to a loss of accuracy. The problem is especially acute for F̂_R in the case of a multi-allele locus, because F̂_R uses an equal weight for each allele at the locus. When the number and frequency differences of alleles at a locus are large, this weighting scheme results in a substantial loss of accuracy. It seems that F̂_R should not be used in practice for highly polymorphic multi-allele loci, such as microsatellites. Compared with MLH that makes no weighting within and between loci, both HL and IR have much improved performances brought about by weighting loci using allele frequency information. The improvements are visible even when allele frequencies are inaccurately estimated (Figure 4) or genotyping errors are present (Figure 5), and increase with the number of alleles per locus (Figure 3).

The three moment estimators of F are unbiased, the likelihood estimator is slightly biased due to the constraint of F⩾0, whereas the three homozygosity metrics are all biased for F. IR is generally much less biased than MLH and HL, and its bias reduces rapidly with an increasing number of loci. Although the four F estimators provide the absolute estimates of F, the three homozygosity metrics yield estimates that indicate relative levels of inbreeding. Measured by the correlation with true values of F, IR, HL, F̂_LR and F̂_C have a similar intermediate performance, the likelihood estimator has the best performance and MLH and F̂_R have the worst performance overall. Measuring performance by correlation coefficient is justified only when the estimates are used in a regression or correlation analysis, such as HFC. More generally, performance is better measured by mean squared error, which accounts for both sampling error and biasness and is valid regardless of the variance of F. When mean squared error is adopted as the criteria, F̂_LR and F̂_C would be better than the three homozygosity metrics.

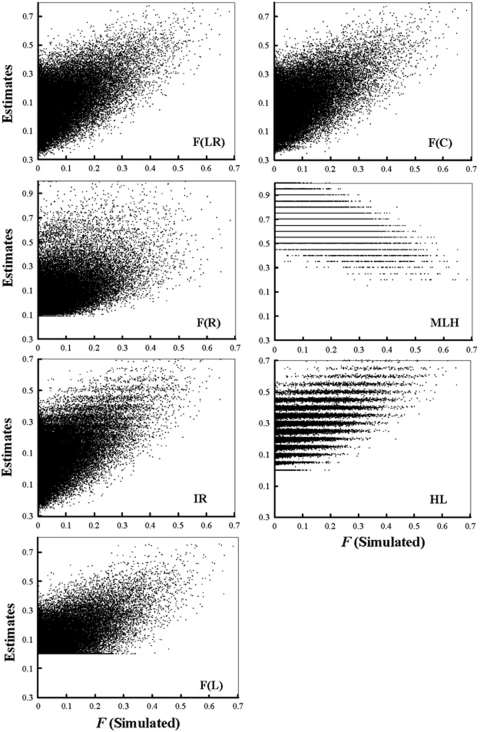
As a performance (accuracy) measurement, the correlation coefficient between an estimator and the true F values is simple and valid, regardless of the degree of bias. Like any other summary statistics, however, it does not provide a complete assessment of the performance. A low correlation coefficient, for example, can be due to a low covariance between F and the estimator, a high variance of the estimator, or both. A scatter graph showing the correlations between the estimated and simulated F values is more informative, but takes too much space. A set of such scatter graphs showing the correlations between each estimator and F can be found in Appendix B. As can be seen, all estimators are highly scattered around the true simulated F value. The F̂_R estimator has especially a high sampling variance, yielding frequently estimates larger than 1, which are out of the scale of the graph.

Allele frequency distributions of the markers affect all estimators, but to different degrees. Some estimators, such as F̂_R, are highly sensitive to the presence of rare alleles, whereas others are resilient. Simulation results are shown in Figures 1,2,3,4 and 5 for a uniform Dirichlet distribution of allele frequencies. In practice, allele frequencies are probably more skewed, yielding more rare alleles than the uniform distribution. I have also conducted simulations assuming a triangular and an equal allele frequency distribution, yielding qualitatively the same conclusions as reached from the simulations using the uniform distribution.

Given the poor performance of MLH compared with the likelihood estimator, it is possible that the low HFCs observed in numerous empirical studies (Chapman et al., 2009; Szulkin et al., 2010) are partially caused by the adoption of this inaccurate metric. Higher HFCs might have been obtained should the likelihood F estimator be used in these empirical studies. The likelihood method can use marker information efficiently and can incorporate null alleles and allelic dropouts. With slight modification, it can use dominant markers (such as AFLPs, see Dasmahapatra et al., 2008) together with codominant markers to estimate F. It can also deal with linkage among genomic markers, if the linkage map of the markers is known (Leutenegger et al., 2003). It seems to be difficult or impossible to cope with these complexities for moment estimators of F or metrics of homozygosity.

It is generally accepted that pedigree data allow a much better inference of inbreeding than genetic markers (Balloux et al., 2004). Although this is probably true in some practical situations, it should be realised that several conditions have to be satisfied for pedigree-derived inbreeding estimates to be more accurate than marker-based estimates. First, the pedigree must be deep enough. Shallow pedigrees spanning just a couple of generations fail to capture a sufficient number of inbreeding loops and thus lead to an underestimation of inbreeding. Furthermore, because of the lack of information about the founders, they are assumed non-inbred and unrelated which may lead to further underestimation of F. Although just a few generations are required to provide a reasonably good estimate of F (Balloux et al., 2004) in balanced pedigrees formed through random mating, a considerably larger number of generations are necessary in unbalanced pedigrees formed by non-random mating, such as avoidance of close inbreeding found in some natural populations and in plant and animal breeding. MacCluer et al. (1983) estimated the inbreeding levels of 5207 standardbred horses from six breeding farms in North America, using the pedigrees traced back as far as 30 ancestral generations. They showed that inbreeding coefficients increase markedly with increasing pedigree depth, levelling off only after 10–12 generations. It is true that a recent common ancestor for the parents of an offspring has a disproportionately large impact on the offspring's F, but there could be many remote common ancestors, remembering that the total number of ancestors roughly double with each generation into the past. Second, the pedigree must be complete and accurate. For most natural populations, pedigrees are difficult to acquire and, if available, are usually incomplete and inaccurate as they are obtained most often from a combination of behavioural observations and marker-based inferences. It is now well recognised that behavioural data are unreliable because of events such as the widespread occurrence of extra-pair mating (for example, Petrie and Kempenaers, 1998). Genetic parentage assignments from marker data (Marshall et al., 1998; Wang and Santure, 2009) are also error prone, with an accuracy depending heavily on the amount of marker information.

It should also be realised that pedigree- and marker-based inbreeding coefficients are conceptually different. The F value calculated from pedigrees gives the expected inbreeding of an individual, or the expected probability of identity by descent of the two alleles at a random locus in the individual's genome. Individuals (say, full siblings) with the same pedigree have the same expected inbreeding, but may have different realised levels of inbreeding. Meiosis is a highly stochastic process. Although half of the DNA making up a gamete is expected to be maternally derived and half is expected to be paternally derived, there is a high stochastic variance about this expectation (Stam, 1980). As a consequence, grandchildren vary in the proportion of DNA they inherit from each of their four grandparents. For humans as an example, while the F value of the offspring of first cousin marriage is expected to be 0.0625, its standard deviation is 0.0243 (Carothers et al., 2006). This variance increases with a decrease in genome size and recombination. Therefore, pedigree-derived F is the expected inbreeding level of individuals possessing the same pedigree and acts as an approximate estimate of individual genome-wide autozygosity (realised inbreeding). In contrast, the F value inferred from markers gives the average realised level of inbreeding at these particular loci of a particular individual. When these markers are taken at random from the genome, it also gives a good estimate of genome-wide inbreeding. Given a sufficient number of markers, they could provide a better estimate of individual genome-wide autozygosity than pedigrees. This is becoming a reality with the rapidly increasing availability of high-density genome-scan data. Marker-based inbreeding estimation also makes it possible to investigate inbreeding-related effects (such as inbreeding depression) using individuals with the same pedigree and thus the same expected F, as their realised levels of inbreeding are variable.

Appendix A

Mean and variance of moment estimators of F

For a locus with k codominant alleles of frequencies p_i (i=1, 2, …, k), the mean and variance of estimator (6) for individuals with inbreeding coefficient F are

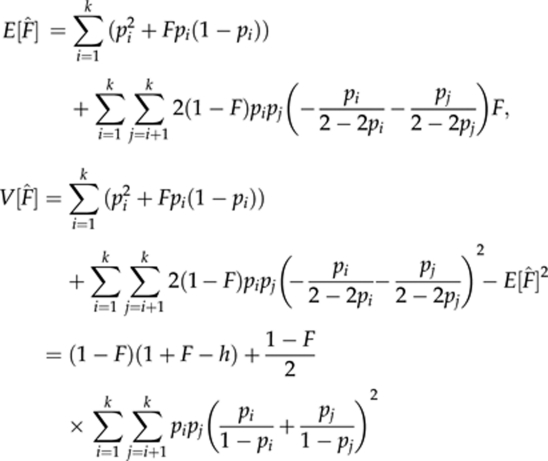
where h is the expected heterozygosity. With low inbreeding (F → 0), the variance is approximately

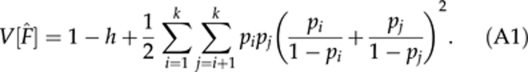Appendix B

Scatter graphs between each estimator and F

The estimates from each estimator and the true simulated F values across 100 000 replicate simulated datasets are plotted in a scatter graph, Figure A. The simulated individual F values were drawn from a beta distribution with a mean and variance of 0.05 and 0.005, respectively. A total of 20 markers, each having 10 alleles with frequencies in a uniform Dirichlet distribution, are used in simulations.

Figure A.

The author declares no conflict of interest.