What Determines the Activity of Antimicrobial and Cytolytic Peptides in Model Membranes

Abstract

We previously proposed three hypotheses relating the mechanism of antimicrobial and cytolytic peptides in model membranes to the Gibbs free energies of binding and insertion into the membrane [Almeida, P.F., and Pokorny, A. (2009) Biochemistry 48, 8083–8093]. Two sets of peptides were designed to test those hypotheses, by mutating the sequences of δ-lysin, cecropin A, and magainin 2. Peptide binding and activity were measured on phosphatidylcholine membranes. In the first set, the peptide charge was changed by mutating basic to acidic residues or vice versa, but the amino acid sequence was not altered much otherwise. The type of dye release changed from graded to all-or-none according to prediction. However, location of charged residues in the sequence with the correct spacing to form salt bridges failed to improve binding. In the second set, the charged and other key residues were kept in the same positions, whereas most of the sequence was significantly but conservatively simplified, maintaining the same hydrophobicity and amphipathicity. This set behaved completely different from predicted. The type of release, which was expected to be maintained, changed dramatically from all-or-none to graded in the mutants of cecropin and magainin. Finally, contrary to the hypotheses, the results indicate that the Gibbs energy of binding to the membrane, not the Gibbs energy of insertion, is the primary determinant of peptide activity.

Irrefutability is not a virtue of a theory (as people often think) but a vice. Every genuine test of a theory is an attempt to falsify it, or to refute it.

Karl Popper, 1963. Conjectures and Refutations.

Our understanding of the relation between the sequence of antimicrobial peptides and their mechanism remains poor. Perhaps the main consensual conclusions are that positive charge on antimicrobial peptides improves binding and, to some extent, determines specificity of these peptides to anionic bacterial membranes; and that sufficient hydrophobicity renders the peptide hemolytic, because binding to the outer monolayer of eukaryotic membranes, which contains almost exclusively zwitterionic and neutral lipids, improves (1–3). Beyond that, we have learned remarkably little about the importance of amino acid sequence in spite of a vast number of studies. It remains impossible to predict mechanism and function from sequence alone.

The cell membrane provides a tightly controlled barrier between cell interior and environment. Protein export involves a secretory pathway from the endoplasmic reticulum, through the Golgi apparatus, to the extracellular matrix. A number of proteins and peptides, however, circumvent the regular transport machinery of the cell and appear to cross the lipid bilayer directly (4). Cell-penetrating peptides (CPPs),¹ for example, appear to accomplished this goal (5). Amphipathic CPPs are similar to antimicrobial peptides and their mechanisms may have more in common than often appreciated (6, 7).

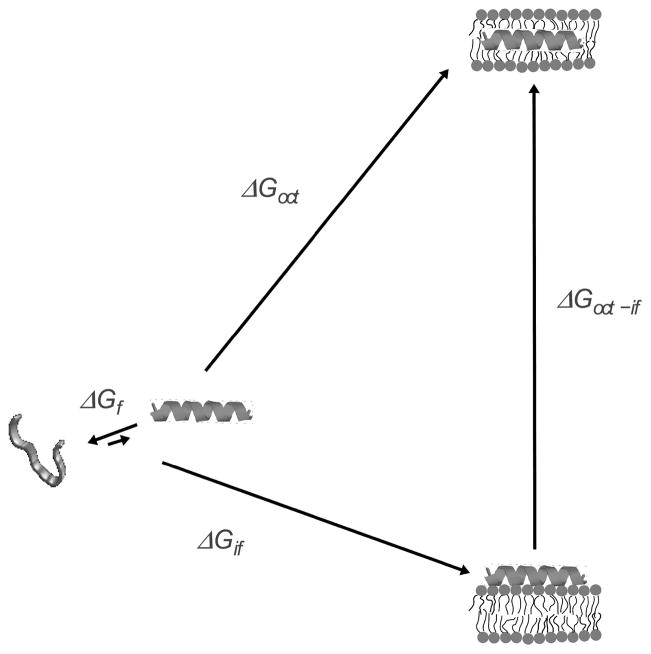
We have proposed three hypotheses to understand the mechanism of membrane-active peptides in model membranes, including antimicrobial, cytolytic, and amphipathic cell-penetrating peptides, on the basis of sequence (6). By mechanism we mean the series of steps in the kinetics leading to membrane disruption, including the process of vesicle leakage. We do not mean the molecular models commonly discussed for the structural arrangements of the peptides in the membrane, such as the barrel-stave (8), carpet (9–11), toroidal pore (12, 13), or sinking-raft models (14, 15). The central idea of the first hypothesis we proposed is that the mechanism of membrane-active peptides is determined by the Gibbs free energy of insertion into the bilayer from the membrane-bound state (6). More precisely, if that energy is smaller than a certain threshold, the peptides are predicted to translocate across the lipid bilayer. This seems to be the case for amphipathic CPPs (16). If the Gibbs free energy of insertion is larger than the threshold, the peptides cannot cross the membrane, and accumulate instead on its surface. A point may be reached when the membrane yields, forming a pore. This distinction is important because peptides that translocate can be used as carriers for delivery of drugs or nucleic acids into cells, whereas those that cause major membrane disruption should be primarily antimicrobial or cytolytic, depending on specificity. According to this hypothesis, the peptide sequence affects the mechanism primarily through its effect on the Gibbs free energy of insertion.

This concept is described more precisely with reference to Figure 1. In water, an equilibrium exists between helical and unfolded conformations of the peptide, which favors the unfolded state. Upon binding to the bilayer/water interface, the peptide folds to an α-helix. The Gibbs energy of binding to the interface is given by $\mathrm{\Delta }{G}_{if}^o$. If we ignore the free energy associated with folding in water, which is typically small compared to the other terms (6), the Gibbs energy of insertion from the surface-bound state should be approximately given by $\mathrm{\Delta }{G}_{\mathit{oct}}^o-\mathrm{\Delta }{G}_{if}^o=\mathrm{\Delta }{G}_{\mathit{oct}-if}^o$, where $\mathrm{\Delta }{G}_{\mathit{oct}}^o$, the Gibbs energy of transfer from water to octanol, is used to estimate transfer to the bilayer hydrophobic core (17). The idea is that $\mathrm{\Delta }{G}_{\mathit{oct}-if}^o$ provides a tool to predict the behavior of the peptides. The Gibbs energy of binding measured experimentally is designated here by $\mathrm{\Delta }{G}_{\mathit{bind}}^o$. It can also be calculated using the Wimley-White interfacial hydrophobicity scale (18–21), and is then designated by $\mathrm{\Delta }{G}_{if}^o$. $\mathrm{\Delta }{G}_{\mathit{oct}}^o$ is calculated with the Wimley-White octanol hydrophobicity scale (18, 22).

FIGURE 1.

Thermodynamic cycle for peptide binding to the membrane interface and insertion into the bilayer. The folding equilibrium in water lies toward the unstructured state and is determined by $\mathrm{\Delta }{G}_f^o$, which is typically small in comparison with the other terms. The Gibbs energy of binding to the interface ( $\mathrm{\Delta }{G}_{if}^o$) includes contributions from the hydrophobic effect and secondary structure formation. Transfer, as an α-helix, from water to the bilayer interior is approximated by transfer to octanol ( $\mathrm{\Delta }{G}_{\mathit{oct}}^o$). The Gibbs energy of transfer from the surface to the interior of the bilayer is approximately $\mathrm{\Delta }{G}_{\mathit{oct}}^o-\mathrm{\Delta }{G}_{if}^o=\mathrm{\Delta }{G}_{\mathit{oct}-if}^o$. Modified with permission from ref (38). Copyright 2007 Elsevier.

Previously, we examined the kinetics and thermodynamics of interaction of a set of amphipathic, α-helical peptides with model membranes (6). This original set consisted of δ-lysin, a hemolytic peptide from Staphylococcus aureus (23); cecropin A, antimicrobial from Hyalophora cecropia (24); magainin 2, antimicrobial from Xenopus laevis (25); and transportan 10 (TP10), an amphipathic CPP (26, 27). For most peptides, $\mathrm{\Delta }{G}_{\mathit{bind}}^o$ was in very good agreement with $\mathrm{\Delta }{G}_{if}^o$ (6, 16). However, for two peptides (δ-lysin and cecropin A) the calculated and experimental binding free energies did not agree. Because these were the only peptides of the set originally examined in which intramolecular salt bridges between side chains could be established, we proposed salt bridge formation on the membrane was the reason for the disagreement in those two cases (6). Formation of an intramolecular salt bridge between acidic and basic groups of the peptide contributes −4 kcal/mol to transfer from water to octanol (28). We suggested that formation of a salt bridge may contribute ≈ −2 kcal/mol to transfer from water to the POPC membrane interface. Using this value, and postulating 2 intramolecular salt bridges in δ-lysin and cecropin A, $\mathrm{\Delta }{G}_{if}^o$ could be brought into agreement with $\mathrm{\Delta }{G}_{\mathit{bind}}^o$ (6).

For clarity and completeness, we now restate the three hypotheses proposed (6). Note also that when $\mathrm{\Delta }{G}_{\mathit{bind}}^o$ is known, this experimental value is used in $\mathrm{\Delta }{G}_{\mathit{oct}-if}^o=\mathrm{\Delta }{G}_{\mathit{oct}}^o-\mathrm{\Delta }{G}_{\mathit{bind}}^o$ instead of $\mathrm{\Delta }{G}_{if}^o$.

1. If $\mathrm{\Delta }{G}_{\mathit{oct}-if}^o\le 20\text{kcal}/\text{mol}$, the peptides can translocate across the bilayer. This should result in graded dye release because translocation provides a means to dissipate the mass imbalance across the bilayer, created by peptide binding. But if $\mathrm{\Delta }{G}_{\mathit{oct}-if}^o>23\text{kcal}/\text{mol}$, the energy barrier for translocation is prohibitively large; the peptides accumulate on the membrane surface until, in a stochastic manner, the membrane yields, releasing the vesicle contents in an all-or-none manner. To be clear, hypothesis 1 contains in fact the following logical structure:

   $$\mathrm{\Delta }{G}_{\mathit{oct}-if}^o\le 20\text{kcal}/\text{mol}\Rightarrow \text{translocation}\Rightarrow \text{graded}\text{release}$$ (1)

   $$\mathrm{\Delta }{G}_{\mathit{oct}-if}^o\ge 23\text{kcal}/\text{mol}\Rightarrow \text{no}\text{translocation}\Rightarrow \text{all}-\text{or}-\text{none}\text{release}$$ (2)

   A “gray zone” may exist for $\mathrm{\Delta }{G}_{\mathit{oct}-if}^o$ between about 20–23 kcal/mol, in which either mechanism may prevail.

2. Formation of intramolecular salt bridges (hydrogen-bonded ion pairs) by the residue side chains can lower $\mathrm{\Delta }{G}_{if}^o$ and $\mathrm{\Delta }{G}_{\mathit{oct}-if}^o$, allowing the peptides to bind better and translocate across the bilayer.

3. The sequence of antimicrobial and other membrane-active peptides can be simplified without altering the peptide mechanism and the type of dye release as long as the Gibbs energies of binding and insertion into the membrane remain approximately constant. The idea is that the thermodynamics of membrane binding and insertion determine the mechanism. Therefore, it should be possible to reduce the diversity of amino acids in the sequence, simplifying it considerably, while preserving the amino acid types to ensure that the peptide remains amphipathic, provided those sequence changes do not alter the thermodynamics of binding and insertion. If this is correct, mutations may occur naturally to impart variation to the sequences, to circumvent acquired bacterial resistance.

TP10 variants were the subject of our previous study, which showed that the changes to the sequence resulted in peptide mechanisms consistent with these hypotheses (16). The results on designed variants of other membrane-active peptide families are presented here.

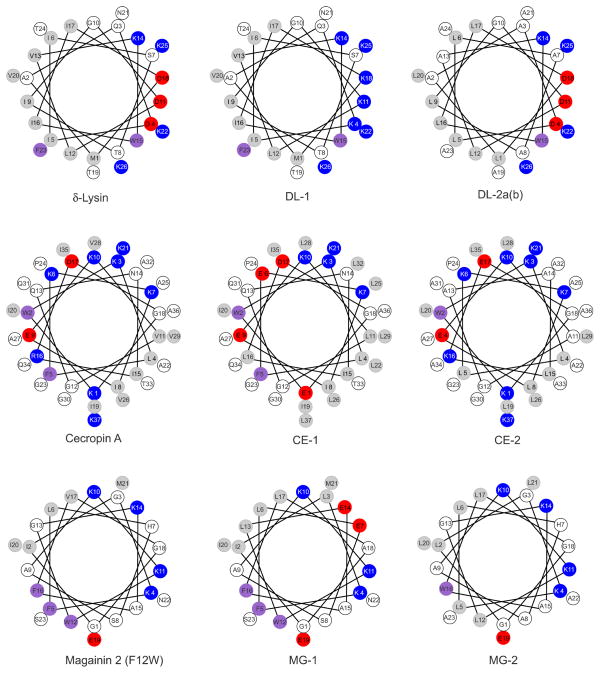
The peptide sequences are shown in Table 1 and their helical wheel projections, in Figure 2. They are divided in two sets and named according to the original peptides from which they are derived: δ-lysin (DL), cecropin A (CE), and magainin 2 (MG). Thus, DL-1 and DL-2 variants are based on δ-lysin; CE-1 and CE-2, on cecropin A; MG-1 and MG-2, on magainin 2. Set 1 consists of DL-1, CE-1, and MG-1; here, charge and putative salt bridges were changed relative to the parent peptides. During design, we tried to keep membrane binding affinity within a measurable range, assuming that the helicity would not change much relative to the parent peptides, while retaining the general amphipathicity of the peptide. Set 1 was designed to test hypothesis 1, that the peptide mechanism depends on the difficulty of peptide insertion. Namely, the release type should be graded or all-or-none depending on whether $\mathrm{\Delta }{G}_{\mathit{oct}-if}^o$ is below or above the threshold. We sought to change peptides between those that can translocate across the membrane (equated with causing graded release) and those that cannot (equated with causing all-or-none release) by engineering mutations that change $\mathrm{\Delta }{G}_{\mathit{oct}-if}^o$ in a predictable way. Furthermore, at least if the mechanism of the peptides does not change with the mutations, the easier the insertion, the faster dye release should be. To alter $\mathrm{\Delta }{G}_{\mathit{oct}-if}^o$, basic residues were mutated to acidic and vice versa, but with minimal other changes to the sequence. This resulted in changes to the net charge of the peptide, and also eliminated or allowed new salt bridges. In this way, hypothesis 2 was also tested.

Table 1.

Parent Set of Peptides and Sets 1 and 2 of Mutants. (Unless indicated, N- and C-termini are free.)

Peptide	Charge (pH 7.5)	Length (residues)	μHa	Sequence
Set of Parent Peptides
δ-Lysin	0	26	7.8	formyl-MAQDIISTIGDLVKWIIDTVNKFTKK
Cecropin A	+7	37	4.9	KWKLFKKIEKVGQNIRDGIIKAGPAVAVVGQATQIAK-amide
Magainin-2 F12W	+3	23	6.9	GIGKFLHSAKKWGKAFVGEIMNS
Set 1 of Mutant Peptides
DL-1	+6	26	7.2	formyl-MAQKIISTIGKLVKWIIKTVNKFTKK
CE-1	+1	37	7.3	EWKLFEKIEKLGQNILDGIIKLGPLLALLGQLTQIAL-amide
MG-1	0	23	9.1	GILKFLESAKKWLEAFLAEIMNS
Set 2 of Mutant Peptides
DL-2a	0	26	7.7	formyl-LAADLLAALGDLAKWLLDALAKAAKK
DL-2b	0	26	8.8	formyl-LAADLLAALGDLLKWLLDALAKLAKK
CE-2	+7	37	5.2	KWKLLKKLEKAGAALKEGLLKAGPALALLGAAAALAK-amide
MG-2	+3	23	7.0	GLGKLLHAAKKLGKAWLGELLAA

^aHydrophobic moment of the complete helix calculated with MPEx using the Wimley-White interfacial scale (18).

FIGURE 2.

Helical wheel projection of the original and variant peptides studied. The colors reflect the hydrophobicities according to the Wimley-White interfacial scale (18). White, hydrophilic or neutral; light gray, hydrophobic; magenta, aromatic; red, negatively charged; and blue, positively charged, at pH 7.5. The only difference between DL-2a and DL-2b is the replacement of Ala 13 and 23 by Leu in DL-2b.

Set 2 consists of DL-2a, DL-2b, CE-2, and MG-2; here, the sequence was simplified, but charge, hydrophobicity, and amphipathicity (hydrophobic moment), were maintained. Set 2 was designed to test hypothesis 3, that is, the importance of amino acid diversity in the sequence. The sequences of the original peptides were simplified to contain a minimal number of amino acid types, while keeping key residues, such as those charged, in place. In practice, this amounted to changing hydrophobic residues to Leu, small polar ones to Ala, and charged residues to Lys or Glu. The peptides of set 2 are experimental analogs of the HP (Hydrophobic/Polar) model (29) that has been extensively studied in protein folding in water. Can these experimental models capture the essence of the activity of antimicrobial peptides?

MATERIALS AND METHODS

Chemicals

DL-1 (purity 93%) was purchased from Bachem (Torrance, CA); DL-2a (95%), CE-2 (95%), and MG-2 (88%), from New England Peptide (Gardner, MA); and DL2b (99%), CE-1 (98%), and MG-1 (95%), from Genscript (Scotch Plains, NJ). Their identity was ascertained by mass spectrometry, and the purity was determined by HPLC, both provided by the manufacturer. δ-Lysin was a gift from Dr. H. Birkbeck (Univ. Glasgow); cecropin A and magainin 2 were purchased from American Peptide Company (Sunnyvale, CA); and magainin 2 F12W was a gift from Dr. R. Biltonen (Univ. Virginia). Stock solutions were prepared by dissolving lyophilized peptide in deionized water or water/ethyl alcohol 1:1 (v/v) (AAPER Alcohol and Chemical, Shelbyville, KY). Stock peptide solutions were stored at −80°C, and kept on ice during experiments. 1-Palmitoyl-2-oleoyl-sn-glycero-3-phosphochol-ine (POPC), 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphatidylethanolamine (POPE), and 1-palmitoyl-2-oleoyl-sn-glycero-3-[phospho-rac-(1-glycerol)] (POPG), in chloroform solution, were purchased from Avanti Polar Lipids (Alabaster, AL). 7-Methoxycoumarin-3-carboxylic acid (7MC) succinimidyl ester, 8-aminonaphtalene-1,3,6-trisulfonic acid (ANTS) disodium salt, p-xylene-bis-pyridinium bromide (DPX), and carboxyfluorescein (CF) were purchased from Molecular Probes/Invitrogen (Carlsbad, CA). Organic solvents (High performance Liquid Chromatography/American Chemical Society grade) were purchased from Burdick & Jackson (Muskegon, MI). Lipids and fluorophores were tested by thin layer chromatography (TLC) and used without further purification. Peptide concentrations were determined by Trp absorbance at 280 nm.

Synthesis of Fluorescent Probes

The syntheses of fluorescent probes, using POPE and a fluorophore attached through an amide bond to the amino group of the ethanolamine, were performed as previously described in detail (30–33), following the method of Vaz and Hallmann (34).

Preparation of Large Unilamellar Vesicles

Large unilamellar vesicles (LUV) were prepared by extrusion through 0.1 μm pore size filters (Nucle-pore, Whatman, Florham, NJ), as previously described (15, 16, 31, 32), in 20 mM MOPS buffer, pH 7.5, 0.1 mM EGTA, 0.02% NaN₃, and 100 mM KCl or appropriately modified, as indicated below. Lipid concentrations were assayed by the Bartlett phosphate method (35), modified as previously described (14).

Circular Dichroism

Peptide secondary structure was determined by circular dichroism (CD) on a Chirascan CD spectrometer (Applied Photophysics, Leatherhead, Surrey, UK), as previously described (16). CD spectra were obtained in aqueous solution, with 1–5 μM peptide, in 10 mM phosphate buffer, pH 7.5, and in the presence of POPC vesicles, at low concentrations (5 μM peptide and 300 μM POPC LUV) and at high concentrations (20 μM peptide and 5 mM POPC LUV). CD measurements of amphipathic peptides on LUV at high lipid concentrations (3–7 mM) yield results equivalent to those obtained with small unilamellar vesicles (SUV), with several advantages (36). To obtain the helicity of the bound peptide at low lipid concentrations, it is necessary to know the dissociation constant (K_D) and the helicity of the peptides in solution in equilibrium with the vesicles. The helicities in solution are difficult to obtain for several of these peptides because of aggregation or adsorption to the cuvette walls in the absence of vesicles. For the membrane-associated peptides, the use of high LUV concentrations (≥ 10 × K_D) has the additional advantage that larger peptide concentrations can be used, while maintaining a low P/L ratio (<1:200). We relied on determinations at high concentrations for the calculation of peptide helicity on the membrane. Nevertheless, determinations at high and low concentrations yielded helical contents on the membrane that differed only by 5–10%. The fractional helicity on the membrane (f_H) was calculated from the average of at least 2 independent samples, according to Luo and Baldwin (37), as previously described (16).

Membrane binding kinetics

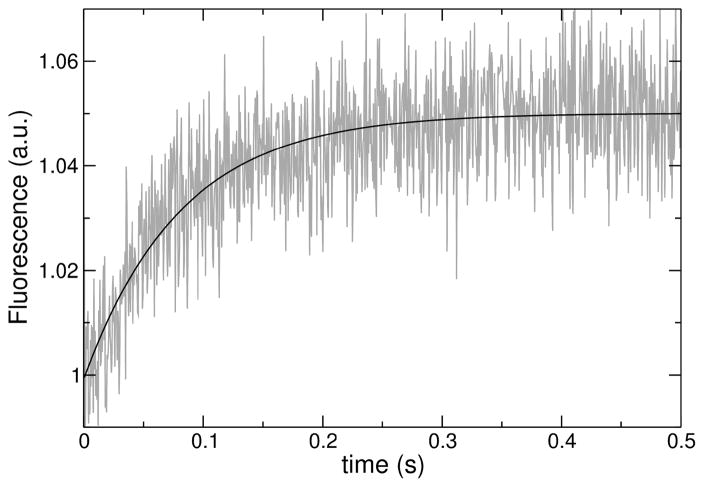
The kinetics of peptide binding to lipid LUV were measured on a stopped-flow fluorimeter (SX.18MV, Applied Photophysics). The fluorescence signal recorded was the emission of 7MC-POPE (maximum at 396 nm) incorporated into the bilayer, upon Förster resonance energy transfer (FRET) from a Trp residue on the peptide, with excitation at 280 nm, as previously described (16, 31–33). After mixing, the concentration of peptide was 0.5–1 μM and the lipid varied between 25 and 400 μM. The kinetics of peptide binding to membranes were analyzed as previously described in detail (31–33). Briefly, each kinetic trace (Figure 3), or the average of several traces from the same sample, was fit with a single exponential rising function, of the form

FIGURE 3.

Example of a curve of binding kinetics, acquired for DL-1 binding to 100 μM POPC LUV. The data correspond to fluorescence emission from the lipid fluorophore 7MC-POPE incorporated in the membrane, through FRET, upon excitation of the Trp residue on the peptide. The line is a single exponential fit to the data.

$$F(t)=a_0[1-exp(-k_{\mathit{app}}t)]+a_1,$$ (3)

where a₀ and a₁ are constants, t is time, and k_app is the apparent rate constant. (In the cases where a very slow process was also apparent, which was not included in k_app, it could be well approximated by a linear ramp.) This rate constant contains contributions from the on- and off-rate constants,

$$k_{\mathit{app}}=k_{on}[L]+k_{\mathit{off}},$$ (4)

where [L] is the lipid concentration, which was varied in a series of different experiments. A plot of k_app against [L] yields k_on from the slope and k_off from the y-intercept.

ANTS/DPX requenching assay

Steady state fluorescence measurements were performed in a spectrofluorimeter (8100 SLM-Aminco, Urbana, IL) upgraded by ISS (Champaign, IL), as previously done for the original peptides (15, 31, 32, 38, 39). In the ANTS/DPX assay (40–42), excitation was at 365 nm (8 nm slit width) and emission at 515 nm (16 nm slit width). The solution encapsulated in the LUVs contained 5 mM ANTS, 10 mM DPX, 20 mM MOPS, pH 7.5, 0.1 mM EGTA, 0.02% NaN₃, and 70 mM KCl. The titrating solution contained 45 mM DPX, 20 mM MOPS, pH 7.5, 0.1 mM EGTA, 0.02% NaN₃, and 30 mM KCl. Following extrusion, the LUVs with encapsulated ANTS and DPX were passed through a Sephadex-G25 column to separate the dye in the external buffer from the vesicles. Typical concentrations were 0.1–2 μM peptide and about 600 μM lipid. The data were analyzed as described in detail by Ladokhin et al. (42). The curve for graded release is described by (41, 42),

$$Q_{in}=\frac{F_i}{F_i^{max}}=\frac{1}{{(1+K_{\mathit{dyn}}{[\text{DPX}]}_0(1-f_{\mathit{out}}))}^{\alpha }){(1+K_{\mathit{sta}}{[\text{DPX}]}_0(1-f_{\mathit{out}}))}^{\alpha })}$$ (5)

where F_i and $F_i^{\mathit{max}}$ are the fluorescence intensities from the vesicle interior with and without quencher (DPX), [DPX]₀ is the initial concentration of DPX encapsulated, f_out is the ANTS fraction outside the vesicles, K_dyn is the dynamic quenching constant, fixed at 50 M⁻¹ in the fits (41), K_sta is the static quenching constant, and α is the ratio of the rates of release of DPX to ANTS.

Carboxyfluorescein release kinetics

Carboxyfluorescein (CF) release kinetics were measured as described before in detail (15, 31–33, 38). Briefly, LUVs of 0.1μm in diameter, containing 50 mM CF, were prepared by extrusion in 20 mM MOPS buffer, pH 7.5, 0.1 mM EGTA, 0.02% NaN₃. Removal of external CF was accomplished by size-exclusion chromatography (Sephadex-G25). The kinetics of CF release, measured by the relief of self-quenching of CF fluorescence, were recorded in a stopped-flow fluorimeter (SX.18MV, Applied Photophysics). The peptide concentration was 1 μM after mixing, in all experiments. The fraction of CF released was determined by comparison of the fluorescence with that obtained upon addition of 1% Triton X-100 (maximal release). The efficiency of dye release was characterized quantitatively, in a model-free way, by the average time constant of dye release (τ) (43, 44),

$$\tau =\frac{\int tf(t)dt}{\int f(t)dt},$$ (6)

where f(t) = dF(t)/dt is the time-derivative of the fractional release as a function of time. This derivative behaves as a probability density function (45, 46).

RESULTS

Peptide secondary structure

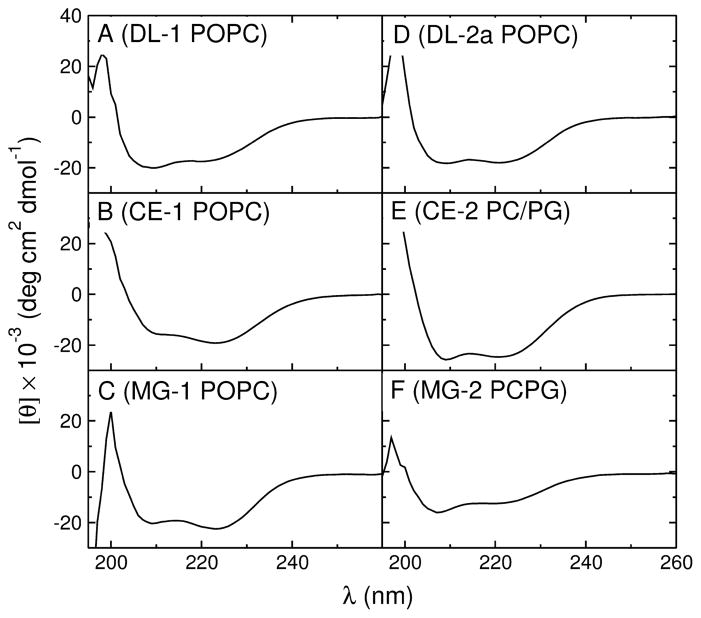
The secondary structure of the peptides in aqueous solution and on the membrane was determined by CD (Figure 4), in LUVs of POPC or POPC:POPG 1:1 (if binding to POPC was weak). The percent helicity of the membrane-associated peptides was obtained from the ellipticity at 222 nm, at a lipid concentration (5 mM) much larger than the dissociation constants (K_D), ensuring that the peptides were fully bound. All peptides were helical on the membrane, usually to a degree similar to that of the corresponding original peptides (Table 3). The helicity on the membrane is necessary to calculate $\mathrm{\Delta }{G}_{if}^o$ with the Wimley-White interfacial scale, using the program Membrane Protein Explorer, MPEx (47). In aqueous solution, however, the helicities were difficult to obtain for several of these peptides. If the helicity in solution is below ≈ 30 %, the experimental error is large, in part because of the low peptide concentrations used (~ 2 μM) to minimize aggregation, and the measurements may not reflect the structure that exists in solution in equilibrium with the membrane. Thus, the helicities in solution, which are not used in any calculation, are approximate and several were rounded to the nearest 5 or 10%, reflecting our estimate of the error. The values calculated using AGADIR (48–53) are included in Table 3 for comparison. (Note that the helicities on the membrane were determined for fully bound peptides and do not rely on the measurements in solution.)

FIGURE 4.

Representative CD spectra of the mutant peptides (20 μM) in 5 mM LUV of POPC, except for CE-2 and MG-2, which were in POPC/POPG 1:1. (A) DL-1, (B) CE-1, (C) MG-1, (D) DL-2a, (E) CE-2, and (F) MG-2.

Table 3.

Thermodynamic and kinetic parameters for the mutant peptides binding and insertion in POPC bilayers at room temperature.

Peptide	$\mathrm{\Delta }{G}_{\mathit{bind}}^o$a (kcal/mol)	$\mathrm{\Delta }{G}_{if}^o$b (kcal/mol)	helix (%)			$\mathrm{\Delta }{G}_{\mathit{oct}}^o$ (kcal/mol)	$\mathrm{\Delta }{G}_{\mathit{oct}-if}^o$c (kcal/mol)	Dye release
			memb.	water				type ANTS/DPX	τ (s)d CF
	exp	calc		exp	calce
δ-Lysin	−8.5	−5.8	100	53	1	21.9	30.4	graded	2.2
DL-1	−7.0	−1.5	52	~20	1	19.3	26.3	all-or-none	4.9
DL-2a	−7.4	−2.3	54	54	35	23.2	30.6	graded	14.8
DL-2b	−5.7	−6.2	77	59	59	19.7	25.4	–	650
Cecropin A	−6.4	−1.7	63	~10	1	31.1	37.5	all-or-none	~15000
CE-1	−7.0	−6.1	55	~30	3	17.3	24.3	all-or-none	35
CE-2	−5.6	−5.7	70	~30	4	29.6	36.2	graded	11000
Magainin-2f	−6.1	−3.8 (−6.2)g	57 (83)	~5	0	20.1	26.2	all-or-none	~20000
MG-1	−7.4	−3.6	69	46	16	18.2	25.6	all-or-none	13.5
MG-2	−6.4	−2.7 (−6.4)	40 (80)	~10	2	19.1	25.5	graded	20000

^aCalculated from the experimentally determined dissociation constant by $\mathrm{\Delta }{G}_{\mathit{bind}}^o=ln{K}_D-2.4\text{kcal}/\text{mol}$.

^bCalculations of $\mathrm{\Delta }{G}_{if}^o$ and $\mathrm{\Delta }{G}_{\mathit{oct}}^o$ were performed with MPEx (47).

^cCalculated using the experimental value $\mathrm{\Delta }{G}_{\mathit{bind}}^o$ for the free energy of binding to the interface.

^dMeasured in LUVs of POPC 50 μM.

^eHelicity in aqueous solution was calculated with AGADIR.

^fBinding was measured with the F12W variant of magainin 2. The calculations assume His is neutral in magainin-2 and MG-2, since the experiments were performed at pH 7.5. The value of $\mathrm{\Delta }{G}_{\mathit{bind}}^o$ for magainin 2 (F12W) on POPC, previously reported as −5.5 kcal/mol (6), which was based on K_D = 5 mM (32), was revised. The value of $\mathrm{\Delta }{G}_{\mathit{bind}}^o=-6.1\text{kcal}/\text{mol}$ listed here is based on a better estimate of K_D = 2 mM (see Table 2).

^gBinding of magainin 2 to POPC is too weak to measure helicity accurately. The value of −3.8 kcal/mol is calculated using the helicity (57%) that we measured in POPC/POPG 1:1. The value of −6.2 is calculated using the helicity (83%) determined from NMR in DPC micelles (64).

Binding to POPC membranes

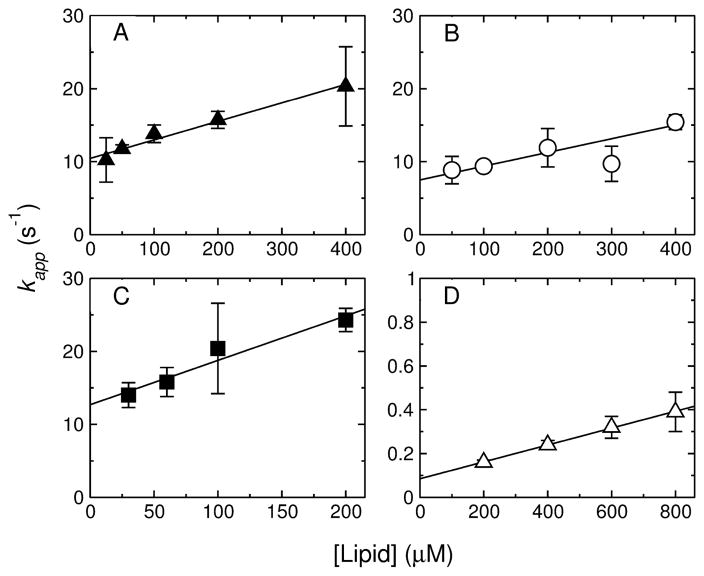
The equilibrium binding constants of the peptides to POPC membranes were determined from the kinetics of binding, measured by stopped-flow fluorescence, using the change in FRET from a Trp residue on the peptide to a lipid fluorophore (7MC-POPE) incorporated in the bilayer (Figure 3). Typically, these measurements were performed in a time scale of about 1 second, to capture only the binding event and avoid contributions from changes imparted to the vesicles by the peptides, which may occur concomitant with deeper insertion. Figure 3 is very representative in showing that the binding process is complete in less than ~ 1 second. A fit of Eq. 3 to the data (Figure 3) yields the apparent rate constant for binding, k_app (31, 32, 38, 39, 58, 59). To obtain the on- and off-rate constants from k_app = k_on [L]+k_off, this experiment was performed as a function of lipid concentration [L]. The results are shown in Figure 5 for DL-1 (A), CE-1 (B), MG-1 (C), and DL-2a (D). (Note that, in all figures, triangles refer to the DL family, circles to the CE family, and squares to the MG family.) The equilibrium dissociation constants were calculated by

FIGURE 5.

Kinetics of peptide binding to LUV of POPC (Dl-1, CE-1, MG-1, and DL-2a) or POPC/POPG 1:1 (CE-2 and MG-2). The apparent rate constant (k_app), obtained from a single exponential fit to the traces of binding kinetics, is plotted against the lipid concentration. (A) DL-1, (B) CE-1, (C) MG-1, and (D) DL-2a. The error bars are standard deviations from 2–4 independent experiments and the lines are linear regressions, which yield k_on from the slope and k_off from the y-intercept. In the case of MG-1 the data are averages from POPC/POPG LUV 50:50, 70:30, 80:20, and 90:10, since there was no detectable dependence on membrane composition. The values of k_on, k_off, and K_D obtained are listed in Table 2.

$$K_D=\frac{k_{\mathit{off}}}{k_{on}}$$ (7)

and are listed in Table 2, together with those of the original peptides, for comparison.

Table 2.

Kinetic and equilibrium constants for binding to POPC bilayers at room temperature. The data for the original peptides is from Almeida and Pokorny (6) and references therein. The estimated relative error in the rate and equilibrium constants is about 30%, except for δ-lysin, where it is larger (see footnote a).

Peptide	KD (μM)	kon M−1s−1	koff s−1
δ-Lysina	30	2 × 103	0.06
DL-1	400	2.5 × 104	10
DL-2a	200	5.5 × 102	0.11
DL-2bb	3400	2.5 × 103	8.6
Cecropin A	1000	2.8 × 105	300
CE-1	400	1.9 × 104	7.5
CE-2	4700	3.0 × 104	140
Magainin-2c	2000	2.8 × 105	550
MG-1	200	6.1 × 104	13
MG-2	1100	2.1 × 104	24

^aMeasuring binding for δ-lysin has been especially difficult, for reasons we do not fully understand. Data was collected previously, for POPC and other unsaturated phosphatidylcholines to which binding is similar (6, 59). On the basis of all those data, the best previous estimate was K_D = 60 μM (6). We have now re-examined the earlier data, and supplemented it with new data (not shown). The numbers listed here are our improved estimates at this point. However, k_on is strikingly small. From our previous estimates (6, 15), the monomer should be the dominant species in solution at a concentration of 0.5 μM, which was used in the binding kinetics. Nevertheless, the small k_on suggests that either the monomer conformation in solution is such that binding is impaired, or that some peptide oligomerization, which is known to occur in solution above 1 μM (14, 54–57), persists at 0.5 μM. If the oligomerization equilibrium contributes to the measured on-rates, the true K_D would be even smaller.

^bData from only one experiment.

^cThe binding data was obtained for the variant F12W of magainin 2, which, like the F16W variant, behaves very similarly to the original magainin (71). The value of K_D = 5 mM (32) was revised. The new estimate of K_D = 2 mM was obtained by direct extrapolation of the K_D in POPC/POPG mixtures, as a function of POPG content in the membrane, to pure POPC. Previously, we had extrapolated the k_on and k_off, and obtained K_D from their ratio (32), but k_on had been overestimated. The new estimates of the rate constants for magainin 2 (F12W) in POPC are listed here.

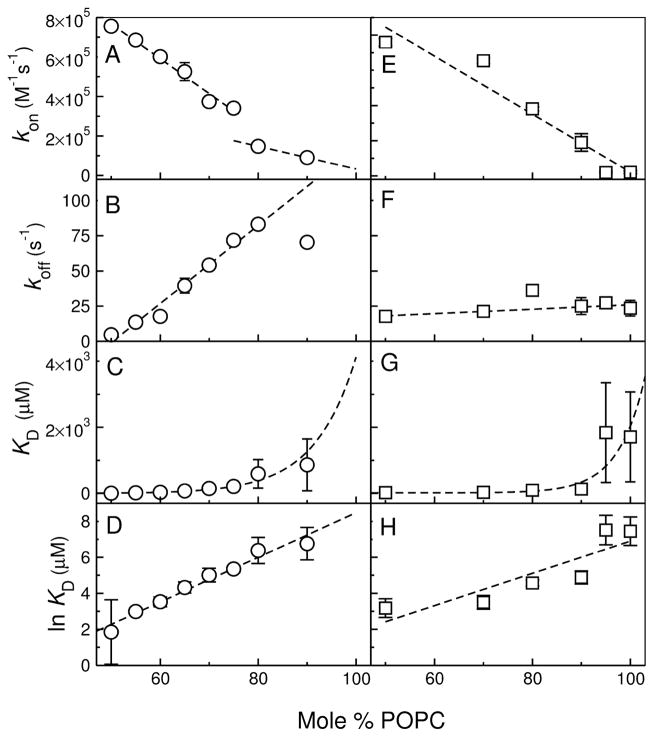
CE-2 and MG-2 bind very weakly to POPC, with K_D in the millimolar range, as the original peptides, cecropin A and magainin 2. To obtain those dissociation constants, k_on and k_off were determined in mixtures of POPC/POPG, varying the POPC content between 50 and 100%, and the results were extrapolated to pure POPC (Figure 6), as previously done for the original peptides (31, 32). The extrapolation using the data from all the lipid mixtures provides a much better estimate of the rate and equilibrium constants for POPC than the direct determination with POPC only. This is because if binding to POPC is weak, the corresponding data are noisier than those acquired in the mixtures containing POPG.

FIGURE 6.

Kinetics of binding of CE-2 (left panels) and MG-2 (right) to LUV as a function of membrane composition, from POPC/POPG 1:1 to pure POPC. The data show the dependence of k_on (A, E), k_off (B, F), K_D (C, D), and ln K_D on the lipid composition. Extrapolation to pure POPC, to which binding is weak, provides the best estimates of the rate and equilibrium constants for CE-2 and MG-2 in POPC, listed in Table 2.

In the case of MG-1, we found that binding to POPC/POPG mixtures is independent of POPG content. This is consistent with MG-1 having no net charge at pH 7.5. However, the FRET signal was better in the presence of POPG, perhaps because of a different position of the Trp or the fluo-rescent moiety of 7MC-POPE in the anionic membranes. Therefore, the data for MG-1 binding to POPC/POPG LUV 50:50, 70:30, 80:20, and 90:10 were all averaged, at each lipid concentration, which is shown in Figure 5C.

The Gibbs free energies of binding to POPC were obtained from the experimental value of K_D by

$$\mathrm{\Delta }{G}_{\mathit{bind}}^o=\mathit{RT}ln{K}_D-\mathit{RT}ln[W],$$ (8)

where [W] = 55.5 M is the molar concentration of water. The term RT ln 55.5 = 2.4 kcal/mol (at room temperature) converts K_D to a partition coefficient of the peptide between lipid and water, with concentrations expressed in mole fraction units. To be able to compare the values of the Gibbs energy of binding derived from experiment ( $\mathrm{\Delta }{G}_{\mathit{bind}}^o$) with those calculated ( $\mathrm{\Delta }{G}_{if}^o$) with the Wimley-White interfacial scale (18–20), mole fraction units must be used. MPEx (47) was employed to calculate $\mathrm{\Delta }{G}_{if}^o$, assuming a free energy $\mathrm{\Delta }{G}_{hb}^o=-0.4\text{kcal}/\text{mol}$ for hydrogen bond formation at the interface, in a helical conformation (21). The values of $\mathrm{\Delta }{G}_{\mathit{bind}}^o$ and $\mathrm{\Delta }{G}_{if}^o$ obtained are listed in Table 3.

Kinetics of dye release

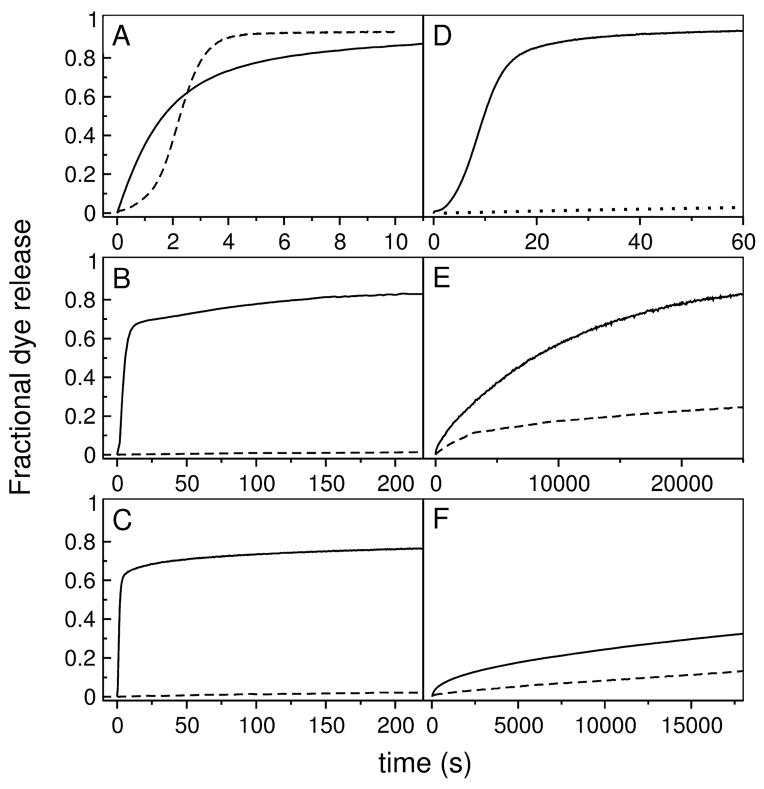
Peptide-induced release of carboxyfluorescein (CF) from lipid vesicles was measured in POPC. Examples of release curves are shown by the solid lines in Figure 7 for set 1 (left panels) and set 2 (right panels). The corresponding curves for the original peptides are shown by the dashed lines for comparison. The overall release rates of DL-1 and δ-lysin are similar, but the shape of the curves is completely different (Figure 7A). CE-1, on the other hand, is dramatically more efficient than cecropin A, which hardly releases from POPC vesicles (Figure 7B). The same is true of MG-1 in comparison with magainin 2 (Figure 7C). DL-2a induces significantly slower release than DL-1 and δ-lysin (Figure 7D); DL-2b induces even slower release (Figure 7D, dotted line). The solid lines in Figures 7E and F show release induced by CE-2 (E) and MG-2 (F) from POPC, which occur in approximately the same timescale as for the original peptides, cecropin A and magainin 2 (dashed lines). The efficiency of dye release is expressed quantitatively by the overall apparent rate constant, which is the inverse of the characteristic average time constant of the process, τ (Eq. 6). The values of τ, obtained under similar experimental conditions, namely at P/L ≈ 1:50, with peptide and lipid concentrations of 0.5–1 μ M and 30–50 μM, respectively, are listed in Table 3.

FIGURE 7.

Kinetics of CF release induced by the mutant peptides (solid lines) from 50 μM POPC LUVs. The curves for the original peptides are shown for comparison (dashed lines) under the same conditions. (A) DL-1 (solid) and δ-lysin (dashed) from POPC; (B) CE-1 (solid) and cecropin A (dashed); (C) MG-1 (solid) and magainin 2 (dashed); (D) DL-2a (solid) and DL-2b (dotted) from POPC; (E) CE-2 (solid) and cecropin A (dashed); and (F) MG-2 and magainin 2 (dashed). Some curves were acquired for longer times, but are shown in the time frames that allow best comparison. In (D), only the beginning of the curve for DL-2b is shown; the curve has the same shape as for Dl-2a, but on a timescale an order of magnitude larger.

Type of dye release: graded or all-or-none

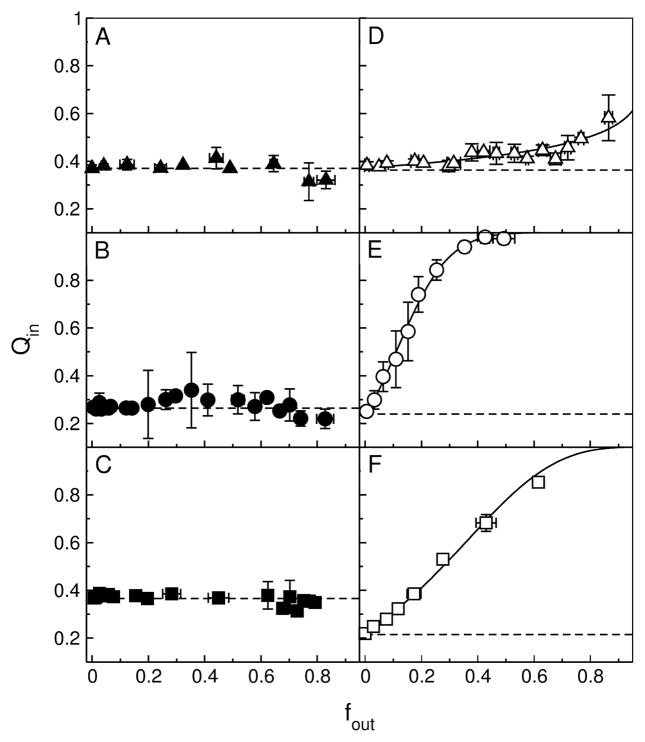
To determine if graded or all-or-none release occurred, the conventional ANTS/DPX requenching assay (40–42) was performed with the mutant peptides, as previously done with the original set. Briefly, if release is all-or-none, the fluorescence inside the vesicles remains constant as ANTS (fluorophore) and DPX (quencher) leak out, resulting in a horizontal line. But if release is graded, the degree of quenching inside the vesicles decreases as DPX leaks out, resulting in a rising curve (40–42). The results of the ANTS/DPX assay for all mutant peptides are shown in Figure 8A–F. The solid lines represent the best fits to the equation for graded release (Eq. 5), and the dashed lines represent all-or-none behavior.

FIGURE 8.

ANTS/DPX requenching assay for the mutant peptides. (A) DL-1 in POPC, (B) CE-1 in POPC, (C) MG-1 in POPC, (D) DL-2a in POPC, (E) CE-2 in POPC/POPG 1:1, and (F) MG-2 in POPC/POPG 1:1. The solid lines in panels D–F (DL-2a, CE-2, and MG-2) represent the best fits to the equation for graded release (Eq. 5). The corresponding fit parameters are, for DL-2a, α = 0.28 and K_sta = 80 M⁻¹; for CE-2, α = 8.5 and K_sta = 140 M⁻¹; and for MG-2, α = 3.0 and K_sta = 140 M⁻¹. For comparison with DL-2a, for δ-Lysin in POPC, the parameters were α = 0.22 and K_sta = 220 M⁻¹ (15). The dashed horizontal lines represent the behavior expected for all-or-none release.

DL-1 exhibits all-or-none behavior in POPC (Figure 8A), whereas δ-lysin was weakly graded (15). CE-1 and MG-1 also exhibit all-or-none behavior in POPC (Figure 8B,C), which is the same as for the original peptides, cecropin A (31, 60) and magainin 2 (32, 61, 62). DL-2a exhibits graded release (Figure 8D), as the original δ-lysin, with similar values of the ratio of DPX/ANTS release rates, α (Eq. 5). For DL-2a and δ-lysin, α = 0.28 and 0.22. Finally, CE-2 and MG-2 also exhibit graded release (Figure 8E,F), in striking contrast with cecropin A and magainin 2, which released in an all-or-none manner from POPC/POPG 1:1. The extreme, graded shape of the curve for CE-2 and MG-2 indicates, furthermore, that DPX is released much faster than ANTS by these peptides, which is reflected in α = 8.5 and 3.0 for CE-2 and MG-2, respectively.

DISCUSSION

Two sets of peptide variants were designed to alter the properties of the original peptides (δ-lysin, cecropin A, and magainin 2) in a way predicted by the hypotheses we had proposed. DL-1 and DL-2 variants were based on δ-lysin; CE-1 and CE-2, on cecropin A; MG-1 and MG-2, on magainin 2 (Table 1 and Figure 2). Set 1 (DL-1, CE-1, and MG-1) was designed to test hypotheses 1 and 2, that the peptide mechanism depends on the difficulty of peptide insertion, which can be altered by intramolecular salt bridges. The dye release should be graded or all-or-none depending on whether $\mathrm{\Delta }{G}_{\mathit{oct}-if}^o$ is below or above the threshold. Set 2 (DL-2a, DL-2b, CE-2, and MG-2) was designed to test hypothesis 3, which states that amino acid diversity in the sequence is not important for the mechanism as long as the thermodynamics of binding and insertion remain the same. Here, the sequences of the original peptides were simplified to contain a minimal number of amino acid types (hydrophobic, polar, charged) in the same positions, but drastically reducing their diversity. In the TP10 family of CPPs that we examined before, the agreement between the Gibbs energies of binding measured experimentally ( $\mathrm{\Delta }{G}_{\mathit{bind}}^o$) and calculated with the Wimley-White interfacial scale ( $\mathrm{\Delta }{G}_{if}^o$) was excellent (16). This is not true of all the peptides now studied.

In the next two sections we compare the experimental value of the Gibbs energy of binding to POPC ( $\mathrm{\Delta }{G}_{\mathit{bind}}^o$) with the value calculated with the Wimley-White scale ( $\mathrm{\Delta }{G}_{if}^o$), which are listed in Table 3. Originally, we reasoned that considering salt bridge formation was justified if $\mathrm{\Delta }{G}_{\mathit{bind}}^o$ was more negative than $\mathrm{\Delta }{G}_{if}^o$ by about 2 kcal/mol or more (6). Putative contributions from salt bridge formation are not included in the calculations of $\mathrm{\Delta }{G}_{if}^o$ and $\mathrm{\Delta }{G}_{\mathit{oct}}^o$ shown in Table 3, but we comment on their possible effects.

Binding to POPC membranes: Test of hypothesis 2

First, let us consider the peptides of set 1. In DL-1, the three acidic residues (Asp) of δ-lysin were converted to basic ones (Lys), imparting to DL-1 a net charge of +6 at pH 7.5, instead of zero as for δ-lysin. Because of the high charge, weak binding of DL-1 to POPC was predicted by the Wimley-White scale ( $\mathrm{\Delta }{G}_{if}^o=-1.5\text{kcal}/\text{mol}$), but we found that $\mathrm{\Delta }{G}_{\mathit{bind}}^o=-7.0\text{kcal}/\text{mol}$ (Table 3). This difference of 5.5 kcal/mol cannot be explained by salt bridge formation because DL-1 does not have any acidic residues. One possible salt bridge between a Lys side chain and the C-terminal carboxylate group would be insufficient to bring $\mathrm{\Delta }{G}_{if}^o$ and $\mathrm{\Delta }{G}_{\mathit{bind}}^o$ into agreement. CE-1 was designed to form one more intramolecular salt bridge than cecropin A, between the N-terminal amino group and Glu2. Peptide binding to POPC was therefore expected to improve relative to cecropin A. Indeed CE-1 binds better than cecropin A to POPC, but for CE-1 $\mathrm{\Delta }{G}_{\mathit{bind}}^o\approx \mathrm{\Delta }{G}_{if}^o$. Thus, the reason for the improved binding is simply the better partitioning to the membrane interface of the amino acid side chains of CE-1, not salt-bridge contributions. MG-1 was designed to form one intramolecular salt bridge (E7/K10, K11 or K10, K11/E13), the EK type being more likely than KE (63). Binding of MG-1 to POPC should be similar to that of magainin 2 if no salt bridge formed, but better if it did. We found that $\mathrm{\Delta }{G}_{\mathit{bind}}^o(-7.4\text{kcal}/\text{mol})$ for MG-1 is significantly more favorable than calculated ( $\mathrm{\Delta }{G}_{if}^o=-3.6\text{kcal}/\text{mol}$), but one salt bridge (the maximum possible) is insuffficient to account for the difference.

The peptides of set 2 have the same distribution of amino acid types as the corresponding original peptides and it was expected that their calculated $\mathrm{\Delta }{G}_{if}^o$ be similar to the original ones. In DL-2b, the experimental values of $\mathrm{\Delta }{G}_{\mathit{bind}}^o$ are fairly close to those calculated. In DL-2a, however, $\mathrm{\Delta }{G}_{if}^o=-2.3\text{kcal}/\text{mol}$ but $\mathrm{\Delta }{G}_{\mathit{bind}}^o=-7.4\text{kcal}/\text{mol}$. Three salt bridges would be sufficient to account for this difference, but it seems unlikely that this would happen only in DL-2a. CE-2 and MG-2 have the same charged amino acid residues as cecropin A and magainin 2, respectively, with net charges of +7 and +3 at pH 7.5. Like the parent peptides, they bind poorly to POPC. Nevertheless, reliable values of K_D in POPC were obtained, by extrapolating K_D in POPC/POPG mixtures, as a function of POPG content, to pure POPC. For CE-2, $\mathrm{\Delta }{G}_{\mathit{bind}}^o=-5.6\text{kcal}/\text{mol}$, in very good agreement with the calculated $\mathrm{\Delta }{G}_{if}^o=-5.7\text{kcal}/\text{mol}$. However, for MG-2 the values are different, $\mathrm{\Delta }{G}_{\mathit{bind}}^o=-6.4$ and $\mathrm{\Delta }{G}_{if}^o=-2.7\text{kcal}/\text{mol}$, and the difference cannot be explained by salt bridge formation. The calculated $\mathrm{\Delta }{G}_{if}^o$ is small because of the low helical content on the membrane (40%).

In general, the value $\mathrm{\Delta }{G}_{if}^o$ cannot be made to match $\mathrm{\Delta }{G}_{\mathit{bind}}^o$ by invoking salt-bridge contributions to binding. Even though formation of those salt bridges cannot be directly determined by the methods used, but only suggested by discrepancies in those two measures of the Gibbs energy of binding, it is clear that salt bridge formation fails to explain all the results reported here. Thus, either intramolecular salt bridges do not form on the membrane interface—even though partner residues were positioned with the correct spacing in the sequence—or they form but provide no significant contribution to $\mathrm{\Delta }{G}_{\mathit{bind}}^o$. This is clearly shown by DL-1 compared to δ-lysin, where elimination of the putative salt bridges failed to abolish the discrepancy between $\mathrm{\Delta }{G}_{if}^o$ and $\mathrm{\Delta }{G}_{\mathit{bind}}^o$. And is corroborated by CE-1 or MG-1, where the possible salt bridges introduced failed to significantly improve binding. Thus, as a general mechanism for enhancing binding, hypothesis 2 is most probably wrong.

Sources of error in the Gibbs energies of binding

What is the source of these discrepancies? Is there a significant error in the experimental values of the Gibbs free energy of binding ( $\mathrm{\Delta }{G}_{\mathit{bind}}^o=\mathit{RT}ln{K}_D-2.4\text{kcal}/\text{mol}$) or in the calculated ones ( $\mathrm{\Delta }{G}_{if}^o$) that can explain the differences? In general, no. Let us consider the error in those thermodynamic parameters. Typically, the relative error in K_D arising from variability in experimental measurements is of the order of 30%, which corresponds to only ≈ 0.2 kcal/mol in $\mathrm{\Delta }{G}_{\mathit{bind}}^o$. A larger source of error arises from the uncertainty regarding peptide translocation, and therefore whether all the lipid or only the outer monolayer of each vesicle should be considered in calculating K_D. This corresponds to a factor of 2 in K_D, which translates into 0.4 kcal/mol in $\mathrm{\Delta }{G}_{\mathit{bind}}^o$. Thus, in the worst case scenario, the cumulative error from those sources is about 0.6 kcal/mol; this is < 10% of a typical value of $\mathrm{\Delta }{G}_{\mathit{bind}}^o=-7.0\text{kcal}/\text{mol}$.

For δ-lysin, DL-2a, DL-2b, CE-1, and MG-1, however, the measurements of K_D (= k_off/k_on ) proved difficult. The signal amplitudes in the stopped-flow fluorescence measurements of binding were small, which suggests that a significant fraction of the peptides was in a state that does not associate with membranes in the short time frame of the binding kinetics. The most likely explanation is that peptide oligomers exist in aqueous solution, which dissociate slowly. It is the monomer that binds to the membrane, and if its concentration is low, the signal is small. These five peptides have low or no net charge at pH 7.5, consistent with a tendency to oligomerize. This is known for δ-lysin above 1 μM (14, 54–57). This idea is corroborated by high helicities in aqueous buffer, considerably higher than expected from AGADIR (53). Oligomerization may distort the measured on- and off-rates, which are used to calculate K_D. Thus, K_D for these five peptides may have a larger error than for the others. However, as discussed below, there is a very good correlation between the experimental values of $\mathrm{\Delta }{G}_{\mathit{bind}}^o$ and the rate of induced dye release, suggesting that the estimate of binding affinities is nearly correct.

Consider now the error in $\mathrm{\Delta }{G}_{if}^o$, calculated with MPEx using the Wimley-White interfacial scale, which originates from uncertainty in the helicity of the peptide on the membrane. Typically, the relative error in peptide helicity on the membrane arising from variability in experimental measurements is of the order of 5%. Using the actual standard deviations obtained in the CD determinations, this yields errors of 0.1–0.6 kcal/mol in $\mathrm{\Delta }{G}_{if}^o$. In DL-1, the error in $\mathrm{\Delta }{G}_{if}^o$ is about 0.2 kcal/mol, clearly insufficient to bridge the difference of 5.5 kcal/mol relative to $\mathrm{\Delta }{G}_{\mathit{bind}}^o$. The helicity would have to be increased from the experimental value of 52 to 95% to make $\mathrm{\Delta }{G}_{if}^o=\mathrm{\Delta }{G}_{\mathit{bind}}^o$. In cecropin A, the error in $\mathrm{\Delta }{G}_{if}^o$ is 0.5 kcal/mol, which is much smaller than the 3.7 kcal/mol difference between $\mathrm{\Delta }{G}_{if}^o$ and $\mathrm{\Delta }{G}_{\mathit{bind}}^o$; in fact, a helicity of 95% on the membrane would be necessary to bring the two values into agreement. In MG-1, $\mathrm{\Delta }{G}_{if}^o=-3.6\text{kcal}/\text{mol}$ with an error of ≈ 0.6 kcal/mol, which is insufficient to bring it even close to $\mathrm{\Delta }{G}_{\mathit{bind}}^o=-7.4\text{kcal}/\text{mol}$. The helicity of MG-1 is 69% in POPC, which is a typical average value for antimicrobial peptides, and even increasing it to 100% would only make $\mathrm{\Delta }{G}_{if}^o=-6.4\text{kcal}/\text{mol}$. As a counterexample, in CE-1 the formal error in $\mathrm{\Delta }{G}_{if}^o$ is 0.1 kcal/mol, but a small increase in helicity, from 55 to 62%, is sufficient to render $\mathrm{\Delta }{G}_{if}^o=\mathrm{\Delta }{G}_{\mathit{bind}}^o$; it is reasonable that CD may underestimate the helicity by 7%.

In the case of magainin 2, the helicity is 57% in POPC/POPG 1:1; using this value, $\mathrm{\Delta }{G}_{if}^o=-3.8\text{kcal}/\text{mol}$, whereas $\mathrm{\Delta }{G}_{\mathit{bind}}^o=-6.1\text{kcal}/\text{mol}$. However, the helicity in pure POPC may be higher; in dodecylphosphocholine (DPC) micelles the helicity is 83% (64), which yields $\mathrm{\Delta }{G}_{if}^o=-6.2\text{kcal}/\text{mol}$, in agreement with the experimental value. A similar situation occurs with MG-2. The CD measurement had to be made in POPC/POPG 1:1 because MG-2 does not bind well to POPC. If the helicity was 80% in pure POPC, the calculated and experimental values would agree. The cases of magainin 2 and MG-2 can thus be explained.

Another factor may be at play in DL-2a, and perhaps to a lesser extent in MG-1. Their helicities in aqueous solution are large, much more than expected from AGADIR, suggesting that the peptides oligomerize in water. When they are mixed with POPC to measure the CD, if only a small fraction dissociates from the oligomers and binds to the membrane, the measured value of the helicity may be heavily weighted by oligomers remaining in solution. But we could not see a change in the CD spectrum of DL-2a added to 5 mM POPC even after a day. It may be a coincidence that the helicities in solution and on the membrane are the same; but it could also be that the amount of peptide bound to lipid is small. In that case, the value of the helicity measured “on the membrane” would be incorrect. If DL-2a were in fact as helical on the membrane as δ-lysin (close to 100%), we would get $\mathrm{\Delta }{G}_{if}^o=-7\text{kcal}/\text{mol}$, in agreement with the experimental value.

In conclusion, in many cases the experimental $\mathrm{\Delta }{G}_{\mathit{bind}}^o$ do not agree with those calculated from the Wimley-White interfacial scale ( $\mathrm{\Delta }{G}_{if}^o$). Whereas these differences can perhaps be attributed to errors in helicity in the cases of magainin 2, MG-2, and DL-2a, the discrepancies observed in cecropin A, δ-lysin, DL-1, and MG-1 are real. There appear to be contributions to binding that are nonadditive and are therefore not captured by the simple sum of the Wimley-White parameters that $\mathrm{\Delta }{G}_{if}^o$ represents. We had previously explained the discrepancies by formation of salt bridges by the side chains of Lys and Arg with Asp and Glu. Now, that explanation is untenable in general. However, the inter-residue spacing was required for formation of salt bridges remains in DL-1, because three Asp residues were changed to Lys, but their positions in the sequence were maintained. These residues are close to each other in space in the folded, helical peptide on the membrane surface. It has recently been shown by simulation, that transfer of spatially close Arg residues to the bilayer interior is nonadditive (65). That is, once a first Arg is transferred to the bilayer and creates a water defect, additional Arg residues can transfer at essentially no energetic cost to the same defect. The presence of a water defect that hydrates the first charge is costly, but additional charges can use that defect for free. Could a similar situation occur with the transfer of the six Lys residues of DL-1 to the membrane interface? If the unfavorable contributions of all but one Lys were considered, a Gibbs energy of transfer $\mathrm{\Delta }{G}_{if}^o=-7.5\text{kcal}/\text{mol}$ would be obtained, which is close to the experimental value of $\mathrm{\Delta }{G}_{\mathit{bind}}^o=-7.0\text{kcal}/\text{mol}$.

Effect of mutations on dye release kinetics

We now compare the effects of mutations on the rate of dye release. The peptide activity toward model membranes was characterized by measuring the kinetics of CF release from LUV, under similar experimental conditions. The release kinetics were quantified by calculating the average characteristic time constants τ, which are listed in Table 3.

The release curves of δ-lysin characteristically exhibit a lag time (Figure 7A). This may be due to oligomerization on the membrane (14, 15) or to an apparent slow on-rate. The observed k_on is indeed small, which could be due to a rate-limiting dissociation of oligomers in solution. On the contrary, dye release by DL-1 has no lag time. Unlike δ-lysin, which has zero net charge at pH 7.5, DL-1 has a charge of +6. This suggests that repulsive electrostatic interactions in DL-1 minimize oligomerization in solution, and corroborates the idea that oligomerization of δ-lysin in solution causes its apparent slow rate of binding. DL-1 was expected to be less efficient than the original δ-lysin, because of a less favorable Gibbs energy of binding. However, the difference in the experimental Gibbs energies of binding is only ≈ 1 kcal/mol only. Accordingly, dye release induced by DL-1 is only a factor of ≈ 2 slower than by δ-lysin (Figure 7A and Table 3).

In the cases of CE-1 and MG-1, the rate of dye release was predicted to increase significantly, compared to cecropin A and magainin 2, and it did. This expectation was based on the improved binding observed ( $\mathrm{\Delta }{G}_{\mathit{bind}}^o$ changed from −6.4 to −7.0 kcal/mol in CE-1, and from −6.1 to −7.4 kcal/mol in MG-1), but also on a lower $\mathrm{\Delta }{G}_{\mathit{oct}―if}^o$ in the case of CE-1, which decreased by 13 kcal/mol relative to cecropin A. As predicted, dye release became dramatically faster for both mutants compared with the original peptides (Figure 7B,C).

DL-2a and DL-2b were expected to exhibit dye release kinetics similar to those of δ-lysin. Indeed, their release curves (Figure 7D) show the sigmoidal shape characteristic of δ-lysin (Figure 7A). The much lower efficiency of DL-2a and DL-2b in dye release, with τ = 14.8 and 650 s compared to 2.2 s for δ-lysin, is probably a consequence of greater extent of oligomerization in solution. As expected, CE-2 and MG-2 are about as inefficient as cecropin A and magainin-2 in causing dye release from POPC LUVs, which occurs in timescales of the order of 10,000 s for these four peptides (Table 3).

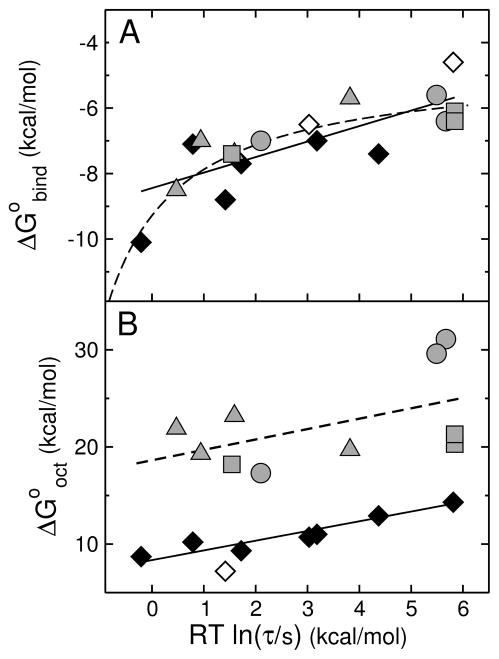
To understand these results, let us consider the Gibbs energies of peptide binding and insertion. The caveats regarding the experimental $\mathrm{\Delta }{G}_{\mathit{bind}}^o$ for some of the peptides notwithstanding, there is a clear correlation between the binding affinity to the membrane and the characteristic time τ of peptide-induced dye release (Figure 9A). Previously, we argued that the mean time constant for dye release (τ) should depend on the Gibbs energy of binding ( $\mathrm{\Delta }{G}_{\mathit{bind}}^o$) and on the activation free energy for insertion in the bilayer (ΔG^‡) through an equation of the Arrhenius type (16),

FIGURE 9.

(A) Gibbs energy of binding to the membrane interface determined experimentally ( $\mathrm{\Delta }{G}_{\mathit{bind}}^o$) as a function of the mean characteristic time τ for CF release from POPC LUVs. Each gray symbol corresponds to a peptide examined here: δ-lysin, DL-1, DL-2a, and DL-2b are shown by gray triangles; cecropin A, CE-1, and CE-2, by gray circles; and magainin 2, MG-1, and MG-2, by gray squares. The data for TP10 variants previously published (16) are shown here for comparison (diamonds): TP10W, TPW-1, TPW-2, and TPW-3; TP10, TP10-COO⁻, TP10W-COO⁻, and TP10-7MC (38, 58). The black symbols correspond to experimental data; the open symbols correspond to TP10 and TP10-COO⁻, for which τ is experimental but the binding affinity is calculated with the Wimley-White scale (neither contains Trp). The straight line is a fit, with a slope of 0.5. The dashed line represents qualitatively the expected behavior limited by diffusion or bilayer response. (B) Gibbs energy of transfer to octanol calculated with the Wimley-White scale ( $\mathrm{\Delta }{G}_{\mathit{oct}}^o$) as a function of the mean characteristic time τ for CF release from POPC LUV. The points correspond to the same peptides as in (A) and the same symbols were used. Again the TP10 variant data are from our previous paper (16). The open circle corresponds to TP10-7MC for which $\mathrm{\Delta }{G}_{\mathit{oct}}^o$was estimated assuming Tyr for the Lys-MC residue (16). The lines are fits, which have slopes of 1.

$$1/\tau =A_o{e}^{-\mathrm{\Delta }{G}_{\mathit{bind}}^o/RT}{e}^{-\mathrm{\Delta }{G}^{‡}/RT}.$$ (9)

The pre-exponential factor A_o includes effects of lipid and peptide concentrations as well as molecular details specific for each peptide family, but should remain fairly constant within a given family under similar experimental conditions. This is the case for the TP10 family (16). According to Eq. 9, if the activation free energy for insertion is $\mathrm{\Delta }{G}^{‡}\approx \mathrm{\Delta }{G}_{\mathit{oct}-if}^o$ (66), and recalling that $\mathrm{\Delta }{G}_{\mathit{oct}-if}^o$ was calculated using the experimental value of $\mathrm{\Delta }{G}_{\mathit{bind}}^o(\mathrm{\Delta }{G}_{\mathit{oct}-if}^o=\mathrm{\Delta }{G}_{\mathit{oct}}^o-\mathrm{\Delta }{G}_{\mathit{bind}}^o)$, we obtain

$$1/\tau =A_o{e}^{-\mathrm{\Delta }{G}_{\mathit{oct}}^o/RT},$$ (10)

which, after taking logarithms and multiplying by −RT, yields

$$\mathrm{\Delta }{G}_{\mathit{oct}}^o=\mathit{RT}ln\tau +\mathit{Const}.$$ (11)

Hence, a linear relation with a slope of 1 is expected between $\mathrm{\Delta }{G}_{\mathit{oct}}^o$ and RT ln τ, which was observed for the family of the cell-penetrating peptide TP10 (Figure 9B, diamonds). When the data for the other three peptide families now examined are compared (Figure 9B, gray symbols), we notice that the dispersion is much larger, though the average behavior is still captured by a straight line with unit slope (dashed). Within each family, the data are too sparse to allow any trends to be gleaned. As a whole, however, it is clear that the mutants of antimicrobial and cytolytic peptides behave differently from the TP10 variants, in that the Gibbs energy of transfer into the nonpolar interior of the membrane is much more unfavorable. A small $\mathrm{\Delta }{G}_{\mathit{oct}-if}^o$, which is a consequence of a small $\mathrm{\Delta }{G}_{\mathit{oct}}^o$, would allow the CPPs, but not the antimicrobial and cytolytic peptides, to translocate across the membrane.

It is also clear from Figure 9 that $\mathrm{\Delta }{G}_{\mathit{bind}}^o$ is a much better overall predictor of the peptide activity (measured by τ) than $\mathrm{\Delta }{G}_{\mathit{oct}}^o$. Previously, based only on the TP10 variants, we thought that the Gibbs energy of insertion was the most important parameter, which led to Eq. 11 (16). Now, with a larger data set, it is apparent that the only point that deviates significantly from the line in Figure 9A is that corresponding to TPW-2, on the left of the plot. A deviation from linearity at very low τ is, however, unavoidable. No matter how good binding is, τ eventually approaches a minimum value (τ_min) that is determined by the diffusion limit for peptide binding to the membrane and by the time of bilayer response. The diffusion limit for binding to LUVs is k_lim ≈ 10⁶ M⁻¹s⁻¹ expressed in terms of lipids (1 LUV ≈ 10⁵ lipids). With a lipid concentration c = 50 μM, this means that the maximum rate of binding is k_lim c = 1/τ_min = 50 s⁻¹. Thus, τ ≥ 0.02 s and RT ln τ ≥ −2.3 kcal/mol. This limit can be only asymptotically approached as $\mathrm{\Delta }{G}_{\mathit{bind}}^o\to -\infty$. The dashed line in Figure 9A depicts qualitatively the expected behavior limited by diffusion or bilayer response. What these results indicate is that binding is the primary step that determines peptide activity.

The Gibbs energy of insertion: Test of hypotheses 1 and 3

We have determined the type of dye release using the ANTS/DPX requenching assay, and confronted the predictions of hypotheses 1 and 3 with the results. The Gibbs energy of insertion was estimated by $\mathrm{\Delta }{G}_{\mathit{oct}-if}^o$, where the experimental value of $\mathrm{\Delta }{G}_{\mathit{bind}}^o$ was used for the Gibbs energy of binding to the interface. These values are listed in Table 3, which also includes a summary of the ANTS/DPX results. According to hypothesis 1, if the type of release provides an indication of peptide translocation, $\mathrm{\Delta }{G}_{\mathit{oct}-if}^o<20\text{kcal}/\text{mol}$ corresponds to graded release and $\mathrm{\Delta }{G}_{\mathit{oct}-if}^o>23\text{kcal}/\text{mol}$ to all-or-none release. These predictions were corroborated by experiment for DL-1, CE-1, and MG-1. Based on our original calculations (which included salt bridges), δ-lysin lay in a “gray zone” between 20–23 kcal/mol; without salt bridges it should be all-or-none, but experimentally it is weakly graded (15). In DL-1 a change to all-or-none release was sought and obtained (Figure 8A). In DL-2a the type of release of δ-lysin was expected to be maintained, and it was (Figure 8D), although without including salt bridges both should be all-or-none. In CE-1 and MG-1 dye release should have remained all-or-none, as in cecropin A (31) and magainin 2 (32, 61, 62), and it did (Figure 8B,C).

The most interesting results, however, were obtained for CE-2 and MG-2. Both peptides had been designed to remain all-or-none, like cecropin A and magainin 2; the sequences were simplified, but the mutations were such that the thermodynamics should not have changed. Indeed, the measured $\mathrm{\Delta }{G}_{\mathit{bind}}^o$ were very close to prediction, and $\mathrm{\Delta }{G}_{\mathit{oct}-if}^o>25\text{kcal}/\text{mol}$ put these two peptides squarely in the all-or-none class. However, dye release is clearly graded (Figure 8E,F). This demonstrates that the simplification of the sequence can dramatically change the type of release, and hypothesis 3 is wrong. The question addressed by hypothesis 3 was whether or not sequence diversity is important. In the mutants CE-2, MG-2 the same amino acid types were kept in the same positions. Namely, polar charged residues were conserved and hydrophobic residues were conserved, but the sequence diversity was reduced to a minimum number of amino acids. The situation is similar in the folding problem of globular proteins in water, when the diversity of amino acids is reduced to only hydrophobic (H) and polar (P), which is embodied in the HP model (29). Whereas the HP model captures many features of the protein folding problem, it does not generate unique native conformations (67). Replacing the HP, two-letter alphabet by a multiletter one, that is, increasing amino acid diversity in the sequence, reduces degeneracy of the folded state (68). Furthermore, two- and three-letter alphabet models fold much less cooperatively than 20-letter ones (69). Experimentally as well, simplified sequences of real proteins fail to fold to unique structures. A three-letter alphabet model of protein G folds to a fluid-like molten globule, but this folded structure is more flexible than the original protein (70). The low-diversity code produces conformations with abundant secondary structure but is not sufficiently specific to yield a unique tertiary structure. The 20-letter alphabet is thought to eliminate unwanted amino acid contacts and avoid aggregation. Clearly, amino acid diversity in the sequence is also fundamental for the activity of these antimicrobial peptide variants.

Hypothesis 1 is not disproved by these results because its most fundamental statement is that translocation requires $\mathrm{\Delta }{G}_{\mathit{oct}-if}^o<20\text{kcal}/\text{mol}$. We had observed that all the peptides whose kinetic mechanism required translocation caused graded release (6). Now, however, it is clear that either the correlation between translocation and graded release breaks down or hypothesis 1 is wrong. Previously, we proposed that graded release occurs because peptides translocate and dissipate the mass imbalance across the membrane before all the dye has time to escape (15). Another possibility, however, is that the peptides constantly but slowly perturb the membrane, without ever translocating or causing a major disruption. In that case, release should be complete; indeed, CE-2 induces complete but graded dye release, consistent with this idea.

Thus, either the first or the second implication in each of the statements (Eqs. 1 and 2) that constitute hypothesis 1 is wrong, but we do not yet know which one. The results obtained with CE-2 and MG-2 show that the type of dye release cannot be predicted on the basis of the Gibbs energy of insertion, and even very conservative changes to the peptide sequence can result in complete switches from all-or-none to graded release. Clearly, it is necessary to determine directly whether the correlation between translocation and graded release holds or not. If the correlation proves correct for CE-2 and MG-2, hypothesis 1 will be disproved. This will be investigated in future work.

CONCLUSION

We have attempted to disprove our hypotheses by examining binding and activity of variants of antimicrobial and cytolytic peptides in model membranes. First, the results indicate that binding to the membrane, not insertion, is the primary determinant of peptide activity. This is contrary to the concept underlying the proposed hypotheses, in which the Gibbs energy of insertion, estimated by $\mathrm{\Delta }{G}_{\mathit{oct}-if}^o$, was central. Nevertheless, $\mathrm{\Delta }{G}_{\mathit{oct}-if}^o$ is much more unfavorable for the families of antimicrobial and cytolytic peptides than for variants of the amphipathic cell-penetrating peptide TP10 previously examined (16). A smaller $\mathrm{\Delta }{G}_{\mathit{oct}-if}^o$ would allow the CPPs, but not the antimicrobial and cytolytic peptides, to translocate across the membrane, as predicted. However, either graded release is not a reliable indicator of peptide translocation or the first hypothesis is wrong. Second, placing acidic and basic residues along the peptide sequence, with the correct spacing for the establishment of salt bridges by their side chains, does not result in consistent improvement of binding. Either these salt bridges do not form at the membrane interface, or they form but do not decrease $\mathrm{\Delta }{G}_{\mathit{bind}}^o$. Third, simplification of the sequence to a few amino acid types, even through very conservative mutations dramatically changes the mechanism of dye release (though not the rate). Thus, amino acid diversity in the sequence seems essential for the function of even these simple polypeptides on the membrane, as it is essential for the folding of globular proteins in water.