Longitudinal Tractography with Application to Neuronal Fiber Trajectory Reconstruction in Neonates

Abstract

This paper presents a novel tractography algorithm for more accurate reconstruction of fiber trajectories in low SNR diffusion-weighted images, such as neonatal scans. We leverage information from a later-time-point longitudinal scan of the neonatal image to obtain more reliable estimates of local fiber orientations. Specifically, we determine the orientation posterior probability at each voxel location by utilizing prior information given by the longitudinal scan, and with the likelihood function formulated based on the Watson distribution. We incorporate this Bayesian model of local orientations into a state-space model for particle-filtering-based probabilistic tracking, catering for the possibility of fiber crossings by modeling multiple orientations per voxel. Regularity of fibers is enforced by encouraging smooth transitions of orientations in subsequent locations traversed by the fiber. Experimental results performed on neonatal scans indicate that fiber reconstruction is significantly improved with less stray fibers and is closer to what one would expect anatomically.

1 Introduction

The human brain is a complex system that is capable of integrating massive amount of information with startling efficiency. A comprehensive description of the architecture of the anatomical connectivity patterns is therefore fundamentally important in cognitive neuroscience and neuropsychology, as it reveals how functional brain states emerge from their underlying structural substrates and provides new mechanistic insights into the association of brain functional deficits with the underlying structural disruption [1].

The neonatal brain provides a window for insights into perhaps the most important phase of human brain development. For this purpose, diffusion-weighted imaging (DWI) plays an indispensable role in the in vivo characterization of brain structural circuity relating different functional regions. However, the utilization of DWI on neonatal subjects for the purpose of connectivity analysis is often impeded by the unreliability of neuronal fiber trajectory reconstruction due to the inherent lower quality of the diffusion-weighted scans. Noisy estimates of local fiber orientations can propagate and accummultate in the course of trajectory reconstruction, especially if the tractography algorithm is greedy in nature, rendering the validity of subsequent tract-based analysis questionable. We present in this paper a remedy to this problem by leveraging prior information from longitudinal scans to improve the accuracy of local fiber orientation estimates for more accurate trajectory reconstruction of the neuronal fibers.

Cook et al. [2] proposed an atlas based approach for better tractography outcome by modifying the stochastic white matter tractography algorithm developed by Friman et al. [3]. An atlas was first generated by computing for each voxel the dyadic tensor of the principal directions from a set of diffusion tensor images. The atlas encapsulates the mean local fiber orientations as well as their degrees of dispersion, serving as prior information to the Bayesian stochastic tractography framework in [3]. This approach, while effective, has two shortcomings: 1) Its formulation is limited to one single orientation per voxel, seriously limiting the ability of the algorithm in accounting for fiber crossing, branching or kissing, and 2) The atlas is not subject-specific, causing loss of fiber tracts in regions where the subject and the atlas disagree.

The contributions of this paper are: 1) The formulation and evaluation of a fiber tractography algorithm that is guided by longitudinal prior information for more robust fiber trajectory reconstruction especially in images with lower SNR, and 2) The evaluation of how modeling multiple fiber orientations per voxel improves tractography outcome in regions with complex diffusion architecture.

2 Approach

2.1 Modeling Local Fiber Orientations

A white matter fiber can be modeled as a finite-length path parameterized by a train of unit length vectors. We use the following notation for such a path: v_(1:T) = {v₍₁₎, … , v_(T)}. We further assume that a fiber path can be traced by tracking the trajectory of a particle travelling in a continuous directional field. Each particle is endowed with an initial speed in an appropriate direction. It then moves with constant speed to position x_(t) according to

$${\mathbf{x}}_{(t+1)}={\mathbf{x}}_{\left(t\right)}+s{\mathbf{v}}_{\left(t\right)}$$ (1)

where t is the time index and s is the step length. To reconstruct the fiber trajectories, we need to determine the probability density function (PDF) of the local fiber orientations f(v_(t)ǀv_(t–1), θ_(t), θ’_(t), D_(t)), where D_(t) = 1, … , Ω is the orientation index. Each voxel may contain up to Ω orientations, as is in the case of high angular resolution diffusion imaging (HARDI). Sets θ_(t) and θ’_(t) are collections of the orientations, and their strengths, in the neighborhood of x_(t) of the neonate and its longitudinal scans, respectively. Specifically, we define a neighborhood N(x_(t)) (e.g., a 3 × 3 × 3 neighborhood) in the vicinity of x_(t) and, for voxel i in the neighborhood, collect all the corresponding orientations ${\mathbf{v}}_{\left(t\right),i}^{\left[D_{\left(t\right)}\right]}$ and their strengths ${\rho }_{\left(t\right),i}^{\left[D_{\left(t\right)}\right]}$ (e.g., magnitudes of the orientation distribution functions), spatially weighted by a Gaussian kernel so that voxels further away from the neighborhood center will be deemphasized. The orientations are first sorted to avoid the bias discussed in [4]. Applying Bayesian theorem, we have

$$f({\mathbf{v}}_{\left(t\right)}\mid {\mathbf{v}}_{(t-1)},{\theta }_{\left(t\right)},{\theta }_{\left(t\right)}^{\prime },D_{\left(t\right)})=\frac{f({\theta }_{\left(t\right)}\mid {\mathbf{v}}_{\left(t\right)},{\mathbf{v}}_{(t-1)},{\theta }_{\left(t\right)}^{\prime },D_{\left(t\right)})f({\mathbf{v}}_{\left(t\right)}\mid {\mathbf{v}}_{(t-1)},{\theta }_{\left(t\right)}^{\prime },D_{\left(t\right)})}{f({\theta }_{\left(t\right)}\mid {\mathbf{v}}_{(t-1)},{\theta }_{\left(t\right)}^{\prime },D_{\left(t\right)})}.$$ (2)

Since the orientations in both images are estimated independently in a voxel-wise fashion, f(θ_(t)ǀv_(t), v_(t–1), θ’_(t), D_(t)) = f(θ_(t)ǀv_(t), D_(t)) and f(θ_(t)ǀv_(t–1), θ’_(t), D_(t)) = f(θ_(t)ǀD_(t)). The equation can then be written as

$$f({\mathbf{v}}_{\left(t\right)}\mid {\mathbf{v}}_{(t-1)},{\theta }_{\left(t\right)},{\theta }_{\left(t\right)}^{\prime },D_{\left(t\right)})=\frac{f({\theta }_{\left(t\right)}\mid {\mathbf{v}}_{\left(t\right)},D_{\left(t\right)})f({\mathbf{v}}_{\left(t\right)}\mid {\mathbf{v}}_{(t-1)},{\theta }_{\left(t\right)}^{\prime },D_{\left(t\right)})}{f({\theta }_{\left(t\right)}\mid D_{\left(t\right)})}.$$ (3)

The factor f(θ_(t)ǀD_(t)) normalizes the posterior probability function to have a unit volume and can thus be written as the integral of the numerator

$$f({\theta }_{\left(t\right)}\mid D_{\left(t\right)})={\int }_{{\mathbf{v}}_{\left(t\right)},{\mathbf{v}}_{(t-1)},{\theta }_{\left(t\right)}^{\prime }}f({\theta }_{\left(t\right)}\mid {\mathbf{v}}_{\left(t\right)},D_{\left(t\right)})f({\mathbf{v}}_{\left(t\right)}\mid {\mathbf{v}}_{(t-1)},{\theta }_{\left(t\right)}^{\prime },D_{\left(t\right)})d{\mathbf{v}}_{\left(t\right)}d{\mathbf{v}}_{(t-1)}d{\theta }_{\left(t\right)}^{\prime }.$$ (4)

In what follows, we will discuss how the likelihood f(θ_(t)ǀv_(t), D_(t)) and prior f(v_(t)ǀv_(t–1), θ’_(t), D_(t)) can be computed.

Likelihood

We assume that the orientations observed in the neighborhood of x_(t) can be regarded as noisy observations of v_(t), characterized by the Watson distribution with probability density function (PDF) [5]

$$f(\mathbf{w}\mid \mu ,\kappa )=C\left(\kappa \right){\mathrm{e}}^{\kappa {\left({\mathbf{w}}^{\mathrm{T}}\mu \right)}^2}.$$ (5)

The parameter μ is a unit vector called the mean orientation and κ is a positive constant called the concentration parameter. The Watson distribution can be thought of as a symmetrization of the Fisher-Von Mises distribution [6] for unit vectors on the sphere. The squared exponential in (5) ensures that the distribution is antipodal symmetric. The density has maxima at ±μ and becomes more concentrated around ±μ as κ increases. The density is also rotationally invariant around ±μ. C(κ) is a normalizing constant to ensure that the density function integrates to unity over the unit sphere. By letting μ = v_(t), the joint distribution, or the likelihood, of the observed orientations θ_(t) can be written as

$$f({\theta }_{\left(t\right)}\mid {\mathbf{v}}_{\left(t\right)},D_{\left(t\right)})=\prod _{(\mathbf{w},\rho )\in {\theta }_{\left(t\right)}^{\left[D_{\left(t\right)}\right]}}C\left(\kappa \right)e^{\rho \kappa {\left({\mathbf{w}}^{\mathrm{T}}{\mathbf{v}}_{\left(t\right)}\right)}^2}$$ (6)

where ${\theta }_{\left(t\right)}^{\left[D_{\left(t\right)}\right]}$ is a subset of θ_(t) consisting only of the group of orientations specified by D_(t). This equation is substituted into the equation for the posterior distribution in (3).

Priors

Via the probability function f(v_(t)ǀv_(t–1), θ’_(t), D_(t)), we encode our prior knowledge about fiber regularity and about orientation from the longitudinal scan. We define the prior probability function as

$$\begin{array}{cc}\hfill f({\mathbf{v}}_{\left(t\right)}\mid & {\mathbf{v}}_{(t-1)},{\theta }_{\left(t\right)}^{\prime },D_{\left(t\right)})\propto \hfill \\ \hfill & \{\begin{array}{cc}{\left[{\mathbf{v}}_{\left(t\right)}^{\mathrm{T}}{\mathbf{v}}_{(t-1)}\right]}^2\left[C\left({\kappa }_{\left(t\right)}^{\prime \left[D_{\left(t\right)}\right]}\right){\mathrm{e}}_{\left(t\right)}^{\prime \left[D_{\left(t\right)}\right]}{\left({\mathbf{v}}_{\left(t\right)}^{\mathrm{T}}{\mu }_{\left(t\right)}^{\prime \left[D_{\left(t\right)}\right]}\right)}^2\right],\hfill & {\mathbf{v}}_{\left(t\right)}^{\mathrm{T}}{\mathbf{v}}_{(t-1)}>0\hfill \\ 0,\hfill & \text{otherwise}.\hfill \end{array}\phantom{\}}\hfill \end{array}$$ (7)

The first term on the right enforces the regularity constraint during fiber reconstruction. The second term transfuses orientation information from the longitudinal scan. The Watson distribution is used to represent the distribution of the orientations in ${\theta }_{\left(t\right)}^{\prime \left[D_{\left(t\right)}\right]}$, with mean orientation ${\mu }_{\left(t\right)}^{\prime \left[D_{\left(t\right)}\right]}$ and concentration parameter ${\kappa }_{\left(t\right)}^{\prime \left[D_{\left(t\right)}\right]}$. Maximum likelihood estimates of the these parameters can be obtained using the method described in [5].

2.2 State-Space Model

Tractography is assumed to be a stochastic process that can be represented using a state-space model with the local fiber orientation v_(t) as the observation, and the orientation index D_(t) as the state. Given the previous oriention v_(t–1) and the current state D_(t), the observation probability is defined according to (3). Noting that the posterior probability for selection of a particular value of the orientation index D_(t) is

$$f(D_{\left(t\right)}\mid {\mathbf{v}}_{(t-1)},{\theta }_{\left(t\right)},{\theta }_{\left(t\right)}^{\prime })=\frac{f({\theta }_{\left(t\right)}\mid {\mathbf{v}}_{(t-1)},{\theta }_{\left(t\right)}^{\prime },D(t\left)\right)f(D_{\left(t\right)}\mid {\mathbf{v}}_{(t-1)},{\theta }_{\left(t\right)}^{\prime })}{f({\theta }_{\left(t\right)}\mid {\mathbf{v}}_{(t-1)},{\theta }_{\left(t\right)}^{\prime })}$$ (8)

and by letting

$$f({\theta }_{\left(t\right)}\mid {\mathbf{v}}_{(t-1)},{\theta }_{\left(t\right)}^{\prime },D(t\left)\right)\propto {\stackrel{‒}{\rho }}_{\left(t\right)}^{\left[D_{\left(t\right)}\right]},f(D_{\left(t\right)}\mid {\mathbf{v}}_{(t-1)},{\theta }_{\left(t\right)}^{\prime })\propto {\left({\mathbf{v}}_{(t-1)}^{\mathrm{T}}{\mu }_{\left(t\right)}^{\prime \left[D_{\left(t\right)}\right]}\right)}^2,$$ (9)

the transition probability can be defined as

$$f(D_{\left(t\right)}\mid {\mathbf{v}}_{(t-1)},{\theta }_{\left(t\right)},{\theta }_{\left(t\right)}^{\prime })\propto {\stackrel{‒}{\rho }}_{\left(t\right)}^{\left[D_{\left(t\right)}\right]}{\left({\mathbf{v}}_{(t-1)}^{\mathrm{T}}{\mu }_{\left(t\right)}^{\prime \left[D_{\left(t\right)}\right]}\right)}^2.$$ (10)

where ${\stackrel{‒}{\rho }}_{\left(t\right)}^{\left[D_{\left(t\right)}\right]}$ denotes the average strength of ${\theta }_{\left(t\right)}^{\left[D_{\left(t\right)}\right]}$. To perform the sequential sampling of fiber paths, we need to draw random samples of the fiber direction from the observation probability (3) and transition probability (10). For drawing samples from complicated and high dimensional PDFs, one can always resort to Markov Chain Monte Carlo (MCMC) techniques. The probability of a path of a given length T is

$$\begin{array}{cc}\hfill f({\mathbf{v}}_{(1:T)}\mid {\theta }_{(1:T)},& {\theta }_{(1:T)}^{\prime })=f(D_{\left(1\right)}\left)f\right({\mathbf{v}}_{\left(1\right)}\mid {\theta }_{\left(1\right)},{\theta }_{\left(1\right)}^{\prime },D_{\left(1\right)})\times \hfill \\ \hfill & {\Pi }_{t=2}^{T}f(D_{\left(t\right)}\mid {\mathbf{v}}_{(t-1)},{\theta }_{\left(t\right)},{\theta }_{\left(t\right)}^{\prime })f({\mathbf{v}}_{\left(t\right)}\mid {\mathbf{v}}_{(t-1)},{\theta }_{\left(t\right)},{\theta }_{\left(t\right)}^{\prime },D_{\left(t\right)}).\hfill \end{array}$$ (11)

Tracking is stopped if the trajectory reaches a voxel with orientation coherence [7]

$${\beta }^{\left[D_{\left(t\right)}\right]}=1-\frac{1}{2}\left\{\sqrt{\frac{{\lambda }_2^{\left[D_{\left(t\right)}\right]}+{\lambda }_3^{\left[D_{\left(t\right)}\right]}}{2{\lambda }_1^{\left[D_{\left(t\right)}\right]}}}+\sqrt{\frac{{\lambda }_2^{\prime \left[D_{\left(t\right)}\right]}+{\lambda }_3^{\prime \left[D\right(t\left)\right]}}{2{\lambda }_1^{\prime \left[D_{\left(t\right)}\right]}}}\right\},{\beta }^{\left[D_{\left(t\right)}\right]}\in [0,1],$$ (12)

falling below a predefined threshold β₀, or simply when the brain boundary is encountered. The λ’s are the eigenvalues of the dyadic tensors of ${\theta }_{\left(t\right)}^{\left[D_{\left(t\right)}\right]}$ and ${\theta }_{\left(t\right)}^{\prime \left[D_{\left(t\right)}\right]}$ [2, 4]. Perfect alignment of the orientations in group D_(t) results in β^[D_(t)] = 1 and an uniform distribution of orientations results in β^[D_(t)] = 0.

3 Results

3.1 Materials

Diffusion-weighted images of 10 infants were acquired at two time points: one month and one year after birth. Diffusion gradients were applied in 42 non-collinear directions with diffusion weighting b = 1000 s/mm², repetition time (TR) = 7,680 ms and echo time (TE) = 82 ms. The scans covered the whole brain with a resolution of 2 × 2 × 2 mm³. Data post-processing includes brain skull removal, motion correction and eddy current correction using algorithms developed and distributed as part of the FMRIB Software Library (FSL) package. Each neonatal (one month) scan was co-registered with their respective longitudinal scan so that they reside in a common space.

3.2 Tractography

To evaluate the effectiveness of the proposed method, we performed tractography based on seeds placed at the points where the midline crosses the splenium of the corpus callosum. 3000 trajectories were initiated from each seed point. The step size was fixed at 1 mm. The maximum allowable orientation coherence was set to 0.1. Various configurations were used:

1. Tractography on the neonatal image alone with no prior information from the longitudinal scan.

2. Tractography on the neonatal image guided by prior information from the longitudinal scan.

3. Tractograph on the longitudinal scan.

4. Tractography on the neonatal image using only the first principal orientation with no prior information.

5. Tractography on the neonatal image guided by longitudinal prior information from the longitudinal scan using only the first principal orientations.

6. Tractography on the longitudinal scan using only the first principal orientations.

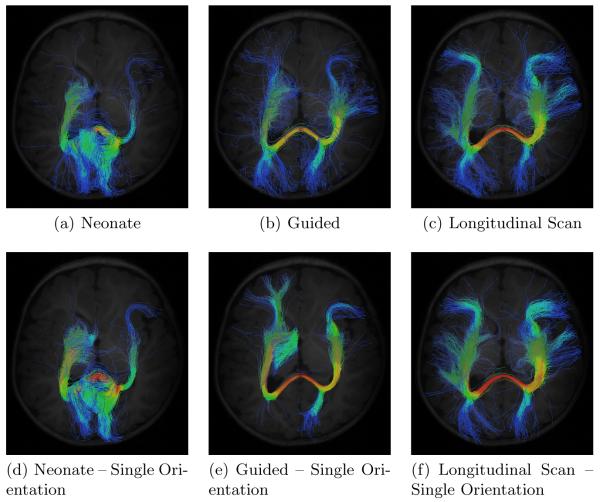
The respective results, shown in Fig. 1, indicate the proposed method (Fig. 1(b)) gives reasonable results. Tractography, when performed based on the orientation information given by the neonate image alone, results in noisy fiber tracts (Fig. 1(a) and Fig. 1(d)). This is not surprising since the neonatal scans typically suffer from lower SNR. The results were improved remarkably by employing prior information given by the longitudinal scan (Fig. 1(c) and Fig. 1(f)). The reconstructed trajectories are generally cleaner with less stray fibers and are in higher agreement with our anatomical understanding of the fibers. Note that by allowing only one orientation per voxel, major fibers are lost. Fig. 1(e) shows that, despite with longitudinal guidance, fibers connecting one of the occipital lobes cannot be correctly preserved and reconstructed.

Fig. 1.

Comparison of the different tractography schemes. (a) Neonate alone, (b) Neonate + Longitudinal Scan, (c) Longitudinal scan alone, (d) Neonate alone (single orientation), (e) Neonate + Longitudinal Scan (single orientation), and (f) Longitudinal scan alone (single orientation).

3.3 Multi- and Single-Orientation Schemes

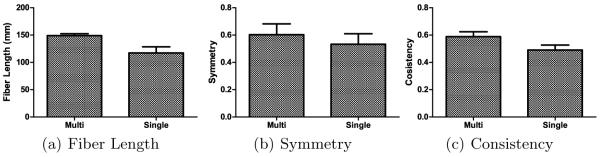
For quantification of the effect of using multi-orientation and single-orientation per voxel on the reconstructed trajectories, various measures were employed. First, we compared the average length of the reconstructed trajectories. A longer length average generally indicates that fiber reconstruction is less likely to be terminated prematurely, which can be due to noisy local fiber orientations. Fig. 2(a) shows that the proposed method results in on average longer trajectories, hinting that by allowing more than one orientation per each voxel results in less chances of premature termination at fiber crossings.

Fig. 2.

Comparison between the multi- and single-orientation schemes using different statistics. Each bar indicates the mean value, and the error bar indicates the corresponding standard error.

Anatomical scans (e.g., T1-weighted and T2-weighted images) of the brain indicate that the brain is mostly symmetrical between the hemispheres. Therefore, one would expect that, to be anatomically sound, the reconstructed trajectories should exhibit some degree of symmetry. For our purpose, we evaluated the degree of symmetry of the reconstructed trajectories by computing the degree of correlation of the connectivity matrices related to the fibers between the left and right hemispheres. Specifically, this was done by parcellating the brain into 116 regions according to the Automated Anatomical Labelling (AAL) atlas [8], computing the connectivity matrix for each hemisphere based only on the (116/2 = 58) ROIs in that particular hemisphere and then computing the normalized scalar product of connectivity matrices of both hemispheres. Each element of the (58 × 58) connectivity matrix records the number of fibers connecting a pair of ROIs. The results, shown in Fig. 2(b), indicates the multi-orientation scheme yields higher inter-hemispheric accuracy compared with the single-orientation scheme, again validating that modelling complex orientation information can be conducive to more accurate reconstruction of fiber trajectories.

Major fiber bundles known to exist in all subjects can be used to test fiber tracking consistency across subjects. Since the seeds used in our evaluation were placed on a major white major structure, we expect the reconstructed trajectories to be relatively consistent across subjects. We tested this by using a similar methodology described in the previous paragraph. But instead of generating the connectivity matrix for each hemisphere separately, we generated a whole brain connectivitiy matrix by considering both hemispheres at the same time. We then computed the mean connectivity matrix over all the 10 subjects. The connectivity matrix of each subject was then compared with this mean matrix (via normalized scalar product) as an indicator of consistency. The higher the similarity of all individual connectivity matrices with the mean matrix, the greater is the consistency. Fig. 2(c) indicates that great consistency can be achieved using the multi-orientation scheme, again validating the effectivenes of the proposed method.

4 Conclusion

We have presented a tractography algorihtm that caters especially for low SNR diffusion-weighted images by leveraging prior information from the respective longitudinal scans. Experimental results performed using neonatal scans indicate that the proposed method yields fiber trajectories that are more consistent with our anatomical understanding. The ability of taking into account multi-orientation information gives further improvement over previous methods by allowing more accurate modeling of complex white matter architecture involving fiber crossings. Precise performance evaluation of tractography algorithms remain difficult since ground truth data are still lacking. Future work entails more extensive assessment of the algorithm based on histological data obtained from excised brains of canine subjects, which will be available in the future as part of the ongoing projects in our group.