Role of the closing base pair for d(GCA) hairpin stability: free energy analysis and folding simulations

Abstract

Hairpin loops belong to the most important structural motifs in folded nucleic acids. The d(GNA) sequence in DNA can form very stable trinucleotide hairpin loops depending, however, strongly on the closing base pair. Replica-exchange molecular dynamics (REMD) were employed to study hairpin folding of two DNA sequences, d(gcGCAgc) and d(cgGCAcg), with the same central loop motif but different closing base pairs starting from single-stranded structures. In both cases, conformations of the most populated conformational cluster at the lowest temperature showed close agreement with available experimental structures. For the loop sequence with the less stable G:C closing base pair, an alternative loop topology accumulated as second most populated conformational state indicating a possible loop structural heterogeneity. Comparative-free energy simulations on induced loop unfolding indicated higher stability of the loop with a C:G closing base pair by ~3 kcal mol⁻¹ (compared to a G:C closing base pair) in very good agreement with experiment. The comparative energetic analysis of sampled unfolded, intermediate and folded conformational states identified electrostatic and packing interactions as the main contributions to the closing base pair dependence of the d(GCA) loop stability.

INTRODUCTION

Hairpin loop structures in nucleic acids are common structural motifs that can be of functional importance as ligand recognition elements or folding initiation sites. A hairpin loop consists of a base paired stem structure and a loop sequence with unpaired or non-Watson–Crick-paired nucleotides. Several trinucleotide sequences at the center of palindromic sequences in DNA can form compact and stable hairpin loops (1–6). Formation of stable DNA hairpin structures may play a role for the expansion of such repeats associated with several genetic diseases (7–10). DNA or RNA hairpins having loops with certain sequences are unusually stable. The GNA trinucleotide motif (G, guanine; A, adenine; N, any nucleotide) in DNA has been found to form particularly stable structures (1,2,5,6,11) even with only two G–C base pairs forming the hairpin stem. A melting transition for disruption of the hairpin structure of >65°C has been reported (1). Structural studies using NMR spectroscopy have revealed a characteristic compact folding topology for the GNA-loop (1,3,6,8) with a B-DNA stem, a sheared G:A loop closing base pair and the central loop base stacking on top of the G:A base pair pointing toward the major groove. Several studies on base modifications and sequence context allowed the analysis on the contribution of individual hydrogen bonds and other non-bonded contacts to the folding stability (11–14).

Interestingly, it was found that for certain DNA and RNA hairpin loops a C:G closing base pair provides significantly enhanced loop stability. For example, changing the closing base pair from C:G to G:C hairpins destabilized the structure by ~2 kcal mol⁻¹ and caused a significant reduction of the melting temperature (11–13). The molecular origin of the unusual loop stability in the context of a C:G closing base pair is still not completely understood. Comparative studies employing the nonlinear finite-difference Poisson–Boltzmann approach combined with experiments at different salt concentrations indicated that electrostatic interactions may play a key role for the stability difference (15,16). However, calculations have only been performed on single-folded hairpin structures and also not for the unfolded state.

DNA trinucleotide hairpin loops have already been investigated in multistart energy minimization (17) employing a generalized Born (GB)-type implicit solvent model to characterize possible stable conformational sub-states. Recently, it has become possible to simulate the folding of the d(gcGCAgc) hairpin structure starting from a single-stranded start conformation using replica-exchange molecular dynamics (REMD) simulations (18). During REMD simulations, several replicas of a system are simulated at different temperatures in parallel allowing for exchanges between replicas at frequent intervals (19–21). In case of the d(gcGCAgc) sequence folded structures, as close as 1.5 Å to the experimental structure were obtained as dominant conformational state in the REMD simulations. Using standard MD simulations at 300 K up to the microsecond regime, it has even become possible to observe folding transitions during continuous MD (cMD) simulations (22). These studies gave important insights into the possible folding pathways, various intermediate states and the role of water molecules during hairpin folding.

In the current study, comparative REMD simulations in explicit solvent of the d(gcGCAgc) and the d(cgGCAcg) motifs in DNA were employed to compare the folding process starting from single-stranded conformations. In both cases, the REMD simulations sampled structures close to the folded state as dominant conformations in the low temperature replicas. However, the distribution of folded conformations and the population of alternative structures differed for both sequences. In addition, Umbrella Sampling (US)–MD simulation were used to compute the free energy profile of hairpin unfolding along a selected reaction coordinate in explicit solvent. It was possible to calculate a potential-of-mean force (PMF) for the unfolding of both hairpin structures. To further elucidate the various stabilizing or destabilizing energetic contributions, continuum solvent calculations were performed on the folded and the unfolded ensembles. In agreement with the experiment, the calculations predict the d(gcGCAgc) motif to form a more stable hairpin compared to the d(cgGCAcg) sequence. The results give insight into the energetic and structural origin of the strong influence of the closing base pair on hairpin stability.

MATERIALS AND METHODS

The extended single-stranded DNA structure of both the sequence d(gcGCAgc) and d(cgGCAcg) were generated using the Nucgen program of the Amber9 package (23) with a B-DNA type geometry followed by energy minimization. Both start structures were neutralized with 6 K+ counterions by using the xleap module of Amber9. The structures were solvated in an octahedral box with approximately 2500 TIP3P (24) water molecules leaving at least 10 Å between the solute atoms and the borders of the box. The fully solvated and neutralized systems were subjected to energy minimization with the sander module of the Amber9 package and using the parm99 force field (25). The parm99 force field was used to allow direct comparison of the present simulations with prior REMD simulations on the same hairpin system (18). Following minimization, both systems were gradually heated from 50 to 300 K with positional restraints (force constant: 50 kcal mol⁻¹Å⁻²) on DNA over a period of 0.25 ns allowing water molecules and ions to move freely. A 9 Å cutoff for the short-range non-bonded interactions was used in combination with the particle mesh Ewald option (26) using a grid spacing of ~0.9 Å to account for long-range electrostatic interactions. The Settle algorithm (27) was used to constrain bond vibrations involving hydrogen atoms. A time step of 1 fs was used during REMD simulations (2 fs for standard MD). During additional 0.25 ns, the positional restraints were gradually reduced to allow finally unrestrained MD simulation of all atoms over a subsequent equilibration time of 2 ns. Equilibrated extended structures were used as start structures for both cMD and REMD simulations.

The REMD simulations were carried out under constant volume using 24 replicas. An exponentially increasing temperature series along the replicas was used, which gives approximately uniform acceptance ratios for exchanges between neighboring replicas with the following simulation temperatures (in Kelvin): 295.0, 297.0, 299.5, 302.0, 304.5, 307.0, 310.0, 313.0, 316.0, 319.6, 323.8, 328.6, 334.0, 340.0, 346.6, 353.8, 361.6, 370.0, 379.0, 388.6, 398.8, 410.6, 422.0 and 434.0. These simulation temperatures resulted in exchange probabilities between neighboring replicas of 25–45% (attempted exchanges every 750 steps, exchange statistics are given in Supplementary Data and Supplementary Table 1s). REMD simulations for both hairpins were continued for 36 ns. For comparison, cMD simulations (100 ns) starting from the same hairpin start structures were run at 300 K for both DNA structures. It is known that the use of the parm99 force field can result in accumulation of coupled transitions of the nucleic acid backbone dihedrals α and γ (termed α/γ flip) in simulations of B-DNA (28). Transitions to the alternative α/γ state were observed during REMD simulations, but no accumulation for dinucleotide steps in the hairpin stem region was found (Supplementary Data and Supplementary Figure 1s). Presumably, the exchanges with higher temperature replicas allow for efficient transitions between different α/γ states. The loop region actually requires a coupled α/γ transition to form the hairpin (6) and an accumulation to up to 25% in the final stage of the REMD was observed (Supplementary Data and Supplementary Figure 1s).

An experimental high-resolution structure of the GCA trinucleotide loop is only available in the context of two flanking T:A base pairs (pdb1ZHU) (3). The reference structures [hairpin structures with the sequences d(gcGCAgc) and d(cgGCAcg), respectively] used for comparison with the current simulation results were constructed by iso-sterical replacement of the T:A base pairs (in the first structure of the 1ZHU entry) by G:C/C:G and C:G/G:C stem base pairs, respectively, using the program Jumna (29). These structures were energy minimized (1000 steps) to remove any residual sterical clashes, which resulted in only very small changes from the experimental loop structure [Root mean square deviation (RMSD) < 0.4 Å)].

US simulations were carried out with a distance restraint between the two phosphorus atoms at both hairpin ends to induce hairpin unfolding (opening). The reaction coordinate corresponded to the distance not involving any projection. For both the hairpin sequences, the folded structures obtained from the REMD simulations (cluster centroid of the most highly populated cluster) were used as start structures. A quadratic penalty function with 2 kcal mol⁻¹ Å⁻² was applied for deviations of distances with respect to the reference distance. The reference distance was increased in steps of 0.5 Å until the hairpin structure adopted an extended single-stranded structure. At each sampling distance window MD simulations (300 K) were carried out for 20 ns and the last 15 ns simulation data were considered for further analysis.

The potential of mean force along the reaction coordinate was calculated using the weighted histogram analysis method (WHAM) (30). Cluster analysis was based on the pair-wise Cartesian RMSD (only heavy atoms) between conformations with an RMSD cutoff of 2 Å and using the kclust program in the MMTSB-tools (31). The Visual molecular dynamics (VMD) program (32) and Pymol (www.pymol.org) were used for visualization of trajectories and for preparation of figures. Molecular Mechanics Poisson Boltzmann Surface Area (MM–PBSA) calculations were used for the energetic analysis of sampled conformations. The molecular mechanics energy term used in MM–PBSA calculations represents the internal bonded energy (energy of bond lengths, bond angles and dihedrals) as well as the non-bonded van der Waals and Coulomb energies. It provides detailed information about the various bonded and non-bonded energy terms that contribute to the stability of the DNA hairpin sequences. Three sets of MM-PBSA calculations were carried out for both hairpin structures, representing folded conformations, intermediate conformations (from US windows representing partially unfolded structures) and conformations representing the fully unfolded and extended form. Each MM–PBSA analysis was performed on 3750 snapshots.

RESULTS AND DISCUSSION

Molecular dynamics simulations on single-stranded and folded structures

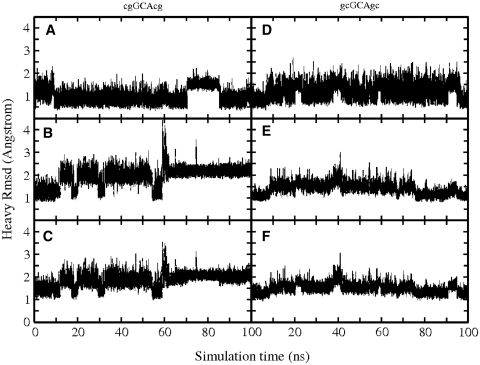
The dynamics of the single stranded and the folded conformation of both DNA sequences were first investigated using cMD simulations (100 ns) at 300 K. The folded forms of both sequences [d(cgGCAcg) and d(gcGCAgc)] stayed overall close to hairpin start structures with an average RMSD (all heavy atoms, excluding all hydrogens) <2.0 Å. Transient conformational transitions can be attributed to fraying of the terminal base pair and fluctuations of the central loop base (Figure 1). The deviation from the folded structure was slightly larger in case of the d(cgGCAcg) structure (compare Figure 1C and F). Continuous MD simulations starting from single-stranded structures showed considerable fluctuations including transitions to collapsed states; however, no transitions to conformations close to the experimentally observed structures were observed (Supplementary Data and Supplementary Figure 2s).

Figure 1.

Root-mean-square deviation (RMSD) with respect to folded hairpin structure, during cMD simulations (100 ns, starting from folded hairpin structures) of the cgGCAcg and gcGCAgc sequences, respectively. Separate plots are given for triloop (GCA) (A and D), stem (B and E) and full structures (C and F).

REMD simulations

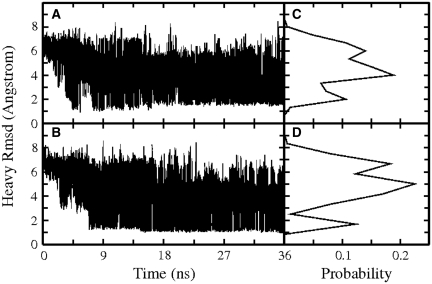
In addition to cMD simulations, REMD simulations of 36 ns were carried out starting from the same single-stranded conformations. The initial RMSD (heavy atoms) of the single-stranded DNA starting conformations was ~7 Å with respect to a folded hairpin reference structure. Frequent exchanges between replicas were observed in both simulations (Supplementary Data and Supplementary Table 1s) as can be judged from the RMSD versus time plots for the lowest temperature replica run (approximately 20000 exchanges between neighboring temperatures within total simulation time, Figure 2).

Figure 2.

RMSD (heavy atoms) of d(cgGCAcg) conformations (A) and d(gcGCAgc) conformations (B) sampled at the lowest temperature run of each REMD with respect to the corresponding folded hairpin reference structure (versus simulation time). The panels (C, D) on the right of each RMSD plot (A, B) correspond to the RMSD probability distributions during the whole 36 ns simulations (lowest temperature replica).

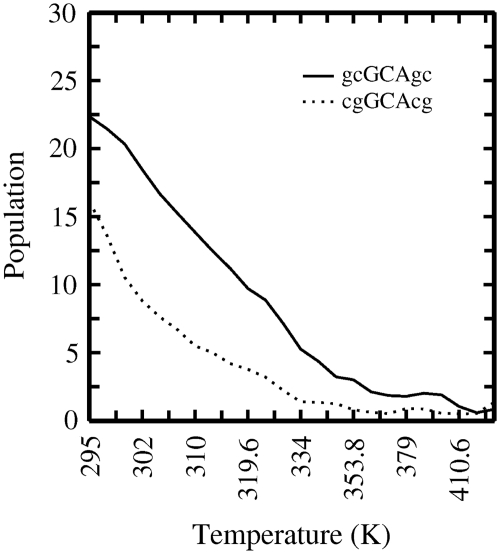
After ~5–6 ns of the REMD simulations conformations close to the folded hairpin structure started to appear in the lowest temperature replica. At around ~9 ns REMD hairpin conformations with an RMSD of ~1.5 Å from the folded hairpin reference structure were sampled in the lowest temperature replica and formed the dominant conformational cluster at ~10–15 ns. The RMSD probability distribution (Figure 2C and D) from REMD simulation indicates that conformations with RMSD <2 Å from the reference structures accounted for ~15–22% of sampled conformations (Figure 3). In cMD simulations on the d(gcGAAgc) sequence, Portella and Orozco (22) indicated the occurrence of 5′-guanine syn conformations that interfered with hairpin formation. Although transitions to guanine syn conformations were observed at the 5′-end of d(gcGAAgc) and the 3′-end of d(cgGCAcg), to similar extends the population (~5% in the lowest temperature replica) was too low to conclude on any influence on the hairpin folding behavior. It might be possible that the frequent exchanges between states during REMD simulations can prevent the accumulation of trapped states that interfere with hairpin folding.

Figure 3.

Population (in percent) of folded states as a function of simulation temperature [continuous curve: d(gcGCAgc); dotted curve: d(cgGCAcg)]. Sampled conformations within 2 Å RMSD from the native structure counted as folded structure.

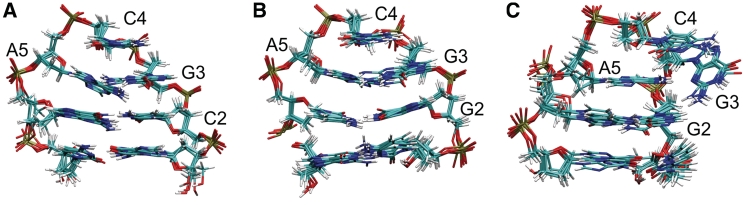
In the case of d(cgGCAcg), the overall folded structure showed a slightly higher RMSD compared to the same hairpin motif, but with the CG closing loop base pair. The folded structures of both sequences included the same characteristic arrangement of loop and stem bases and a similar H-bonding pattern as the experimental structure of the GCA triloop motif (Figure 4). In the case of the d(cgGCAcg) sequence, the RMSD probability distribution (Figure 2C and D) indicates a second peak deviating by ~2.5 Å from the folded reference structure. It corresponds to an alternatively folded conformational cluster with the same stem structure, but differences in the conformational arrangement of the central triloop compared to the native form. The G:A sheared base pair is replaced by the A5 stacked on the C:G closing base pair and hydrogen bonded to G3 via a single H1N6–N3 bond. A second hydrogen bond between G3(H2N4) and G2(N7) is formed. The G3 adopts a partially looped-out form in this structure (Figure 4). For the d(cgGCAcg) sequence, the conformational cluster representing this alternatively folded form is about half to two-third as populated as the conformation representing the native structure and hydrogen bonding pattern [<0.1% populated in case of the d(gcGCAgc) sequence]. It is interesting to note that a triloop topology very similar to this alternative triloop structure has been found in the experimental structure of a GUA triloop in RNA (33, Supplementary Data and Supplementary Figure S3). It should be emphasized that additional peaks in the RMSD distributions of the REMD simulations around 4–5 Å (Figure 2C and D) do not correspond to single conformational clusters, but represent a large variety of compact and extended conformational states (even a completely extended DNA structure deviates from the folded hairpin by ~6 Å).

Figure 4.

(A) Superposition of four representative conformations from the most populated cluster obtained during the final stage of the REMD folding simulations on the d(gcGCAgc) structure. The RMSD of the sampled structure was within 2 Å of the experimental structure. (B) Same for the d(cgGCAcg) sequence. (C) Second most populated conformational cluster of the d(cgGCAcg) sequence with an RMSD of ~2.5 Å from the native loop structure and an altered triloop topology missing the G:A sheared base pair. All members of this cluster contain a partially looped out G3 that forms one hydrogen bond with A5 and a second hydrogen bonding contact with G2.

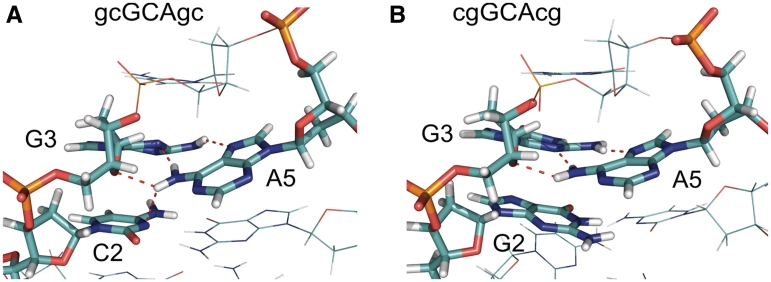
However, even the native-like folded structures obtained as dominant conformational clusters (with lowest free energy) for both sequences indicate interesting structural differences that can help to explain the observed differences in hairpin stability. For the d(gcGCAgc) sequence, a superposition of REMD-sampled native-like structures indicates that the sheared G:A base pair is slightly twisted allowing the N6H2 group of A5 to form simultaneously two hydrogen bonding contacts (the N6H1 with the N3 of G3 and the N6H2 with the exposed O2 of C2), in addition to the H-bond between G3(N4H1) and A5(N3) (Figures 4 and 5). Note, that such favorable pattern was also indicated by Blose et al. (15) and found in the high-resolution NMR structure of the related d(gcGAAgc) hairpin loop (6). This pattern is not possible for the d(cgGCAcg) sequence (because there is no appropriate acceptor in G2), and consequently the G:A pair adopts a more planar conformation compared to the d(gcGCAgc) case (illustrated in Figures 4 and 5).

Figure 5.

(A) Hydrogen bonding network formed between C2 (O2′-atom) and A5 (H1N6-atom) as well as two hydrogen bonds formed between G3 and A5 in the sheared base pair geometry in case of the d(gcGCAgc) hairpin. (B) For the d(cgGCAcg) hairpin only the sheared base pair hydrogen bonds are possible (dashed lines). The structures correspond to representative conformations of the most populated conformational cluster (in the lowest temperature replica) of the REMD simulations starting from unfolded single-stranded DNA.

Moody and Bevilacqua (11) studied the influence of inserting spacers at various positions on the stability of the cGCAg as well as the gGCAc motifs. Interestingly, for the cGCAg only the insertion before the G of the loop resulted in a significant destabilization of the loop (by ~1.6 kcal mol⁻¹). This effect was not observed for the gGCAc motif (11). In case of the present structure for the d(gcGCAgc) sequence, the spacer insertion between C2 and G3 would result in the disruption of the proposed hydrogen bonding contact between A5 and C2, which can explain the experimentally observed free energy change that is equivalent to the loss of one hydrogen bond contact. In contrast, for the d(cgGCAcg) sequence such contact is not possible in agreement with the experimental observation for this case.

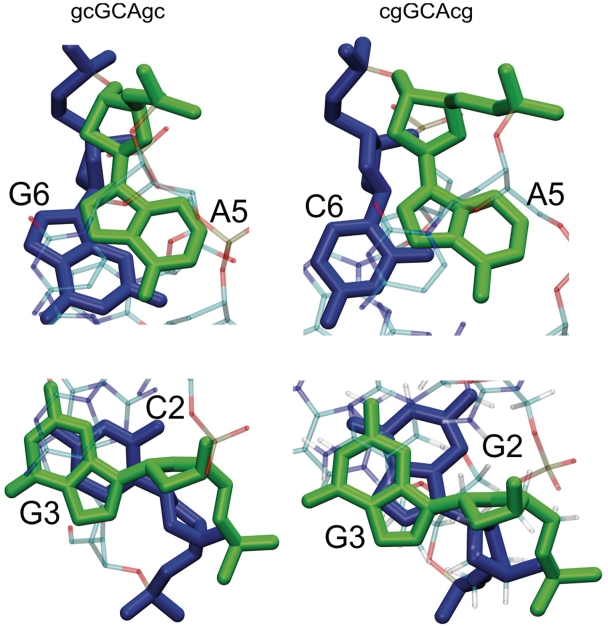
In addition to the hydrogen bonding pattern, differences in stacking of the G:A pair on the closing C:G or G:C pair may contribute to the stability difference. Both folded conformations indicate nearest neighbor stacking of the G3 base on the C2 or G2 base, respectively (Figure 6), and also very similar stacking of the central loop base (C4) on the sheared G:A loop pair. However, there are significantly more stacking contacts (in terms of close atom–atom pairs) between the A5 and G6 in case of the d(gcGCAgc) sequence compared to stacking contacts between A5 and C6 for the less stable d(cgGCAcg) hairpin motif (Figure 6, upper panel). Furthermore, in case of the d(gcGCAgc) hairpin cross-stacking of G3 and G6 as well as between C2 and A5 involves electrostatically favorable contacts between the partially positively charged amino groups (G3–N4 and A5–N6) and partially negative O6′ and O2′ of G6 and C2, respectively, not present in the folded d(cgGCAcg) hairpin. Blose et al. (16) arrived at qualitatively similar conclusions in a structural and electrostatic analysis of experimental structures of RNA tetraloops with different closing base pairs.

Figure 6.

Stacking pattern of nucleotides flanking the central triloop motif in the most populated near-native conformational cluster. (Upper panels) Stick representation of nucleotides A5 (green) and G6 (blue) in a representative structure of the folded d(gcGCAgc) hairpin conformational cluster (view along the helical axis of the stem). In case of the cgGCAcg hairpin, the stacking involves C6 (blue) and A5 (green) (lower panels). Stick representation of nucleotides G3 (green) and C2 (blue) in a representative structure of the d(gcGCAgc) hairpin conformational cluster (view along the helical axis of the stem). For the d(cgGCAcg) hairpin the stacking involves G2 (instead of C2).

When considering only the hairpin structure with an RMSD <2 Å as folded state [excluding the alternatively folded state in case of the d(gcGCAgc) sequence], a folded population of ~22% versus 15% was found in case of d(gcGCAgc) versus d(cgGCAcg) motif, respectively (Figure 3). At least for the d(gcGCAgc) case (with a T_m = 67°C), a higher population of folded states at the lowest simulation temperature is expected. It indicates that probably significantly longer simulation times (even with the use of REMD) are required to achieve convergence of the sampled population of folded states. Nevertheless, to get a qualitative indication on the difference in melting behavior one can compare the temperature at which the population of the folded structure has dropped to half of the population at the lowest temperature. This corresponds to ~318 K for the d(gcGCAgc) versus 308 K for the d(cgGCAcg) motif (Figure 3), respectively. Both the absolute melting temperature for the hairpin structures as well as the difference due to a different closing base pair are smaller compared to the corresponding experimental values. The result indicates that longer simulation times are necessary for a full convergence of the sampled populations. It is also possible that force field artifacts contribute to the deviation from experiment. However, it is also known that the stability of hairpin loops depends significantly on the salt concentration (16). Experimental melting temperatures are typically measured at a salt concentration of 1 M (NaCl) and due to increased phosphate–phosphate repulsion the stability of the folded hairpin decreases significantly at lower salt concentration (16).

US simulations of hairpin unfolding

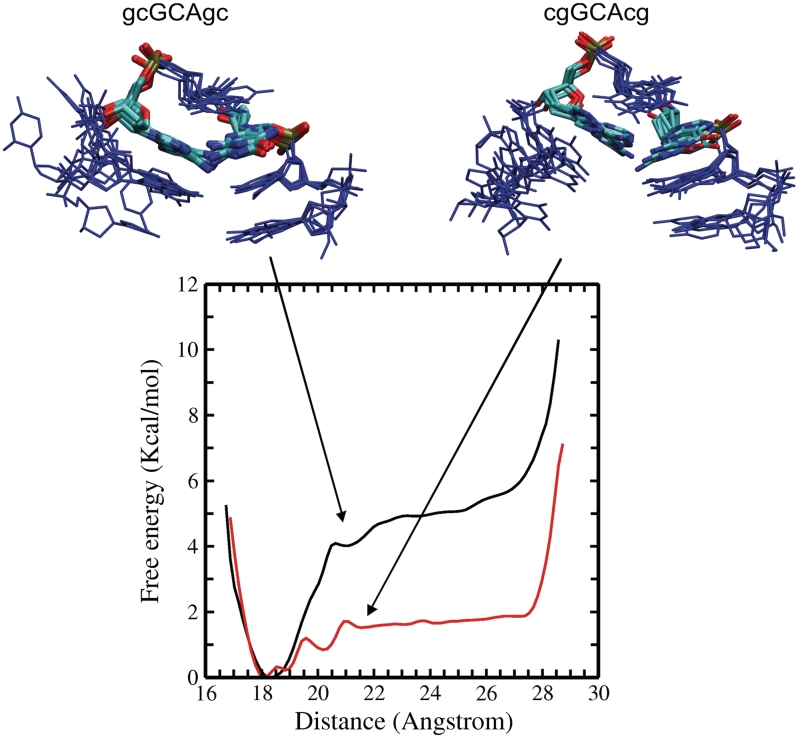
In order to further compare the stability of the hairpin structure with respect to a single-stranded DNA conformation for both DNA sequences, US–MD simulations starting from the folded hairpin were performed. A quadratic restraining potential between the phosphorus atoms of the two ends of the DNA hairpin structure was applied. Starting from a reference distance of 18 Å, the reference distance in the restraining potential was increased gradually in 0.5 Å steps up until a distance of 28 Å was reached. At each distance window 20 ns MD simulations (5 ns equilibration followed by 15 ns data gathering) were performed. The WHAM of the sampled states indicates an overall free energy difference of ~5 kcal mol⁻¹ in case of the d(gcGCAgc) sequences and a significantly smaller value of ~1.9 kcal mol⁻¹ in case of the d(cgGCAcg) sequence (Figure 7). In the US simulations, the unfolded state of the hairpins is represented by conformers with distances of the terminal phosphorous atoms in the range of ~21–28 Å. This corresponds to an idealized model and one should note that it is possible that the unfolded state of the hairpins may also contain states with smaller distance of the terminal phosphate groups.

Figure 7.

Calculated free energy change (PMF) obtained from US simulations along the distance of the terminal phosphate groups starting from folded hairpin conformations. The upper panels show a superposition of sampled intermediate conformations [left panel: d(gcGCAgc) and right panel: d(cgGCAcg)] obtained from the US window at 20.5 Å phosphate–phosphate distance. Nucleotides are shown in blue except for G3 and A5 (atom color code). In case of the gcGCAgc sequence the sheared G3:A5 arrangement is frequently preserved, whereas in case of the cgGCAcg, it is largely replaced by a G3:A5 contact similar to the structure observed in the second most populated cluster from the REMD of the d(cgGCAcg) hairpin.

For the cGCAg loop motif, an experimentally determined free energy contribution of −3.69 kcal mol⁻¹ has been reported and −0.63 kcal mol⁻¹ for the gGCAc case (11). The empirical free energy increment of adding another C:G pair to the stem amounts to approximately −2.0 kcal mol⁻¹, which results in a total free energy of −5.7 kcal mol⁻¹ of forming the d(gcGCAgc) hairpin versus −2.6 kcal mol⁻¹ of forming the d(cgGCAcg) hairpin structure. The empirical free energies are slightly larger than the free energies obtained from the US–MD simulations. However, as discussed above, the lower salt concentration during the simulation decreases the hairpin stability relative to experimental situation at 1 M salt. The calculated difference in hairpin forming free energy of ~3.1 kcal mol⁻¹ is, however, in excellent agreement with experiment [3.06 kcal mol⁻¹ (11)].

The transition along the selected reaction coordinate occurs quite abruptly and cooperatively indicating that once the stem base pairs start to break the rest of the structure is also significantly destabilized. For the folded and the completely unfolded forms of the two structures, the sampled conformational states are similar. However, comparison of dominant conformational states at the sampling intervals associated with the regime of largest changes in free energy indicates some differences in sampled states. First, in case of the d(gcGCAgc) sequence, the triloop conformation and the closing base pair remain largely intact and the added end-to-end distance restraint is largely fulfilled by the unstacking of the terminal base pair (Figure 7). In case of the d(cgGCAcg) sequence, loss of the terminal base pair results in further opening of the rest of the hairpin structure (Figure 7). The opening of hairpin and stem base pairs occurs almost simultaneously. The triloop structural motif starts to deviate significantly from the folded hairpin form. Interestingly, it frequently adopts a pattern of bases in the triloop similar to the arrangement found for the second dominant conformational state of this hairpin in the REMD simulations (see above and Figure 4). The agreement of sampled loop states in the REMD (starting from unfolded state) and US–MD simulations supports the relevance of this alternative base arrangement for the folding/unfolding of the d(cgGCAcg) structure.

Energetic analysis of sampled states

Due to the large potential energy fluctuations in explicit solvent simulations, the analysis of sampled states was performed after replacing the explicit solvent and ions by a dielectric continuum and a salt distribution function (MM–PBSA). The calculations were carried out on trajectories from the US intervals representing the folded hairpin structure, the intermediate partially folded conformers (corresponding to a distance window with the reference distance of 20.5 Å) and the completely unfolded structures (distances: 26.5 Å), respectively. Note, that the interval representing the folded state consists of a relatively narrow distribution of conformations, whereas the unfolded state consists of a variety of conformers. For each case, 3750 snapshots were analyzed and used to obtain ensemble averages. Interestingly, for the unfolded case the total MM–PBSA energies are very similar for the two sequences (Table 1).

Table 1.

Energetic analysis of sampled states of both DNA hairpins during US simulation

Energy components	cgGCAcg			gcGCAgc
	Folded	Intermediate	Unfolded	Folded	Intermediate	Unfolded
Ebonded	319 (±13)	317 (±22)	315 (±25)	320 (±13)	316 (±25)	315 (±19)
EVDW	−45 (±5)	−47 (±6)	−31 (±6)	−48 (±5)	−46 (±7)	−31 (±6)
ECoulomb	−842 (±11)	−795 (±11)	−778 (±12)	−853 (±12)	−832 (±11)	−782 (±12)
Esolvation	−967 (±10)	−1000 (+/20)	−1016 (±23)	−958 (±11)	−967 (±19)	−1012 (±17)
Etot	−1524 (±10)	−1513 (±12)	−1496 (±12)	−1528 (±10)	−1516 (±14)	−1496 (±12)

MM–PBSA energies (in kcal mol⁻¹) are averages over the last 15 ns of US (3750 frames, standard deviations are given in parenthesis). Same symbols for energetic contributions as in legend of Figure 8.

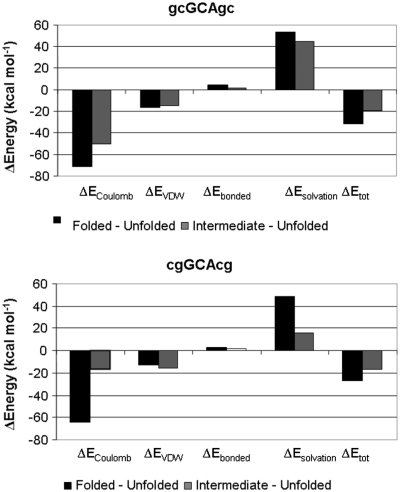
This is, however, expected since both sequences contain the same number and type of nucleotides and for this end-to-end distance regime the sampled states contain fluctuating and largely unstacked single-stranded conformations. Hence, each unfolded strand can be considered as the same set of independent nucleotides with little interaction. Comparing folded and unfolded ensembles indicates an energetic preference of the folded state by −27.6 kcal mol⁻¹ for the d(cgGCAcg) case and −31.9 kcal mol⁻¹ for the d(gcGCAgc) sequence, respectively (Figure 8). The difference (−4.3 kcal mol⁻¹) is close to the experimental stability difference of the two hairpins (−3.06 kcal mol⁻¹). It should be emphasized that these numbers do not include conformational entropy contributions; however, solvation effects and therefore also changes in solvent entropy are at least in principle accounted for. The MM–PBSA energies do not correspond to free energies, but also not to pure enthalpic contributions. Nevertheless, it is interesting to note that experimental enthalpy changes of hairpin formation [−33 kcal mol⁻¹ for the cGCAg motif, (11)] are at least of very similar magnitude as the calculated changes in MM–PBSA energies.

Figure 8.

Differences in calculated MM–PBSA energies between folded and completely unfolded hairpin structure (black), and between intermediate (sampled at a terminal phosphate distance of 20.5 Å) and completely unfolded hairpin structures (gray). Energetic contributions correspond to differences in E_coulomb (pair-wise electrostatic Coulomb energy), E_VDW (van der Waals packing energy), E_bonded (energy of bonds, bond angles and dihedral angles), E_solvation (polar and non-polar solvation energy) and E_tot (total energy difference).

The calculations emphasize the importance of electrostatic interactions and to a lesser degree van der Waals packing forces as the origin of the closing base pair effect on hairpin stability. This agrees with the above structural analysis of the sampled folded structures. The important role of electrostatic interactions for the closing base pair stabilization has already been emphasized by Bevilacqua and coworkers (15,16) based on the analysis of single structures of the folded hairpin state. Comparing the MM–PBSA components of folded, intermediate and unfolded states indicates that especially electrostatically the intermediate states of the d(gcGCAcg) case are more similar to the folded form, whereas the opposite was observed for the less stable d(cgGCAcg) sequence. Here, the electrostatic components are more similar to the unfolded states. This agrees with the type of structures sampled in the intermediate regime as described above and also indicates the tendency of the less stable hairpin sequence to rapidly relief the ‘electrostatic stress’ due to some unfavorable contacts in the fold hairpin structure. Taken together the MM–PBSA analysis indicates a stronger preference of the folded hairpin structure of the d(gcGCAgc) sequence versus d(cgGCAcg) sequence of ~2.3 kcal mol⁻¹. This is in good agreement with the results from PMF calculations and in qualitative agreement with experiment. The stronger preference is due to more favorable electrostatic and van der Waals (vdW) packing interactions of the folded versus unfolded states. It could be helpful for a more accurate characterization in future studies to investigate the energetic contributions to the hairpin stability using quantum mechanical approaches.

CONCLUSIONS

Closing base pairs make an important contribution to the stability of hairpin structures in DNA and RNA. Using REMD simulations it was possible to obtain folded hairpin structures of two DNA triloop hairpins that differed in the closing base pair. For both cases, a folded structure in close agreement with available experimental structures was obtained as most populated conformational cluster. However, for the less stable hairpin sequence, a substantial amount of an alternatively folded hairpin conformation was sampled with a different arrangement of the central triloop. This may indicate a structural heterogeneity of the loop in case of a G:C closing base pair. The possibility that this alternative fold is an artifact of the force field cannot be completely excluded. However, intriguingly, a similar arrangement of loop nucleotides has been found in an experimental RNA triloop structure with a similar sequence [central cGUAg (33)]. In addition, even the folded forms of the two sequences with a correctly formed sheared G:A base pair differ in fine structure and offer structural explanations for the differences in hairpin stability: both US simulations as well as the MM–PBSA trajectory analysis consistently predict stability differences of the two triloop structures that are in very good agreement with experiment. The calculations indicate that differences in electrostatic and vdW packing interactions of the folded form are responsible for the strong influence of the closing base pair on hairpin stability. This agrees with the more qualitative structural interpretation of additional hydrogen bonding contacts and better stacking interactions in the folded d(gcGCAgc) versus the corresponding d(cgGCAcg) structures obtained from the REMD simulations.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

Funding for open access charge: Deutsche Forschungsgemeinschaft (grant Za153/17) (to M.Z.).

Conflict of interest statement. None declared.