Effective Saturation: a More Informative Metric for Comparing Peak Separation in One- and Two-Dimensional Separations

Abstract

A theoretical comparison is made of the numbers of observed peaks in one-dimensional (1D) and two-dimensional (2D) separations having the same peak capacity, as calculated from the traditional metric of resolution. The shortcoming of the average minimum resolution of statistical overlap theory (SOT) for this comparison is described. A new metric called the “effective saturation” is introduced to ameliorate the shortcoming. Unlike the “saturation”, which is the usual metric of peak crowding in SOT, the effective saturation is independent of the average minimum resolution and can be determined using traditional values of resolution and peak capacity. Our most important finding is that under a wide range of practical conditions, 1D and 2D separations of the same mixture produce almost equal numbers of observed peaks when the traditional peak capacities of the separations are the same, provided that the effective saturation and not the usual saturation is used as the measure of crowding. This is the case when peak distributions are random and when edge effects are minor. The numerical results supporting this finding can be described by empirical functions of the effective saturation, including one for the traditional peak capacity needed to separate a given fraction of mixture constituents as observed peaks. The near equality of the number of observed peaks in 1D and 2D separations based on the effective saturation is confirmed by simulations. However, this equality is compromised in 2D separations when edge effects are large. The new finding does not contradict previous predictions by SOT of differences between 1D and 2D separations at equal saturation. Indeed, the simulations reaffirm their validity. Rather, the usual metric, i.e., the saturation, is just not as simple a metric for comparing 1D and 2D separations as is the new metric, i.e., the effective saturation. We strongly recommend use of the new metric for its great simplifying effect.

Introduction

In a recent paper by Stoll, Wang, and Carr, the practical resolving power of one-dimensional (1D) and two-dimensional (2D) separations was compared by determining the peak capacities and numbers of observed peaks in both the fully optimized 1DLC and practical comprehensive 2DLC of a corn-seed extract [1]. The peak capacities of both separation types were calculated at unit resolution, with the 2D peak capacity including corrections for the fraction of separation space occupied by peaks and the broadening of first-dimension peaks due to undersampling. The ratio of the 1D and 2D peak capacities, and the ratio of the numbers of observed peaks, were compared at different analysis times. Both ratios approached unity at 5 minutes, with optimized 1DLC being superior at shorter times and practical 2DLC being superior at longer times. At 5 minutes, however, the same peak capacity produced the same number of observed peaks in both separations.

This finding is an apparent contradiction of point-process statistical-overlap theory (SOT), which predicts that a mixture will produce fewer observed peaks in a 2D separation than in a 1D separation having the same peak capacity [2]. In part, the difference occurs because the peak coordinates in the 2D separation of Stoll et al. are weakly correlated. More importantly, the resolutions determining the peak capacity in the two cases are different. The resolution used by Stoll et al. is the traditional metric, whereas the resolution of SOT is the average minimum resolution [3,4], a value that is often misunderstood and is reviewed below. The two resolutions typically are not the same.

This experimental finding stimulated us to ask the question: should a complex mixture produce the same number of observed peaks in 1D and 2D separations with the same peak capacity, when that capacity is calculated using the traditional metric of resolution? The answer is relevant, since almost all experimentalists compare the two separation types using traditional metrics of resolution and peak capacity. It also indicates which separation type is superior, all other matters being equal. Interestingly, this problem has not been addressed by theory. The most general answer must depend on the specific way in which peaks are distributed in the separations (e.g., strongly correlated, weakly correlated, or random). This paper answers the question for separations containing random distributions of peaks by introducing a new metric of peak crowding, which we call the effective saturation. This metric assimilates the average minimum resolution and for the first time permits us to make SOT calculations of peak overlap using the traditional metrics for resolution and peak capacity. These calculations facilitate a more useful comparison of 1D and 2D separations by SOT, whose predictions are not changed but simply are expressed relative to the effective saturation. On doing so, some very interesting results are found.

Theory

Average minimum resolution

Some background on the average minimum resolution is useful. In SOT, the intervals between peaks and the heights of peaks are assumed to be governed by probability distributions, from which various attributes of the separation (e.g., number of mixture constituents, peak widths, etc.) can be calculated from a large ensemble of similar separations [2,3,5–11]. In particular, point-process SOT allows one to calculate the average number of observed peaks in the separation ensemble. Several reviews have been published [12–16]. In SOT, peaks must be separated by some minimum resolution if they are to belong to two different observed peaks [3]. In other words, this minimum resolution is required to observe a separation. The minimum resolution depends on the requirements of the separation [17], and in recent years it has been mostly identified with the production of maxima. Therefore, a “peak” is the concentration profile of a single mixture constituent, whereas an “observed peak” is a detected maximum in the separation and may contain one or more constituents. The minimum resolution differs for pairs of peaks having different sizes: it can be as small as 0.5 for peaks of equal height, and it can even be substantially greater than 1 for peaks of vastly different heights. All combinations of peak heights must be considered, with the average of the minimum resolutions determining the average number of observed peaks. This average is called the average minimum resolution and its numerical value is usually designated as $R_s^{\ast }$. In the first studies of SOT, $R_s^{\ast }$ was an empirical parameter [17–19]. With subsequent experimental [15,19–22] and theoretical [15,23] evidence that peaks in multi-constituent separations often have an exponential (or near exponential) distribution of heights, researchers studied the effect of this height distribution on $R_s^{\ast }$ by simulating multi-constituent separations [23–25] and calculating the resolution distribution using Monte Carlo simulation [26] and rigorous theory [27]. The rigorous theory is the most elegant work and showed that $R_s^{\ast }$ is 0.725 for Gaussian peaks having equal standard deviations and an exponential distribution of heights [27]. However, this value allows SOT to predict the correct number of observed peaks only when the degree of peak crowding is small [11,28]. The reason is simple: it is based on the overlap of only two peaks, whereas observed peaks in real separations subject to extensive peak overlaps often contain more than two constituents.

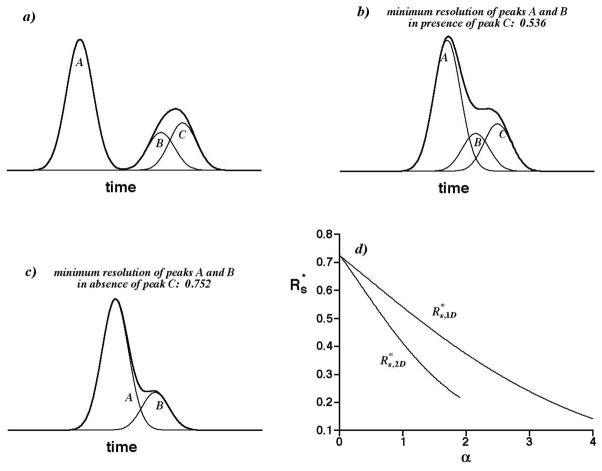
The importance of multi-constituent peak overlap to the minimum resolution is illustrated in Figure 1. Figure 1a shows two observed peaks (maxima) formed from three Gaussian peaks labeled A, B, and C. The peak A is a singlet, whereas peaks B and C overlap to form a doublet. In Figure 1b, the singlet A has been shifted toward the doublet, until two distinct maxima barely are observed. Further shifting causes the singlet to fuse with the doublet, forming a triplet with a single maximum. Therefore, the resolution of peaks A and B, 0.536, is its minimum value, with A and B belonging to different observed peaks. Interestingly, it is less than the minimum resolution of peaks A and B, 0.752, that barely produces two observed peaks in the absence of peak C (see Figure 1c). The reason is simple: even though the doublet is broadened more than the singlet, its maximum is shifted away from the singlet even more than it is broadened. Consequently, the peaks A and B can approach more closely at minimum resolution in the presence of peak C than in its absence. This trend extends to observed peaks that are triplets, quartets, etc., with the implication that the minimum resolution is not fixed but decreases with increasing peak crowding.

Figure 1.

a) Individual Gaussian peaks A, B, and C (——) and the detected signal from them (——). b) As in a), but with peak A shifted until two observed peaks (maxima) are barely observed. Axes are scaled as in a). c) As in b) but peak C is absent. d) Graph of the average minimum resolution $R_s^{\ast }$ vs. the saturation α for 1D separations ( $R_{s,1D}^{\ast }$) and 2D separations ( $R_{s,2D}^{\ast }$).

Clearly, it is easy to envision a case in which the height of peak C is so small that the minimum resolution of peaks A and B is nearly independent of C. In general, however, the decrease must be addressed. Equations based on SOT and predicting this decrease have been published for both 1D separations [28] and 2D separations [11]. Figure 1d shows the predicted dependence of $R_s^{\ast }$ on the “saturation” α, when peaks have an exponential distribution of heights and are distributed randomly throughout the separation. The saturation is a metric of peak crowding that increases with increasing peak overlap; it is defined precisely below. As it approaches zero, all observed peaks become singlets and the limiting $R_s^{\ast }$ discussed earlier, 0.725, is appropriate. As it increases, however, many observed peaks become doublets, triplets, etc., causing $R_s^{\ast }$ to systematically decrease and to become less than 0.5. The average minimum resolution for 2D separations, $R_{s,2D}^{\ast }$, is smaller than its counterpart for 1D separations, $R_{s,1D}^{\ast }$, at all positive saturations. The two functions differ, because the ways in which peaks can overlap, and likelihood of peak overlap, differ in the two separation types. These $R_s^{\ast }$ functions work very well with SOT, facilitating the prediction of accurate numbers of observed peaks when overlap is severe [11,28]. Indeed, the failure to address their variation results in poor predictions when overlap is severe [11,28].

However, the variations cause a number of ensuing complications. As shown below, the saturation depends on $R_{s,1D}^{\ast }$ in 1D separations and on ${(R_{s,2D}^{\ast })}^2$ in 2D separations, but these values themselves depend on the saturation (see Figure 1d) and consequently numerical methods are required to determine them. More important, the 1D and 2D peak capacities defined by SOT are inversely proportional to $R_{s,1D}^{\ast }$ and ${(R_{s,2D}^{\ast })}^2$ [3,4], which means they themselves are functions of saturation. This is a very undesirable property, which is totally at odds with the traditional concept of peak capacity as an invariant metric of the maximum number of peaks that can be contained in a separation space.

Perhaps most importantly, the variation of $R_{s,1D}^{\ast }$ and $R_{s,2D}^{\ast }$ with saturation greatly complicates the comparison of 1D and 2D separations by SOT. One interpretation of the saturation is the ratio of the number of mixture constituents (or peaks) to the peak capacity defined relative to $R_s^{\ast }$ [3,4]. Accordingly, for a given mixture the peak capacities of 1D and 2D separations are equal at the same saturation. However, since the size of a peak-capacity unit is proportional to $R_s^{\ast }$ [3,4] and since $R_{s,2D}^{\ast }<R_{s,1D}^{\ast }$ at all positive saturations, the unit is relatively smaller in 2D separations than in 1D ones. Consequently, at equal saturations the separations are not compared under identical conditions, and the significance of the comparison -- even if correct -- is ambiguous.

In contrast, the effective saturation eliminates this ambiguity. Relative to the effective saturation, 1D and 2D separations of randomly distributed peaks can easily be compared by SOT using equal traditional peak capacities having units of the same relative size.

Terminology and assumptions

The terminology of Schoenmakers et al. [29] for multi-dimensional separations is used when possible. It is assumed that the peaks in both 1D and 2D separations are randomly distributed and have an exponential distribution of heights. It also is assumed that the standard deviation ¹σ of Gaussian peaks in 1D separations is constant, and that the standard deviations ¹σ and ²σ of bi-Gaussian peaks in 2D separations are constant although they can differ between dimensions. The invariance of ¹σ and ²σ is consistent with results for well optimized gradient methods (e.g., solvent in LC and temperature in GC). Finally, it is assumed that 2D separations are rectangular, as they are in most beds and gels, and in comprehensive separations. The spatial lengths or temporal durations (i.e., the extents) of a 1D separation and the first dimension of a 2D separation are ¹D; the extent of the second dimension is ²D. The arbitrary resolution ¹R_s determines the traditional peak capacity ¹n_c of a 1D separation and the first dimension of a 2D separation; the arbitrary resolution ²R_s determines the traditional peak capacity ²n_c of the second dimension. These constant resolutions have no relation to the SOT functions $R_{s,1D}^{\ast }$ and $R_{s,2D}^{\ast }$. By “traditional peak capacity”, we mean the metric used by most researchers as defined below. In general, the subscripts “1D” and “2D” are used as needed with variables common to 1D and 2D separations but having different characteristics (e.g., $R_{s,1D}^{\ast }$ and $R_{s,2D}^{\ast }$). However, the subscripts are dropped on comparing the variables (e.g., the label $R_s^{\ast }$ for the ordinate of Figure 1d).

Effective saturation

In accordance with SOT, the saturation α_1D of a 1D separation is normally defined as [3]

$${\alpha }_{1D}\equiv 4\overline{m}{}^1\sigma R_{s,1D}^{\ast }/{}^{1}D$$ (1)

where m̄ is a statistical metric for the number of mixture constituents (or peaks). The value of $R_{s,1D}^{\ast }$ in Eq. 1 is not arbitrary: it must be chosen from the graph in Figure 1d, such that the result on the right-hand-side of Eq. 1 equals the corresponding value of α_1D in the graph [28]. For any m̄, ¹σ, and ¹D, only one coordinate satisfies this condition.

The definition of the traditional peak capacity of a 1D separation, or the first dimension of a 2D separation, is [30]

$${{}^{1}n}_c={}^{1}D/({}^{1}w{{}^{1}R}_s)$$ (2)

where ¹w = 4 ¹σ is the first-dimension peak width. Eqs. 1 and 2 can be combined to obtain a new metric, the effective saturation α_e,1D of a 1D separation

$${\alpha }_{e,1D}=\overline{m}{}^{1}w/{}^{1}D=\overline{m}/({{}^{1}R}_s{{}^{1}n}_c)={\alpha }_{1D}/R_{s,1D}^{\ast }$$ (3)

The great appeal of Eq. 3 is that it depends only on the number of mixture constituents m̄ and the separation attributes ¹w and ¹D. It is independent of resolution, as shown by the first term on the right-hand-side of Eq. 3. Therefore, the presence of ¹R_s in the second expression on the right-hand-side can easily give rise to confusion; it is only a scaling factor that expresses the effective saturation in terms of the traditional peak capacity ¹n_c, with ¹n_c and ¹R_s being inversely proportional. For example, the effective saturation is the same for a traditional peak capacity ¹n_c of 500 at ¹R_s = 1 and a traditional peak capacity of 1000 at ¹R_s = 0.5, because ¹D/¹w is 500 in both cases. The second and third expressions of Eq. 3, which researchers can evaluate easily from measured peak widths and the dimension extent, are related to SOT predictions using the final expression in Eq. 3. In brief, the predictions are evaluated at saturation α_1D as in previous studies, and the associated effective saturation α_e,1D then is calculated by dividing α_1D by the corresponding $R_{s,1D}^{\ast }$ value in Figure 1d. At first glance, this does not seem to excise the average minimum resolution, since the $R_{s,1D}^{\ast }$ value is needed. However, as is shown below, the calculation only needs to be made once, with the SOT predictions ultimately expressed in terms of the convenient metric, α_e,1D.

In accordance with SOT, the saturation α_2D of a 2D separation is defined as [4,11]

$${\alpha }_{2D}\equiv 4\pi \overline{m}{}^1\sigma {}^2\sigma {(R_{s,2D}^{\ast })}^2/({}^{1}D{}^{2}D)$$ (4)

As before, the value of $R_{s,2D}^{\ast }$ in Eq. 4 is not arbitrary; it must be chosen from the graph in Figure 1d, such that the result on the right-hand-side of Eq. 4 equals the corresponding value of α_2D in the graph [11]. Only one coordinate satisfies this condition.

The traditional peak capacity of the second dimension of a 2D separation is

$${{}^{2}n}_c={}^{2}D/({}^{2}w{{}^{2}R}_s)$$ (5)

where ²w = 4 ²σ is the second-dimension peak width. Eqs. 2, 4, and 5 can be combined with the expression for the traditional 2D peak capacity n_c,2D [31]

$$n_{c,2D}={{}^{1}n}_c{{}^{2}n}_c$$ (6)

to define the effective saturation α_e,2D of a 2D separation

$${\alpha }_{e,2D}=\overline{m}{}^{1}w{}^{2}w/({}^{1}D{}^{2}D)=\overline{m}/(n_{c,2D}{{}^{1}R}_s{{}^{2}R}_s)=4{\alpha }_{2D}/[\pi {(R_{s,2D}^{\ast })}^2]$$ (7)

As before, the appeal of Eq. 7 is that it depends only on m̄ and the separation attributes ¹w, ²w, ¹D, and ²D. It is independent of resolution; as before, the resolution factors ¹R_s and ²R_s in the third expression simply describe α_e,2D in terms of the traditional 2D peak capacity n_c,2D, with n_c,2D and the product ¹R_s ²R_s being inversely proportional. The value of α_e,2D appropriate to saturation α_2D is found by dividing α_2D by the square of the corresponding $R_{s,2D}^{\ast }$ value in Figure 1d and then multiplying by 4/π.

It is common to use peak capacities as metrics of separation efficiency. Eqs. 3 and 7 show that expressing the effective saturation relative to traditional peak capacities requires definition of the resolutions ¹R_s and ²R_s. As discussed above, different combinations of traditional peak capacity and resolution give the same effective saturation α_e, but one specific combination is particularly interesting. By comparing Eqs. 3 and 7 at equal α_e, one sees that 1D and 2D separations of the same mixture of m̄ constituents have the same traditional peak capacities (¹n_c = n_c,2D), when the ¹R_s value for the 1D separation equals the product, ¹R_s ²R_s, for the 2D separation. When ¹R_s = ²R_s = 1 as is often assumed, the traditional 1D and 2D peak capacities are equal for the same m̄ and α_e.

The effective saturation has properties that are desirable in SOT. To take advantage of them, one must associate the SOT predictions of the number of observed peaks p at saturation α with the effective saturation α_e.

SOT predictions of p relative to saturation α

The average number of observed peaks (maxima) p_1D in a 1D separation of m̄ randomly distributed peaks is [3,28]

$$p_{1D}=\overline{m}exp(-{\alpha }_{1D})$$ (8)

Similarly, the average number of observed peaks (maxima) p_2D in an unbounded 2D separation of m̄ randomly distributed peaks is [2,10,11]

$$p_{2D}=4\overline{m}{\alpha }_{2D}exp(-4{\alpha }_{2D})/[1-exp(-4{\alpha }_{2D})]$$ (9)

Obviously, any real 2D separation actually has boundaries. Here, the word “unbounded” means that the “edge effect” is negligible. The edge effect describes the fact that there is a lower probability for peak overlap near boundaries (i.e., the edges and corners) of a multi-dimensional separation space than in the center of the space. It exists because there are no peaks outside the boundaries available to overlap with peaks just inside and near the boundaries [10]. As a result, the probability of finding an observed peak and thus the average number of observed peaks in the edge region must be somewhat larger than in the central region and thus the total number of observed peaks will be larger than Eq. 9 predicts. The edge effect in 2D SOT has been modeled successfully, and the theory and equations to predict p_2D are given elsewhere [10,11]. They show that the edge effect increases with decreasing constituent number, increasing saturation, and increasing aspect ratio (i.e., the ratio of ¹n_c and ²n_c at equal resolution). Although such predictions are reported in this paper, the equations are not cited because they are relatively cumbersome and the detail is not necessary.

Procedures

Simulations of 1D and 2D separations containing 100 to 1000 peaks (or mixture constituents) with randomly distributed coordinates and exponentially distributed heights were calculated as detailed elsewhere [11,28]. A repetition of this detail here is not instructive. The results reported below are the average numbers of maxima observed in 50 simulations. The predictions of p by SOT were calculated from Eqs. 8 and 9 (or from edge-effect corrected equations [10,11]) as functions of the saturation (α). The same predictions then were expressed relative to the effective saturation (α_e) by using Figure 1d and the right-hand-side of Eqs. 3 and 7.

Results and Discussion

SOT results relative to saturation α

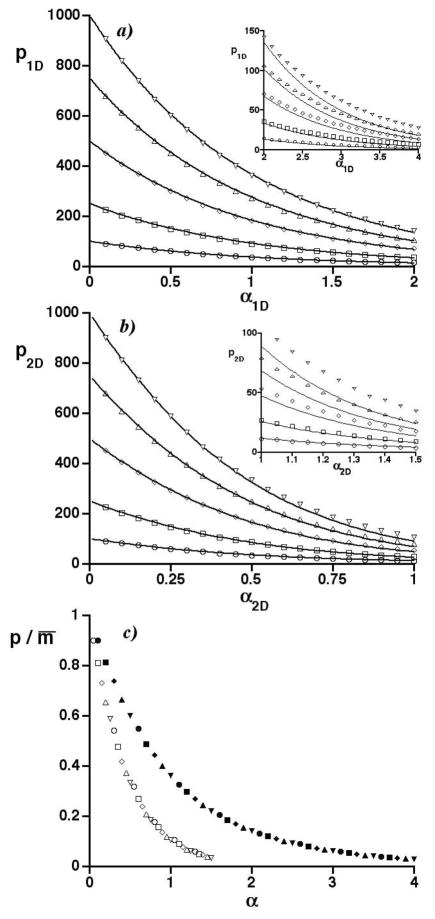
Figure 2 reports graphs of SOT predictions and simulation results expressed relative to the traditional metric of peak crowding, the saturation α. These are similar to others reported elsewhere [11,28] and are discussed only briefly to set the stage for the new, more important results. Figure 2a is a graph of the average number of observed peaks in 1D separations (p_1D) vs. the 1D saturation (α_1D) for numbers of mixture constituents (m) from 100 to 1000. The simulation results are given by the symbols; the curves are SOT predictions calculated from Eq. 8. The inset shows the results at large α_1D. Figure 2b is a graph of the average number of observed peaks in 2D separations (p_2D) vs. the 2D saturation (α_2D) for the same constituent numbers and an aspect ratio of one (for which the edge effect is minimal [10]). The simulation results are given by symbols; the curves are the edge-effect corrected SOT predictions. The inset shows results at large α_2D. The variation of $R_s^{\ast }$ with saturation shown in Figure 1d is included in both the 1D and 2D predictions. The predictions are in very good agreement with simulations except at high saturation, where overlap is severe (e.g., p/m̄ < 0.1).

Figure 2.

a) Graph of the average number of observed peaks in 1D separations (p_1D) vs. the 1D saturation (α_1D) for numbers of randomly distributed constituents m equaling 100 (○), 250 (□), 500 (◇), 750 (△), and 1000 (∇). Curves are SOT predictions. Inset shows results at large α_1D. b) As in a) but for 2D separations having an aspect ratio of one. c) Graph of the ratio of the average numbers of observed peaks to mixture constituents (p/m̄) vs. the saturation (α) of 1D and 2D separations. Selected simulation results in a) and b) are represented by filled and open symbols, respectively. Symbol types are the same as in a) and b), e.g., circles for m = 100.

Figure 2c contains selected simulation results from Figures 2a and 2b and shows that the ratio of the average numbers of observed peaks to mixture constituents (p/m̄) decreases more rapidly with saturation in 2D separations than in 1D ones. This is consistent with theory. As observed above, at the same saturation 1D and 2D separations have the same peak capacities for the same number of mixture constituents. However, since $R_{s,2D}^{\ast }<R_{s,1D}^{\ast }$, the 2D separation space is proportionally smaller than the 1D one. Consequently, it is not surprising that the 2D separation is worse. The traditionally defined saturation is simply not a good metric for comparing the separations.

It is useful to note that the 2D peak capacity of SOT is larger than the product of the first and second dimension peak capacities by the geometrical factor, 4/π [32,33]. If the 2D peak capacity of SOT were defined instead by this traditional product [33], then m̄ constituents would have the same 1D and 2D peak capacities when α_1D equals πα_2D/4, and the variable α_2D in Eq. 9 would be replaced by πα_2D/4. Under this condition, however, $R_{s,2D}^{\ast }$ is still less than $R_{s,1D}^{\ast }$ (results not shown), and the 1D and 2D peak-capacity units still have different relative sizes. Unsurprsingly, p_2D is still less than p_1D.

SOT results relative to effective saturation α_e

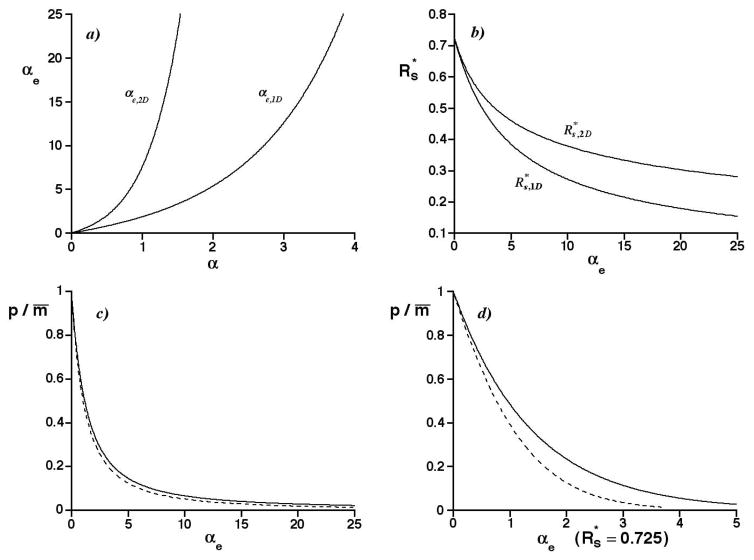
Figure 3a is a plot of the effective saturation α_e vs. the saturation α for 1D and 2D separations, as calculated from Eqs. 3 and 7, and Figure 1d. In both cases, the effective saturation increases rapidly with α but the 2D separations do so even more rapidly. Perhaps the most striking result is the rapidity of the increase, with α_e approaching 25 for the larger α ranges in Figures 1d and 2. The choice of unit resolution (¹R_s = ²R_s = 1) as the basis for the α_e values corresponds to traditional peak capacities that are 25 times smaller than the average number of mixture constituents. Thus a coupling of SOT with α_e can offer insight into separations at very high peak crowding.

Figure 3.

a) Graph of the effective saturation α_e vs. the saturation α for 1D separations (α_e,1D) and 2D separations (α_e,2D). b) Graph of the average minimum resolution $R_s^{\ast }$ vs. the effective saturation α_e for 1D separations ( $R_{s,1D}^{\ast }$) and 2D separations ( $R_{s,2D}^{\ast }$). c) Graph of the p/m̄ ratio vs. the effective saturation α_e for 1D separations (——; calculated from Eqs. 3 and 8, and Figure 1d) and unbounded 2D separations (- - -; calculated from Eqs. 7 and 9, and Figure 1d). d) As in c), but with α_e determined by $R_s^{\ast }=0.725$.

Figure 3b is a plot of the average minimum resolution $R_s^{\ast }$ vs. the effective saturation α_e. Here, the values of $R_s^{\ast }$ in Figure 1d are unchanged but are now referenced to α_e instead of α. Because α_e,_2D increases much more rapidly with α than does α_e,_1D (see Figure 3a), $R_{s,2D}^{\ast }$ is now “stretched out” along the abscissa and is larger than $R_{s,1D}^{\ast }$ at any positive α_e, in contrast to the graphs in Figure 1d.

1D and unbounded 2D separations

Figure 3c shows the predicted fraction of mixture constituents appearing as observed peaks, p/m̄, vs. α_e for 1D and unbounded 2D separations. The graph is the exact analog of Figure 2c but the dependent variable (p/m̄) is referenced to α_e instead of α. The solid curve for 1D separations was calculated from Eq. 8, divided by m̄; the dashed curve for unbounded 2D separations was calculated from Eq. 9, divided by m̄. In both cases the p/m̄ predictions were not changed but only referenced to α_e using Figure 1d, and Eqs. 3 and 7. The two curves are essentially the same, with p_2D/m̄ being slightly smaller than p_1D/m̄ at large α_e. The greatest deviation between the curves at any α_e is less than 0.037. The close agreement is obtained only by including the variation with α of the functions $R_s^{\ast }$ in Figure 1d, thus justifying the importance of their derivation. This is shown in Figure 3d, which is identical to Figure 3c except that α_e is calculated using a fixed value of $R_s^{\ast }$, set equal to its limiting value (0.725) at zero saturation. Here the p/m̄ ratios diverge at even small α_e, which has a much smaller range than in Figure 3c because $R_s^{\ast }$ is constant.

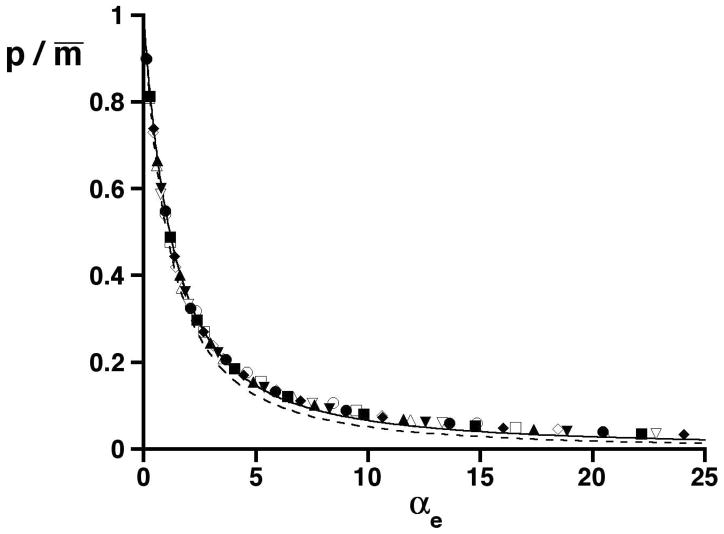
This is a most important and profoundly simple finding. It means that 1D and unbounded 2D separations of randomly distributed peaks produce almost the same numbers of observed peaks over a wide range in α_e, when equal 1D and 2D traditional peak capacities calculated at unit resolution are used. This assertion is supported by Figure 4, which shows selected simulation data for 1D and 2D separations in Figures 2a and 2b. The data are referenced to α_e, expressed as the ratio of the average numbers of observed peaks to mixture constituents, and superimposed on the curves first shown in Figure 3c. The results are almost identical at the same α_e and also agree well with predictions. The near equality of 1D and unbounded 2D separations means that, all other matters aside, researchers should choose the separation method (1D vs. 2D) having the greater traditional peak capacity, regardless of dimensionality. Usually, this will be the 2D separation.

Figure 4.

Graph of the ratio of the average numbers of observed peaks to mixture constituents (p/m̄) vs. the effective saturation (α_e). Selected simulation results for 1D separations in Figure 2a and 2D separations in Figure 2b are represented by filled and open symbols, respectively. Symbol types are the same as in Figure 2. The curves for the p/m̄ ratio in Figure 3c are shown.

This is arguably one of SOT’s most important insights, but its earlier predictions are not wrong. In fact, Figure 2 shows they are correct. However, it is clear that the saturation α is a much less useful metric than the effective saturation α_e for comparing 1D and 2D separations, due primarily to the undesirable properties of the average minimum resolution $R_s^{\ast }$. When these properties are removed by assimilating $R_s^{\ast }$ into the effective saturation, the near equality of 1D and unbounded 2D separations in terms of the number of observed peaks becomes very evident.

To some extent the new terminology “effective saturation” was modeled on the classical chromatographic term, “effective plate number”. The virtue of the effective plate number is that it allows chromatographic formats to be more evenhandedly compared in terms of resolution than does the conventionally defined plate number. The resulting equation for resolution and effective plate number involves an implicit dependence of retention factor whereas the equation for resolution and plate number involves an explicit dependence on retention factor [32]. This is very analogous to the situation existing in Eqs. 3 and 7, with various functions of the effective saturation (e.g., the average number of observed peaks) depending implicitly on $R_s^{\ast }$.

A question of fundamental interest is, why are the p/m̄ ratios for 1D and unbounded 2D separations nearly equal at the same effective saturation? Perhaps the agreement is testimony to the soundness of the traditional peak capacity as a metric. If this metric is meaningful, then one might expect that the provision of equal numbers of “units” in which to place 1D and 2D peaks should produce the same p/m̄ ratio, provided that the distribution of peaks is the same in both cases (e.g., random). This indeed is the case.

The fact that peak overlap in 1D and unbounded 2D separations is about the same at the same effective saturation is very relevant to the work of Stoll et al. [1] discussed in the Introduction. Other recent work by Stoll and the authors of this paper showed that the manner in which the traditional 2D peak capacity is partitioned between the first and second dimensions does not have much impact on the number of observed peaks [34]. Given these results and our current findings, we conclude that 2DLC will produce more observed peaks than fully optimized 1DLC, at least for separation times greater than 5 minutes. This may not be the case in GC × GC as pointed out by Blumberg and coworkers [35].

Empirical fit to graphs of p/m̄ vs. α_e

Although the curves in Figures 3a – 3c are predicted from theory, they lack analytical expressions because the variation of $R_s^{\ast }$ with α, on which α_e depends, was computed by the numerical solution to multiple equations [11,28]. However, they are described well by various empirical fits in the Appendix. Here, we discuss the results of a fit of Eq. 10 to the p/m̄ ratios in Figure 3c

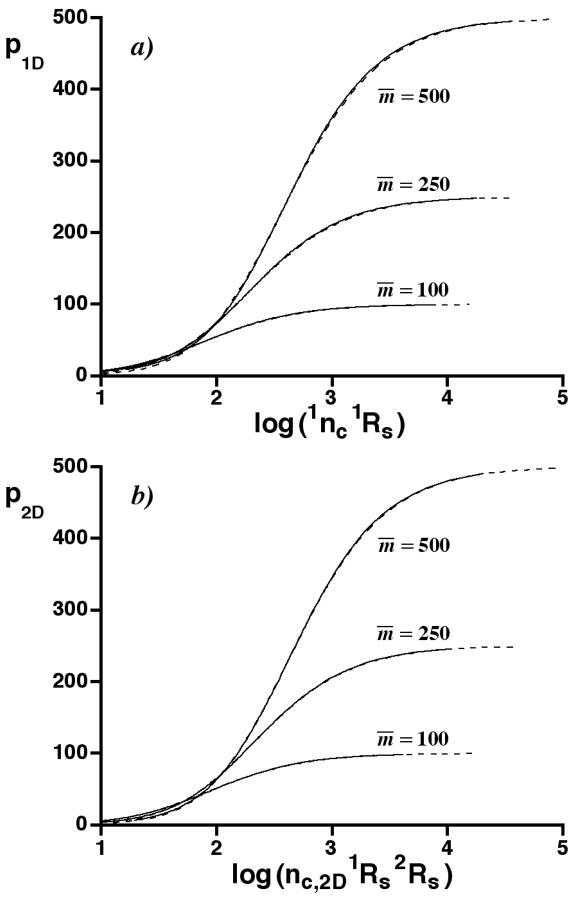
$$p/\overline{m}\approx \frac{1}{1+{\beta }_1{\alpha }_e+{\beta }_2{\alpha }_e^2};0\le {\alpha }_e\le 25$$ (10)

where the β’s are fitting coefficients. Eq. 10 can easily be solved to obtain the traditional peak capacities (scaled by resolutions), ¹n_c ¹R_s and n_c,_2D ¹R_s ²R_s, needed to separate m̄ mixture constituents into p observed peaks. The solution, which is given in the Appendix, is a remarkably simple and useful result for designing 1D and 2D separations. Figures 5a and 5b are graphs of p vs. the logarithm of the 1D and 2D traditional peak capacities for different m̄, as calculated from Figure 3c and the solution to Eq. 10. The agreement between the numerical and analytical results is excellent. The analytical results extend to larger traditional peak capacities, simply because the numerical results have a limited range. As an example, the solution to Eq. 10 shows that n_c,2D ¹R_s ²R_s must be 1355 for an unbounded 2D separation of m̄ = 500 constituents to produce p = 375 observed peaks, and it must be increased to about 3940 for the separation to produce 450 observed peaks. The corresponding ¹n_c ¹R_s values for a 1D separation are about 1210 and 3540. In these calculations, both m̄ and p are statistical averages, and some fluctuation about them is expected in any given separation. The calculations and Figure 5 reaffirm a previous prediction of SOT: the number of mixture constituents must be much less than the peak capacity, if most of them are to be resolved. Further a slightly higher peak capacity is needed for a 2D separation than a 1D one.

Figure 5.

a) Graph of p_1D vs. log (¹n_c ¹R_s) for 1D separations calculated from Figure 3c (——) and the solution to Eq. 10 (- - -), with m̄ = 100, 250, and 500. b) As in a), but a graph of p_2D vs. log (n_c,2D ¹R_s ²R_s) for unbounded 2D separations.

Eq. 10 can be used to calculate relationships other than the p/m̄ ratio. For example, the average number of observed peaks p is the product of Eq. 10 and m̄. In addition, the fraction of the traditional 1D peak capacity used in producing 1D observed peaks, p_1D/¹n_c, is the product of Eq. 10 and ¹R_sα_e,1D (see Eq. 3). Similarly, p_2D/n_c,2D is the product of Eq. 10 and ¹R_s ²R_s α_e,2D (see Eq. 7).

Bounded 2D separations and the edge effect

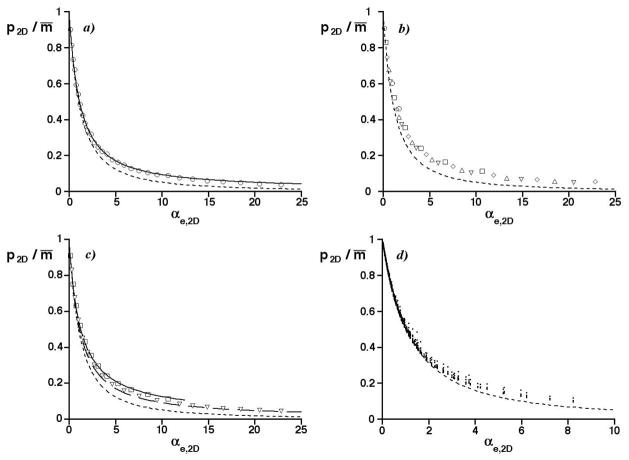
Unfortunately, the edge effect complicates the near equality of 1D and 2D separations, even when SOT is referenced to the effective saturation. For example, the 2D simulation results in Figure 4 are slightly larger than predicted by Eq. 9 due to a small edge effect. This is confirmed in Figure 6a, which is a graph of the ratio of the average numbers of observed peaks to mixture constituents (p_2D/m̄) vs. the 2D effective saturation α_e,2D for the smallest constituent number, m = 100 (the edge effect increases with decreasing m [10]). The solid curve represents the edge-effect corrected prediction, whereas the dashed curve represents the unbounded 2D separation. At large α_e,2D, the former describes the results better than the latter.

Figure 6.

Graphs of the ratio of the average numbers of observed peaks to mixture constituents (p_2D/m̄) vs. the effective saturation (α_e,2D). The prediction for an unbounded 2D separation is shown (- - -). a) Circles are simulation results in Figure 2b for m = 100; solid curve is the edge-effect corrected prediction for m̄ = 100. Aspect ratio: one. b) As in a) but for simulation results having an aspect ratio of 40. Symbols have the same meaning as in Figure 2b. c) As in b) but for m’s of 250 and 1000, with edge-effect corrected predictions for m̄ = 250 (——) and m̄ = 1000 (– –). d) As in a), but with the effective saturation α_e,2D including the peak broadening factor < β>, Eq. 11. Circles are average results from 1436 sets of simulated c-2D separations with 100 to 550 randomly distributed peaks, aspect ratios of 40 or less, and t_s/¹σ ratios between 0.2 and 16 [34].

The edge effect in 2D separations also increases as the aspect ratio departs from unity [10]. Figure 6b is a graph of p_2D/m̄ vs. α_e,2D for the same m’s as before, but now the aspect ratio is 40 (i.e., the peak capacity of one dimension is 40 times greater than the other). At large α_e,2D, the simulation results are larger than predicted for the unbounded 2D separation, as represented by the dashed curve. They also show a small dependence on m. However, they are described well by the edge-effect corrected theory, as shown in Figure 6c for average constituent numbers m̄ of 250 (solid curve) and 1000 (coarsely dashed curve). The prediction for m̄ = 250 does not span the full α_e,2D range, because of limitations on theory [10].

These differences are not surprising. Although in principle 1D separations are subject to an edge effect, only the first and last peaks in the separation lack neighboring peaks on one side, with minor consequences unless the constituent number is small [5]. In contrast, a greater fraction of all the peaks are near boundaries in a 2D separation.

The edge effect can be substantial in severely undersampled comprehensive 2D (c-2D) separations, in which the profiles of observed peaks are extensively broadened in the first dimension. This occurs because severe undersampling can increase the aspect ratio, particularly when ¹n_c is smaller than ²n_c (e.g., by 5-fold or more) [34]. Such combinations occur in 2DLC when an inefficient first-dimension separation (e.g., size exclusion or ion exchange) is coupled to an on-line, efficient second-dimension separation (e.g., RPLC). Recent work has shown that the average peak width ¹w of first-dimension Gaussian peaks after sampling is 4 <β> ¹σ, where

$$<\beta >\approx \sqrt{1+0.21{(t_s/{}^1\sigma )}^2}$$ (11)

and t_s is the sampling time in the first dimension [34,36]. Since the effective saturation is proportional to ¹w (see Eq. 7), it is also proportional to <β> in c-2D separations of randomly distributed peaks. Figure 6d is a graph of p_2D/m̄ vs. α_e,2D, with <β> included in the calculation of α_e,2D. The symbols represent the average results of 1436 sets of simulated c-2D separations (with 50 simulations per set) in a recent publication [34]. The c-2D separations had aspect ratios of 40 or less and contained 100 to 550 randomly distributed peaks sampled over the dimensionless sampling periods, 0.2 ≤ t_s/¹σ ≤ 16. These periods determined <β>, Eq. 11. The dashed curve is the result for an unbounded 2D separation. The results show the same trends as in Figures 6a – 6c, with excellent agreement at small α_e,2D and small deviations at relatively large α_e,2D.

Figure 6 shows that accurate predictions of the p_2D/m̄ ratio for 2D separations having large edge effects cannot always be made from theory for an unbounded 2D separation, even relative to the effective saturation. At large effective saturations, the actual p_2D/m̄ ratio can exceed its unbounded 2D counterpart, and the edge-effect corrected theory must be used for accuracy. Since this theory depends in a complex manner on m̄, the effective saturation, and the aspect ratio, it is not possible to construct a universal curve. The conditions under which edge effects can be neglected will be described in a future publication. For now, we simply will argue that the edge effect may not always require quantitative treatment, because it is largest when the p_2D/m̄ ratio is small (see Figure 6). Since a small ratio indicates the separation is poor, it may not be necessary to know with accuracy how poor it is: it may suffice simply to know that it is poor. Therefore, researchers may find it convenient to use Eq. 10 as an approximation to the p_2D/m̄ ratio even when the edge effect is large, with an awareness that the prediction will be too small.

Effective saturation in correlated 2D separations

Commonly peaks in real 2D separations are not entirely randomly distributed. Usually their coordinates are positively correlated because the separation mechanisms in the two dimensions are not fully independent. Based on recent work, we have every reason to think that the average number of observed peaks in a correlated 2D separation and the effective saturation α_e,2D are related [34]. However, the exact relationship differs for different distributions of peak coordinates and cannot be predicted at this time. The study of such relationships clearly is important but is best deferred to another publication due to its complexity.

Conclusions

The prediction by Eqs. 8 and 9 of nearly equal p/m̄ ratios for 1D and unbounded 2D separations at equal effective saturations α_e is one of the most important results thus far obtained from SOT. It shows that these separations are almost identical, with one having little or no advantage over the other in terms of the separation produced by a given traditional peak capacity. In contrast, the separation power appears to be very different, when interpreted relative to the usual SOT metric of peak crowding, the saturation α. We think that the effective saturation is the metric that experimentalists prefer, as it is based on traditional resolutions and peak capacities that are simple to measure. The ease with which the empirical result, Eq. 10, can be used to predict the p/m̄ ratio and related quantities (e.g., p, the ratio of p to the traditional peak capacity, and the traditional peak capacity needed to separate m̄ constituents into p observed peaks) should greatly assist experimentalists in characterizing and optimizing separations having very high effective saturations (e.g., 25).

Extensions of SOT have been published to address shortcomings of Eqs. 8 and 9, such as the variations of peak density and standard deviation that are common in 1D and 2D separations [37,38]. Similar extensions can be made to Eq. 10 or equations in the Appendix. However, to do so here would detract from the main theme of this paper, namely that relative to the effective separation 1D and unbounded 2D separations of randomly distributed peaks are essentially the same.

It is evident that simulations of 1D and 2D separations of randomly distributed peaks having the same traditional peak capacity could have been developed long ago and used to establish their near equality on an empirical basis. However, the theoretical basis for the equality would have been lacking. It is satisfying that SOT provides that basis.

Appendix

Fits to curves in Figures 3a – 3c

Over the range, 0 ≤ α_e ≤ 25, a simple useful fit to the graphs of p/m̄ vs. α_e in Figure 3c is given by Eq. A1 and in the text by Eq. 10

$$p/\overline{m}\approx \frac{1}{1+{\beta }_1{\alpha }_e+{\beta }_2{\alpha }_e^2}$$ (A1)

with β_1,1D = 0.775 ± 0.002 and β_2,1D = 0.0750 ± 0.0009 for 1D separations, and with β_1,2D = 0.862 ± 0.002 and β_2,2D = 0.111 ± 0.001 for unbounded 2D separations. The algebraic differences between the curves in Figure 3c and Eq. A1 (i.e., the residuals) never exceed 0.0051. Eq. A1 is useful, because it can easily be solved for the scaled traditional peak capacities, ¹n_c ¹R_s and n_c,2D ¹R_s ²R_s, required to separate m̄ constituents into p observed peaks

$$\frac{\overline{m}}{\sqrt{{\left(\frac{{\beta }_1}{2{\beta }_2}\right)}^2+\frac{1-p/\overline{m}}{{\beta }_{2}p/\overline{m}}}-\frac{{\beta }_1}{2{\beta }_2}}$$ (A2)

As p/m̄ approaches unity, Eq. A2 approaches infinity, indicating that infinitely large traditional peak capacities are required for total separation as we expect. The dashed curves in Figure 5 were calculated from Eq. A2 and the β’s reported above.

Because the curves in Figure 3c are almost the same at any α_e, some researchers may prefer not to distinguish them. Eq. A1 can be fit to the average of their cubic splines (the curves themselves cannot be averaged because their α_e’s differ), with β_1,ave = 0.837 ± 0.004 and β_2,ave = 0.081 ± 0.001 (the subscript, “ave”, refers to the average p/m̄ ratio). The algebraic differences between the average p/m̄ ratio and the fit never exceed 0.013. Unsurprisingly, the β_ave’s lie between the dimension-specific β’s reported above. Over the range, 0.10 ≤ p/m̄ ≤ 1, the traditional peak capacities predicted by Eq. A2 using the β_ave’s differ by at most ±10% from those predicted using the dimension-specific β’s.

The p/m̄ ratios at different α_e also can be estimated from fits that preserve the SOT equations in their original form. Over the range, 0 ≤ α_e ≤ 25, the variation of the average minimum resolution $R_s^{\ast }$ with α_e in Figure 3b can be fit with

$$R_{s,1D}^{\ast }\approx \frac{0.725}{1+{\beta }_3{({\alpha }_{e,1D})}^{{\beta }_4}}$$ (A3)

$$R_{s,2D}^{\ast }\approx \frac{0.725}{\sqrt{1+{\beta }_5{({\alpha }_{e,2D})}^{{\beta }_6}}}$$ (A4)

with β₃ = 0.1942 ± 0.0005, β₄ = 0.930 ± 0.001, β₅ = 0.351 ± 0.002, and β₆ = 0.880 ± 0.002. The algebraic differences between the curves in Figure 3b, and Eqs. A3 and A4, never exceed 0.0060. Eqs. A3 and A4 can be combined with Eqs. 3 and 7 to express the saturation α in terms of α_e

$${\alpha }_{1D}={\alpha }_{e,1D}{R}_{s,1D}^{\ast }\approx \frac{0.725{\alpha }_{e,1D}}{1+{\beta }_3{({\alpha }_{e,1D})}^{{\beta }_4}}$$ (A5)

$${\alpha }_{2D}={\alpha }_{e,2D}\pi {\left(R_{s,2D}^{\ast }\right)}^2/4\approx \frac{0.413{\alpha }_{e,2D}}{1+{\beta }_5{({\alpha }_{e,2D})}^{{\beta }_6}}$$ (A6)

Eqs. A5 and A6 approximate the curves in Figure 3a (although with reversed axes). They can be substituted into Eqs. 8 and 9 to estimate p as a function of α_e. The algebraic differences between these p estimates, divided by m̄, and the curves in Figure 3c never exceed 0.0049. Eq. A6 also can be used to estimate p using edge-effect corrected theory.