Abstract
The thermal deactivation of TEM-1 β-lactamase was examined using two experimental techniques: a series of isothermal batch assays and a single, continuous, non-isothermal assay in an enzyme membrane reactor (EMR). The isothermal batch-mode technique was coupled with the three-state “Equilibrium Model” of enzyme deactivation, while the results of the EMR experiment were fitted to a four-state “molten globule model”. The two methods both led to the conclusions that the thermal deactivation of TEM-1 β-lactamase does not follow the Lumry-Eyring model and that the Teq of the enzyme (the point at which active and inactive states are present in equal amounts due to thermodynamic equilibrium) is at least 10 °C from the Tm (melting temperature), contrary to the idea that the true temperature optimum of a biocatalyst is necessarily close to the melting temperature.
Keywords: biocatalysis, enzyme catalysis, enzyme models, Equilibrium Model, protein folding
Introduction
The operational stability of a biocatalyst is an important characteristic in determining the suitability of that catalyst in a given process. It is well-understood that catalytic activity tends to increase with temperature, but that in the case of enzymes, elevated temperature also leads to thermal deactivation, due to a loss of integrity of the active site.[1,2] When kept at elevated temperatures for extended time periods, enzymes will undergo denaturation to a permanently inactive state. Some enzymes are capable of recovering catalytic activity after relatively short incubations at elevated temperatures which induce a loss of activity.[3,4] The Equilibrium Model (Scheme 1) captures this phenomenon by including a reversible transition between active and inactive states, and has been shown to be valid for all of the enzymes (approximately 40) on which it has been tested.[5–8]
Scheme 1.
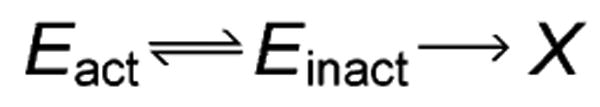
The Equilibrium Model.
By treating the reversible transition between Eact and Einact as a van't Hoff-type equilibrium, and the transition from Einact to X as a time-dependent, first-order decay with Arrhenius-type rate constant, one can derive an expression for the observed reaction rate as a function of temperature and elapsed time.[5,6] Transition state theory is utilized to define the three quantities involved in the deactivation model, according to Equations 1–3. These are kcat (turnover number of enzyme), Keq (equilibrium constant between Eact and Einact), and kinact (first-order rate constant for decay from Einact to X). The description of the Einact to X step in the Equilibrium Model is not intended to preclude the presence of multiple, inactive intermediate unfolding states, though it makes no distinction between such states.[8]
| (1) |
| (2) |
| (3) |
Under isothermal conditions, the values of kcat, Keq, and kinact remain fixed, and depend only on the activation and deactivation parameters of the enzyme at that temperature: ΔGcat (activation energy for enzyme-catalyzed reaction), ΔGinact (activation energy for the Einact to X transition), ΔHeq (enthalpy change for the Eact to Einact transition), and Teq (temperature at which [Eact] = [Einact]). When isothermal conditions exist, the expression for the reaction rate Vmax, as a function of temperature and time, is given by Equation (4), where E0 is the initial enzyme concentration.
| (4) |
By substituting the results of Equations (1)–(3) into Equation (4), the values of ΔGcat, ΔGinact, ΔHeq, and Teq may be estimated by fitting experimental data of reaction rate vs. temperature vs. time to the model.[9] The established method for estimating these parameters is to perform an array of activity-progress curves (including isothermal deactivation), while holding the initial enzyme concentration, E0, constant. After several temperatures have been examined, all progress curves are fitted to a three-dimensional surface plot using Powell's algorithm to determine the global minimum of the sum of squares deviation between the experimental curves and the model.[9]
Recently, a method was developed for determining the optimum operating temperature for a biocatalyst using a single, continuous assay rather than an array of isothermal experiments.[10,11] This method utilizes an enzyme membrane reactor (EMR) for soluble enzyme, or a packed-bed reactor for immobilized enzyme, to subject a single sample of enzyme to a continuous, positive, most often linear temperature gradient. Since time and temperature are functionally related in such a linear ramp scheme, the reaction rate may be expressed as a function of a single variable (either time or temperature), plus all of the intrinsic activation and deactivation parameters listed in Equations (1)–(3).
As certain enzymes are known to lose catalytic activity before the onset of complete unfolding (i.e. the global loss of secondary structure often associated with the Tm of the enzyme),[1] the model used with the continuous temperature ramp experiment assumes that the biocatalyst follows a four-state deactivation model. This four-state model is similar to the Equilibrium Model but allows for two separate inactive states. The native state, N, is in equilibrium with a “molten globule” state, M, which has undergone slight conformational changes that render it inactive. Herein, states N and M are taken to be functionally equivalent to Eact and Einact, respectively, in the Equilibrium Model. The four-state model includes a second equilibrium between M and another unfolded state, U, which has unfolded in the sense that it has experienced a widespread loss of secondary structure. This “molten globule” unfolding model is shown in Scheme 2.
Scheme 2.
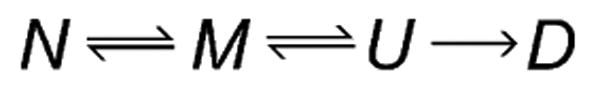
The four-state “molten globule” deactivation model.
The “molten globule” unfolding model (Scheme 2) assumes that the enzyme must first enter the unfolded state U before it may become permanently denatured and that there are no pathways for denaturation directly from the native or molten globule states. It uses the same parameter as the Equilibrium Model, Keq, to describe the van't Hoff equilibrium between states N and M. The first-order denaturation constant for state U, kinact, is also the same for both models. The molten globule model, however, contains the additional parameter, Kmg = [U]/[M], shown in Equation (5), where Tmg is the temperature at which [M] = [U].
| (5) |
Hence, the four-state model assumes a heterogeneous population of inactive enzyme and seeks to capture both the Teq and the traditional Tm of the enzyme. Both of these values, which do not necessarily coincide with each other, are important when designing and characterizing a stable biocatalyst.[8]
When biocatalyst deactivation data is collected in a system which is operated as a continuous stirred-tank reactor (CSTR), the degree of substrate conversion, X, is given as a function of temperature, according to Equation (6).
| (6) |
Equation (6) contains the system parameters V (reactor volume), [S]0 (substrate feed concentration), and v (feed volumetric flow rate). Both kcat and [N] vary over the course of the experimental run as temperature is ramped up, and are readily expressed as functions of either time or temperature in the case of a linear heating ramp (the relationship T = T0+mt applies, where m is the rate of increase of the reactor temperature). The value of kcat is given by Equation (1), and the value of [N] is derived by combining the definitions of Keq and Kmg, the mass balance on species N, M, U, and D, and the first-order denaturation rate law which states d[D]/dt = kinact[U].
| (7) |
| (8) |
| (9) |
Upon rearrangement, and application of the chain rule, Equation 9 is transformed into a first-order differential equation for which K1 = d(Keq)/dt and K2 = d(Kmg)/dt. The rate of disappearance of native enzyme at any time (or temperature) according to Scheme 2 is given by Equation (10).
| (10) |
Unlike the three-state, isothermal Equilibrium Model in which all of the equilibrium constants and the deactivation rate constant are constant through the course of an experimental run, this four-state, non-isothermal model equation is not readily integrated analytically. However, provided that the continuous temperature ramp experiment is started at any temperature well below the Tm of the enzyme, such that Kmg ≪ Keq, Equation (10) may be solved numerically by assuming an initial value of [N]0 = E0/(1+Keq).
Essentially, the continuous ramp method uses variable Keq, kcat, and kinact, whereas the Equilibrium Model (in isothermal batch-mode) allows these all to be held constant. Both methods, however, assume the intrinsic activation and deactivation parameters (ΔGcat, ΔGinact, ΔHeq, Teq) remain nearly constant over the entire temperature range of interest.
In this work, we have studied the thermal deactivation of an enzyme, TEM-1 β-lactamase from Escherichia coli, using both the isothermal batch techniques and the continuous EMR temperature ramp, on the same batch of enzyme, in order to assess the relative strengths of the two methods. Previously, a metallo-β-lactamase from Bacillus cereus has been studied using the batch-mode method with the Equilibrium Model, but a Class A β-lactamase such as TEM-1 has not been investigated to date using this method.[6,12,13]
Experimental Section
Materials
TEM-1 β-lactamase (E.C. 3.5.2.6) was over-expressed in Escherichia coli and purified from the expression medium via ammonium sulfate precipitation and ion exchange chromatography as in Rogers et al.[11] Penicillin G potassium salt was purchased from USB Corp. (Cleveland, OH). Coomassie Protein Assay Reagent was obtained from Thermo Scientific (Rockford, IL). All other chemicals used were of analytical grade.
Batch-mode experimental setup
Enzyme activity was measured using a Thermospectronic Helios γ-spectrophotometer equipped with a Thermospectronic single-cell Peltier-effect cuvette holder. This system was networked to a computer installed with Vision32 (Version 1.25, Unicam) software for recording absorbance vs. time data. Quartz cuvettes with a 5 mm path length were used during the course of all experiments, due to their favorable optical and heat transfer properties. The cuvette was kept isothermal during the course of each experimental run and a Cole-Parmer Digi-Sense thermocouple thermometer was used to ensure there was no temperature gradient larger than 0.1 °C within the cuvette, or from the beginning to the end of the run. Runs were discarded and repeated if a temperature gradient was detected. The thermometer and the temperature control bath were calibrated using a Cole-Parmer NIST-traceable glass thermometer.
Assay conditions
The reaction mixture consisted of an aqueous solution of 50 mm sodium phosphate buffer and 4.4 mm penicillin G at pH 7.0. For each run, 1.0 mL of reaction mixture was added to the cuvette, along with a 2 mm diameter Teflon-coated stir wire, and the system was allowed to thermally equilibrate for a minimum of 5 min. A stock solution of enzyme, with concentration determined by Bradford assay (measurement of A280 in the presence of Coomassie Protein Assay Reagent), was used to prepare a sample with a final concentration of 32 μg mL−1. After thermal equilibration, 5 μL of the enzyme solution (for a total enzyme concentration of 5.5 nm) was injected directly into the cuvette using a positive displacement pipettor and the contents of the cuvette were agitated rapidly for 3 seconds using the preheated stir wire. After stirring was completed, the software began recording absorbance data.
The hydrolysis of penicillin G by TEM-1 β-lactamase was observed by monitoring the absorbance shift at 252 nm. At this wavelength, the unreacted substrate exhibited an extinction coefficient of ε252 = 682 m−1 cm−1 and the fully hydrolyzed mixture exhibited an extinction coefficient of ε252 = 213 m−1 cm−1. This difference of 469 m−1 cm−1 between the substrate and product remained constant throughout the entire temperature range of this study. The combination of substrate concentration, cuvette path length, and enzyme loading was chosen such that the starting absorbance never exceeded 1.5 AU (to preclude instrument saturation), and the substrate conversion never exceeded approximately 40% at any of the temperatures examined. Hence, the substrate concentration was never lower than about 2.6 mm; a value over 100 times the published KM of the enzyme for penicillin G at 25 °C.[14] The linearity of the instrument response over the absorbance range 0.5–1.5 AU was confirmed by running a dilution series of unreacted substrate solution (R2 = 0.995). Reactions were allowed to proceed for 120 seconds, with data points acquired at two-second intervals.
Batch-mode data analysis
Triplicate assays were performed at each temperature, and the absorbance vs. time data were converted to reaction rate vs. time data. The average of the three rates at each time point was used to construct a single progress curve of reaction rate vs. elapsed assay time for each given temperature. The progress curves were smoothed using a Loess transformation (SigmaPlot 2001 for Windows) to eliminate noise from the data, and the smoothed curves for all temperatures were initially fitted to the Equilibrium Model using MATLAB, with initial parameter estimates of ΔGcat = 85 kJ mol−1, ΔGinact = 100 kJ mol−1, ΔHeq = 120 kJ mol−1, Teq = 320 K. The fitting parameters resulting from the first MATLAB run were used as improved initial estimates for a second MATLAB run, which provided the final values.[9]
Continuous-mode EMR experimental setup
Substrate conversion vs. time data were collected in an EMR which was configured to operate as a CSTR. A single sample of enzyme was charged to a reactor with a working volume of 10.0 mL and a solution of 200 mm sodium phosphate buffer and 20 mm penicillin G was continuously fed to the reactor at a rate of 1.25 mL min−1. The buffer system was selected and tested to ensure that the pH remained at 6.8–7.0 over the entire experimental temperature range and all levels of substrate conversion. The penicillin G feed solution was kept refrigerated at 4 °C during experiments to preclude thermal degradation. To counteract the effects of enzyme absorption to the membrane surface, a loading of 1.0 mg mL−1 bovine serum albumin (BSA), which exhibited no activity toward the substrate, was charged to the reactor. Control runs were performed at 4 °C, in the absence of thermal enzyme deactivation, to rule out the effects of membrane absorption and shear stress damage to the enzyme due to stirring. Zero activity loss was detected after 36 hrs of reactor operation during the control runs.
After a one-hour equilibration period at the initial temperature of 295 K, the reactor temperature was progressively increased to 330 K using a linear temperature ramp of 2 Khr−1. The substrate conversion was monitored by measuring the optical rotation of the reactor effluent stream via an in-line polarimeter with a sample cell which was kept at 25 °C by external water bath. At 25 °C, the specific optical rotation of the substrate mixture was α589 = 107° M−1 while that of the product was α589 = 57° M−1. To account for background thermal degradation of the substrate, a calibration curve was constructed by first running pure unreacted feed and then completely hydrolyzed product through the entire temperature ramp.
Continuous-mode data analysis
The conversion vs. time data were smoothed with the MATLAB Curve Fitting Toolbox, using a Robust Loess method with span = 85. The smoothed experimental data were fitted according to Equations (6) and (10), using an iterative solving procedure to minimize the sum of squared residuals by adjusting the fitting parameters. Two different numerical techniques were used to solve the initial value problem (IVP) of Equation (10): an implicit Euler method with a time interval of Δt = 120 s and an area-under-the-curve approximation according to the trapezoidal rule, with a time interval of Δt = 120 s.
In addition, a model was generated which omitted the folding state, U, and assumed only a three-state model equivalent to the Equilibrium Model. An attempt was then made to fit the continuous EMR data to this three-state model for purposes of comparison, using the area-under-the-curve approximation per the trapezoidal rule for the numerical integration.
Results and Discussion
Batch-Mode Results
A total of ten progress curves for the enzyme were measured, each in triplicate, over the temperature range from 292 K to 332 K. The temperature spacing between progress curves was varied through the course of the experiments, and two of the progress curves were measured at high temperatures, such that the initial reaction rate had fallen below its peak value (i.e. the temperature was above Topt). The experimental data for rate vs. temperature vs. time, overlaid with the rate predicted by the MATLAB routine according to Equation (4), is shown in Figure 1.
Figure 1.
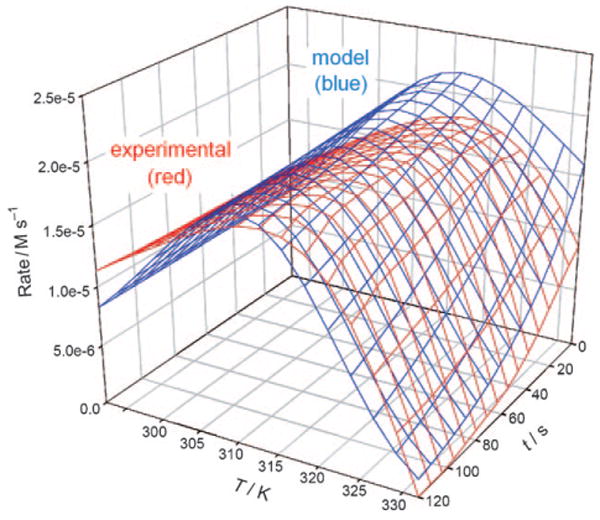
Isothermal batch mode results (experimental vs. model).
Continuous-mode EMR Results
Figure 2 depicts the experimental data from the continuous EMR temperature ramp experiment, overlaid with three different model predictions: the four-state molten globule model using the implicit Euler technique, the four-state molten globule model using the trapezoidal rule, and the three-state Equilibrium Model. The values of the deactivation parameters which were found by the various experimental methods and model fitting procedures are shown in Table 1.
Figure 2.
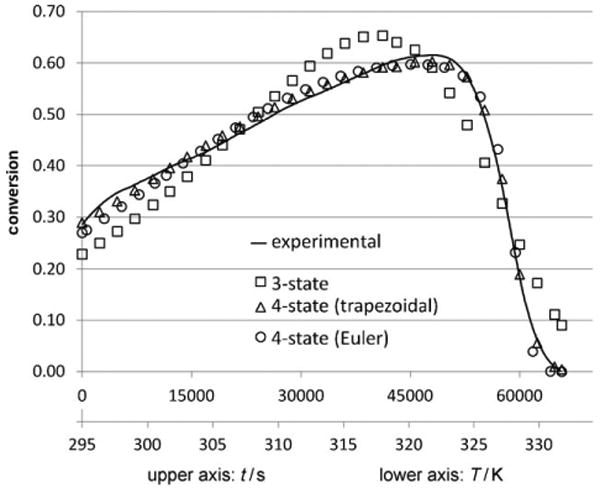
Continuous temperature ramp EMR results (fitted to models).
Table 1.
Estimation of deactivation parameters by isothermal batch-mode tests and continuous temperature ramp EMR methods (standard deviations for batch isothermal data are shown in parentheses).
| Method | ΔGcat [kJ mol−1] | ΔHeq [kJ mol−1] | Teq [K] | ΔHmg [kJ mol−1] | Tmg [K] | ΔGinact [kJ mol−1] | Σ(residual)2 |
|---|---|---|---|---|---|---|---|
| batch isothermal | 53.6 (0.04) | 98.5 (2.0) | 313.8 (0.3) | – | – | 92.1 (0.2) | – |
| EMR (four-state, Euler) | 54.0 | 64.6 | 317.9 | 716.5 | 328.6 | 101.2 | 0.1835 |
| EMR (four-state, trapezoidal) | 54.2 | 74.9 | 309.2 | 699.7 | 324.7 | 100.6 | 0.0497 |
| EMR (three-state, trapezoidal) | 54.8 | 69.4 | 330.5 | – | – | 101.0 | 1.7198 |
Comparison of Models to Experimental Data
Figures 1 and 2 show the experimental data for the batch-mode and continuous methods, respectively, overlaid with the predictions of the models. One conspicuous feature of the experimental data for both the isothermal batch and temperature ramp methods is that the early (low-temperature) segment of the curve shows a near-linear increase of activity with temperature. In the absence of any deactivation effects in this regime, one would expect the curve to be concave upward, more closely resembling an Arrhenius-type activation profile. The near-linear increase in the isothermal batch-mode data suggests the onset of activity loss at a temperature well below the traditional Tm of TEM-1 β-lactamase, which is 51.5 °C as evidenced by interpretation of the circular dichroism spectrum.[15] It is clear that a different effect must be responsible for the activity loss in the vicinity of 310–315 K, more than 10 °C below the Tm, contrary to the widely held belief that the optimum operating temperature of a biocatalyst is very close (within a degree or two) to its melting temperature, but is expected for an enzyme following the Equilibrium Model.[10,16] This may only hold true for those enzymes for which global secondary structure and active site integrity are compromised simultaneously.
The three-state deactivation model resulted in a relatively poor fit to the continuous non-isothermal data from the EMR. Similar to the fit of the Equilibrium Model to the batch results in Figure 1, the three-state deactivation model, numerically integrated by the trapezoidal rule, tends to underestimate the enzyme activity on the low-temperature end of the EMR experiment, anticipating an Arrhenius-type increase as temperature rises. It can be clearly seen that the predicted slope of the rate vs. temperature trend, in the low-temperature regime, is significantly greater than that of the experimental data, for both the three-state batch and three-state temperature ramp models.
Notably, however, the three-state isothermal Equilibrium Model (MATLAB routine) resulted in a relatively good fit to the batch data in the high temperature regime, particularly near the Teq of 314 K, whereas the three-state EMR model was unable to converge upon a good fit in this regime. One explanation for this inequality could be the large difference in time scales between the two experimental methods. At temperatures a few degrees below the Teq, denaturation during the course of the experimental run may be nearly invisible in the two-minute isothermal batch assay. The three-state EMR model, however, is forced to include the cumulative effects of denaturation over a much longer time, as the time between each data point in the EMR model is 120 s, the same length as the entire progress curve of the batch model.
Thus, at a moderate temperature, which is apparently “non-denaturing” as seen in the shorter batch assay, a significant amount of time has passed in the continuous EMR run and there is already much less active enzyme present than if the enzyme were being exposed to that temperature for the first time. Indeed, it has been previously shown in the literature that insufficient monitoring time, particularly at higher temperatures, can disguise the equilibrium character of inactivation and thus make it difficult to fit data to a model which would remain consistent in longer assays.[17] Effects such as uncooperative unfolding and grace-period inactivation can influence the accuracy of such short-term assays. Currently, the effects of varying the temperature ramp rate in the continuous EMR are under further investigation.[11]
There is ample evidence in the literature that several strains of β-lactamase follow a four-state unfolding mechanism.[18–20] It has been previously established by use of guanidinium chloride denaturation experiments that TEM-1 β-lactamase does not follow a simple “one-step, two-state” folding mechanism, but rather exhibits a thermodynamically stable intermediate state in equilibrium with the native and unfolded states, likely influenced by the cis/trans isomerization of Xaa–Pro peptide bonds.[21] This intermediate state, described in the literature, is modeled here to correspond to the molten globule state of the four-state model.
The batch-mode isothermal Equilibrium Model and the non-isothermal four-state temperature ramp models, remarkably, were in good agreement with respect to the location of the Teq, though the batch-mode Equilibrium Model predicted a higher ΔHeq, which may be because the three-state model is converging on an intermediate value somewhere between the enthalpy change necessary to enact a conformational change at the active site (ΔHeq of the four-state model), and the enthalpy change associated with the onset of unfolding (ΔHmg of the four-state model). The four-state model makes a distinction between these two transitions, in which the molten globule state M exhibits no activity but also does not readily become permanently denatured, whereas the unfolded state is much more readily denatured, an effect which corresponds to the sudden loss of activity in the vicinity of Tmg. In addition, the nature of the Equilibrium Model equation is such that ΔHeq is subject to relatively high errors.[6,9] Discrepancies between the two models may be due to the fact that the Equilibrium Model treats the Einact to X transition as a single event, although not necessarily via a single product.[7] Alternatively, it may be due to the fact that, for this enzyme, data for the Equilibrium Model has only been collected for two minutes. The value of Tmg predicted by the temperature ramp four-state trapezoidal model (the better fit of the two four-state models) is 51.7 °C, which coincides almost exactly with the documented Tm of the enzyme, as measured by circular dichroism.[15]
The values for ΔGinact predicted by the four-state continuous model were somewhat higher than those from the three-state batch-mode Equilibrium Model. Again, this may be attributable to the fact that there is a very large time-scale difference between the two experiments, and the prediction of the first-order denaturation rate constant kinact may appear to be quite different during a two-minute assay than over the course of several hours.
The ΔGcat value of 54.2 kJ mol−1 predicted by the continuous four-state trapezoidal model gives a turnover number of 1530 s−1 at 25 °C, which is in excellent agreement with the literature value of 1500 s−1 for TEM-1 using penicillin G as a substrate.[22] The predicted ΔGcat was slightly lower in the three-state batch-mode Equilibrium Model, at 53.6 kJ mol−1, corresponding to a turnover number of 2550 s−1 at 25 °C. The discrepancy between these two values could be a consequence of experimental error associated with the Bradford assay in determining the initial enzyme concentration, or it may be due to determinations of kcat having been made under conditions for which not all of the enzyme is active.[7,23] However, the difference is not far from the sum of the fitting and experimental errors expected for the determination of Equilibrium Model parameters.[9]
The four-state continuous temperature ramp models predict the ΔHmg to be nearly an order of magnitude higher than the ΔHeq value, which is in agreement with the notion that the conformational shift needed to render the enzyme inactive is slight compared to the complete unfolding of the enzyme.[7,8,24,25] The value of 700 kJ mol−1 for the enthalpy change upon unfolding is in the typical range for globular proteins such as β-lactamase I from Bacillus cereus, which exhibits a denaturation enthalpy of 646 kJ mol−1, although this is low compared with subtilisin.[26]
The two numerical integration methods used with the four-state model (implicit Euler method and trapezoidal rule) predicted nearly the same values for ΔGcat, ΔHmg, and ΔGinact. The two methods produced slightly different predictions for the Tmg, which may be due to the different behavior of the two integration techniques in the vicinity of Tmg. The trapezoidal rule method, which resulted in a better overall fit, was particularly more effective than the implicit Euler method at tracking the experimental data in this regime where the rate of change of conversion with respect to time is high. The significant difference between the two models was in their predictions of ΔHeq and Teq. The implicit Euler method showed a higher Teq with a lower energy barrier, while the trapezoidal method showed the converse arrangement. Nevertheless, both methods confirmed that ΔHeq was about an order of magnitude less than the ΔHmg indicated by both the four-state continuous experiment and CD data from literature and that the Teq was at least 10 °C lower than Tmg (i.e. melting temperature Tm).
Conclusions
Whereas the three-state Equilibrium Model (Scheme 1) did not result in a good fit to the data obtained by the continuous temperature ramp method, it resulted in a relatively good fit to the isothermally obtained batch data, although the predicted value of ΔGcat was slightly low and the abbreviated increase of actual reaction rate with temperature was not fully captured by the model. The four-state deactivation model (Scheme 2), especially when the steep changes around Tmg were tracked by a routine employing the trapezoidal rule rather than Euler's method, resulted in an excellent fit to the data collected by the continuous temperature ramp EMR experiment, and furthermore showed good agreement with the batch-mode Equilibrium Model regarding the location of Teq, the temperature of transition between native, active enzyme and conformationally compromised, inactive enzyme.
Whereas the four-state model contains a higher number of fitting parameters and should admittedly result in an improved fit over the three-state model, there is, as discussed earlier, copious evidence in the literature which indicates TEM-1 unfolds via a four-state mechanism. Both the three-state Equilibrium Model and four-state continuous model were effective at pinpointing the transition between active and inactive enzyme. The finding of two distinct transitions in the temperature ramp EMR model corroborates the previously established notion that Teq is separate from Topt, with the latter depending on a mix of Teq, ΔGcat, and ΔHeq.[5–7] Both are important to engineers who wish to characterize and design biocatalysts. It is clear that the difference in timescale of these two experimental modes may affect the parameters predicted by model fitting. Denaturing effects which may be ignored during an assay lasting only a few minutes will have a greater effect on models which seek to capture the cumulative deactivation over several hours. A high degree of uncooperativity in the process of transitioning between native and denatured states is likely one source of discrepancy between the two experimental methods.
The discontinuous Equilibrium Model batch method has a string of advantages. The collection of an array of isothermal progress curves, while labor-intensive compared to the continuous temperature ramp experiment, can be fitted to a model which is mathematically straightforward in that all temperature-dependent equilibrium constants remain unchanged during progress curves. The batch method also uses smaller quantities of substrates, buffers, and other reagents and can be performed with commonplace instrumentation and equipment, so there is no need to configure a CSTR. In the current study with TEM-1 β-lactamase, the Equilibrium Model was equally as capable as the more complex four-state continuous model in identifying the Teq of the enzyme. So far, all enzymes for which Equilibrium Model data has been collected obey the model.[7,8]
The temperature ramp method, although it is faster and requires minimal direct monitoring, and furthermore utilizes a single injection of enzyme (minimizing systematic error), requires a model which relies on numerical integration techniques due to the complicated behavior of native enzyme population when temperature increases with time. However, the ability of the continuous EMR system, in conjunction with the four-state deactivation model, appears to be a powerful tool for examining multiple thermodynamic transitions (N to M as well as M to U), both of which are of great importance in biocatalyst design, in a single experiment. This technique can likely be extended to other biocatalysts which do not deactivate according to a simple two-state cooperative mechanism.
Acknowledgments
The authors would like to give many thanks to Colin Monk at University of Waikato for his technical assistance with the MATLAB Equilibrium Model software and to Christian Albert, visiting scientist from Technische Universität München, for his experimental work on TEM-1 β-lactamase deactivation. T.A.R. gratefully acknowledges support from the National Institute of Health (Grant 5R01AI064817-02).
Contributor Information
Dr. Roy M. Daniel, Email: r.daniel@waikato.ac.nz.
Dr. Andreas S. Bommarius, Email: andreas.bommarius@chbe.gatech.edu.
References
- 1.Manetto GD, La Rosa C, Grasso DM, Milardi D. J Therm Anal Calorim. 2005;80:263–270. [Google Scholar]
- 2.Aymard C, Belarbi A. Enzyme Microb Technol. 2000;27:612–618. doi: 10.1016/s0141-0229(00)00258-1. [DOI] [PubMed] [Google Scholar]
- 3.Vieille C, Zeikus GJ. Microbiol Mol Biol Rev. 2001;65:1–43. doi: 10.1128/MMBR.65.1.1-43.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Machado MF, Saraiva JM. Biotechnol Lett. 2005;27:1233–1239. doi: 10.1007/s10529-005-0023-y. [DOI] [PubMed] [Google Scholar]
- 5.Daniel RM, Danson MJ, Eisenthal R. Trends Biochem Sci. 2001;26:223–225. doi: 10.1016/s0968-0004(01)01803-5. [DOI] [PubMed] [Google Scholar]
- 6.Peterson ME, Eisenthal R, Danson MJ, Spence A, Daniel RM. J Biol Chem. 2004;279:20717–20722. doi: 10.1074/jbc.M309143200. [DOI] [PubMed] [Google Scholar]
- 7.Daniel RM, Danson MJ, Hough DW, Lee CK, Peterson ME, Cowan DA. Enzyme stability and activity at high temperatures. In: Thomas T, Sidiqui KS, editors. Protein Adaptation in Thermophiles. Pub Nova Science; 2009. pp. 1–34. [Google Scholar]
- 8.Daniel RM, Danson MJ, Eisenthal R, Lee CK, Peterson ME. Biochem Soc Trans. 2007;35:1543–1546. doi: 10.1042/BST0351543. [DOI] [PubMed] [Google Scholar]
- 9.Peterson ME, Daniel RM, Danson MJ, Eisenthal R. Biochem J. 2007;402:331–337. doi: 10.1042/BJ20061143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Gibbs PR, Uehara CS, Neunert U, Bommarius AS. Biotechnol Prog. 2005;21:762–774. doi: 10.1021/bp049609k. [DOI] [PubMed] [Google Scholar]
- 11.T. A. Rogers, A. S. Bommarius, unpublished results.
- 12.Peterson Michelle Emma. PhD thesis. University of Waikato; 2005. Evidence for a third thermal parameter of enzymes. [Google Scholar]
- 13.Peterson ME, Eisenthal R, Danson MJ, Spence A, Daniel RM. J Biol Chem. 2005;280:6915–6922. [Google Scholar]
- 14.Lejeune A, Pain RH, Charlier P, Frere J, Matagne A. Biochemistry. 2008;47:1186–1193. doi: 10.1021/bi701927y. [DOI] [PubMed] [Google Scholar]
- 15.Wang X, Minasov G, Shoichet BK. Proteins Struct Funct Genet. 2002;47:86–96. [PubMed] [Google Scholar]
- 16.Eisenthal R, Peterson ME, Daniel RM, Danson MJ. Trends Biotechnol. 2006;24:289–292. doi: 10.1016/j.tibtech.2006.05.004. [DOI] [PubMed] [Google Scholar]
- 17.Polakovic M, Vrabel P. Process Biochem. 1996;31:787–800. [Google Scholar]
- 18.Uversky VN, Ptitsyn OB. Biochemistry. 1994;33:2782–2791. doi: 10.1021/bi00176a006. [DOI] [PubMed] [Google Scholar]
- 19.Vijayakumar S, Vishveshwara S, Ravishanker G, Beveridge DL. Biophys J. 1993;65:2304–2312. doi: 10.1016/S0006-3495(93)81288-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Bone S. Phys Med Biol. 1994;39:1801–1809. doi: 10.1088/0031-9155/39/11/002. [DOI] [PubMed] [Google Scholar]
- 21.Vanhove M, Raquet X, Frere J. Proteins Struct Funct Genet. 1995;22:110–118. doi: 10.1002/prot.340220204. [DOI] [PubMed] [Google Scholar]
- 22.Mathonet P, Deherve J, Soumillion P, Fastrez J. Protein Sci. 2006;15:2323–2334. doi: 10.1110/ps.062303606. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Lee CK, Daniel RM, Shepherd C, Saul D, Cary SC, Danson MJ, Eisenthal R, Peterson ME. FASEB J. 2007;21:1934–1941. doi: 10.1096/fj.06-7265com. [DOI] [PubMed] [Google Scholar]
- 24.Lee Charles Kai-Wu. PhD thesis. University of Waikato; 2007. Eurythermalism of a deep-sea symbiosis system from an enzymological aspect. [Google Scholar]
- 25.Daniel RM, Danson MJ, Eisenthal R, Lee CK, Peterson ME. Extremophiles. 2008;12:51–59. doi: 10.1007/s00792-007-0089-7. [DOI] [PubMed] [Google Scholar]
- 26.Arriaga P, Menendez M, Villacorta JM, Laynez J. Biochemistry. 1992;31:6603–6607. doi: 10.1021/bi00143a034. [DOI] [PubMed] [Google Scholar]


