Abstract
The description of excited state dynamics in energy transfer systems constitutes a theoretical and experimental challenge in modern chemical physics. A spectroscopic protocol that systematically characterizes both coherent and dissipative processes of the probed chromophores is desired. Here, we show that a set of two-color photon-echo experiments performs quantum state tomography (QST) of the one-exciton manifold of a dimer by reconstructing its density matrix in real time. This possibility in turn allows for a complete description of excited state dynamics via quantum process tomography (QPT). Simulations of a noisy QPT experiment for an inhomogeneously broadened ensemble of model excitonic dimers show that the protocol distills rich information about dissipative excitonic dynamics, which appears nontrivially hidden in the signal monitored in single realizations of four-wave mixing experiments.
Keywords: excitation energy transfer, nonlinear spectroscopy, quantum information processing, open quantum systems, quantum biology
Excitonic systems and the processes triggered upon their interaction with electromagnetic radiation are of fundamental physical and chemical interest (1–6). In nonlinear optical spectroscopy (NLOS), a series of ultrafast femtosecond pulses induces coherent vibrational and electronic dynamics in a molecule or nanomaterial, and the nonlinear polarization of the excitonic system is monitored both in the time and frequency domains (7, 8). To interpret these experiments, theoretical modeling has proven essential, framed within the Liouville space formalism popularized by Mukamel (7). Implicit in these calculations is the evolution of the quantum state of the dissipative system in the form of a density matrix. The detected polarization contains information of the time dependent density matrix of the system, although not in the most transparent way. An important problem is whether these experiments allow quantum state tomography (QST)—that is, the determination of the density matrix of the probed system at different instants of time (9, 10). A more ambitious question is if a complete characterization of the quantum dynamics of the system can be performed via quantum process tomography (QPT) (11, 12), a protocol that we define in the next section. In this article, we show that both QST and QPT are possible for the single-exciton manifold of a coupled dimer of chromophores with a series of two-color photon-echo (PE) experiments. We also present numerical simulations on a model system and show that robust QST and QPT is achievable even in the presence of experimental noise as well as inhomogeneous broadening. This article provides a conceptual presentation, and interested readers may find derivations and technical details in SI Appendix.
Basic Concepts of QPT
Consider a quantum system that interacts with a bath. We can describe the full state of the system and the environment at time T by the density matrix ρtotal(T). The reduced density matrix of the system is ρ(T) = TrB ρtotal(T), where the trace is over the degrees of freedom of the bath. If the initial state is a product, ρtotal(0) = ρ(0)⊗ρB(0) (always with the same initial bath state ρB(0)), then the evolution of the system may be expressed as a linear transformation (13):
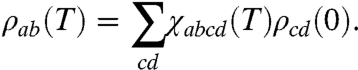 |
[1] |
The central object of this article is the process matrix χ(T), which is independent of the initial state ρ(0). As opposed to master equations that are written in differential form, Eq. 1 can be regarded as an integrated equation of motion for every T. It holds both for Markovian and non-Markovian dynamics of the bath, and it always leads to positive density matrices. Note that χ(T) completely characterizes the dynamics of the system. Preserving Hermiticity, trace, and positivity of ρ(T) imply, respectively, the relations (section I of SI Appendix)
| [2] |
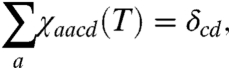 |
[3] |
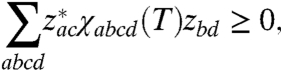 |
[4] |
where z is any complex valued vector. Using Eqs. 2 and 3, for a system in a d-dimensional Hilbert space, χ(T) is determined by d4 - d2 real valued parameters (11). Operationally, QPT can be defined as an experimental protocol to obtain χ(T). Spectroscopically, χ(T) may be reconstructed by measuring ρ(T) (i.e., performing QST) given some choice of initial state ρ(0), where the ρ(0) are chosen successively from a complete set of initial states (14–17). Because we are interested in energy transfer dynamics, this procedure shall be performed at several values of T. In this article, we show how to perform QPT for a model coupled excitonic dimer using two-color heterodyne photon-echo experiments.
Description of the System and Its Interaction with Light
Consider an excitonic dimer interacting with a bath of phonons. The excitonic part of the Hamiltonian, describing the system with the environment frozen in place, is given by (4, 8, 18):
| [5] |
where 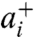 and
and 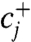 (ai and cj) are creation (annihilation) operators for site i∈{A,B} and delocalized j∈{α,β} excitons, respectively. ωA ≠ ωB are the first and second site energies, J ≠ 0 is the Coulombic coupling between the chromophores. We define the average of site energies
(ai and cj) are creation (annihilation) operators for site i∈{A,B} and delocalized j∈{α,β} excitons, respectively. ωA ≠ ωB are the first and second site energies, J ≠ 0 is the Coulombic coupling between the chromophores. We define the average of site energies 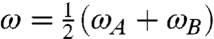 , difference
, difference 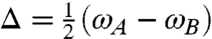 , and mixing angle
, and mixing angle 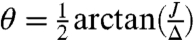 . Then cα = cos θaA + sin θaB, cβ = - sin θaA + cos θaB, ωα = ω + Δ sec 2θ, and ωβ = ω - Δ sec 2θ. For convenience, we define the single-exciton states
. Then cα = cos θaA + sin θaB, cβ = - sin θaA + cos θaB, ωα = ω + Δ sec 2θ, and ωβ = ω - Δ sec 2θ. For convenience, we define the single-exciton states 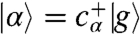 ,
, 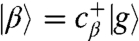 , where
, where 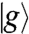 is the ground state, and the biexcitonic state
is the ground state, and the biexcitonic state 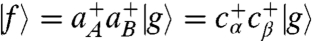 . The model Hamiltonian does not account for exciton–exciton binding or repulsion terms, so the energy level of the biexciton is ωf = ωα + ωβ = ωA + ωB. Denoting ωij ≡ ωi - ωj, we have ωαg = ωfβ and ωβg = ωfα.
. The model Hamiltonian does not account for exciton–exciton binding or repulsion terms, so the energy level of the biexciton is ωf = ωα + ωβ = ωA + ωB. Denoting ωij ≡ ωi - ωj, we have ωαg = ωfβ and ωβg = ωfα.
We are interested in the perturbation of the excitonic system due to three laser pulses:
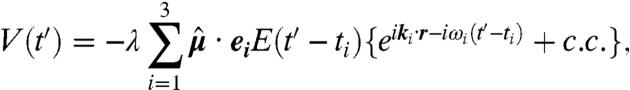 |
[6] |
where λ is the intensity of the electric field, assumed weak, 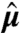 is the dipole operator, and ei, ti, ki, ωi denote the polarization *, time center, wavevector, and carrier frequency of the i-th pulse. E(t′) is the slowly varying pulse envelope, which we choose to be Gaussian with fixed width σ for all pulses, E(t′) = e-t′2/2σ2. The polarization induced by the pulses on the molecule located at position r is given by
is the dipole operator, and ei, ti, ki, ωi denote the polarization *, time center, wavevector, and carrier frequency of the i-th pulse. E(t′) is the slowly varying pulse envelope, which we choose to be Gaussian with fixed width σ for all pulses, E(t′) = e-t′2/2σ2. The polarization induced by the pulses on the molecule located at position r is given by 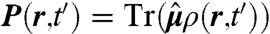 . This quantity can be Fourier decomposed along different wavevectors as
. This quantity can be Fourier decomposed along different wavevectors as 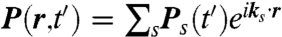 , where the ks are linear combinations of wavevectors of the incoming fields. Radiation is produced due to the polarization (proportional to iP(r,t′)). We can choose to study a single component Ps by detecting only the radiation moving in the direction ks. This is achieved by interfering the radiation with a fourth pulse moving in the direction ks, called the local oscillator (LO) (7). In particular, we shall be interested in the time-integrated signal in the photon-echo (PE) direction, k4 = kPE = -k1 + k2 + k3. This heterodyne-detected signal
, where the ks are linear combinations of wavevectors of the incoming fields. Radiation is produced due to the polarization (proportional to iP(r,t′)). We can choose to study a single component Ps by detecting only the radiation moving in the direction ks. This is achieved by interfering the radiation with a fourth pulse moving in the direction ks, called the local oscillator (LO) (7). In particular, we shall be interested in the time-integrated signal in the photon-echo (PE) direction, k4 = kPE = -k1 + k2 + k3. This heterodyne-detected signal 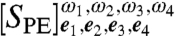 , where the subscripts indicate the polarizations of the four light pulses and the superscripts indicate their carrier frequencies, is proportional to
, where the subscripts indicate the polarizations of the four light pulses and the superscripts indicate their carrier frequencies, is proportional to
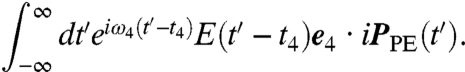 |
[7] |
Spatial integration over the volume of probed molecules selects out the component PPE(t′) from the P(r,t′). The time integration yields a signal that is proportional to the components of PPE(t′)·e4 oscillating at the frequencies of the LO, which is centered about ω4 †. In this excitonic model, the only optically allowed transitions are between states differing by one excitation, so the only nonzero matrix elements of 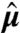 are μij = μji for ij = αg, βg, fα, fβ (section II of SI Appendix).
are μij = μji for ij = αg, βg, fα, fβ (section II of SI Appendix).
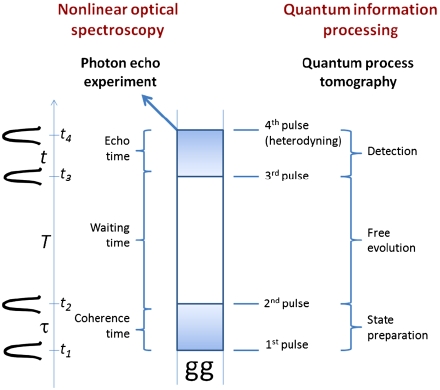
In the following section, we present the main results of our study. We show that a carefully chosen set of two-color rephasing PE experiments can be used to perform a QPT of the first exciton manifold (Fig. 1). The preparation of initial states is achieved using the first two pulses at t1 and t2. Initial states spanning the single-exciton manifold are produced by using the four possible combinations of two different carrier frequencies for the first two pulses. In the terminology of PE experiments, these pulses define the so-called coherence time interval τ = t2 - t1. The time interval between the second and third pulses, called the waiting time T = t3 - t2, defines the quantum channel (11), which we want to characterize by QPT. Finally, we carry out QST of the output density matrix at the instant t3. This task is indirectly performed by using the third pulse to selectively generate new dipole-active coherences, which are detected upon heterodyning with the fourth pulse at t4, that is, after the echo time t = t4 - t3 has elapsed. Varying the third and fourth pulse frequencies yields sufficient linear equations for QST. This procedure naturally concludes the protocol of the desired QPT.
Fig. 1.
A set of photon echo experiments can be regarded as a QPT. Pulses are centered about t1,t2,t3,t4. Time flows upward in the diagram. The four pulses define the coherence (τ), waiting (T) times, and echo ( t) times. This experiment, in the language of quantum information processing, can be regarded as consisting of three stages: initial state preparation, free evolution, and detection of the output state of the waiting time.
Results
For purposes of the QPT protocol, we assume that the structural parameters ωαg, ωβg, μαg, μβg, μfα, and μfβ are all known. Information about the transition frequencies can be obtained from a linear absorption spectrum, whereas the dipoles can be extracted from X-ray crystallography (19). As shown in recent work of our group, with enough data from the PE experiments, it is also possible to extract these parameters self-consistently (20, 21). We proceed to describe the steps of the PE experiment on a coupled dimer that yield a QPT.
Initial State Preparation.
Before any electromagnetic perturbation, the excitonic system is in the ground state 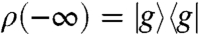 . After the first two pulses in the k1, k2 directions act on the system, the effective density matrix
. After the first two pulses in the k1, k2 directions act on the system, the effective density matrix  (at T = 0) is created. This density is second order in λ and, combined with the third and fourth pulses, directly determines the signal. By applying second order perturbation theory and the rotating-wave approximation (RWA), we can define an effective initial state (Fig. 2 A–D and section III of SI Appendix):
(at T = 0) is created. This density is second order in λ and, combined with the third and fourth pulses, directly determines the signal. By applying second order perturbation theory and the rotating-wave approximation (RWA), we can define an effective initial state (Fig. 2 A–D and section III of SI Appendix):
 |
[8] |
This state evolves during the waiting time T to give
| [9] |
which holds for T ≳ 3σ, that is, after the action of the first two pulses has effectively ended. Eq. 9 is of the form of Eq. 1, and therefore appealing for our QPT purposes. The purely imaginary coefficients  for p∈{α,β} are proportional to the frequency components at ωpg of the pulse that is centered at ωi:
for p∈{α,β} are proportional to the frequency components at ωpg of the pulse that is centered at ωi:
 |
[10] |
and the propagator of the optical coherence 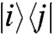 is
is
| [11] |
which, for simplicity, has been taken to be the product of a coherent oscillatory term beating at a frequency ωij and an exponential decay with dephasing rate Γij, assumed to be known. Θ(τ) is the Heaviside function, so the propagator is finite only for times τ≥0. We have kept only the -k1 and +k2 components because those are the only contributions to the signal at kPE.
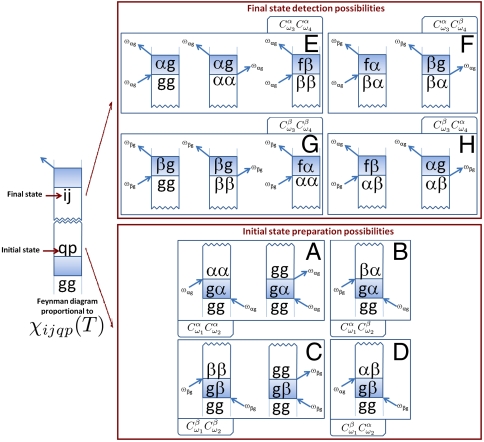
Fig. 2.
Possible state preparations and detections. We list all the possible preparations and detections of elements of the density matrix at the waiting time T via a rephasing PE experiment. The double-sided Feynman diagrams above list all the possible processes detected in a rephasing PE experiment. Each diagram is related to an element χijqp(T) due to the prepared state 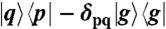 at the beginning of the waiting time and the detected state ij at the end of it. By combining the preparations in A, B, C, and D, with the detections in E, F, G, and H, 16 different types of processes can be enumerated, which can be classified according to the pulse frequencies of the associated perturbations.
at the beginning of the waiting time and the detected state ij at the end of it. By combining the preparations in A, B, C, and D, with the detections in E, F, G, and H, 16 different types of processes can be enumerated, which can be classified according to the pulse frequencies of the associated perturbations.
Eq. 8 has a simple interpretation and can be easily read off from the Feynman diagrams depicted in Fig. 2 A–D. Because we will be selecting only light in the kPE direction, we keep only the portion of the first pulse proportional to eiω1(t-t1) and only the portion of the second pulse proportional to e-iω2(t-t2) in Eq. 6. Then, because the state before any perturbation is 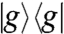 , the first pulse can only resonantly excite the bra in the RWA (7), generating an optical coherence
, the first pulse can only resonantly excite the bra in the RWA (7), generating an optical coherence 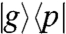 (where p∈{α,β}) with amplitude
(where p∈{α,β}) with amplitude 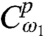 . This coherence undergoes free evolution for time τ under
. This coherence undergoes free evolution for time τ under 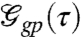 before the second pulse perturbs the system. In the RWA, this second pulse can act on the ket of
before the second pulse perturbs the system. In the RWA, this second pulse can act on the ket of 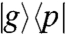 to yield
to yield 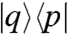 with amplitude
with amplitude 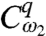 and on the bra to create a hole
and on the bra to create a hole 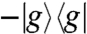 with amplitude
with amplitude 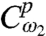 , producing Eq. 8. The amplitude of this prepared initial state is proportional to the alignment of the corresponding transition dipole moments with the polarization of the incoming fields. Once the initial state is prepared, it evolves via χ(T), which is the object we want to characterize. A possible problem is the contamination of the initial states by terms proportional to a hole
, producing Eq. 8. The amplitude of this prepared initial state is proportional to the alignment of the corresponding transition dipole moments with the polarization of the incoming fields. Once the initial state is prepared, it evolves via χ(T), which is the object we want to characterize. A possible problem is the contamination of the initial states by terms proportional to a hole 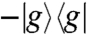 every time there is a single-exciton manifold population
every time there is a single-exciton manifold population 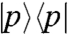 . This is not a difficulty if we assume:
. This is not a difficulty if we assume:
| [12] |
that is, if the ground state population does not transform into any other state via free evolution. This is reasonable because we may ignore processes where phonons can induce upward optical transitions. We similarly neglect spontaneous excitation from the single to double exciton states.
One can see from Eq. 8 that a set of four linearly independent initial states can be generated by manipulating the frequency components of the pulses through 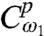 and
and 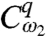 . It is sufficient to consider a pulse toolbox of two waveforms that create
. It is sufficient to consider a pulse toolbox of two waveforms that create 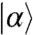 and
and 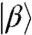 with different amplitudes. For instance, by centering one waveform at ω+ in the vicinity of ωαg and the other at ω- close to ωβg , we can simultaneously have:
with different amplitudes. For instance, by centering one waveform at ω+ in the vicinity of ωαg and the other at ω- close to ωβg , we can simultaneously have:
| [13] |
for purely imaginary numbers C′ ≠ C′′. The conceptually simplest choice, which we shall denote the maximum discrimination choice (MDC) and is best for QPT purposes, is two waveforms each resonant with only one transition, so C′≫C′′, and we can neglect C′′. Four linearly independent initial states can be prepared by choosing the waveform of each of the first two pulses from this pulse toolbox.
Evolution.
The system evolves during the waiting time T after the initial state is prepared. Transfers between coherences and populations are systematically described by χ(T). The components of 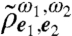 evolve in time, described by χ(T), without assuming any particular model for the bath or system-bath interaction, other than Eq. 12. By definition, the amplitude of the ij component of
evolve in time, described by χ(T), without assuming any particular model for the bath or system-bath interaction, other than Eq. 12. By definition, the amplitude of the ij component of 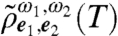 is proportional to χijqp(T), with the exception of the gg component, which is proportional to χggpq(T) + δpq due to the contamination of the hole in the initial state. We note that deexcitation transfers from the single-exciton manifold to elements involving the ground state (gg,gα,gβ, gα, gβ) are expected to be small, because such processes are also unlikely to occur on femtosecond time scales due to either the phonon or the photon bath. Detailed analysis shows that our protocol can detect decay into gg but not into gα or gβ. We shall keep these χggqp(T) terms in our equations in order to monitor amplitude leakage errors from the single-exciton manifold, providing a consistency check for treating the single-exciton manifold as an effective TLS in the time scale of interest.
is proportional to χijqp(T), with the exception of the gg component, which is proportional to χggpq(T) + δpq due to the contamination of the hole in the initial state. We note that deexcitation transfers from the single-exciton manifold to elements involving the ground state (gg,gα,gβ, gα, gβ) are expected to be small, because such processes are also unlikely to occur on femtosecond time scales due to either the phonon or the photon bath. Detailed analysis shows that our protocol can detect decay into gg but not into gα or gβ. We shall keep these χggqp(T) terms in our equations in order to monitor amplitude leakage errors from the single-exciton manifold, providing a consistency check for treating the single-exciton manifold as an effective TLS in the time scale of interest.
Detection.
The last two pulses provide an indirect QST of the state after the waiting time. The third perturbation along +k3 and centered at time t3 will selectively probe certain coherences and populations of 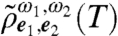 . As an illustration (see Fig. 2 E and F), the component of the pulse matching the transition energy ωαg = ωfβ and proportional to
. As an illustration (see Fig. 2 E and F), the component of the pulse matching the transition energy ωαg = ωfβ and proportional to 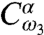 will, in the RWA, promote the resonant transitions
will, in the RWA, promote the resonant transitions 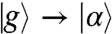 and
and 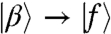 on the ket side, and the conjugate resonant transitions
on the ket side, and the conjugate resonant transitions 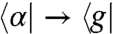 and
and 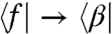 on the bra side, the latter of which are irrelevant as we are ignoring transfers to the biexciton state during the waiting time. These transitions will generate two sets of optically active coherences in the echo interval: αg, fβ that oscillate at frequency ωαg, and βg, fα that oscillate at ωβg. These sets generate a polarization that interferes with the LO yielding signals proportional to
on the bra side, the latter of which are irrelevant as we are ignoring transfers to the biexciton state during the waiting time. These transitions will generate two sets of optically active coherences in the echo interval: αg, fβ that oscillate at frequency ωαg, and βg, fα that oscillate at ωβg. These sets generate a polarization that interferes with the LO yielding signals proportional to 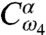 and
and 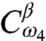 , respectively. The propagator for the echo time is taken to be as in Eq. 11. A similar analysis can be repeated for the
, respectively. The propagator for the echo time is taken to be as in Eq. 11. A similar analysis can be repeated for the 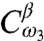 term. Analogously to the preparation stage, the same toolbox of two different waveforms for the third and the fourth pulses allows discrimination of all final states of
term. Analogously to the preparation stage, the same toolbox of two different waveforms for the third and the fourth pulses allows discrimination of all final states of 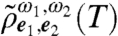 . Fig. 2 depicts double-sided Feynman diagrams for all possible combinations of preparations and detections with four pulses each chosen from two waveforms, yielding 16 experiments. By keeping track of these processes, the signal
. Fig. 2 depicts double-sided Feynman diagrams for all possible combinations of preparations and detections with four pulses each chosen from two waveforms, yielding 16 experiments. By keeping track of these processes, the signal 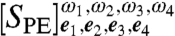 may be compactly written as (section IV of SI Appendix):
may be compactly written as (section IV of SI Appendix):
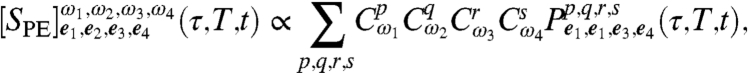 |
[14] |
where the proportionality constant is purely real, and the expression holds for T,t > 3σ. The terms 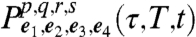 are loosely polarizations (in fact, they are proportional to i times polarizations) ‡ and are given by
are loosely polarizations (in fact, they are proportional to i times polarizations) ‡ and are given by
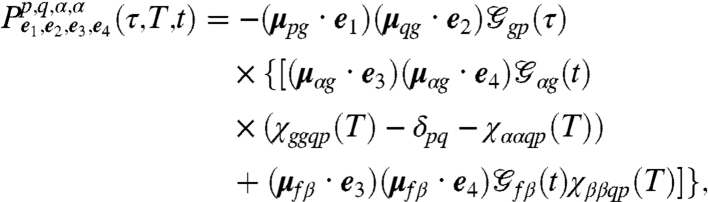 |
[15] |
and
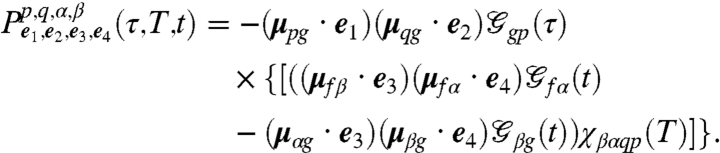 |
[16] |
The remaining terms 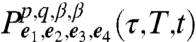 ,
, 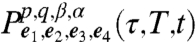 follow upon the interchange α↔β. Eqs. 14–16 are the main result of this article. Each
follow upon the interchange α↔β. Eqs. 14–16 are the main result of this article. Each 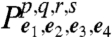 represents the observed signal if the first (second, third, fourth) laser pulse is resonant only with the p (q,r,s) transition. The total measured signal
represents the observed signal if the first (second, third, fourth) laser pulse is resonant only with the p (q,r,s) transition. The total measured signal 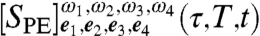 is a weighted sum of these
is a weighted sum of these 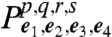 . Eqs. 15 and 16 show that each
. Eqs. 15 and 16 show that each 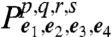 is a linear combination of elements of χ(T), corresponding to the prepared initial states and detected final states. After collecting the 16 signals
is a linear combination of elements of χ(T), corresponding to the prepared initial states and detected final states. After collecting the 16 signals 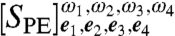 with each pulse carrier frequency ωi chosen from {ω+,ω-} as in Eq. 13, with fixed polarizations ei, Eq. 14 can be inverted to yield the elements of χ(T) associated with the single-exciton manifold of the dimer, hence accomplishing the desired QSTs and QPT at once. Notice that in principle, for a given value of waiting time T, the one-dimensional (1D) measurements associated with a single set of τ, t values is enough for purposes of QPT of the single-exciton manifold. In the most typical measurements, the sample has isotropically distributed chromophores, so Eq. 14 must be modified to include isotropic averaging
with each pulse carrier frequency ωi chosen from {ω+,ω-} as in Eq. 13, with fixed polarizations ei, Eq. 14 can be inverted to yield the elements of χ(T) associated with the single-exciton manifold of the dimer, hence accomplishing the desired QSTs and QPT at once. Notice that in principle, for a given value of waiting time T, the one-dimensional (1D) measurements associated with a single set of τ, t values is enough for purposes of QPT of the single-exciton manifold. In the most typical measurements, the sample has isotropically distributed chromophores, so Eq. 14 must be modified to include isotropic averaging 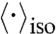 (section VI of SI Appendix). Because the present QPT protocol does not rely on different polarization settings, we will assume for simplicity that each of the 16 experiments is carried out with (e1,e2,e3,e4) = (z,z,z,z). Further technical details of the QPT protocol can be found in the next section as well as in sections V–XII of SI Appendix.
(section VI of SI Appendix). Because the present QPT protocol does not rely on different polarization settings, we will assume for simplicity that each of the 16 experiments is carried out with (e1,e2,e3,e4) = (z,z,z,z). Further technical details of the QPT protocol can be found in the next section as well as in sections V–XII of SI Appendix.
Important Observations.
Difference between a standard PE experiment and QPT. In the current practice of NLOS, model Hamiltonians with free parameters for the excitonic system, the bath, and the interaction between them are postulated, and the experimental spectra are fit to the model via calculation of response functions, from which structural and dynamical information is extracted (22). In our language, such experiments involve fitting models to complicated combinations of quantum processes associated with χ(T). QPT requires only a model for the excitonic system but not for the bath or the system–bath coupling, making it suitable for probing systems where the bath dynamics are unknown. By definition, QPT extracts the elements of χ(T), allowing a straightforward analysis of processes directly associated with the density matrix, such as dephasing and relaxation.
QPT can also be performed with control of time delays τ, t instead of frequency control. Although 1D measurements suffice for QPT, suppose the signal is collected for many values of τ and t. Upon appropriately defined Fourier transformations of the signal along these variables, a two-dimensional electronic spectrum (2D-ES) can be constructed where the coherence propagators of Eq. 11 manifest as four resonances about ωαg and ωβg along both axes (8, 20, 23). An important observation follows: The frequencies of the coherent evolutions in the coherence and echo times are the same as the frequencies of the first transition and the LO detection. By varying t and τ, a 2D-ES provides the frequency-controlled information of the first and fourth pulses. Hence, it is possible to make the first and fourth pulses sufficiently broadband that their frequency components at the αg and βg transitions are of similar magnitude. Then, the 16 1D experiments can be replaced with four 2D-ES where the second and third pulses are frequency-controlled. A caveat in this identification is the assumption that the optical coherences evolve in a form like Eq. 11, without errors of coherence transfers (sections VII and IX of SI Appendix).
-
Extension to overlapping pulses. The discussion above assumed negligible pulse overlaps. Remarkably, Eqs. 14, 15, and 16 still hold in general for any τ,t≥0 and T > 3σ, with the exception that
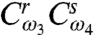 in Eq. 14 must be replaced by
in Eq. 14 must be replaced by
to account for the fact that the third pulse must act in the sample before the LO can detect the polarization (section IV B of SI Appendix). In the case of well-separated pulses, t≫σ, Eq. 17 reduces to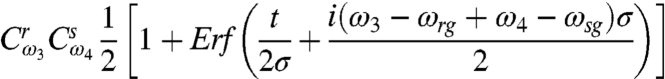
[17] 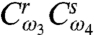 .
.The measurements of the real and imaginary part of the PE signal in the τ,t = 0 limit are recognized with the names of transient dichroism (TD) and transient birefringence (TB), respectively (24), and are very interesting for QPT. For resonant TD/TB (ω3 + ω4 = ωrs + ωsg), Eq. 17) reduces to
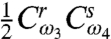 , which shows that the LO monitors only half of the original polarization because it interferes with the polarization as it is generated. Consider such a resonant TD/TB experiment where, even though the pulses can achieve frequency selectivity, they are short in the sense that
, which shows that the LO monitors only half of the original polarization because it interferes with the polarization as it is generated. Consider such a resonant TD/TB experiment where, even though the pulses can achieve frequency selectivity, they are short in the sense that  , where λ is a characteristic reorganization energy scale of the bath. In this situation, the bath state will not evolve during the action of the first two pulses, allowing unambiguous preparation of initial excitonic states tensored with the same initial equilibrium bath configuration (section VIII of SI Appendix), yielding a consistent QPT. Also, for τ, t = 0, the free evolution of the optical coherences does not contribute to the signal, and the short time scale σ does not allow for errors of population or coherence transfers to occur in the preparation or detection stages. Hence, a highlight of the TD/TB signal is that it is determined exclusively by the dynamics of the single-exciton manifold. Scenarios where the TD/TB configuration is preferred compared to the PE are excitonic systems coupled to highly non-Markovian baths (25–28).
, where λ is a characteristic reorganization energy scale of the bath. In this situation, the bath state will not evolve during the action of the first two pulses, allowing unambiguous preparation of initial excitonic states tensored with the same initial equilibrium bath configuration (section VIII of SI Appendix), yielding a consistent QPT. Also, for τ, t = 0, the free evolution of the optical coherences does not contribute to the signal, and the short time scale σ does not allow for errors of population or coherence transfers to occur in the preparation or detection stages. Hence, a highlight of the TD/TB signal is that it is determined exclusively by the dynamics of the single-exciton manifold. Scenarios where the TD/TB configuration is preferred compared to the PE are excitonic systems coupled to highly non-Markovian baths (25–28). Numerical stability of QPT. An investigation of the stability properties of the matrices associated with the reconstruction of χ(T) from the 16 enumerated experiments shows that our protocol is very robust upon the variation of the structural parameters of the system—namely, the ratio between the two dipole norms dB/dA, the angle between the site dipoles ϕ, and the mixing angle θ. General exceptions occur at the vicinity of θ = 0,
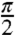 where the coupling J vanishes, as well as for
where the coupling J vanishes, as well as for 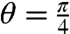 ,
, 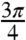 and dB/dA = 1—that is, the homodimer case (sections XI A and B of SI Appendix).
and dB/dA = 1—that is, the homodimer case (sections XI A and B of SI Appendix).
Numerical Example.
To test the extraction of χ from experimental spectra, we consider a dimer with Hamiltonian parameters that are on the order of previously reported experiments consisting of light harvesting systems (18, 29) (ωA = 12,881 cm-1, ωB = 12,719 cm-1, J = 120 cm-1 yielding θ = 0.49). We assume a toolbox of two carrier frequencies ω+ = 13,480 cm-1 and ω- = 12,130 cm-1, respectively, so that ωi∈{ω+,ω-} for all i, and the width of the pulses to be FWHM = 28.3 fs in intensity, which corresponds to σ = 40 fs in amplitude. The parameters satisfy the MDC condition with C′/C′′ = 20. The pulses are long enough to guarantee the selectivity of the produced exciton but short enough to allow for the evolution of the bath induced excitonic dynamics to be monitored. We choose dB/dA = 2 and ϕ = 0.3. We present simulations on the QPT for this system, where each chromophore is linearly coupled to an independent Markovian bath of harmonic oscillators. The dissipative effects are modeled through a secular Redfield model at temperature 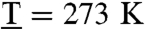 (section X of SI Appendix).
(section X of SI Appendix).
Because we are working in the MDC regime, the signals in Eq. 14 are simply proportional to 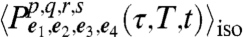 . Fig. 3 plots the 16 real parts of the
. Fig. 3 plots the 16 real parts of the 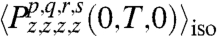 values,§ which can be regarded as signals from the TD/TB setting, or as PE signals with the coherence and echo time propagators factored out. They have been calculated via an isotropic average of Eqs. 15 and 16 (sections VI and XI-B). In our simulations, we consider an inhomogeneously broadened ensemble of 10,000 dimers with diagonal disorder. The site energies are drawn from Gaussian distributions centered about ωA and ωB, respectively, both with standard deviation of σinh = 40 cm-1. For every waiting time T, the signal is calculated with this fixed ensemble. After a normalization step, the signals are of O(1) or smaller. Additional noise simulating experimental errors due to laser fluctuations is included. This consists of independent realizations at every waiting time T of Gaussian noise on the measured signals with zero mean and σlaser = 0.05 standard deviation.
values,§ which can be regarded as signals from the TD/TB setting, or as PE signals with the coherence and echo time propagators factored out. They have been calculated via an isotropic average of Eqs. 15 and 16 (sections VI and XI-B). In our simulations, we consider an inhomogeneously broadened ensemble of 10,000 dimers with diagonal disorder. The site energies are drawn from Gaussian distributions centered about ωA and ωB, respectively, both with standard deviation of σinh = 40 cm-1. For every waiting time T, the signal is calculated with this fixed ensemble. After a normalization step, the signals are of O(1) or smaller. Additional noise simulating experimental errors due to laser fluctuations is included. This consists of independent realizations at every waiting time T of Gaussian noise on the measured signals with zero mean and σlaser = 0.05 standard deviation.
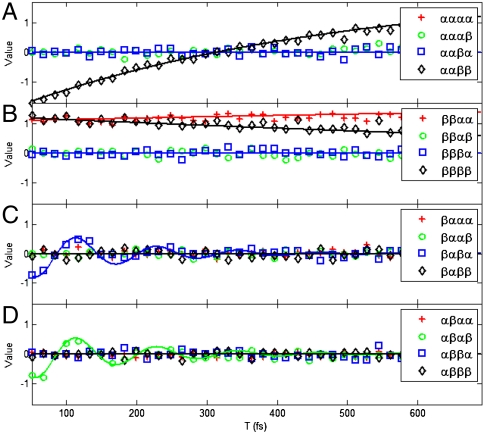
Fig. 3.
Polarization signals from 16 two-color experiments for fixed τ = t = 0. The legends pqrs correspond to the real parts of the isotropically averaged signals 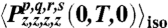 . The panels are organized by QPT initial state: A for
. The panels are organized by QPT initial state: A for 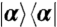 , B for
, B for 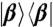 , C for
, C for 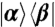 , and D for
, and D for 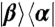 . The ideal signals are depicted as continuous functions whereas the simulations with inhomogeneous broadening and noise are represented as discrete points of the same color. The imaginary parts show a similar agreement between ideal and noisy results.
. The ideal signals are depicted as continuous functions whereas the simulations with inhomogeneous broadening and noise are represented as discrete points of the same color. The imaginary parts show a similar agreement between ideal and noisy results.
Fig. 3 plots the ideal and inhomogeneously broadened, noisy signals as continuous and discrete points, respectively. The ideal signals are calculated from a single dimer with no disorder and without laser fluctuations. All plots start at T = 3σ = 51 fs, because for earlier times, the initial states are not yet effectively prepared. Errors in experimental signals 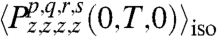 translate into errors of reconstructed χ(T). An estimate of the amplification of relative errors is set by the condition numbers of the matrices to be inverted, which is lower than κ = 2.9 for our set of parameters dB/dA, θ, ϕ (section XI B of SI Appendix). Reconstruction of χ must respect the known symmetries, Eqs. 2–4. Eqs. 2 and 3 are built into the corresponding matrix equations, but Eq. 4 must be included by using a semidefinite programming routine. The latter is implemented using the open-source package CVX (30), and the result is Fig. 4, which shows the discrete points representing the reconstructed elements of χ(T) from noisy data on top of the ideal results plotted as continuous functions of T. The relative error of the inverted χ(T) averages to 0.12. Notice that despite the significant inhomogeneous broadening and noise, there is remarkable agreement between the ideal and the reconstructed values. This finding is reminiscent of studies due to Humble and Cina (31).
translate into errors of reconstructed χ(T). An estimate of the amplification of relative errors is set by the condition numbers of the matrices to be inverted, which is lower than κ = 2.9 for our set of parameters dB/dA, θ, ϕ (section XI B of SI Appendix). Reconstruction of χ must respect the known symmetries, Eqs. 2–4. Eqs. 2 and 3 are built into the corresponding matrix equations, but Eq. 4 must be included by using a semidefinite programming routine. The latter is implemented using the open-source package CVX (30), and the result is Fig. 4, which shows the discrete points representing the reconstructed elements of χ(T) from noisy data on top of the ideal results plotted as continuous functions of T. The relative error of the inverted χ(T) averages to 0.12. Notice that despite the significant inhomogeneous broadening and noise, there is remarkable agreement between the ideal and the reconstructed values. This finding is reminiscent of studies due to Humble and Cina (31).
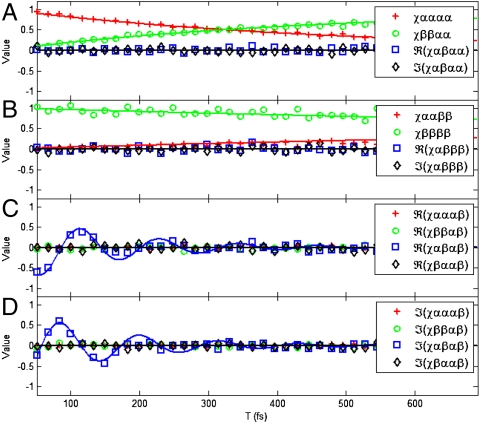
Fig. 4.
Elements of χ(T) for the numerical example. The true values are shown as a continuous function, whereas the discrete points represent the extraction from noisy data. The panels are organized according to the initial state, A for 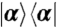 , B for
, B for 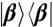 , and C and D for
, and C and D for 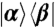 .
.
Fig. 4 illustrates the final objective of a coupled dimer QPT, namely, the process matrix χ(T). Each panel shows processes of the density matrix as a function of T, conditional on the initial state being αα (A), ββ (B), or αβ (C and D), with the ideal T-dependence. The detailed balance condition in the Redfield model implies that 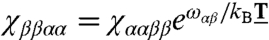 , which can be seen in panels A and B. Also, note that due to the secular approximation, coherence-to-population and the reverse processes are zero. Note that all the decoherence processes in our model occur within a time scale of hundreds of femtoseconds, with the αβ coherence evolving through about three periods before practically vanishing (C and D). Clearly, a more complex interplay of the excitonic system with the phonon bath is possible (32), but this example illustrates the essence of the type of information that can be obtained through QPT.
, which can be seen in panels A and B. Also, note that due to the secular approximation, coherence-to-population and the reverse processes are zero. Note that all the decoherence processes in our model occur within a time scale of hundreds of femtoseconds, with the αβ coherence evolving through about three periods before practically vanishing (C and D). Clearly, a more complex interplay of the excitonic system with the phonon bath is possible (32), but this example illustrates the essence of the type of information that can be obtained through QPT.
Conclusions
In this article, we have introduced QPT as a powerful tool to systematically characterize the dynamics of excitonic systems in condensed phases. We identified the coherence, waiting, and echo intervals of the PE experiment with the state preparation, free evolution, and detection stages of a QPT. In order to achieve selective state preparation and detection, we suggested frequency control through pulses of two different colors, although scenarios with time delays and pulse polarizations as control knobs were also discussed here and elsewhere (20, 33). By choosing between these colors for each of the four pulses, 16 experiments can be carried out, which yield all the elements of χ(T) related to the single-exciton manifold. An analysis of the reconstruction of χ(T) in the presence of inhomogeneous broadening and experimental noise was provided, and the simulation on a model system shows that QPT of an excitonic system in condensed phase is a very plausible goal.
Equipped with χ(T), which completely characterizes the excitonic dynamics, a plethora of questions can be rigorously answered about it. Some examples are: Can the bath be described as Markovian? If so, does the secular approximation hold, or can a population spontaneously be transferred to a coherence (34)? If not, what is its degree of non-Markovianity (35, 36)? Does a given master equation accurately describe the dynamics of the system? What is the time scale of each decoherence process? Are the baths coupled to each chromophore correlated (37, 38)? How much entanglement is induced in the system upon photoexcitation (39)? Once these questions are answered, interesting questions of control (40) and manipulation of excitons can be asked.
In summary, a QIP approach to nonlinear spectroscopy via QPT offers novel insights on the ways to design experiments in order to extract information about the quantum state of the energy transfer system. We believe this work bridges a gap between theoretical and experimental studies on excitation energy transfer from the QIP and physical chemistry communities, respectively.
Supplementary Material
Acknowledgments.
We acknowledge stimulating discussions with Hohjai Lee, Dylan Arias, Patrick Wen, and Keith Nelson. This work was supported by the Center of Excitonics, an Energy Frontier Research Center funded by the US Department of Energy, Office of Science, Office of Basic Energy Sciences under Award Number DESC0001088 and the Harvard University Center for the Environment.
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1110642108/-/DCSupplemental.
*We use the word polarization in two different ways: to denote (a) the orientation of oscillations of the electric field and (b) the density of electric dipole moments in a material. The meaning should be clear by the context.
†More precisely, the monitored signal is proportional to 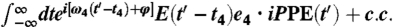 , where two experiments are conducted by varying the phase φ of the LO with respect to the emitted polarization to extract the real and imaginary terms of Eq. 7. For purposes of our discussion, it is enough to consider the complex valued signal.
, where two experiments are conducted by varying the phase φ of the LO with respect to the emitted polarization to extract the real and imaginary terms of Eq. 7. For purposes of our discussion, it is enough to consider the complex valued signal.
‡By comparing Eqs. 7 and 14, we notice that both 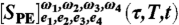 and
and 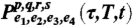 are related to iPPE via a real proportionality constant. Although we shall denote
are related to iPPE via a real proportionality constant. Although we shall denote 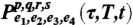 loosely as a polarization, when referring to its real and imaginary parts, we must remember that they are proportional to the real and imaginary parts of the signal
loosely as a polarization, when referring to its real and imaginary parts, we must remember that they are proportional to the real and imaginary parts of the signal 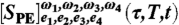 , and to the imaginary and real parts of the actual polarization PPE, respectively.
, and to the imaginary and real parts of the actual polarization PPE, respectively.
§The imaginary parts are not presented due to lack of space, but they show similar features.
References
- 1.Khalil M, Demirdöven N, Tokmakoff A. Vibrational coherence transfer characterized with fourier-transform 2d ir spectroscopy. J Chem Phys. 2004;121:362–373. doi: 10.1063/1.1756870. [DOI] [PubMed] [Google Scholar]
- 2.Stone KW, et al. Two-quantum 2D FT electronic spectroscopy of biexcitons in GaAs quantum wells. Science. 2009;324:1169–1173. doi: 10.1126/science.1170274. [DOI] [PubMed] [Google Scholar]
- 3.Collini E, Scholes GD. Coherent intrachain energy migration in a conjugated polymer at room temperature. Science. 2009;323:369–373. doi: 10.1126/science.1164016. [DOI] [PubMed] [Google Scholar]
- 4.Womick JM, Moran AM. Exciton coherence and energy transport in the light-harvesting dimers of allophycocyanin. J Phys Chem B. 2009;113:15747–15759. doi: 10.1021/jp907644h. [DOI] [PubMed] [Google Scholar]
- 5.Panitchayangkoon G, et al. Long-lived quantum coherence in photosynthetic complexes at physiological temperature. Proc Natl Acad Sci USA. 2010;107:12766–12770. doi: 10.1073/pnas.1005484107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Harel E, Fidler AF, Engel GS. Real-time mapping of electronic structure with single-shot two-dimensional electronic spectroscopy. Proc Natl Acad Sci USA. 2010;107:16444–16447. doi: 10.1073/pnas.1007579107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Mukamel S. Principles of Nonlinear Optical Spectroscopy. Oxford: Oxford Univ Press; 1995. [Google Scholar]
- 8.Cho M. Two Dimensional Optical Spectroscopy. Boca Raton, FL: CRC; 2009. [Google Scholar]
- 9.Dunn TJ, Walmsley IA, Mukamel S. Experimental determination of the quantum-mechanical state of a molecular vibrational mode using fluorescence tomography. Phys Rev Lett. 1995;74:884–887. doi: 10.1103/PhysRevLett.74.884. [DOI] [PubMed] [Google Scholar]
- 10.Humble TS, Cina JA. Molecular state reconstruction by nonlinear wave packet interferometry. Phys Rev Lett. 2004;93:060402. doi: 10.1103/PhysRevLett.93.060402. [DOI] [PubMed] [Google Scholar]
- 11.Nielsen MA, Chuang IL. Quantum Computation and Quantum Information. Cambridge, UK: Cambridge Univ Press; 2000. [Google Scholar]
- 12.Mohseni M, Lidar DA. Direct characterization of quantum dynamics. Phys Rev Lett. 2006;97:170501. doi: 10.1103/PhysRevLett.97.170501. [DOI] [PubMed] [Google Scholar]
- 13.Sudarshan ECG, Mathews PM, Rau J. Stochastic dynamics of quantum-mechanical systems. Phys Rev. 1961;121:920–924. [Google Scholar]
- 14.Weinstein YS, et al. Quantum process tomography of the quantum fourier transform. J Chem Phys. 2004;121:6117–6133. doi: 10.1063/1.1785151. [DOI] [PubMed] [Google Scholar]
- 15.Myrskog SH, Fox JK, Mitchell MW, Steinberg AM. Quantum process tomography on vibrational states of atoms in an optical lattice. Phys Rev A. 2005;72:013615. [Google Scholar]
- 16.Bialczak RC, et al. Quantum process tomography of a universal entangling gate implemented with Josephson phase qubits. Nat Phys. 2010;6:409–413. [Google Scholar]
- 17.Shabani A, et al. Efficient measurement of quantum dynamics via compressive sensing. Phys Rev Lett. 2011;106:100401. doi: 10.1103/PhysRevLett.106.100401. [DOI] [PubMed] [Google Scholar]
- 18.Kjellberg P, Brüggemann B, Pullerits T. Two-dimensional electronic spectroscopy of an excitonically coupled dimer. Phys Rev B. 2006;74:024303. [Google Scholar]
- 19.Liu ZF, et al. Crystal structure of spinach major light-harvesting complex at 2.72 angstrom resolution. Nature. 2004;428:287–292. doi: 10.1038/nature02373. [DOI] [PubMed] [Google Scholar]
- 20.Yuen-Zhou J, Aspuru-Guzik A. Quantum process tomography of excitonic dimers from two-dimensional electronic spectroscopy. i. General theory and application to homodimers. J Chem Phys. 2011;134:134505. doi: 10.1063/1.3569694. [DOI] [PubMed] [Google Scholar]
- 21.Lott GA, Perdomo-Ortiz A, Utterback JK, Aspuru-Guzik A, Marcus AH. Conformation of self-assembled porphyrin dimers in liposome vesicles by phase-modulation 2D fluorescence spectroscopy. Proc Natl Acad Sci USA. 2011;108:16521–16526. doi: 10.1073/pnas.1017308108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Khalil M, Demirdoven N, Tokmakoff A. Coherent 2D IR spectroscopy: Molecular structure and dynamics in solution. J Phys Chem A. 2003;107:5258–5279. [Google Scholar]
- 23.Jonas DM. Two-dimensional femtosecond spectroscopy. Annu Rev Phys Chem. 2003;54:425–463. doi: 10.1146/annurev.physchem.54.011002.103907. [DOI] [PubMed] [Google Scholar]
- 24.Cho M, Fleming GR, Mukamel S. Nonlinear response functions for birefringence and dichroism measurements in condensed phases. J Chem Phys. 1993;98:5314–5326. [Google Scholar]
- 25.Cina JA, Kilin DS, Humble TS. Wavepacket interferometry for short-time electronic energy transfer: Multidimensional optical spectroscopy in the time domain. J Chem Phys. 2003;118:46–61. [Google Scholar]
- 26.Biggs JD, Cina JA. Using wave-packet interferometry to monitor the external vibrational control of electronic excitation transfer. J Chem Phys. 2009;131:224101. doi: 10.1063/1.3257596. [DOI] [PubMed] [Google Scholar]
- 27.Biggs JD, Cina JA. Calculations of nonlinear wave-packet interferometry signals in the pump-probe limit as tests for vibrational control over electronic excitation transfer. J Chem Phys. 2009;131:224302. doi: 10.1063/1.3257597. [DOI] [PubMed] [Google Scholar]
- 28.Hanna G, Geva E. Multidimensional spectra via the mixed quantum-classical Liouville method: Signatures of nonequilibrium dynamics. J Phys Chem B. 2009;113:9278–9288. doi: 10.1021/jp902797z. [DOI] [PubMed] [Google Scholar]
- 29.Lee H, Cheng YC, Fleming GR. Coherence dynamics in photosynthesis: Protein protection of excitonic coherence. Science. 2007;316:1462–1465. doi: 10.1126/science.1142188. [DOI] [PubMed] [Google Scholar]
- 30.Grant M, Boyd S. CVX: Matlab software for disciplined convex programming, version 1.21. 2011.
- 31.Humble T, Cina J. Nonlinear wave-packet interferometry and molecular state reconstruction in a vibrating and rotating diatomic molecule. J Phys Chem B. 2006;110:18879–18892. doi: 10.1021/jp0567669. [DOI] [PubMed] [Google Scholar]
- 32.Leggett AJ, et al. Dynamics of the dissipative two-state system. Rev Mod Phys. 1987;59:1–85. [Google Scholar]
- 33.Rebentrost P, Shim S, Yuen-Zhou J, Aspuru-Guzik A. Characterization and quantification of the role of coherence in ultrafast quantum biological experiments using quantum master equations, atomistic simulations, and quantum process tomography. Procedia Chem. 2010;3:332–346. [Google Scholar]
- 34.Ishizaki A, Fleming GR. On the adequacy of the Redfield equation and related approaches to the study of quantum dynamics in electronic energy transfer. J Chem Phys. 2009;130:234110. doi: 10.1063/1.3155214. [DOI] [PubMed] [Google Scholar]
- 35.Cheng YC, Engel GS, Fleming GR. Elucidation of population and coherence dynamics using cross-peaks in two-dimensional electronic spectroscopy. Chem Phys. 2007;341:285–295. [Google Scholar]
- 36.Rebentrost P, Aspuru-Guzik A. Communication: Exciton-phonon information flow in the energy transfer process of photosynthetic complexes. J Chem Phys. 2011;134:101103. doi: 10.1063/1.3563617. [DOI] [PubMed] [Google Scholar]
- 37.Ishizaki A, Fleming GR. Theoretical examination of quantum coherence in a photosynthetic system at physiological temperature. Proc Natl Acad Sci USA. 2009;106:17255–17260. doi: 10.1073/pnas.0908989106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Kofman AG, Korotkov AN. Two-qubit decoherence mechanisms revealed via quantum process tomography. Phys Rev A. 2009;80:042103. [Google Scholar]
- 39.Sarovar M, Ishizaki A, Fleming G, Whaley K. Quantum entanglement in photosynthetic light-harvesting complexes. Nat Phys. 2010;6:462–467. [Google Scholar]
- 40.Brumer PW, Shapiro M. Principles of the Quantum Control of Molecular Processes. Hoboken, NJ: Wiley-Interscience; 2003. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.