Mathematical properties of F_st between admixed populations and their parental source populations

Abstract

We consider the properties of the F_st measure of genetic divergence between an admixed population and its parental source populations. Among all possible populations admixed among an arbitrary set of parental populations, we show that the value of F_st between an admixed population and a specific source population is maximized when the admixed population is simply the most distant of the other source populations. For the case with only two parental populations, as a function of the admixture fraction, we further demonstrate that this F_st value is monotonic and convex, so that F_st is informative about the admixture fraction. We illustrate our results using example human population-genetic data, showing how they provide a framework in which to interpret the features of F_st in admixed populations.

1. Introduction

The well-known “fixation index” F_st quantifies the extent to which a polymorphic population is subdivided into subpopulations (Wright (1951), Excoffier (2001), Rousset (2001), Balding (2003), Holsinger and Weir (2009)). In a definition due to Nei (1973, 1987), F_st is defined in terms of the expected heterozygosity of the overall population and the mean expected heterozygosity across the subpopulations:

• Definition The expected heterozygosity in a population for a given locus with I distinct alleles is defined as $H=1-{\displaystyle {\sum }_{i=1}^I}{p}_i^2$, where p_i is the frequency of allele i.

• Definition At a given locus, the fixation index, F_st, is defined as F_st = (H_t − H_s)/H_t, where H_t is the expected heterozygosity of the overall population, and H_s is the mean expected heterozygosity across subpopulations.

Assuming that the subpopulations have equal contribution to the total population, H_t is computed by pooling the various subpopulations in equal proportion, and H_s is calculated by weighting the various subpopulations equally. Recall that F_st always lies between 0 and 1, and that F_st is 0 if and only if H_t = H_s, meaning that the pooled population is unstructured. F_st increases as the genetic differentiation between the various subpopulations increases, and the theoretical maximum of 1 is reached if and only if each subpopulation is entirely monomorphic (and homozygous).

We consider the fixation index in the context of admixture, where one population arises from the amalgamation of multiple populations, typically after a long period of relative isolation for the founding groups. Admixture scenarios have been abundant over the course of human history, and for admixture events that have occurred recently, the admixture process has left a detectable signature in the genomes of admixed individuals. For example, the contributions of European, Native American, and African populations to the genetic history of African American (Parra et al. (1998, 2001), Salas et al. (2005), Tang et al. (2006b), Tishkoff et al. (2009), Zakharia et al. (2009), Bryc et al. (2010a)) and Hispanic and Mestizo (Bonilla et al. (2004), Seldin et al. (2007), Tang et al. (2007), Wang et al. (2008), Risch et al. (2009), Silva-Zolezzi et al. (2009), Bryc et al. (2010b)) populations have been the focus of much investigation. Genetic studies of admixture have further been of interest not only for what they reveal about population history, but also because admixed populations can be used in locating disease-associated genomic regions through methods that search in admixed individuals for regions of the genome with excess ancestry from the ancestral population in which a disease is more prevalent (reviewed by McKeigue (2005), Reich and Patterson (2005), Smith and O’Brien (2005), Seldin (2007), Buerkle and Lexer (2008), Zhu et al. (2008),Winkler et al. (2010)).

In an admixture setting, we provide a theoretical framework for explaining the properties of F_st between admixed populations and their parental populations. We examine the values of F_st between pairs of populations, in which one member of the pair is an admixed population and the other is one of its parental source populations. After introducing notation and an example dataset in Section 2, in Section 3, we prove our main theorem, which concerns the value of F_st between a population formed by admixture of K founding populations and a specific one of the K founding populations. We show that for any K ≥ 2, considering all admixture combinations for a given set of founding populations, this F_st expression is maximized when the admixed population is in fact one of the other founding populations. In Section 4, we then consider the special case of K = 2 founding populations, proving in Section 4.1 that F_st is monotonic and convex in the admixture coefficient. Section 4.2 uses microsatellite genotype data on Mestizo populations to demonstrate that F_st values predicted using our theoretical results closely match observed F_st values. Section 4.3 then suggests an estimator of admixture on the basis of F_st. Finally, in Section 5, we summarize the main results and discuss their broader implications.

2. Notation and data

We use a simplified form of the F_st value between two populations that have the same contribution to the total population and that when pooled together produce a polymorphic population. Denote by p_1i the frequency of allele i in population 1 and by p_2i the frequency of allele i in population 2. We then have

$$\begin{array}{cc}\hfill H_t& =1-{\displaystyle \sum _{i=1}^I}{\left[\frac{1}{2}(p_{1i}+p_{2i})\right]}^2=1-\frac{1}{4}{\displaystyle \sum _{i=1}^I}{(p_{1i}+p_{2i})}^2\hfill \\ \hfill H_s& =\frac{1}{2}\left[\right(1-{\displaystyle \sum _{i=1}^I}{p}_{1i}^2)+(1-{\displaystyle \sum _{i=1}^I}{p}_{2i}^2\left)\right]=1-\frac{1}{2}{\displaystyle \sum _{i=1}^I}(p_{1i}^2+p_{2i}^2)\hfill \\ \hfill H_t-H_s& =\frac{1}{4}{\displaystyle \sum _{i=1}^I}[2p_{1i}^2+2p_{2i}^2-{(p_{1i}+p_{2i})}^2]=\frac{1}{4}{\displaystyle \sum _{i=1}^I}{(p_{1i}-p_{2i})}^2\hfill \\ \hfill F_{\mathit{\text{st}}}& =\frac{H_t-H_s}{H_t}=\frac{\frac{1}{4}{\displaystyle {\sum }_{i=1}^I}{(p_{1i}-p_{2i})}^2}{1-\frac{1}{4}{\displaystyle {\sum }_{i=1}^I}{(p_{1i}+p_{2i})}^2}=\frac{{\displaystyle {\sum }_{i=1}^I}{(p_{1i}-p_{2i})}^2}{4-{\displaystyle {\sum }_{i=1}^I}{(p_{1i}+p_{2i})}^2}.\hfill \end{array}$$ (1)

Table 1 summarizes the notation for the scenario in which K ≥ 2 founding populations give rise to an admixed population. Denote by r_i the frequency of allele i in the admixed population. Let γ_k represent the admixture fraction corresponding to population k, so that fraction γ_k of the ancestry of the admixed population derives from source population k. The admixed population then has

$$r_i={\displaystyle \sum _{k=1}^K}{\gamma }_k{p}_{\mathit{\text{ki}}},$$

where γ_k ≥ 0 for 1 ≤ k ≤ K and ${\displaystyle {\sum }_{k=1}^K}{\gamma }_k=1$. We assume throughout the paper that there exists at least one pair of founding populations, k and ℓ, for which $\underset{¯}{p_k}\ne \underset{¯}{p_{\ell }}$. This assumption corresponds to an assumption that the founding populations do not all have identical allele frequencies.

Table 1.

Notation.

Type of quantity	Symbol	Description
Indices	i = 1,…, I	Index over alleles
	k = 1,…, K	Index over populations
Allele frequencies	pki	Frequency of allele i in population k
	$\underset{¯}{p_k}$	Vector of allele frequencies for population k
	ri	Frequency of allele i in the admixed population
Admixture fractions	γk	Admixture fraction for population k
	γ̲	Vector of admixture fractions

The example scenarios that we consider use a subset of the data from Wang et al. (2008), consisting of genotypes of 249 Mestizos, 160 Europeans, 463 Native Americans, and 123 Africans at 678 autosomal microsatellite loci. The Mestizo samples provide an example of admixture primarily between European and Native American founding populations, and to a lesser extent, African populations. In our analyses, we focus on the European and Native American contributions, treating the full Mestizo sample as an admixed population and the European and Native American samples as its founding populations. In each of the population samples, except where otherwise specified (in particular, in Section 4.2), we treat the sample allele frequencies from Wang et al. (2008) as the parametric allele frequencies.

3. General case: K founding populations

Our goal in this section is to examine F_st to a specific founding population over the space of admixture vectors possible for a population admixed among a given collection of K founding populations. We begin by providing an expression for F_st between the admixed population and a specific founding population. Without loss of generality, we investigate F_st between population 1 and the admixed population. Using eq. 1 and viewing F_st as a function of two allele frequency vectors, we have

$$F_{\mathit{\text{st}}}(\underset{¯}{p_1},\underset{¯}{r})=\frac{{\displaystyle {\sum }_{i=1}^I}{(p_{1i}-{\displaystyle {\sum }_{k=1}^K}{\gamma }_k{p}_{ki})}^2}{4-{\displaystyle {\sum }_{i=1}^I}{(p_{1i}+{\displaystyle {\sum }_{k=1}^K}{\gamma }_k{p}_{ki})}^2}.$$ (2)

In Theorem 2, we obtain a result concerning the maximum over admixed populations of F_st between the admixed population and an arbitrarily chosen founding population. We first prove a preliminary result involving F_st between one population and a population formed by admixture of two other populations.

Lemma 1 (Three-population lemma). Denote by $\underset{¯}{p_1},\underset{¯}{p_2},\underset{¯}{p_3}$ the vectors corresponding to the allele frequencies of three populations. Consider a population formed by admixture between populations 2 and 3, where γ ∈ [0, 1] represents the admixture fraction for population 2. Then

$$\underset{\gamma \in [0,1]}{\text{max}}{F}_{\mathit{\text{st}}}[\underset{¯}{p_1},\gamma \underset{¯}{p_2}+(1-\gamma )\underset{¯}{p_3}]=\text{max}\{F_{\mathit{\text{st}}}(\underset{¯}{p_1},\underset{¯}{p_2}),F_{\mathit{\text{st}}}(\underset{¯}{p_1},\underset{¯}{p_3})\}.$$

Proof. We start by applying eq. 1 to calculate F_st between population 1 and the population formed by admixture of populations 2 and 3. We also introduce some additional variables, δ_13i = p_1i − p_3i, δ_23i = p_2i − p_3i, and τ_13i = p_1i + p_3i, for 1 ≤ i ≤ I, to simplify the notation. Then

$$\begin{array}{cc}{F}_{\mathit{\text{st}}}[\underset{¯}{p_1},\gamma \underset{¯}{p_2}+(1-\gamma )\underset{¯}{p_3}]\hfill & =\frac{{\displaystyle {\sum }_{i=1}^I}{[p_{1i}-\gamma p_{2i}-(1-\gamma )p_{3i}]}^2}{4-{\displaystyle {\sum }_{i=1}^I}{[p_{1i}+\gamma p_{2i}+(1-\gamma )p_{3i}]}^2}\hfill \\ \hfill & =\frac{{\displaystyle {\sum }_{i=1}^I}{({\delta }_{13i}-\gamma {\delta }_{23i})}^2}{4-{\displaystyle {\sum }_{i=1}^I}{({\tau }_{13i}+\gamma {\delta }_{23i})}^2}.\hfill \end{array}$$ (3)

We denote the function $F_{\mathit{\text{st}}}[\underset{¯}{p_1},\gamma \underset{¯}{p_2}+(1-\gamma )\underset{¯}{p_3}]$ by G(γ), to emphasize the fact that we aim to maximize this quantity with respect to γ. To calculate the derivative of G(γ), we first do some preliminary calculations:

$$\begin{array}{cc}\hfill \frac{d}{d\gamma }{\displaystyle \sum _{i=1}^I}{({\delta }_{13i}-\gamma {\delta }_{23i})}^2& =-2{\displaystyle \sum _{i=1}^I}{\delta }_{23i}({\delta }_{13i}-\gamma {\delta }_{23i})\hfill \\ \hfill \frac{d}{d\gamma }[4-{\displaystyle \sum _{i=1}^I}{({\tau }_{13i}+\gamma {\delta }_{23i})}^2]& =-2{\displaystyle \sum _{i=1}^I}{\delta }_{23i}({\tau }_{13i}+\gamma {\delta }_{23i}).\hfill \end{array}$$

Putting these results together, we obtain

$$\frac{d}{d\gamma }G(\gamma )=\frac{-2[{\displaystyle {\sum }_{i=1}^I}{\delta }_{23i}({\delta }_{13i}-\gamma {\delta }_{23i})][4-{\displaystyle {\sum }_{i=1}^I}{({\tau }_{13i}+\gamma {\delta }_{23i})}^2]+2[{\displaystyle {\sum }_{i=1}^I}{({\delta }_{13i}-\gamma {\delta }_{23i})}^2][{\displaystyle {\sum }_{i=1}^I}{\delta }_{23i}({\tau }_{13i}+\gamma {\delta }_{23i})]}{{[4-{\displaystyle {\sum }_{i=1}^I}{({\tau }_{13i}+\gamma {\delta }_{23i})}^2]}^2}.$$

The denominator is always positive, so we focus on the numerator to see where it is greater or less than 0. We denote half the numerator by E(γ), and note that E(γ) is a polynomial in γ, of degree at most 2. We denote the coefficients of γ², γ, and 1 in E(γ), by a, b, and c, respectively, and calculate them individually:

$$\begin{array}{cc}a\hfill & =-2\left({\displaystyle \sum _{i=1}^I}{\delta }_{23i}^2\right)\left({\displaystyle \sum _{i=1}^I}{p}_{1i}{\delta }_{23i}\right)\hfill \\ b\hfill & =4\left({\displaystyle \sum _{i=1}^I}{\delta }_{23i}^2\right)(1-{\displaystyle \sum _{i=1}^I}{p}_{1i}{p}_{3i})\hfill \\ c\hfill & =-4\left({\displaystyle \sum _{i=1}^I}{\delta }_{13i}{\delta }_{23i}\right)+\left({\displaystyle \sum _{i=1}^I}{\delta }_{13i}{\delta }_{23i}\right)\left({\displaystyle \sum _{i=1}^I}{\tau }_{13i}^2\right)+\left({\displaystyle \sum _{i=1}^I}{\tau }_{13i}{\delta }_{23i}\right)\left({\displaystyle \sum _{i=1}^I}{\delta }_{13i}^2\right).\hfill \end{array}$$ (4)

We next show that E(γ) is increasing or decreasing on [0, 1]. If a = 0, then E(γ) is linear, and the claim is trivial (a and b cannot both be zero, because a = b = 0 implies that populations 2 and 3 have identical allele frequencies). Suppose a ≠ 0. We show that the position of the vertex of the parabola E(γ) = aγ² + bγ + c, or −b/(2a), is not in (0, 1). We first note that $1={\displaystyle {\sum }_{i=1}^I}{p}_{1i}\ge {\displaystyle {\sum }_{i=1}^I}{p}_{1i}{p}_{3i}$, so that b ≥ 0. Consequently, if −b/(2a) > 0, then a < 0 and ${\displaystyle {\sum }_{i=1}^I}{p}_{1i}{p}_{2i}>{\displaystyle {\sum }_{i=1}^I}{p}_{1i}{p}_{3i}$. If 0 < −b/(2a) < 1, then we also have $1-{\displaystyle {\sum }_{i=1}^I}{p}_{1i}{p}_{3i}<{\displaystyle {\sum }_{i=1}^I}{p}_{1i}{p}_{2i}-{\displaystyle {\sum }_{i=1}^I}{p}_{1i}{p}_{3i}$, which means that $1<{\displaystyle {\sum }_{i=1}^I}{p}_{1i}{p}_{2i}$. This inequality clearly does not hold, because $1={\displaystyle {\sum }_{i=1}^I}{p}_{1i}\ge {\displaystyle {\sum }_{i=1}^I}{p}_{1i}{p}_{2i}$. As a result, −b/(2a) ∉ (0, 1), so that the extrema of E(γ) on [0, 1] must occur at γ = 0 and γ = 1. It follows that E(γ) is either increasing or decreasing for γ ∈ (0, 1).

To demonstrate that E(γ) is increasing, we show that E(1) > E(0):

$$\begin{array}{cc}E(1)-E(0)\hfill & =-2\left({\displaystyle \sum _{i=1}^I}{\delta }_{23i}^2\right)\left({\displaystyle \sum _{i=1}^I}{p}_{1i}{\delta }_{23i}\right)+4\left({\displaystyle \sum _{i=1}^I}{\delta }_{23i}^2\right)(1-{\displaystyle \sum _{i=1}^I}{p}_{1i}{p}_{3i})\hfill \\ \hfill & =2\left({\displaystyle \sum _{i=1}^I}{\delta }_{23i}^2\right)(2-{\displaystyle \sum _{i=1}^I}{p}_{1i}{p}_{2i}-{\displaystyle \sum _{i=1}^I}{p}_{1i}{p}_{3i}).\hfill \end{array}$$

We note that ${\displaystyle {\sum }_{i=1}^I}{\delta }_{23i}^2>0$ by the assumption that populations 2 and 3 do not have identical allele frequencies, and $2={\displaystyle {\sum }_{i=1}^I}{p}_{2i}+{\displaystyle {\sum }_{i=1}^I}{p}_{3i}>{\displaystyle {\sum }_{i=1}^I}{p}_{1i}{p}_{2i}+{\displaystyle {\sum }_{i=1}^I}{p}_{1i}{p}_{3i}$. This inequality is strict by this same assumption, as population 1 cannot have identical allele frequencies to both populations 2 and 3. Consequently, E(1) > E(0), and E(γ) is increasing on γ ∈ [0, 1]. Note that if populations 2 and 3 were switched, so that we instead considered the value of $F_{\mathit{\text{st}}}[\underset{¯}{p_1},(1-\gamma )\underset{¯}{p_2}+\gamma \underset{¯}{p_3}]$ rather than $F_{\mathit{\text{st}}}[\underset{¯}{p_1},\gamma \underset{¯}{p_2}+(1-\gamma )\underset{¯}{p_3}]$, then E(1) − E(0) would not change, and we would reach the same conclusion that E(1) > E(0) and E(γ) is increasing on the interval.

Three possibilities exist for the location of 0: E(1) > E(0) ≥ 0, E(1) > 0 > E(0) or 0 ≥ E(1) > E(0). Because E(γ) only differs from $\frac{d}{d\gamma }G(\gamma )$ by a positive factor, these three possibilities correspond to three possibilities for the shape of G(γ) on γ ∈ [0, 1]: G(γ) is increasing, G(γ) is decreasing up to a point, then increasing, or G(γ) is decreasing. In each of these three cases, it follows that

$$\underset{\gamma \in [0,1]}{\text{max}}{F}_{\mathit{\text{st}}}[\underset{¯}{p_1},\gamma \underset{¯}{p_2}+(1-\gamma )\underset{¯}{p_3}]=\underset{\gamma \in [0,1]}{\text{max}}G(\gamma )=\text{max}\{G(0),G(1)\}=\text{max}\{F_{\mathit{\text{st}}}(\underset{¯}{p_1},\underset{¯}{p_2}),F_{\mathit{\text{st}}}(\underset{¯}{p_1},\underset{¯}{p_3})\}.$$ (5)

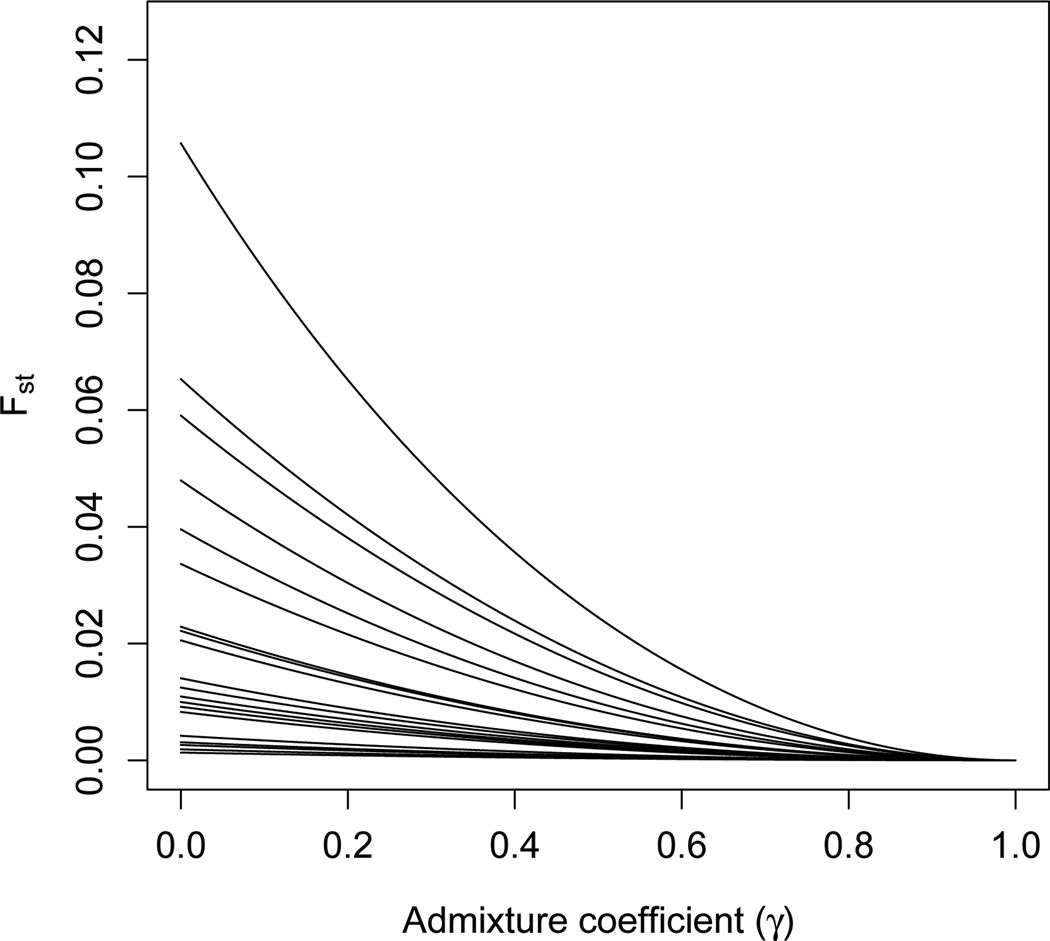
The result of this lemma is illustrated on a data example in Figure 1, in which log₁₀[G(γ)] is plotted against γ. In this case, population 1 represents a Mestizo admixed population, and populations 2 and 3 represent European and Native American populations, respectively. For each of twenty loci considered, as in the lemma, the maximum of the function is located either at γ = 0 or at γ = 1.

Figure 1.

F_st between a population and a hypothetical second population that is admixed between two other populations. log₁₀[G(γ)], seen as a function of γ, is plotted against γ, where G(γ) is $F_{\mathit{\text{st}}}[\underset{¯}{p_1},\gamma \underset{¯}{p_2}+(1-\gamma )\underset{¯}{p_3}]$, (eq. 3). Populations 1, 2, and 3 represent populations of Mestizo, European, and Native American descent, respectively, and $\underset{¯}{p_1},\underset{¯}{p_2}\text{ and }\underset{¯}{p_3}$ are based on allele frequencies estimated from Wang et al. (2008). Twenty randomly selected loci are considered, with each curve representing a different locus. The dots indicate the maxima for individual curves. In accordance with Lemma 1, for γ ∈ [0, 1], the maximal value of log₁₀[G(γ)], and therefore of G(γ), is always at γ = 0 or γ = 1.

We now use the three-population lemma to prove that for any K, F_st between a population formed by admixture of K founding populations and a specific one of those founding populations is maximized when the admixed population is in fact one of the other K − 1 founding populations.

Theorem 2. Denote by $\underset{¯}{p_1},\dots ,\underset{¯}{p_K}$ the vectors corresponding to the allele frequencies of K populations. Consider a population formed by admixture between the K populations, where γ_k ∈ [0, 1] represents the admixture fraction for population k, for 1 ≤ k ≤ K, such that ${\displaystyle {\sum }_{k=1}^K}{\gamma }_k=1$. Then

$$\underset{\underset{¯}{\gamma }}{\text{max}}{F}_{\mathit{\text{st}}}[\underset{¯}{p_1},{\gamma }_1\underset{¯}{p_1}+\dots +{\gamma }_K\underset{¯}{p_K}]=\text{max}\{F_{\mathit{\text{st}}}(\underset{¯}{p_1},\underset{¯}{p_2}),\dots ,F_{\mathit{\text{st}}}(\underset{¯}{p_1},\underset{¯}{p_K})\}.$$ (6)

Proof. We prove this result by induction on K.

• Step 1: K = 2. Taking $\underset{¯}{p_1}\text{ and }\underset{¯}{p_2}$ in place of $\underset{¯}{p_2}\text{ and }\underset{¯}{p_3}$, respectively, Lemma 1 already demonstrates the result in the case that K = 2:

  $$\underset{\gamma \in [0,1]}{\text{max}}{F}_{\mathit{\text{st}}}[\underset{¯}{p_1},\gamma \underset{¯}{p_1}+(1-\gamma )\underset{¯}{p_2}]=\text{max}\{F_{\mathit{\text{st}}}(\underset{¯}{p_1},\underset{¯}{p_1}),F_{\mathit{\text{st}}}(\underset{¯}{p_1},\underset{¯}{p_2})\}=F_{\mathit{\text{st}}}(\underset{¯}{p_1},\underset{¯}{p_2}),$$

  where, for simplicity, we replace γ₁ by γ and γ₂ by 1 − γ.
• Step 2: K → K + 1. We now show that if the result in eq. 6 holds for K populations, then it also holds for K + 1 populations (with γ_K+1 > 0):

  $$\begin{gathered} F_{\mathit{\text{st}}}[\underset{¯}{p_1},{\gamma }_1\underset{¯}{p_1}+\dots +{\gamma }_{K-1}\underset{¯}{p_{K-1}}+{\gamma }_K\underset{¯}{p_K}+{\gamma }_{K+1}\underset{¯}{p_{K+1}}] \\ =F_{\mathit{\text{st}}}[\underset{¯}{p_1},{\gamma }_1\underset{¯}{p_1}+\dots +{\gamma }_{K-1}\underset{¯}{p_{K-1}}+({\gamma }_K+{\gamma }_{K+1})(\frac{{\gamma }_K}{{\gamma }_K+{\gamma }_{K+1}}\underset{¯}{p_K}+\frac{{\gamma }_{K+1}}{{\gamma }_K+{\gamma }_{K+1}}\underset{¯}{p_{K+1}}\left)\right] \\ \le \text{max}\{F_{\mathit{\text{st}}}(\underset{¯}{p_1},\underset{¯}{p_2}),\dots ,F_{\mathit{\text{st}}}(\underset{¯}{p_1},\underset{¯}{p_{K-1}}),F_{\mathit{\text{st}}}(\underset{¯}{p_1},\frac{{\gamma }_K}{{\gamma }_K+{\gamma }_{K+1}}\underset{¯}{p_K}+\frac{{\gamma }_{K+1}}{{\gamma }_K+{\gamma }_{K+1}}\underset{¯}{p_{K+1}}\left)\right\}, \end{gathered}$$

  where the last step follows by the inductive hypothesis, eq. 6, for the case with K populations. The expression $[{\gamma }_K/({\gamma }_K+{\gamma }_{K+1})]\underset{¯}{p_K}+[{\gamma }_{K+1}/({\gamma }_K+{\gamma }_{K+1})]\underset{¯}{p_{K+1}}$ has the form $\gamma \underset{¯}{p_K}+(1-\gamma )\underset{¯}{p_{K+1}}$, with γ_K/(γ_K + γ_K+1) taking on the role of γ. Consequently, using Lemma 1,

  $$F_{\mathit{\text{st}}}[\underset{¯}{p_1},\frac{{\gamma }_K}{{\gamma }_K+{\gamma }_{K+1}}\underset{¯}{p_K}+\frac{{\gamma }_{K+1}}{{\gamma }_K+{\gamma }_{K+1}}\underset{¯}{p_{K+1}}]\le \text{max}\{F_{\mathit{\text{st}}}(\underset{¯}{p_1},\underset{¯}{p_K}),F_{\mathit{\text{st}}}(\underset{¯}{p_1},\underset{¯}{p_{K+1}})\},$$

  so that

  $$F_{\mathit{\text{st}}}[\underset{¯}{p_1},{\gamma }_1\underset{¯}{p_1}+\dots +{\gamma }_{K-1}\underset{¯}{p_{K-1}}+{\gamma }_K\underset{¯}{p_K}+{\gamma }_{K+1}\underset{¯}{p_{K+1}}]\le \text{max}\{F_{\mathit{\text{st}}}(\underset{¯}{p_1},\underset{¯}{p_2}),\dots ,F_{\mathit{\text{st}}}(\underset{¯}{p_1},\underset{¯}{p_{K-1}}),F_{\mathit{\text{st}}}(\underset{¯}{p_1},\underset{¯}{p_K}),F_{\mathit{\text{st}}}(\underset{¯}{p_1},\underset{¯}{p_{K+1}})\}.$$

  Thus, the induction is complete, and we have shown that the result in eq. 6 holds for arbitrary K.

The theorem is sensible, in that considering all possible populations admixed among a given collection of source populations, the most “distant” populations from source population 1 are combinations that do not include ancestry from population 1. The theorem demonstrates that the most distant admixed population according to F_st is precisely one of the remaining source populations, it is not a nontrivial mixture of those source populations, either with each other or with population 1.

An interesting corollary of Theorem 2 is that given a set of K founding populations, considering all admixed populations that can be constructed from those founding populations, the value of F_st between an admixed population and the founding population from which it is maximally distant, or max_{k∈{1,…,K}} $F_{\mathit{\text{st}}}(\underset{¯}{p_k},\underset{¯}{r})$, is bounded above by the maximal F_st among pairs of founding populations, or max_{k,ℓ∈{1,…,K}} $F_{\mathit{\text{st}}}(\underset{¯}{p_k},\underset{¯}{p_{\ell }})$. This result is obtained by simply noting that given k, as a result of the theorem, $F_{\mathit{\text{st}}}(\underset{¯}{p_k},\underset{¯}{r})$ is bounded above by max_{ℓ∈{1,…,K}} $F_{\mathit{\text{st}}}(\underset{¯}{p_k},\underset{¯}{p_{\ell }})$, and by then taking the maximum over k. Thus, according to the F_st measure, an admixed population can be no more distant from any of its founding populations than the two most distant among the founding populations are from each other.

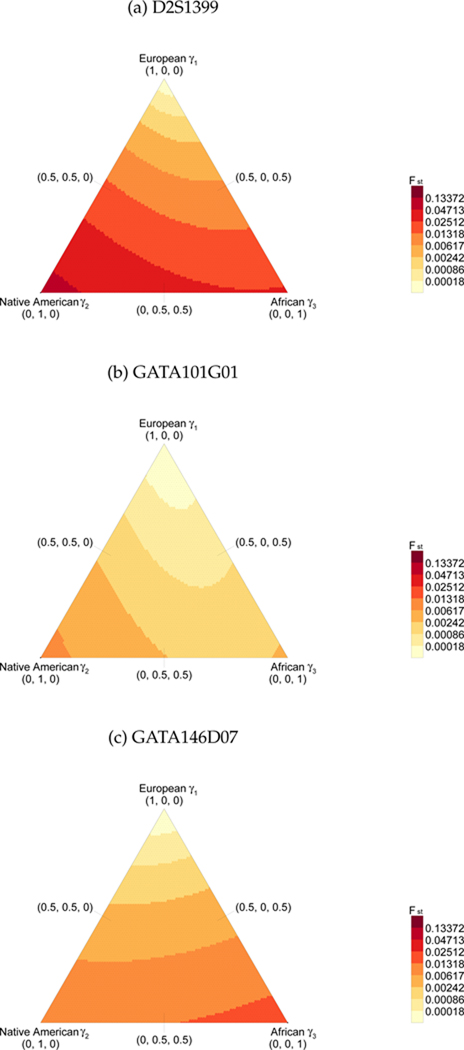
Three examples illustrating the theorem with K = 3 are presented in Figure 2. Sample allele frequencies for three genetic loci in three populations — European, Native American, and African — are used as $\underset{¯}{p_1},\underset{¯}{p_2}\text{ and }\underset{¯}{p_3}$, respectively. The triangular region shown in the figure for a given locus represents the space of possible admixture vectors (γ₁, γ₂, γ₃). For each locus, the maximal value of F_st between the admixed population and population 1 occurs either at the corner represented by γ₂ = 1 or at the corner represented by γ₃ = 1, as established in the theorem.

Figure 2.

F_st between a population and hypothetical admixtures of that population with two other populations. $F_{\mathit{\text{st}}}[\underset{¯}{p_1},{\gamma }_1\underset{¯}{p_1}+{\gamma }_2\underset{¯}{p_2}+{\gamma }_3\underset{¯}{p_3}]$, seen as a function of γ̲, is plotted for all possible values of γ̲ (eq. 2). Populations 1, 2, and 3 represent populations of European, Native American, and African descent, respectively, and $\underset{¯}{p_1},\underset{¯}{p_2}\text{ and }\underset{¯}{p_3}$ are based an allele frequencies estimated from Wang et al. (2008). Three loci are considered. In each triangle, the admixture fractions γ₁, γ₂, and γ₃ vary along the three axes, and darker colors correspond to higher values of F_st. In accordance with Theorem 2, considering all possible γ̲, the maximal value of F_st is always at γ₂ = 1 or γ₃ = 1. (A) Locus D2S1399. (B) Locus GATA101G01. (C) Locus GATA146D07.

4. Special case: Two founding populations

We now consider the special case in which only two founding populations give rise to an admixed population. We can simplify the notation of the previous section, so that γ = γ₁, 1 − γ = γ₂, τ_i = p_1i + p_2i, and δ_i = p_1i − p_2i. Using eq. 1, the F_st value between population 1 and the admixed population can be written as

$$\begin{array}{cc}{F}_{\mathit{\text{st}}}[\underset{¯}{p_1},\gamma \underset{¯}{p_1}+(1-\gamma )\underset{¯}{p_2}]\hfill & =\frac{{\displaystyle {\sum }_{i=1}^I}{[p_{1i}-\gamma p_{1i}-(1-\gamma )p_{2i}]}^2}{4-{\displaystyle {\sum }_{i=1}^I}{[p_{1i}+\gamma p_{1i}+(1-\gamma )p_{2i}]}^2}\hfill \\ \hfill & =\frac{{(1-\gamma )}^2{\displaystyle {\sum }_{i=1}^I}{\delta }_i^2}{4-{\displaystyle {\sum }_{i=1}^I}{({\tau }_i+\gamma {\delta }_i)}^2}.\hfill \end{array}$$ (7)

Thus, in this case, F_st is a function only of the admixture fraction, γ, and the sums and differences of the allele frequencies of the two founding populations. The K = 2 case has fewer parameters than the general case of arbitrary K, and it is therefore possible to more precisely examine the properties of F_st as a function of the single admixture coefficient γ.

We first note that it was shown in the proof of Theorem 2 that the maximal F_st between population 1 and the admixed population is obtained when the admixed population is in fact population 2, so that γ = 0:

$$\underset{\gamma \in [0,1]}{\text{max}}{F}_{\mathit{\text{st}}}[\underset{¯}{p_1},\gamma \underset{¯}{p_1}+(1-\gamma )\underset{¯}{p_2}]=F_{\mathit{\text{st}}}(\underset{¯}{p_1},\underset{¯}{p_2}).$$

4.1. F_st is monotonic and convex in the admixture coefficient

For the case with two founding populations, it is of interest to determine whether F_st behaves in a predictable way as a function of γ. We now show that F_st between a founding population and the admixed population is monotonic in the admixture coefficient.

Theorem 3. As a function of γ, $F_{\mathit{\text{st}}}[\underset{¯}{p_1},\gamma \underset{¯}{p_1}+(1-\gamma )\underset{¯}{p_2}]$ is decreasing for γ ∈ [0, 1].

Proof. Let α = 1 − γ. We can use portions of the proof of Lemma 1, with $\underset{¯}{p_1}$ in the role of $\underset{¯}{p_3}$. Following the proof of Lemma 1, for $F_{\mathit{\text{st}}}[\underset{¯}{p_1},\alpha \underset{¯}{p_2}+(1-\alpha )\underset{¯}{p_1}]$, E(α) = aα² + bα + c. Plugging in α = 0, E(α) = c. Noting in eq. 4 that δ_13i = 0 when $\underset{¯}{p_3}=\underset{¯}{p_1}$, we get E(0) = 0. We then have E(1) > E(0) ≥ 0, so that G(α) is increasing on α ∈ [0, 1]. As a result, $G(1-\alpha )=G(\gamma )=F_{\mathit{\text{st}}}[\underset{¯}{p_1},\gamma \underset{¯}{p_1}+(1-\gamma )\underset{¯}{p_2}]$ is decreasing in γ on γ ∈ [0, 1].

The theorem supports the intuitive perspective that increasing the admixture fraction from source population 2 increases the genetic divergence of an admixed population from source population 1. We can in fact prove a stronger result. Not only is $F_{\mathit{\text{st}}}[\underset{¯}{p_1},\gamma \underset{¯}{p_1}+(1-\gamma )\underset{¯}{p_2}]$ monotonic in γ, we can also show that it is convex as a function of the admixture fraction.

Theorem 4. As a function of γ, $F_{\mathit{\text{st}}}[\underset{¯}{p_1},\gamma \underset{¯}{p_1}+(1-\gamma )\underset{¯}{p_2}]$ is convex for γ ∈ [0, 1].

Proof. It suffices to demonstrate that the second derivative of $F_{\mathit{\text{st}}}[\underset{¯}{p_1},\gamma \underset{¯}{p_1}+(1-\gamma )\underset{¯}{p_2}]$ as a function of γ is nonnegative. We insert $\underset{¯}{p_1}\text{ and }\underset{¯}{p_2}$ in place of $\underset{¯}{p_2}\text{ and }\underset{¯}{p_3}$, respectively, in the proof of Lemma 1. Thus, we aim to show that $\frac{d^{2}G(\gamma )}{d{\gamma }^2}>0$. We have:

$$\begin{array}{cc}\frac{d}{d\gamma }G(\gamma )\hfill & =\frac{-2[{\displaystyle {\sum }_{i=1}^I}{\delta }_i({\delta }_i-\gamma {\delta }_i)][4-{\displaystyle {\sum }_{i=1}^I}{({\tau }_i+\gamma {\delta }_i)}^2]+[{\displaystyle {\sum }_{i=1}^I}{({\delta }_i-\gamma {\delta }_i)}^2][2{\displaystyle {\sum }_{i=1}^I}{\delta }_i({\tau }_i+\gamma {\delta }_i)]}{{[4-{\displaystyle {\sum }_{i=1}^I}{({\tau }_i+\gamma {\delta }_i)}^2]}^2}\hfill \\ \hfill & =2(1-\gamma )\left({\displaystyle \sum _{i=1}^I}{\delta }_i^2\right)\left\{\frac{-[4-{\displaystyle {\sum }_{i=1}^I}{({\tau }_i+\gamma {\delta }_i)}^2]+(1-\gamma ){\displaystyle {\sum }_{i=1}^I}{\delta }_i({\tau }_i+\gamma {\delta }_i)}{{[4-{\displaystyle {\sum }_{i=1}^I}{({\tau }_i+\gamma {\delta }_i)}^2]}^2}\right\}.\hfill \end{array}$$

To verify that the second derivative of G(γ) is nonnegative, we need only show that $\frac{1}{2{\displaystyle {\sum }_{i=1}^I}{\delta }_i^2}\frac{d^{2}G(\gamma )}{d{\gamma }^2}$ is nonnegative. Consider the following expressions:

$$\begin{array}{cc}{E}_1(\gamma )\hfill & =4+{\displaystyle \sum _{i=1}^I}{\delta }_i^2-{\displaystyle \sum _{i=1}^I}{\tau }_i^2-2\gamma {\displaystyle \sum _{i=1}^I}{\tau }_i{\delta }_i-2\gamma {\displaystyle \sum _{i=1}^I}{\delta }_i^2\hfill \\ E_2(\gamma )\hfill & =4-{\displaystyle \sum _{i=1}^I}{({\tau }_i+\gamma {\delta }_i)}^2\hfill \\ E_3(\gamma )\hfill & =4-{\displaystyle \sum _{i=1}^I}{\tau }_i^2-{\displaystyle \sum _{i=1}^I}{\tau }_i{\delta }_i-\gamma {\displaystyle \sum _{i=1}^I}{\tau }_i{\delta }_i-\gamma {\displaystyle \sum _{i=1}^I}{\delta }_i^2\hfill \\ E_4(\gamma )\hfill & ={\displaystyle \sum _{i=1}^I}{\delta }_i({\tau }_i+\gamma {\delta }_i).\hfill \end{array}$$

We note some relationships between these expressions:

$$E_1(\gamma )=E_2(\gamma )+{(1-\gamma )}^2{\displaystyle \sum _{i=1}^I}{\delta }_i^2$$ (8)

$$E_3(\gamma )=E_2(\gamma )-(1-\gamma )E_4(\gamma ).$$ (9)

Using eq. 9,

$$\frac{1}{2{\displaystyle {\sum }_{i=1}^I}{\delta }_i^2}\frac{d}{d\gamma }G(\gamma )=\frac{-(1-\gamma )E_3(\gamma )}{E_2^2(\gamma )}.$$ (10)

Differentiating the individual expressions and then combining them,

$$\begin{array}{cc}\hfill \frac{d}{d\gamma }[-E_3(\gamma )]& =\frac{d}{d\gamma }\{-[4-{\displaystyle \sum _{i=1}^I}{({\tau }_i+\gamma {\delta }_i)}^2]+(1-\gamma ){\displaystyle \sum _{i=1}^I}{\delta }_i({\tau }_i+\gamma {\delta }_i)\}={\displaystyle \sum _{i=1}^I}{\tau }_i{\delta }_i+{\displaystyle \sum _{i=1}^I}{\delta }_i^2\hfill \\ \hfill \frac{d}{d\gamma }[-(1-\gamma )E_3(\gamma )]& ={\displaystyle \sum _{i=1}^I}{\tau }_i{\delta }_i+{\displaystyle \sum _{i=1}^I}{\delta }_i^2-\gamma {\displaystyle \sum _{i=1}^I}{\tau }_i{\delta }_i-\gamma {\displaystyle \sum _{i=1}^I}{\delta }_i^2+4-{\displaystyle \sum _{i=1}^I}{\tau }_i^2-{\displaystyle \sum _{i=1}^I}{\tau }_i{\delta }_i-\gamma {\displaystyle \sum _{i=1}^I}{\tau }_i{\delta }_i-\gamma {\displaystyle \sum _{i=1}^I}{\delta }_i^2=4+{\displaystyle \sum _{i=1}^I}{\delta }_i^2-{\displaystyle \sum _{i=1}^I}{\tau }_i^2-2\gamma {\displaystyle \sum _{i=1}^I}{\tau }_i{\delta }_i-2\gamma {\displaystyle \sum _{i=1}^I}{\delta }_i^2=E_1(\gamma )\hfill \\ \hfill \frac{d}{d\gamma }[E_2^2(\gamma )]& =\frac{d}{d\gamma }{[4-{\displaystyle \sum _{i=1}^I}{({\tau }_i+\gamma {\delta }_i)}^2]}^2=-4[4-{\displaystyle \sum _{i=1}^I}{({\tau }_i+\gamma {\delta }_i)}^2][{\displaystyle \sum _{i=1}^I}{\delta }_i({\tau }_i+\gamma {\delta }_i)]=-4E_2(\gamma )E_4(\gamma ).\hfill \end{array}$$

We now differentiate eq. 10 and use the expressions above, obtaining:

$$\begin{array}{c}\frac{1}{2{\displaystyle {\sum }_{i=1}^I}{\delta }_i^2}\frac{d^{2}G(\gamma )}{d{\gamma }^2}\ge 0\hfill \\ \iff \frac{d}{d\gamma }\left[\frac{-(1-\gamma )E_3(\gamma )}{E_2^2(\gamma )}\right]\ge 0\hfill \\ \iff E_1(\gamma )E_2^2(\gamma )-4(1-\gamma )E_3(\gamma )E_2(\gamma )E_4(\gamma )\ge 0\hfill \\ \iff E_1(\gamma )E_2(\gamma )-4(1-\gamma )E_3(\gamma )E_4(\gamma )\ge 0.\hfill \end{array}$$

The last step follows because E₂(γ) ≥ 0, as E₂(γ) corresponds to four times the (nonnegative) heterozygosity of the pooled population consisting of population 1 and the admixed population with allele frequency vector $\gamma \underset{¯}{p_1}+(1-\gamma )\underset{¯}{p_2}$. By applying eqs. 8 and 9 and simplifying, we obtain:

$$\begin{array}{cc}{E}_1(\gamma )E_2(\gamma )-4(1-\gamma )E_3(\gamma )E_4(\gamma )\hfill & =E_2^2(\gamma )+\left[{(1-\gamma )}^2{\displaystyle \sum _{i=1}^I}{\delta }_i^2\right]E_2(\gamma )-4(1-\gamma )E_2(\gamma )E_4(\gamma )+4{(1-\gamma )}^2{E}_4^2(\gamma )\hfill \\ \hfill & ={[E_2(\gamma )-2(1-\gamma )E_4(\gamma )]}^2+{(1-\gamma )}^2{\displaystyle \sum _{i=1}^I}{\delta }_i^2{E}_2(\gamma )\ge 0\hfill \end{array}$$

because both terms are nonnegative.

An illustration of Theorems 3 and 4 appears in Figure 3. The same twenty loci from Figure 1 are used; populations 1 and 2 are the European and Native American populations, respectively. For each locus, the F_st value between population 1 and a population formed by the admixture of populations 1 and 2 can be seen to be decreasing and convex in γ ∈ [0, 1], where γ is the admixture fraction for population 1.

Figure 3.

F_st between a population and a hypothetical admixture of that population with a second population. $F_{\mathit{\text{st}}}[\underset{¯}{p_1},\gamma \underset{¯}{p_1}+(1-\gamma )\underset{¯}{p_2}]$, seen as a function of γ, is plotted against γ (eq. 7). Populations 1 and 2 represent populations of European and Native American descent, respectively, and $\underset{¯}{p_1}\text{ and }\underset{¯}{p_2}$ are based on allele frequencies estimated from Wang et al. (2008). The same twenty randomly selected loci as in Figure 1 are considered, with each curve representing a different locus. In accordance with Theorems 3 and 4, F_st is always decreasing and convex in γ.

4.2. Comparison of predicted F_st to observed F_st

When allele frequencies are available on both the admixed population and the founding populations, we are able to calculate the observed F_st value between a specific founding population and a population formed by admixture of multiple founding populations. For example, it is possible to calculate the observed F_st between an African-American population and a putative African founding population, or between a Mestizo population and a putative European founding population. In practice, the true founding populations are not precisely known, no longer exist, or may not have data available, so that in general, only an approximation is possible.

In such cases, our results provide a way of predicting the F_st value between a population formed by an admixture of multiple founding populations and a specific founding population, on the basis of measured allele frequencies and admixture coefficients. The predicted F_st value can be calculated when the allele frequencies and the admixture coefficients are available or can be estimated for the founding populations. Estimation of the admixture fractions at a given locus for the various founding populations can be achieved via maximum likelihood (Millar (1987)) or other techniques.

For the Wang et al. (2008) data, we estimated the fraction of European ancestry in the Mestizo population at each of the 678 loci, treating the European and Native American populations as founding populations. This approach followed the procedure of Schroeder et al. (2009), with all of the various subgroups in the Mestizo sample of Wang et al. (2008) pooled together (indeed the admixture estimates are the same as those used in the “Combined admixed sample” analysis in Table 1 of Schroeder et al. (2009)). Following Schroeder et al. (2009), for any allele present in at least one individual in the Mestizo population but not present in both founding populations, and for each founding population that did not possess the allele, a single copy of the allele was artificially added to that ancestral population. Sample allele frequencies that were then obtained for Europeans and Native Americans were treated as true allele frequencies for use in the maximum likelihood inference of the European admixture proportion, assuming Hardy-Weinberg equilibrium in the admixed population. Maximum likelihood estimates were obtained numerically and were used to obtain the predicted F_st according to eq. 7.

The observed and predicted F_st values for individual loci are compared in Figure 4. In general, we find that the observation closely matches the prediction. In most cases (549 of 678 loci), however, the prediction provides an underestimate of the observed value. This systematic underestimation might arise from the use of estimated rather than true values to obtain the prediction; in particular, the prediction relies on both the estimated allele frequencies and the maximum likelihood estimate of γ obtained from the same data used to estimate the allele frequencies.

Figure 4.

Predicted and observed F_st. (A) The predicted and observed F_st values between an admixed Mestizo population and a European founding population are plotted against the European admixture fraction γ in the Mestizo population, estimated by maximum likelihood. The prediction is based on eq. 7, using the European and Native American allele frequencies estimated from Wang et al. (2008) as $\underset{¯}{p_1}\text{ and }\underset{¯}{p_2}$, respectively, together with the maximum likelihood estimate of γ. The observation is based on F_st estimated from eq. 1, inserting estimated allele frequencies from Wang et al. (2008) on European and Mestizo populations. (B) The observed F_st value is plotted against the predicted F_st value. The identity line is shown in gray. In both panels, each point represents one of the 678 loci used. The correlation coefficient between the predicted and observed F_st values is 0.978.

4.3. An admixture estimator on the basis of F_st

As an alternative to use of an estimated admixture coefficient to predict F_st, an observed F_st value between a population formed by admixture of two founding populations and a specific founding population can be used as a way of estimating the admixture fraction. In the case of two founding populations, the quadratic equation in eq. 7 can be solved to provide an estimator in the style of the method of moments. This approach is reasonable, as the monotonicity result in Theorem 3 indicates that for fixed allele frequencies, γ is identifiable from F_st. The resulting estimator is non-parametric, in that it does not make assumptions on the form of the probability distribution of the allele frequencies at a given locus:

$${\widehat{\gamma }}_{\pm }=\frac{({\displaystyle {\sum }_{i=1}^I}{\delta }_i^2-F_{\mathit{\text{st}}}{\displaystyle {\sum }_{i=1}^I}{\delta }_i{\tau }_i)\pm \sqrt{{({\displaystyle {\sum }_{i=1}^I}{\delta }_i^2-F_{\mathit{\text{st}}}{\displaystyle {\sum }_{i=1}^I}{\delta }_i{\tau }_i)}^2-(1+F_{\mathit{\text{st}}})({\displaystyle {\sum }_{i=1}^I}{\delta }_i^2)({\displaystyle {\sum }_{i=1}^I}{\delta }_i^2+F_{\mathit{\text{st}}}{\displaystyle {\sum }_{i=1}^I}{\tau }_i^2-4F_{\mathit{\text{st}}})}}{(1+F_{\mathit{\text{st}}}){\displaystyle {\sum }_{i=1}^I}{\delta }_i^2}.$$ (11)

It can be shown that γ̂₊ ≥ 1 for all possible values of F_st and the δ_i and τ_i. Therefore, if γ̂₋ is between 0 and 1, it is chosen as the estimate. In the case in which γ̂₋ < 0, 0 is chosen as the estimate, and if γ̂₋ > 1, 1 is chosen as the estimate.

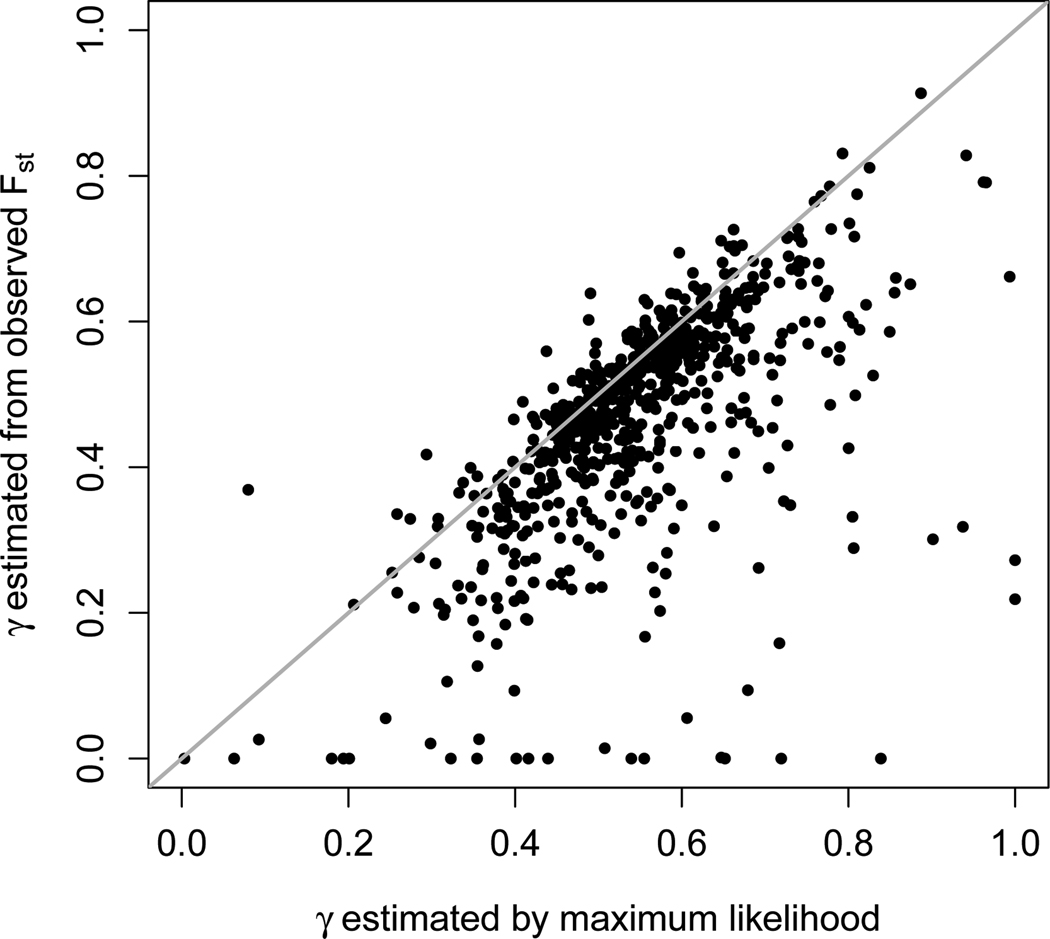
For the example data, Figure 5 presents a plot of the estimate of γ from the observed F_st versus the maximum likelihood estimate of γ, with Europeans and Native Americans as populations 1 and 2, and with Mestizos as the admixed population. The correlation between the estimates from these two methods is 0.618, and in general, the moment estimator produces smaller estimates than the maximum likelihood method, including several estimates of zero in cases where maximum likelihood obtains a positive value.

Figure 5.

Admixture estimates obtained from observed F_st (eq. 11) versus estimates obtained by maximum likelihood. The plot represents a scenario in which a European and a Native American population are the founding populations and a Mestizo population is the admixed population, and allele frequencies estimated from Wang et al. (2008) on all three populations are used to estimate γ, the European admixture fraction in the Mestizo population. The identity line is shown in gray, and each point represents one of the 678 loci used. The correlation coefficient between the two sets of estimates is 0.618.

5. Discussion

In this paper, we have considered the F_st measure in the context of admixed populations. We have explored the F_st value between a population formed by the admixture of K founding populations and one of those founding populations. In the general case of arbitrary K ≥ 2, we have demonstrated that this value is maximized when the admixed population is in fact one of the other founding populations. In the particular case of K = 2, this F_st value is monotonic and convex in the admixture fraction. We have also provided a formula for predicting F_st in an admixed population on the basis of the estimated admixture coefficient and the allele frequencies in the founding populations, producing very similar values to those observed in an empirical example utilizing the data of Wang et al. (2008).

Further, we discussed a non-parametric method of estimating the admixture fraction from the observed F_st values, and we compared it to the maximum likelihood method. In general, the non-parametric estimator is useful primarily for the purpose of illustrating the close relationship between F_st and the admixture coefficient, and its statistical properties are likely to be poorer than those of modern genome-based approaches to admixture estimation (Falush et al. (2003), Hoggart et al. (2004), Tang et al. (2006a), Sankararaman et al. (2008) Alexander et al. (2009), Price et al. (2009), Engelhardt and Stephens (2010)). However, as a straightforward formula that is calculated from quantities that are easily obtained, it provides a convenient approach when a computationally simple initial estimate is desirable.

Our results can provide a basis for interpreting F_st in admixed populations. In particular, in the case in which K = 2, the monotonicity and convexity of F_st in the admixture coefficient imply that F_st is informative about the level of admixture, and vice versa. This relationship can be a useful starting point for measurement of admixture, and a comparison of observed and predicted F_st values can be used as an initial check on the extent to which estimates of the admixture fraction obtained by maximum likelihood or other algorithms are sensible.

We note several limitations of our work. First, our admixture model does not involve a mechanistic evolutionary process, considering only the linear combination of allele frequencies that occurs when an admixed population is produced instantaneously from a set of source populations. Second, we examine admixture only at the population level, disregarding variation that might exist in admixture levels across individuals within a population. Third, as in many methods for analysis of admixed populations, we caution that our work presumes that the source populations for a given admixed population have been correctly specified. It is encouraging, however, that in spite of these concerns, the predicted F_st values generally agree with the values observed in our empirical example. As illustrated by the results presented here, further analysis of the properties of F_st in an admixture setting will continue to facilitate the understanding of population-genetic issues in the context of admixture research.