Extracellular Proton Modulation of the Cardiac Voltage-Gated Sodium Channel, Na_V1.5

Abstract

Low pH depolarizes the voltage dependence of voltage-gated sodium (Na_V) channel activation and fast inactivation. A complete description of Na_V channel proton modulation, however, has not been reported. The majority of Na_V channel proton modulation studies have been completed in intact tissue. Additionally, several Na_V channel isoforms are expressed in cardiac tissue. Characterizing the proton modulation of the cardiac Na_V channel, Na_V1.5, will thus help define its contribution to ischemic arrhythmogenesis, where extracellular pH drops from pH 7.4 to as low as pH 6.0 within ∼10 min of its onset. We expressed the human variant of Na_V1.5 with and without the modulating β₁ subunit in Xenopus oocytes. Lowering extracellular pH from 7.4 to 6.0 affected a range of biophysical gating properties heretofore unreported. Specifically, acidic pH destabilized the fast-inactivated and slow-inactivated states, and elevated persistent I_Na. These data were incorporated into a ventricular action potential model that displayed a reduced maximum rate of depolarization as well as disparate increases in epicardial, mid-myocardial, and endocardial action potential durations, indicative of an increased heterogeneity of repolarization. Portions of these data were previously reported in abstract form.

Introduction

Voltage-gated sodium (Na_V) channels are responsible for action potential (AP) propagation in most excitable cells. Each channel is composed of a pore-forming α-subunit and one or more modulating β-subunits (1–3). The α-subunit forms the functional pore of the channel and is composed of four homologous domains (DI–DIV) consisting of six transmembrane α-helices (S1–S6) (1,4). Helices S1–S4 form the channel's voltage sensor, primarily mediated by a high concentration of positively charged lysines and arginines positioned every third residue within each S4 helix (5). The S5 and S6 helices combine with the extracellular loops that link them (p-loops) to form the functional pore and selectivity filter of the channel (6).

Shortly after activation, the intracellular DIII–DIV linker, acting as a hinged lid, occludes the cytoplasmic side of the channel pore and effectively blocks further ion permeation (7). This process is called fast inactivation because it occurs in the time frame of several milliseconds. In response to prolonged depolarization or rapid, successive depolarizations, Na_V channels enter a slow-inactivated state (8). Slow inactivation is molecularly and pharmacologically distinct from fast inactivation and requires a much longer time period to occur, developing over the time frame of seconds (9,10). The mechanism of slow inactivation is poorly understood, but it is believed to be due to a constriction of the extracellular pore mediated by long-distance interactions within the channel (8). Together, the fast-inactivated and slow-inactivated states regulate Na_V channel availability and therefore cellular excitability.

Mutations in Na_V1.5 channels, the primary Na_V channel isoform found in cardiac tissue, that alter the stability of the fast- or slow-inactivated states are the underlying cause of several congenital disorders, including long QT syndrome type III and Brugada syndrome (11). Additionally, extrinsic factors acting directly and/or indirectly on Na_V1.5 channels can alter their functional properties. Changes in Na_V channel function during cardiac acidosis are believed to contribute to cardiac arrhythmia. During cardiac ischemia, extracellular pH drops from pH 7.4 to as low as pH 6.0 within ∼10 min of its onset (12). As proton levels increase, the voltage dependencies of both activation and steady-state fast inactivation (SSFI) are depolarized (13–20). Additionally, protonation of p-loop carboxylate amino acids causes a reduction of single-channel conductance with a pKa ∼ pH 6.0 and complete block at pH ∼ 4.0 (18,19). Recordings from intact cardiomyocytes have shown similar reductions in peak I_Na and shifts in the voltage dependencies of activation and SSFI (21,22), although Murphy et al. (23) reported no significant shifts at pH 6.6.

A complete description of the effects of protons on Na_V1.5 channel kinetics has not been reported. An improved understanding of the isoform-specific effects of protons on Na_V1.5 channel kinetics will enhance the treatment of the deleterious and arrhythmogenic effects of cardiac ischemia. In this work we expressed the human variant of the cardiac Na_V channel, hNa_V1.5, in Xenopus oocytes. We demonstrate that reducing extracellular pH destabilizes both the fast-inactivated and slow-inactivated states and leads to an increase in persistent I_Na. Data obtained at pH 7.4 (control) and pH 6.0 were incorporated into a ventricular AP model. The model displayed arrhythmogenic characteristics when pH 6.0 data were used.

Materials and Methods

Molecular biology

The human variant of the pore-forming α-subunit, hNa_V1.5, in SP6-4T was graciously donated by Dr. Chris Ahern (University of British Columbia, Vancouver, Canada). hNa_V1.5 DNA was linearized with the use of XbaI (Invitrogen, Carlsbad, CA). The β₁ subunit in pBluescript was linearized with the use of HindIII (Invitrogen). A T7 mMESSAGE mMACHINE high-yield capped RNA transcription kit (Applied Biosystems, Carlsbad, CA) was used to complete the transcription.

Oocyte preparation

We terminally anesthetized female frogs (Xenopus laevis; Boreal Northwest, St. Catharines, Canada) by placing them in 2 g/L tricaine solution until they were unresponsive. Oocytes were surgically removed, and theca and follicular layers were enzymatically removed by ∼1 h agitation of semi-intact lobes in a calcium-free solution containing (in mM) 96 NaCl, 2 KCl, 20 MgCl₂, 5 HEPES, and supplemented with 1 mg/ml type 1a collagenase (Sigma-Aldrich, Oakville, Canada). The collagenased oocytes were then washed and sorted in calcium-free solution and finally incubated overnight at 19°C with SOS+ media containing (in mM) 96 NaCl, 2 KCl, 1.8 CaCl₂, 1 MgCl₂, 5 HEPES, 2.5 sodium pyruvate, supplemented with 100 mg/L gentamicin sulfate and 5% horse serum. Stage V-VI oocytes were coinjected with 50 nL of cRNA encoding hNa_V1.5 with or without the β₁ subunit. Injected oocytes were incubated at 19°C in SOS+ media for 3–10 days before recording was performed. All surgical and animal care procedures were completed in accordance with the policies and procedures of the Simon Fraser University Animal Care Committee and the Canadian Council of Animal Care (24).

Data acquisition

Macroscopic current recordings were made using a CA-1B amplifier (Dagan, Minneapolis, MN) in the cut-open mode. Data were low-pass-filtered at 10 kHz, digitized at 50 kHz with the use of an ITC-16 interface (HEKA Elektronics, Mahone Bay, Canada), and then recorded with Patchmaster version 2x41 (HEKA Elektronics) running on an iMac (Apple Canada, Markham, Canada). The oocytes were placed in a cut-open, voltage-clamp, triple-bath setup as previously described (25). The cells were then permeabilized via bottom-bath perfusion with an intracellular solution containing (in mM) 9.6 NaCl, 88 KCl, 5 HEPES, 11 EGTA, titrated to pH 7.4 and supplemented with 0.1% saponin. After 1–2 min of exposure, a saponin-free intracellular solution was washed in. The extracellular solution of the top and middle chambers contained (in mM) 96 NaCl, 4 KCl, 1.8 CaCl₂, 1 MgCl₂, and 5 HEPES. For recordings of extracellular pH below 6.5, HEPES was substituted with 5 mM MES. Bath chambers were temperature controlled at 21°C by means of a Peltier device run by a TC-10 temperature controller (Dagan, Minneapolis, MN).

Pulse protocols

Cells were maintained at a holding potential of −100 mV between all protocols. Unless otherwise stated, leak subtraction was completed online using a −p/4 protocol from a holding potential of −100 mV. I/V relationships were measured with 20 ms depolarizations between −100 mV and +40 mV, in 10 mV increments, from a 500 ms prepulse of −120 mV. SSFI was measured by stepping from a 30 ms, −150 mV holding potential to alternating 500 ms prepulses between −120 and 0 mV in 10 mV increments, and then to a 0 mV test pulse. We measured the time and voltage dependence of fast-inactivation recovery using a double-pulse protocol by depolarizing the membrane to 0 mV for 500 ms to fully fast-inactivate the channels. The membranes were then stepped to an interpulse potential between −150 and −80 mV in 10 mV increments. The current recovered during the interpulse was assessed during a second depolarization to 0 mV, 0–50 ms into the interpulse. To measure the rate of onset of closed-state fast inactivation, the membrane potential was held at −150 mV for 30 ms and stepped to a conditioning pulse of −70 to −40 mV in 10 mV increments. Available current was measured with a 0 mV test pulse 0–50 ms into the interpulse.

Prolonged versions of the fast inactivation protocols were used to measure slow inactivation. Steady-state slow inactivation (SSSI) was measured by holding membranes at −150 mV for 30 s to recover channels from the slow-inactivated state and then stepping to alternating, 60 s conditioning pulses between −150 mV and −10 mV in 20 mV increments. Membrane voltage was then hyperpolarized to −150 mV for 20 ms to allow recovery of fast-inactivated but not slow-inactivated channels, and then depolarized to a 0 mV test pulse to measure the remaining channel availability. The rate of recovery from slow inactivation was measured by depolarizing the membrane to 0 mV for 60 s to fully slow-inactivate the channels. The membrane potential was then stepped to an interpulse potential (−150 mV), 0.2–30 s in duration, before the recovered current was measured with a 0 mV test pulse. To measure the rate of slow inactivation onset, cells were held at −150 mV for 30 s, stepped to a prepulse potential (0 mV) for 0–60 s, hyperpolarized to −150 mV for 20 ms to allow recovery of fast-inactivated but not slow-inactivated channels, and the available current was then measured with a 0 mV test pulse.

We measured window currents using a slowly depolarizing ramp protocol from −100 mV to +20 mV at 0.1 mV/ms. We assessed the absolute window current by directly comparing the average window current at pH 6.0 with that observed at pH 7.4. By normalizing the ramp currents to the peak current amplitude at −40 mV of their respective pH values, we assessed the relative window current. We subtracted leak and endogenous currents offline using average currents recorded from eight uninjected oocytes at pH 7.4 and pH 6.0. To measure use-dependent inactivation, cells were depolarized to 0 mV for 230 ms and hyperpolarized to −90 mV for 150 ms (∼2.6 Hz) 250 times. The elevated frequency, which coincides with a 156 bpm heart rate, was sufficient to generate a measurable reduction in current due to inactivation while remaining within the range of physiological depolarization and frequency values. The ratio of depolarization to repolarization was chosen based on Bazett's formula to generate a healthy QT duration, calculated as QTc = 371 (26). To ensure the appropriate pulse frequency, no leak subtraction was used in use-dependent inactivation recordings.

Data analysis

We analyzed the activation, fast-inactivation, and slow-inactivation data as described in the Supporting Material using Fitmaster v. 2x32 (HEKA Elektronics) and Igor Pro v. 5.01 (Wavemetrics, Lake Oswego, OR) run on an iMac. Additionally, data plotted as a function of pH were fitted with the Hill equation:

$$\text{f}\left(\text{x}\right){=\text{Y}}_0+\frac{\left({\text{Y}}_{\text{M}}-{\text{Y}}_0\right)}{\left[1+{\left(\frac{{\text{X}}_{1/2}}{\text{X}}\right)}^b\right]}$$ (1)

where Y_M and Y₀ are the maximum and minimum values of the fit, respectively; X_1/2 is the midpoint of the curve; X is the pH; and b is the rate.

We performed statistical analyses with Student's t-test and analysis of variance (ANOVA), where appropriate, using Instat (Graphpad, La Jolla, CA). All data are reported as the mean ± SE and statistical significance was taken at p < 0.05.

AP model

A detailed description of the parameters used is provided in Table S1, Table S2, and Table S3. We programmed the original ten Tusscher et al. (27) model into Python code using the modules NumPy (Enthought, Austin, TX) and matplotlib (John Hunter). The code was then updated to include calcium current and slow delayed potassium current equations (28,29). A late persistent sodium current was added according to the formulas of Hund and Rudy (30). We replaced the maximal sodium conductance value with the Luo-Rudy dynamic model (31) value to better reflect our experimental data. The slow delayed rectifier potassium conductance (G_Kr) was changed to incorporate the role of internal calcium concentrations on G_Ks (32). The late sodium maximal conductance value was changed to reflect the data collected by Zygmunt et al. (33). These data show different persistent sodium currents in different layers of the ventricular myocardium. The sodium current slow-inactivation time constants collected were normalized to those collected by Richmond et al. (34) and then fitted with two separate exponential equations. Finally, we incorporated our data for steady-state conductance and inactivation curves, fast- and slow-inactivation time constants of both recovery and onset, and normalized late sodium currents into the model to reflect the different sodium current properties at pH 7.4 versus pH 6.0. The sodium current data were Q10 adjusted according to the methods of ten Tusscher et al. (27) and Nagatomo et al. (35). The model was run for epicardial, mid-myocardial, and endocardial ventricular cardiomyocytes at 1 and 3 Hz.

Results

Activation

We measured the peak current of the hNa_V1.5 channel, coexpressed with the β₁ subunit, using extracellular solution titrated to pH 8.0–4.4. Sample traces recorded at pH 7.4 and pH 6.0 are shown in Fig. 1 A. Fig. 1 B, inset, shows the peak current amplitude normalized to control (pH 7.4) plotted as a function of extracellular pH and fitted with the Hill equation (Eq. 1; pKa = 6.1). Normalized conductance was plotted as a function of test potential and fitted with a Boltzmann function (Eq. S2). At pH 6.0, the midpoint (V_1/2) of activation was significantly and reversibly depolarized from −33.2 ± 0.9 mV to −27.7 ± 1.6 mV (n = 42 and 16, respectively; p < 0.05), and the apparent valence (z) significantly decreased from 3.4 ± 0.1 e to 2.8 ± 0.1 e (p < 0.05; Fig. 1 B). For a broader view of the effect of pH on activation of hNa_V1.5+β₁, channels, we plotted the change in the V_1/2 and z of activation as a function of extracellular pH and fitted the data with Eq. 1, producing pKa = 6.2 and pKa = 6.0, respectively (n = 3–14; Fig. 1 C). An ANOVA revealed significant shifts in the V_1/2 and z of activation at pH 6.0, 5.4, and 5.0, compared with pH 7.4 (p < 0.05). At pH 6.0, the time to peak current at 0 mV was significantly increased from 897.2 ± 39.6 μs to 1168.2 ± 67.7 μs (n = 14, p < 0.01; Fig. 1 D).

Figure 1.

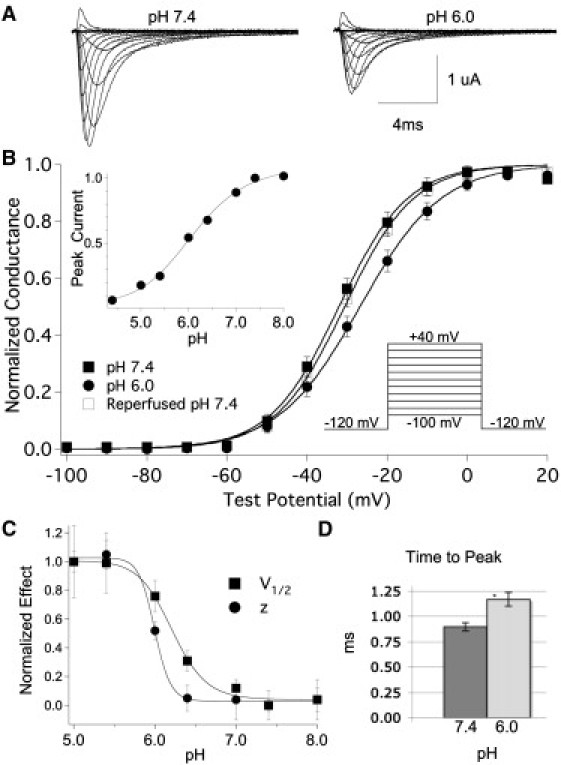
Low pH depolarizes Na_V1.5+β₁ activation. (A) Sample traces recorded at pH 7.4 and pH 6.0. (B) Normalized conductance of Na_V1.5+β₁, plotted as a function of test potential, with extracellular pH 7.4 (filled squares), pH 6.0 (circles), and after reperfusion of pH 7.4 (open squares). The inset shows the pulse protocol used and the proton block curve, pKa = 6.1. (C) Effect of pH on V_1/2 (squares) and z (circles) is normalized and plotted as a function of pH and fitted with the Hill equation. pKa values are 6.2 and 6.0, and the rates are −29 and −61 for V_1/2 and z, respectively. (D) Time to peak current, measured at 0 mV. All data points are mean ± SE; ^∗ denotes statistically significant at p < 0.05.

Fast inactivation

To assess the voltage dependence of SSFI in hNa_V1.5+β₁ channels, we plotted the peak current amplitudes (sample traces in Fig. 2 A, inset) as a function of the prepulse potential and fitted them with a Boltzmann function (Eq. S3) as shown in Fig. 2 A. At pH 6.0, the V_1/2 of the SSFI curve was significantly and reversibly depolarized from −76.6 ± 0.5 mV to −73.2 ± 0.7 mV (n = 28 and 11, respectively; p < 0.05). An ANOVA revealed significant shifts in the V_1/2 of SSFI at pH 6.0, 5.4, and 5.0, compared with the V_1/2 at pH 7.4 (n = 6–28). The effects of pH changes on z were not statistically significant when compared with pH 7.4. At pH 8.0, however, z was significantly different from that obtained at pH 5.4 and 5.0. The V_1/2 voltages of SSFI plotted as a function of pH displayed a linear trend (data not shown).

Figure 2.

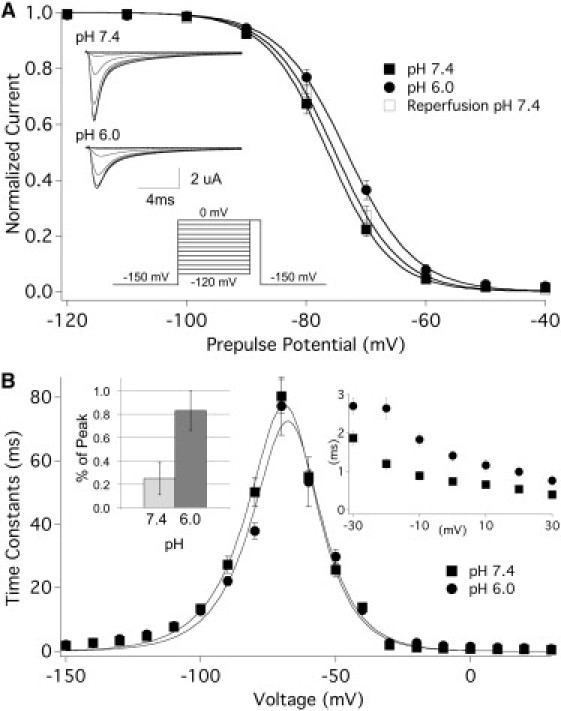
Low pH destabilizes SSFI in Na_V1.5+β₁. (A) SSFI at pH 7.4 (filled squares), pH 6.0 (circles), and after reperfusion of pH 7.4 (open squares), shown by plotting peak current against prepulse potential. The inset depicts the pulse protocol used, as well as sample SSFI current traces recorded at pH 7.4 and pH 6.0. (B) Time constants of recovery (−150 to −80 mV) and onset of closed-state (−70 to −40 mV) and open-state (−30 to 30 mV) fast inactivation plotted as a function of voltage. The inset displays an expanded view of open-state fast inactivation as well as persistent current reported as percent of peak current.

We measured the time constants of fast inactivation at pH 7.4 and pH 6.0 by fitting the decay of current (open-state onset) or the change in peak current (closed-state onset and recovery) with a single exponential function (Eq. S4). We then plotted the time constants as a function of voltage and fitted them with an Eyring model (Eq. S5, Fig. 2 B). We observed no major changes in the peak of the curve or any values for closed-state inactivation, measured between −70 mV and −40 mV. In contrast, the time constants of open-state fast inactivation, measured between −30 mV and +30 mV (Fig. 2 D, inset), were significantly increased at pH 6.0. Also, the time constants of recovery were significantly decreased at pH 6.0, from 27.3 ± 1.2 ms to 22.1 ± 0.7 ms at −90 mV (n = 19 and 16, respectively; p < 0.001), and from 50.2 ± 2.6 ms to 37.8 ± 1.5 ms at −80 mV (n = 14 and 12, respectively; p < 0.0001). Persistent current, measured at the end of a 100 ms test pulse to −20 mV (reported here as percent of peak current), was significantly increased from 0.25 ± 0.14% at pH 7.4 to 0.83 ± 0.17% at pH 6.0 (Fig. 2 B, inset; n = 4, p < 0.01).

Window current occurs over a voltage range in which channels activate but fail to fast-inactivate. We used two methods to assess window currents: overlaying the conductance (Fig. 1 B) and SSFI (Fig. 2 A) curves (see Fig. 3 A), and using a slow ramp protocol to measure quasi-steady state currents (Fig. 3, B and C). Reducing the extracellular pH reduced the total charge of the absolute window current by 29%, 146 μC at pH 7.4 and 103 μC at pH 6.0 (Fig. 3 B). The peak of the window current was also decreased from 18.0 nA to 12.0 nA and shifted from −43.0 mV to −36.7 mV at pH 7.4 and 6.0, respectively. We assessed the area bounded by overlaying the normalized activation/SSFI curves, as well as ramp currents normalized to peak current at −40 mV, and found that the area of relative window current was increased at pH 6.0 by 78% and 72%, respectively (Fig. 3, A and C).

Figure 3.

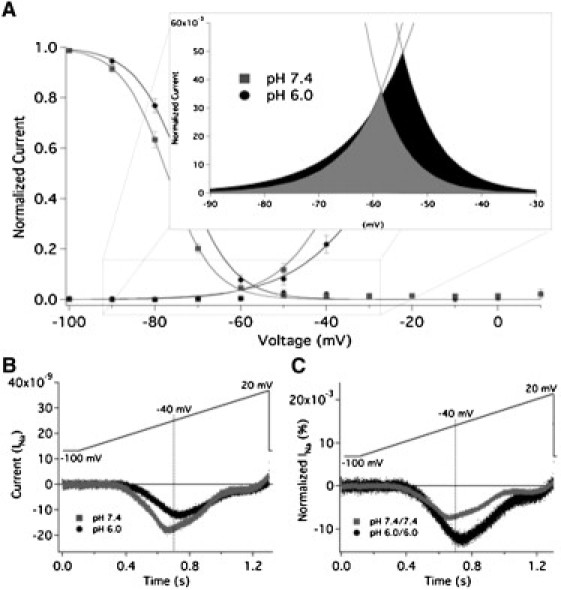
Low pH modulates window currents in Na_V1.5+β₁. (A) Overlay of activation and SSFI curves recorded from Na_V1.5+β₁ with extracellular pH 7.4 (squares) and 6.0 (circles). The inset shows an expanded view from −90 mV to −30 mV. Window currents are highlighted in gray (pH 7.4) and black (pH 6.0). We calculated relative window current at pH 7.4 and 6.0 by integrating the area under the overlay of the Boltzmann fits for conductance and SSFI. pH 6.0 significantly increased the area of window current, measured in arbitrary units (AU), from 0.54 ± 0.07 AU to 0.96 ± 0.15 AU (n = 6, p = 0.0098). The shift in the peak of the window current was not statistically significant (p > 0.05). (B) Averaged ramp currents from nine oocytes recorded at pH 7.4 (gray) and pH 6.0 (black). The total charge from ramp currents was reduced by 29% at pH 6.0 relative to pH 7.4. (C) Averaged ramp currents shown in panel B normalized to peak current at −40 mV at pH 7.4 or 6.0. There was an increase in the relative ramp current at pH 6.0, from 62.0 AU at pH 7.4 and 106.7 AU at 6.0.

Slow inactivation

We examined the proton modulation of hNa_V1.5+β₁ slow inactivation. Normalized current measured from SSSI protocols at pH 7.4 and 6.0 is plotted as a function of prepulse potential and fitted with a modified Boltzmann function (Eq. S3) in Fig. 4 A. pH had no effect on the V_1/2, z, or maximum probability of SSSI. In contrast, the rate of slow inactivation recovery at −150 mV changed from a biexponential fit at pH 7.4 (τ₂ = 240 ± 17 ms, τ₁ = 2.73 ± 0.26 s, n = 10) to a monoexponential fit at pH 6.0 (τ = 502 ± 167 ms, n = 4) and appears accelerated (Fig. 4 B). Additionally, the time constant of slow inactivation onset at 0 mV was significantly increased from 7.78 ± 0.72 s to 12.23 ± 0.85 s (n = 7 and 4, respectively; p = 0.009; Fig. 4 C). Similar effects were observed for recovery and onset at −130 mV and +20 mV, respectively (data not shown). These data suggest that the observed effects were not limited to specific voltages.

Figure 4.

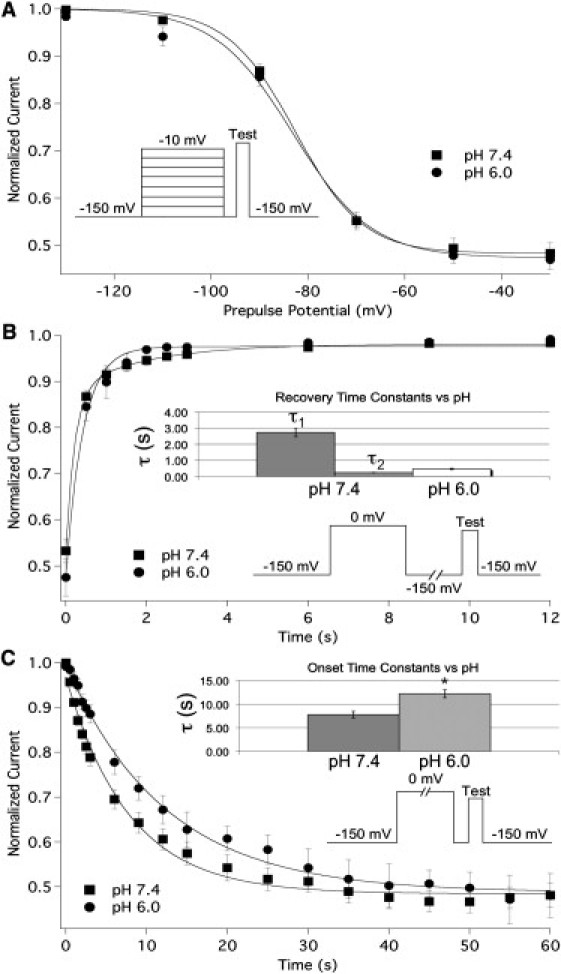
Low pH alters the kinetics of slow inactivation in Na_V1.5+β₁. (A) SSSI measured at pH 7.4 (squares) and pH 6.0 (circles). Peak normalized current is plotted as a function of prepulse potential and fitted with our modified Boltzmann function. (B) The rate of recovery from slow inactivation at −150 mV. Normalized current is plotted as a function of time and fitted with a double (pH 7.4) or single (pH 6.0) exponential. (C) The rate of onset of slow inactivation at 0 mV. Normalized current is plotted as a function of time and fitted with a single exponential. The bar graphs in Fig. 2, B and C, show the time constants of recovery and onset, respectively. The pulse protocols used are displayed in the insets of panels A, B, and C, respectively. All data points are mean ± SE; ^∗ indicates statistical significance at p < 0.05.

Use-dependent inactivation

To acquire a more physiologically relevant measure of the effect of pH on hNa_V1.5+β₁ function, we measured use-dependent inactivation using a pulse protocol designed to mimic a human ventricular AP. Cells were depolarized to 0 mV for 230 ms and then hyperpolarized to −90 mV for 150 ms to simulate an elevated heart rate of ∼160 beats per minute. Peak currents from 250 consecutive pulses were recorded and normalized to the first pulse, and then plotted as a function of time and fitted with a double exponential equation (Eq. S4) as shown in Fig. 5 A. At pH 6.0, the fast and slow time constants of use-dependent inactivation were significantly increased from 3.00 ± 0.18 s to 4.99 ± 0.36 s (n = 7, p = 0.0008) and 19.31 ± 0.99 s to 23.3 ± 1.31 s (n = 7, p = 0.037), respectively (Fig. 5 B). The relative amplitude of the slow component was significantly decreased from 20.98 ± 1.73% to 16.75 ± 1.66% (n = 7, p = 0.011), and the asymptote of the fit to current decay was significantly increased from 56.9 ± 1.6% to 64.5 ± 1.33% (n = 7, p < 0.0001; Fig. 5, A and C). We observed a significant elevation of the asymptote at pH 6.4 and 6.0 (recorded at pH 8.0, 7.0, 6.4, and 6.0; n = 5–8; Fig. 5 C). A few recordings were run for up to 1000 pulses, and 250 pulses was found to be a reliable indicator of the asymptote of use-dependent inactivation and the steady state of slow inactivation, because no further decrease in current amplitude was measured from the 250th to the 1000th pulse.

Figure 5.

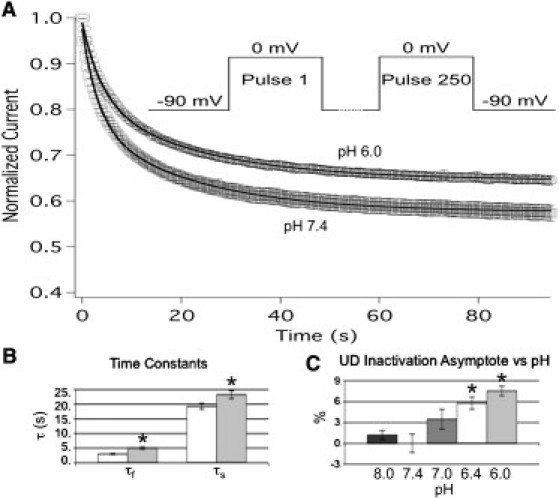
Low pH inhibits use-dependent inactivation in Na_V1.5+β₁. pH modulation of use-dependent inactivation was measured at pH 7.4 (squares) and pH 6.0 (circles). (A) The data were normalized to the first pulse, plotted as a function of time, and fitted with a double exponential. Lines depict respective fits with a double exponential equation, and the pulse protocol used is displayed in the inset. (B) Values derived from double exponential fits at pH 7.4 (open) and pH 6.0 (filled). The fast (τ_f) and slow (τ_s) time constants of use-dependent inactivation were significantly increased at pH 6.0 (gray) compared with pH 7.4 (white). (C) Change in the asymptote of use-dependent inactivation plotted as a function of pH. Values obtained at pH 7.4 were significantly different from those obtained at pH 6.4 and 6.0. All data points are mean ± SE; ^∗ indicates statistical significance at p < 0.05.

Role of the β₁ subunit

Given its known role in Na_V channel function (2,10,36–38), we investigated whether the presence of the β₁ subunit altered pH modulation of hNa_V1.5 channels. We expressed the hNa_V1.5 α-subunit alone in Xenopus oocytes and then recorded channel activation, fast inactivation, slow inactivation, and use-dependent inactivation, as previously described. Extracellular pH 6.0 still significantly altered the V_1/2 of activation and SSFI, and elevated the asymptote of use-dependent inactivation in Na_V1.5 alone (n = 5–10, p < 0.05; Fig. S1). The effects of extracellular pH 6.0 on the hNa_V1.5 α-subunit alone were nearly identical to those observed with hNa_V1.5+β₁. A direct comparison of the shifts in V_1/2, as well as the asymptote of use-dependent inactivation, suggested a reduced effect of lowered pH in the absence of β₁. The difference in the effects of pH 6.0 on channel kinetics between Na_V1.5+β₁ and Na_V1.5 alone, however, were not statistically significant.

AP modeling

To assess the contribution of the observed changes in Na_V1.5 channel function in response to acidosis on AP morphology, we incorporated Na_V1.5+β₁ data into a ventricular AP model (Fig. 6 and Fig. S2) (27). Models were run for epicardial, mid-myocardial, and endocardial cardiomyocytes at 1 and 3 Hz, incorporating Na_V1.5+β₁ data recorded with the extracellular solution titrated to either pH 7.4 or pH 6.0. Figure 6 and Fig. S3 show that the changes in Na_V1.5+β₁ function at pH 6.0 acted to prolong mid-myocardial APs over epicardial and endocardial APs. The AP duration (APD)₉₀ was increased in epicardial, mid-myocardial, and endocardial APs at pH 6.0 compared with pH 7.4, recorded at 1 Hz (348–353 ms, 361–378 ms, and 348–354 ms, respectively). The APs obtained with pH 6.0 data also displayed an 11 mV reduction in the peak depolarization (from 40 mV to 29 mV), a 5 mV increase in the threshold for AP firing (from −51 mV to −46 mV), and a 60% reduction in the maximum AP upstroke velocity (V_max; from 197 mV/ms to 81 mV/ms). Similar effects were also observed at 3 Hz (data not shown).

Figure 6.

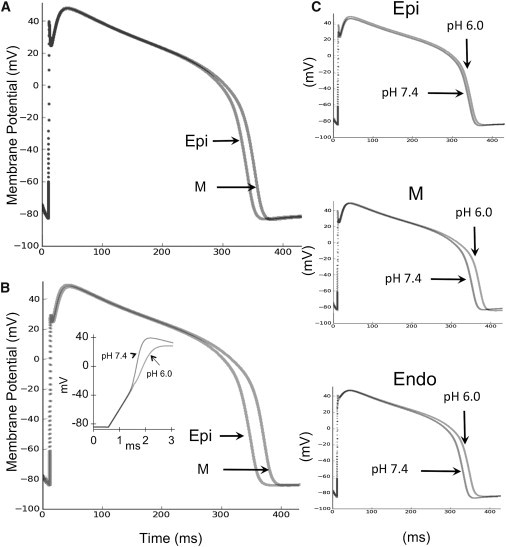
A ventricular AP model is altered by Na_V1.5+β₁ proton modulation. Overlay of simulated epicardial (Epi) and mid-myocardial (M) ventricular APs incorporating Na_V1.5+β₁ data recorded with the extracellular solution titrated to pH 7.4 (A) or pH 6.0 (B). Na_V1.5+β₁ currents recorded at pH 6.0 preferentially prolonged mid-myocardial APs over epicardial and endocardial APs. At pH 6.0, the APD₉₀ was increased from 348 ms to 353 ms (epicardial), 361 ms to 378 ms (mid-myocardial), and 348 ms to 354 ms (endocardial). APs obtained using pH 6.0 data also displayed an 11 mV reduction in their peak depolarization (40 mV to 29 mV) and a 5 mV increase in the threshold for AP firing (−51 mV to −46 mV), and reduced the maximum rate of the AP upstroke by 60% (197 mV/ms to 81 mV/ms) (inset). The inset displays an expanded view of the initial rise of a mid-myocardial cell AP at pH 7.4 and 6.0. (C) Epicardial, mid-myocardial, and endocardial ventricular APs display the preferential increase of mid-myocardial APs with pH 6.0 data.

Discussion

A reduction in extracellular pH, such as during myocardial ischemia, triggers an array of arrhythmogenic alterations in cardiac tissue. Although a reduction in internal pH also occurs, the extracellular pH has been shown to change more dramatically (see Crampin et al. (39) and Bers (40) for reviews). Given the location of Na_V1.5 channels and the relative reduction in extracellular versus intracellular pH, exploration of extracellular proton modulation is prudent. Although we did not measure internal pH during our recordings, the rapid reversibility of Na_V1.5 channel proton modulation, along with the stability of intracellular pH of oocytes during prolonged exposure to reduced extracellular pH (41,42), suggests that intracellular pH underwent only a minimal change (if any) during these recordings. The alterations in I_Na described here are therefore attributable to extracellular protons. The role played by Na_V1.5 channel proton modulation in arrhythmogenesis is unclear, and a detailed kinetic analysis of the effects of acidosis on Na_V1.5 channels is lacking. Here we provide such an analysis and demonstrate that protons destabilized the fast- and slow-inactivated states, and increased both persistent and apparent window I_Na. When these biophysical effects are incorporated into a simulation of the epicardial, mid-myocardial, and endocardial APs, they appear to promote disparate prolongation of the APD across the ventricular wall and may therefore contribute to arrhythmogenesis.

Effects on activation

We found that low extracellular pH reduced peak current, reversibly depolarized the voltage dependence of activation, and increased the time to peak current by 30%. The pH-dependent shift in V_1/2 and z of activation was similar to that of proton block, which may suggest that the residues responsible for proton block are also responsible for the changes in voltage-dependent gating properties. Of interest, the change in valence plotted as a function of pH and fitted with a Hill equation had a pKa = 6.0. A direct comparison of the Hill curves of V_1/2 and z reveals similar pKa values but very different slopes (Fig. 1 C). The effect on V_1/2 is observed at a higher pH than the effect on z, but they reach full effect at the same pH. Further, the pH at which the curves reach their maxima does not coincide with the baseline plateau of proton block of hNa_V1.5+β₁; instead, it more resembles the plateau of Na_V1.4 proton block, which has a pH-independent current of ∼14% (18,19). Replacement of C373 with the homologous residue in Na_V1.4 channels, a tyrosine, introduces a similar pH-independent current in Na_V1.5 channels (18). The reverse mutation in Na_V1.4 channels (Y401C) removed the pH-independent current (18). Although protonation of C373 may be unnecessary for the effects on the voltage dependence of activation gating, the effect on V_1/2 and z could occur as the result of titration of the outer pore carboxylates previously mentioned.

Effects on inactivation

Fast inactivation

Our data show that low pH reversibly destabilizes the fast-inactivated state. Destabilization of fast inactivation is a well-documented trigger for cardiac arrhythmia (11). We observed an increase in the relative window current at pH 6.0 versus pH 7.4 (Fig. 3, A and C), although the absolute window current was reduced (Fig. 3 B). Also, the rates of recovery from the fast-inactivated state were significantly accelerated at −80 mV and −90 mV, the rates of open-state inactivation were significantly reduced at −30 mV through +30 mV, and persistent I_Na was significantly increased (Fig. 2). The slowed onset of open-state inactivation would be expected to delay the initial repolarization of the cardiac AP, whereas increased window current, acting in concert with accelerated recovery and the increase in persistent I_Na, would be expected to increase the probability of channels reopening during the AP plateau. Together, these effects on inactivation would slow the rate and increase the heterogeneity of repolarization, a prediction that is supported by our epicardial, mid-myocardial, and endocardial modeling data.

Slow inactivation

The stability of the slow-inactivated state is mediated, at least in part, by amino acid residues within Na_V channel p-loops. Altering the electrostatic environment within the pore alters the properties of slow inactivation. Extracellular elevation of permeable cations has been shown to speed recovery, slow the onset, and decrease the maximum probability of slow inactivation in Na_V1.5 channels (43). Here, the rate of slow inactivation onset was significantly reduced and the rate of recovery from slow inactivation appeared to be accelerated at pH 6.0. In contrast, there was no effect on SSSI. Additionally, the maximum probability of SSSI increased with removal of fast inactivation in Na_V1.5 channels (9), and we observed a destabilization of the fast-inactivated state. The mutual association of protons and slow inactivation at the pore seems sufficient to assume some effect of protons on SSSI (44); however, we observed none. Why pH affected the rates of slow inactivation but not SSSI is unclear. A positive charge on the extra- and intracellular sides of DII-S4 has been shown to affect slow inactivation (44,45). Proton modulation of Na_V1.5 channel slow inactivation may occur closer to the channel's voltage sensor and not the pore, which could explain the mutual effects on fast and slow inactivation. That being said, it seems parsimonious to suggest that protons act on slow inactivation through a similar mechanism to that observed by Townsend and Horn (43), who showed that positive charges binding at outer vestibule carboxylates inhibit closing of the slow inactivation gate.

Use-dependent inactivation

A use-dependent analysis allows us to frame a more physiological picture of the interplay between the various states of the channel and the dynamic nature of cardiac muscle tissue. Each depolarizing pulse in the use-dependent protocol is much longer than even the greatest time constant of fast inactivation. Therefore, it is unlikely that the effect on use-dependent inactivation by pH can be attributed to modulation of fast inactivation kinetics. Time constants measured for fast inactivation (Fig. 2 D) tell us that, at most, only 4% of the effect on the asymptote of use-dependent inactivation could be attributed to changes in fast inactivation recovery.

The changes in slow-inactivation recovery and onset therefore explain the majority of the differences in use-dependent inactivation. The time constants of slow inactivation are small enough to permit channels to accumulate in the slow-inactivated state over the course of our protocol. By inhibiting slow-inactivation onset and accelerating slow-inactivation recovery, the channels reach a lower level of steady-state, use-dependent inactivation. The effects on the time constants of use-dependent inactivation can therefore be attributed to proton modulation of slow inactivation. We did not explore the role of stimulation frequency in this study, but this might be expected to further affect how the channels respond to changes in pH.

AP model and relation to arrhythmia

Protons interact with a wide range of proteins and produce an altered and arrhythmogenic AP morphology during cardiac acidosis. By incorporating our data into a ventricular AP model and leaving all other model parameters unchanged, we can predict the independent contribution of Na_V1.5 channel proton modulation to changes in AP morphology during acidosis without the confounding and complicated effects of proton modulation of other cardiac proteins. Using our data, we observed that all of our AP models display two major characteristics: First, proton modulation of Na_V1.5 channel currents produces a 60% decrease in V_max (Fig. 6 B, inset). We attribute the reduction in V_max to the reduced Na_V1.5+β conductance. In the intact myocardium, this would be expected to cause a reduction in the velocity of AP propagation, an arrhythmogenic effect that occurs during local ischemia (23). Second, our model predicts prolonged ventricular APDs (Fig. 6, A and B, and Fig. S2 C). A prolonged APD would increase the likelihood of early afterdepolarizations, similar to what is observed in individuals suffering from long QT syndrome type III (46). Of interest, the increases in persistent I_Na predominantly prolonged mid-myocardial APs (≈18 ms) as opposed to epicardial (≈6 ms) or endocardial (≈7 ms) APs. This is expected because the longer mid-myocardial AP plateau allows a greater contribution from persistent I_Na. The predominant extension of mid-myocardial APD would be expected to increase the heterogeneity of repolarization across the ventricular wall, a known trigger for reentrant arrhythmia in the intact myocardium (47,48). The time between the peak and baseline of the ECG T-wave (T_peak-T_end), indicative of epicardial and mid-myocardial AP repolarization, respectively, is one index that is used to estimate transmural dispersion of repolarization (49). Although our modeling data do not allow us to derive an exact T_peak-T_end value, they demonstrate that the T_peak-T_end would most likely increase, and this would be expected to increase the likelihood of arrhythmia (48).

Numerous additional changes in myocyte physiology occur during cardiac ischemia that could affect the role of Na_V1.5 channels in arrhythmogenesis. For example, membrane depolarization from the ischemia-induced rise in extracellular [K⁺] may cause further reductions in Na_V1.5 channel availability. Changes in Ca²⁺ dynamics, stemming from elevated extra- and intracellular proton concentrations, would also alter AP morphology. We used the ten Tusscher-Noble model to assess how proton modulation of Na_V1.5 might affect the morphology of a ventricular AP, and our findings suggest that the APD is prolonged, albeit in the absence of the above-mentioned changes. Further complex and extensive modeling studies incorporating our observations into a model that includes the numerous changes seen in other channels and proteins would likely produce interesting and important findings.

Conclusion

Our results demonstrate that heightened extracellular proton concentrations destabilize both the fast-inactivated and slow-inactivated states in Na_V1.5 channels. These effects display arrhythmogenic properties when incorporated into a ventricular AP model.