Thermodynamic efficiency and mechanochemical coupling of F₁-ATPase

Abstract

F₁-ATPase is a nanosized biological energy transducer working as part of F_oF₁-ATP synthase. Its rotary machinery transduces energy between chemical free energy and mechanical work and plays a central role in the cellular energy transduction by synthesizing most ATP in virtually all organisms. However, information about its energetics is limited compared to that of the reaction scheme. Actually, fundamental questions such as how efficiently F₁-ATPase transduces free energy remain unanswered. Here, we demonstrated reversible rotations of isolated F₁-ATPase in discrete 120° steps by precisely controlling both the external torque and the chemical potential of ATP hydrolysis as a model system of F_oF₁-ATP synthase. We found that the maximum work performed by F₁-ATPase per 120° step is nearly equal to the thermodynamical maximum work that can be extracted from a single ATP hydrolysis under a broad range of conditions. Our results suggested a 100% free-energy transduction efficiency and a tight mechanochemical coupling of F₁-ATPase.

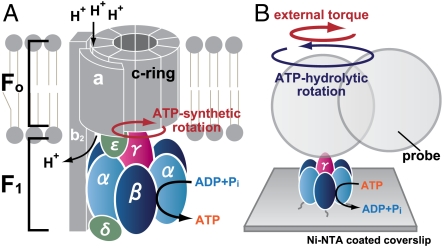
ATP synthase F_oF₁ plays a central role in the cellular energy transduction by synthesizing most ATP in virtually all organisms, including bacteria, chloroplasts, and mitochondria (1, 2). This enzyme consists of two motors: F_o-motor, which is embedded in the membrane, and F₁-motor (F₁-ATPase), which protrudes from the membrane (Fig. 1A). F₁-motor is a reversible motor/generator. As part of F_oF₁-ATP synthase, it acts as a generator. Proton flux through the F_o-motor along the transmembrane electrochemical potential drives rotation of the F_o-motor’s c-ring. Because the rotor subunit (γ-shaft) of F₁-motor is coupled with the c-ring (3–5), c-ring rotation forces γ-shaft to rotate. Under these conditions, F₁-motor synthesizes ATP from ADP and phosphate (P_i) (6–8). On the other hand, when isolated, F₁-motor works as a motor, hydrolyzing ATP to ADP and P_i and rotating the γ-shaft counter to the direction it takes during ATP-synthetic rotations (9–12) (Fig. 1B). An ATP hydrolysis makes a 120° rotation of the γ-shaft.

Fig. 1.

F_oF₁-ATP synthase and F₁-motor. (A) F_oF₁-ATP synthase consists of F_o-motor (ab₂c_n) and F₁-motor (α₃β₃γδε). The variable n depends on species. (B) The α₃β₃γ subcomplex of F₁-motor. By adhering F₁-motor to a glass surface and attaching a probe of dimeric particles to the γ-shaft, its rotation can be observed under optical microscope. By using electrorotation method, we can induce a controlled external torque on the probe particle.

Despite the critical role played by F₁-motor as a mechanochemical energy transducer, information about its energetics remains limited compared to that of the reaction scheme (13–15). In fact, fundamental questions remain unanswered; these questions include how efficiently F₁-motor can convert energy between the chemical free energy change of an ATP hydrolysis (Δμ) and mechanical work. Previous studies (12, 16) suggested that F₁-motor works at a high efficiency in the sense that the work against viscous drag during a rotational step in the absence of external torque is nearly equal to Δμ. However, this efficiency should be distinguished from the free-energy transduction efficiency because the work against viscous drag finally dissipates as heat to the surrounding environment and cannot be fully utilized further (17). To evaluate the efficiency of the mechanochemical free-energy transduction, it is required to examine the work against a conservative external load.

The above question has not been addressed clearly for F₁-motor in experiments compared to extensive theoretical studies (18, 19) and experimental studies on linear motors (20, 21) because it has been a challenge to apply an external torque of precisely controlled magnitude. In this study, we adhered F₁-motor’s stator subunits to a glass surface and applied external, ATP-synthetic direction torque to the probe particle attached to the γ-shaft by using an electrorotation method (16, 22–24). This method allowed us to create a model system of F_oF₁-ATP synthase, wherein we could examine the synthetic-direction rotations and the energetics of an isolated F₁-motor while precisely controlling both the external torque and the chemical potential of ATP hydrolysis.

Results

Stepwise Rotations in the ATP-Synthetic Direction.

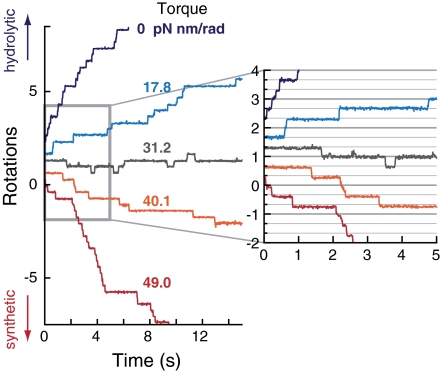
In the absence of external torque (0 pN nm/rad), F₁-motor rotated in discrete 120° steps at a low ATP concentration (denoted by [ATP]) and in the presence of ADP and P_i (Fig. 2). The rate-limiting step, observed as a pausing (or dwell) between steps in the trajectory, corresponds to the ATP waiting state; binding of ATP triggers the 120° rotation (12). When we applied an opposing torque against hydrolytic rotation on the probe particle, duration of the dwells increased, and the rotational rate decreased accordingly. Under a sufficiently strong torque, we observed rotation in the ATP-synthetic direction, with three steps per rotation. At an intermediate magnitude of torque (31.2 pN nm/rad), the probe particle showed bidirectional stepwise fluctuations with 120° steps and stalled on average. It is noteworthy that in this stalled state the rotation neither froze at a specific angular position nor displayed freely rotating Brownian motion.

Fig. 2.

Rotational trajectories under external torque (0.4 μM ATP, 4 μM ADP, 1 mM P_i) of the same F₁-motor molecule.

In a previous study (23) where an ATP regeneration system was used to drastically reduce [ADP], and where P_i was not explicitly included, rotations in the synthetic direction were not observed even under a strong torque (up to approximately 100 pN nm/rad). Our results indicate that ADP and P_i are necessary for F₁-motor to rotate in the synthetic direction, implying that ADP and P_i are incorporated into F₁-motor and that ATP is synthesized during the synthetic direction rotation. The ATP synthesis under mechanically forced rotations has been demonstrated by using magnetic tweezers (6, 7). In those experiments, the angular position of the probe rather than torque was controlled. As we have shown, the present method with a controlled external torque enables us to examine mechanical responses such as the stepwise rotations in the ATP-synthetic direction. We will see that, furthermore, this method provides fruitful information about the energetics and mechanochemical coupling of F₁-motor.

Rotational Rate and Stall Torque Under Mechanochemical Control.

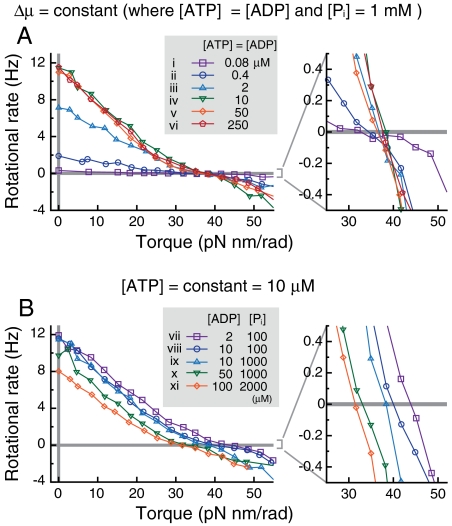
Fig. 3 shows the torque dependency of rotational rates under various concentrations of ATP, ADP, and P_i. First, we varied [ATP] and [ADP] under the constraint that [ATP] = [ADP], and [P_i] = 1 mM. The free rotational rates, or the rotational rates in the absence of external torque, varied significantly depending on [ATP]( = [ADP]); they increased as [ATP] increased because ATP binding was the rate-limiting step. At high [ATP] (> 10 μM), the free rotational rates were saturated because of a viscous friction and had similar values (ca. 11 Hz). On the other hand, the stall torque (N_stall) under which the rotational rate vanishes, was almost the same except at extremely low [ATP]( = [ADP]) (Fig. 3A). Note that the free energy change liberated by a single ATP hydrolysis is

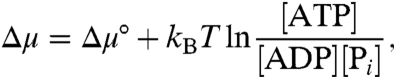[1]

which is constant under the present conditions, except for a minor difference of Δμ° due to changes in variables such as the ionic strength and concentration of free Mg²⁺, because the ratio [ATP]/[ADP][P_i] is constant. When we varied Δμ while holding [ATP] constant at 10 μM, N_stall was markedly different (Fig. 3B) whereas the free rotational rates were relatively similar compared to those in Fig. 3A.

Fig. 3.

Torque dependency of the mean rotational rates under various concentrations of ATP, ADP, and P_i. (A) [ATP] = [ADP], and [P_i] = 1 mM. Because the ratio [ADP][P_i]/[ATP] is constant, Δμ is constant (see Eq. 1). (B) [ATP] = 10 μM while varying [ADP] and [P_i] to control Δμ. Data from approximately 15 molecules were averaged under each condition. In total, data of 92 and 74 molecules are used in A and B, respectively. The mean rotational rates are calculated as follows: Because the magnitude of the imposed torque varies from particle to particle, we divided the horizontal axis into bins (width is 7 pN nm/rad except for the case in the absence of external torque) and took an average of the torque and rotational rates in each bin.

When either [ADP] (Fig. 3, vii, viii, ix, and x) or [P_i] (viii, ix) alone were increased, N_stall decreased. On the other hand, when only [ATP] was increased (v, x), N_stall increased. Thus, ADP and P_i facilitated rotation in the synthetic direction, whereas ATP had the opposite effect. These results again suggest that ADP and P_i are incorporated into F₁-motor and that ATP is synthesized during synthetic direction rotations. See Fig. S1 for data of individual molecules.

Maximum Work During a 120° Rotation is Equal to Δμ.

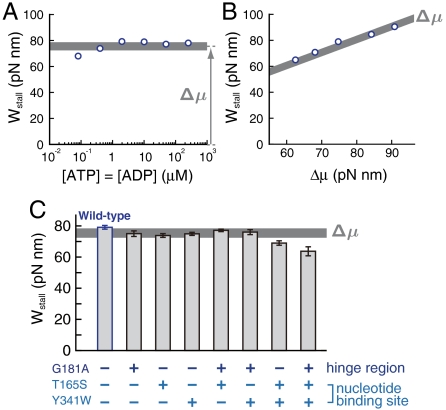
Under an opposing torque of N, F₁-motor performs W ≡ N × 120° work against the external torque during a 120° rotation. Therefore, W_stall ≡ N_stall × 120° is equivalent to the maximum work performed by F₁-motor during a 120° rotation. We found that W_stall is nearly equal to Δμ under a variety of conditions (Fig. 4 A and B, see Fig. S2 for the method to estimate the stall torque). Note that Δμ is the thermodynamic limitation for the work extractable from an ATP hydrolysis. When [ATP] and [ADP] are extremely low (0.08 μM), W_stall was significantly smaller than Δμ (see Table S1 for the t test). At low [ADP], it is possible that there are slippery rotations in the synthetic direction, during which ADP is not incorporated and, therefore, ATP is not synthesized.

Fig. 4.

W_stall [the stall torque × 120° (2π/3)] of the wild type and mutants. (A and B) W_stall of the wild type under conditions corresponding to those in Fig. 3 A and B, respectively. Error bars (standard errors) are smaller than the symbols. (C) W_stall of the mutants under 10 μM ATP, 10 μM ADP, and 1 mM P_i. Error bars are standard errors. The thick lines indicate the value of Δμ. The standard free energy difference Δμ° is different among literatures; the thickness of these lines indicates the estimation variance of Δμ (see Table S1 and Table S2 for details).

Proper Torque Generation Requires only a Partial Binding of Nucleotides.

It is still unclear how the F₁-motor generates torque (25–27). To investigate the amino acid residues critical for the torque generation, we measured the stall torque of various mutants. We mutated one or more of the following three β-subunit’s amino acid residues (Fig. S3): one in the hinge region [βG181A (28)], and two around the ATP binding site [βT165S (29) and βY341W (30)]. βT165 interacts with the phosphate moiety via Mg²⁺, whereas βY341 has a hydrophobic interaction with the adenine ring moiety. βG181 undergoes a large change in the dihedral angle of peptide bond during rotation. The mutant including all of these three mutations is known to have a smaller free rotational rate than the wild type (31), suggesting that it has a smaller torque against a viscous load.

The W_stall values of the mutants including both βT165S and βY341W were significantly smaller than that of the wild type, whereas those of the remaining mutants were nearly equal to that of the wild type (Fig. 4C, see also Fig. S4 and Table S2). These results imply that proper torque generation requires only a partial binding of nucleotides at either the phosphate moiety and the adenine ring. On the other hand, βG181A had little effect on stall torque; this result is consistent with a previous result suggesting that βG181A does not affect torque against a viscous load (28). Although βG181A clearly changes its dihedral angle when the β subunit undergoes a conformational transition from open to closed, the role of the hinge region in torque generation is still unclear. To reveal its role, future study should examine the effects of mutations in the hinge region.

Mechanochemical Coupling.

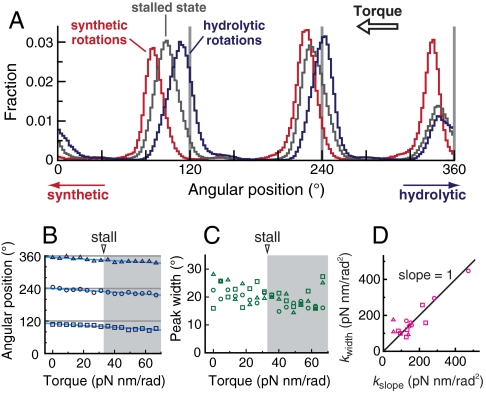
We next focus on the stepping motion to evaluate the mechanochemical coupling. The angular distribution had three peaks corresponding to the ATP waiting states at low [ATP] in the absence of external torque (Fig. 5A). This distribution was maintained as we applied torque, even when the rotation almost stalled and when rotating in the synthetic direction. For quantitative analysis, we fitted the angular distribution of each peak by the Gaussian function: A exp{-[θ - θ₀(N)]²/2σ²(N)}, where A is the height of the peak, θ is the angular position, θ₀(N) is the angular position of the peak in the presence of torque (N), and σ(N) is the width. We found that the angular positions of the peaks shifted in the direction of the applied torque with a linear dependence on torque overall (Fig. 5B). On the other hand, the peak width had little dependency on torque (Fig. 5C). We confirmed Einstein relation, that is, the spring constant calculated from the peak width, 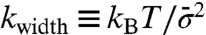, where 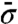is the mean of σ over N, and that calculated from the torque dependency of the peak displacement, k_slope, which is the slope of a linear fitting curve of θ₀(N), coincided well (Fig. 5D). These results suggest that the displacement of the peak’s angular position under torque is simply due to a shift of the equilibrium angular position during a dwell; the angular position of the dwell observed during synthetic direction rotations is equivalent to that of the ATP waiting state during hydrolytic direction rotations.

Fig. 5.

Torque dependency of angular distributions under 0.4 μM ATP, 4 μM ADP, and 1 mM P_i. (A) Angular distributions of three peaks of a molecule under hydrolytic rotations in the absence of torque (blue), around the stalled state (gray, torque = 31.2 pN nm/rad), and under the synthetic-direction rotations (red, 49.0 pN nm/rad). Bin width is 2°. (B) Angular positions of the peaks (symbols) and linear fitting curves (solid lines). In the shaded region, F₁-motor rotates in the synthetic direction. (C) Width of the peaks. The data of the same molecule are used for plotting A, B, and C. (D) Validation of Einstein relation. Spring constants calculated by different two methods are plotted. Different symbols correspond to different molecules (15 dwells of five molecules).

Note that the estimated spring constant reflects not only the internal stiffness of the motor but also the external one such as the linker between the γ-shaft and the probe and that between the α₃β₃-ring and the glass surface (32, 33). Okuno et al. has estimated the internal and external stiffness to be k_in = 223 pN nm/rad² and k_ex = 72.6 pN nm/rad², respectively, in their system, which yield the total stiffness that the probe feels of 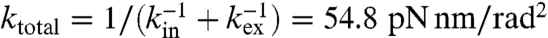(32). In our system, k_total was typically 150 pN nm/rad² (Fig. 5D). Given that k_in = 223 pN nm/rad² as estimated by Okuno et al., k_ex was estimated to be 458 pN nm/rad² typically. The large difference of k_ex from their estimation is expected be due to the difference of the preparation of the probe. Thus, the total stiffness that the probe feels is dominated by the internal stiffness of the motor in our system. The broad distribution of the spring constants (Fig. 5D) is supposed to be due to the small distortion of the motor’s structure by the interaction between the motor and the glass surface.

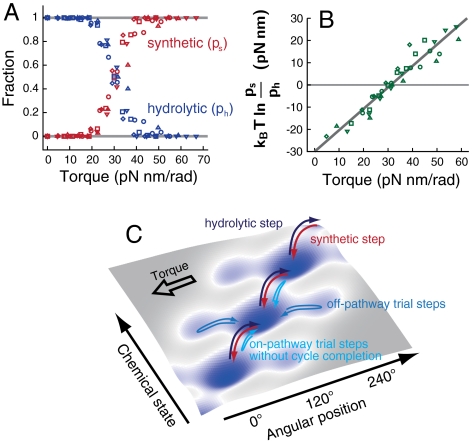
The equivalence of the pausing states during rotations in both the directions leads to a simple model that the bidirectional stepwise rotations of F₁-motor can be modeled as jumps among three discrete states with 120° spacings. For further analysis, we counted the number of steps in both the directions. Fig. 6A shows the fraction of steps in the synthetic direction, p_s, and in the hydrolytic direction, p_h( = 1 - p_s), under torque. As we increased the magnitude of torque, p_s increased and then balanced with p_h (the stalled state). The logarithmic ratio of p_s to p_h depended linearly on torque (Fig. 6B):

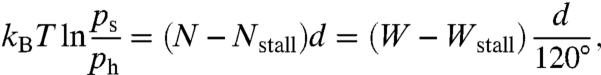[2]

where the fitting parameters d and N_stall were 55° and 31.2 pN nm/rad, respectively. W_stall = N_stall × 120° = 65.3 pN nm was nearly equal to Δμ under this condition (65.2 pN nm). The value of d provides valuable information about the mechanochemical coupling, which will be discussed later.

Fig. 6.

Step analysis of the rotational trajectories under 0.4 μM ATP, 4 μM ADP, and 1 mM P_i. Different symbol corresponds to different molecule (five molecules in total). (A) Occurrence probabilities of steps in the synthetic direction (p_s, red) and hydrolytic direction (p_h, blue). (B) The ratio p_s/p_h depends exponentially on the torque. (C) Free energy landscape and possible pathways.

Discussion

When examining the maximum torque generated by F₁-motors, previous studies have focused on the stepping torque, that is, the rotational velocity during the step between dwells multiplied by the rotational frictional coefficient of the probe (12, 34). We found that the rotation neither froze at a specific angular position nor displayed freely rotating Brownian motion, even in the stalled state; rather it showed bidirectional stepwise fluctuations (Fig. 2). Thus, the stepping torque does not vanish and the F₁-motor appears capable of exerting torque during the stalled state; instead, the occurrence probabilities of steps in the hydrolytic and synthetic directions are balanced. Therefore, it is essential to distinguish between the stepping torque and the stall torque. The former is determined basically by the mechanical properties, or by the structure, of the F₁-motor. On the other hand, the latter is determined by both the chemical potential of the ATP hydrolysis and the mechanical properties of the F₁-motor.

The coincidence between the maximum work performed by F₁-motor during the 120° rotation (W_stall) and the chemical free energy change of an ATP hydrolysis (Δμ) suggests that F₁-motor serves as a highly efficient mechanochemical free-energy transducer of F_oF₁-ATP synthase at almost 100% thermodynamic efficiency. For such a high efficiency to be achieved, a tight mechanochemical coupling is expected, that is, one ATP is hydrolyzed during every hydrolytic-direction step, whereas one ATP is synthesized during every synthetic direction step.

On the other hand, in a tightly coupled system in the rigorous meaning of this term, the ratio of the occurrence frequencies of the forward and backward chemical cycles (denoted as π_s and π_h) is expected to satisfy k_BT ln(π_s/π_h) = (N - N_stall)d, where d is the step size corresponding to a chemical cycle and is 120° here, to be consistent with the detailed balance condition or fluctuation theorem (18, 35–38); π_s/π_h depends only on the free energy difference between states independently of the system’s detail. However, d was significantly smaller than 120° when we used the ratio of step fractions in both the directions, p_s/p_h, as the estimation of π_s/π_h (Fig. 6B). This result is reasonable given that there are rotational steps without the completion of chemical cycles. That is, because a single rotational step comprises multiple chemical processes, it is possible that the γ-shaft starts to rotate but sometimes returns to the initial state before the chemical cycle completes (39). In addition to such on-pathway incomplete steps, off-pathway steps without accompanying any chemical transitions might occur (Fig. 6C). Because such an off-pathway step results in an unstable state, the γ-shaft will return to the initial state immediately without rotating further. When we use Eq. 2 for the estimation of d, these trial round-trip steps with incomplete chemical cycles decrease the estimation value of d as follows: When we count m incomplete round-trip steps in addition to the steps accompanying complete chemical cycles (n_s and n_h), π_s/π_h = n_s/n_h and p_s/p_h = (n_s + m)/(n_h + m). Because of the upward concavity of logarithmic function, | ln π_s/π_h| > | ln p_s/p_h|. More detailed statistical analysis of rotational steps would be helpful for better understanding of the energetics and mechanochemical coupling (39). However, the most essential approach is to evaluate not only mechanical response but also chemical response by directly observing the binding and release of ATP and ADP (13, 40) in the presence of controlled torque.

It is known that the hydrolytic 120° step is resolved to two substeps of 80° and 40° (12, 41, 42). During the pause after 80° step (catalytic dwell), ATP is hydrolyzed and a phosphate is released. Because its duration is only milliseconds long, we did not observe it during free hydrolytic rotations with the large probe used in this study. However, we did not observe corresponding pauses during hydrolytic rotations under load and even during synthetic direction rotations. This result suggests that the duration of the catalytic dwells has little torque dependency. For better understanding, it maybe productive to investigate the effect of external torque on catalytic dwells of the βE190D mutant with low ATPase activity (41, 42).

Materials and Methods

Rotation Assay.

The observation chamber was constructed by essentially the same method in the previous study (16, 23). F₁ molecules derived from a thermophilic Bacillus PS3 with mutations for the rotation assay (His₆-αC193S/W463F, His₁₀-β, γS107C/I210C, denoted by wild type) (7) and other mutations indicated were adhered on a coverslip functionalized by Ni²⁺-nitrilotriacetic (NTA) acid. Rotations of the γ-shaft were probed by streptavidin-coated dimeric polystyrene particles (diameter = 0.287 μm, Seradyn) attached to the biotinylated γ-shaft.

Observation was performed at 24.5 ± 1.5 °C in a buffer containing 5 mM 3-morpholinopropanesulfonic acid (MOPS)-K, indicated amount of MgATP, MgADP, and P_i, and 1 mM excess of MgCl₂ over ATP and ADP (pH 6.9) on a phase-contrast upright microscope (Olympus) with a 100× objective (Olympus), at 1,800 Hz using a high-speed camera (Imperx), an interface board (National Instruments), and a laboratory-made capturing software developed on LabView 8.6 (National Instruments). Such a high frequency recording prevents the finite exposure time effect for the estimation of the spring constant (32). The angular position of the probe was estimated by using an algorithm based on the principal component analysis, which reduces the effect of the instrumental noise. The data including a long pause presumably due to the MgADP-inhibited state (43) are excluded from the analysis.

Electrorotation Method.

We have four electrodes patterned with a spacing of 50 μm on the bottom glass surface of the chamber (16, 23) (Fig. S5). By applying 15-MHz sinusoidal voltages with a phase shift of π/2 on the electrodes using a function generator (NF Corporation) and four voltage amplifiers (NF Corporation), an electric field rotating at 15 MHz was generated in the center of the electrodes. Under this rotating electric field, a dipole moment rotating at 15 MHz were induced on the probe particle. Because there is a phase delay between the electric field and dipole moment, the probe is subjected to a constant torque. The magnitude of torque is proportional to the square of the voltages’ amplitude and the volume of the dielectric objects. The temperature rise problem reported in the previous study (23) was avoided by reducing the ionic strength of the buffer and reducing the distance between the top and bottom glasses using thinner spacers [SaranWrap (Asahi Kasei) with silicone grease]. The distance between the top and bottom glass surfaces was 15–20 μm. Temperature rise caused by the electric field was measured by the same method used in ref. 23 and found to be at most 1.0 °C, which was comparable to the temperature variance of the environment.

Torque Calibration.

We controlled the magnitude of the torque by varying the amplitude of the applied voltage. The magnitude of torque (N) is proportional to the square of the voltages’ amplitude (A): N ≡ αA². The coefficient α depends on various parameters such as the height and ionic strength of the chamber and the volume of the probe particle. Therefore, it is required to evaluate α in each chamber. Previously, assuming that torque is similar among particles in the same chamber, we estimated α using rotational Brownian particles (16, 23). In this study we developed a unique method to evaluate α, which provides a better estimation; α can be directly obtained using the particle with which we take data.

In ref. 16, we showed that the velocity fluctuation-dissipation theorem (44) holds in the high frequency region for the rotating probe particle attached to the F₁-ATPase;

[3]

Here, 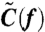is the Fourier transform of the auto-correlation function of the rotational velocity 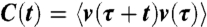at a frequency f. 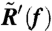is the real part of the Fourier–Laplace transform of the linear-response function R(t), which satisfies 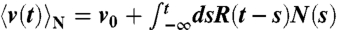, where 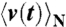denotes the ensemble average of the rotational velocity under a sufficiently small probe torque N(t). The mean rotational velocity is 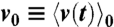in the absence of external torque. Because of the causality, R(t) = 0 if t < 0. Given that we apply a sufficiently small sinusoidal torque N(t) = N₀ sin(2πf₀t) of a frequency f₀ and obtain a velocity profile 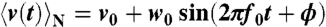, it is easily shown that 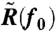becomes

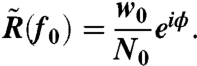[4]

Note that w₀ and ϕ depend on f₀. By measuring the response (w₀ and ϕ) and fluctuation [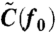] of the rotational velocity at sufficiently high frequency f₀, we obtain α by using Eq. 3, Eq 4, and 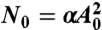, where A₀ is the amplitude of the sinusoidal amplitude-modulation of the electrorotation voltages used for applying sinusoidal probe torque:

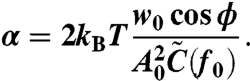[5]

The actual experimental procedure was as follows: We calculated 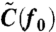from the rotational trajectories in the absence of external torque by a fast Fourier method (45) (Fig. S6A). Measurement of w₀ and ϕ was performed in the following manner (Fig. S7). We observed the time course of the rotational velocity v(t) under a sufficiently small sinusoidal torque at a frequency f₀ = 300 Hz. Sinusoidal torque was obtained by modulating the amplitude of the applied voltage periodically. We took an ensemble average 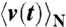for each period of T = 1/f₀, fitted by a sinusoidal function 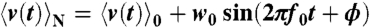for evaluating w₀ and ϕ, and calculated α by using Eq. 5. The response curve under a sinusoidal probe torque was well-fitted by a sinusoidal function (Fig. S6B), suggesting that the response function was measured in the linear-response regime around the steady state.

Step Analysis.

Steps in the rotational trajectories were identified by using an algorithm based on Hidden Markov Modeling and the Viterbi algorithm (45). The validity of this method was checked by eye. In this method, we modeled the stepping motion as jumps among three discrete states. We denote the state at a frame k (1 ≤ k ≤ L) as s_k (1 ≤ s_k ≤ 3) and define a score function: 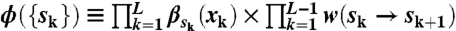. Here, {x_k} is the rotational trajectory, β_s(x) is the probability that x is observed at a state s, and w(s → s^′) is a transition probability from s to s^′. We obtained 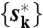that maximizes ϕ({s_k}) by Viterbi algorithm and calculated the fraction of steps (p_h and p_s). We estimated β_m(x) by fitting the angular distribution by Gaussian functions and w(s → s^′) is not known a priori. Therefore, for obtained 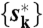, we optimized w(s → s^′) to maximize 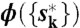. We repeated these two optimizations until the convergence.