Transcription factor network reconstruction using the living cell array

Abstract

The objective of identifying transcriptional regulatory networks is to provide insights as to what governs an organism’s long term response to external stimuli. We explore the coupling of the living cell array (LCA), a novel microfluidics device which utilizes fluorescence levels as a surrogate for transcription factor activity with reverse Euler deconvolution (RED) a computational technique proposed in this work to decipher the dynamics of the interactions. It is hypothesized that these two methods will allow us to first assess the underlying network architecture associated with the transcription factor network as well as specific mechanistic consequences of transcription factor activation such as receptor dimerization or tolerance.

The overall approach identifies evidence of time-lagged response which may be indicative of mechanisms such as receptor dimerization, tolerance mechanisms which are evidence of various receptor mediated dynamics, and feedback loops which regulate the response of an organism to changing environmental conditions. Furthermore, through the exploration of multiple network architectures, we were able to obtain insights as to the role each transcription factor plays in the overall response and their overall redundancy in the organism’s response to external perturbations. Thus, the LCA along with the proposed analysis technique is a valuable tool for identifying the possible architectures and mechanisms underlying the transcriptional response.

1. Introduction

Transcription factors are proteins representing an important mediator in controlling the levels of mRNA. When activated, these transcription factors bind to the upstream regions of DNA and cause the up/down regulation of mRNA production. The challenges which arise in building models that describe transcription factor activity (TFA) and their interactions come from the fact that the level of TFA need not correlate with the amount of the transcription factor present due requirements for activation such as phosphorylation or dimerization (Samet et al., 2002) and post-translational modifications (Tootle and Rebay, 2005). Furthermore, the fact that functional binding sites exist on the promoter of transcription factors suggests that these factors are involved in complex cross-regulatory interactions (Kyrmizi et al., 2006; Nelson et al., 2004).

To identify the interactions between transcription factors (TF) and their targets, experimental techniques such as transcription factor prediction or Chip–chip experiments (Lee et al., 2002) have been developed. These techniques focus primarily upon the genomic sequences to identify which transcription factors interact with the upstream regions of various genes. Computational methods, on the other hand, such as Boolean networks (Shmulevich et al., 2002), Petri-nets (Goss and Peccoud, 1998) combine both transcription factor prediction and mRNA expression levels (Segal et al., 2003) in an attempt to identify network architectures from gene expression. The methods that combine genomic sequence and gene expression information make the implicit assumption that the activity of a transcription factor, i.e., its potential for impacting gene regulation, is associated with the levels of the corresponding mRNA. However, it is well known that this need not be the case as best exemplified by the activity models proposed for the NFkB family of transcription factors (Hoffmann et al., 2002). The computational prediction of transcription factor activities is an active area of research and a number of very promising methodologies have already been proposed for the in silico prediction of TFA based on transcriptional data (Boscolo et al., 2004; Boulesteix and Strimmer, 2005; Kao et al., 2004a; Liao et al., 2003; Tran et al., 2005).

The living cell array (LCA) (King et al., 2007, 2008) presents a unique experimental platform that allows for the direct estimation of the activity of a transcription factor. Rather than focusing upon the binding of transcription factors, or mRNA expression changes, it utilizes fluorescent reporters that respond to the levels of active transcription factors, via specially designed plasmids utilizing known transcription factor binding motifs. Given the novel nature of its experimental design, the LCA offers the opportunity to decipher mechanisms driving the cross-activation of assemblies of transcription factors. Furthermore, owing to the design of the microfludics device, one can simultaneously obtain the levels of TFA under multiple stimuli with high temporal resolution. This greatly improves our ability to decipher the interactions between the different transcription factors because we are no longer constrained by limitations in the data, where the number of genes measured is much greater than the number of conditions or time points in which they are measured as in the case where transcriptional networks were reconstructed from microarray data (Somorjai et al., 2003).

In this paper, we propose reverse Euler decomposition (RED) as a computational framework enabling us to take advantage of the benefits offered by the LCA. Combining this computational framework along with the experimental system of the LCA, it is possible to not only isolate TF interactions but also to quantify numerically, the evidence of nonlinear phenomena that are present in biological systems (Hemberg and Barahona, 2007). Identifying these non-linear interactions is important because they provide evidence of specific mechanistic effects that govern transcriptional activation. We focus primarily upon a set of transcription factors known to play a role in inflammation, and we hypothesize that it is possible to de-convolve the aggregate TFA responses and we will demonstrate the consistency between what is currently known about these transcription factors and our predictions.

2. Methods

2.1. The LCA

The LCA is a microfluidics device which utilizes cells transfected with reporter plasmids. These reporter plasmids comprise of an unstable green fluorescent protein (GFP), a minimal promoter, and four repeats of a transcription factor’s consensus sequence (Wieder et al., 2005). Therefore, when a transcription factor is in its active state, it binds to the plasmid thereby causing the synthesis of an unstable GFP (Thompson et al., 2004b). In this system, the fluorescence levels act as a surrogate for the amount of activated transcription factor present within the system. Due to the artificial construction of these plasmids, the fluorescence level of a given reporter should be determined only through the activated level of its associated transcription factor. However, it was found that under multiple stimulation profiles, there was a significant level of cross talk. We hypothesize that such cross-talk is due to interactions between the different transcription factors i.e., the activation of transcription factor A can cause the up/down regulation in the activity of transcription factor B. Guided by the interest in hepatic inflammation, the reporter cell lines were designed to probe the dynamics of transcription factors associated with inflammation (Thompson et al., 2004a). Appropriate soluble stimuli were designed that stimulate the dynamic cellular microenvironment and would enable the systematic characterization of the cellular responses. Specifically, the NFκβ transcription factor was induced by TNF-α, AP-1 induced by IL-1, STAT3 induced by IL-6, ISRE induced by INF-γ, GRE induced by Dexamethasone, Table 1.

Table 1.

The soluble factors and the transcription factors they are associated with.

Soluble factor stimulus	Reporter gene
TNF-α	NFkB (GGGAATTTCC)
IL1	AP1 (TGAGTCA)
IL6	STAT3 (TTCCCGAA)
IFN-γ	ISRE (GAAACTGAAACT)
Dexamethasone	GRE (AGAACAAAATGTTGT)

Heat shock element (HSE) was excluded from this table because it did not have a soluble factor directly associated with it.

2.2. Deconvolution of network interactions

The construction of the LCA experiment allows us to monitor the temporal dynamics of a system of TFs as they respond to a continuous infusion of soluble signals designed to activate specific TFs. In a hypothetical scenario only one factor should be activated for a given infusion of its corresponding activation signal. However, due to the cross-talk between TFs indirect interactions emerge which manifest themselves through the coordinated activation of an ensemble of factors. To decipher the emerging dynamic of the network of interacting TFs we need to first define an appropriate model for the dynamics of the system.

In its most general form, the dynamics of any dynamical system can be described as:

$$\frac{\text{dTFA}(i,t)}{\text{d}t}=F(\text{TFA}(j,t),j=1,\dots ,N_{\text{TF}})+s(i)\forall t;i=1,\dots ,N_{\text{TF}}$$ (1)

where N_TF denotes the total number of TFs in the network and TFA(i,t) represents the activity of transcription factor i, F represents an arbitrary function which incorporates and convolutes the underlying dynamics of the interacting TFs. The component s(i) expresses the effect of the activation event of a transcription factor. In the context of the LCA design it corresponds to a constant infusion of a soluble factor activating the TF and it is considered to be the known external stimulus that activates the transcriptional machinery. Essentially, in this model, we suggest that the dynamics of TFA can be described through an appropriate, yet to be determined, function (F) which is dependent upon the TF activity itself, and a forcing function s, which may or may not be a function of time indicating a specific and direct activation of a transcription factor. In the context of LCA, the forcing function is assumed to be independent of time since it is presumed that the soluble factors continuously activate the TFs through infusion. The activity of the TFs is quantified through the monitoring of the expression of the corresponding reporter genes.

A widely used simplification (Mjolsness et al., 1991) approximates (1) as:

$$\frac{\text{dTFA}(i,t)}{\text{d}t}=\left[\sum _{j=1}^{N_{\text{TF}}}f(i,j,t)·\text{TFA}(j,t)\right]+s(i)\forall t;i,j=1,\dots ,N_{\text{TF}}$$ (2)

This transformation effectively makes use of the assumption that the effect of the network of interacting TFs is additive and therefore the driving dynamics, as defined by the function F(TFA), can be decomposed into ${\sum }_{j=1}^{N_{\text{TF}}}f(i,j,t)·\text{TFA}(j,t)$. Underlying the transformation is the understanding that the transcription factors do not form significant interacting complexes, and that transcription factors interact with each other independently (D’Haeseleer et al., 1999). While in some cases, transcription factors do form large interacting complexes; our careful selection of transcription factors used in the experiment do not involve these interactions and thus the additive assumption may be used. Furthermore, the model assumes a connection weight that maps the influence of one transcription factor to another (Boulesteix and Strimmer, 2005; Kao et al., 2004b). Thus, the, yet to be determined, functions f(i,j,t) describes the influence of TF i to the activity of TF j at time t.

Several methods have been proposed that solve for the functions f(i,j,t). A commonly invoked assumption is that the interaction strength, quantified through f(i,j,t), is not a function of time (Dasika et al., 2004; Gardner et al., 2003; Guthke et al., 2005). This treats the interactions as scalars representing effectively the network connectivity strength. For instance the network identification by multiple regression, NIR, (Gardner et al., 2003) assumes that the transcriptional dynamics are measured at steady state, and therefore eliminate the contribution of time upon f(i,j,t) whereas other methods, such as Dasika et al. (2004) and Schmitt et al. (2004), use time delays as a method of identifying when in time there exists a significant interaction, thus removing the explicit temporal modeling as well.

Given the lack of sufficient conditions in the experimental data, most algorithms must also account for the fact that using the available experimental data, the problem is ill defined i.e., there are more variables than equations in the formulation. As a result, numerous ingenuous approaches have been proposed that make use of innovative ideas to overcome such limitations. In that respect NIR constrains the number of allowed connections for to the number of conditions measured (Gardner et al., 2003), whereas (Guthke et al., 2005) use singular value decomposition (SVD) to reduce the number of genes whose profiles need to be reconstructed. Network component analysis (NCA) (Liao et al., 2003) rigorously defines the number of active interactions which can be present. By gauging the effect of unmeasured transcription factors have upon gene expression profiles, NCA establishes a set of related connectivity structures such that the solutions differ by a diagonal scaling matrix. It should be noted that NCA does account for the temporal evolution of the interaction strengths.

However, when TFA(i,t) is known at a relatively high temporal resolution one could in principle argue that a numerical estimate of the interaction dynamics, as expressed by f(i,j,t) can be obtained. In the case of a single variable—single equation, the system is fully determined at each time point. Therefore, if the dynamics of ẋ = f (x) and represented via the decomposition dx/dt = α(t) x(t), it is possible to determine α(t) in a numerical sense provided that both dx/dt and x are known. This is done simply by assuming that the dynamics expressed as can be resolved at each time point by simply evaluating α(t) as:

$$\alpha (t)=\frac{{\left(\frac{\text{d}x}{\text{d}t}\right)}_{\text{estimated}}}{x{(t)}_{\text{measured}}}$$ (3)

This process is essentially the reverse of Euler integration in which α(t) and x(t = 0) are known and we wish to reconstruct the dynamics of x(t) in a numerical sense. The aforementioned calculation assumes an accurate estimate of the rate of change of x(t) based on the measured values of x(t). Because we assume that at each time point a single parameter needs to be determined, α(t), then the system is fully determined and assuming that the operation in (3) is possible the instantaneous dynamics can be resolved. However, with N_TF transcription factors measured under a single stimulus, at each time point there are effectively $N_{\text{TF}}^2$ unknowns, f(i,j,t), ∀t, since each transcription factor may be interacting with every other transcription factor. To fully account for these unknowns, it is necessary to evaluate the set of differential equations under at least N_TF different starting points or different conditions for the problem to be fully defined. The LCA framework allows for the concurrent definition of such multiple experimental perturbations by the introduction of either independent soluble signals, or combinations of such signals in an effort to activate groups of TFs simultaneously. The key advantage of utilizing the LCA is that for each transcription factor measured, it is reasonably straightforward to add one or more conditions such that the system is fully defined. This is because each condition represents the stimulation of the system with a stimulatory soluble factor, denoted earlier by s(i). It is important to note that in both our formulation as well as the experimental system, multiple combinations of soluble factors can be utilized as separate conditions. Therefore, no simplifying assumptions need to be made regarding the complexity of the network.

We refer to the process of generating an approximation to f(i,j,t) as RED. In a similar fashion to Euler Integration, we seek a numerical solution to the problem. However instead of defining the problem as finding a numerical representation of the response, TFA(i,t), as in the case of Euler Integration, we shall be looking for a numerical representation for f(i,j,t), which is normally known analytically in Euler integration but unknown in our case, and hence the moniker RED.

Thus the purpose of RED is to evaluate numerically the interactions dynamics, f(i,j,t) at each time point. Given the available experimental data, we are effectively performing a least squares estimation at each time point through the minimization of an appropriate norm:

$$\begin{array}{l}\Vert {\frac{\text{dTFA}(i,t)}{\text{d}t}|}_{\text{estimated}}-\left(\left[\sum _{j=1}^{N_{\text{TF}}}f(i,j,t)·\text{TFA}(j,t){\mid }_{\text{measured}}\right]+s(i)\right)\Vert \\ \forall t;i,j=1,\dots ,N_{\text{TF}}\end{array}$$ (4)

Furthermore, given the time resolution, the derivative of each transcription factor’s activity level can be accurately estimated via smoothing splines (Rice and Rosenblatt, 1983). Thus, the rate of change of TFA(i,t) is numerically estimated given the measurements of TFA(i,t). The minimization of the norm essentially minimizes the error between the rate of change of TFA as measured from the data and the rate of change in TFA as predicted by the model. In this formulation, f(i,j,t), represents the contribution of one transcription factor upon the activity of another TF at any given time point.

However, from an analysis point of view a critical question which emerges is whether the network of interacting TFs possesses any special structural characteristics. In other words, we are concerned as to whether the network is composed of fully interacting elements, or whether direct links between specific TFs do not exist. These would effectively be translated to

$$\exists (i,j)ɜ:f(i,j,t)=0\forall t$$ (5)

In order to address this question, we will couple the deconvolution of the dynamics, based on the minimization of (4), with mathematical programming formulations that allow for the optimal identification of the network architecture, i.e., direct links between TFs, as well as the deconvolution of the network dynamics. In fact we present two modeling approaches, one which optimally determines interactions, and a second formulation which utilizes an a priori network architecture. This a priori network architecture may be the result of other analysis such as prediction algorithms for transcription factor binding (Haverty et al., 2004), chip–chip experiments (Lee et al., 2002), or other algorithms such as Boolean networks which link the activity of a given gene with its particular activator (Kauffman et al., 2003).

2.3. Global network reconstruction via reverse Euler deconvolution

The LCA provides the opportunity to generate multiple realizations of the TFA dynamics based on the multiple systemic perturbations through the infusion of soluble factors activating the target TFs. In order to explore the wealth of the data and to extract what would appear to be the underlying interaction dynamics representative of the systemic response across a number of conditions, we deconvolute simultaneously, at each time point, all the experimentally generated profiles. Therefore, at each time point a number of conditions, equal to the number of TFs in the system, are used for the estimation of the dynamics. In order to render the problem computationally tractable and maintain a linear nature, we opt to utilize the L-1 norm as opposed to the more widely used L-2 norm:

$$\begin{array}{l}\left|{\frac{\text{dTFA}(i,t)}{\text{d}t}|}_{\text{estimated}}-(\left[\sum _{j=1}^{N_{\text{TF}}}f(i,j,t)·\text{TFA}(j,t){\mid }_{\text{measured}}\right]+s(s))\right|\\ =\epsilon (i,t)\forall t;i=1,\dots ,N_{\text{TF}}\end{array}$$ (6)

The global network reconstruction formulation simultaneously attempts to identify the most probable network architecture, i.e., a network architecture which yields the lowest error as well as the numerical solution for f(i,j,t). Therefore, the network reconstruction optimization problem reconciling the dynamics over a number of external disturbances, k is defined as follows:

$$\begin{array}{l}min:\sum _{i=1}^{N_{\text{TF}}}\sum _{k=1}^{N_c}\sum _{t=1}^T{\epsilon }^{+}(i,k,t)+{\epsilon }^{-}(i,k,t)\\ \text{subject}\text{to}:\\ {\frac{\text{dTFA}(i,k,t)}{\text{d}t}|}_{\text{estimated}}-\left(\sum _{j=1}^{N_{\text{TF}}}[f(i,j,t)·\text{TFA}(j,k,t){\mid }_{\text{measured}}+\beta (i,j)·s(j,k)]\right)\\ ={\epsilon }^{+}(i,k,t)-{\epsilon }^{-}(i,k,t)\forall i,k,t\\ -N(i,j)·M\le f(i,j,t)\le N(i,j)·M\forall i,j,t\\ \beta (i,j)\le \{\begin{array}{ll}0\hfill & \text{if}i=j\hfill \\ M\hfill & \text{otherwise}\hfill \end{array}\\ \beta (i,j)\ge \{\begin{array}{ll}0\hfill & \text{if}i=j\hfill \\ -M\hfill & \text{otherwise}\hfill \end{array}\\ \sum _{j=1}^{N_{\text{TF}}}N(i,j)\ge 1,\forall i\\ \sum _{i=1}^{N_{\text{TF}}}N(i,j)\ge 1,\forall j\\ {\epsilon }^{+}(i,k,t),{\epsilon }^{-}(i,k,t)\in {\mathbb{R}}^{+}\forall i,k,t\\ f(i,j,t),\beta (i,k)\in \mathbb{R}\forall i,j,k,t\\ i=1,\dots ,N_{\text{TF}},k=1,\dots ,N_c,t=1,\dots ,T\\ N(i,j)=\{\begin{array}{ll}1\hfill & \text{if}\text{TF}i\text{regulates}\text{TF}j\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}\\ s(i,k)=\{\begin{array}{ll}1\hfill & \text{if}\text{soluble}\text{factor}k\text{activates}\text{TF}k\hfill \\ \hfill & \text{otherwise}\hfill \end{array}\end{array}$$ (7)

The variables β(i,j) indicate the level of activation of TF i in the presence of soluble signal j, N_c denotes the total number of simultaneous stimulation experiments. The introduction of this term was necessary because in the experimental design, there is no guarantee that each reporter plasmid will respond in the same way to an identical level of its stimulatory factor. For a single time point, there is a total of n+n^2 variables which need to be addressed. The LCA allows us to compensate for this through the use of composite inputs in which multiple stimulatory factors are used at once thus allowing for the relatively easy introduction of another condition thus eliminating this problem. However, since β remains a constant, over the experimental time course, we actually have t*n²+n variables with t*n*(n+1) equations thus making the system over-defined after the introduction of an additional condition. Formulation (6) concurrently reconciles the measurements based on k perturbation experiments. The L-1 norm is simulated through the use of appropriate positive slack variables. The prior information is hard-coded in the parameters N(i,j). The only provision at this point is that we assume that each TF has at least one regulator and that each factor regulates at least one member of the network.

2.4. Network reconstruction via bi-clustering

Prior information can be readily incorporated into the mathematical programming framework for conducting RED, whether based on Chip–chip experiments (Harbison et al., 2004) or computational transcription factor prediction (Cartharius et al., 2005). Aside from sequence-based prior information, in the form of known or putative binding interactions, gene expression experiments have also been suggested for elucidating network interactions (Hartemink, 2005) and thus postulating putative interactions. In the context of the LCA we have previously shown how a novel bi-clustering methodology can identify possible networks of interacting transcription factors based on the measured TFA (Yang et al., 2007). The use of a bi-clustering technique to determine the network architecture was predicated upon the hypothesis that local interactions could be isolated as groups of reporter genes with highly correlated activity under multiple stimulation profile, and from these local interactions, it would be possible to construct a network that can be used to rationalize the response obtained from the LCA. The bi-clustering itself is performed via a mixed integer linear programming (MILP) method. The key innovation with this method over those of previous bi-clustering methods (Cheng and Church, 2000; Kluger et al., 2003; Yoon et al., 2005), lies in its ability to find bi-clusters with arbitrary overlaps which allows it to represent networks which are more complete than those which find independent bi-clusters. A bi-partite graph can then be generalized into a directed graph with corresponding feedback loops so long as there is a method to transform the nodes that lie in the output layer (sink) into a node in the input layer (source). In the LCA, the input layer consists of the individual soluble factors used for stimuli such as those given in Table 1. Since these soluble factors have a one to one correspondence with the transcription factors, the nodes in the input layer in Fig. 1, can be replaced with their corresponding transcription factors. To convert the bi-partite network into a form usable by RED, we assume that the direct stimulation of a reporter can only occur via its associated soluble factor, Table 1. All of the other interactions must therefore be secondary. Therefore, if a bi-cluster contains a stimulatory factor of TNF-α and was found to stimulate both NFkB and STAT3, we would hypothesize that there is a direct link between TNF-α and NFkB, while the stimulation of STAT3 must occur downstream of NFkB. Because STAT3 must occur downstream of NFkB, we hypothesize that there is some process linking NFkB to STAT3 of which there is a mechanism and dynamic which we seek to obtain evidence for. The details of the methodology are discussed in (Yang et al., 2007).

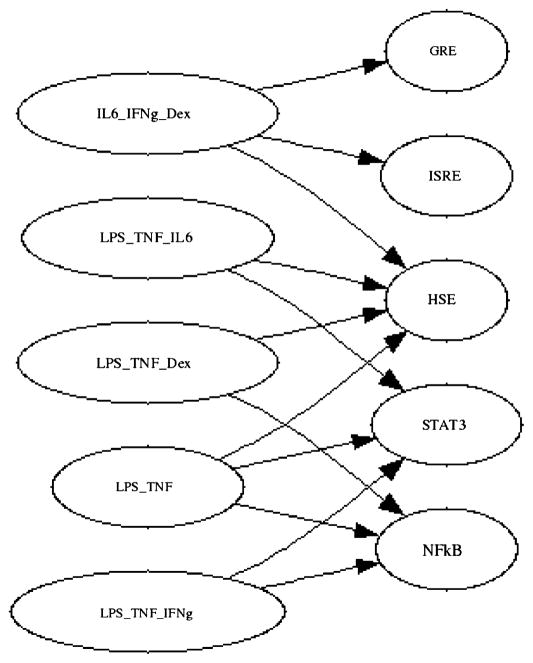
Fig. 1.

The resultant bi-partite network obtained from bi-clustering the LCA data. The nodes on the left are the input layer and the ones on the right are the output layer which consists of the reporter genes. Despite being in the experimental data, neither IL1 or its associated transcription factor AP1 were found to be in a bi-cluster.

Processing the bi-clustering result in this fashion yields the network given in Fig. 2. Most of the nodes and their stimulatory factors are associated with each other with the exception of lipopolysaccharide (LPS) and heat shock element (HSE). LPS represents a non-specific inducer of inflammation and therefore does not have a direct reporter associated with itself, and HSE did not have a specific inducer associated with it. Given that the focus is on the interactions between the transcription factors, HSE was included in the network while LPS was not. One of the notable features about this network is that AP1 appears to be disconnected from the rest of the network. This is due to the fact that while it is measured and directly stimulated in the experiment, it was not found in any of the bi-clusters given in Fig. 1. To convert the network from Figs. 1 to 2, we make the primary assumption that the reporter genes in the LCA can only be stimulated via their individual transcription factor. Therefore, if TNF-α stimulates any other reporters aside from NFkB, it must first stimulate NFkB, and this stimulation of NFkB results in signaling cascade, which will eventually lead to the stimulation of that transcription factor. Such an activation may occur because the transcription factor which is directly activated by the soluble signal binds to the upstream region of another soluble signal, such as NFkB binding to the upstream region of IL-6 (Gealy et al., 2007), or via a more indirect route utilizing intermediate signaling molecules. Therefore, if a link is present between a soluble factor and a transcription factor reporter which it was not designed to directly activate such as TNF-α and any reporter which is not NFkB, then a link is drawn between NFkB and that reporter. The direct links are introduce in the deconvolution optimization framework by activating appropriate entries of the N matrix in (6) based on the structure of directed graph from the bi-clustering results, though the incorporation of the constraint (7):

$$\begin{array}{l}-N(i,j)·M\le f(i,j,t)\le N(i,j)·M\forall i,j,t\\ N(i,j)=\{\begin{array}{ll}1\hfill & \text{if}\text{TF}i\text{regulates}\text{TF}j\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}\end{array}$$ (7a)

Fig. 2.

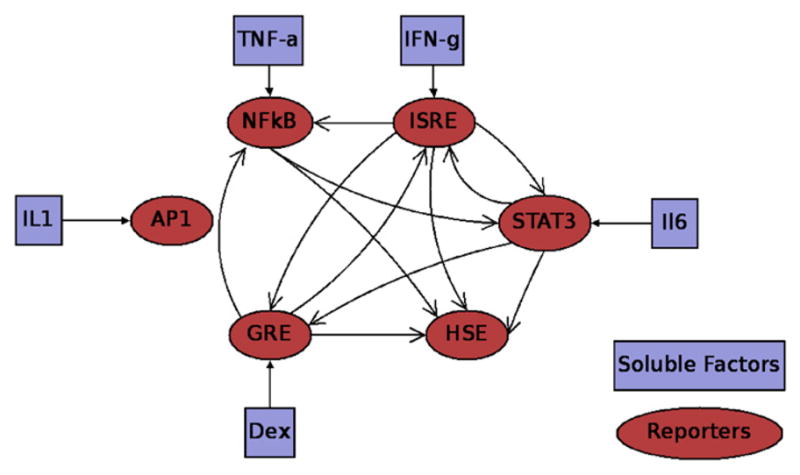
The directed graph associated with the bi-clustering result. AP-1 is unconnected because it was not found to be part of any bi-cluster.

If certain connections are known not to be present, the corresponding interaction dynamics elements f(i,j,t) can be readily eliminated from the deconvolution.

2.5. Generalized reconstruction

A tantalizing question related to the in silico reconstruction of interaction networks is whether a core of dominant, or otherwise significant interactions can be identified. Various computational methodologies have been proposed that attempt to qualify network interactions in an effort to further prune connectivity and, hopefully, reveal and underlying critical core of significant interactions (Gao et al., 2004; Van Someren et al., 2001). In the context of the optimization framework, we model this selection through the introduction of appropriate binary variables λ(i,j) which denote the existence of a direct interaction between two factors, i and j. In order to evaluate the overall complexity of the deconvolution, the problem is solved parametrically with respect to the total number of possible connections (N_TF×N_TF). The introduction of the parameter 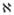controls the complexity of the deconvolution. The detailed formulation of the mixed-integer optimization problem is provided in (8).

$$\begin{array}{l}min:\sum _{i=1}^{N_{\text{TF}}}\sum _{k=1}^{N_c}\sum _{t=1}^T{\epsilon }^{+}(i,k,t)+{\epsilon }^{-}(i,k,t)\\ \mathit{subjectto}:\\ {\frac{\text{dTFA}(i,k,t)}{\text{d}t}|}_{\text{estimated}}-\left(\sum _{j=1}^{N_{\text{TF}}}[f(i,j,t)·\text{TFA}(j,k,t){\mid }_{\text{measured}}+\beta (i,j)·s(j,k)]\right)\\ ={\epsilon }^{+}(i,k,t)-{\epsilon }^{-}(i,k,t)\forall i,k,t\\ \beta (i,j)\le \{\begin{array}{ll}0\hfill & \text{if}i=j\hfill \\ M\hfill & \text{otherwise}\hfill \end{array}\\ \beta (i,j)\ge \{\begin{array}{ll}0\hfill & \text{if}i=j\hfill \\ -M\hfill & \text{otherwise}\hfill \end{array}\\ -\lambda (i,j)·M\le f(i,j,t)\le \lambda (i,j)·M\forall i,j,t\\ \sum _{j=1}^{N_{\text{TF}}}\lambda (i,j)\ge 1,\forall i\\ \sum _{i=1}^{N_{\text{TF}}}\lambda (i,j)\ge 1,\forall j\\ \sum _{i=1}^{N_{\text{TF}}}\sum _{j=1}^{N_{\text{TF}}}\lambda (i,j)=\mathbb{N}\le N_{\text{TF}}\times N_{\text{TF}}\\ {\epsilon }^{+}(i,k,t),{\epsilon }^{-}(i,k,t)\in {\mathbb{R}}^{+}\forall i,k,t\\ f(i,j,t),\beta (i,k)\in \mathbb{R}\forall i,j,k,t\\ i=1,\dots ,N_{\text{TF}},k=1,\dots ,N_c,t=1,\dots ,T\\ \lambda (i,j)\in \{0,1\},\lambda (i,j)=\{\begin{array}{ll}1\hfill & \text{if}\text{TF}i\text{regulates}\text{TF}j\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}\\ s(i,k)=\{\begin{array}{ll}1\hfill & \text{if}\text{soluble}\text{factor}k\text{activates}\text{TF}k\hfill \\ \hfill & \text{otherwise}\hfill \end{array}\end{array}$$ (8)

The binary variable λ(i,j) serves a dual role: they can be treated as the “N” variables of (7) which model the known absence of specific interactions, or force the existence of certain interactions, but can also serve as the variable to be used for the optimal selection of required interaction elements in the overall regulatory network. We have already demonstrated the possibility of developing such mixed-integer optimization methodologies in the context of modeling transcription regulatory networks (Foteinou et al., 2008).

2.6. Evaluation of dynamics

The overall hypothesis behind utilizing the RED is that the numerical response f(i,j,t) may provide insight as to the under-lying processes which drive the observed changes in the activity of transcription factors. The functions f(i,j,t) essentially represent how the various mechanisms transform the amount of active transcription factors into a signal which is then used to activate a secondary transcription factor. Treating the transcriptional network as a circuit analog, we can exploit the fact that many of the simple network architectures which we have obtained have well characterized step responses. Because the LCA utilizes a step input as the stimulatory profile for its soluble factors, we ought to be able to draw direct comparisons between the responses we see and the characteristic inputs. Previous work in electrical engineering has gone so far as to design automatic classifiers which categorize the step response based upon their circuit architecture (Leva and Piroddi, 1996; Piroddi and Leva, 2007), we have elected to determine significant network architectures through visual inspection due to the significantly different responses of the network architectures.

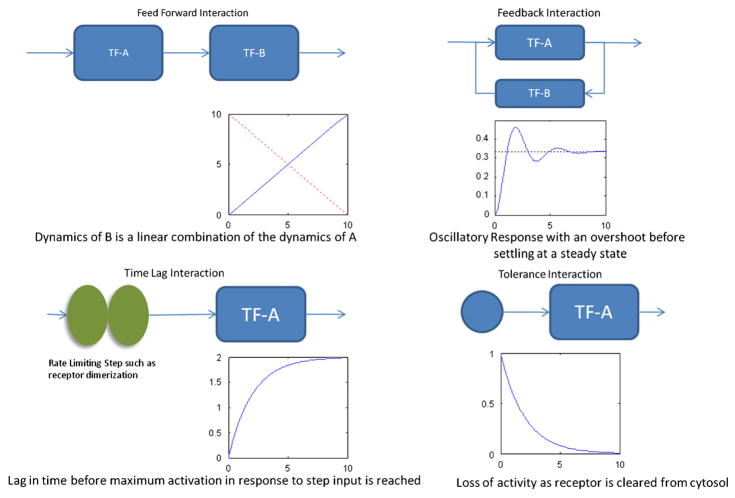
We have elected to look for evidence of four types of dynamic interactions. The two which correspond to different network architectures (Rao and Arkin, 2001) are feed forward (Mangan and Alon, 2003) and feedback (Milo et al., 2002), whereas time lag, and tolerance mechanisms correspond to dynamic responses of the individual transcription factors. Identifying interaction motifs that eventually constitute the overall structure of a regulatory network is a very active research area and numerous methodologies have been developed to assess the emergence of local structures (Zhu et al., 2007). While there are other methods for evaluating the statistical significance of each of the fits (Dudbridge and Koeleman, 2004) we will be evaluating the possibility of developing specific network sub-structures by evaluating the dynamics of the interactions, f(i,j,t). The feed forward response represents the simplest response. In the feed forward interaction between transcription factors A→B, strength of the up/down-regulation of B is dependent upon the activation of A and hence the activity of A’s reporter, within a multiplicative factor. Time lagged dynamics can represent either intermediate transcription factors such as A→X→B in which X is an unknown factor, or events that that have a relatively slower rate limiting step such as the interaction between multiple sub-units. Feedback interactions emerge when the activation of transcription factor B, goes back and affects the activation of transcription factor A in addition to the standard feed forward response. The tolerance mechanism is a response which involves the loss of activation despite continued activation. In the LCA, there is a continuous infusion of the soluble signal, and therefore, this response should be quite evident. One of the possible mechanisms for this response is the loss of various receptors in the cytosol under continuous stimulation. Fig. 3 shows these basic interactions and the expected responses of the system. In addition to these simple models, the motifs can be combined for composite responses such as profiles that have both a time delay and tolerance effect.

Fig. 3.

Expected network motifs and their expected responses. These interactions have a set response to a step input which is part of the experimental design. In these hypothetical interactions the x-axis represents time and the y-axis represents the interaction strengths.

3. Results

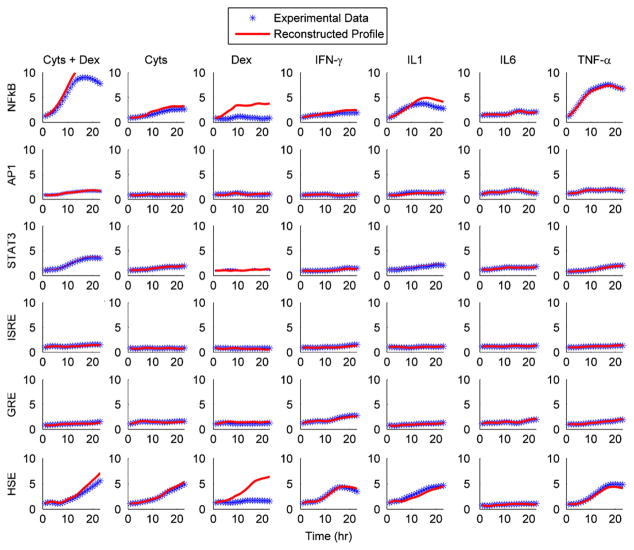
Despite fitting the derivatives rather than the florescence values obtained from the LCA, we were still able to get accurate fits for the data, Fig. 4. In Fig. 4, we attempted to simulate the original experimental data via conducting a forward Euler integration via

Fig. 4.

The reconstruction of the profiles obtained from the living cell array.

$$\text{TFA}(i,k,t+1)=\text{TFA}(i,k,t)+h\ast \left(\sum _{j=1}^{N_{\text{TF}}}[f(i,j,t)·\text{TFA}(j,k,t){\mid }_{\text{measured}}+\beta (i,j)·s(j,k)]\right)$$

to show that from our numerical representation f(i,j,t) it is possible to accurately reconstruct the signal. However, one issue with this reconstruction is the fact that there is significant error propagation. Due to the recurrence from of standard Euler integration, the errors from previous time points are incorporated into the prediction for later time points (Dunn et al., 2006). Thus certain reconstructions such as the one where NFkB is stimulated via Dexamethasone show a reconstruction with deviated significantly. Even so, for the most part, most of the reconstructions appear to be accurate reflection of the underlying data.

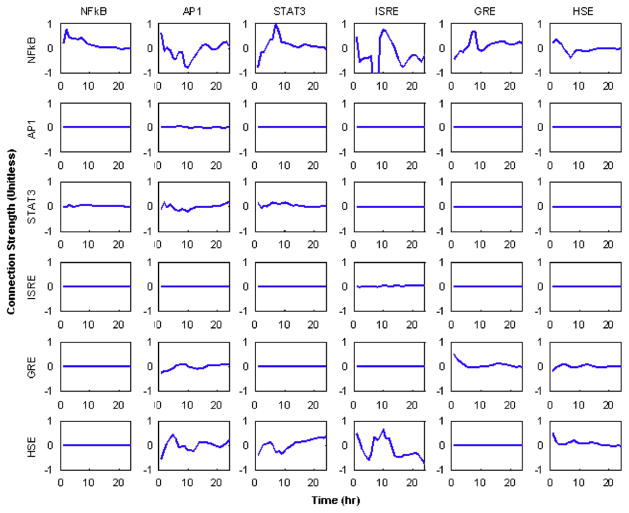
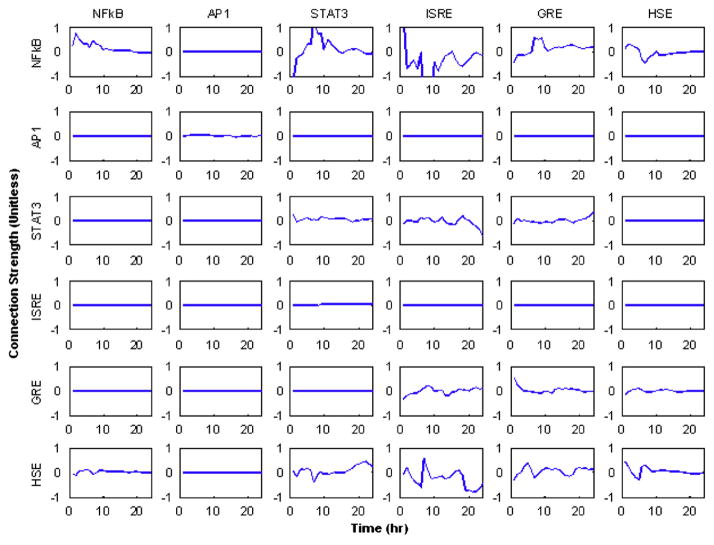
3.1. Fully connected network

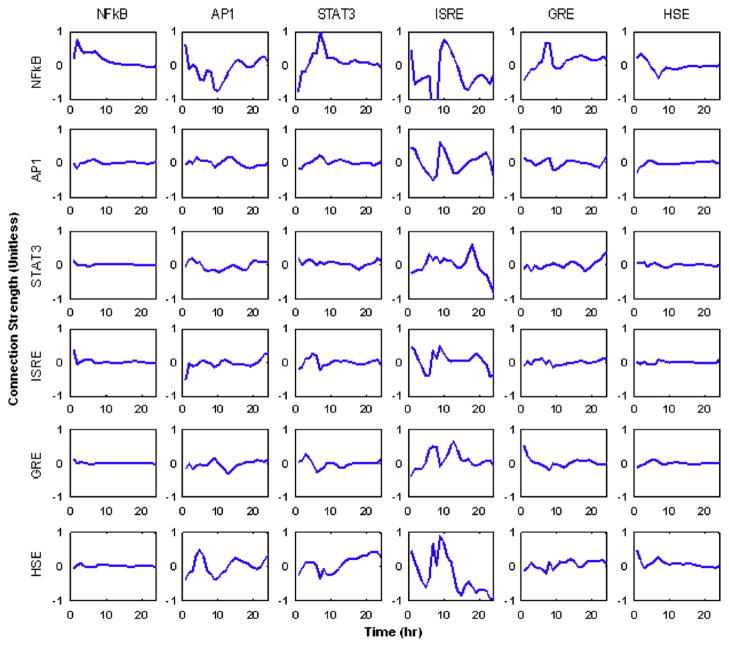
In Fig. 5 the profiles of the time varying weights f(i,j,t) are given. In this figure, there is evidence as to how each of the transcription factors interacts with others as well as themselves. Each row corresponds to the individual transcription factors whose activity we seek to reconstruct, and each column corresponds to the effect a specific transcription factor has upon the other factors within the system. The matrix in Fig. 5 represents an incidence matrix in which the outgoing connections for a given transcription factor are represented as columns, and the incoming connections are indicated as rows. Therefore, the first row corresponds to the factors which affect the activity of NFkB, whereas the first column represents the effect NFkB has upon other transcription factors. In these figures, a negative value for f(i,j,t) represents down-regulation effect whereas positive value represent an up-regulation event i.e., an increase in the activity of one transcription factor decreases the activity of another and vise versa. From the profiles, we believe that evidence points to the fact that many of the dynamic processes are regulated by feedback control loops and therefore the simple notion that genes are only up or down-regulated may be too simplistic. For instance the stimulation of NFkB via GRE appears to be initially down-regulated, but also have a time period in which it is up-regulated after which it remains constant.

Fig. 5.

The dynamics of the interaction strengths calculated with a fully connected network. It is possible to see effects similar to those predicted via the motif patterns in Fig. 3.

From the results, it may seem obvious which of the connections can be removed, i.e., those which show very low levels of activity. However, this may not always be the case. For instance, the STAT3→STAT3 interaction which corresponds to the stimulation of STAT3 by IL6 seems to be at a rather low level and can be removed. However, this connection needs to be included due to the design of the system in which STAT3 is stimulated via its soluble factor. Therefore, it is not immediately obvious as to which connection should be removed. Such ambiguities therefore lead up to the next formulation in which the network is solved.

3.2. Freely optimized network

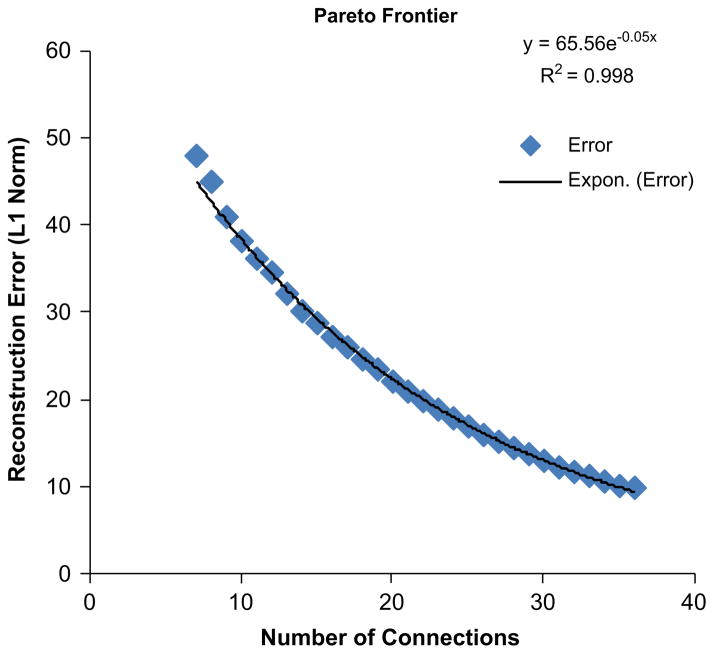
The freely optimized network solves the problem parametrically from six to 36 connections. The lower bound for the number of connections corresponds to the fact that each transcription factor needs to have some form of regulation, either via its soluble factor, or due to the effects of another transcription factor. The upper bound for the number of connections is the number of connections for a fully connected network. One of the problems with solving for the network in this manner is that it is difficult to tell a priori how many connections are needed. This then requires one to solve exhaustively for all possible number of connections. The trade-off between complexity and the quality of fit is expressed as the pareto frontier. The pareto frontier indicated that one cannot obtain a better solution unless one increases the complexity of the problem being solved is given in Fig. 6.

Fig. 6.

The Pareto frontier.

The pareto frontier for this system does not exhibit a typical “knee” feature which allows us to determine whether a sufficient number of connections have been obtained. The progression of the pareto frontier shows an exponentially decaying response. This fit an exponential curve with an R² of 0.997 indicating the high quality of fit. This signifies that the formulation for freely optimizing the network obtains relatively more important connections early rather than later. We hypothesize that the reason for this response is due to the small scale of the experimental data. Due to the fact that these transcription factors all related to inflammation, it is not surprisingly that all of the transcription factors may be part of a larger interconnected network. The small scale of the data means that many intermediate transcription factors are not present and therefore none of the links are truly redundant.

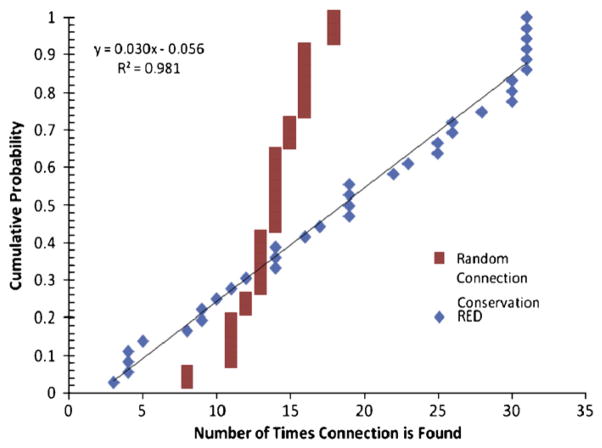
Though RED is unable to determine outright the number of connections present in the system, we hypothesized that it may still be able to give the relative importance of a given connection between two transcription factors. By solving the formulation from six to 36 connections, we expect the more important interactions to appear early and then to be conserved in solutions containing more connections. Therefore, if a set of interactions were present in a solution of size N, we would expect the great majority of the interactions would be present in solutions with more than N connection. Therefore, the most important interaction would be found first, and conserved throughout all the other solutions, the second most important interaction found second, etc. Plotting the number of times an interaction is present amongst the different solutions we obtain Fig. 7 which exhibits this behavior. There is a smooth linear progression of importance, whereas had the interactions been included at random, a connection would have been conserved an intermediate number of times (15) with a small amount of variability.

Fig. 7.

The number of times a link is conserved over the different solutions. Under RED there is a clear trend in the importance of links where as randomly assigned connects appear at a relatively consistent rate.

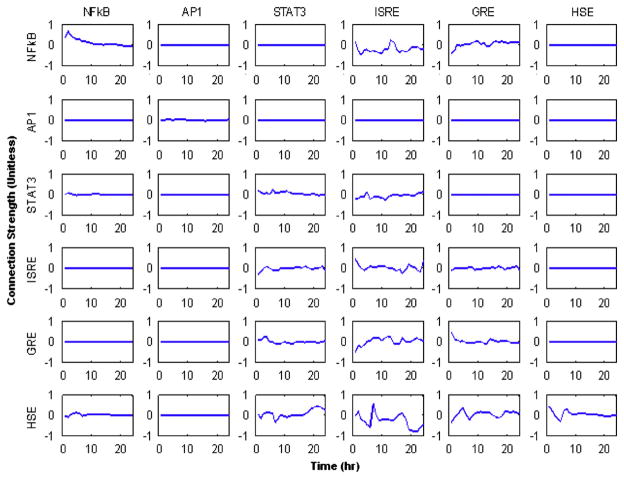
Given the structure of the pareto frontier, it is relatively difficult to determine the optimal number of connections. In Fig. 8, the dynamics are shown for 18 connections which represent half of all possible connections utilized. What is remarkable about the reconstructed dynamics is that for the links that are common between the networks most of the profiles seem similar in quality as in the fully connected network. This suggests that the reconstruction is reasonably robust not only in the way the individual links are incorporated, but also in the way the dynamics are obtained.

Fig. 8.

The freely optimized network corresponding to 18 connections. It is notable that many of the dynamics are very similar to that of a fully connected network. The model formulation does not force the connections to be bi-directional or symmetric.

3.3. Bi-clustered network

One of the strengths of utilizing this formulation is that outside information can be incorporated, thus allowing for the ability to examine other network architectures. The primary reason as stated previously was that the use of a priori information could greatly reduce the computational complexity of the problem by reducing either the number of free binary variables or eliminating them outright. While the bi-clustering formulation is also an MILP formulation, the bi-clustering formulation scales better in terms of the number of binary variables needed for a given problem size having 2N binary variables as opposed to N² binary variables as in the case of the fully optimized network. Therefore, one of the questions is what the trade-off between runtime and reconstruction error is. Since the bi-clustered network itself consists of 18 connections, this result was compared with the fully optimized network with 18 connections.

Normally the simplest method for assessing the “correctness” of a network is to assess the error associated with the reconstruction. In the presented formulation this is indicated by the L1 norm, which is the sum of the positive and negative slacks. The overall range of possible errors ranges from above fifty to a minimum of 9.9. Since in the fully optimized network, we attempt to select network architectures with the lowest error, we have to determine whether the bi-clustered network represents a good trade-off between the ability to reconstruct the dynamics and its decrease in run time. To evaluate this, we wanted to see whether on average randomly generated networks have a higher error associated with them than a bi-clustered network. Generating 1000 random networks, we found that the mean error for the networks was 36.8632 with a standard deviation of 4.2, whereas the bi-clustered network corresponded to an error of 30.31. Therefore, while the bi-clustered network does not reconstruct the profiles as accurately as either the freely optimized network or the fully connected network, we hypothesize that it does capture many salient features of these networks due to a reconstruction error which is significantly lower than that of a randomly generated network. Therefore, while the bi-clustered network does not yield an optimal reconstruction, it may function as an adequate approximation of the structures present within a given biological network. One of the advantages of utilizing bi-clustering to first determine the underlying structure is rather than the freely optimizing the network structure is the fact that bi-clustering coupled with the formulation in Eq. (3) yields an operation that requires less binary variables which at a first approximation yields far lower runtimes. Therefore, the use of bi-clustering may be considered as a trade-off between accuracy and run time. Because there are differences between the network architecture generated via RED and bi-clustering, we wish to determine whether these differences lead to changes in the dynamics of f(i,j,t), Fig. 9, and whether the changes in dynamics can be explained due to mechanistic differences between the two solutions. For instance the NFkB/GRE interaction appears to have moved from a feedback dynamic to a standard feed forward interaction. The most glaring differences between the networks generated via RED and the ones generated via bi-clustering is fact that AP-1 no longer affects or is affected by the rest the network, and HSE does not have any outgoing connections. Given the qualitative differences between the networks, the question which arises is whether the change in dynamics is due to the loss of AP-1’s effect upon the system or HSE’s effect upon the system.

Fig. 9.

The reconstructed dynamics of the network obtained via bi-clustering. What is notable is the change of the response of NFkB to Dexamethasone stimulation (GRE) which turned from more of a direct interaction from a feedback interaction.

3.4. Constrained optimized network

One of the things which we observed with the bi-clustered network was the fact that AP-1 was not incorporated into the network, and there were no outgoing links for HSE. Therefore, we manually remove the connections associated with AP-1 and then allow the optimizations framework to evaluate the presence of the rest of the network. This allows us to assess the role of HSE independently of AP-1. Doing so, we can see that the feed back dynamics associated with NFkB in response to GRE stimulation has returned as well as the response to ISRE. From this result it appears that the response of NFkB to both IFN-γ and Dexamethasone are in part affected by HSE, Fig. 10. Moreover, without AP-1 affecting the dynamics of HSE, we see a large change in the dynamics of other transcription factors, thereby suggesting that AP-1 plays an important role in HSE activation.

Fig. 10.

The response of the system when outgoing nodes from HSE were enabled, but the outgoing connections from AP1 were not.

4. Discussion

4.1. Evaluation of multiple network architectures

The most obvious question one has with multiple network architectures is which of the proposed network architectures is correct, in which the simplest answer is which network yielded the lowest reconstruction error. However, at this point it would be incorrect to suggest that the small proof of principle implementation of the LCA would yield the correct underlying network. Therefore while it is reasonably simple to rank the different gene network architectures by their reconstruction error, it may be more informative to decipher how different networks relate to each other in terms of their response.

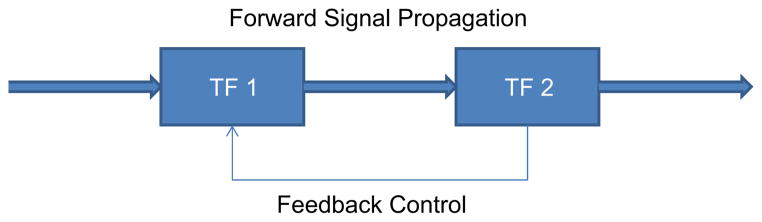
We hypothesize that for a given network architecture, the removal of a link may have a minimal impact upon the dynamics of the rest of the system and thus be a sign of its redundancy. Secondly, the removal of an important link could significantly alter the reconstructed dynamics of the system thus signaling that the removal of a link is incompatible with the measured response, i.e., that while the data can still be fitted to the model, the intrinsic response of the architecture is different from what was measured experimentally. The most obvious changes would be if the removal of the link causes the response of the rest of the interactions of a given transcription factor to significantly change. However, there exists a third case which we hypothesize is more interesting, which is the loss of a link which changes the dynamic response of f(i,j,t) in a mechanistically relevant manner. This would be akin to a mutation in which the changes in an organism’s response are only evident during times of stress (Frenkel et al., 1999). Candidates for such a response would be found in feedback loops, Fig. 11, where one of the links is responsible for signal propagation and the other link is responsible for regulating the response within a certain range. Under reasonable stimulation, it is possible that the feedback portion may be redundant, and the dynamics associated with the forward–forward portion may transform from a dynamic that is characteristic of a feedback mechanism to that of a feed forward mechanism.

Fig. 11.

The two portions of a feedback element, one of which plays a role in the forward signal propagation, whereas the second connection is responsible for regulating the overall range of the response. During times of normal stimulation, the feedback link may not play a large role in the overall response.

4.2. Predicted result of NFkB activation

The transcription factor interaction with the clearest activity profile is the activation of NFkB in response to TNF-α stimulation. This profile was present in all four solutions, Figs. 5, 8–10. It is possible to see a clear lag in the activity of the transcription factor to the step response, in which it takes a non-trivial amount of time to reach a maximum, after which there is a return to baseline. This is indicative of a time lagged response coupled with a tolerance mechanism. This dynamic provides evidence of a rate limiting event in NFkB thus accounting for time lag before a maximum value is reached. This rate limiting step could be due to the time it takes for the subunits to be released from IkB (Campbell and Perkins, 2004) or via a rate limiting dimerization step. The return to baseline despite continuous infusion of the TNF-α signal illustrates that the NFkB shows a tolerance like response under prolonged administration of inflammatory cytokines (Sass et al., 2002). One result which is unexpected is the fact that NFkB activation seems to have a low level of effect upon the other inflammatory cytokines, but seems to be significantly affected by the activity of the other inflammatory cytokines. This suggest that while TNF-α is an important mediator of inflammation, its reporter NFkB lies downstream in comparison to the other inflammatory transcription factors which were measured in this experiment. This result was consistent over the different solutions which leads us to the belief that this response is both highly robust, as well as the fact that the experiment yielded data of high quality for this particular transcription factor.

4.3. Predicted result of AP1 activation

The perturbation of the system through an administration of IL1 did not seem to have a large impact upon the AP-1 reporter in any of the solutions. This suggests that the reporter gene for AP-1 activation may need to be optimized. The level of up/down regulation of the AP-1 reporter in response to IL1 activation is low in contrast to the dynamics seen via the HSE, and NFkB reporters. This was evident in the fully connected and freely optimized networks, Figs. 5 and 8, and as such the effect of the soluble factor IL1 is evident within the system, though not through its individual reporter. In the solutions of the fully connected and freely optimized networks given in Fig. 5 and 8 there appears to be a feedback mechanism associated with AP1 and HSE, with an oscillatory behavior in the weights. We see that in the freely optimized network, there is still a great deal of commonality in the response of f(i,j,t) between the two cases despite the removal of the effects of GRE and NFkB upon the system. With the removal of AP1 however, we see that there exists a major change in the dynamics of the rest of the system, Figs. 9 and 10. Computationally, this means that the loss of AP1 as a connection, requires significant alterations to the dynamics of other transcription factors in order to fit the data. We hypothesize that this effect is due to HSE repressing the synthesis of IL1 which is the activator of AP-1 (Xie et al., 2002), and that IL1 affects the phosphorylation of various heat shock proteins (Saklatvala et al., 1991). The combination of these two factors suggests the existence of a cycle and therefore the need for a feedback interaction between the two elements.

It may be tempting to suggest that the effect of AP1 upon the rest of the system can predicted merely the magnitude of its interaction. However, this is not necessarily the case as seen in the interactions of the other transcription factors with NFkB. What we see is that even with the removal of AP1, Fig. 10, from the solution, the interaction dynamics of the other transcription factors with NFkB are still reasonably consistent and that it requires the removal of both HSE and AP1 before there exists a significant change.

4.4. Predicted result of STAT3 activation

Similar to the results obtained with the IL1 stimulation, the IL6 stimulation did not appear to have a large effect upon the induction of its reporter. This dynamic was again present in all of the solutions that were obtained. This evidence suggests that the sequence of the reporter could perhaps be better designed. Specifically, while these reporters are able to show qualitative changes, they may be optimized to show greater fold change when activated. In spite of the low fold change in STAT3 reporter activation, there was a significant alteration in the activity of the NFkB reporter by IL6. This was present in three of the four solutions, Figs. 5, 8 and 10, being present in the solutions where the network was determined via the MILP formulation and absent when utilizing the bi-clustered network. This activation appears to have a feedback-type dynamic for NFkB. In the literature, it has been reported that IL6 is induced by TNF-α, an activator of NFkB (Yamada et al., 1997) as well evidence that IL6 down-regulates the activity of NFkB (Hatzigeorgiou et al., 1993). This combination of effects points to the existence of the feedback mechanism as suggested via the reconstructed dynamics. The other reporters in response to IL6 stimulation have inconsistent results and connectivity. Given that the connection strengths of STAT3 to the other transcription factors is low, this suggests that perhaps the connections may not actually exist, or that IL6 represents a relatively non-specific inducer of inflammation and that while it affects many system, its individual contribution to the dynamics of the measured reporters is reasonably low.

4.5. Predicted result of ISRE activation

While many of the transcription factor interactions seem to have dynamics which are similar to those predicted via the network motifs in Fig. 3, the responses for IFN-γ stimulation do not. This may be due to the highly connected nature of IFN-γ due to its central role in the JAK-STAT pathway (Levy, 1995). Aside from the interconnectedness of the IFN-γ, the networks generated via the full optimization, and the bi-clustering both appear to reflect the fact that ISRE is consistently more connected than any of the other elements. Due to small scale of the system, the effect of IFN-γ on the other factors may be in reality mediated through several intermediates. Without these intermediates, the effect of IFN-γ upon the system represents the combination of the effects of these different intermediates, thereby obscuring the direct effect that IFN-γ has upon the system. However, the pseudo-oscillatory behavior may be indicative of a significant amount of feedback that underlies an organism’s response to IFN-γ, and may be due to factors which have not been previously identified.

4.6. Predicted result of GRE activation

One of the interesting aspects of corticosteroid stimulation is the fact that under direct stimulation of corticosteroids, the signals obtained for processing were very noisy, Fig. 12, as evidenced by the lack of repeatability in the measurements. The reason for this lack of signal fidelity is due to the fact that the majority of the inflammatory cytokines are down-regulated by corticosteroids. Working off a baseline fluorescence of the reporters being zero, the down-regulation of this signal means that the measurements are dominated by noise. To compensate for this, the experimental system also included composite stimulus represented by an infusion of all the inflammatory cytokines with the addition of Dexamethasone. This allows for a baseline fluorescence to be obtained and the effect of Dexamethasone to be de-convolved from the system. The ability for these interactions to be de-convolved is an important one because it shows that composite stimuli can be used successfully in the optimization framework and presents less of a problem in the network generation than the bi-clustering formulation. The response of the system to Dexamethasone provides similar insights into the mechanism of corticosteroid activity. Unlike the response of NFkB to a step input of TNF-α, the response of the Dexamethasone upon its reporter GRE is a decreasing function indicative of a tolerance mechanism, Figs. 5, 8–10. Therefore, the maximum effect of corticosteroids occurs early and there is no delay before a maximum is reached. This suggests that unlike NFkB, there is no rate limiting step between the binding of the corticosteroid to the glucocorticosteroid receptor (GR) and the activation of the transcription factor. This suggests that the dimerization event is not rate-limited, i.e., there is a sufficiently high concentration of endogenous GR present in the system which the rate of dimerization occurs fast enough where it is not detectable given the time resolution of our system.

Fig. 12.

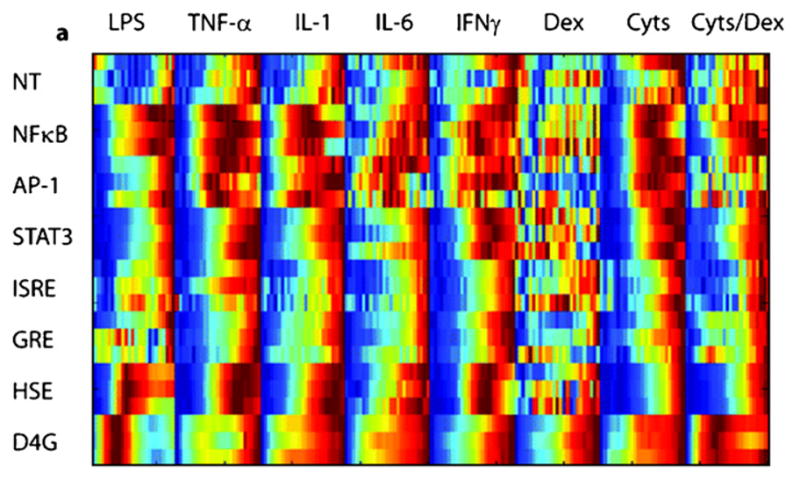
The raw data from the living cell array. Note that the data for the singular stimulation by Dexamethasone is relatively noisy (King et al., 2007).

Another interesting aspect of Dexamethasone stimulation is the response of the NFkB reporter in response to activated GRE. The currently accepted notion is that the activation of GRE down-regulated NFkB, thus damping the inflammatory response. However, one of the interesting aspects of this response is evident when the response over different solutions is compared. In the bi-clustering solution where the contributions from STAT3 and HSE were not included in the dynamics of NFkB, we see a clear shift from a feedback mechanism to that of a standard feed-forward response in which the strength of GRE’s effect upon NFkB is directly related to the amount that GRE is stimulated. This suggests that unlike AP1, STAT3 and HSE play an important role in mediating the feedback mechanism that regulates the response of NFkB to corticosteroids.

4.7. Outstanding issues

The issue of unmeasured and missing transcription factors poses a significant problem when it comes to interpreting the results of the data. It is difficult to determine whether or not the dynamics represent the direct interactions between two transcription factors, or whether the dynamics reported by the algorithm are a composite of multiple interactions. For the purposes of this manuscript, the interactions which were analyzed further were selected based upon how well they reflected the responses of standard transcriptional network motifs. Utilizing this method, it was possible to identify the mechanics and dynamics for a subset of the interactions and predict the existence of more complex responses for the rest. The ideal solution for this problem is through a more comprehensive LCA in which many more transcription factors would be measured rather than just such a small subset as was used here. Another issue which needs to be resolved is the issue of scale. The formulation will fit profiles that show the greatest magnitude change over those with a smaller magnitude in change. This is problematic because it depends upon the fluorescence reported via the LCA apparatus. Therefore, dynamics which show a greater fold change had the appearance of their connections prioritized when solving the problem parametrically. This means that the appearance of a connection dependent both on the biological importance as well as the signal to noise ratio of the reporter sequence. Therefore, while we were reasonably sure as to the quality of the dynamics for NFkB and GRE, we were less sure about the dynamics associated with the other reporters. A possible solution to this issue may be to obtain proper calibration curves for each of the reporter plasmids such that the overall range of fluorescence can be calibrated from minimum to maximum values and then normalized accordingly.

5. Conclusions

The LCA, given its ability to easily obtain combinations of transcription factor activation under different stimulation profiles with very high temporal resolution offers a new and powerful method to probe the underlying transcriptional network. Along with simple network building and determining which transcription factors actively regulate each other, the LCA combined with RED allows for the assessment of possible network connectivity structures as well as giving intuitions as to the dynamics of the interactions. While solving the MILP formulation is computationally expensive, the optimization framework allows for the incorporation of a previously generated network which may not be optimal sufficiently similar to the true underlying structure. This sub-optimal network has profiles which are oftentimes very similar to those of the optimal network. However, in the cases where the profiles are different, there is often a significant rationale behind the differences such as loss of feedback loops with the removal of a given node. Therefore the loss of nodes or interactions degrades the response of the system gracefully rather than catastrophically inwhich no useful information can be extracted.

With these interactions, it is then possible to predict important underlying mechanistic properties such as feed forward networks, tolerance mechanisms, feed-back networks, and time delay properties. Even in the small proof of principles example provided here, these network motifs are illustrated in the dataset. For instance, we were able to clearly see the tolerance mechanism associated with corticosteroid stimulation, as well as the initial down-regulatory effect of corticosteroids. Other effects visible were time-lagged effects of NFkB due the necessity of sub-unit dimerization. Given that the evidence of these effects are present in our small scale system, we are confident that the same framework can be expanded to much larger systems in which much less is known about the system. Such interactions are almost as important as determining which transcription factors interact because they provide the foundation of the dynamical system which controls the response of an organism to outside stimulus.