Automatic segmentation of the facial nerve and chorda tympani in pediatric CT scans

Abstract

Purpose: Cochlear implant surgery is used to implant an electrode array in the cochlea to treat hearing loss. The authors recently introduced a minimally invasive image-guided technique termed percutaneous cochlear implantation. This approach achieves access to the cochlea by drilling a single linear channel from the outer skull into the cochlea via the facial recess, a region bounded by the facial nerve and chorda tympani. To exploit existing methods for computing automatically safe drilling trajectories, the facial nerve and chorda tympani need to be segmented. The goal of this work is to automatically segment the facial nerve and chorda tympani in pediatric CT scans.

Methods: The authors have proposed an automatic technique to achieve the segmentation task in adult patients that relies on statistical models of the structures. These models contain intensity and shape information along the central axes of both structures. In this work, the authors attempted to use the same method to segment the structures in pediatric scans. However, the authors learned that substantial differences exist between the anatomy of children and that of adults, which led to poor segmentation results when an adult model is used to segment a pediatric volume. Therefore, the authors built a new model for pediatric cases and used it to segment pediatric scans. Once this new model was built, the authors employed the same segmentation method used for adults with algorithm parameters that were optimized for pediatric anatomy.

Results: A validation experiment was conducted on 10 CT scans in which manually segmented structures were compared to automatically segmented structures. The mean, standard deviation, median, and maximum segmentation errors were 0.23, 0.17, 0.18, and 1.27 mm, respectively.

Conclusions: The results indicate that accurate segmentation of the facial nerve and chorda tympani in pediatric scans is achievable, thus suggesting that safe drilling trajectories can also be computed automatically.

INTRODUCTION

Cochlear implantation (CI), a surgical technique, is routinely performed to restore hearing ability for patients that experience bilateral, severe hearing loss.¹ In CI, an electrode array is surgically placed in the cochlea, via either a natural opening (the round window) or a surgical opening (cochleostomy), for electrical stimulation of the auditory nerve. The electrode array receives signals from externally worn components consisting of a microphone, a sound processor, a signal transmitter, and a signal receiver. The microphone senses sound waves. Then, the sound processor decomposes the sound waves, in a process that usually involves Fourier analysis, and converts them into electrical signals that can be transmitted to the signal transmitter. Finally, the signal transmitter relays the electrical signals to an internally implanted receiver that, in turn, transmits the electrical signals to the electrode array.

In traditional CI procedures, access to the cochlea is achieved by a wide excavation of the temporal bone region of the skull and manually accessing the cochlea through the facial recess. Recently, we introduced a minimally invasive image-guided CI technique called percutaneous cochlear implantation (PCI).² PCI achieves access to the cochlea by drilling a single linear channel from the outer skull into the cochlea via the facial recess. The facial recess is a region approximately 2.5 mm wide bounded posteriorly by the facial nerve that controls ipsilateral facial mimetic motion and anteriorly by the chorda tympani that controls ipsilateral taste to the tip of the tongue. The drilling trajectory is computed by algorithms that we developed to find a path that targets the cochlea and optimally preserves the safety of critical ear anatomy structures such as the ossicles, ear canal, facial nerve, and chorda tympani.³ Drilling is constrained to follow the computed trajectory by a patient-customized micro-stereotactic drill guide, called a microtable, which was designed by our group.⁴ The PCI approach involves the following four steps: (1) preoperative planning, (2) intraoperative registration, (3) drill guide fabrication, and (4) drill guide mounting and drilling.

Step 1: Preoperative planning

Prior to CI surgery, a CT scan of the patient’s head containing the ear region is acquired. Then, the ear structures are automatically identified and accurately segmented.^{5, 6} Based on the segmented structures, a safe drilling trajectory is computed automatically.³

Step 2: Intraoperative registration

On the day of surgery, three fiducial markers are implanted, typically at the most inferior (mastoid tip), posterior, and superior positions of the temporal bone. The marker consists of an anchor that is screwed into the bone, a metal sphere that serves as a fiducial marker, and a tubular extender that connects the two. A CT scan of the part of the head containing the markers and ear region is obtained using a CT scanner (e.g., xCAT ENT Mobile from Xoran Technologies, Ann Arbor, MI; voxel size 0.3 × 0.3 × 0.4 mm³). Next, the acquired intraoperative and preoperative CT scans are isotropically downsampled by a factor of 4 and rigidly registered using a 6 DOF (translation and rotation in three dimensions) transformation. Then, the regions of the ear are cropped from both images and subsequently registered using a 12 DOF (translation, rotation, scale, and skew in three dimensions) affine transformation. The transformations are automatically estimated with an intensity-based registration method that maximizes the mutual information between the images.^{7, 8} Usually, the preoperative image is acquired a few days before the surgery, but for cases where there is a substantial time gap between the preoperative CT and the surgery, this affine registration is necessary to account for local deformations caused by growth of the temporal bone. Using the compound affine transformation, the drilling trajectory generated from the preoperative plan is transformed into the intraoperative image space, i.e., the space in which the fiducial markers are located. Finally, the centers of the markers are identified by a semiautomatic method developed by our group that starts with a user provided seed point.^{9, 10}

Step 3: Drill guide fabrication

The microtable used as a patient specific drill guide is manufactured from a slab of Ultem (Quadrant Engineering Plastic Products, Reading, PA). The tabletop of the microtable has four holes. In three of them, legs are affixed that connect it to the fiducial markers. The drill bit is guided through the fourth hole (targeting hole). Fabrication of the microtable requires determining the location and depth of the four holes. These values are determined so that the targeting hole is collinear with the planned drilling trajectory. A component of the intraoperative software developed by our group is used to generate the command files that are used by a CNC machine (e.g., Ameritech CNC, Broussard Enterprise, Inc., Santa Fe Springs, CA) to manufacture the microtable. The CNC machine takes less than 3 min to complete the fabrication of the microtable.

Step 4: Drill guide mounting and drilling

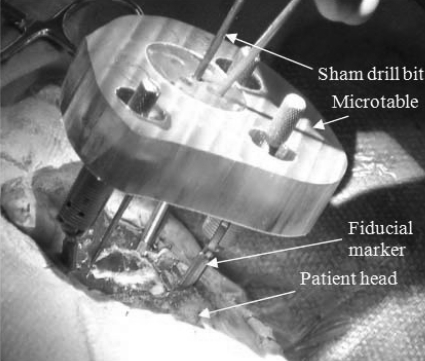
Once the microtable is fabricated, it is mounted on the marker spheres, and a drill press is attached to the targeting hole. Finally, drilling is performed to just lateral to the facial recess with a wide bore drill bit (4 mm diameter) and through the facial recess and more medially with a 1.5 mm diameter drill bit. The bit is guided through the targeting hole along the preoperatively planned drilling trajectory and perpendicular to the tabletop of the microtable. Figure 1 shows a microtable mounted on a patient’s head with a sham drill bit inserted during clinical validation testing.

Figure 1.

Microtable mounted on a patient head.

Challenges in segmentation

The facial nerve, which controls the movement of the ipsilateral face, and the chorda tympani, which controls the sense of taste, are sensitive anatomical structures that are in close proximity to the desired CI drilling trajectory. Thus, to compute a safe insertion trajectory that will avoid damage to these structures, the facial nerve and chorda tympani need to be segmented. The effectiveness of traditional segmentation methods, such as atlas-based segmentation, is limited since the facial nerve and chorda tympani are thin structures (0.8–1.7 mm and 0.3–0.8 mm in diameter, respectively), exhibit poor contrast with adjacent structures, and are surrounded by highly variable anatomy. To accurately segment these structures, we developed an automatic segmentation method that relies on a statistical model of the structures.⁵ The models include intensity and shape information that varies with position along the medial axis of the respective structures. We are now extending the PCI concept to pediatric patients. This requires segmenting the facial nerve and chorda tympani in pediatric CT scans. While doing so, we learned that substantial differences exist between the ear anatomies of adults and children. This led to poor segmentation of the facial nerve and chorda tympani when a model of adult anatomy was used to segment a pediatric CT.

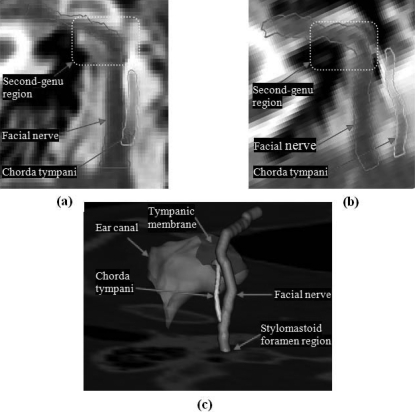
The facial nerve is a thin tubular structure that travels through the temporal bone. In the second-genu region, the facial nerve bends and travels between the stapes and lateral semicircular canal. The facial nerve then continues in the mastoid portion of the temporal bone and exits through the stylomastoid foramen. Figure 2 shows the facial nerve and chorda tympani. To visualize the full length of the structures in panels (a) and (b), we mapped the 3D centerlines of the structures onto the coronal plane. This mapping was used to create a thin-plate-spline (TPS)-based transformation that was then used to interpolate the CT images to the same plane. It is clearly seen in panels (a) and (b) that the facial nerve makes a sharper turn in pediatric patients than it does in adult patients. The chorda tympani typically branches from the vertical segment of the facial nerve approximately 1–2.5 mm superior to the stylomastoid foramen and runs at an angle to the tympanic membrane as shown in panel (c). During our study, we have observed that in some pediatric cases, the chorda tympani enters the temporal bone near the stylomastoid foramen. Panel (a) in Fig. 2 shows a chorda tympani of an adult patient that branches from the vertical segment of the facial nerve, whereas panel (b) shows a chorda tympani of an infant that originates near the stylomastoid foramen, instead of branching from the vertical segment of the facial nerve. We have also observed that the angle and position at which the chorda tympani originates in pediatric cases exhibit higher interpatient variation than in adult cases.

Figure 2.

Comparison of facial nerve and chorda tympani structures in an adult and a pediatric CT scans. (a) Contours of facial nerve and chorda tympani in an adult CT. (b) Contours of facial nerve and chorda tympani in a pediatric CT. (c) 3D rendering of the anatomy.

To address the issue of anatomical differences, we have constructed a new model for pediatric patients, and we have employed the same segmentation algorithm that we used for adults with parameters optimized for pediatric populations. We report that, with this new model, accurate and automatic segmentation of the facial nerve and chorda tympani is achievable in pediatric patients.

METHODS

Data

A total of 22 pediatric scans, with age range of 11 months to 16 yr, were used in this study. The images were acquired from different scanners. Typical scan resolution is 512 × 512 × 130 voxels of 0.3 × 0.3 × 0.4 mm³ size. Out of the 22 scans, one was selected as a reference (atlas) volume, 11 were used as training volumes in order to generate the model, and the other ten were used as test volumes. The atlas volume was chosen based on subjective criteria, i.e., there was strong contrast between bone and soft tissue in the image, the spatial resolution of the image was high, the size of the patient’s head was representative of the data set, and the patient’s head was roughly located near the center of the image and oriented in the transverse direction.

Segmentation approach

The general approach we use to segment the structure involves extracting the centerline of the structure and then expanding it into the full structure using a standard level set method.¹¹ In order to find the centerline in a target volume, we use a minimal cost path algorithm. To provide the minimum cost path algorithm with a priori intensity and shape costs, we create a model of the structure. The model is designed so that it can be aligned with the target volume.

Model generation

The model is composed of statistical intensity and shape information associated with each voxel along the centerline of the structure of interest (SOI). The model centerline is defined as the centerline of the manually delineated SOI in the atlas volume. Each model centerline voxel is associated with statistical values of three features: intensity, width, and unit orientation vector. These values are computed as an ensemble average of the respective feature values measured from all the training scans’ corresponding centerline points. The model is used to both define a cost function for centerline extraction and to create a speed function. The speed function defines the rate of expansion at each voxel for the level set algorithm, which expands the centerline into the full structure.¹¹ The model data are stored only on the left ear of the reference volume. The right ear is modeled by reflecting the left ear model across the midsagittal plane, which is possible due to the symmetry of the human head.¹²

The model generation process, outlined in Fig. 3, consists of the following four steps: (a) the SOIs are manually segmented in the reference and training scans. The manual segmentations were created by a student rater and later corrected by two experienced physicians. (b) The training images are aligned with the reference image by applying a series of three affine registrations. The first is a surface-based registration computed to correct the size difference between the reference and training images. This is necessary because the size of the head in the pediatric population varies substantially. This variability can be problematic for standard image registration algorithms, which are sensitive to initial position. Thus, the skull surfaces of the training volumes are first registered to the skull surface of the reference volume using the iterative closest point (ICP) algorithm.¹³ This minimizes the sum of squared distances between all points from the reference surface to their closest points on the training surface. The surfaces of the skulls are extracted using the marching cubes algorithm, which creates triangle models of constant intensity surface from 3D image data.¹⁴ For some volumes, manual initialization (rotation and translation) of the surface-based registration is necessary- because the images are acquired with the head in various positions (rotation and translation from the center of the field of view) due to patient sedation. Next, an intensity-based affine registration is applied to the images, after being downsampled by a factor of four in each dimension. Once global alignment of the training images with the reference images is achieved, the part of the scan with the ear anatomy is cropped from the training volumes using a bounding box on the region of interest projected from the reference volume. Finally, the cropped images are registered using an intensity-based affine registration applied at full resolution. The intensity-based registrations use Powell’s direction method and Brent’s line search algorithm¹⁵ to optimize the mutual information^{7, 8} between the images and estimate a transformation matrix with 12 DOF (three rotations, translations, scales, and skews). Applying registration on the whole volumes at a lower resolution followed by registration of the cropped regions at full resolution is computationally more efficient and, in our experience, leads to improved accuracy in the region of interest. (c) The manual delineations of the SOIs in the training volumes are projected onto the affinely registered reference space using the compound registration transformation. Then, centerlines of the manual segmentations are extracted using a topology preserving voxel thinning algorithm.¹⁶ At each point along the extracted centerlines, values of structure width, intensity, and curve orientation are measured and stored. The orientation vector at each voxel is estimated using central differences, except for the first and last voxels where forward and reverse differences are used. (d) The reference volume is nonrigidly registered to each affinely registered training volume using an intensity-based nonrigid registration technique¹⁷ that registers images by maximizing a normalized mutual information-based objective function.¹⁸ Centerline points from the reference volume are projected onto each affinely registered training volume using the obtained nonrigid deformation field. A correspondence, based on the minimum Euclidean distance, is established between each reference centerline point and the closest point from each affinely registered training volume’s centerline. This results in one corresponding point in each training volume for every reference point. Subsequently, statistical values of width, intensity, and orientation features at each point along the model centerline are computed as the average of the measurements from its set of corresponding points. Features are measured on the affinely registered training images.

Figure 3.

Model-generation steps.

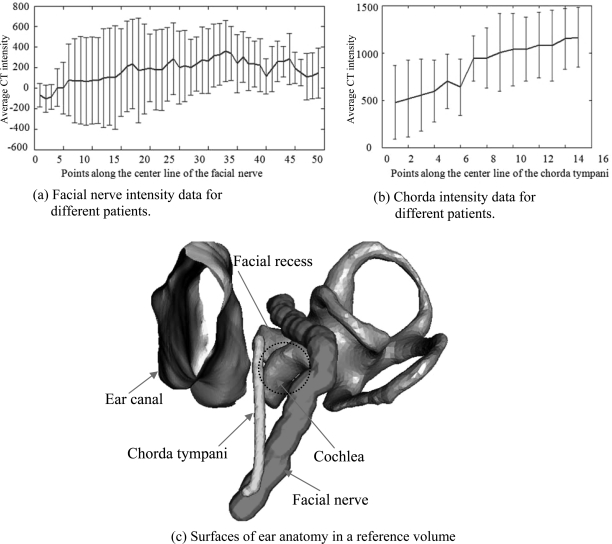
The above model generation process is applied to both the facial nerve and chorda tympani to create models for these two structures. In Fig. 4, panel (c) shows the surfaces of the facial nerve and chorda in the reference volume. The mean and standard deviation of the intensity (in Hounsfield units) along the facial nerve and chorda tympani in the pediatric population is shown in panels (a) and (b), respectively. These panels clearly show that the intensity of the structures in CT scans changes along their length. It also shows that there is a considerable variation in intensity at each point along the length. This represents a challenge to segmentation methods that rely on a single threshold or even on intensity distributions.

Figure 4.

Pediatric structures model data. (a) Facial nerve intensity data for different patients. (b) Chorda intensity data for different patients. (c) Surfaces of ear anatomy in a reference volume.

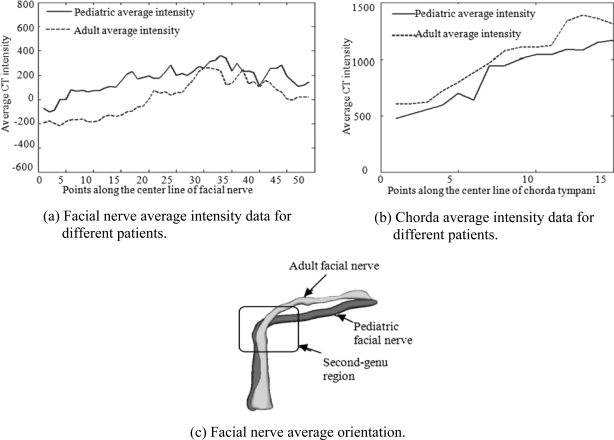
Figure 5 demonstrates the differences in intensity and shape characteristics between adult and pediatric models. Panel (a) compares the average intensity profiles of the facial nerve in the two populations. Although the two functions have a similar trend, the intensities along the pediatric facial nerve are consistently higher. The average intensity profile of the chorda in the pediatric volumes, shown in panel (b), is consistently lower compared to the adult model. Surface models of the average adult and average pediatric facial nerves are shown in panel (c). It is clearly shown that, on average, the facial nerve in the second-genu region makes a sharper turn for pediatric than for adult individuals. In order to create this image, the pediatric model is projected onto the adult image space using the transformation matrix obtained by applying a series of affine registrations, as described in step (b) of the model generation procedure, to align pediatric and adult images. These intensity and shape differences explain the limited success we achieved when applying an adult model of the anatomy to segment pediatric images. Thus, we have constructed a new pediatric model for pediatric patients and employed the same segmentation algorithm we used for adults with parameters optimized for pediatric populations.

Figure 5.

Adult and pediatric population statistical model. (a) Facial nerve average intensity data for different patients. (b) Chorda average intensity data for different patients. (c) Facial nerve average orientation.

Structure segmentation

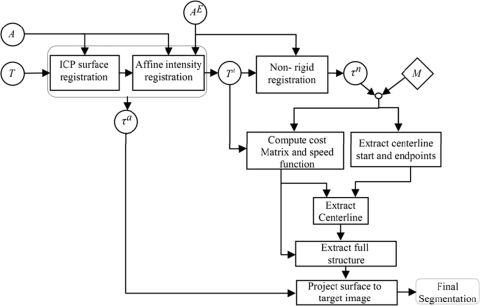
Once created, the models can be used to segment the structures in a target image using the model-based segmentation algorithm we have developed, called the navigated optimal medial axis and deformable-model (NOMAD) algorithm.¹⁹ The flow chart in Fig. 6 shows the structure segmentation process in a target image. In the flow chart, a circle represents an image when the inside text is a Roman letter and a transformation when it is a Greek letter. Rectangles represent operations on images. The diamond represents model information. T is the target image we want to segment, A is the atlas image, and A^E is the ear region of the atlas image. T is first affinely registered to A and A^E in order to produce T^A. Then, A^E is nonrigidly registered to T^A using the adaptive bases nonrigid registration algorithm.¹⁷ Subsequently, the model centerline points are projected onto T^A using τⁿ, the nonrigid registration deformation field. Next, for each voxel in T^A, the closest point on the projected centerline is found and a correspondence is established between that voxel and the model point. Based on the correspondence, a cost matrix, speed function, and the start and end points of the structure centerline are computed. The cost matrix and start and end points are supplied to a minimum cost path algorithm to extract structure centerline. A standard level set algorithm uses the speed function to expand the extracted centerline to full structure segmentation. Finally, the segmented surface is projected back onto T using τ^a, the affine transformation matrix.

Figure 6.

Structure segmentation flow chart.

The expressions of the cost terms associated with each feature are presented in Table Table I.. The parameters α and β are used to adjust the relative importance of each feature in the overall cost of a transition from one voxel to a neighboring voxel. The table reports the values of each of these parameters, followed by the sensitivity of the results to each parameter, as will be discussed later. A voxel in T^A is represented by x. M_I(x) and $\overrightarrow{M_o(\mathit{x})}$ are model intensity and orientation values associated with the projected model point that is nearest to x. $\overrightarrow{\mathit{t}}$ is the curve orientation at x. Nbhd(x) is the set of 26 voxels that are in the neighborhood of voxel x. Term 1 penalizes deviation of intensity from the intensity predicted by the model. This cost term is zero when the intensity at voxel x is equal to the intensity predicted by the model M_I(x). We set the value of the normalization in this term to 2000, since, based on qualitative observations, the difference in intensity between a target and reference point is not more than 2000. Term 2 penalizes curve orientation in a direction different from the direction predicted by the model. Transitions in the direction of the predicted orientation have a cost of zero, while transitions in the opposite direction have a maximum cost. Term 3 is a model-independent term that favors voxels that are local intensity minima. The cost term is zero when the intensity at x is a local minimum and is highest when the intensity at x is a local maximum. The total cost associated with a transition from one point to a new point is the sum of term (1) and term (3) at the new point, and term (2) evaluated in the direction of the transition to the new point. This results in a 3-D cost matrix.

Table 1.

Expression of cost terms for centerline extraction.

	Cost term	Purpose	Facial nerve		Chorda tympani
	α	Β	α	β
1	β[|TA(x)-MI(x)|∕2000]α	Penalizes deviation from intensity predicted by model	1.7|30%*	2.4|50%	3.4|80%	11.5|40%
2	$\beta {\left[\left(1-\frac{\overrightarrow{\mathit{t}}·\overrightarrow{M_o(\mathit{x})}}{\left|\overrightarrow{\mathit{t}}\right||\overrightarrow{M_o(\mathit{x})\left|\right|}}\right)∕2\right]}^{\alpha }$	Penalizes deviation from orientation predicted by model	2.4|60%	12.5|50%	4.0|30%	1.0|80%
3	$\beta {[1-\left(\frac{\#\{\mathit{y}\hspace{1em}\mathrm{in}\hspace{1em}\mathit{Nbhd}(\mathit{x})\mathrm{:}{T}^A(\mathit{y})>T^A(\mathit{x})\}}{\#\{\mathit{y}\hspace{1em}\mathit{in}\hspace{1em}\mathit{Nbhd}(\mathit{x})\}}\right)]}^{\alpha }$	Penalizes deviation from local intensity minima	4.0|40%	1.0|40%	1.2|70%	1.5|70%

^*Percentile represents allowable variation in coefficient resulting in < 0.5 mm change in total segmentation error.

The start and end points of the facial nerve are identified as the center of mass of the most inferior 5% and the most anterior 5% of the projected facial nerve mask, i.e., the mask obtained after the manually delineated facial nerve mask in the atlas is projected onto T^A. For the chorda tympani, the start and end points were identified in the adult population also as the center of mass of the most inferior 5% and most superior 5% of the projected chorda mask. However, in the pediatric population, this did not lead to an accurate segmentation of the chorda tympani because this structure is more variable in its starting position and orientation. To correct this, we delineated chorda tympani masks both in the reference and in each training image such that they extend 2–3 mm inferior to their true starting positions. This increases the chances for the NOMAD algorithm to arrive at an accurate localization of the chorda tympani when it reaches the region of interest.

Once the starting points, the ending points, and the cost matrix are computed, the structure centerline is computed as the optimal path in the cost matrix using a minimum cost path finding algorithm.²⁰ Since the chorda tympani is a very thin structure, we complete its full segmentation by assigning a radius of 0.325 mm at each point of the centerline. Full structure segmentation of the facial nerve is accomplished by a standard geometric deformable model based on level sets. The generated centerlines are used to initialize the evolution. The rate of evolution at each centerline point is specified using the speed function, which is defined as the sum of the two expressions shown in Table Table II.. The parameters γ and δ are used to adjust the relative importance of each feature in the speed function. As is done in Table Table I., the value of, and sensitivity of the algorithm to, each parameter is given in Table Table II.. The first term in the speed function slows the rate when width at each centerline point is smaller, whereas the second term slows the rate when the local intensity deviates from the intensity predicted by the model. In a typical use of level set techniques, the process iterates until convergence. Here, we fix the number of iterations to three because the lack of contrast between the structure and its surrounding leads to leakage. Thus, the values of δ and γ have been estimated on the training scans to lead to full structure segmentation in three iterations.

Table 2.

Speed function for level set expansion.

			Facial nerve
	Speed function	Purpose	δ	γ
1	e[γMw(x)δ]	Slows the rate of propagation when the structure width is small	0.5|60%	1.0|60%
2	e[-γ(|TA(x)-MI(x)|∕2000δ]	Slows the rate of propagation when the local intensity deviates from the predicted value	0.2|50%	1.1|70%

Segmentation validation

We used two quantitative distance measures to evaluate our segmentation accuracy, which we call automatic-to-manual (AM) and manual-to-automatic (MA). To compute these distances, the surface voxels of the manual and automatic surfaces are identified. Once this is done, the MA error is computed as the Euclidean distance from each voxel on the manual surface to the closest voxel in the automatic segmentation. Similarly, the AM error is computed as the distance from each voxel on the automatic surface to the closest voxel in the manual segmentation. The nonsymmetric AM and MA errors reduce to zero when the manual and automatic segmentations are in complete agreement.

The manual delineation of the structures on the testing scans was done by a student and corrected by two experienced physicians. The manual segmentations were generated only for the segments of the structures that are in close proximity with the drilling trajectory. For the facial nerve, those segments are the mastoid (vertical) and the tympanic (horizontal) segments. For the chorda, the region of interest is the segment that runs from the stylomastoid foramen to the tympanic membrane. Validation experiments were performed on the ten test volumes. A statistical model is created using the reference and the training volumes. Each test volume is then segmented using that statistical model. The parameter values used for segmentation (see Tables 1, Table II.) are selected using the procedure described in Sec. 2F

Parameter selection

The values of α and β in the cost terms (see Table Table I.) and the values of γ and δ in the speed function (see Table Table II.) were modified heuristically on the training scans until an acceptable value of the total maximum AM or MA error was found. Once good values of the parameters were obtained, each of these values were modified in 5% increments in the direction that decreased the maximum AM or MA error, until converging to a value for which the error clearly increased. The final parameter value was chosen in the generally flat region preceding the convergence value. To characterize the sensitivity of the algorithm to these parameter values, each parameter was then modified, also on the training scans, with 10% increments and decrements until the maximum AM or MA error increased by 0.5 mm. The sensitivity of the algorithm to the parameter values was then measured as the percent deviation of the parameters at which this increase in error occurs. The final parameter values and the sensitivity of the algorithm to each parameter are presented in Tables 1, Table II.

RESULTS

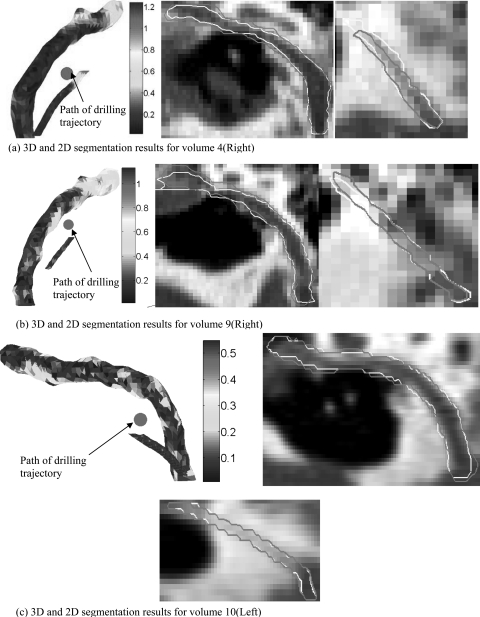
The results of the validation performed on the ten test volumes are presented in Table Table III.. Shown in the table are the values of mean, standard deviation, interquartile range, median, and maximum errors in millimeters for both the facial nerve and chorda tympani. The errors are measured using the two evaluation metrics, MA and AM, as discussed above. The mean and median errors for the structures are approximately 0.2 mm (<1 voxel). Maximum errors are 1.3 mm for the facial nerve and 1.2 mm for the chorda tympani. To assist in the interpretation of the results, 2D and 3D renderings for three of the experiments are shown in Fig. 7. Two experiments that resulted in large segmentation errors are presented in panels (a) and (b), respectively. In panel (c), renderings of an experiment that resulted in low overall error are presented. Manual segmentation contours are in light yellow and automatic contours are in dark purple. In the 3D visualizations, the color encodes the distance in millimeters to the closest point on the corresponding manual surface. Each 3D rendering shows a view of the segmentations along the path-of-flight of the planned drilling channel (position marked with red circle) computed using the automatic segmentations. The largest chorda segmentation error can be seen at its superior endpoint in panel (a). Errors occurred in this region adjacent to the tympanic membrane in several experiments. This is because the chorda and surrounding structures are highly variable and lack contrast in CT in this region. The variability is so extreme that manual identification can be challenging. In panel (b), the largest facial nerve error can be seen near the end of its horizontal segment. This also is a region where error maxima occur in several experiments.

Table 3.

AM and MA segmentation errors on the ten test scans. Total refers to the mean, standard deviation, median, and max errors for all scans.

(a) Facial nerve segmentation errors measured in millimeters
		Facial nerve
		Mean		Std. deviat		Median		Max		I. Q. range
Volume	Ear	AM	MA	AM	MA	AM	MA	AM	MA	AM	MA
1	Left	0.35	0.28	0.2	0.15	0.35	0.23	0.84	0.69	0.31	0.22
2	Left	0.19	0.25	0.11	0.12	0.19	0.23	0.53	0.72	0.16	0.14
3	Right	0.2	0.24	0.14	0.12	0.2	0.22	0.86	0.89	0.24	0.16
4	Right	0.26	0.21	0.21	0.11	0.26	0.19	1.27	0.7	0.25	0.15
5	Left	0.13	0.18	0.1	0.09	0.13	0.18	0.51	0.43	0.12	0.07
6	Right	0.23	0.27	0.15	0.13	0.23	0.25	0.95	0.81	0.25	0.19
7	Left	0.22	0.25	0.16	0.12	0.22	0.23	1.14	0.84	0.19	0.13
8	Left	0.26	0.22	0.16	0.1	0.26	0.19	0.91	0.58	0.15	0.11
9	Right	0.31	0.26	0.19	0.13	0.31	0.23	1.13	0.77	0.3	0.19
10	Left	0.14	0.18	0.09	0.07	0.14	0.17	0.55	0.58	0.13	0.1
total		0.23	0.24	0.17	0.12	0.18	0.21	1.27	0.89	0.22	0.15

(b) Chorda tympani segmentation errors measured in millimeters
		Chorda tympani
		Mean		Std. devia		Median		Max		I.Q. range
Volume	Ear	AM	MA	AM	MA	AM	MA	AM	MA	AM	MA
1	Left	0.15	0.11	0.04	0.03	0.13	0.11	0.27	0.23	0.1	0.1
2	Left	0.1	0.09	0.03	0.05	0.1	0.07	0.24	0.35	0.09	0.07
3	Right	0.1	0.11	0.04	0.09	0.11	0.07	0.33	0.62	0.06	0.06
4	Right	0.32	0.3	0.28	0.28	0.14	0.13	1.25	1.07	0.15	0.12
5	Left	0.13	0.11	0.05	0.06	0.1	0.09	0.32	0.35	0.07	0.06
6	Right	0.09	0.07	0.02	0.02	0.09	0.06	0.17	0.13	0.08	0.06
7	Left	0.1	0.11	0.04	0.09	0.09	0.07	0.33	0.62	0.03	0.04
8	Left	0.16	0.14	0.04	0.05	0.14	0.12	0.3	0.32	0.14	0.12
9	Right	0.2	0.19	0.06	0.07	0.21	0.16	0.32	0.38	0.14	0.13
10	Left	0.09	0.07	0.02	0.02	0.09	0.06	0.17	0.16	0.09	0.06
total		0.14	0.13	0.1	0.1	0.1	0.08	1.24	1.07	0.09	0.06

Figure 7.

Segmentation result. (a) 3D and 2D segmentation results for volume 4(R). (b) 3D and 2D segmentation results for volume 9(R). (c) 3D and 2D segmentation results for volume 10(L).

DISCUSSION AND CONCLUSIONS

The percutaneous cochlear implantation surgery technique we have introduced requires the segmentation of the facial nerve and chorda tympani to compute a safe drilling trajectory. In previous work presented by our group, the segmentation of these structures was achieved using an algorithm that relies on a statistical model generated from an adult population. We tested this algorithm on a pediatric population with limited success due to the substantial differences between adult and pediatric anatomy. The differences are observed in the second-genu region of the facial nerve where the nerve makes a sharper turn in children than it does in adult patients. In addition, we observed variation in the starting position of the chorda tympani across patients. Typically, the chorda tympani branches from the vertical segment of the facial nerve. However, in pediatric patients, it is not uncommon for it to exit from the stylomastoid foramen alone. In this work, to correct for the anatomical differences, a pediatric-specific statistical model is built and the same segmentation algorithm employed on adults is used for the segmentation of the facial nerve and chorda tympani in the pediatric population.

In both the pediatric and adult implementations (see Tables 1, Table II. of Ref. 5), the algorithm is less sensitive to the speed function parameters {δ, γ} than those of the optimal path cost function {α, β}. In the adult implementation, the orientation term is weighted the lowest for both the facial nerve and chorda tympani. In the pediatric implementation, the orientation term is weighted the lowest for the chorda tympani. In contrast to the adult implementation, the orientation term is weighted the highest for the facial nerve in the pediatric implementation. We attribute this to the sharp turn of the facial nerve in pediatric individuals, which requires higher shape cost.

The automatic segmentation algorithm was evaluated on ten CT scans, resulting in mean, standard deviation, median, and maximum errors of 0.237, 0.121, 0.214, and 1.273 mm, respectively, for the facial nerve. These results are 0.141, 0.1, 0.1, and 1.241 mm for the chorda tympani. Thus, the segmentation algorithm was able to achieve subvoxel mean error distance for both structures. Although the maximum distances are substantial, they are highly localized. For the facial nerve, these errors typically occur near the end of its horizontal segment. Accuracy in this region is less vital for PCI since it is not immediately adjacent to the facial recess.

Drilling trajectories were computed using each set of automatic segmentations. All trajectories were assessed in the patients’ CTs by an experienced surgeon and judged to be safe. The results we have obtained thus suggest that the percutaneous cochlear implant approach is a viable approach for pediatric patients. To date, this technique has been successfully used to perform planning prospectively on six pediatric patients in the pediatric PCI clinical validation study we are currently conducting.

The main limitation of the approach is that manual initialization is required for registration of the atlas and target images when there are substantial differences in head size, position, and orientation between the images. This is because large misalignments are not always corrected by the automatic intensity-based registration methods described in Sec. 2C Future work will include further automation of this process as well as continuing the clinical validation of the algorithm as a tool for safely planning pediatric PCI surgeries.