Polymer physics of the cytoskeleton

Abstract

The cytoskeleton is generally visualized by light or electron microscopy as a meshwork of protein filaments that spans the space between the nuclear envelope and the plasma membrane. In most cell types, this meshwork is formed by a three dimensional composite network of actin filaments, microtubules (MT), and intermediate filaments (IF) together with the host of proteins that bind to the sides or ends of these linear polymers. Cytoskeletal binding proteins regulate filament length, crosslink filaments to each other, and apply forces to the filaments. One approach to modeling the mechanical properties of the cytoskeleton and of cell in general is to consider the elements of the cytoskeleton as polymers, using experimental methods and theoretical models developed for traditional polymers but modified for the much larger, stiffer, and fragile biopolymers comprising the cytoskeleton. The presence of motor proteins that move actin filaments and microtubules also creates a new class of active materials that are out of thermodynamic equilibrium, and unconstrained by limitations of the fluctuation-dissipation theorem. These active materials create rich opportunities for experimental design and theoretical developments. The degree to which the mechanics of live cells can usefully be modeled as highly complex polymer networks is by no means certain, and this article will discuss recent progress in quantitatively measuring cytoskeletal polymer systems and relating them to the properties of the cell.

1. Introduction

A cell is filled with a complex system of polymers. In the nucleus, meter long DNA strands are compacted in micron sized packages that store genetic information but reveal relevant sequences to transcriptional machinery. The cell membrane is essentially a self-assembled 2-D copolymer composed of hundreds of different lipid subunits with a bilayer. In between the nucleus and the cell membrane lies a network of biopolymer filaments known as the cytoskeleton, which is directly responsible for determining cell shape, generating mechanical forces, resisting externally imposed forces, and transducing extracellular biochemical and mechanical stimuli to the cytoplasm [1**]. In most cell types, this meshwork is formed by a three dimensional composite network of actin filaments, microtubules (MT), and intermediate filaments (IF) together with the proteins that control the assembly and attachments of these linear polymers. Cytoskeletal binding proteins regulate filament length, crosslink filaments to each other, and apply forces to the filaments. One approach to modeling the mechanical properties of the cell is to consider it as a complex soft material with mechanical properties dominated by the longest, most abundant, and most crosslinked polymers within it. In this approximation, filamentous actin (F-actin) has been generally thought to dominate cell mechanics and the properties of purified actin networks, modulated by binding proteins and other cytoskeletal filaments are presumed to be a useful starting point to interpret whole cell mechanics. This approach benefits from a rich theoretical understating of synthetic polymer networks, modified for the unusual shapes and stiffness of cytoskeletal polymers.

Modeling the cell as a system of polymer networks is a relatively recent idea, influenced heavily by electron, fluorescence, and atomic force microscopy images of the filaments spanning the intercellular space. Earlier studies of cell mechanics considered the cell as a colloidal system [2], and indeed the cell interior is far more crowed by membrane-bound organelles, large protein complexes, and other nano or micron-scaled objects than it is by the cytoskeleton, which occupies only on the order of a few percent of the cell’s volume. The colloidal nature of the cell has recently been re-emphasized by studies of cell mechanics interpreted in terms of a soft glass [3]. How these two aspects of the cell: a low volume fraction cytoskeleton and a high volume fraction of imbedded objects combine to achieve the mechanical properties for cell function remains to be established [4*], and this article will focus on recent studies that examine the mechanical properties of single cytoskeletal filaments or the networks they form in order to test whether they can account for the properties of the cell.

2. Major components of the cytoskeleton

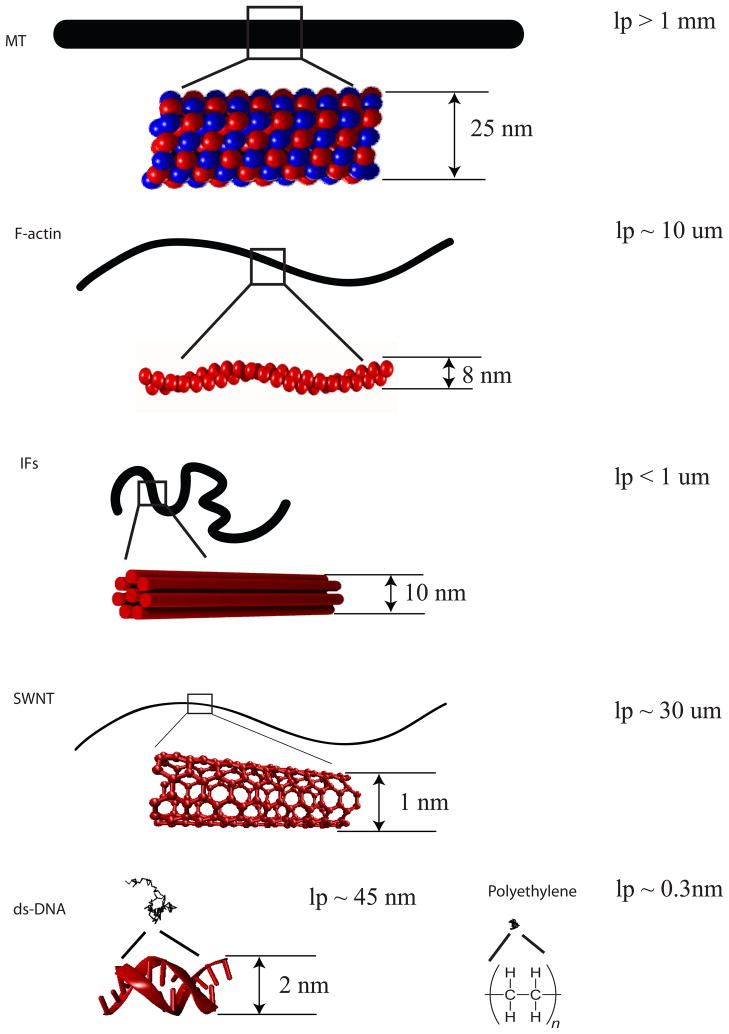
There are three major types of the cytoskeleton filaments: microtubules, actin filaments, and intermediate filaments. These filaments differ from each other in their molecular structure, function and mechanical properties, as depicted in Figure 1. The most striking feature of cytoskeletal polymers, and one that creates unique material properties, is the enormous bending stiffness of these filaments in comparison to synthetic polymers or even other biopolymers such as DNA. As figure 1 shows, the end to end length of all three cytoskeletal polymers is far greater than that of conventional polymers of the same contour length, and therefore these filaments have unique ability to form networks and elastic materials at very low volume fractions. For example, F-actin form gels at volume fractions as low as 0.001%, while the gelation of synthetic polymers occur at volume fraction of at least 3 orders of magnitude higher.

Figure 1. Elongated structure of cytoskeletal filaments.

Microtubules, F-actin, and intermediate filaments with contour length 10 um are drawn at the same scale in comparison to single wall carbon nanotubes, double strand DNA, and polyethylene of the same contour length.

2.1 MTs

Microtubules are polymers of the globular proteins α and β-tubulin dimers. The tubulin dimers polymerize head to tail into polarized protofilaments. Approximately 13 parallel protofilaments arrange in a staggered manner to form a hollow tube of 25 nm in diameter [5*]. Even though they are the stiffest of all known biopolymers, with persistence length more than 1 mm, microtubules appear not to dominate the mechanics of the cytoskeleton, perhaps because they are not stably crosslinked to each other or to other parts of the cytoskeleton. However, their presence can significantly modify the elasticity of actin networks, for example [6*] and can alter the compressibility of networks formed by more flexible polymers [7].

2.2 F-actin

Actin filaments are polymerized from globular actin monomers. An actin filament can be regarded as two parallel protofilaments that twist around each other into a right-handed helix with a diameter of 8 nm. For both MTs and actin, filament growth and organization are regulated by many factors, including ionic concentrations and a variety of capping, binding, branching, and severing proteins. F-actin appears to be the primary mechanical component of the cytoskeleton. While providing mechanical support to the cells, the actin network is connected to trans-membrane adhesion proteins. This connection facilitates the transduction of intracellular and extracellular mechanical signals, which allow cells to detect and respond to both chemical and mechanical signals from their extra-cellular environment [8].

2.3 IFs

Intermediate filaments are composed of eight parallel protofilaments held together by lateral hydrophobic and electrostatic interactions, and a hierarchy of inter-subunit interactions results in the mature IF structure [9*, 10]. The protofilaments are made of staggered tetramers of IF proteins. Each IF protein has a coiled-coil structure that also contains non-helical elements [11]. The intermediate filaments have an average diameter of 10 nm, which is larger than the actin filaments but smaller than that of the microtubules. The “intermediate” however originally referred to their size compared to the smaller actin filaments (thin filaments) and larger myosin filaments (thick filaments) seen in electron micrographs of muscle cells [12]. Whereas very similar MT and actin variants exist in nearly all eukaryotic cell types, IF species are far more varied but expressed by fewer organisms and cell types [13**].

3. Mechanical properties of individual cytoskeletal filaments

From a mechanic perspective the most striking difference among the cytoskeletal filament types in their bending stiffness (Figure 1). Stiffness of polymer filaments can be quantified by their persistence length, l_p, which is defined as the length scale for the decay of the tangent-tangent correlation along the filament, and is proportional to the stiffness of the polymer. If a polymer can be modeled as a uniform cylinder, l_p= k_B/kT, where k_B is the bending modulus of the filament. Usually l_p is easier than k_B to measure, and the force needed to deform a filament is inferred from l_p, but recent studies of the coupling between bending or stretching and twisting F-actin suggest that simultaneous application of torque, tension, or bending as some actin binding proteins appear to do, can have more profound effects on F-actin than suggested by l_p alone [14, 15*]. For complex filaments like microtubules, where sliding between protofibrils can occur during MT bending, the relation between l_p and k_B is not a simple proportionality, and some experiments and models predict a contour length-dependent persistence length [16, 17].

The ratio between persistence length (l_p) and the contour length (l_c) differentiates the polymer filaments into three regimes. When l_c≫l_p, the filaments are flexible, i.e. thermal energy can cause large transverse fluctuations so that a filament looks like a Gaussian polymer chain with a Kuhn length of 2l_p. In the limit of l_p≫l_c, filaments are stiff and do not show transverse thermal undulations but move in solution as rigid rods driven by thermal energy. Semi-flexible filaments lie between these two limits, and l_c and l_p are on the same order of magnitude.

For filaments with micrometer long contour length, the three types of cytoskeleton filaments fall in these three stiffness regimes respectively. Intermediate filaments are the softest among the three major types of cytoskeleton filaments. Their l_p is reported to range from 200 nm to slightly over 1 μm and is IF type dependent [18, 19]. The very small persistence length of the 10 nm diameter IF containing many coiled-coil dimer subunits per cross-section is surprising since the persistence length of a single coiled-coil dimer such as tropomyosin is itself approximately 100 nm. [20]. The thinner, semiflexible F-actin is an order of magnitude stiffer than IFs and has a persistence length ranging from 3–17 um [21], which is comparable to the typical filament length. Microtubules are considered as stiff polymers with l_p > 1mm [21].

Compared to IFs, MTs and F-actin are relatively brittle filaments and rupture under elongational strains less than approximately 10%. Intermediate filaments, in contrast, can bear much larger extensional strain than MTs and F-actin. Several types of intermediate filaments have been stretched to over 200% of their resting length without breaking [9, 22]. This large extensibility is attributed to the hierarchical structure of IFs that allows partial unfolding of subunits without breakage of the filament.

4 Polyelectrolyte properties - counterion crosslinking

All three cytoskeletal filaments are strong polyelectrolytes with anionic surface charge density as shown in Figure 3 similar to that of double stranded DNA (~1 e/nm²). Polyelectrolyte properties appear to be especially important for neurofilaments (NFs), which in addition to having the largest surface charge density also have long unstructured polypeptide domains (sidearms) that extend away from the neurofilament surfaces. In many respects NFs resemble brush polymers, and the combination of steric and electrostatic repulsions between sidearm affects both single NFs and NF networks in a manner that depends on the ionic composition of the solution [19, 23**].

Figure 3. Surface charge density of cytoskeletal filaments.

The charge density of F-actin, microtubules and two types of IFs Surface charge density was calculated from the amino acid sequence for the human variants of these proteins derived from GenBank without regard to post-translational modifications, except for actin, where amino acid processing and binding of charged ligands contribute a significant amount of charge to the protein. The charge per length of IFs is calculated from the amino acid sequence of IF subunits before post-translational modifications and the assumptions that all IFs contain 32 monomers in the cross-section of a 10 nm cylindrical filament . The molar ratio of neurofilament triplet proteins is taken as NFH:NFM:NFL = 1:2:6. The value for actin is for post-translationally modified beta-actin, the most prominent non-muscle cytoplasmic actin isoform assuming 370 monomers per micron of 8 nm filament and that each monomer binds 1 Mg²⁺ and 1 ADP^3-. Microtubule charge assumes 1625 tubulin dimers per micron of 25 nm diameter MT, with each dimer binding 2 Mg²⁺ and 2 GDP^3-. The calculated charge per length of the filament was divided by the diameter of each filament type.

Surface charge effects also enable crosslinking of IFs networks by divalent metal ions. Mg²⁺ and Al³⁺ have been well characterized as effective crosslinkers of NFs [24], and recent studies expand the range of divalent ions and IF types to show that divalent metal ions in general can act as effective crosslinkers within IF gels [25*–27].

5. Elasticity of semiflexible polymer networks

Compared to flexible polymer networks which are generally well modeled by classic rubber elasticity theory, semiflexible polymer gels exhibit novel mechanical properties due to their finite filament stiffness and often very low volume fraction.

5.1. Frequency dependence

The elasticity of semiflexible polymer networks is dominated by the dynamics of individual network filament and is frequency dependent. Two distinct regimes can be observed in the frequency dependence of the shear storage modulus, G’, for crosslinked cytoskeletal polymer networks. At time scales typically ranging a few decades below and above 1 s, a plateau region is observed in which G’ is nearly independent of frequency or scales with a very low fractional exponent, typically on the order of 0.1, determined mainly by the network architecture, filament density and crosslinker density. At high frequencies, G’ shows a different power law dependence on frequency with a scaling exponent of 0.75, reflecting the high-frequency the behavior of single polymers [28].

5.2. Strain stiffening

Semiflexible polymer networks show nonlinear elasticity at medium strain levels in the form of strain stiffening, i.e. the elastic moduli of these gels become larger at larger strains. A broad spectrum of biopolymers including F-actin and several intermediate filament types form gels with increased elastic moduli at larger deformations [18, 26, 28–30*]. The origin of strain stiffening in networks of semi-flexible or rod-like polymers has been addressed by several recent theories. When the persistence length of the filament is comparable to the mesh size or distance between cross-links within the network, the strain stiffening emerges from an entropic model that considers how thermal fluctuations of semiflexible polymers are constrained as the end-to-end distance of filament segments between crosslinks changes when the sample is deformed [29, 31*, 32] (Figure 2A). Networks formed by much stiffer and thicker fibers, such as actin bundles, also exhibit strain stiffening, but the degree of strain stiffening appears to be less than that of the intermediate filaments, and thermal motions of these stiffer fibers would appear not to play a significant role in their response. In these cases strain-stiffening depends on alignment of fibers in the strain direction and a shift from soft bending modes to stiffer stretching modes as the fibers reorient [33*–36]. Filament alignment and changes in crosslinking can also contribute to network stiffening under strain as shown in Figure 2B [37]. Generation of internal stress by activation of motor proteins within crosslinked network can further contribute to stiffening (Figure 2C) [38**]. In stressed networks Brownian dynamics simulations show that the elasticity of crosslinked actin networks shifts from entropic at low internal stress and low crosslink density to enthalpic at high prestress and higher crosslink density [39] so in real systems a mixture of all these effects is likely to determine cytoskeletal rheology.

Figure 2. Effect of actin binding proteins and molecular motors on rheological properties of cytoskeletal networks.

(A) Strain stiffening in isotropic semiflexible polymer networks (adapted from [45] ) due to the nonlinear force extension of individual filaments. (B) Flexible cross-linkers in the actin network lead to strain stiffening of the network (adapted from [37]). (C) Myosin motors in the crosslinked actin network generate internal tension that stiffen the network (adapted from [25]).

5.3. Strain softening and dissipation

At large stresses, cytoskeletal polymer networks show strain softening. Although breaking of individual polymer strands can lead to network failure, recent work with actin and IF networks shows that the stress – induced unbinding of crosslinkers also leads to network softening [40–42]. Crosslinker unbinding, either due to the external force or due to the kinetics of transient crosslinking, allows actin filaments to locally rearrange and leads to dissipation of energy [41, 43]. Once the local stress is relaxed, the crosslinker can rebind to the filaments and network elasticity can recover [40*,41*,42*].

5.4. Negative normal stress

Another novel feature of semiflexible network rheology is that a pure shear deformation causes the network to shrink in the direction perpendicular to the direction of shear stress. The internal stress leading to such a shrinkage is called a negative normal stress, which tends to pull the surfaces under shear toward each other (Figure 2A). When cross-linked networks of F-actin, IFs, or other biopolymers are sheared, the stress directed orthogonal to the strain direction increases quadratically with shear strain and can have a magnitude close to that of the shear stress [44]. Flexible polymer gels generally have negligible normal stress, and at high strains exhibit a positive normal stress that is much smaller than the shear stress. Thermal model for semi-flexible filaments account for negative normal stress by the force-displacement relation for single filaments for which less force is needed to compress such a filament than to stretch it [44, 45] (Figure 2A). Non-thermal models of stiff filaments also predict negative normal stress, because compressed filaments can buckle and so reduce upward forces relative to the increased downward forces produced by stretched filaments [46*]. Some models predict that the normal stresses can be even greater than shear stresses under some conditions [33].

6. Rheological properties of cells compared to those of polymer networks

Cells exhibit frequency dependent linear viscoelastic moduli with scaling exponents characteristic of stress relaxation in semiflexible polymer networks [18, 28, 47, 48]. This correspondence suggests that actin, microtubules, and intermediate filaments dominate the viscoelastic response of cells. It is worth noting that under physiological conditions, cells are subject to highly nonlinear strains of both externally and internally generated origins. Comparing the mechanical properties of actin gels with and without myosin motors shows that the ATP dependent myosin motor activity not only affects the frequency response of the linear viscoelastic moduli, but also generates internal tension to stiffen the actin network [38**, 49, 50]. The assumption that cell mechanics in vivo can be inferred from its linear viscoelastic properties, as in simple materials, is thus called into question.

Some studies have also shown that cells exhibit strain stiffening in response to stress or deformation. The precise origin of the strain stiffening response of cells is not fully understood. In addition to orientation, alignment, and the pulling out of entropic fluctuations of the cytoskeleton filaments under shear, it may also reflect important contributions from pre-stress due to active elements such as molecular motors [38**, 50–52]. Interestingly, the flexible cross-linkers can also contribute to network strain stiffening. At low strains, elastic modulus of the network is dominated by the contribution from stretching the flexible cross-linkers. The nonlinear force extension curve of flexible cross-linkers, which are modeled as worm-like chains, gives rise to the non-linear elasticity for actin networks linked by soft cross-linkers [25, 37, 53].

7. Conclusion

Rheological behavior of cells shares characteristics of nearly every class of semiflexible polymers reviewed here. However, viewed as a polymer network, the cell is arguably the most challenging to characterize and interpret of all semiflexible polymer networks. The complexity arises in large part from the fact that there are a variety of load-bearing elements and heterogeneous substructures inside cells. These elements and structures are coupled mechanically through both passive (mechanical) and active (ATP-dependent) processes and have multiple timescales of response. Additionally, most cells contain endogenous molecular force sensors that trigger biochemical signaling pathways, which can actively modulate cellular stiffness in response to shear forces with specific characteristics, a process known as mechanosensing. From the polymer physics point of view, the cell is therefore an active, exotic, and hierarchically-structured polymer network.

Highlights.

• Cytoskeletal polymers have unique rheology that depends on filament stiffness

• Cytoskeletal gels stiffen at moderate strain and reversibly soften at high strain

• Motor proteins strongly alter cytoskeletal network and cell viscoelasticity