Risk Prediction for Prostate Cancer Recurrence Through Regularized Estimation with Simultaneous Adjustment for Nonlinear Clinical Effects

Abstract

In biomedical studies, it is of substantial interest to develop risk prediction scores using high-dimensional data such as gene expression data for clinical endpoints that are subject to censoring. In the presence of well-established clinical risk factors, investigators often prefer a procedure that also adjusts for these clinical variables. While accelerated failure time (AFT) models are a useful tool for the analysis of censored outcome data, it assumes that covariate effects on the logarithm of time-to-event are linear, which is often unrealistic in practice. We propose to build risk prediction scores through regularized rank estimation in partly linear AFT models, where high-dimensional data such as gene expression data are modeled linearly and important clinical variables are modeled nonlinearly using penalized regression splines. We show through simulation studies that our model has better operating characteristics compared to several existing models. In particular, we show that there is a non-negligible effect on prediction as well as feature selection when nonlinear clinical effects are misspecified as linear. This work is motivated by a recent prostate cancer study, where investigators collected gene expression data along with established prognostic clinical variables and the primary endpoint is time to prostate cancer recurrence. We analyzed the prostate cancer data and evaluated prediction performance of several models based on the extended c statistic for censored data, showing that 1) the relationship between the clinical variable, prostate specific antigen, and the prostate cancer recurrence is likely nonlinear, i.e., the time to recurrence decreases as PSA increases and it starts to level off when PSA becomes greater than 11; 2) correct specification of this nonlinear effect improves performance in prediction and feature selection; and 3) addition of gene expression data does not seem to further improve the performance of the resultant risk prediction scores.

1. Introduction

In biomedical research, it is of substantial interest to build prediction scores for risk of a disease using high-dimensional biomarker data such as gene expression data for clinical endpoints subject to censoring, e.g., time to the development or recurrence of a disease. This process typically involves a feature selection step, which identifies important biomarkers that are predictive of the risk. When some clinical variables have been established as the risk factors of a disease, it is preferred to use a feature selection procedure that also accounts for these clinical variables. Using observed data with censored outcomes, our goal is to build risk prediction scores using high-dimensional data through feature selection while simultaneously adjusting for effects of clinical variables that are potentially nonlinear.

1.1. A Prostate Cancer Study

This article is motivated by a prostate cancer study. An important challenge in prostate cancer research is to develop effective predictors of future tumor recurrence following surgery in order to determine whether immediate adjuvant therapy is warranted. Thus, biomarkers that could predict the likelihood of success for surgical therapies would be of great clinical significance. In this study, each patient underwent radical prostatectomy following a diagnosis of prostate cancer, and their radical prostatectomy specimens were collected immediately after the surgery and subsequently formalin-fixed and paraffin-embedded (FFPE). More recently, the investigators isolated RNA samples from these specimens and performed DASL (cDNA-mediated Annealing, Selection, extension and Ligation) expression profiling on these RNA samples using a custom-designed panel of 1536 probes for 522 prostate cancer relevant genes. The DASL assay is a novel expression profiling platform based upon massively multiplexed real-time polymerase chain reaction applied in a microarray format, and more importantly, it allows quantitative analysis of RNA from FFPE samples whereas traditional microarrays do not (Bibikova et al., 2004; Abramovitz et al., 2008). In addition, important clinical variables were also collected, two of which, prostate specific antigen (PSA) and total gleason score, are known to be associated with prostate cancer risk and prognosis and are of particular interest. The primary clinical endpoint in this study is time to prostate cancer recurrence. The research questions of interest include 1) identifying important probes that are predictive of the recurrence of prostate cancer after adjusting for important clinical variables; 2) constructing and evaluating risk prediction scores; and 3) determining whether the inclusion of the gene expression data improves the prediction performance. It was also suspected that PSA may have a nonlinear effect on the clinical endpoint. In this article, we will develop and apply a new statistical model, which allows us to answer these questions.

1.2. Feature Selection and Prediction in AFT

The accelerated failure time (AFT) model is an important tool for the analysis of censored outcome data (Cox and Oakes, 1984; Kalbfleisch and Prentice, 2002). Compared to the more popular proportional hazard (PH) model (Cox, 1972), the AFT model is, as suggested by Sir David Cox (Reid, 1994), “in many ways more appealing because of its quite direct physical interpretation,” especially when the response variable is not related to survival time. Furthermore, when prediction is of primary interest, the AFT model is arguably more attractive, since it models the mean of the log-transformed outcome variable whereas the Cox PH model estimates the hazard functions.

Classic AFT models assume that the covariate effects on the logarithm of the time-to-event are linear, in which case one could use standard rank-based techniques for estimation and inference (Tsiatis, 1990; Ying, 1993; Jin et al., 2003) and perform a lasso-type (Tibshirani, 1996) variable selection (Johnson, 2008; Cai, Huang and Tian, 2009). Regarding existing variable selection and prediction procedures, there are two unsatisfying products. First, the linearity assumption may not hold in real data. For example, Kattan (2003a) showed that relaxing the linearity assumption of the Cox PH model improved predictive accuracy in the setting of predicting prostate cancer recurrence with low-dimensional data. Second, an unsupervised implementation of the regularized variable selection procedure can inadvertently remove clinical variables that are known to be scientifically relevant and can be measured easily in practice. We will address both concerns in our extensions of AFT models.

1.3. Partly Linear Models

It has been well established that linear regression models are insufficient in many applications and it is more desirable to allow for more general covariate effects. Nonlinear modeling of covariate effects is less restrictive than the linear modeling approach and thus is less likely to distort the underlying relationship between an outcome and covariates. However, new challenges arise when including nonlinear covariate effects in regression models. In particular, nonparametric regression methods encounter the so-called “curse of dimensionality” problem, i.e., the convergence rate of the resulting estimator decreases as the dimension of the covariates increases (Stone, 1980), which is further exacerbated when the dimension of the covariates is high. The partly linear model of Engle et al. (1986); Härdle, Liang and Gao (2000); Ruppert, Wand and Carroll (2003) provides a useful compromise to model the effect of some covariates nonlinearly and the rest linearly. Specifically, for the i-th subject, let T_i be a univariate endpoint of interest for the i-th subject, and ${\mathbf{\text{Z}}}_i={(Z_i^{(1)},\dots ,Z_i^{(d)})}^{\text{T}}(d\times 1)$ and ${\mathbf{\text{X}}}_i={(X_i^{(1)},\dots ,X_i^{(q)})}^{\text{T}}(q\times 1)$ denote high-dimensional features of interest (say gene expression levels) and established clinical variables, respectively. Then one partly linear model of interest is

$${\mathit{\text{T}}}_i=\varphi ({\mathbf{\text{X}}}_i)+{\vartheta }^{\text{T}}{\mathbf{\text{Z}}}_i+{\varepsilon }_i,$$ (1)

where ϑ = (ϑ₁, …, ϑ_d)^T is a parameter vector of interest, φ is an unspecified function, and the errors (ε_i) are independently and identically distributed (i.i.d.) and follow an arbitrary distribution function F_ε. Special cases of this model have been used in varied applications across many disciplines including econometrics, engineering, biostatistics, and epidemiology (Härdle, Liang and Gao, 2000). In this article, we consider Model (1) for T_i subject to right-censoring, and hence the observed data are ${\{({\stackrel{\sim }{\mathit{\text{T}}}}_i,{\delta }_i,{\mathbf{\text{Z}}}_i,{\mathbf{\text{X}}}_i)\}}_{i=1}^n$, where T̃_i = min(T_i, C_i), δ_i = I(T_i ≤ C_i), and C_i is a random censoring event. We note that T_i is the log-transformed survival time in survival analysis, and we refer to Model (1) as partly linear AFT models.

In the absence of censoring, the nonparametric function φ in Model (1) can be estimated using kernel methods (Härdle, Liang and Gao, 2000) (references therein) and smoothing spline methods (Engle et al., 1986; Heckman, 1986). For partly linear AFT models, one can extend the basic weighting scheme of Koul, Susarla and van Ryzin (1981), where one treats censoring like other missing data problems (Tsiatis, 2006) and inversely weights the uncensored observations by the probability of being uncensored, i.e. so-called inverse-probability weighted (IPW) estimators. A close cousin to the IPW methodology is censoring unbiased transformations (Fan and Gijbels, 1996) (ch. 5 and references therein), which effectively replaces a censored outcome with a suitable surrogate before complete-data estimation procedures are applied. Both IPW kernel-type estimators and censoring unbiased transformations in the partly linear model have been studied for AFT models (Liang and Zhou, 1998; Wang and Li, 2002). Since both aforementioned approaches make stronger assumptions than rank estimation of AFT models (Cai, Huang and Tian, 2009), we focus on extending rank estimation to meet our needs.

We here consider a general penalized loss function for partly linear AFT models

$$\underset{\vartheta ,\varphi \in \Phi }{min}{ℒ}_n(\varphi ,\vartheta )+\gamma J(\varphi ),$$ (2)

where ℒ_n is the loss function for observed data and J(φ) imposes some type of penalty on the complexity of φ. Our approach is to replace ℒ_n with the Gehan (1965) loss function (Jin et al., 2003) and model φ using penalized regression splines; our focus is to build risk prediction scores. To minimize the penalized loss function (2), the insight into the optimization procedure is due, in part, to Koenker, Ng and Portnoy (1994), who noted that the optimization problem in quantile smoothing splines can be solved by L₁-type linear programming techniques and proposed an interior point algorithm for the problem. Li, Liu and Zhu (2007) built on this idea to propose an entirely different path-finding algorithm for more general nonparametric quantile regression models. Along similar lines, when J(φ) is taken as a L₁ norm as in penalized regression splines (Ruppert and Carroll, 1997), the optimization problem of (2) is essentially an L₁ loss plus L₁ penalty problem, and can also be solved by L₁-type linear programming techniques, which will be exploited in our approach to the optimization problem. Once the basic spline framework is adopted, we show that our estimator can be generalized through additive models for q > 1 and variable selection in the linear component. The additive structure of nonlinear components (Hastie and Tibshirani, 1990) is adopted to further alleviate the issue of curse of dimensionality. To the best of our knowledge, there is no similar work in the partly linear or partly additive model for censored or uncensored data using Cox or AFT models, and we are the first to conduct systematic investigation on the impact of mis-specified nonlinear effects on prediction and feature selection using AFT models for high-dimensional data.

More recently, Chen, Shen and Ying (2005) proposed stratified rank estimation for Model (1) and Johnson (2009) proposed a regularized extension. However, their stratified methods are fundamentally different from ours in several aspects. First and foremost, the stratified estimators do not provide an estimate of the nonlinear effect of the stratifying variable, namely, φ̂(X), and hence the lasso extension proposed by Johnson (2009) focused on variable selection only. It is evident that φ̂(X) plays an important role in prediction; since the stratified estimators in Johnson (2009) can only use ϑ̂^TZ for prediction, their performance suffers, which will be shown in our numerical studies. By contrast, our approach provides an estimate of φ(X), which in turn can be used to improve prediction performance. Second, the numerical algorithm proposed in Johnson (2009) can only handle the case of d < n and their numerical studies are limited to such cases, whereas we here investigate the high-dimensional settings with d > n. Third, as will be shown in our numerical results, our proposed method outperforms the stratified estimators in feature selection as well.

The rest of the article is organized as follows. In Section 2, we present the details of the methodology. In Section 3, we investigate the operation characteristics of the proposed approach through simulation studies. In Section 4, we analyze the prostate cancer study and provide answers to the research questions of interest. We conclude this article with some discussion remarks in Section 5.

2. Methodology

2.1. Regression Splines in Partly Linear AFT model

We first consider a simplified case for the partly linear AFT model (1), where X_i is assumed to be univariate, i.e. q = 1 and X_i ≡ X_i, and then Model (1) reduces to

$${\mathit{\text{T}}}_i=\varphi (X_i)+{\vartheta }^{\text{T}}{\mathbf{\text{Z}}}_i+{\varepsilon }_i.$$ (3)

Let 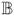(x) = {B₁(x), …, B_M(x)}^T (M ≤ n) be a set of basis functions. We use a regression spline model for φ(·), which asserts that φ(x) = 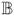(x)^Tβ, for some. β ∈ ℜ^M. Popular bases include B-splines, natural splines, and truncated power series basis (Ruppert, Wand and Carroll, 2003). As explained in Section 2.2, we will use the truncated power series basis of degree p without the intercept term, i.e., $\mathbb{\text{B}}(x)={\{x,\dots ,x^p,{(x-{\kappa }_1)}_{+}^p,\dots ,{(x-{\kappa }_r)}_{+}^p\}}^{\text{T}}$, where (κ₁,…, κ_r) denotes a set of r knots, and (u)₊ = uI(u ≥ 0). Hence, M = p + r. Throughout, we use equally spaced percentiles as knots and set p = 3, i.e., the cubic splines, unless otherwise noted. Let θ ≡ (β, ϑ) denote the parameters of interest. Then, define θ̂_RS ≡ (β̂,ϑ̂)= argmin_β,ϑℒ_n(β, ϑ), where

$${ℒ}_n(\beta ,\vartheta )=n^{-2}\sum _{i=1}^n\sum _{j=1}^n{\delta }_i{(e_i-e_j)}_{-},$$ (4)

with e_i = T̃_i−β^T 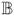(X_i) − ϑ^TZ_i and c₋ = max(0, −c). Because Model (3) has been “linearized”, we can apply existing rank-based estimation techniques for the usual linear AFT models. In particular, Jin et al. (2003) noted that the minimizer of ℒ_n(β, ϑ) is also the minimizer of

$$\sum _{i=1}^n\sum _{j=1}^n{\delta }_i\left|e_i-e_j\right|+\left|\zeta -({\beta }^{\text{T}},{\vartheta }^{\text{T}})\sum _{k=1}^n\sum _{l=1}^n{\delta }_k{D}_{lk}\right|,$$

for a large constant ζ, where $D_{lk}={\{\mathbb{\text{B}}{(X_l)}^{\text{T}},{\mathbf{\text{Z}}}_l^{\text{T}}\}}^{\text{T}}-{\{\mathbb{\text{B}}{(X_k)}^{\text{T}},{\mathbf{\text{Z}}}_k^{\text{T}}\}}^{\text{T}}$. Evidently, the minimizer of this new loss function may be viewed as the solution to a L₁ regression of a pseudo response vector V = (V₁, …, V_S)^T (S × 1) on a pseudo design matrix W = (W₁, …, W_S)^T (S × (M + d)). It can be readily shown that V is of the form {δ_i(T̃_i − T̃_j), …, ζ}^T and W is of the form ${\left({\delta }_i{D}_{ij},\dots ,{\sum }_{k=1}^n{\sum }_{l=1}^n{\delta }_k{D}_{lk}\right)}^{\text{T}}$, where δ_i(T̃_i − T̃_j) and ${\delta }_i{D}_{ij}^{\text{T}}$ go through all i and j with δ_i = 1, and hence S denotes the number of pseudo observations in V. Consequently, we have

$${\hat{\theta }}_{\text{RS}}={\text{argmin}}_{\beta ,\vartheta }\sum _{s=1}^S\left|V_s-{\theta }^{\text{T}}{\mathbf{\text{W}}}_s\right|.$$ (5)

The fact that θ̂_RScan be written as the L₁ regression estimate facilitates the numerical techniques, which will be used for our subsequent estimators.

2.2. Penalized Regression Splines in Partly Linear AFT Models

When regression splines are used to model nonlinear covariates effects, it is crucial to choose the optimal number and location of knots (κ₁, …, κ_r). It is well known that too many knots may lead to overfitting whereas too few may not be sufficient to capture non-linear effects (Ruppert, Wand and Carroll, 2003). The penalized regression spline regression approach (Eilers and Marx, 1996; Ruppert and Carroll, 1997; Li and Ruppert, 2008; Claeskens, Krivoboko and Opsomer, 2009) handles this problem by starting with a very large number of knots and applying regularization to avoid overfitting. In addition, a penalized regression spline with L₁ penalty corresponds to a Bayesian model with double exponential or Laplace priors and is known to be able to accommodate large jumps when using the truncated polynomial basis functions (Ruppert and Carroll, 1997). While the truncated power series basis is often used for penalized regression spline (Ruppert and Carroll, 1997), one can use other bases such as B-splines basis in penalized regression spline models and the results should not differ as long as two sets of bases span the same space of functions (Li and Ruppert, 2008). We adopt the L₁ penalty and consider the penalized regression spline estimator

$${\widehat{\theta }}_{\text{PRS}}(\gamma )={\text{argmin}}_{\beta ,\vartheta }\left\{{ℒ}_n(\beta ,\vartheta )+\gamma \sum _{m=p+1}^M\left|{\beta }_m\right|\right\},$$ (6)

referred to as the partly linear AFT estimator, where γ is a regularization parameter and is used to achieve the goal of knot selection. Using the L₁ loss function in (5) and a data augmentation technique for regularized L₁ regression, θ_PRS(γ) may be found easily for a given γ. Namely, define $\mathbf{\text{V}}\ast ={({\mathbf{\text{V}}}^{\text{T}},0_r^{\text{T}})}^{\text{T}}$, W* = [W^T,(0_r×p, D_r, 0_r×d)^T]^T, and D_r = γI_r, where 0_r is a r-vector of zeros, 0_r×p (0_r×d) is a r × p (r × d) matrix of zeros and I_r an r-dimensional identity matrix. Then, θ̂_PRS(γ) is found through the L₁ regression of V* on W*. γ can be selected through cross validation or generalized cross validation (Ruppert, Wand and Carroll, 2003).

2.3. Variable Selection and Prediction in Partly Linear AFT Models

Finally, we consider variable selection for the high-dimensional features (Z) in the partly linear AFT model (3) by extending the penalized regression spline estimator θ̂_PRS(γ). Let λ be another regularization parameter and consider the minimizer to the L₁ regularized loss function

$${\widehat{\theta }}_{\text{PRS}(1)}(\gamma ,\lambda )={\text{argmin}}_{\beta ,\vartheta }\left\{{ℒ}_n(\beta ,\vartheta )+\gamma \sum _{m=p+1}^M\left|{\beta }_m\right|+\lambda \sum _{j=1}^d\left|{\vartheta }_j\right|\right\}.$$ (7)

which is also referred to as the lasso partly linear AFT model estimator. The data augmentation scheme used in Section 2.2 applies to the regularized estimator in (7) as well. Define the pseudo response vector ${\mathbf{\text{V}}}^{†}={({\mathbf{\text{V}}}^{\text{T}},0_{r+d}^{\text{T}})}^{\text{T}}$ and the pseudo design matrix

$${\mathbf{\text{W}}}^{†}={\left[{\mathbf{\text{W}}}^{\text{T}},{\left(\begin{array}{ccc}{0}_{r\times p}& \gamma I_r& 0_{r\times d}\\ 0_{d\times p}& 0_{d\times r}& \text{diag}({\lambda }_1,\dots ,{\lambda }_d)\end{array}\right)}^{\text{T}}\right]}^{\text{T}}.$$

For fixed γ and λ, the estimate is computed as the L₁ regression estimate of V^† on W^†. To select γ and λ, we can use two approaches, namely the cross validation (CV) and generalized cross validation (GCV) (Tibshirani, 1997; Cai, Huang and Tian, 2009). The K–fold CV approach chooses the values of γ and λ that maximize the Gehan loss function (4). The GCV approach chooses the values of γ and λ that maximize the criteria, ℒ_n(β, ϑ)/(1 − d_γ, λ/n)², where n is the number of observations and d_γ,λ is the number of nonzero estimated coefficients for the basis functions ( (X)) and linear predictors (Z), i.e., the number of nonzero estimates in (β̂, ϑ̂). Note that d_γ,λ depends on γ and λ. Once θ_PRS(1) is obtained, one can build prediction scores as φ̂(X) + ϑ̂^TZ.

2.4. Extension to Additive Partly Linear AFT Models

When X_i is of q-dimension (q > 1) in the partly linear model (1), estimation is more difficult due to the issue of curse of dimensionality, even when q is moderately large and in the absence of censoring. For our partly linear AFT model, we propose to use an additive structure for φ to further alleviate the problem, namely an additive partly linear AFT model,

$$T_i=\sum _{j=1}^q{\varphi }_j(X_i^{(j)})+{\vartheta }^{\text{T}}{\mathbf{\text{Z}}}_i+{\varepsilon }_i,$$ (8)

where φ_j's (j = 1, …, q) are unknown functions. Similar to what is discussed in Section 2.2, penalized regression splines can be used for the additive partly linear model to conduct knot selection for each nonlinear effect, ${\varphi }_j(X_i^{(j)})(j=1,\dots ,q)$. The variable selection for Z as discussed in Section 2.3 can also be extended to this additive partly linear AFT model. When q is large and it is also of interest to conduct feature selection among q additive nonlinear effects, one can modify the regularization term for β in the loss function (6) and (7); specifically one can regularize all β, i.e., $\gamma {\sum }_{m=1}^M\left|{\beta }_m\right|$, as opposed to regularizing only the terms that correspond to the set of jumps in the pth derivative, i.e., $\gamma {\sum }_{m=p+1}^M\left|{\beta }_m\right|$. Similarly, we can modify the data augmentation scheme to obtain the parameter estimates for these models.

2.5. Numerical Implementation For High-dimensional Data

In Section 2.1-2.4, the parameters are estimated using L₁ regression models through a data augmentation scheme such as (5), which can be readily implemented using the quantreg package in R. While this algorithm works well when the total number of parameters is small relative to the sample size, it becomes very slow and starts to fail as the number of parameters gets close to or greater than the effective sample size after accounting for censoring. As an alternative, we extended a numerical algorithm developed for efficient computation of rank estimates for AFT models (Conrad and Johnson, 2010) to compute the proposed estimators, in particular, the estimator in (7). In essence, this method approximates a L₁ regularized loss function with a smooth function and subsequently optimizes the smoothed objective function using a Limited-Broyden-Fletcher-Goldfarb-Shanno (L-BFGS) algorithm (Nocedal and Wright, 2006), which is implemented in Matlab. This method speeds up the computation substantially and can handle the case of high-dimensional data. We have compared these two algorithms and they give very similar results when both are applicable, i.e., Z is of low dimension.

3. Simulation Studies

We conducted extensive simulation studies to evaluate the operating characteristics of the proposed models including estimation, feature selection and most importantly prediction, in comparison with several existing models.

3.1. Estimation

We considered a case of single Z_i and single X_i, i.e., Model (3), and focused on the estimation of the regression coefficient ϑ and its sampling variance. In this setup, no feature selection is involved. To facilitate comparisons, our simulation study details were adapted from those given by Chen, Shen and Ying (2005) and Johnson (2009). The random variable Z_i was generated from a standard normal distribution, and X_i was generated through X_i = 0.25Z_i + U_i, where U_i follows a uniform distribution Un(−5, 5) and completely independent of all other random variables. In Model (3), we let ϑ = 1 and ε_i ∼ N(0, 1) and mutually independent of (X_i, Z_i). We considered linear and quadratic effects, i.e., φ(X_i) = 2X_i and $\varphi (X_i)=X_i^2$, respectively. Finally, censoring random variables were simulated through $C_i=\varphi (X_i)+Z_i\vartheta +U_i^{\ast }$, where $U_i^{\ast }$ follows Un(0, 1). As a result, the proportion of censored outcomes ranges from 20% to 30%. We compared several estimators, the partly linear AFT model (PL-AFT) with r knots (r = 2 and 4), which was fit using the loss function (6), the stratified estimator in Chen, Shen and Ying (2005) (S_K-AFT) where K denotes the number of strata, the standard linear AFT model with both X_i and Z_i modeled linearly (AFT), and an AFT model with true φ plugged in (AFT-φ). Two sample sizes were used, n = 50 and n = 100.

Our simulation results show that the CV and GCV methods give similar results, so we report only the results using GCV. Table 1 summarizes the mean bias, standard deviation (SD) and mean squared error (MSE) of ϑ̂ over 200 Monte Carlo data sets, and it also provides the range of standard errors for the performance measure in each column, where all numbers are multiplied by 1000. In all cases, the proposed partly linear AFT estimator outperforms the stratified estimators as well as the standard AFT estimator in terms of MSE, and its performance is comparable to that of the estimator using the true φ. The number of knots has little impact on the performance of our proposed estimator. The standard linear AFT estimator exhibits the largest bias and MSE when φ is not linear, indicating that it is important to adjust for the nonlinear effect of X even when one is only interested in the effect of Z. While the stratification step in the S_K-AFT method results in reduced bias when the number of strata is large, it has larger SD and MSE compared to PL-AFT. Furthermore, in the settings of our interest, no method has been proposed for choosing K in the S_K-AFT method, which is not obvious either, leading to a further shortcoming of this method over the others.

Table 1.

Simulation results for parameter estimation (ϑ̂) based on 200 Monte Carlo data sets, where ϑ = 1. PL-AFT, partly linear AFT model with r knots; S_K-AFT, stratified AFT estimator with K strata; AFT, standard linear AFT model with both X_i and Z_i modeled linearly; and AFT-φ, AFT model with true φ plugged in. Range of SEs, the range of SEs for the corresponding performance measure in each column. NA, SE of a performance measure can not be computed for SD. All numbers are multiplied by 1000.

	φ(X) = 2X			φ(X) = 2X2
	Bias	SD	MSE	Bias	SD	MSE
	n = 50
PL-AFT (r = 2)	-12	159	25	-2	166	28
PL-AFT (r = 4)	-10	159	25	-1	168	28
S5-AFT	95	288	92	-65	436	195
S10-AFT	28	223	50	-43	299	91
S25-AFT	31	303	93	-38	381	146
AFT	-4	153	23	21	1214	1475
AFT-φ	-7	154	24	-5	158	25
	n = 100
PL-AFT (r = 2)	-9	113	13	-2	115	13
PL-AFT (r = 4)	-9	113	13	-1	115	13
S10-AFT	44	163	29	-23	210	45
S25-AFT	1	157	25	-9	185	34
S50-AFT	-7	193	37	8	209	44
AFT	-8	113	13	71	755	575
AFT-φ	-9	113	13	-2	111	12
Range of SEs	8-21	NA	1-12	8-86	NA	1-209

3.2. Feature Selection

In our second set of simulation studies, we focused on simultaneous estimation and feature selection for Z_i as well as prediction. The regression function still consisted of a nonlinear effect of a single covariate X_i, but we increased the dimension of the linear predictors (Z_i) to d = 8. Z_i were generated from a multivariate normal with a mean equal to 0_d and (j, k)th element of the covariance matrix equal to ρ^|j−k| (ρ = 0, 0.5, 0.9). The covariate Xi was generated through X_i = 0.5Z_1i + 0.5Z_2i + 0.5Z_3i + U_i, where U_i is Un(−1, 1) and independent of all other random variables. This corresponds to a case where Z₁ and Z₂ have both direct and indirect effect through X on the outcome whereas Z₃ has only an indirect effect on the outcome. The true regression coefficients for Z are set to ϑ = (Δ, Δ, 0, 0, 0, Δ, 0, 0)′, where Δ = 1 and 0.5 represent a strong signal (effect size) and a weak signal (effect size), respectively. In this case, the three important covariates (namely, Z₁, Z₂, and Z₆) can potentially be highly correlated. The effect of X_i was generated from $\varphi (X_i)=({0.2}_{\ast }{X}_i+{0.5}_{\ast }{X}_i^2+{0.15}_{\ast }{X}_i^3)I(X_i>=0)+({0.05}_{\ast }{X}_i)I(X_i<0)$, where I(·) is the indicator function. This setup mimics a practical setting where the effect of the clinical variable (X) on the outcome is ignorable when X is less than a threshold level (X = 0); but as X increases past the threshold level, its effect becomes appreciable. The log survival time T_i was then generated using Equation (3), where ε_i follows N(0, 1) and is mutually independent of (X_i, Z_i). The censoring random variable was simulated according to the rule, $C_i=\varphi \left(X_i\right)+{\vartheta }^{\text{T}}{\mathbf{\text{Z}}}_i+U_i^{\ast }$, where $U_i^{\ast }$, follows the uniform distribution Un(0, 6). The resulting proportion of censoring ranges from 20% to 30%.

We compared six models: (1) the lasso partly linear AFT model (Lasso-PL) with r = 6 which was fit using the loss function (7); (2) the lasso stratified model (Lasso-S_K) (Johnson, 2009) where K denotes the number of strata; (3) the lasso linear AFT model assuming a linear effect for both X_i and Z_i (Lasso-L); (4) the standard linear AFT model (AFT); (5) the lasso linear Cox PH model assuming a linear effect for both X_i and Z_i (Lasso-Cox) (Tibshirani, 1997; Goeman, 2010); and (6) the so-called oracle partly linear model (Oracle) with ϑ₃, ϑ₄, ϑ₅, ϑ₇ and ϑ₈ fixed at 0 and r = 6 for the penalized splines. We are not aware of any existing Cox PH model that can handle both nonlinear covariate effects and feature selection in high-dimensional data. Since the data were generated under a true AFT model and the PH assumption underlying the Cox model is violated, we are primarily interested in feature selection when comparing the Lasso-Cox model. The oracle model, while unavailable in practice, may serve as an optimal bench mark for the purpose of comparisons. In each instance of regularized methods, GCV was used to tune the regularization parameters, λ and/or γ.

In each simulation run, a training sample of size n = 125 and a testing sample of size 10n were generated. To evaluate parameter estimation, we monitored the sum of squared errors (SSE) for ϑ̂ defined as (ϑ̂ − ϑ)^T(ϑ̂ − ϑ). To evaluate feature selection, we monitor the proportion of zero coefficients being set to zero $(P_C\equiv {\sum }_{i=1}^{d}I({\widehat{\vartheta }}_i=0)I({\vartheta }_i=0)/{\sum }_{i=1}^{d}I({\vartheta }_i=0))$, for which 1 is the optimal value, and the proportion of nonzero coefficients being set to zero $(P_I\equiv {\sum }_{i=1}^{d}I({\widehat{\vartheta }}_i=0)I({\vartheta }_i\ne 0)/{\sum }_{i=1}^{d}I({\vartheta }_i\ne 0))$, for which 0 is the optimal value. To assess the prediction performance, we considered two mean squared prediction errors, ${\text{MSPE}}_1\equiv {(10n)}^{-1}{\sum }_{j=1}^{10n}{\left[\widehat{\varphi }(X_j)-\varphi (X_j)+{(\widehat{\vartheta }-\vartheta )}^{\text{T}}{\mathbf{\text{Z}}}_j\right]}^2$, and ${\text{MSPE}}_2\equiv {(10n)}^{-1}{\sum }_{j=1}^{10n}{\left[{(\widehat{\vartheta }-\vartheta )}^{\text{T}}{\mathbf{\text{Z}}}_j\right]}^2$, where j goes through the observations in the testing sample. MSPE₁ is the squared prediction error using both nonlinear and linear components in Model (3), and MSPE₂ is the squared prediction error using only linear components in Model (3). For AFT models, MSPE₁ and MSPE₂ can be considered as metrics of prediction performance on the log-transformed scale. Note that the stratified Lasso model does not provide an estimate of φ(X), so MSPE₁ is not applicable for Lasso-S_K. For each simulation setting, the performance measures were averaged over 400 Monte Carlo data sets. For the performance measure in each column, the range of standard errors was computed.

Our simulation results are summarized in Table 2. First, the performance of the standard linear AFT model (AFT) is not satisfactory in terms of both prediction and feature selection. We now restrict the discussion to the regularized estimators. In all cases, our Lasso-PL estimator exhibits lowest SSE, MSPE₁ and MSPE₂ among regularized estimators; in particular, its MSPE₁ and MSPE₂ are comparable to that of the Oracle estimator and are substantially lower than other regularized estimator. In terms of feature selection, Lasso-PL, Lasso-L and Lasso-Cox correctly identify the majority of the regression coefficients that are zero (P_C); Lasso-PL has higher P_C than Lasso-L when ρ = 0 or 0.5 and their P_C's are comparable in the presence of high correlation (ρ = 0.9); and Lasso-L has considerably higher P_C than Lasso-Cox in all cases. By comparison, the lasso stratified models (Lasso-S_K) only identify less than 30% of true zeros in some cases and roughly half of the true zeros in the rest of the cases. When there is no correlation and the signal is strong, all Lasso estimators successfully avoid setting nonzero coefficients to zero i.e, P_I equal to or close to 0. However, as the correlation gets stronger, P_I increases for all estimators to various degrees. When ρ = 0.9, P_I becomes appreciable for Lasso-L, whereas it remains moderate for Lasso-PL.

Table 2.

Simulation results for evaluating feature selection and prediction performance based on 400 Monte Carlo data sets, where n = 125 and d = 8. Lasso-PL, Lasso partly linear AFT model; Lasso-S_K, Lasso stratified model with K strata; Lasso-L, Lasso linear AFT model assuming a linear effect for both X_i and Z_i; Lasso-Cox, Lasso linear Cox model assuming a linear effect for both X_i and Z_i; AFT, standard AFT model assuming linear effects for both X_i and Z_i without regularization; and Oracle, oracle partly linear model with zero coefficients being set to 0. Δ, effect size; SSE, sum of squared errors for ϑ̂; P_C, proportion of zero coefficients being set to zero; P_I, proportion of nonzero coefficients being set to zero; MSPE₁, squared prediction error using both nonlinear and linear components; and MSPE₂, squared prediction error using only linear components. Range of SEs, range of SEs for the corresponding performance measure in each column. NA, a performance measure is not applicable for an estimator. All numbers are multiplied by 1000.

	Δ = 1					Δ = 0.5
	SSE	PC	PI	MSPE1	MSPE2	SSE	PC	PI	MSPE1	MSPE2
	ρ= 0
Lasso-PL	8	734	0	244	67	8	724	0	237	67
Lasso-S2	23	482	0	NA	186	23	453	1	NA	185
Lasso-S4	16	582	0	NA	127	15	565	2	NA	122
Lasso-S8	20	424	0	NA	161	20	438	8	NA	159
Lasso-L	12	639	0	997	100	12	611	0	990	99
Lasso-Cox	NA	488	0	NA	NA	NA	543	17	NA	NA
AFT	18	0	0	982	142	18	0	0	982	143
Oracle	4	1000	0	153	29	4	1000	0	207	30
	ρ = 0.5
Lasso-PL	11	767	0	225	74	11	777	2	296	75
Lasso-S2	38	403	0	NA	341	40	412	8	NA	353
Lasso-S4	21	569	0	NA	171	20	599	5	NA	146
Lasso-S8	26	540	0	NA	218	26	594	15	NA	204
Lasso-L	19	720	0	2894	126	19	748	16	2943	121
Lasso-Cox	NA	562	0	NA	NA	NA	612	14	NA	NA
AFT	33	0	0	2839	212	32	0	0	2878	202
Oracle	5	1000	0	175	31	5	1000	0	248	32
	ρ = 0.9
Lasso-PL	45	739	2	373	118	39	758	113	337	130
Lasso-S2	126	502	16	NA	592	106	500	152	NA	595
Lasso-S4	77	582	4	NA	184	60	596	124	NA	170
Lasso-S8	118	236	6	NA	338	96	424	135	NA	390
Lasso-L	92	751	31	6571	245	65	778	270	6738	262
Lasso-Cox	NA	596	8	NA	NA	NA	651	153	NA	NA
AFT	224	0	0	6483	337	226	0	0	6612	354
Oracle	17	1000	0	320	55	17	1000	0	288	54
Range of SEs	0.1-8	0-24	0-5	8-76	1-23	0.2-8	0-26	0-13	10-81	1-25

3.3. Prediction in the Presence of High-dimensional Data

We conducted a third set of simulations to explore the impact of noise levels on the prediction performance in the presence of high-dimensional data (i.e., d ≥ n), and compared four models, namely, Lasso-PL, Lasso-S_K, Lasso-L and Lasso-Cox. We note that the standard AFT model is not applicable for high-dimensional data. The simulation setup paralleled that in Section 3.2. The differences are noted as follows. The sample size was fixed to n = 100 and the number of linear predictors was d ≥ 100, and let ϑ₁ = ϑ₂₆ = ϑ₅₁ = ϑ₇₆ = 1 and all other ϑ's be 0. Let X = 0.5Z₁₀ + 0.5Z₃₅ + 0.5Z₆₀ + U_i, where U_i follows Un(−1, 1). Through these changes, we investigated a case where the significant linear predictors (Z) are not highly correlated. The censoring random variable was generated similar to that in Section 3.2 with a different uniform distribution such that the censoring probability is approximately 40%. Since MSPE₁ and MSPE₂ are not applicable in the presence of censoring in practice, we computed another metric of prediction performance using the testing sample, namely, the c statistic for censored data, which measures the proportion of concordance pairs based on observed and predicted outcomes and ranges between 0 and 1 with 1 indicating perfect prediction (Kattan, 2003a,b; Steyerberg et al., 2010). In particular, the comparison with Lasso-Cox is focused on c statistics. Again, for Lasso-S_K, MSPE₁ was not applicable and ϑ̂^TZ_j was used to compute c statistic; for the performance measure in each column, the range of standard errors was computed.

Table 3 summarizes the prediction performance for d = 100, d = 500 and d = 1500 over 400 Monte Carlo data sets. In the presence of high-dimensional data, Table 3 shows that the proposed Lasso-PL always achieves the best prediction performance in terms of the c statistic as well as MSPE₁ and MSPE₂, and Lasso-Cox always has lower c than Lasso-PL and Lasso-L. By and large, the prediction performance of Lasso-S_K is comparable to that of Lasso-L and is considerably worse than Lasso-PL in all cases, and in particular, the absence of the estimated nonlinear effect in X leads to substantial loss in the c statistic. While Lasso-PL estimates the nonlinear effect of X well in all cases, the prediction error due to the linear predictors (MSPE₂) starts to dominate as d increases. Since all significant predictors are in the first 100 predictors, the cases of d = 1500 and d = 500 simply add 1100 and 400 noise predictors, respectively, compared to the case of d = 100. Our results indicate that as the noise level increases the prediction performance deteriorates for all models. For Lasso-L models, the prediction error due to mis-specified nonlinear effect of X remains substantial in all cases. In this setup, when correlation is weak or moderate (ρ = 0 or 0.5), the impact of correlation on prediction performance is moderate, in particular, in terms of c; however, as correlation becomes very strong (ρ = 0.9), the prediction performance improves considerably in terms of c for all methods.

Table 3.

Simulation results for evaluating prediction performance in the presence of high-dimensional data based on 400 Monte Carlo data sets, where n = 100. Lasso-PL, Lasso partly linear AFT model; Lasso-S_K, Lasso stratified model with K strata; Lasso-L, Lasso linear AFT model assuming a linear effect for both X_i and Z_i; and Lasso-Cox, Lasso linear Cox model assuming a linear effect for both X_i and Z_i. MSPE₁, the squared prediction error using both nonlinear and linear components; MSPE₂, the squared prediction error using only linear components; and c, the c-statistic for censored data. Range of SEs, range of SEs for the corresponding performance measure in each column. NA, a performance measure is not applicable for a estimator. All numbers are multiplied by 1000.

	d = 100		c	d = 500		c	d= 1500		c
	MSPE1	MSPE2		MSPE1	MSPE2		MSPE1	MSPE2
	ρ = 0
Lasso-PL	412	349	860	989	897	840	1685	1543	796
Lasso-S2	NA	676	811	NA	1589	768	NA	2310	711
Lasso-S4	NA	560	812	NA	1428	780	NA	2182	718
Lasso-S8	NA	529	811	NA	1454	775	NA	2208	716
Lasso-L	1441	568	829	2752	1666	784	3719	2496	697
Lasso-Cox	NA	NA	798	NA	NA	749	NA	NA	684
	ρ = 0.5
Lasso-PL	389	330	860	1034	937	839	1659	1518	797
Lasso-S2	NA	637	810	NA	1653	766	NA	2270	716
Lasso-S4	NA	525	812	NA	1472	777	NA	2152	725
Lasso-S8	NA	491	811	NA	1512	774	NA	2196	721
Lasso-L	1418	550	829	2803	1720	781	3703	2513	701
Lasso-Cox	NA	NA	799	NA	NA	749	NA	NA	690
	ρ = 0.9
Lasso-PL	387	328	875	1084	1124	852	1795	1909	811
Lasso-S2	NA	529	841	NA	1314	815	NA	2059	769
Lasso-S4	NA	474	842	NA	1422	812	NA	2253	759
Lasso-S8	NA	455	841	NA	1618	805	NA	2473	744
Lasso-L	1476	480	852	2274	1152	836	3179	1849	802
Lasso-Cox	NA	NA	840	NA	NA	825	NA	NA	796
Range of SEs	9-20	8-23	0.6-2	32-56	32-52	1-4	47-61	47-57	2-5

We performed additional simulations for a higher censoring rate, 60%, and for different regression coefficient values, e.g., ϑ₁ = ϑ₂ = ϑ₃ = ϑ₅₀ = 1 and all other ϑ's set to 0, i.e., the first three significant predictors are highly correlated. Under all scenarios, the results on comparisons between different models remain the same, but the prediction performance worsens as the censoring rate increases.

In summary, the proposed lasso partly linear AFT model achieves best performance in all three areas: estimation, feature selection and prediction. While the lasso stratified estimator performs reasonably well in estimation, its performance in feature selection and prediction is not satisfactory. When a covariate effect is nonlinear, the performance of Lasso-L worsens, and the deterioration can be substantial in terms of prediction. When the PH assumption does not hold, the performance of Lasso-Cox is considerably worse than Lasso-L. Furthermore, if prediction is of primary interest, our results suggest that it is advantageous to build prediction scores using data with less noise variables.

4. Data Analysis: the Prostate Cancer Study

We analyzed the data from the prostate cancer study, which included 78 patients. The outcome of interest is time to prostate cancer recurrence, which starts on the day of prostatectomy and is subject to censoring; the observed survival time ranges from 2 months to 160 months and the censoring rate is 57.7%. In the data analysis, the log-transformed survival time was used to fit AFT models. Gene expression data using 1536 probes and two clinical variables (PSA and gleason score) were measured from samples collected at the baseline (i.e., right after the surgery) and were used in our analysis. Since replicate RNA samples were collected and measured from some subjects, we averaged the gene expression data over multiple RNA samples from a same subject before subsequent analysis. The gleason score in this data set ranges only between 5 and 9 and 91% of patients had a score of either 6 or 7; combining this with suggestions from the investigators, the total gleason score was dichotomized as ≥ 7 or not.

Before the data analysis, all gene expression measurements were preprocessed and standardized to have mean 0 and unit standard deviation. Subsequently, Cox PH models were fit for each individual probe and all probes were then ranked according to their score test statistics from the largest (J = 1) to the smallest (J = 1536). This ranking procedure serves two purposes. First, it simplifies the presentation of the results, since we can refer to each probe using its ranking. Second, a pre-selection step using this ranking procedure is used when evaluating the prediction performance in Section 4.2, which is similar to what is often used in detecting differentially expressed genes. We note that the use of Cox PH models is of no particular importance, which simply provides a way to rank the probes; one can use other models such as AFT models.

4.1. Feature Selection

Before building prediction scores, we conducted feature selection using the following models, the Lasso-PL with r = 10, Lasso-S_K, Lasso-L, and Lasso-Cox. In the Lasso-PL model (3), X_i is PSA, which is modeled using penalized splines, and Z include the binary clinical variable, gleason score, as well as the complete set or a subset of 1536 probes. Similarly, in the Lasso-S_K model, stratification is based on PSA.

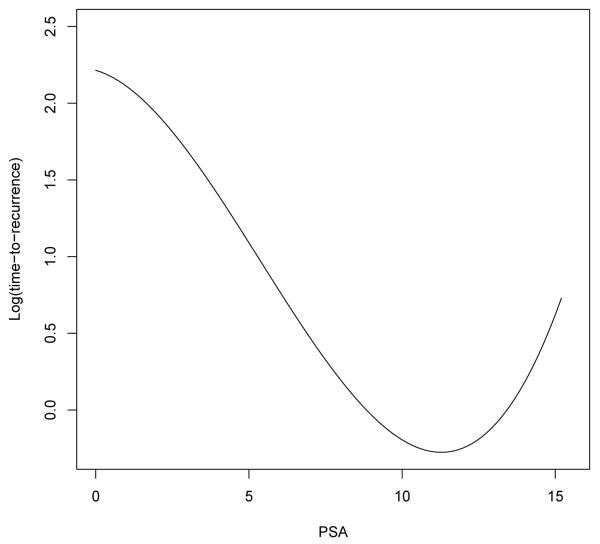
We first conducted an analysis using the complete set of 1536 probes. The results on feature selection are summarized in Table 4. A linear effect of PSA was included in the Lasso-L model and was estimated to be nonzero, which further justifies the inclusion of PSA in other models; on the other hand, the total gleason score is not selected by any of the methods. Figure 1 shows the estimated effect of PSA using Lasso-PL; specifically, the time to recurrence initially decreases as PSA increases and then starts to increase slightly as PSA goes beyond 11. After further examination of the data, we found that most patients had PSA values ranging from 0-15.2, but three had PSA values of 18.43, 26 and 32.10. More importantly, all subjects with PSA> 15.2 had censored outcomes; consequently, it is not appropriate to project the estimated φ(X) beyond 15.2. We also suspect that the increasing trend towards the right tail is an artifact of the data and the effect of PSA instead levels off when it is greater than 11, given that an increase in the time to recurrence as PSA increases does not seem plausible clinically.

Table 4. Feature selection for the prostate cancer study.

Method	Selected Probes
Lasso-PL	1, 2, 4, 12, 16, 31, 38, 46, 63
Lasso-S2	1, 4, 8, 12, 16, 31, 46, 63, 382, 906
Lasso-S4	1, 4, 12,16,29,31,36,38,46,56,70,78,310,382,390,591,1500
Lasso-S8	1, 4, 8, 9, 16, 18, 31,36,37,38,46,56,57,70,78,178,237,271,310,855,1500
Lasso-L	1, 2, 4, 8, 9, 16, 31, 46, 63, 70, 136
Lasso-Cox	2, 4, 8, 11, 14, 16, 22, 31, 46, 52, 63

Fig 1.

Estimated nonlinear effect of PSA on the prostate cancer recurrence after surgery (φ̂(X)).

In terms of feature selection for the probe data, the Lasso-PL model selects the least number of features, among which Probe 4, 16, 31, and 46 are selected by all six models, Probe 1 selected by five models, Probe 63 selected by four models and Probe 2, 12 and 38 selected by three models. In other words, all probes selected by Lasso-PL are selected by at least half of all models, whereas other models select some probes that are not shared by the rest of the models and are likely to be noise. This agrees with the simulation results, i.e., in the presence of moderate to strong correlation among predictors, the other models tend to select a larger number of noise features. In addition, the difference between the Lasso-PL method and the Lasso-L method is likely due to the nonlinear effect of PSA.

4.2. Prediction Performance

To internally evaluate the prediction performance, the data were randomly split into a training sample (60%) and a validation sample (40%). Due to the high censoring rate, this step was stratified on the censoring status to avoid extreme imbalance of censoring rates between the training and validation samples. The models of interest were fit using the training sample and were then used to construct the predictive risk score for cancer recurrence, say, φ̂(X) + ϑ̂^TZ for Lasso-PL, for subjects in the validation sample. Subsequently, the c statistic was computed in the validation sample. This procedure was repeated 1000 times and the average c statistic is used for evaluating the prediction performance of different models.

We compared the following model and data combinations: Lasso-PL with r = 10 using 1536 probes and 2 clinical variables with PSA modeled non-linearly; Lasso-L and Lasso-Cox using 1536 probes and 2 clinical variables; Lasso-PL with r = 10 using 2 clinical variables plus top 25 probes with PSA modeled nonlinearly, where the top 25 probes were selected within each training sample; Lasso-L and Lasso-Cox using 2 clinical variables plus top 25 probes; partly linear AFT and Cox models (PL-AFT and PL-Cox) using 2 clinical variables only with PSA modeled nonlinearly through a penalized spline; linear AFT and Cox model (AFT and Cox) using 2 clinical variables only. Note that we did not use Lasso-S_K, since it does not estimate the nonlinear effect of PSA.

Table 5 presents the mean c statistic computed using each model and data combination. Partly linear models have higher average c than linear models in all settings and for both AFT and Cox models, indicating that the mis-specified effect of PSA leads to worse prediction performance. In all cases, AFT models have similar or higher average c compared to their corresponding Cox models. The average c for Lasso-PL using all 1536 probes is slightly less than PL-AFT using only clinical variables, whereas Lasso-L and Lasso-Cox using all 1536 probes have substantially lower c than AFT and Cox using only clinical variables. Furthermore, when a pre-selection step was included to choose the top 25 probes first, we observe small improvement in c for Lasso-L and Lasso-Cox and no improvement for Lasso-PL, which is likely due to that the correctly modeled PSA effect plays the most important role in prediction and the addition of gene expression data does not seem to further improve prediction.

Table 5. Prediction performance in the data analysis: mean c statistic.

All 1536 probes
Lasso-PL	Lasso-L		Lasso-Cox
0.653	0.561		0.553
Top 25 probes
Lasso-PL	Lasso-L		Lasso-Cox
0.653	0.567		0.572
Clinical variables only
PL-AFT	AFT	PL-Cox	Cox
0.665	0.644	0.658	0.644

In summary, our analyses suggest that 1) the relationship between the baseline PSA and prostate cancer recurrence is likely nonlinear, i.e., the time to recurrence decreases as PSA increases and it starts to level off when PSA becomes greater than 11; 2) the correct specification of this nonlinear effect improves performance in prediction and feature selection; and 3) the addition of gene expression data does not seem to further improve the prediction performance. However, given that the sample size in this study is small, our results need to be validated in a future study, preferably with a larger sample size.

5. Discussion

We have investigated statistical approaches for prediction of clinical end points that are subject to censoring. Our research shows that correctly specifying nonlinear effects improves performance in both prediction and feature selection for both low-dimensional and high-dimensional data. While the proposed models can be used for high-dimensional data, caution needs to be exercised in practice, since the sample size is often small in real-life studies. This is especially true when prediction is of primary interest and feature selection is less of a concern. As the regularized methods achieve sparsity, they shrink the coefficients of the important predictors. In finite samples, such shrinkage becomes more pronounced as the noise level (i.e., the number of noise predictors) increases; as a result, the prediction performance deteriorates, which is reflected in our simulations and data analysis.

We investigated two numerical methods for fitting proposed models. The first algorithm is implemented through a L₁ regression, which is slow for large data sets or when the number of predictors is large relative to the sample size and fails when d > n. These limitations are especially serious for censored data. For example, in our data example, the first algorithm started to have convergence issues if d > 25 probes were used, in particular, when cross-validation was used or internal validation was performed for evaluating prediction performance. The second algorithm as described in Section 2.5 can deal with high-dimensional data, and its solutions are fairly close to those obtained using the first method when both are applicable. Consequently, we recommend the use of the second algorithm in practice.

In this paper, we focus on the performance for prediction as well as feature selection in finite samples through extensive numerical studies, and the theoretical properties of the proposed methods are likely inherited from those of regularized linear AFT models and penalized splines, which are beyond the scope of this article and are a topic for future research. Nevertheless, our numerical results provide empirical evidence to suggest that the proposed approach is likely to enjoy the properties on feature selection that are possessed by regularized estimation in linear AFT models (Cai, Huang and Tian, 2009) and in stratified AFT models (Johnson, 2009).

Several metrics have been proposed for assessing the performance of prediction models, and Steyerberg et al. (2010) provides a nice review on this subject; however, it is well known that censoring presents additional challenges in developing such metrics (Begg et al., 2000; Gonen and Heller, 2005; Steyerberg et al., 2010). In our simulations and data example, we used the extended c statistic to evaluate the prediction performance in the presence of censored data; despite its ease of use, this metric uses only concordant and disconcordant information and hence leads to loss of information. Furthermore, while the existing metrics for censored data are applicable for AFT models, no metric has been proposed to take advantage of the unique feature of AFT models, namely, they model the log-transformed outcome and can provide prediction on the log-transformed scale, which is not trivial and is another topic for our future research.