Theory and simulation of diffusion-influenced, stochastically gated ligand binding to buried sites

Abstract

We consider the diffusion-influenced rate coefficient of ligand binding to a site located in a deep pocket on a protein; the binding pocket is flexible and can reorganize in response to ligand entrance. We extend to this flexible protein-ligand system a formalism developed previously [A. M. Berezhkovskii, A, Szabo, and H.-X. Zhou, J. Chem. Phys. 135, 075103 (2011)10.1063/1.3609973] for breaking the ligand-binding problem into an exterior problem and an interior problem. Conformational fluctuations of a bottleneck or a lid and the binding site are modeled as stochastic gating. We present analytical and Brownian dynamics simulation results for the case of a cylindrical pocket containing a binding site at the bottom. Induced switch, whereby the conformation of the protein adapts to the incoming ligand, leads to considerable rate enhancement.

INTRODUCTION

Many ligand-binding proteins have binding sites located in deep pockets. To calculate the diffusion-influenced binding rate coefficient in such a situation, in a previous paper¹ we developed a general formalism for breaking the overall problem into an exterior problem and an interior problem. In the exterior problem, the ligand is restricted to the bulk solution outside the binding pocket and is absorbed by the entrance to the pocket. In the interior problem, the ligand is confined to the pocket and binds to the final binding site. To connect between the exterior and interior problems, an approximation was invoked that the protein-ligand pair distribution function stays equilibrated over the cross section of the binding pocket, resulting in a special boundary condition for the interior problem. It was assumed that the protein molecule is rigid. In the present work, we remove this last assumption, allowing the binding pocket to be conformationally flexible. We focus on conformational fluctuations of a bottleneck (or lid) and the binding site, and model these conformational fluctuations as stochastic gating.

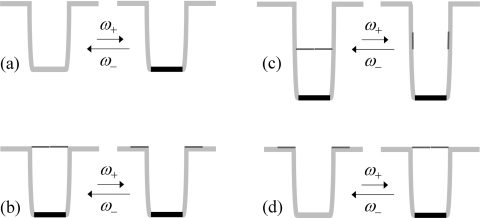
We deal with three gating situations (Fig. 1), all motivated by actual protein-ligand systems. In the first, referred to as gating binding-site, the binding site switches between inert and reactive conformations (Fig. 1a). The second situation, referred to as gated access, has a bottleneck or gate, either at the entrance to or midway along the binding pocket (Figs. 1b, 1c), that switches between closed and open conformations. Acetylcholineseterase features such a gate midway along a tunnel leading to the active site.² In the third situation, referred to as gating binding-pocket, ligand entrance to the binding pocket induces both the closure of a lid and the switch of the binding site from being inert to being reactive (Fig. 1d). Oritidine-5-phosphate decarboxylase,³trp RNA-binding attenuation protein,^{4, 5} and many other ligand-binding proteins are examples of this situation.

Figure 1.

Gating situations studied in the present paper. (a) A buried binding site that switches between inert and reactive conformations. (b) A buried binding site that has gated access. The gate is at the entrance of the binding pocket. (c) The gated access situation, with the gate midway along the binding pocket. (d) A binding pocket that switches between an open lid/inert binding-site state and a closed lid/reactive binding-site state.

The gating binding-site situation was first studied theoretically by McCammon and Northrup.⁶ A subsequent solution by Szabo et al.⁷ has guided other theoretical and simulation studies.^{8, 9, 10, 11, 12, 13} In these studies, the binding site was modeled as switching between a reactive (i.e., absorbing) conformation and an inert (i.e., reflecting) conformation. The transition rates, ω₊ and ω_–, between the two conformations were assumed to be fixed, regardless of whether the ligand is far away or near the binding site,

$$\mathrm{reflecting}\underset{{\omega }_{-}}{\overset{{\omega }_{+}}{\rightleftarrows }}\mathrm{absorbing}.$$ (1.1)

By making the approximation that the flux of the pair distribution function is constant over the binding site in the absorbing conformation, Szabo et al.⁷ derived the following result for the steady-state rate constant $k_{\mathrm{G}}^{\mathrm{ss}}$ in the gating binding-site situation:

$$\frac{1}{k_{\mathrm{G}}^{\mathrm{ss}}}=\frac{1}{k^{\mathrm{ss}}}+\frac{{\omega }_{-}}{{\omega }_{+}}\frac{1}{\omega \widehat{k}\left(\omega \right)},$$ (1.2)

where ω = ω₊ + ω_–; $\widehat{k}\left(s\right)$ denotes the Laplace transform of the time-dependent rate coefficient k(t) in the ungated situation, in which the binding site is always absorbing; and k^ss is the steady-state limit of k(t) [i.e., $k^{\mathrm{ss}}=k\left(\infty \right)={\lim }_{s\to 0}s\widehat{k}\left(s\right)$]. Later it was found that,¹⁰ when generalized to the time-dependent problem, the constant-flux approximation is equivalent to assuming that the pair distribution function stays equilibrated over the binding site. The time-dependent rate coefficient, k_G(t), in Laplace space has the form

$$\frac{1}{s{\widehat{k}}_{\mathrm{G}}\left(s\right)}=\frac{1}{s\widehat{k}\left(s\right)}+\frac{{\omega }_{-}}{{\omega }_{+}}\frac{1}{(s+\omega )\widehat{k}(s+\omega )},$$ (1.3)

which at s = 0 reduces to Eq. 1.2. The formalism presented in the previous paper¹ can be used to find $\widehat{k}\left(s\right)$ when the binding site is located inside a deep pocket.

We first studied the gated access situation in 1998.¹⁴ The transition rates between the closed and open conformations of the gate were fixed (also denoted by ω_±), regardless of where the ligand was located. By making the approximation that the flux of the pair distribution function is constant over the gate when it is in the open conformation, it was possible to break the overall problem into an exterior problem and an interior problem. The exterior and interior regions are separated by the gate. The overall rate constant can be written as

$$\frac{1}{k_{\mathrm{G}}^{\mathrm{ss}}}=\frac{1}{k_{\mathrm{E};\mathrm{G}}^{\mathrm{ss}}}+\frac{1}{k_{\mathrm{I};\mathrm{G}}^{\mathrm{ss}}},$$ (1.4a)

where $k_{\mathrm{E};\mathrm{G}}^{\mathrm{ss}}$ is the rate constant for ligands in the exterior region being absorbed by the fluctuating gate and can be found by Eq. 1.2. The other quantity $k_{\mathrm{I};\mathrm{G}}^{\mathrm{ss}}$ is a rate constant from the interior problem, in which the ligands are reflected by the closed gate but maintain the equilibrium distribution over the open gate, leading to

$$\frac{1}{k_{\mathrm{I};\mathrm{G}}^{\mathrm{ss}}}=\frac{1}{k_{\mathrm{I}}^{\mathrm{ss}}}+\frac{{\omega }_{-}}{{\omega }_{+}}\frac{1}{\omega {\widehat{j}}_{\mathrm{I}}\left(\omega \right)},$$ (1.4b)

where ${\widehat{j}}_{\mathrm{I}}\left(s\right)$ is the Laplace transform of the total flux, j_I(t), across the open gate, and $k_{\mathrm{I}}^{\mathrm{ss}}=j_{\mathrm{I}}\left(\infty \right)={\lim }_{s\to 0}s{\widehat{j}}_{\mathrm{I}}\left(s\right)$. Equations 1.4 have been used to study substrate binding to acetylcholinesterase¹⁵ and permeant ion binding to an internal site in a transmembrane ion channel.^{16, 17}

Recently, it was recognized that more realistic modeling requires variable transition rates between the alternative conformations of the binding site and the gate.¹⁸ In the gating binding-site situation, we expect that the transition rates favor the reflecting conformation while the ligand is far away but would favor the absorbing conformation while the ligand is inside the binding pocket. The change in transition rates comes about due to the protein-ligand interactions inside the binding pocket. With such variable transition rates, two popular binding mechanisms, conformational selection and induced fit, emerge as extremes when the timescale of the conformational transitions is either much longer or much shorter than the timescale of the diffusional approach to the binding pocket. The conformational-selection and induced-fit extremes provide lower and upper bounds of the ligand binding rate constant, respectively, and the values of the two bounds become close when the range of the protein-ligand interactions is longer than the binding pocket.¹⁹ A similar conclusion was reached regarding how the conformational switch of a protein nonspecifically bound to DNA affects the binding rate to a specific site.²⁰ Following the terminology of that paper, we refer to the scenario of fixed transition rates between alternative conformations as “indifferent switch,” and the scenario of variable transition rates as “induced switch.”

As mentioned above, Eqs. 1.2, 1.3, 1.4 were obtained by applying the constant-flux approximation, either over the binding site or over the gate. Compared to the constant-flux approximation, the formalism presented in the previous paper¹ appears to be superior for dealing with a binding site located inside a deep pocket, leading to more accurate results for the rate coefficient in the ungated situation. Here, we adapt the basic idea of that paper¹ to derive a boundary condition over the entrance to the binding pocket for the three gating situations illustrated in Fig. 1. We go beyond previous studies by treating both the indifferent-switch scenario and the induced-switch scenario. We present explicit results for the case of a cylindrical pocket containing a binding site at the bottom. We find that induced switch leads to significant enhancement of the protein-ligand binding rate over the indifferent-switch scenario. We also use Brownian dynamics (BD) simulations to obtain exact results for the protein-ligand binding rate coefficient and show that the analytical results derived in this paper are accurate to within 1.5%.

The rest of the paper is organized as follows. In Sec. 2, we summarize the results of the previous paper¹ for an ungated cylindrical pocket and compare them against BD simulations. We then present the gating binding-site situation in Sec. 3. In Sec. 4, we consider a gating circular binding site on an otherwise inert plane, which is a special case of the cylindrical binding pocket when the depth is zero. We test the results of Sec. 3 in this special case both analytically and against BD simulations. This is followed by the gated access situation in Sec. 5 and the gating binding-pocket situation in Sec. 6. We end the paper with some concluding remarks, drawing particular attention on how the present work can be the basis for treating molecular flexibility in BD simulations of protein-ligand binding.

THE UNGATED CYLINDRICAL POCKET

Formalism for breaking into exterior and interior problems

The formalism developed in the previous paper¹ for breaking the overall problem into an exterior problem and an interior problem can be illustrated by the case of a binding site located at the bottom of a cylindrical pocket. In the exterior region, the pair distribution function G(r, t) satisfies the Smoluchowski equation

$$\frac{\partial G}{\partial t}=\nabla ·\left\{D{e}^{-\beta U\left(\mathbf{r}\right)}\nabla \left[e^{\beta U\left(\mathbf{r}\right)}G\right]\right\},$$ (2.1)

with the initial condition

$$G(\mathbf{r},0)=e^{-\beta U\left(\mathbf{r}\right)}$$ (2.2)

and the boundary condition

$$G(\mathbf{r},t)=1\mathrm{as}r\to \infty .$$ (2.3)

The basic assumption of the previous paper is that the distribution function undergoes rapid equilibration over the cross section of the cylindrical pocket:

$$G(\mathbf{r},t)\approx e^{-\beta U\left(\mathbf{r}\right)}f(x,t)\mathrm{if}0\le x\le L,$$ (2.4)

where x is the coordinate along the cylindrical axis and L is the length of the cylindrical pocket. Then the reduced one-dimensional distribution function in the pocket, g(x, t), defined as

$$g(x,t)=\int \int \mathit{\text{dydz}}G(\mathbf{r},t),$$ (2.5)

satisfies

$$\frac{\partial g}{\partial t}=\frac{\partial }{\partial x}\left[D{e}^{-\beta V\left(x\right)}\frac{\partial e^{-\beta V\left(x\right)}g}{\partial x}\right]\equiv \mathcal{L}g,$$ (2.6)

where ∫∫dydz represents an integration over the cylindrical cross section at position x; V(x) is the one-dimensional potential of mean force given by

$$e^{-\beta V\left(x\right)}={\sigma }^{-1}\int \int \mathit{\text{dydz}}{e}^{-\beta U\left(\mathbf{r}\right)},$$ (2.7)

with σ denoting the cross sectional area of the cylindrical pocket. Binding at x = 0 is specified by a radiation boundary condition

$$\mathcal{J}g(0,t)\equiv D{e}^{-\beta V\left(x\right)}{\left.\frac{\partial e^{\beta V\left(x\right)}g(x,t)}{\partial x}\right|}_{x=0}={\kappa }_{0}g(0,t),$$ (2.8)

where κ₀ is the reactivity. Either side of the last identity gives the overall rate coefficient k(t). The initial value of the rate coefficient is

$$k_0={\kappa }_0\sigma e^{-\beta V\left(0\right)}.$$ (2.9)

The approximation of Eq. 2.4 is the basis of an ansatz for the distribution function in the exterior region. In Laplace space, this takes the form

$$\widehat{G}(\mathbf{r},s)={\widehat{A}}_1\left(s\right)\widehat{H}(\mathbf{r},s)+{\widehat{A}}_2\left(s\right)e^{-\beta U\left(\mathbf{r}\right)},$$ (2.10)

which involves H(r, t), the distribution function for the exterior problem that satisfies an absorbing boundary condition on the entrance to the cylindrical pocket. To determine the coefficients ${\widehat{A}}_1\left(s\right)$ and ${\widehat{A}}_2\left(s\right)$, we note that G(r, t), H(r, t), and exp[–βU(r)] all go to 1 as r → ∞. Therefore,

$${\widehat{A}}_1\left(s\right)+s{\widehat{A}}_2\left(s\right)=1.$$ (2.11)

To find a second identity, we specializing Eq. 2.10 to x = L, the entrance to the cylindrical pocket. Here, H(r, t) = 0 since the entrance is absorbing for H(r, t). Integrating over the entrance, we have

$$\widehat{g}(L,s)={\widehat{A}}_2\left(s\right)\sigma e^{-\beta V\left(L\right)}.$$ (2.12)

The last two identifies allow us to find

$${\widehat{A}}_1\left(s\right)=1-\frac{s\widehat{g}(L,s)}{\sigma e^{-\beta V\left(L\right)}}.$$ (2.13)

Finally, the boundary condition for g(x, t) at x = L is obtained by calculating the flux of Eq. 2.10. Noting that total flux of H(r, t) at x = L is the rate coefficient k_E(t) for ligands in the exterior region being absorbed by the entrance to the cylindrical pocket and that the flux of exp[–βU(r)] is zero, we find

$$\mathcal{J}\widehat{g}(L,s)=\left(1-\frac{s\widehat{g}(L,s)}{\sigma e^{-\beta V\left(L\right)}}\right){\widehat{k}}_{\mathrm{E}}\left(s\right).$$ (2.14)

A formal solution

In Laplace space, Eq. 2.6 takes the form

$$s\widehat{g}(x,s)-\sigma e^{-\beta V\left(x\right)}=\mathcal{L}\widehat{g}(x,s).$$ (2.15)

The radiation boundary condition of Eq. 2.8 takes the form

$$\mathcal{J}\widehat{g}(0,s)={\kappa }_0\widehat{g}(0,s).$$ (2.16)

We construct the solution in the form

$$\widehat{g}(x,s)=\frac{1}{s}\sigma e^{-\beta V\left(x\right)}+\widehat{B}\left(s\right)\widehat{q}(x,s),$$ (2.17)

where $\widehat{q}(x,s)$ satisfies

$$s\widehat{q}(x,s)=\mathcal{L}\widehat{q}(x,s),$$ (2.18a)

subject to the boundary conditions

$$-\mathcal{J}\widehat{q}(L,s)=\frac{s{\widehat{k}}_{\mathrm{E}}\left(s\right)}{\sigma e^{-\beta V\left(L\right)}}\widehat{q}(L,s),$$ (2.18b)

$$\widehat{q}(0,s)=\frac{1}{s}\sigma e^{-\beta V\left(0\right)}.$$ (2.18c)

It can be verified that Eq. 2.17 satisfies Eq. 2.15 and the boundary condition of Eq. 2.14. Using the remaining boundary condition of Eq. 2.16, we have

$$\widehat{B}\left(s\right)\mathcal{J}\widehat{q}(0,s)=\left(\frac{1}{s}+\widehat{B}\left(s\right)\right)k_0.$$ (2.19)

Solving for $\widehat{B}\left(s\right)$, we finally find

$$\frac{1}{s\widehat{k}\left(s\right)}\equiv \frac{1}{s\mathcal{J}\widehat{g}(0,s)}=\frac{1}{k_0}+\frac{1}{-s\mathcal{J}\widehat{q}(0,s)}.$$ (2.20)

A number of results in Sec. 3 will be expressed in terms of $\widehat{q}(x,s)$. Its boundary condition at x = L, given by Eq. 2.18b, is a radiation type in Laplace space, with reactivity given by $\frac{s{\widehat{k}}_{\mathrm{E}}\left(s\right)}{\sigma e^{-\beta V\left(L\right)}}$. ${\widehat{k}}_{\mathrm{E}}\left(s\right)$ must be determined by solving the exterior problem. If the potential is zero outside the cylindrical pocket, an excellent approximation is²¹

$$\frac{s{\widehat{k}}_{\mathrm{E}}\left(s\right)}{4Da}=1+\frac{\pi }{4}a\lambda +\frac{(\pi ∕4-1)a\lambda }{\pi (4-\pi )∕({\pi }^2-8)+a\lambda },$$ (2.21)

where a is the radius of the absorbing disk, which is also the top of the cylindrical pocket. Equation 2.21 was constructed to reproduce the first two terms of the expansions of ${\widehat{k}}_{\mathrm{E}}\left(s\right)$ in s for both large s and small s, corresponding to short and long times, respectively. In particular, it gives the correct steady-state limit $k_{\mathrm{E}}^{\mathrm{ss}}=4Da$.²² In Sec. 4, we will extend this result to the case where the disk is partially absorbing and stochastically gated, by applying Eq. 2.18b to the special case L = 0.

The steady-state rate constant k^ss is of particular interest, which can be obtained by taking the s → 0 limit. Solving the steady-state version of Eqs. 2.18, we find

$$\frac{1}{-\mathcal{J}{q}^{\mathrm{ss}}\left(0\right)}=\frac{1}{k_{\mathrm{E}}^{\mathrm{ss}}}+{\int }_0^{L}dx\frac{1}{D\sigma e^{-\beta V\left(x\right)}}.$$ (2.22)

Using this in the steady-state limit of Eq. 2.20, we obtain the expression for the steady-state rate constant:

$$\frac{1}{k^{\mathrm{ss}}}=\frac{1}{k_{\mathrm{E}}^{\mathrm{ss}}}+\frac{1}{k_{\mathrm{I}}^{\mathrm{ss}}},$$ (2.23a)

where

$$\frac{1}{k_{\mathrm{I}}^{\mathrm{ss}}}=\frac{1}{k_0}+{\int }_0^{L}dx\frac{1}{D\sigma e^{-\beta V\left(x\right)}}$$ (2.23b)

can be recognized as the rate constant for ligands in the interior region when the pair distribution function on the entrance is maintained at its equilibrium value exp[–βU(r)].¹⁴ This expression for k^ss was given in the previous paper.¹

A constant-linear potential in the cylindrical pocket

An explicit expression for $\widehat{k}\left(s\right)$ was given in the previous paper¹ for the case of a linear potential in the cylindrical pocket. For a constant potential: βV(x) = βV₀ for 0 ⩽ x ⩽ L, Eq. 2.18a becomes

$$s\widehat{q}(x,s)=D\frac{d^2\widehat{q}(x,s)}{d{x}^2}.$$ (2.24)

The solution has the form

$$\widehat{q}(x,s)={\widehat{B}}_1\left(s\right)e^{\lambda x}+{\widehat{B}}_2\left(s\right)e^{-\lambda x},$$ (2.25)

where

$$\lambda ={(s∕D)}^{1∕2}.$$ (2.26)

After determining ${\widehat{B}}_1\left(s\right)$ and ${\widehat{B}}_2\left(s\right)$ by using the boundary conditions of Eqs. 2.18b, 2.18c, we find

$$\frac{1}{s\widehat{k}\left(s\right)}=\frac{1}{k_0}+\frac{\lambda \coth \left(\lambda L\right)+s{\widehat{k}}_{\mathrm{E}}\left(s\right)∕D\sigma e^{-\beta V_0}}{s{\widehat{k}}_{\mathrm{E}}\left(s\right)\lambda \coth \left(\lambda L\right)+s\sigma e^{-\beta V_0}}.$$ (2.27)

The steady-state rate constant is

$$\frac{1}{k^{\mathrm{ss}}}=\frac{1}{k_{\mathrm{E}}^{\mathrm{ss}}}+\frac{1}{k_0}+\frac{L}{D\sigma e^{-\beta V_0}}.$$ (2.28)

For a potential that bridges the linear and constant potentials,

$$V\left(x\right)=\left\{\begin{array}{c}\hfill V_0,\mathrm{if}0<x\le L_1\\ \hfill V_0(L-x)∕\Delta ,\mathrm{if}{L}_1<x<L\end{array}\right.,$$ (2.29)

where Δ = L − L₁, the rate coefficient can also be obtained. The result is

$$\frac{1}{s\widehat{k}\left(s\right)}=\frac{1}{k_0}+\frac{\lambda \coth \left(\lambda L_1\right)+\alpha ∕D\sigma e^{-\beta V_0}}{\alpha \lambda \coth \left(\lambda L_1\right)+s\sigma e^{-\beta V_0}},$$ (2.30a)

where

$$\begin{array}{c}\hfill \frac{1}{\alpha }=e^{\beta V_0}\frac{{\lambda }_2\coth \left({\lambda }_2\Delta \right)-\beta V_0∕2\Delta +s{\widehat{k}}_{\mathrm{E}}\left(s\right)∕D\sigma }{s{\widehat{k}}_{\mathrm{E}}\left(s\right){\lambda }_2\coth \left({\lambda }_2\Delta \right)+s\sigma +\beta V_{0}s{\widehat{k}}_{\mathrm{E}}\left(s\right)∕2\Delta },\end{array}$$ (2.30b)

with λ₂ = [s/D + (βV₀/2Δ)²]^1/2.

Comparison against BD simulations

The first algorithm for obtaining the steady-state rate constant from BD simulations was developed by Northrup et al.²³ From ligand trajectories started on a spherical surface enclosing the entire protein molecule, one obtains the capture probability, i.e., the fraction of trajectories that lead to reaction at the binding site rather than escape to infinity. The rate constant is proportional to the capture probability. For a binding site located in a deep pocket, the capture probability may become extremely small, rendering this algorithm ineffective.²⁴ This algorithm was originally developed for rigid protein molecules, but has been applied to a gated access situation.²⁵ A potential problem with the algorithm in the induced-switch scenario will be noted below in Subsection 5B.

We developed an alternative algorithm, which yields the full time-dependent rate coefficient.²⁶ The ligand trajectories are started from the binding site. One then obtains the survival probability S(t) as a function of time. The rate coefficient is given by k(t) = k(0)S(t). Here, we use this algorithm to obtain k(t) for the cylindrical binding pocket with the constant-linear potential of Eq. 2.29. The algorithm was recently applied to a gating binding-site situation under induced switch.¹⁹

In Fig. 2, we compare the analytical expression for k(t) given by Eqs. 2.30 against BD simulation results. Data are presented for βV₀ = –3 and L₁/L = 0.2 to 0.8. Very good agreement is seen (difference < 1%), validating the formalism developed in the previous paper¹ for breaking the ligand-binding problem into an exterior problem and an interior problem.

Figure 2.

Comparison of analytical (solid lines) and BD simulation (symbols) results for the rate coefficient in the constant-linear potential of Eq. 2.29. Results at four values of L₁/a are shown in different colors according to the key in the figure. Other parameters are: κ₀ = 0.1D/a; L/a = 5; and βV₀ = –3.

THE GATING BINDING-SITE SITUATION

Indifferent switch

In the indifferent-switch scenario, the binding site switches between a (partially) absorbing conformation and a reflecting conformation according to Eq. 1.1. The pair distribution function, G_g(r, t), now depending on the conformation g, which is either a (for absorbing) or r (for reflecting), of the binding site, satisfies the equations

$$\frac{\partial G_{\mathrm{a}}}{\partial t}=\nabla ·\left\{D{e}^{-\beta U\left(\mathbf{r}\right)}\nabla \left[e^{\beta U\left(\mathbf{r}\right)}{G}_{\mathrm{a}}\right]\right\}-{\omega }_{-}{G}_{\mathrm{a}}+{\omega }_{+}{G}_{\mathrm{r}},$$ (3.1a)

$$\frac{\partial G_{\mathrm{r}}}{\partial t}=\nabla ·\left\{D{e}^{-\beta U\left(\mathbf{r}\right)}\nabla \left[e^{\beta U\left(\mathbf{r}\right)}{G}_{\mathrm{r}}\right]\right\}+{\omega }_{-}{G}_{\mathrm{a}}-{\omega }_{+}{G}_{\mathrm{r}}.$$ (3.1b)

The outer boundary values are

$$G_{\mathrm{g}}(\mathbf{r},t)=p_{\mathrm{g}}\mathrm{as}r\to \infty ,$$ (3.2a)

where

$$p_{\mathrm{a}}={\omega }_{+}∕\omega ;p_{\mathrm{r}}={\omega }_{-}∕\omega .$$ (3.2b)

We now work in Laplace space. By forming the combinations

$$\widehat{G}(\mathbf{r},s)={\widehat{G}}_{\mathrm{a}}(\mathbf{r},s)+{\widehat{G}}_{\mathrm{r}}(\mathbf{r},s),$$ (3.3a)

$$\widehat{F}(\mathbf{r},s)=p_{\mathrm{r}}{\widehat{G}}_{\mathrm{a}}(\mathbf{r},s)-p_{\mathrm{a}}{\widehat{G}}_{\mathrm{r}}(\mathbf{r},s),$$ (3.3b)

we transform Eqs. 3.1 to

$$s\widehat{G}-e^{-\beta U\left(\mathbf{r}\right)}=\nabla ·\left\{D{e}^{-\beta U\left(\mathbf{r}\right)}\nabla \left[e^{\beta U\left(\mathbf{r}\right)}\widehat{G}\right]\right\},$$ (3.4a)

$$s_1\widehat{F}=\nabla ·\left\{D{e}^{-\beta U\left(\mathbf{r}\right)}\nabla \left[e^{\beta U\left(\mathbf{r}\right)}\widehat{F}\right]\right\},$$ (3.4b)

where s₁ = s + ω.

In analogy to Eq. 2.10, we make the following ansatz:

$$\widehat{G}(\mathbf{r},s)={\widehat{A}}_1\left(s\right)\widehat{H}(\mathbf{r},s)+{\widehat{A}}_2\left(s\right)e^{-\beta U\left(\mathbf{r}\right)},$$ (3.5a)

$$\widehat{F}(\mathbf{r},s)={\widehat{B}}_1\left(s\right)\widehat{H}(\mathbf{r},s_1)+{\widehat{B}}_2\left(s\right)e^{-\beta U\left(\mathbf{r}\right)}.$$ (3.5b)

Following the steps of Subsection 2A, we arrive at the following boundary conditions for the reduced one-dimensional distribution functions ${\widehat{g}}_{\mathrm{g}}(x,s)$ in the cylindrical pocket:

$$\mathcal{J}\widehat{g}(L,s)=\left(1-\frac{s\widehat{g}(L,s)}{\sigma e^{-\beta V\left(L\right)}}\right){\widehat{k}}_E\left(s\right),$$ (3.6a)

$$-\mathcal{J}\widehat{f}(L,s)=\frac{s_1{\widehat{k}}_{\mathrm{E}}\left(s_1\right)}{\sigma e^{-\beta V\left(L\right)}}\widehat{f}(L,s),$$ (3.6b)

where $\widehat{g}(x,s)$ and $\widehat{f}(x,s)$ are linear combinations of ${\widehat{g}}_{\mathrm{a}}(x,s)$ and ${\widehat{g}}_{\mathrm{r}}(x,s)$ that are analogous to Eqs. 3.3:

$$\widehat{g}(x,s)={\widehat{g}}_{\mathrm{a}}(x,s)+{\widehat{g}}_{\mathrm{r}}(x,s),$$ (3.7a)

$$\widehat{f}(x,s)=p_{\mathrm{r}}{\widehat{g}}_{\mathrm{a}}(x,s)-p_{\mathrm{a}}{\widehat{g}}_{\mathrm{r}}(x,s).$$ (3.7b)

Corresponding to Eqs. 3.4, we have

$$s\widehat{g}-\sigma e^{-\beta V\left(x\right)}=\mathcal{L}\widehat{g},$$ (3.8a)

$$s_1\widehat{f}=\mathcal{L}\widehat{f}.$$ (3.8b)

Following Eq. 2.17, we can write the solution of Eqs. 3.8 as

$$\widehat{g}(x,s)=\frac{1}{s}\sigma e^{-\beta V\left(x\right)}+{\widehat{C}}_1\left(s\right)\widehat{q}(x,s),$$ (3.9a)

$$\widehat{f}(x,s)={\widehat{C}}_2\left(s\right)\widehat{q}(x,s_1),$$ (3.9b)

which by design satisfies the boundary conditions at x = L given by Eq. 3.6. The boundary conditions at x = 0 are

$$\mathcal{J}{\widehat{g}}_{\mathrm{a}}(0,s)={\kappa }_0{\widehat{g}}_{\mathrm{a}}(0,s),$$ (3.10a)

$$\mathcal{J}{\widehat{g}}_{\mathrm{r}}(0,s)=0.$$ (3.10b)

Using these to determine the coefficients ${\widehat{C}}_1\left(s\right)$ and ${\widehat{C}}_2\left(s\right)$, we finally find the rate coefficient for the present gating binding-site situation to be

$$\begin{array}{ccc}\hfill \frac{1}{s{\widehat{k}}_{\mathrm{G}}\left(s\right)}& \equiv & \frac{1}{s\mathcal{J}{\widehat{g}}_{\mathrm{a}}(0,s)}=\frac{1}{p_{\mathrm{a}}{k}_0}+\frac{1}{-s\mathcal{J}\widehat{q}(0,s)}\hfill \\ & & +\frac{p_{\mathrm{r}}}{p_{\mathrm{a}}}\frac{1}{-s_{1}J\widehat{q}(0,s_1)}.\hfill \end{array}$$ (3.11a)

Using Eq. 2.20 for the ungated rate coefficient $\widehat{k}\left(s\right)$, we can write ${\widehat{k}}_{\mathrm{G}}\left(s\right)$ as

$$\frac{1}{s{\widehat{k}}_{\mathrm{G}}\left(s\right)}=\frac{1}{s\widehat{k}\left(s\right)}+\frac{{\omega }_{-}}{{\omega }_{+}}\frac{1}{(s+\omega )\widehat{k}(s+\omega )},$$ (3.11b)

which is just Eq. 1.3.

Taking the s → 0 limit of Eq. 3.11a and using Eqs. 2.22, 2.23b, we obtain the steady-state rate constant

$$\frac{1}{k_{\mathrm{G}}^{\mathrm{ss}}}=\frac{1}{k_{\mathrm{E}}^{\mathrm{ss}}}+\frac{1}{k_{\mathrm{I}}^{\mathrm{ss}}}+\frac{{\omega }_{-}}{{\omega }_{+}}\left[\frac{1}{k_0}+\frac{1}{-\omega \mathcal{J}\widehat{q}(0,\omega )}\right].$$ (3.11c)

For a constant potential inside the binding pocket, use of Eqs. 2.27, 2.28 in Eq. 3.11b leads to the following expression:

$$\begin{array}{ccc}\hfill \frac{1}{k_{\mathrm{G}}^{\mathrm{ss}}}& =& \frac{1}{k_{\mathrm{E}}^{\mathrm{ss}}}+\frac{1}{p_{\mathrm{a}}{\kappa }_0\sigma e^{-\beta V_0}}+\frac{L}{D\sigma e^{-\beta V_0}}\hfill \\ & & +\frac{p_{\mathrm{r}}}{p_{\mathrm{a}}}\frac{\nu \coth \left(\nu L\right)+\omega {\widehat{k}}_{\mathrm{E}}\left(\omega \right)∕D\sigma e^{-\beta V_0}}{\omega {\widehat{k}}_{\mathrm{E}}\left(\omega \right)\nu \coth \left(\nu L\right)+\omega \sigma e^{-\beta V_0}},\hfill \end{array}$$ (3.11d)

where ν = (ω/D)^1/2.

Induced switch

For an actual protein molecule, the transition rates ω_± between the absorbing conformation and the reflecting conformation will depend on the position of the ligand. Concomitantly, the protein-ligand interaction potential will be conformation-dependent. These position-dependent transition rates ω_±(r) and conformation-dependent potentials U_g(r) satisfy the following detailed balance condition:^{18, 19}

$$\frac{{\omega }_{+}\left(\mathbf{r}\right)}{{\omega }_{-}\left(\mathbf{r}\right)}=\frac{{\omega }_{\infty +}}{{\omega }_{\infty -}}{e}^{-\beta [U_{\mathrm{a}}\left(\mathbf{r}\right)-U_{\mathrm{r}}\left(\mathbf{r}\right)]},$$ (3.12)

in which ω_∞± are the transition rates at r = ∞ [where U_g(r) = 0]. In a typical system, the transition rates will change from favoring the reflecting conformation while the ligand is far away to favoring the absorbing conformation while the ligand is near the binding site. The governing equations for the pair distribution functions G_g(r, t) become¹⁹

$$\begin{array}{ccc}\hfill \frac{\partial G_{\mathrm{a}}}{\partial t}& =& \nabla ·\left\{D{e}^{-\beta U_{\mathrm{a}}\left(\mathbf{r}\right)}\nabla \left[e^{\beta U_{\mathrm{a}}\left(\mathbf{r}\right)}{G}_{\mathrm{a}}\right]\right\}\hfill \\ & & -{\omega }_{-}\left(\mathbf{r}\right)G_{\mathrm{a}}+{\omega }_{+}\left(\mathbf{r}\right)G_{\mathrm{r}},\hfill \end{array}$$ (3.13a)

$$\frac{\partial G_{\mathrm{r}}}{\partial t}=\nabla ·\left\{D{e}^{-\beta U_{\mathrm{r}}\left(\mathbf{r}\right)}\nabla \left[e^{\beta U_{\mathrm{r}}\left(\mathbf{r}\right)}{G}_{\mathrm{r}}\right]\right\}+{\omega }_{-}\left(\mathbf{r}\right)G_{\mathrm{a}}-{\omega }_{+}\left(\mathbf{r}\right)G_{\mathrm{r}}.$$ (3.13b)

We now present explicit results for this induced-switch scenario. First we make the reasonable assumption that, in the exterior region, the interaction potential is independent of the conformation of the binding site, and correspondingly the transition rates take the fixed values ω_±. Second we assume that, throughout the cylindrical pocket, the one-dimensional potentials of mean force V_g(x) are constant, and the transition rates are also constant and denoted as ω_I±. The governing equations for the reduced one-dimensional distribution functions ${\widehat{g}}_{\mathrm{g}}(x,s)$ are

$$s{\widehat{g}}_{\mathrm{a}}-p_{\mathrm{a}}\sigma e^{-\beta V_{\mathrm{a}}}=D\frac{d^2{\widehat{g}}_{\mathrm{a}}}{d{x}^2}-{\omega }_{\mathrm{I}-}{\widehat{g}}_{\mathrm{a}}+{\omega }_{\mathrm{I}+}{\widehat{g}}_{\mathrm{r}},$$ (3.14a)

$$s{\widehat{g}}_{\mathrm{r}}-p_{\mathrm{r}}\sigma e^{-\beta V_{\mathrm{r}}}=D\frac{d^2{\widehat{g}}_{\mathrm{r}}}{d{x}^2}+{\omega }_{\mathrm{I}-}{\widehat{g}}_{\mathrm{a}}-{\omega }_{\mathrm{I}+}{\widehat{g}}_{\mathrm{r}}.$$ (3.14b)

For later reference, we define

$${\omega }_{\mathrm{I}}={\omega }_{\mathrm{I}+}+{\omega }_{\mathrm{I}-},$$ (3.15a)

$$p_{\mathrm{Ia}}={\omega }_{\mathrm{I}+}∕{\omega }_{\mathrm{I}},$$ (3.15b)

$$p_{\mathrm{Ir}}={\omega }_{\mathrm{I}-}∕{\omega }_{\mathrm{I}}.$$ (3.15c)

Using the linear combinations of Eqs. 3.7, we transform the above equations to

$$s\widehat{g}-\sigma e^{-\beta V_{\mathrm{eff}}}=D\frac{d^2\widehat{g}}{d{x}^2},$$ (3.16a)

$$s_{\mathrm{I}1}\widehat{f}=D\frac{d^2\widehat{f}}{d{x}^2},$$ (3.16b)

where

$$e^{-\beta V\mathrm{eff}}=p_{\mathrm{a}}{e}^{-\beta V_{\mathrm{a}}}+p_{\mathrm{r}}{e}^{-\beta V_{\mathrm{r}}}$$ (3.17)

and s_I1 = s + ω_I.

The boundary conditions at x = L are analogous to Eq. 3.6, now given by

$$\mathcal{J}{\widehat{g}}_{\mathrm{E}}\left(s\right)=\left(1-\frac{s{\widehat{g}}_{\mathrm{E}}\left(s\right)}{\sigma e^{-\beta V_{\mathrm{E}}}}\right){\widehat{k}}_{\mathrm{E}}\left(s\right),$$ (3.18a)

$$-\mathcal{J}{\widehat{f}}_{\mathrm{E}}\left(s\right)=\frac{s_1{\widehat{k}}_{\mathrm{E}}\left(s_1\right)}{\sigma e^{-\beta V_{\mathrm{E}}}}{\widehat{f}}_{\mathrm{E}}\left(s\right),$$ (3.18b)

where s₁ = s + ω and

$$e^{\beta V_{\mathrm{E}}}{\widehat{g}}_{\mathrm{E}}\left(s\right)=e^{\beta V_{\mathrm{a}}}{\widehat{g}}_{\mathrm{a}}(L,s)+e^{\beta V_{\mathrm{r}}}{\widehat{g}}_{\mathrm{r}}(L,s),$$ (3.19a)

$$e^{\beta V_{\mathrm{E}}}{\widehat{f}}_{\mathrm{E}}\left(s\right)=p_{\mathrm{r}}{e}^{\beta V_{\mathrm{a}}}{\widehat{g}}_{\mathrm{a}}(L,s)-p_{\mathrm{a}}{e}^{\beta V_{\mathrm{r}}}{\widehat{g}}_{\mathrm{r}}(L,s),$$ (3.19b)

$$\mathcal{J}{\widehat{g}}_{\mathrm{E}}\left(s\right)=\mathcal{J}{\widehat{g}}_{\mathrm{a}}(L,s)+\mathcal{J}{\widehat{g}}_{\mathrm{r}}(L,s),$$ (3.19c)

$$\mathcal{J}{\widehat{f}}_{\mathrm{E}}\left(s\right)=p_{\mathrm{a}}\mathcal{J}{\widehat{g}}_{\mathrm{a}}(L,s)-p_{\mathrm{r}}\mathcal{J}{\widehat{g}}_{\mathrm{r}}(L,s).$$ (3.19d)

The last relations are based on the continuity conditions of $e^{\beta V_{\mathrm{g}}}{\widehat{g}}_{\mathrm{g}}$ and $\mathcal{J}{\widehat{g}}_{\mathrm{g}}$. In terms of $\widehat{g}$ and $\widehat{f}$, we can write them as

$$\begin{array}{ccc}\hfill e^{\beta V_{\mathrm{E}}}{\widehat{g}}_{\mathrm{E}}\left(s\right)& =& e^{\beta V_{\mathrm{eff}}}\widehat{g}(L,s)+(e^{\beta V_{\mathrm{a}}}-e^{\beta V_{\mathrm{r}}})\widehat{f}(L,s)\hfill \\ & =& e^{\beta V_{\mathrm{eff}}}[\widehat{g}(L,s)-(\Delta p∕p_{\mathrm{Ia}}{p}_{\mathrm{Ir}})\widehat{f}(L,s)],\hfill \end{array}$$ (3.20a)

$$\begin{array}{ccc}\hfill e^{\beta V_{\mathrm{E}}}{\widehat{f}}_{\mathrm{E}}\left(s\right)& =& e^{\beta V_{\mathrm{a}}+\beta V_{\mathrm{r}}-\beta V_{\mathrm{eff}}}\widehat{f}(L,s)\hfill \\ & =& e^{\beta V_{\mathrm{eff}}}(p_{\mathrm{a}}{p}_{\mathrm{r}}∕p_{\mathrm{Ia}}{p}_{\mathrm{Ir}})\widehat{f}(L,s),\hfill \end{array}$$ (3.20b)

$$\mathcal{J}{\widehat{g}}_{\mathrm{E}}\left(s\right)=\mathcal{J}\widehat{g}(L,s),$$ (3.20c)

$$\mathcal{J}{\widehat{f}}_{\mathrm{E}}\left(s\right)=\Delta p\mathcal{J}\widehat{g}(L,s)+\mathcal{J}\widehat{f}(L,s),$$ (3.20d)

where

$$\Delta p=p_{\mathrm{Ia}}{p}_{\mathrm{r}}-p_{\mathrm{Ir}}{p}_{\mathrm{a}}=p_{\mathrm{Ia}}-p_{\mathrm{a}}=p_{\mathrm{r}}-p_{\mathrm{Ir}}.$$ (3.21)

The boundary conditions at x = 0 are still given by Eqs. 3.10.

The steady-state solution of Eqs. 3.16 has the form

$$g^{\mathrm{ss}}\left(x\right)=B_1+B_{2}x,$$ (3.22a)

$$f^{\mathrm{ss}}\left(x\right)=C_1{e}^{{\nu }_{\mathrm{I}}x}+C_2{e}^{-{\nu }_{\mathrm{I}}x},$$ (3.22b)

where ν_I = (ω_I/D)^1/2. Using the boundary conditions of Eqs. 3.10, 3.18 to determine the coefficients, we find the rate constant under induced switch to be

$$\begin{array}{c}\hfill \frac{1}{k_{\mathrm{G}}^{\mathrm{ss}}}=\frac{1}{k_{\mathrm{E}}^{\mathrm{ss}}}+\frac{1}{p_{\mathrm{Ia}}{\kappa }_0\sigma e^{-\beta V_{e\mathrm{ff}}}}+\frac{L}{D\sigma e^{-\beta V_{e\mathrm{ff}}}}+\frac{p_{\mathrm{Ir}}}{p_{\mathrm{Ia}}}\frac{{\displaystyle \left(1+\frac{\Delta p^2}{p_{\mathrm{Ir}}^2}\right){\nu }_{\mathrm{I}}\coth \left({\nu }_{\mathrm{I}}L\right)+\frac{p_{\mathrm{a}}{p}_{\mathrm{r}}}{p_{\mathrm{Ia}}{p}_{\mathrm{Ir}}}\frac{\omega {\widehat{k}}_{\mathrm{E}}\left(\omega \right)}{D\sigma e^{-\beta V_{\mathrm{eff}}}}+\frac{2\Delta p}{p_{\mathrm{Ir}}}\frac{{\nu }_{\mathrm{I}}}{\sinh \left({\nu }_{\mathrm{I}}L\right)}}}{(p_{\mathrm{a}}{p}_{\mathrm{r}}∕p_{\mathrm{Ia}}{p}_{\mathrm{Ir}})\omega {\widehat{k}}_{\mathrm{E}}\left(\omega \right){\nu }_{\mathrm{I}}\coth \left({\nu }_{\mathrm{I}}L\right)+{\omega }_{\mathrm{I}}\sigma e^{-\beta V_{\mathrm{eff}}}}.\end{array}$$ (3.23)

It can be easily verified that, when ω_I± = ω_± and V_eff = V₀, Eq. 3.23 reduces to the indifferent-switch result of Eq. 3.11d. When gating is infinitely slow (i.e., ω and ω_I → 0), conformational selection emerges as the binding mechanism and the rate constant is

$$\frac{1}{k_{\mathrm{CS}}^{\mathrm{ss}}}=\frac{1}{p_{\mathrm{a}}}\left(\frac{1}{k_{\mathrm{E}}^{\mathrm{ss}}}+\frac{1}{{\kappa }_0\sigma e^{-\beta V_{\mathrm{a}}}}+\frac{L}{D\sigma e^{-\beta V_{\mathrm{a}}}}\right).$$ (3.24a)

This $k_{\mathrm{CS}}^{\mathrm{ss}}$ result can be recognized as the product of p_a and the rate constant for an always-absorbing binding site, as to be expected.^{18, 19} When gating is infinitely fast (i.e., ω and ω_I → ∞), induced fit emerges as the binding mechanism and the rate constant is

$$\frac{1}{k_{\mathrm{IF}}^{\mathrm{ss}}}=\frac{1}{k_{\mathrm{E}}^{\mathrm{ss}}}+\frac{1}{p_{\mathrm{Ia}}{\kappa }_0\sigma e^{-\beta V_{e\mathrm{ff}}}}+\frac{L}{D\sigma e^{-\beta V_{e\mathrm{ff}}}},$$ (3.24b)

which is produced by an always-absorbing binding site with reactivity p_Iaκ₀ and a potential V_eff, also to be expected.^{18, 19}

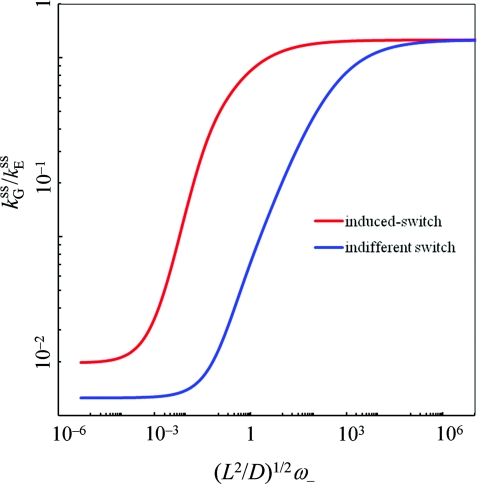
In Fig. 3, we compare $k_{\mathrm{G}}^{\mathrm{ss}}$ given by Eq. 3.23 for the induced-switch scenario against the counterpart given by Eq. 3.11d for the indifferent-switch scenario. Two significant differences can be seen. First, the decrease in $k_{\mathrm{G}}^{\mathrm{ss}}$ in the slow-gating limit is smaller under induced switch than under indifferent switch. More importantly, the shift of $k_{\mathrm{G}}^{\mathrm{ss}}$ toward the upper bound in the fast-gating limit occurs at much lower values of the conformational transition rates. This means that, under induced switch, the ligand binding rate constant becomes maximal even at relatively low conformational transition rates.

Figure 3.

$k_{\mathrm{G}}^{\mathrm{ss}}$ (scaled by $k_{\mathrm{E}}^{\mathrm{ss}}=4Da$) for a gating binding site under either induced switch (red curve) or indifferent switch (blue curve). The indifferent-switch scenario has a constant potential V₀ = V_eff in the binding pocket. Parameters are as follows: κ₀ = ∞; L/a = 5; p_a/p_r = 0.01; p_Ia/p_Ir = 10; e^−βVa = 10³; and e^−βVr = 1.

One example of the gating binding-site situation presented here is a gate located midway along the binding pocket. That case will be discussed in Subsection 5C.

THE GATING CIRCULAR BINDING SITE

The problem of an absorbing disk located on an otherwise inert plane has attracted considerable attention as a model for protein-ligand binding and for electrode.^{21, 22, 27, 28, 29, 30}. The rate coefficient ${\widehat{k}}_{\mathrm{E}}\left(s\right)$ for such a binding site is given by Eq. 2.21. When the depth L = 0, the cylindrical binding pocket considered in Secs. 2, 3 reduces to a circular binding site on an inert plane. Therefore, by setting L = 0, the preceding results for partial absorption and stochastic gating apply to the circular binding site. The rate coefficient ${\widehat{k}}_{\mathrm{E};\mathrm{G}}\left(s\right)$ under stochastic gating will play a key role in Secs. 5, 6. Here, we check the accuracy of the results.

Setting L = 0 in Eq. 2.18b and using Eq. 2.18c, we obtain

$$-\mathcal{J}\widehat{q}(0,s)=s{\widehat{k}}_{\mathrm{E}}\left(s\right).$$ (4.1)

Using this result in Eq. 2.20, we obtain the following expression for the rate coefficient ${\widehat{k}}_{\mathrm{Ep}}\left(s\right)$ when the disk is partially absorbing:

$$\frac{1}{s{\widehat{k}}_{\mathrm{Ep}}\left(s\right)}=\frac{1}{{\kappa }_0\sigma }+\frac{1}{s{\widehat{k}}_{\mathrm{E}}\left(s\right)}.$$ (4.2)

This was first proposed by Zwanzig and Szabo.²¹ For the case where the disk switches stochastically between a partially absorbing conformation and a reflecting conformation, using Eq. 4.1 in Eq. 3.11a, we find that the rate coefficient ${\widehat{k}}_{\mathrm{Ep};\mathrm{G}}\left(s\right)$ is related to ${\widehat{k}}_{\mathrm{E};\mathrm{G}}\left(s\right)$, the rate coefficient when absorption is complete rather than partial, via

$$\frac{1}{s{\widehat{k}}_{\mathrm{Ep};\mathrm{G}}\left(s\right)}=\frac{1}{p_{\mathrm{a}}{\kappa }_0\sigma }+\frac{1}{s{\widehat{k}}_{\mathrm{E};\mathrm{G}}\left(s\right)},$$ (4.3)

where p_a = ω₊/ω is the probability that the disk is in the absorbing conformation. ${\widehat{k}}_{\mathrm{E};\mathrm{G}}\left(s\right)$ in turn is given by

$$\frac{1}{s{\widehat{k}}_{\mathrm{E};\mathrm{G}}\left(s\right)}=\frac{1}{s{\widehat{k}}_{\mathrm{E}}\left(s\right)}+\frac{{\omega }_{-}}{{\omega }_{+}}\frac{1}{(s+\omega ){\widehat{k}}_{\mathrm{E}}(s+\omega )},$$ (4.4)

which conforms to Eq. 1.3. Below we demonstrate the accuracy of Eqs. 4.3, 4.4 analytically and by BD simulations.

Expansion of ${\widehat{k}}_{Ep;G}\left(s\right)$ at small s

In 1996, we derived a general result for the long-time asymptote of any time-dependent rate coefficient, which in Laplace space takes the form¹⁰

$$s\widehat{k}\left(s\right)=k^{\mathrm{ss}}\left[1+\frac{k^{\mathrm{ss}}}{2\pi D}{(s∕D)}^{1∕2}+\cdots \right]$$ (4.5a)

for small s. (The factor 2π would be 4π if the ligand were allowed to approach infinity from all directions.) It can be easily verified that the small s expansion of ${\widehat{k}}_{\mathrm{E}}\left(s\right)$ in Eq. 2.21 conforms to Eq. 4.5a, with $k_{\mathrm{E}}^{\mathrm{ss}}=4Da$. We now show that ${\widehat{k}}_{\mathrm{E};\mathrm{G}}\left(s\right)$ given by Eq. 4.4 also conforms to Eq. 4.5a. To that end, we first express Eq. 4.5a in an equivalent form:

$$\frac{1}{s\widehat{k}\left(s\right)}=\frac{1}{k^{\mathrm{ss}}}-\frac{1}{2\pi D}{(s∕D)}^{1∕2}+\cdots .$$ (4.5b)

Note that the coefficient of the s^1/2 term on the right-hand side of Eq. 4.5b only depends on the diffusion constant D. The expansion of the first term on the right-hand side of Eq. 4.4 already contributes such an s^1/2 term. Therefore the expansion of the second term on the right-hand side of Eq. 4.4 must not have an s^1/2 term. This is indeed the case, since in the second term s appears in the form of s + ω, and the expansion of (s + ω)^1/2 does not have an s^1/2 term.

In Eq. 4.3, a constant term is added on the right-hand side. Since the constant term cannot contribute an s^1/2 term, we find that ${\widehat{k}}_{\mathrm{Ep};\mathrm{G}}\left(s\right)$ given by Eq. 4.3 also conforms to Eq. 4.5b and hence the correct small-s (i.e., long-time) behavior of Eq. 4.5a.

Expansion of ${\widehat{k}}_{\mathrm{E};\mathrm{G}}\left(s\right)$ at large s

Oldham²⁷ derived the first two terms in the short-time expansion of k_E(t). In Laplace space, the corresponding large-s expansion takes the form

$$s{\widehat{k}}_{\mathrm{E}}\left(s\right)=D\sigma {(s∕D)}^{1∕2}+\pi Da+\cdots .$$ (4.6a)

The first term, known as the Cottrell term, corresponds to a uniform flux into the surface area of the absorbing disk; the second term corresponds to the flux through the rim of the disk. Note that the expansion of $(s+\omega ){\widehat{k}}_{\mathrm{E}}(s+\omega )$ has the same two leading terms:

$$(s+\omega ){\widehat{k}}_{\mathrm{E}}(s+\omega )=D\sigma {(s∕D)}^{1∕2}+\pi Da+\cdots .$$ (4.6b)

In Appendix A, we calculate the two leading terms of ${\widehat{k}}_{\mathrm{E};\mathrm{G}}\left(s\right)$. Each is the corresponding term in Eq. 4.6a scaled by p_a, leading to

$$s{\widehat{k}}_{\mathrm{E};\mathrm{G}}\left(s\right)=p_{\mathrm{a}}D\sigma {(s∕D)}^{1∕2}+\pi p_{\mathrm{a}}Da+\cdots .$$ (4.7)

Using Eqs. 4.6 in Eq. 4.4, one can easily verify that the resulting expansion for ${\widehat{k}}_{\mathrm{E};\mathrm{G}}\left(s\right)$ agrees with Eq. 4.7.

BD simulations

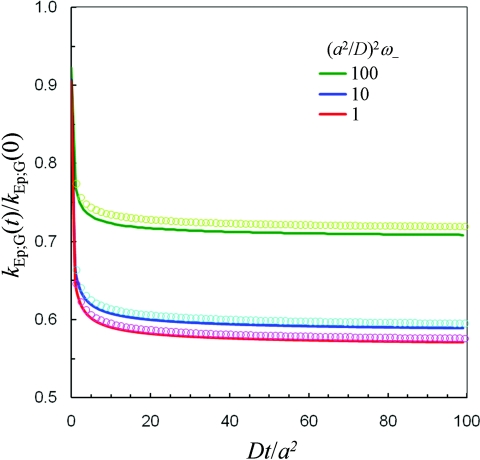
In Fig. 4, we compare k_{Ep; G}(t) given by Eqs. 4.3, 4.4 against BD simulation results for three sets of ω_± values. The analytical formulas only understate slightly (<1.5%) the simulation results.

Figure 4.

Comparison of analytical (solid lines) and BD simulation (symbols) results for the rate coefficient of binding to a gating disk. Results at three values of (a²/D)^1/2ω_– are shown in different colors according to the key in the figure. Other parameters are: κ₀ = D/a; and (a²/D)^1/2ω₊ = 100.

THE GATED ACCESS SITUATION

Indifferent switch

We now consider the case where a stochastic gate is present at the entrance to the cylindrical pocket (Fig. 1b). The open and closed conformations will be denoted with subscripts o and c, respectively. The governing equation for the pair distribution function G_g(r, t) here is analogous to Eqs. 3.1. However, while exp[βU(r)]G_o(r, t) is continuous across the pocket entrance, G_c(r, t) here satisfies the reflecting boundary condition on the entrance. The exterior problem now involves a gating binding site on the pocket entrance. This is just the problem dealt with in Sec. 4. Let the pair distribution for that problem be denoted as H_g(r, t). Analogous to Eq. 2.10, we make the ansatz

$${\widehat{G}}_{\mathrm{o}}(\mathbf{r},s)={\widehat{A}}_1\left(s\right){\widehat{H}}_{\mathrm{o}}(\mathbf{r},s)+{\widehat{A}}_2\left(s\right)e^{-\beta U\left(\mathbf{r}\right)}.$$ (5.1)

This leads to the following boundary condition for the reduced distribution function ${\widehat{g}}_{\mathrm{o}}(x,s)$ at x = L:

$$\mathcal{J}{\widehat{g}}_{\mathrm{o}}(L,s)=\left(1-\frac{s{\widehat{g}}_{\mathrm{o}}(L,s)}{p_{\mathrm{o}}\sigma e^{-\beta V\left(L\right)}}\right){\widehat{k}}_{\mathrm{E};\mathrm{G}}\left(s\right),$$ (5.2a)

where ${\widehat{k}}_{\mathrm{E};\mathrm{G}}\left(s\right)$ is the rate coefficient calculated from H_g(r, t). The boundary condition at x = L is reflecting for ${\widehat{g}}_{\mathrm{c}}(x,s)$; hence,

$$\mathcal{J}{\widehat{g}}_{\mathrm{c}}(L,s)=0.$$ (5.2b)

The boundary conditions at x = 0 are

$$\mathcal{J}{\widehat{g}}_{\mathrm{o}}(0,s)={\kappa }_0{\widehat{g}}_{\mathrm{o}}(0,s),$$ (5.3a)

$$\mathcal{J}{\widehat{g}}_{\mathrm{c}}(0,s)={\kappa }_0{\widehat{g}}_{\mathrm{c}}(0,s).$$ (5.3b)

We again combine ${\widehat{g}}_{\mathrm{o}}(x,s)$ and ${\widehat{g}}_{\mathrm{c}}(x,s)$ in analogy to Eqs. 3.7. The resulting $\widehat{g}(x,s)$ and $\widehat{f}(x,s)$ are governed by Eqs. 3.8. The boundary conditions at x = 0 can be written as

$$\mathcal{J}\widehat{g}(0,s)={\kappa }_0\widehat{g}(0,s),$$ (5.4a)

$$\mathcal{J}\widehat{f}(0,s)={\kappa }_0\widehat{f}(0,s).$$ (5.4b)

We introduce two specific solutions to the equation

$$s\widehat{i}(x,s)=\mathcal{L}\widehat{i}(x,s).$$ (5.5)

The first, ${\widehat{i}}_1(x,s)$, is specified by the boundary conditions

$$\mathcal{J}{\widehat{i}}_1(L,s)=0,$$ (5.6a)

$${\widehat{i}}_1(0,s)=\frac{1}{s}\sigma e^{-\beta V\left(0\right)}.$$ (5.6b)

The second, ${\widehat{i}}_2(x,s)$, is specified by the boundary conditions

$${\widehat{i}}_2(L,s)=\frac{1}{s}\sigma e^{-\beta V\left(L\right)},$$ (5.7a)

$$\mathcal{J}{\widehat{i}}_2(0,s)={\kappa }_0{\widehat{i}}_2(0,s).$$ (5.7b)

Using ${\widehat{i}}_1(x,s)$ and ${\widehat{i}}_2(x,s)$, we can construct $\widehat{g}(x,s)$ and $\widehat{f}(x,s)$ as

$$\widehat{g}(x,s)=\frac{1}{s}\sigma e^{-\beta V\left(x\right)}+{\widehat{B}}_1\left(s\right){\widehat{i}}_1(x,s)+{\widehat{B}}_2\left(s\right){\widehat{i}}_2(x,s),$$ (5.8a)

$$\widehat{f}(x,s)=\widehat{C}\left(s\right){\widehat{i}}_2(x,s_1).$$ (5.8b)

By design $\widehat{f}(x,s)$ satisfies the boundary condition of Eq. 5.4b. Determining the three coefficients of Eqs. 5.8 using the boundary conditions of Eqs. 5.2, 5.4a, we obtain the rate coefficient ${\widehat{k}}_{\mathrm{G}}\left(s\right)$ in the present gated access situation:

$$\begin{array}{ccc}\hfill s{\widehat{k}}_{\mathrm{G}}\left(s\right)\equiv s\mathcal{J}\widehat{g}(0,s)& =& {\displaystyle \frac{-s\mathcal{J}{\widehat{i}}_1(0,s)}{1-s\mathcal{J}{\widehat{i}}_1(0,s)∕k_0}+\frac{s{\widehat{i}}_1(L,s)∕\sigma e^{-\beta V\left(L\right)}}{1-s\mathcal{J}{\widehat{i}}_1(0,s)∕k_0}}\hfill \\ & & \times \frac{1}{{\displaystyle \frac{1}{s\mathcal{J}{\widehat{i}}_2(0,s)}+\frac{\mathcal{J}{\widehat{i}}_2(L,s)}{\mathcal{J}{\widehat{i}}_2(0,s)}\frac{1}{s{\widehat{k}}_{\mathrm{E};\mathrm{G}}\left(s\right)}+\frac{{\omega }_{-}}{{\omega }_{+}}\frac{\mathcal{J}{\widehat{i}}_2(L,s)}{\mathcal{J}{\widehat{i}}_2(0,s)}\frac{1}{s_1\mathcal{J}{\widehat{i}}_2(L,s_1)}}}.\hfill \end{array}$$ (5.9)

At the steady state (i.e., s → 0), $s\mathcal{J}{\widehat{i}}_1(0,s)=0$ and $s\mathcal{J}{\widehat{i}}_2(0,s)=s\mathcal{J}{\widehat{i}}_2(L,s)=k_{\mathrm{I}}^{\mathrm{ss}}$ [given by Eq. 2.23b]. Correspondingly, the steady-state rate constant is

$$\frac{1}{k_{\mathrm{G}}^{\mathrm{ss}}}=\frac{1}{k_{\mathrm{E};\mathrm{G}}^{\mathrm{ss}}}+\frac{1}{k_{\mathrm{I}}^{\mathrm{ss}}}+\frac{{\omega }_{-}}{{\omega }_{+}}\frac{1}{\omega \mathcal{J}{\widehat{i}}_2(L,\omega )}.$$ (5.10)

The sum of the last two terms corresponds to the rate constant $k_{\mathrm{I};\mathrm{G}}^{\mathrm{ss}}$:

$$\frac{1}{k_{\mathrm{I};\mathrm{G}}^{\mathrm{ss}}}=\frac{1}{k_{\mathrm{I}}^{\mathrm{ss}}}+\frac{{\omega }_{-}}{{\omega }_{+}}\frac{1}{\omega \mathcal{J}{\widehat{i}}_2(L,\omega )},$$ (5.11)

for an interior problem, in which the pair distribution function $h_{\mathrm{g}}^{\mathrm{ss}}\left(x\right)$ satisfies the following boundary conditions at x = L:

$$h_{\mathrm{o}}^{\mathrm{ss}}\left(L\right)=p_{\mathrm{o}}\sigma e^{-\beta V\left(L\right)},$$ (5.12a)

$$\mathcal{J}{h}_{\mathrm{c}}^{\mathrm{ss}}\left(L\right)=0.$$ (5.12b)

That is, the pair distribution function takes the equilibrium value if the gate is open and is reflected if the gate is closed. With the identification of $\mathcal{J}{\widehat{i}}_2(L,\omega )$ and ${\widehat{j}}_{\mathrm{I}}\left(\omega \right)$, Eq. 5.11 is just Eq. 1.4b. To prove Eq. 5.11, one just has to recognize that Eq. 5.2a leads to Eq. 5.12a when $k_{\mathrm{E};\mathrm{G}}^{\mathrm{ss}}$ → ∞. Now, in that limit Eq. 5.10 becomes Eq. 5.11.

Note that Eq. 5.10 bears some resemblance to the $k_{\mathrm{G}}^{\mathrm{ss}}$ result for the gating binding-site situation given by Eq. 3.11c, with ${\widehat{i}}_2(x,s)$ here playing a similar role as $\widehat{q}(x,s)$ there. For a constant potential inside the binding pocket, solving ${\widehat{i}}_2(x,s)$ in analogy to $\widehat{q}(x,s)$ in Subsection 2C, we find the rate constant to be

$$\begin{array}{ccc}\hfill \frac{1}{k_{\mathrm{G}}^{\mathrm{ss}}}& =& \frac{1}{k_{\mathrm{E};\mathrm{G}}^{\mathrm{ss}}}+\frac{1}{{\kappa }_0\sigma e^{-\beta V_0}}+\frac{L}{D\sigma e^{-\beta V_0}}\hfill \\ & & +\frac{p_{\mathrm{c}}}{p_{\mathrm{o}}}\frac{\nu \coth \left(\nu L\right)+k_0∕D\sigma e^{-\beta V_0}}{k_0\nu \coth \left(\nu L\right)+\omega \sigma e^{-\beta V_0}},\hfill \end{array}$$ (5.13)

where k₀=κ₀σe^−βV₀ and ν = (ω/D)^1/2. When ω → ∞, the last term disappears and $k_{\mathrm{G}}^{\mathrm{ss}}$ → k^ss, the rate constant when the gate stays in the open conformation.^{14, 31} Note also the similarity between Eq. 5.13 and the counterpart, Eq. 3.11d, in Subsection 3A. The $k_{\mathrm{G}}^{\mathrm{ss}}$ result for a linear potential in the binding pocket and κ₀ = ∞ was given previously.¹⁷

Induced switch

We now consider the case where the transitions rates when the ligand is outside the gate are different from those inside the gate. The latter are denoted as ω_I±. The induced-switch model considered here is similar to that described in Subsection 3B. In particular,

$$\frac{{\omega }_{\mathrm{I}+}}{{\omega }_{\mathrm{I}-}}=\frac{{\omega }_{+}}{{\omega }_{-}}{e}^{-\beta (V_{\mathrm{o}}-V_{\mathrm{c}})}.$$ (5.14a)

Or, in terms of the equilibrium probabilities of the open and closed conformations,

$$\frac{p_{\mathrm{Io}}}{p_{\mathrm{Ic}}}=\frac{p_{\mathrm{o}}}{p_{\mathrm{c}}}{e}^{-\beta (V_{\mathrm{o}}-V_{\mathrm{c}})}.$$ (5.14b)

The boundary condition of Eq. 5.2a now becomes

$$\mathcal{J}{\widehat{g}}_{\mathrm{o}}(L,s)=\left(1-\frac{s{\widehat{g}}_{\mathrm{o}}(L,s)}{p_{\mathrm{Io}}\sigma e^{-\beta V_{\mathrm{eff}}\left(L\right)}}\right){\widehat{k}}_{\mathrm{E};\mathrm{G}}\left(s\right).$$ (5.15)

The interior problem is essentially the same as in the indifferent-switch case of Subsection 5A, but with ω_± replaced by ω_I± and V₀ replaced by V_eff. Making these replacements in Eq. 5.13, we find the rate constant for the interior problem now to be given by

$$\begin{array}{ccc}\hfill \frac{1}{k_{\mathrm{G}}^{\mathrm{ss}}}& =& \frac{1}{k_{\mathrm{E};\mathrm{G}}^{\mathrm{ss}}}+\frac{1}{{\kappa }_0\sigma e^{-\beta V_{\mathrm{eff}}}}+\frac{L}{D\sigma e^{-\beta V_{\mathrm{eff}}}}\hfill \\ \hfill & & +\frac{p_{\mathrm{Ic}}}{p_{\mathrm{Io}}}\frac{{\nu }_{\mathrm{I}}\coth \left({\nu }_{\mathrm{I}}L\right)+{\kappa }_0∕D}{{\kappa }_0\sigma e^{-\beta V_{\mathrm{eff}}}{\nu }_{\mathrm{I}}\coth \left({\nu }_{\mathrm{I}}L\right)+{\omega }_{\mathrm{I}}\sigma e^{-\beta V_{\mathrm{eff}}}}.\hfill \end{array}$$ (5.16)

One might have expected that, in the induced-switch case, the ligand inside the gate would favor the closed conformation of the gate (i.e., p_Ic/p_Io ≫ 1), such that the ligand would be trapped, assuring its ultimate binding. Indeed, if one naively applies the BD simulation algorithm of Northrup et al.,²³ the calculated capture probability and hence the ligand-binding rate constant would increase with increasing p_Ic/p_Io. However, Eq. 5.16 shows that $k_{\mathrm{G}}^{\mathrm{ss}}$ decreases with increasing p_Ic/p_Io. This inverse relationship would be correctly predicted by our BD simulation algorithm,²⁶ since the survival probability of a ligand started from the binding site, and hence k_G(t), would decrease with increasing p_Ic/p_Io.

The inverse relationship between $k_{\mathrm{G}}^{\mathrm{ss}}$ and p_Ic/p_Io can be rationalized in the following way. The ratio of $k_{\mathrm{G}}^{\mathrm{ss}}$ and the unbinding rate constant is the binding constant, which is determined by protein-ligand interactions at the binding site³² and hence in the present case is independent of p_Ic/p_Io. Therefore $k_{\mathrm{G}}^{\mathrm{ss}}$ and the unbinding rate constant should have the same dependence on p_Ic/p_Io. Now, clearly the unbinding rate constant decreases with increasing p_Ic/p_Io. We can thus conclude that $k_{\mathrm{G}}^{\mathrm{ss}}$ should also decrease with increasing p_Ic/p_Io. That the BD simulation algorithm of Northrup et al. may predict the opposite trend suggests that one should be cautious in applying this method to systems involving induced switch.

Gate located midway along the binding pocket

When the gate is located midway along the binding pocket (Fig. 1c), the results presented in Subsections 5A, 5B are still valid, except that ${\widehat{k}}_{\mathrm{E};\mathrm{G}}\left(s\right)$ now represents the rate coefficient for binding to a site represented by the fluctuating gate. That problem is just what is modeled by the gating binding-site situation of Sec. 3 – the open gate corresponds to the binding site in the absorbing conformation and the closed gate corresponds to the reflecting conformation. ${\widehat{k}}_{\mathrm{G}}\left(s\right)$ there, with κ₀ set to infinity, is just ${\widehat{k}}_{\mathrm{E};\mathrm{G}}\left(s\right)$ for the present case.

THE GATING BINDING-POCKET SITUATION

Finally, we consider the situation where the ligand once entering the binding pocket induces both the closure of the lid and the switch of the binding site from the inert conformation to the reactive conformation. In principle, the lid and the binding site will have different dynamics, though these can be coupled. Here, we consider the extreme case, depicted in Fig. 1d, where the open lid is always coincident with the inert binding site and the closed lid is always with the reactive binding site. The switches between the two states are stochastic. In the opposite extreme, not considered here, the lid and the binding site would be modeled as independent stochastic gates.

The solution of the rate coefficient for the gating binding-pocket situation as defined above is very similar to that presented in Sec. 5 for the gated access situation. The boundary conditions on the lid are the same as the corresponding results there. However, the boundary conditions on the binding site are different. Instead of Eqs. 5.3, we now have

$$\mathcal{J}{\widehat{g}}_{\mathrm{o}}(0,s)=0,$$ (6.1a)

$$\mathcal{J}{\widehat{g}}_{\mathrm{c}}(0,s)={\kappa }_0{\widehat{g}}_{\mathrm{c}}(0,s),$$ (6.1b)

which express the coincidence between the open lid and inert binding site and between the closed lid and reactive binding site. The boundary conditions of the gating binding-pocket situation at the lid are the same as those of the gated access situation but at the binding site are the same as those of the gating binding-site situation. In this sense, the gating binding-pocket situation is a hybrid of the gated access situation and the gating binding-site situation.

Indifferent switch

Suppose that the transition rates between the open lid/inert binding-site state and the closed lid/reactive binding-site state have fixed values ω_± regardless where the ligand is located. Note that as far as the binding site is concerned the notations for the transition rates are the same as those used for the gating binding-site situation (Fig. 1a), but as far as the lid is concerned the present notations correspond to an interchange of ω₊ and ω_– used for the gated access situation (Fig. 1b). The only impact of this interchange is on ${\widehat{k}}_{\mathrm{E};\mathrm{G}}\left(s\right)$ (the rate coefficient for binding to the fluctuating lid). It is understood that the ${\widehat{k}}_{\mathrm{E};\mathrm{G}}\left(s\right)$ result of Sec. 4 is used below with the interchange of ω₊ and ω_–.

We only present results for the steady-state limit. In analogy to the steady-state versions of Eqs. 5.8, we may write the solution of the one-dimensional pair distribution functions as

$$g^{\mathrm{ss}}\left(x\right)=\sigma e^{-\beta V\left(x\right)}+B_1{i}_1^{\mathrm{ss}}\left(x\right)+B_2{i}_2^{\mathrm{ss}}\left(x\right),$$ (6.2a)

$$f^{\mathrm{ss}}\left(x\right)=C_1\left(\omega \right){\widehat{i}}_1(x,\omega )+C_2\left(\omega \right){\widehat{i}}_2(x,\omega ).$$ (6.2b)

Determining the coefficients using the boundary conditions at x = L and x = 0, we find the steady-state rate constant to be

$$\begin{array}{ccc}\hfill {\displaystyle \frac{1}{k_{\mathrm{G}}^{\mathrm{ss}}}}& =& \frac{1}{k_{\mathrm{E};\mathrm{G}}^{\mathrm{ss}}}+\frac{1}{k_{\mathrm{I}}^{\mathrm{ss}}}+\frac{p_{\mathrm{c}}}{p_{\mathrm{o}}}\frac{1}{\omega \mathcal{J}{\widehat{i}}_2(L,\omega )}\hfill \\ & & {\displaystyle +\frac{p_{\mathrm{c}}}{p_{\mathrm{o}}}\frac{\omega {\widehat{i}}_1(L,\omega )}{\sigma e^{-\beta V\left(L\right)}}\frac{\mathcal{J}{\widehat{i}}_2(0,\omega )}{\mathcal{J}{\widehat{i}}_2(L,\omega )}\frac{1}{-\omega \mathcal{J}{\widehat{i}}_1(0,\omega )}}\hfill \\ & & {\displaystyle +\frac{p_{\mathrm{o}}}{p_{\mathrm{c}}}\left[\frac{1}{k_0}+\frac{1}{-\omega \mathcal{J}{\widehat{i}}_1(0,\omega )}\right]}\hfill \\ & & {\displaystyle +\frac{\omega {\widehat{i}}_1(L,\omega )}{\sigma e^{-\beta V\left(L\right)}}\frac{2}{-\omega \mathcal{J}{\widehat{i}}_1(0,\omega )}.}\hfill \end{array}$$ (6.3)

Compared to Eq. 5.10, it can be seen that the first three terms give the rate constant of the gated access situation. The presence of the additional terms means that the rate constant here for the gating binding-pocket situation is lower. The decrease in rate constant is understandable since now, in addition to the fluctuating lid, the fluctuating binding site serves to further reduce $k_{\mathrm{G}}^{\mathrm{ss}}$. Moreover, instead of a monotonic dependence on p_c/p_o, $k_{\mathrm{G}}^{\mathrm{ss}}$ decreases when p_c/p_o becomes either too small or too big and is maximal when p_c/p_o = 1. The decrease of $k_{\mathrm{G}}^{\mathrm{ss}}$ at both extremes of p_c/p_o comes about due to the coincidence of open lid and inert binding site and of closed lid and reactive binding site in the present model. An open lid allows the ligand to enter the binding pocket but the accompanying inert binding site would not allow ligand binding. Conversely, a closed lid would prevent the ligand to enter the binding pocket, regardless of the fact that the closed lid is accompanied by a reactive binding site.

Like Eq. 5.11 in the gated access situation, the terms beyond the first one in Eq. 6.3 express the rate constant $k_{\mathrm{I};\mathrm{G}}^{\mathrm{ss}}$ for the interior problem in which the pair distribution function satisfies the boundary conditions of Eqs. 5.11. For a constant potential in the binding pocket, explicit solution of ${\widehat{i}}_1(x,s)$ and ${\widehat{i}}_2(x,s)$ leads to the following expression for $k_{\mathrm{I};\mathrm{G}}^{\mathrm{ss}}$:

$$\begin{array}{ccc}\hfill \frac{1}{k_{\mathrm{I};\mathrm{G}}^{\mathrm{ss}}}& =& \frac{1}{p_{\mathrm{c}}{\kappa }_0\sigma e^{-\beta V_0}}+\frac{L}{D\sigma e^{-\beta V_0}}+\left(\frac{p_{\mathrm{c}}}{p_{\mathrm{o}}}+\frac{p_{\mathrm{o}}}{p_{\mathrm{c}}}\right)\frac{\nu \coth \left(\nu L\right)}{\omega \sigma e^{-\beta V_0}}\hfill \\ & & +\frac{2\nu }{\omega \sigma e^{-\beta V_0}\sinh \left(\nu L\right)}.\hfill \end{array}$$ (6.4)

Induced switch

Similar to the gated access situation, the rate constant in the induced-switch case can be obtained from Eq. 6.4, the result for the indifferent-switch case, by replacing ω_± with ω_I± and V₀ with V_eff, leading to

$$\begin{array}{ccc}\hfill \frac{1}{k_{\mathrm{I};\mathrm{G}}^{\mathrm{ss}}}& =& \frac{1}{p_{\mathrm{Ic}}{\kappa }_0\sigma e^{-\beta V_{\mathrm{eff}}}}+\frac{L}{D\sigma e^{-\beta V_{\mathrm{eff}}}}+\left(\frac{p_{\mathrm{Ic}}}{p_{\mathrm{Io}}}+\frac{p_{\mathrm{Io}}}{p_{\mathrm{Ic}}}\right)\hfill \\ & & \times \frac{{\nu }_{\mathrm{I}}\coth \left({\nu }_{\mathrm{I}}L\right)}{{\omega }_{\mathrm{I}}\sigma e^{-\beta V_{e\mathrm{ff}}}}+\frac{2{\nu }_{\mathrm{I}}}{{\omega }_{\mathrm{I}}\sigma e^{-\beta V_{\mathrm{eff}}}\sinh \left({\nu }_{\mathrm{I}}L\right)}.\hfill \end{array}$$ (6.5)

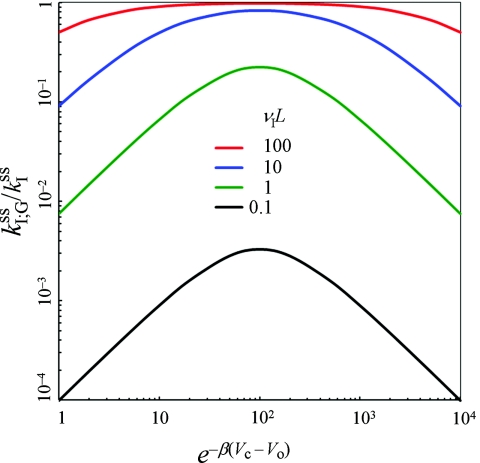
According to Eq. 5.14b, the ratio p_Ic/p_Io can be tuned by varying the difference in potential, V_c – V_o, between the closed lid/reactive binding-site state and open lid/inert binding-site state. The variation in V_c – V_o allows for an optimal rate enhancement over the indifferent-switch case, as shown in Fig. 5. The enhancement is particularly significant at low transition rates between the two alternative states.

Figure 5.

The rate constant $k_{\mathrm{I};\mathrm{G}}^{\mathrm{ss}}$ (scaled by $k_{\mathrm{I}}^{\mathrm{ss}}=D\sigma e^{-\beta V_{\mathrm{eff}}}∕L$) for the interior problem in the gating binding-pocket situation. The indifferent-switch scenario is represented by e^{−β(Vc – Vo)} = 1. Results at four values of ν_IL = (L²/D)^1/2ω_I, representing the ratio of the diffusional timescale and the conformational transition timescale, are shown in different colors according to the key in the figure. Other parameters are: κ₀ = ∞; p_c/p_o = 0.01; e^−βVeff = 10.

p_Ic/p_Io approaches 1 as V_c – V_o becomes more and more negative, eventually leading to a decrease in the binding rate constant (Fig. 5). This is consistent with the slow binding and unbinding expected of a lid that has a high probability of closure when the ligand is inside the binding pocket. The slow unbinding achieved via such a lid may be a desired kinetic property in some circumstances.

CONCLUDING REMARKS

We have extended to flexible protein-ligand systems the formalism for breaking the problem of calculating the diffusion-influenced binding rate coefficient into an exterior problem and an interior problem. Conformational switches of a lid over the binding pocket, a bottleneck along the binding pocket, and the binding site are considered. It is found that under induced switch, whereby the conformation of the protein adapts to the incoming ligand, considerable rate enhancement can be achieved over the indifferent-switch scenario.

To realistically model protein-ligand systems, we have to replace idealized geometries by an atomic representation, which necessitates the use of Brownian dynamics simulations. Treating molecular flexibility in BD simulations is extremely expensive²⁵ and hence most BD simulations have treated protein and ligand molecules as rigid. For systems in which conformational fluctuations are essential for ligand binding, the rigid treatment has resulted in unrealistically loose reaction criteria.^{24, 33} The present work of breaking the calculation of rate constants into exterior and interior problems opens the door to a new class of algorithms, which allows molecules to be treated as flexible in BD simulations. The exterior problem requires long BD simulations, but during these simulations the molecules can be treated as rigid. The rate coefficient produced by these simulations is then used for the outer boundary condition of the interior problem. Because now the ligand is confined to the binding pocket, only short BD simulations are required, and one can afford to treat the molecules as flexible. Algorithmic development along this line will be reported in the future.

APPENDIX A: DERIVATION OF EQ. 4.7

Here, we derive the first two terms in the large-s expansion of ${\widehat{k}}_{\mathrm{E};\mathrm{G}}\left(s\right)$, which is the rate coefficient for a disk that switches between an absorbing conformation and a reflecting conformation. Following Oldham,²⁷ the first term corresponds a uniform flux into the surface area of the disk. In the present case, the pair distribution function, G_g(x, t), where g = a (for absorbing) or r (for reflecting) satisfies the equations

$$\frac{\partial G_{\mathrm{a}}}{\partial t}=D\frac{{\partial }^2{G}_{\mathrm{a}}}{{\partial }^{2}x}-{\omega }_{-}{G}_{\mathrm{a}}+{\omega }_{+}{G}_{\mathrm{r}},$$ (A1a)

$$\frac{\partial G_{\mathrm{r}}}{\partial t}=D\frac{{\partial }^2{G}_{\mathrm{r}}}{{\partial }^{2}x}+{\omega }_{-}{G}_{\mathrm{a}}-{\omega }_{+}{G}_{\mathrm{r}}.$$ (A1b)

Here, we set x = 0 at the surface of the disk. The boundary conditions are

$$G_{\mathrm{a}}(0,t)=0,$$ (A2a)

$${\left.D\frac{\partial G_{\mathrm{r}}(x,t)}{\partial x}\right|}_{x=0}=0,$$ (A2b)

$$G_{\mathrm{g}}(\infty ,t)=p_{\mathrm{g}}.$$ (A2c)

The initial values of G_g(x, t) are also those given by Eq. A2c.

To solve Eqs. A1, we form the following linear combinations:

$$G(x,t)=G_{\mathrm{a}}(x,t)+G_{\mathrm{r}}(x,t),$$ (A3a)

$$F(x,t)=p_{\mathrm{r}}{G}_{\mathrm{a}}(x,t)-p_{\mathrm{a}}{G}_{\mathrm{r}}(x,t).$$ (A3b)

These transform Eqs. A1 into

$$\frac{\partial G(x,t)}{\partial t}=D\frac{{\partial }^{2}G(x,t)}{{\partial }^{2}x},$$ (A4a)

$$\frac{\partial F}{\partial t}=D\frac{{\partial }^{2}F}{{\partial }^{2}x}-\omega F.$$ (A4b)

The solution in Laplace space has the form

$$\widehat{G}(x,s)=\frac{1}{s}-B_1{e}^{-\lambda x},$$ (A5a)

$$\widehat{F}(x,s)=B_2{e}^{-{\lambda }_{1}x},$$ (A5b)

where λ = (s/D)^1/2 and λ₁ = [(s + ω)/D]^1/2. Applying the boundary conditions of Eqs. A2a, A2b, we find

$$B_1=\frac{1}{s}\frac{p_{\mathrm{a}}}{p_{\mathrm{a}}+p_{\mathrm{r}}\lambda ∕{\lambda }_1},$$ (A6a)

$$B_2=-\frac{1}{s}\frac{p_{\mathrm{a}}{p}_{\mathrm{r}}\lambda ∕{\lambda }_1}{p_{\mathrm{a}}+p_{\mathrm{r}}\lambda ∕{\lambda }_1}.$$ (A6b)

The total flux into the surface area of the disk is

$${\left.\widehat{j}\left(s\right)=D\sigma \frac{\partial G_{\mathrm{a}}(x,t)}{\partial x}\right|}_{x=0}=\frac{D\sigma }{s}\frac{p_{\mathrm{a}}\lambda }{p_{\mathrm{a}}+p_{\mathrm{r}}\lambda ∕{\lambda }_1}.$$ (A7a)

The leading term in the large-s expansion is

$$\widehat{j}\left(s\right)=\frac{p_{\mathrm{a}}D\sigma {(s∕D)}^{1∕2}}{s}+\cdots$$ (A7b)

which is the first term on the right-hand side of Eq. 4.7.

The second term in the large-s expansion of ${\widehat{k}}_{\mathrm{E};\mathrm{G}}\left(s\right)$ corresponds to the flux through the rim of the disk. The flux per unit rim length is the same as that into the edge of a half-plane that switched between absorbing and reflecting; the other half-plane is always reflecting. We carry out the calculation of the edge problem by following Phillips and Jansons,²⁹ who used Laplace and Kontorovich-Lebedev transforms to calculate the flux into the edge of an ungated half-plane. The Kontorovich-Lebedev transform is convenient for dealing with wedge-shaped boundaries. For a function f(ρ), the Kontorovich-Lebedev transform is

$$\overline{f}\left(\zeta \right)={\int }_0^{\infty }d\rho \frac{f\left(\rho \right)}{\rho }{K}_{i\zeta }\left(\lambda \rho \right),$$ (A8a)

where K_ν(x) denoted a modified Bessel function of the second kind. The inverse is

$$f\left(\rho \right)=\frac{2}{{\pi }^2}{\int }_0^{\infty }d\zeta \overline{f}\left(\zeta \right)K_{i\zeta }\left(\lambda \rho \right)\zeta \sinh \left(\pi \zeta \right).$$ (A8b)

We use polar coordinates (ρ, ϕ) on the plane perpendicular to the edge of the gated half-plane. The pair distribution function, G_g(ρ, ϕ, t), satisfies the equations

$$\frac{\partial G_{\mathrm{a}}}{\partial t}=D\left[\frac{1}{\rho }\frac{\partial }{\partial \rho }\rho \frac{\partial G_{\mathrm{a}}}{\partial \rho }+\frac{1}{{\rho }^2}\frac{{\partial }^2{G}_{\mathrm{a}}}{{\partial }^2\phi }\right]-{\omega }_{-}{G}_{\mathrm{a}}+{\omega }_{+}{G}_{\mathrm{r}},$$ (A9a)

$$\frac{\partial G_{\mathrm{r}}}{\partial t}=D\left[\frac{1}{\rho }\frac{\partial }{\partial \rho }\rho \frac{\partial G_{\mathrm{r}}}{\partial \rho }+\frac{1}{{\rho }^2}\frac{{\partial }^2{G}_{\mathrm{r}}}{{\partial }^2\phi }\right]+{\omega }_{-}{G}_{\mathrm{a}}-{\omega }_{+}{G}_{\mathrm{r}}.$$ (A9b)

We set ϕ = 0 on the gated half-plane. For sake of generality we assume that the reflecting half plane is at ϕ = ϕ₀; the case of actual interest is ϕ₀ = π. The boundary conditions are

$$G_{\mathrm{a}}(\rho ,0,t)=0,$$ (A10a)

$${\left.D\frac{\partial G_{\mathrm{r}}(\rho ,\phi ,t)}{\partial \phi }\right|}_{\phi =0}=0,$$ (A10b)

$${\left.D\frac{\partial G_{\mathrm{g}}(\rho ,\phi ,t)}{\partial \phi }\right|}_{\phi ={\phi }_0}=0.$$ (A10c)

We again form the linear combinations of Eqs. A3, leading to

$$\frac{\partial G}{\partial t}=D\left[\frac{1}{\rho }\frac{\partial }{\partial \rho }\rho \frac{\partial G}{\partial \rho }+\frac{1}{{\rho }^2}\frac{{\partial }^{2}G}{{\partial }^2\phi }\right],$$ (A11a)

$$\frac{\partial F}{\partial t}=D\left[\frac{1}{\rho }\frac{\partial }{\partial \rho }\rho \frac{\partial F}{\partial \rho }+\frac{1}{{\rho }^2}\frac{{\partial }^{2}F}{{\partial }^2\phi }\right]-\omega F.$$ (A11b)

By first taking the Laplace transform with respect to t and then taking the Kontorovich-Lebedev transform with respect to ρ, we find

$$\begin{array}{ccc}& & \widehat{G}(\rho ,\phi ,s)\hfill \\ & & =\frac{1}{s}-\frac{2}{{\pi }^2}{\int }_0^{\infty }d\zeta (B_1{e}^{\zeta \phi }+B_2{e}^{-\zeta \phi })K_{i\zeta }\left(\lambda \rho \right)\zeta \sinh \left(\pi \zeta \right),\hfill \end{array}$$ (A12a)

$$\begin{array}{ccc}& & \widehat{F}(\rho ,\phi ,s)\hfill \\ & & =\frac{2}{{\pi }^2}{\int }_0^{\infty }d\zeta (B_3{e}^{\zeta \phi }+B_4{e}^{-\zeta \phi })K_{i\zeta }\left({\lambda }_1\rho \right)\zeta \sinh \left(\pi \zeta \right).\hfill \end{array}$$ (A12b)

Applying the boundary conditions of Eqs. A10, we have

$$\begin{array}{c}{\displaystyle \frac{2}{{\pi }^2}{p}_{\mathrm{a}}{\int }_0^{\infty }d\zeta (B_1+B_2)K_{i\zeta }\left(\lambda \rho \right)\zeta \sinh \left(\pi \zeta \right)}\hfill \\ {\displaystyle -\frac{2}{{\pi }^2}{\int }_0^{\infty }d\zeta (B_3+B_4)K_{i\zeta }\left({\lambda }_1\rho \right)\zeta \sinh \left(\pi \zeta \right)=\frac{p_{\mathrm{a}}}{s},}\hfill \end{array}$$ (A13a)

$$\begin{array}{c}{\displaystyle \frac{2}{{\pi }^2}{p}_{\mathrm{r}}{\int }_0^{\infty }d\zeta (B_1-B_2)K_{i\zeta }\left(\lambda \rho \right)\zeta \sinh \left(\pi \zeta \right)}\hfill \\ {\displaystyle +\frac{2}{{\pi }^2}{\int }_0^{\infty }d\zeta (B_3-B_4)K_{i\zeta }\left({\lambda }_1\rho \right)\zeta \sinh \left(\pi \zeta \right)=0,}\hfill \end{array}$$ (A13b)

$$\begin{array}{c}{\displaystyle \frac{2}{{\pi }^2}{p}_{\mathrm{a}}{\int }_0^{\infty }d\zeta (B_1{e}^{\zeta {\phi }_0}-B_2{e}^{-\zeta {\phi }_0})K_{i\zeta }\left(\lambda \rho \right)\zeta \sinh \left(\pi \zeta \right)}\hfill \\ {\displaystyle -\frac{2}{{\pi }^2}{\int }_0^{\infty }d\zeta (B_3{e}^{\zeta {\phi }_0}-B_4{e}^{-\zeta {\phi }_0})K_{i\zeta }\left({\lambda }_1\rho \right)\zeta \sinh \left(\pi \zeta \right)=0,}\hfill \end{array}$$ (A13c)

$$\begin{array}{c}{\displaystyle \frac{2}{{\pi }^2}{p}_{\mathrm{r}}{\int }_0^{\infty }d\zeta (B_1{e}^{\zeta {\phi }_0}-B_2{e}^{-\zeta {\phi }_0})K_{i\zeta }\left(\lambda \rho \right)\zeta \sinh \left(\pi \zeta \right)}\hfill \\ {\displaystyle +\frac{2}{{\pi }^2}{\int }_0^{\infty }d\zeta (B_3{e}^{\zeta {\phi }_0}-B_4{e}^{-\zeta {\phi }_0})K_{i\zeta }\left({\lambda }_1\rho \right)\zeta \sinh \left(\pi \zeta \right)=0.}\hfill \end{array}$$ (A13d)

We are only interested in the large-s limit. In this limit, λ₁ → λ. Consequently, Eqs. A13 lead to

$$\begin{array}{ccc}& & p_{\mathrm{a}}(B_1+B_2)-(B_3+B_4)\hfill \\ & & =\frac{p_{\mathrm{a}}}{s}{\int }_0^{\infty }d\rho \frac{1}{\rho }{K}_{i\zeta }\left(\lambda \rho \right)=\frac{p_{\mathrm{a}}}{s}\frac{\pi ∕2}{\zeta \sinh (\pi \zeta ∕2)},\hfill \end{array}$$ (A14a)

$$p_{\mathrm{r}}(B_1-B_2)+(B_3-B_4)=0,$$ (A14b)

$$p_{\mathrm{a}}(B_1{e}^{\zeta {\phi }_0}-B_2{e}^{-\zeta {\phi }_0})-(B_3{e}^{\zeta {\phi }_0}-B_4{e}^{-\zeta {\phi }_0})=0,$$ (A14c)

$$p_{\mathrm{r}}(B_1{e}^{\zeta {\phi }_0}-B_2{e}^{-\zeta {\phi }_0})+(B_3{e}^{\zeta {\phi }_0}-B_4{e}^{-\zeta {\phi }_0})=0.$$ (A14d)

In evaluating the integral in Eq. A14a we have used formulas 6.561.16 and 8.322.1 of Gradshteyn and Ryzhik.³⁴ The coefficients are then

$$B_1=\frac{p_{\mathrm{a}}}{s}\frac{\pi ∕2}{\zeta \sinh (\pi \zeta ∕2)}\frac{1}{e^{2\zeta {\phi }_0}+1},$$ (A15a)

$$B_2=\frac{p_{\mathrm{a}}}{s}\frac{\pi ∕2}{\zeta \sinh (\pi \zeta ∕2)}\frac{e^{2\zeta {\phi }_0}}{e^{2\zeta {\phi }_0}+1},$$ (A15b)

$$B_3=-\frac{p_{\mathrm{a}}{p}_{\mathrm{r}}}{s}\frac{\pi ∕2}{\zeta \sinh (\pi \zeta ∕2)}\frac{1}{e^{2\zeta {\phi }_0}+1},$$ (A15c)

$$B_4=-\frac{p_{\mathrm{a}}{p}_{\mathrm{r}}}{s}\frac{\pi ∕2}{\zeta \sinh (\pi \zeta ∕2)}\frac{e^{2\zeta {\phi }_0}}{e^{2\zeta {\phi }_0}+1}.$$ (A15d)

Now, we find

$$\begin{array}{ccc}\hfill \widehat{G}(\rho ,\phi ,s)& =& \frac{1}{s}-\frac{p_{\mathrm{a}}}{s}\frac{2}{\pi }{\int }_0^{\infty }d\zeta \frac{\cosh \left[({\phi }_0-\phi )\zeta \right]}{\cosh \left({\phi }_0\zeta \right)}\hfill \\ & & \times K_{i\zeta }\left(\lambda \rho \right)\cosh (\pi \zeta ∕2).\hfill \end{array}$$ (A16)

The case where the whole plane is gated is equivalent to the case of a reflecting half-plane at ϕ₀ = π/2. The “excess” pair distribution function is

$$\begin{array}{ccc}\hfill \Delta \widehat{G}(\rho ,\phi ,s)& =& \widehat{G}(\rho ,\phi ,s)-\widehat{G}(\rho ,\phi ,s){|}_{{\phi }_0=\pi ∕2}\hfill \\ & =& {\displaystyle \frac{p_{\mathrm{a}}}{s}\frac{2}{\pi }{\int }_0^{\infty }d\zeta \frac{\cosh \left[(\pi ∕2-\phi )\zeta \right]\cosh \left({\phi }_0\zeta \right)-\cosh \left[({\phi }_0-\phi )\zeta \right]\cosh (\pi \zeta ∕2)}{\cosh \left({\phi }_0\zeta \right)}{K}_{i\zeta }\left(\lambda \rho \right)}\hfill \\ & =& {\displaystyle \frac{p_{\mathrm{a}}}{s}\frac{2}{\pi }{\int }_0^{\infty }d\zeta \frac{\sinh \left[({\phi }_0-\pi ∕2)\zeta \right]\sinh \left(\phi \zeta \right)}{\cosh \left({\phi }_0\zeta \right)}{K}_{i\zeta }\left(\lambda \rho \right).}\hfill \end{array}$$ (A17)

The total flux per unit edge length is

$$\begin{array}{ccc}\hfill \widehat{j}\left(s\right)& =& D{\int }_0^{\infty }d\rho {\left.\frac{1}{\rho }\frac{\partial \Delta \widehat{G}(\rho ,\phi ,s)}{\partial \phi }\right|}_{\phi =0}\hfill \\ & =& \frac{p_{\mathrm{a}}D}{s}\frac{2}{\pi }{\int }_0^{\infty }d\zeta \frac{\zeta \sinh \left[({\phi }_0-\pi ∕2)\zeta \right]}{\cosh \left({\phi }_0\zeta \right)}{\int }_0^{\infty }d\rho \frac{1}{\rho }{K}_{i\zeta }\left(\lambda \rho \right)\hfill \\ & =& \frac{p_{\mathrm{a}}D}{s}\frac{2}{\pi }{\int }_0^{\infty }d\zeta \frac{\zeta \sinh \left[({\phi }_0-\pi ∕2)\zeta \right]}{\cosh \left({\phi }_0\zeta \right)}\frac{\pi ∕2}{\zeta \sinh (\pi \zeta ∕2)}\hfill \\ & =& \frac{p_{\mathrm{a}}D}{s}{\int }_0^{\infty }d\zeta \frac{\sinh \left[({\phi }_0-\pi ∕2)\zeta \right]}{\cosh \left({\phi }_0\zeta \right)\sinh (\pi \zeta ∕2)}.\hfill \end{array}$$ (A18a)

For the case of interest to us, ϕ₀ = π. In this case, Eq. A18a becomes

$$\widehat{j}\left(s\right)=\frac{p_{\mathrm{a}}D}{s}{\int }_0^{\infty }d\zeta \frac{1}{\cosh \left(\pi \zeta \right)}=\frac{p_{\mathrm{a}}D}{2s}$$ (A18b)

Multiplying by the circumference 2πa of the disk, we arrive at the second term on the right-hand side of Eq. 4.7.