AREM: Aligning Short Reads from ChIP-Sequencing by Expectation Maximization

Abstract

High-throughput sequencing coupled to chromatin immunoprecipitation (ChIP-Seq) is widely used in characterizing genome-wide binding patterns of transcription factors, cofactors, chromatin modifiers, and other DNA binding proteins. A key step in ChIP-Seq data analysis is to map short reads from high-throughput sequencing to a reference genome and identify peak regions enriched with short reads. Although several methods have been proposed for ChIP-Seq analysis, most existing methods only consider reads that can be uniquely placed in the reference genome, and therefore have low power for detecting peaks located within repeat sequences. Here, we introduce a probabilistic approach for ChIP-Seq data analysis that utilizes all reads, providing a truly genome-wide view of binding patterns. Reads are modeled using a mixture model corresponding to K enriched regions and a null genomic background. We use maximum likelihood to estimate the locations of the enriched regions, and implement an expectation-maximization (E-M) algorithm, called AREM (aligning reads by expectation maximization), to update the alignment probabilities of each read to different genomic locations. We apply the algorithm to identify genome-wide binding events of two proteins: Rad21, a component of cohesin and a key factor involved in chromatid cohesion, and Srebp-1, a transcription factor important for lipid/cholesterol homeostasis. Using AREM, we were able to identify 19,935 Rad21 peaks and 1,748 Srebp-1 peaks in the mouse genome with high confidence, including 1,517 (7.6%) Rad21 peaks and 227 (13%) Srebp-1 peaks that were missed using only uniquely mapped reads. The open source implementation of our algorithm is available at http://sourceforge.net/projects/arem.

1. Introduction

In recent years, high-throughput sequencing coupled to chromatin immunoprecipitation (ChIP-Seq) has become one of the premier methods of analyzing protein-DNA interactions (Park, 2009). The ability to capture a vast array of protein binding locations genome-wide in a single experiment has led to important insights in a number of biological processes, including transcriptional regulation, epigenetic modification and signal transduction (Mikkelsen et al., 2007; Ouyang et al., 2009; Blow et al., 2010; Seo et al., 2009). Numerous methods have been developed to analyze ChIP-Seq data and typically work well for identifying protein-DNA interactions located within non-repeat sequences. However, identifying interactions in repeat regions remains a challenging problem since sequencing reads from these regions usually cannot be uniquely mapped to a reference genome. We present novel methodology for identifying protein-DNA interactions in repeat sequences.

ChIP-Seq computational analysis typically consists of two tasks: one is to identify the genomic locations of the short reads by aligning them to a reference genome, and the second is to find genomic regions enriched with the aligned reads, which is often termed peak finding. Eland, MAQ, Bowtie, and SOAP are among the most popular for mapping short reads to a reference genome (Cox, 2007; Langmead et al., 2009; Li et al., 2008a,b) and provide many or all of the potential mappings for a given sequence read. Once potential mappings have been identified, significantly enriched genomic regions are identified using one of several available tools (Fejes et al., 2008; Ji et al., 2008; Mortazavi et al., 2008; Zhang et al., 2008; Spyrou et al., 2009; Zang et al., 2009; Blahnik et al., 2010; Qin et al., 2010; Salmon-Divon et al., 2010). Some peak finders are better suited for histone modification studies, others for transcription factor binding site identification. These peak finders have been surveyed on several occasions (Kharchenko et al., 2008; Pepke et al., 2009; Wilbanks and Facciotti, 2010).

Many short reads cannot be uniquely mapped to the reference genome. Most peak finding workflows throw away these non-uniquely mapped reads, and as a consequence have low power for detecting peaks located within repeat regions. While each experiment varies, only about 60% (our data) of the sequence reads from a ChIP-Seq experiment can be uniquely mapped to a reference genome. Therefore, a significant portion of the raw data is not utilized by the current methods. There have been proposals to address the non-uniquely mapped reads in the literature by either randomly choosing a location from a set of potential ones (Kagey et al., 2010; Schmid and Bucher, 2010) or by taking all potential alignments (Mortazavi et al., 2008), but most peak callers are not equipped to deal with ambiguous reads.

We propose a novel peak caller designed to handle ambiguous reads directly by performing read alignment and peak-calling jointly rather than in two separate steps. In the context of ChIP-Seq studies, regions enriched during immunoprecipitation are more likely the true genomic source of sequence reads than other regions of the genome. We leverage this idea to iteratively identify the true genomic source of ambiguous reads. Under our model, the true locations of reads and binding peaks are treated as hidden variables, and we implement an algorithm, AREM, to estimate both iteratively by alternating between mapping reads and finding peaks.

Two ChIP-Seq datasets were used in this study: (1) cohesin, a new dataset generated in house, and (2) Srebp-1, a previously published dataset (Seo et al., 2009). We generated the cohesin dataset by performing ChIP-Seq using mouse embryonic fibroblasts and an antibody targeting Rad21 (Zeng et al., 2009), a subunit of cohesin. Cohesin is an essential protein complex required for sister chromatid cohesion. In mammalian cells, cohesin binding sites are present in intergenic, promoter and 3′ regions—especially in connection with CTCF binding sites (Rubio et al., 2008; Liu et al., 2009). It was found that cohesin is recruited by CTCF to many of its binding sites, and plays a role in CTCF-dependent gene regulation (Wendt et al., 2008; Nativio et al., 2009). Cohesin has been shown to bind to repeat sequences in a disease-specific manner (Zeng et al., 2009), making it a particularly interesting candidate for our study.

The second dataset is Srebp-1, a transcription factor important in allostatic regulation of sterol biosynthesis and membrane lipid composition (Hagen et al., 2010). This particular dataset (Seo et al., 2009) examines the genomic binding locations for Srebp-1 in mouse liver. Regulation of expression by Srebp-1 is important for regulation of cholesterol; repeat-binding for this transcription factor has not been shown previously (Yokoyama et al., 1993; Hagen et al., 2010). We choose these datasets because both proteins have well characterized regulatory motifs, allowing us to directly test the validity of our peak finding method.

On a 2.8-Ghz CPU, AREM takes about 20 minutes and 1.6-GB RAM to call peaks from over 12 million alignments and about 30 minutes and 6-GB RAM to call peaks from nearly 120 million alignments. Each dataset takes less than 40 iterations to converge. AREM is written in Python, is open-source, and is available at http://sourceforge.net/projects/arem.

2. Methods

2.1. Notations

Let 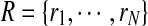denote a set of reads from a ChIP-Seq experiment with read 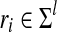, where Σ = {A, C, G, T}, l is the length of each read, and N denotes the number of reads. Let 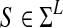denote the reference sequence to which the reads will be mapped. In real applications, the reference sequence usually consists of multiple chromosomes. For notational simplicity, we assume the chromosomes have been concatenated to form one reference sequence.

We assume that for each read we are provided with a set of potential alignments to the reference sequence. Denote the set of potential alignments of read r_i to S by 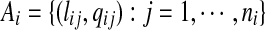, where l_ij and q_ij denote the starting location and the confidence score of the j-th alignment, and n_i is the total number of potential alignments. We assume for all j, and use it to account for both sequencing quality scores and mismatches between the read and the reference sequence. There are several programs available to generate the initial potential alignments and confidence scores.

2.2. Mixture model

We use a generative model to describe the likelihood of observing the given set of short reads from a ChIP-Seq experiment. Suppose the ChIP procedure results in the enrichment of K non-overlapping regions in the reference sequence S. Denote the K enriched regions (also called peak regions) by 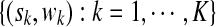, where s_k and w_k represent the start and the width, respectively, of the i-th enriched region in S. Let 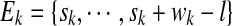denote the set of locations in the enriched region k that can potentially generate a read of length l. Let 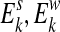denote the start and width of region k. We will use E₀ to denote all locations in S that are not covered by .

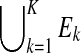We use variable 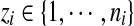to denote the true location of read r_i, with z_i = j representing that r_i originates from location l_ij of S. In addition, we use variable 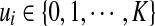to label the type of region that read r_i belongs to. u_i = k represents that read r_i is from the non-enriched regions of S if k = 0, and is from k-th enriched region otherwise. Both z_i and u_i are not directly observable, and are often referred to as the hidden variables of the generative model.

Let P(r_i|z_i = j, u_i = k) denote the conditional probability of observing read r_i given that r_i is from location l_ij and belongs to region k. Assuming different reads are generated independently, the log likelihood of observing R given the mixture model is then

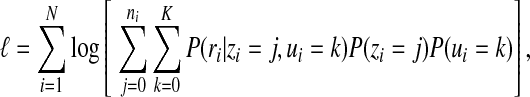where P(z_i) and P(u_i) represent the prior probabilities of the location and the region type, respectively, of read r_i. P(z_i) is set according to the confidence scores of different alignments

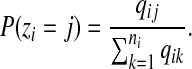(1)

P(u_i) depends on both the width and the enrichment ratio of each enriched region. Denote the enrichment ratio of the ChIP regions versus non-ChIP regions by α, which is often significantly impacted by the quality of antibodies used in ChIP experiments. We parametrize the prior distribution on region types as follows

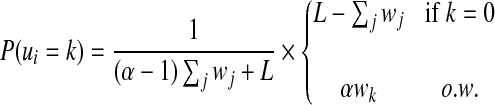(2)

2.3. Parameter estimation

The conditional probability P(r_i|z_i = j, u_i = k) can be modeled in a number of different ways. For example, bell-shaped distributions are commonly used to model the enriched regions. However, for computational simplicity, we will use a simple uniform distribution to model the enriched regions. If read r_i comes from one of the enriched regions, i.e., k ≠ 0, we assume the read is equally likely to originate from any of the potential positions within the enriched region, that is,

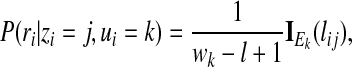(3)

where I_A(x) is the indicator function, returning 1 if 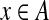and 0, otherwise.

If the read is from non-enriched regions, i.e., k = 0, we use 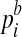to model the background probability of an arbitrary read originating from location i of the reference sequence. (We assume 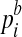has been properly normalized such that 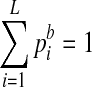.) Then the conditional probability P(r_i|z_i = j, u_i = k) for the case of k = 0 is modeled by

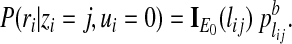(4)

Numerous ChIP-Seq studies have demonstrated that the locations of ChIP-Seq reads are typically non-uniform, significantly biased toward promoter or open chromatin regions (Park, 2009). The 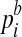's takes this ChIP and sequencing bias into account, and can be inferred from control experiments typically employed in ChIP-Seq studies.

Next we integrate out the u_i variable to obtain the conditional probability of observing r_i given only z_i

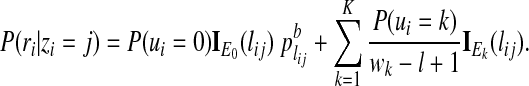(5)

Note that because 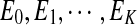are disjoint, only one term in the above summation can be non-zero. This property significantly reduces the computation for parameter estimation since we do not need to infer the values of u_i variables any more.

The log likelihood of observing R given the mixture model can now be written as

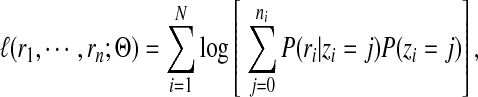(6)

where 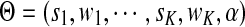denotes the parameters of the mixture model. We estimate the values of these unknown parameters using maximum likelihood estimation

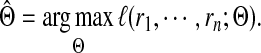(7)

2.4. Expectation-maximization algorithm

We solve the maximum likelihood estimation problem in Eq. (7) through an expectation-maximization (E-M) algorithm. The algorithm iteratively applies the following two steps until convergence:

Expectation step: Estimate the posterior probability of alignments under the current estimate of parameters Θ^(t):

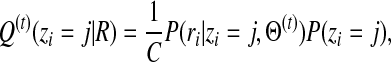(8)

where C is a normalization constant.

Maximization step: Find the parameters Θ^(t+1) that maximize the following quantity,

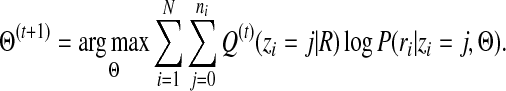(9)

2.5. Implementation of E-M updates

The mixture model described above contains 2K + 1 parameters. Since K, the number of peak regions, is typically large, ranging from hundreds to hundreds of thousands, exactly solving Eq. (9) in the maximization step is nontrivial. Instead of seeking an exact solution, we identify the K regions from the data by considering all regions where the number of possible alignments is significantly enriched above the background.

For a given window of size w starting at s of the reference genome, we first calculate the number of reads located within the window, weighted by the current estimation of posterior alignment probabilities,

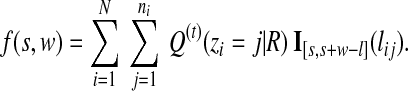(10)

We term this quantity the foreground read density. As a comparison, we also calculate a background read density b(s, w), which is estimated using either reads from the control experiment or reads from a much larger extended region covering the window. Different ways of calculating background read density are discussed in (Zhang et al., 2008).

Provided with both background and foreground read densities, we then define an enrichment score ø(s, w) to measure the significance of read enrichment within the window starting at position s with width w. For this purpose, we assume the number of reads are distributed according to a Poisson model with mean rate b(s, w). If f (s, w) is an integer, the enrichment score is defined to be φ(s, w) = −log₁₀(1 − g(f, b)), where

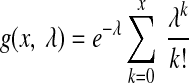(11)

denotes the chance of observing at least x Poisson events given the mean rate of λ. However, if f (s, w) is not an integer, the enrichment score cannot be defined this way. Instead, we use a linear extrapolation to define the enrichment score 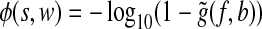, where function 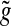is defined as

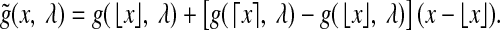(12)

If two potential alignments of a read have the same confidence score and are located in two peak regions with equal enrichment, the update of posterior alignment probabilities in Eq. (8) will assign equal weight to these two alignments. This is so because we have assumed that peak regions have the same enrichment ratio as described in Eq. (2), which is not true as some peak regions are more enriched than others in real ChIP experiments. To address this issue, we have also implemented an update of the posterior probabilities that takes the calculated enrichment scores into account as

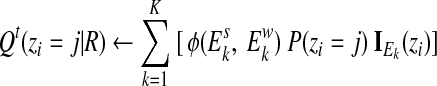(13)

which is then normalized. In practice, we found this implementation usually behaves better than the one without using enrichment scores.

We use entropy to quantify the uncertainty of alignments associated with each read. For read i, the entropy at iteration t is defined to be

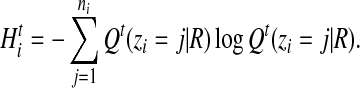(14)

We stop the E-M iteration when the relative square difference between two consecutive entropies is small, that is, when

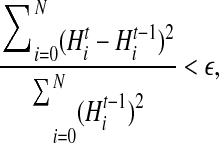(15)

where ε = 10⁻⁵ for results reported in this article.

AREM seeks to identify the true genomic source of multiply-aligning reads (also called multireads). Many of the multireads will map to repeat regions of the genome, and we expect repeats to be included in the K potentially enriched regions. To prevent repeat regions from garnering multiread mass without sufficient evidence of their enrichment, we impose a minimum enrichment score. Effectively, unique or less ambiguous multireads need to raise enrichment above noise levels for repeat regions to be called as peaks. The minimum enrichment score is a parameter of our model, and its effect on called peaks is explored in Results.

3. Results

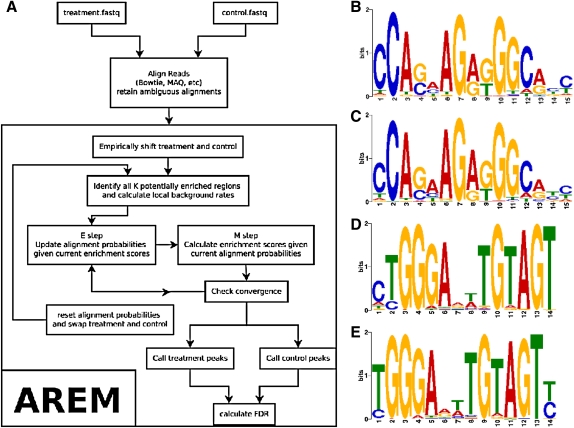
Building on the methodology of the popular peak-caller model-based analysis of ChIP-Seq (MACS) (Zhang et al., 2008), we implement AREM, a novel peak caller designed to handle multiple possible alignments for each sequence read. AREM's peak caller combines an initial sliding window approach with a greedy refinement step and iteratively aligns ambiguous reads. We use two ChIP-Seq datasets in this study: Rad21 and Srebp-1. Rad21, a subunit of the structural protein cohesin, contained 7.2 million treatment reads and 7.4 million control reads (our data). Srebp-1, a regulator of cholesterol metabolism, had 7.7 million treatment reads and 6.4 million control reads (Seo et al., 2009) (Fig. 1).

FIG. 1.

(A) AREM workflow diagram. (B–E) DE novo discovery of motifs. From top to bottom: (B) CTCF in MACS peaks from uniquely mapping reads, (C) CTCF in AREM's peaks with multireads, (D) Srebp-1 in MACS peaks from uniquely mapping reads and (E) Srebp-1 in AREM peaks with multireads.

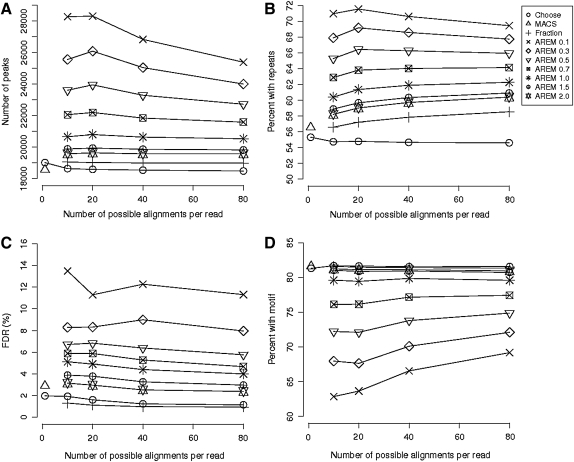
Using AREM, we identify 19,935 Rad21 peaks covering more than 10 million base pairs at a low False Discovery Rate (FDR) of 3.7% and 1,474 Srebp-1 peaks covering nearly 1 million bases at a moderate FDR of 8%. For comparison, we also called peaks using MACS and SICER (Zang et al., 2009), another popular peak finding program. To compare our results, we use FDR and motif presence as indicators of bona fide binding sites.

3.1. AREM identifies additional binding sites

We seek to benchmark both AREM's peak-calling and its multiread methodology. To benchmark peak-calling, we limit all reads to their best alignment and run AREM, MACS and SICER. In the Rad21 dataset, AREM identifies 456 more peaks than MACS and 1920 more peaks than SICER but retains a similar motif presence (81.6% MACS, 82.5% SICER, 81.3% AREM) and has a lower FDR (2.8% MACS, 12.7% SICER, 1.9% AREM) (Table 1). For Srebp-1, AREM identifies more than double the number of peaks compared to MACS and 816 more than SICER, though the FDR is slightly higher (4.85% MACS, 9% SICER, 8% AREM), and motif presence is slightly lower (46.6% MACS, 59% SICER, 39% AREM). In both datasets, AREM appears to be more sensitive to true binding sites, picking up more total sites with motif instances, although it trades off some specificity in Srebp-1 (seen Appendix).

Table 1.

Comparison of Peak-Calling Methods for Cohesin and Srebp-1.

Method	No. of alignments	No. of peaks	Peak bases	FDR	New peaks	Motif	Repeat
Cohesin
MACS	2,368,229	18,556	9,546,641	2.8%	—	81.67%	56.55%
SICER	2,368,229	17,092	17,374,108	12.71%	—	82.55%	70.42%
AREM 1	2,368,229	19,012	9,353,567	1.9%	—	81.32%	55.30%
AREM 10	7,616,647	19,881	10,225,479	3.8%	1,404	81.04%	58.88%
AREM 20	12,312,878	19,935	10,531,465	3.7%	1,517	80.88%	59.66%
AREM 40	20,527,010	19,863	10,744,836	3.2%	1,546	80.93%	60.34%
AREM 80	34,537,311	19,820	10,972,796	2.9%	1,538	80.73%	60.91%
Srebp-1
MACS	10,482,005	721	495,968	4.85%	—	46.60%	53.95%
SICER	10,482,005	622	963,778	9.0%	—	59.00%	77.33%
AREM 1	10,482,005	1,438	880,284	8.0%	—	39.08%	53.47%
AREM 10	28,347,869	1,815	996,346	10.5%	262	39.22%	56.04%
AREM 20	44,493,532	1,748	959,646	8.0%	227	39.95%	55.97%
AREM 40	72,453,642	1,685	983,459	8.2%	248	40.34%	56.46%
AREM 80	118,744,757	1,695	987,746	7.3%	272	40.66%	56.73%

Three peak callers (MACS, SICER, and AREM) were run on both datasets. For AREM, the maximum number of retained alignments per read is varied (from 1 to 80). The total number of peaks and bases covered by peaks is reported as well as the FDR by swapping treatment and control. For both datasets, AREM's minimum enrichment score was fixed at 1.5 with 20 maximum alignments per read. For comparison, the motif background rate of occurence was 4.5% (CTCF) and 27% (Srebp-1) in 100,000 genomic samples, sized similarly to Rad21 MACS peaks and Srebp-1 MACS peaks, respectively.

To see if AREM can identify true sites that are not significant without multireads, we performed peak-calling with multireads, removing peaks that overlapped with those identified using AREM without multireads. Up to 1,546 (8.1%) and 272 (18.9%) previously unidentified peaks were called from Rad21 and Srebp-1, respectively. These new peaks have a similar motif presence compared to previous peaks but overlap with annotated repeat regions more often.

3.2. AREM's sensitivity is increased with ambiguous reads

Several methods for dealing with ambiguous reads have been proposed, including retaining all possible mappings, retaining one of the mappings chosen at random, and distributing weight equally among the mappings. The first option will clearly lead to false positives, particularly in repeat regions as the number of retained mappings increases. We compare the latter two methods to our E-M implementation, varying the number of retained reads and summarizing the results in Table 1. Although both random selection and fractionating reads increases the number of peaks called, our E-M method outperforms them, yielding 1,546 more peaks for Rad21, and 272 for Srebp-1 with comparable quality. As the number of retained alignments increases, the disparity gets smaller. AREM shows fairly consistent results across datasets with a large increase in total number of alignments (nearly 40-fold for Rad21 and over 10-fold for Srebp-1).

For a given sample, the iterations show a continued shift of the max alignment probabilities to either 1 or 0. This shift is consistent across datasets with larger numbers of max alignments (data not shown), but does depend on other parameters. What is apparent is that AREM's E-M heuristic performs well, allowing for significant shift toward a “definitive” alignment; at the same time, it does not force a shift on reads with too little information, preventing misalignment and resulting spurious peak-calling.

3.3. AREM is sensitive to repeat regions

An important parameter in our model is the minimum enrichment score for all K regions. Since repeat regions have such similar sequence content, many reads will share the same repetitive elements. If one of the shared repeat elements has a slightly higher enrichment score by chance, the E-M method will iteratively shift probability into that repeat region, snowballing the region into what appears to be a full-fledged sequence peak. To distinguish repetitive peaks arising by small enrichment fluctuations from true binding sites within or adjacent to repetitive elements, we impose a minimum enrichment score on all regions. Using lower threshold scores, our method may include false positives from these random fluctuations. However, true binding peaks near repetitive elements may be missed if the score is too high.

To explore the effect of varying the minimum enrichment score, we varied the minimum score from 0.1 to 2, keeping the maximum number of alignments fixed at 20. For Rad21, we see a declining number of discovered peaks ranging from 28,305 to 19,634 peaks. In addition to a decline in discovered peaks as minimum enrichment score increases, we also see a decrease in the reported FDR and the percent of peaks in repeat regions from 11.28% to 2.95% FDR and 71.56% to 59.02%. Lastly, the percent of peaks with motif increases from 63.64% to 81.12%. These additional peaks appear to be of lower quality: motifs are largely absent from them, and the FDR is much higher (Fig. 2).

FIG. 2.

Graphs displaying varying parameters and number of possible alignments per read. (A) Total number of peaks discovered. (B) Percentage of peaks with repetitive sequences. (C) False discovery rate. (D) Percentage of peaks with motif.

For our method, detecting peaks near repeat regions is a tradeoff between sensitivity and specificity. As the minimum score increases, the method approaches the uniform or “fraction” distribution, in which only the initial mapping quality scores (and not the enrichment) affect alignment probabilities. The fraction method is explored explicitly, showing increased power compared to unique reads only, but decreased sensitivity to true binding sites compared to other AREM runs.

4. Discussion

Repetitive elements in the genome have traditionally been problematic in sequence analysis. Since sequenced reads are short and repetitive sequences are similar, many equally likely mappings may exist for a given read. Our method uses the low-coverage unique reads near repeat regions to evaluate which potential alignments for each read are the most likely. Our method's sensitivity to repeat regions is adjustable, but increasing sensitivity may introduce false positives. Further refinement of our methodology may lead to increased specificity.

Our results imply that functional CTCF binding sites exist within repeat regions, revealing an interesting relationship between repetitive sequence and chromatin structure. Another application of our method would be to explore the relationship between repetitive sequence and epigenetic modifications such as histone modifications. Regulation of and by transposable elements has been linked to methylation marks (Huda and Jordan, 2009), and transposable elements have a major role in cancers (Chuzhanova et al., 2003). Better identification of histone modifications in regions of repetitive DNA increases our understanding of key regulators of genome stability and diseases sparked by translocations and mutations.

5. Appendix

5.1. Alignment

We aligned the data using Bowtie (Langmead et al., 2009) with the Burrows-Wheeler index provided by the Bowtie website. The index is based on the unmasked MM9 reference genome from the UCSC Genome Browser (Rhead et al., 2009). We clipped the first base of all raw reads to remove sequencing artifacts and allowed a maximum of two mismatches in the first 28 bases of the remaining sequence. We generated several alignment collections for both Srebp-1 and Rad21 by varying k, the maximum number of reported alignments. We restricted our study to search the 1, 10, 20, 40, and 80 best alignments. Table 1 shows that the total number of alignments was only starting to plateau at k = 80, indicating that many sequences have more than 80 possible alignments, for practicality we restricted our search as above. We calculated map confidence scores from Bowtie output as in Li et al. (2008a). We also provide an option for using the aligner's confidence scores directly rather than recalculating them from mismatches and sequence qualities. During preparation of the sequencing library, unequal amplification can result in biased counts for reads. To eliminate this bias, we limit the number of alignments to one for each start position on each strand. In particular, we choose the best alignment (based on quality score) for each position; in the event that all alignments have the same quality score, we choose a random read to represent that particular position.

5.2. Peak finding

Our peak finding method is an adapted version of the MACS (Zhang et al., 2008) peak finder. Like MACS, we empirically model the spatial separation between +/− strand tags and shift both treatment and control tags. We also continue MACS' conservative approach to background modeling, using the highest of three rates as the background (in this study, genome-wide or within 1,000 or 10,000 bases). As a divergence from MACS, we use a sliding window approach to identify large potentially enriched regions then use a smoothened greedy approach to refine called peaks. We call peaks within this large region by greedily adding reads to improve enrichment, but avoid local optima by always looking up to the full sliding window width away. The initial large regions correspond to the K regions used for the E-M steps of Section 2.5. During the E-M steps, local background rates are used as during final peak-calling. Peaks reported in this study are above a p-value of 10⁻⁵. All enrichment scores and p-values are calculated using the poisson linear interpolation described in equation 12. Once E-M is complete on the treatment data and peaks are called, we reset the treatment alignment probabilities, swap treatment and control and rerun the algorithm, including E-M steps, to determine the False Discovery Rate (FDR). For all algorithms tested in this study, we define the FDR as the ratio of peaks called using control data to peaks called using treatment data. This method of FDR calculation is common in ChIP-Seq studies (Zhang et al., 2008; Zang et al., 2009).

5.3. Motif finding

Motif presence helps determine peak quality, as shown in Boeva et al. (2010). To determine if our new peaks were of the same quality as the other peaks, we performed de novo motif discovery using MEME Bailey and Elkan, 1995 version 4.4. Input sequence was limited to 150 bp (Rad21) and 200 bp (Srebp-1) around the summit of the peaks called by MACS from uniquely mapping reads. All sequences were used for Srebp-1, while 1,000 sequences were randomly sampled a total of 5 times for Rad21. The motif signal was strong in both datasets and we extracted the discovered motif position weight matrix (PWM) for further use. We also performed the motif search using Srebp-1 and CTCF motifs catalogued in Transfac 11.3, and found similar results. For the CTCF motif, we did genomic sampling (100,000 samples) to identify a threshold score corresponding to a z-score of 4.29. For Srebp-1, we used the threshold score reported by MEME (Fig. 1).

Acknowledgments

We thank the Liu lab for releasing MACS as open-source, and R. Chien, Y. Chen, and N. Infante for helpful discussions. This work was partly supported by the NSF (grant DBI-0846218 to X.X.) and the NIH (grant HD062951 to K.Y.). D.N. and J.B. were supported by the NIH/NLM Bioinformatics (training grant T15LM07443).

Disclosure Statement

No competing financial interests exist.