Statistical investigation of position-specific deformation pattern of nucleosome DNA based on multiple conformational properties

Abstract

The histone octamer induced bending of DNA into the super-helix structure in nucleosome core particle, is very unique and vital for DNA packing into chromatin. We collected 48 nucleosome crystal structures from PDB and applied a multivariate analysis on the nucleosome structural data. Based on the anisotropic nature of DNA structure, a principal conformational subspace (PCS) is derived from multiple properties to represent the most significant variances of nucleosome DNA structures. The coupling of base pair-oriented parameters with sugar phosphate backbone parameters presented in principal dimensionalities reveals two main deformation modes that have supplemented the existing physical model. By using sequence alignment-based statistics, a positiondependent conformational map for the super-helical DNA path is established. The result shows that the crystal structures of nucleosome DNA have much consistency in position-specific structural variations and certain periodicity is found to exist in these variations. Thus, the positions with obvious deformation patterns along the DNA path in nucleosome core particle are relatively conservative from the perspective of statistics.

Background

Nucleosome is the elementary structure unit of eukaryotic chromatin, which works as the first step in packaging the large genomes into the cell nucleus and directly influences DNA replication, recombination, repair and transcription. It has been proved that the bending of the core DNA along the superhelical path is very anisotropic, in which the degree of overall curvature is about twice of that in the uniform ideal super-helix [1]. Compared with the highly conserved structures of the four types of histone in the core octamer, DNA sequences are much more varied and flexible to accommodate the sharp conformational changes under different environments. In order to describe the DNA microstructure, a considerable number of conformational properties have been defined [2]. Based on these properties, a lot of work has been done to reveal the stereochemical traits and the deformation mechanism of DNA molecules. These results have led to a clearer understanding of the geometrical nature of the basic A-, B-form DNA that comes from oligomers [3, 4] and the small DNA-protein complexes [5, 6]. The knowledge about DNA deformation induced by the histone octamer, however, is more complicated because it depends on the coordination of the structural setting of each part to finally form the 1.67-turn superhelix. Previous studies on the nucleosome DNA structure usually choose one or several nucleosome core particles (NCPs) to summarize the deformation characteristics of the DNA and construct structural and physical models for the super-helix path in terms of step parameters, groove width, bending angle, inter-atomic forces or deformation energy scores [7–9]. Tolstorukov et al. established the roll-and-slide model in which slide makes major contribution to the super-helical pitch and roll accounts for the DNA bending [10]. Bishop applied a Fourier-filtering strategy to the six base-pair step parameters from several nucleosome crystal structures, to identify the necessary amount of Fourier components that each parameter needs to reconstruct a highresolution model of the nucleosome superhelix [11]. Becker et al. established a mechanical model for the histone-DNA binding by calculating forces and torques acting on each base pair along the super-helical path [12]. Morozov et al. extended Olson’s DNA elastic energy function by adding a weighted part of histone-DNA interaction energy to build a biophysical model for the intrinsic sequence dependence of nucleosome formation [13]. Although a lot of interesting conclusions have been made, they are specific to certain core particles used in the studies and the structural measurement via one or a few properties only emphasizes deformation in certain dimensions. With an increasing number of determined nucleosome crystal structures, it is now possible to study whether a consistency of deformation patterns relative to the global organization exists among NCPs with variant DNA and histone sources. We apply a multivariate analysis on the nucleosome structure database and establish a position-dependent conformational map for the superhelical DNA paths. A principal conformational subspace (PCS) is built to represent the most significant variances of the original structural database. Based on the statistics of the variation along the principal dimensionalities, the positions or regions that have distinct deformation patterns are identified. The statistical result shows that there is a high consistency as to the position-specific structural contribution to the overall superhelix among the crystal structures of nucleosome.

Methodology

Structural data of NCPs

The experimental database is constructed by collecting 6870 base pair steps from 48 nucleosome crystal structures in the Protein Data Bank (PDB), including 1AOI, 1EQZ, 1F66, 1ID3, 1KX5, 1KX4, 1KX3, 1M1A, 1M19, 1M18, 1P3P, 1P3O, 1P3M, 1P3L, 1P3K, 1P3I, 1P3G, 1P3F, 1P3B, 1P3A, 1P34, 1S32, 2CV5, 1U35, 1ZLA, 2F8N, 2FJ7, 2NZD, 2NQB, 2PYO, 3B6G, 3B6F, 3C1C, 3C1B, 3KUY, 3LJA, 3KWQ, 3LEL, 3AFA, 3A6N, 3MGS, 3MGR, 3MGQ, 3MGP, 3KXB, 3MVD, 3LZ0 and 3LZ1. The pdb file of 3LEL contains two spatially independent nucleosome cores and hence the actual total number of nucleosome sequences used in our study is 49. The software 3DNA is used to derive the conformational parameters from the raw pdb file [14]. In order to describe a typical base pair step unit, we incorporate three types of structural parameters: (1) sugar phosphate backbone, (2) base pair and (3) base pair step. The first type includes main-chain torsion angles (α, β, γ, δ, ε and ζ), a pseudorotation angle (amplitude τm and phase angle P) that indicates the sugar ring puckering and glycosidic bond torsion angle (χ) [2]. The second and the third type respectively describe the relative orientation of the two complementary bases (shear, stretch, stagger, buckle, propeller and opening) and the stacking interactions of two sequential base pair steps (shift, slide, rise, tilt, roll and twist) [2]. Due to the double strand nature of DNA, each unit has two sets of sugar phosphate backbone parameters, and hence a single observation in the database is a vector with 30 dimensions (see supplementary material)

Principal component analysis

PCA is a useful tool in exploratory data analysis and it reveals the projection of original parameters onto the direction that stands for the largest variations. By applying PCA to the database we aim at finding a principal conformational subspace (PCS) to represent the most significant original structural fluctuations [15]. Standard algorithms are used here. The covariance matrix C with elements Cab measures the relationship between the original structural dimensions. C_ab = <(x_a ― <x_a>) (x_b ― <x_b>) > (Equation 1), where x is the standardized values of original structural parameters and <> means the average over all observations in the nucleosome database. The matrix of eigenvectors U diagonalizes the covariance matrix C. U_T CU = D (Equation 2), where D is the diagonal matrix of eigenvalues λ₁,…λ₃₀. The eigenvectors in matrix U describe the harmonic contribution of original dimensions to each principal component and the eigenvalues measure the variances that each PC accounts for. The principal components with the largest eigenvalues are then selected to construct the principal conformational subspace (PCS). For any given observation θ_n, its score in any collective dimension of the PCS is calculated as given in supplementary material.

Statistical analysis of position-specific structural contribution

For each nucleosome, the PCS scores of its constituent parts, are calculated and related to the positions at which they occur. The scores are then converted to scaled scores of 0 to 1, in which 0 and 1 respectively represent the minimum and maximum score in a certain nucleosome path. By doing so, we can highlight the positions of relative larger geometrical fluctuations for each nucleosome path. The conversion of the original score υ_k,m to the scaled score z_k,m is defined as given in supplementary material. Additionally, original scores at each position are summed up and averaged over all the paths. The averaged results are then analyzed using the Fourier Transform to detect whether periodicity exists in the geometrical variation along the superhelix path. The frequency spectrum of the position-specific geometrical variation sequence is defined as given in supplementary material.

Discussion

The principal conformational subspace

The eigenvalues of the first three principal components derived from the nucleosome crystal structure database are all larger than 2, which separate them from the subsequent PCs. So we use (PC1, PC2, PC3) to define the principal conformational subspace because in a less explicit situation the special conformational information may just be implied in several most significant eigenvectors. The loadings of PC1 are evenly distributed on all the original structural parameters except for buckle (Table 1, see supplementary material). Another parameter τm2 also has very limited but not negligible projection on PC1. It means that upon the fluctuation along PC1, the buckle angle between two complementary bases and the sugar pucker amplitude of the second backbone strand remain still, when other torsions and displacements are changing. By contrast, δ₁, ζ₁, χ₁, β₂, ε₂, χ₂, P₂, slide, roll and twist are dominant in PC1, and from the geometrical meaning of these parameters, the PC1 can be described as a ribose ring oriented coordinate that emphasizes the slide-roll-twist variations. For PC2, the loadings are also very evenly distributed on various parameters except that the step parameter tilt almost has no reflection in this eigenvector. From the coefficients comparison of PC2 with PC1, we can see that the slide-roll-twist coupling is more emphasized in PC2 while the anti-correlations of roll with slide and twist found in both PCs are the same. It should be noted that the five backbone torsion angles (α, β, γ, δ, ζ) of each strand have significant and even projections. PC2 therefore can be characterized as a backbone-torsion-oriented-coordinate that emphasizes the slide-roll-twist and sugar- pucker variations. For PC3, buckle, shift and ε₂ dominate. PC3 also has considerable loadings on stagger, opening, rise, tilt, twist and τ_m2. As far as the absolute values of coefficients of corresponding parameters are concerned, the weights on the two strands are not in equilibrium. So overall PC3 is a collective coordinate that is based on the glycosidic bond torsion as well as sugar pucker of strand II and lays stress on the behaviors of complementary base pairs and the step structural variations in terms of shift, rise, tilt and twist, which is completely different from PC1 and PC2. The average structure shows that the two strands of backbone have very similar mean conformational parameters, which indicates that the backbone on the whole maintains a good symmetry or balance between its double strands during DNA bending into the 1.67 super-helical turns. From the standard deviation values, which measure the spread of data points from their mean, it can be seen that the two strands also have similar fluctuation levels. Nevertheless, the coordinates of PCs, especially PC3, have some bias on one of the two strands, which is in the form of exerting different coefficients on the same backbone parameters of the two strands. Thus, it is inferred that the two strands of backbone play diverse and uneven roles in the PCs.

Position-specific deformation pattern along the nucleosome DNA path

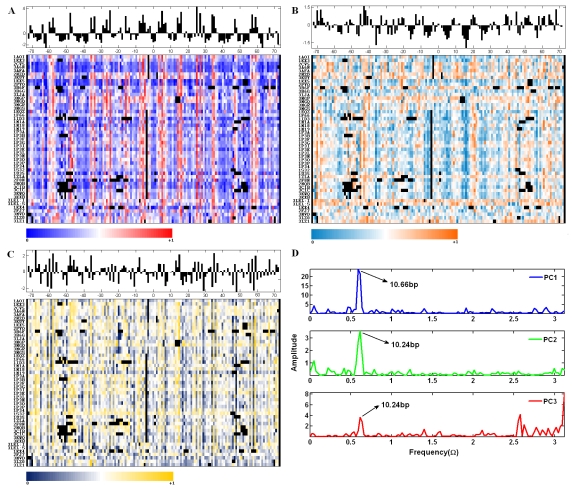
It can be seen that there are regular patterns in the sequential structural variations in terms of scaled PC1, PC2 and PC3 scores (Figure 1a, 1b and 1c). The histograms of the averaged original PC score, over all the nucleosome paths, give a general and statistical structural characterization of the constituent parts. We assume that the position-specific original PC scores are a function of position. By averaging PC scores on certain position over all the nucleosomes, the noise hidden in the data can be reduced greatly. The Fourier analysis on the curve of average value vs. position shows that the structural variation along the nucleosome path is periodic (Figure 1d). In the case of PC1 curve, a 10.66bp-periodicity is revealed, while for the PC2 and PC3 curve, a slightly different periodicity, 10.24bp, is obtained. We also applied the Fourier analysis on the 30 original structural parameters. It is found that stagger and roll have the 10.24bp periodicity while slide and twist have the 10.66bp periodicity. The backbone parameter ε and ζ also have obvious periodicities, but for different nucleosomes, their periodicities have some fluctuations of being either 10.24bp or 10.66bp. Another backbone parameter β has been observed to have a predominant 10.24bp or 10.66bp periodicity in some but not all nucleosomes. The rest parameters do not have any predominant periodicity. Therefore, it is concluded that despite of the significant projections of various parameters on the PCs, the global bending of nucleosome DNA is mainly implemented by stagger, roll, slide, twist, β, ε and ζ variations. The variations described in terms of these parameters, however, are not strictly synchronous with each other. Positions with extreme PC scores that exceed the standard deviation range are marked along the two halves relative to the dyad axis. Based on the probabilities of positions with extreme PC scores, it is possible to identify positions of overall importance for the nucleosome structure. Here, only those with over 40% probability of having extreme PC scores are recognized as important “building blocks”. It is found that some positions do not stand in isolation but with adjacent positions to form a short region, such as ­42˜­41, ­25˜­ 24, ­15˜­14, 14˜16/17, 34˜35 and 40˜41. In particular, a fair number of positions have more than one kind of extreme PC scores, which means that they have multiple deformation patterns. We separate twenty regions with relatively strong deformation patterns measured by either or some principal dimensionalities: ­69˜­57, ­47˜­41, ­38, ­35˜­33, ­29, ­25˜­24, ­ 15˜­14, ­10, ­7˜­3, 3˜7, 14˜22, 25˜29, 34˜36, 40˜41, 45˜48, 52, 55˜59, 63˜64, 67˜68 and 71. Compared with other parts along the nucleosome path, these regions are more inclined to take distinct deformation patterns. It can be found that their distributions are not strictly symmetric to the dyad point and have irregular intervals between any two neighboring ones.

Figure 1.

The profiles of structural variations described by the values under principal dimensionalities and periodicities hidden in the variations. (a), (b) and (c): the spectrums of sequential structural variations in terms of scaled PC1, PC2 and PC3 scores respectively for the 49 nucleosome paths. Original scores of PC1, PC2 and PC3 are converted to a color-coded value range of 0˜1. The inserted blanks for an optimal alignment and the base pairs deleted by 3DNA are represented by black squares in spectrums and are excluded from the statistics. The histograms above the spectrums stand for the averaged value of position-specific original scores over all the nucleosomes. (d) The frequency spectrums based on the Fourier Transform on the averaged PC scores varying with positions.

Conclusion

The statistical analysis on the experimentally determined crystal structures of nucleosomes in the PDB reveals that the conformational settings along the 145˜147bp sequence are obviously position-specific. The behaviors of the base pair steps, the puckering of the ribose ring and related backbone torsions jointly represent the major structural variation that is reflected in the PCs defined in our study. The structural variation characterized by the PC scores is periodic along the nucleosome path. The periodicity 10.66bp and 10.24bp acquired in our research are consistent with the 10˜11bp periodicity reported in previous research, but our result is based purely on the structural properties while the commonly accepted 10˜11bp periodicity is usually the product of genome sequence content analysis. Finally, the significant structural contributors that are evaluated by their scores on PC1, PC2 and PC3 have been proven to follow certain distribution patterns. Some positions are highlighted by more than one kind of PC score, implying that the local structures on these positions have multiple deformation patterns. The high probabilities of certain positions (or regions) having extreme PC values prove that the crystal structures of nucleosome DNA have much consistency in position-specific structural variations.