On the Confounds among Retest Gains and Age-Cohort Differences in the Estimation of Within-Person Change in Longitudinal Studies: A Simulation Study

Abstract

Although longitudinal designs are the only way in which age changes can be directly observed, a recurrent criticism involves to what extent retest effects may downwardly bias estimates of true age-related cognitive change. Considerable attention has been given to the problem of retest effects within mixed effects models that include separate parameters for longitudinal change over time (usually specified as a function of age) and for the impact of retest (specified as a function of number of exposures). Because time (i.e., intervals between assessment) and number of exposures are highly correlated (and are perfectly correlated in equal interval designs) in most longitudinal designs, the separation of effects of within-person change from effects of retest gains is only possible given certain assumptions (e.g., age convergence). To the extent that cross-sectional and longitudinal effects of age differ, obtained estimates of aging and retest may not be informative. The current simulation study investigated the recovery of within-person change (i.e., aging) and retest effects from repeated cognitive testing as a function of number of waves, age range at baseline, and size and direction of age-cohort differences on the intercept and age slope in age-based models of change. Significant bias and Type I error rates in the estimated effects of retest were observed when these convergence assumptions were not met. These simulation results suggest that retest effects may not be distinguishable from effects of aging-related change and age-cohort differences in typical long-term traditional longitudinal designs.

The extent of changes in cognitive function with increasing age has been examined using both cross-sectional and longitudinal designs. In cross-sectional designs, between-person age differences are used as a proxy for within-person age changes, and the resulting inferences about aging are thus subject to many well-known biases, including cohort effects, self-selection effects, mortality effects, and other inferential problems (Baltes, Cornelius, & Nesselroade, 1979; Baltes & Nesselroade, 1979; Hofer & Sliwinski, 2006; and Schaie, 1965, 2008). In contrast, both cross-sectional age differences and longitudinal age changes can be observed directly in longitudinal designs of persons varying in initial age, necessitating the examination of additive and/or interactive effects of age-cohort differences (i.e., incremental effects of cross-sectional age related to birth cohort and population selection effects) in estimating aging-related change.

Despite their relative advantages, a recurrent criticism of longitudinal designs involves to what extent retest or practice effects – performance gains due to repeated test exposure – may bias estimates of true aging-related change. In discussing retest effects within the context of cognitive testing specifically, we distinguish between practice effects, or improvement due to repetition of the same or similar materials, and instead will refer more generally to retest effects, or changes in performance due to previous exposure to the testing materials, environment, and procedures. To the extent that performance is improved due to familiarity with the testing material, reduction of anxiety, or general practice of the skills involved, then the magnitude of age-related decline observed at subsequent occasions may be reduced artificially, with the largest effect of retest gain typically observed between the first two occasions. Although the problem of retest effects in longitudinal studies of aging has long been identified (e.g., Baltes, 1968; Schaie 1965), it has been difficult to address in practice. Given that most studies use widely-spaced measurement occasions (i.e., of sufficient duration in which systematic change over time is expected to occur) that are relatively constant across individuals, the effects of aging-related change and retest gains within a given individual in such designs are inherently confounded.

One way to approach the problem of distinguishing retest from aging is with group-based designs. For example, the Seattle Longitudinal Study (Schaie, 1996) includes a new age-matched cohort at the second occasion for each age group, so that the extent to which retest effects result in differential estimates of age differences between cohorts can be evaluated explicitly. Although retest effects are partly responsible in such designs for group differences between those for whom the second occasion is actually the second versus those for whom it is only the first, group differences may also be due to selective attrition, in that the returning participants may be higher functioning and healthier than the age cohort initially sampled.

To combat such a problem, Thorvaldsson, Hofer, Berg, and Johansson (2006) report analyses from a wait-list control design, in which performance of persons from age 85-99 who had previously been assessed from age 70-81 was compared to that of persons who were not previously assessed. Thus, performance from age 85-99 would be primarily due to aging in the first group, but would be a function of both aging and retest in the second group. They found significant retest effects for level of performance in vocabulary and spatial reasoning only, both of which may have resulted from repeated use of the same stimulus materials. No differences between the retest groups were found for estimates of aging-related change. Unfortunately, such group-based approaches cannot be informative for examining the effect of retest at the individual level, leading to the development of other methods for quantifying retest effects.

Statistical Control of Retest Effects

An alternative way in which researchers have attempted to distinguish retest from aging is through statistical control in random effects models, in which separate parameters are estimated for longitudinal change over time (specified as a function of age) and for the impact of retest (specified as a function of number of test exposures) (e.g., Ferrer, Salthouse, Stewart, & Swartz, 2004; Ferrer, Salthouse, McArdle, Stewart, & Schwartz, 2005; McArdle, Ferrer-Caja, Hamagami, & Woodcock, 2002; Rabbitt, Diggle, Smith, Holland, & McInnes, 2001; Rabbitt, Diggle, Smith, & McInnes, 2004; Rabbitt, Lunn, & Wong, 2008; Salthouse, Schroeder, & Ferrer, 2004). A simple example of this type of age-based retest model is shown in Equation 1:

$$\begin{array}{cc}\hfill & \text{Level}1:{\mathrm{y}}_{\mathrm{t}\mathrm{i}}={\beta }_{0\mathrm{i}}+{\beta }_{1\mathrm{i}}\left({\text{Age}}_{\mathrm{t}\mathrm{i}}\right)+{\beta }_{2\mathrm{i}}\left({\text{Retest}}_{\mathrm{t}\mathrm{i}}\right)+{\mathrm{e}}_{\mathrm{t}\mathrm{i}}\hfill \\ \hfill & \text{Level}2:{\beta }_{0\mathrm{i}}={\gamma }_{00}+{\mathrm{U}}_{0\mathrm{i}}{\beta }_{1\mathrm{i}}={\gamma }_{10}+{\mathrm{U}}_{1\mathrm{i}}{\beta }_{2\mathrm{i}}={\gamma }_{20}\hfill \end{array}$$ (1)

in which y_ti is the outcome at time t for individual i. The level-1 model describes within-person change over time as a function of an individual intercept and two individual processes: time-varying age and time-varying retest, with a residual at each occasion for each individual (e_ti). The level-2 model then describes the expected mean of each term in the model for change (the fixed intercept γ₀₀, the fixed age slope γ₁₀, and the fixed retest slope γ₂₀,), also including terms that allow each individual to deviate randomly from those mean values (the random intercept U_0i and the random age slope U_1i). Usually the retest slope is modeled as fixed rather than random (i.e., assumed constant over persons, so without U_2i), though not always (e.g., Ferrer et al., 2005).

Although the example model in Equation 1 includes only a linear effect of time-varying age, other polynomial functions of age (e.g., quadratic effects) or nonlinear functions of age (e.g., exponential effects) can be specified instead as needed. Further, parameters for retest have been included in a variety of ways, such as a single “boost” improvement after the first occasion (i.e., using a function of 0-1-1-1…1 across occasions), distinct improvement at each subsequent occasion (i.e., via a series of dummy codes that either contrast the baseline occasion with each subsequent occasion or specify the incremental retest effect at each subsequent occasion), continual improvement as a function of number of test occasions (i.e., 1-2-3-4…), or as an estimated latent basis function across occasions (i.e., 0-?-?-?…1). Critically, whereas age is specified as a function of exact time between occasions, retest is not – only the number of test exposures is relevant for indexing retest (and not the exact time elapsed between test exposures).

Retest models like that depicted in Equation 1 can only be estimated in studies in which age and measurement occasion are not perfectly correlated, such as when there is a wide age range at the beginning of the study, variable retest intervals (i.e., time is unbalanced), or both. Studies employing such retest models have suggested that estimates of age-related change are likely to have downward bias unless retest effects are controlled statistically, and that retest effects can persist for many years. Positive gains attributed to retest effects have been reported to persist even given a test interval of 7-8 years (Rabbitt et al., 2004; Rabbitt, Lunn, Ibrahim, & McInnes, 2009; Salthouse et al., 2004), suggesting that efforts to minimize retest effects by using widely-spaced measurement occasions may not be successful.

In addition to distorting average aging effects, an additional problem is to what extent differential retest effects across persons can distort individual aging effects, such that persons who benefit more from retest effects than others could appear to be differentially spared by the effects of aging. Unfortunately, most of these studies have not had sufficient data with which to estimate individual differences in retest effects. Further, the findings from those studies that have examined predictors of retest effects have conflicted. While some studies have found retest effects to be unrelated to age (Ferrer et al., 2004; Rabbitt et al., 2001; 2004; Salthouse et al., 2004) or unrelated to attrition due to death or dropout (Rabbitt et al., 2008), other studies have reported that retest gains were weaker in older persons (Ferrer et al., 2005; Rabbitt et al., 2008) or weaker in persons with the highest and lowest levels of cognitive ability (Rabbitt et al., 2008). Further, some studies have found retest effects to be only weakly related across domains (Salthouse & Tucker-Drob, 2008), whereas other studies have found stronger relationships (e.g., Ferrer et al., 2005), but controlling for these retest relationships does not always appear to significantly attenuate the age slope correlations across domains (e.g., Ferrer et al., 2005).

Assumptions of Retest Models

Models for statistical control of retest effects typically rely on a number of assumptions when applied in long-term longitudinal studies. The major aim of retest models is to estimate the aging-related change that would have been obtained at subsequent occasions without repeated testing. Because the quantity of “naive” performance cannot be observed directly in any research design where there is reactivity to repeated testing, it is important to recognize what is assumed in order to quantify retest effects within these models. The first assumption when using occasion to operationalize retest is that the size of the retest effect depends solely on the number of previous assessments, and does not depend on the time interval between assessments (e.g., Ferrer et al., 2004; Ferrer et al., 2005; McArdle et al., 2002; Salthouse et al., 2004). In other words, regardless of whether a second measurement occasion occurs one month or seven years after the first (i.e., a variable time-lag between occasions), it should be affected by the same degree of retest simply because it is the second occasion (and the same is true for other occasions as well).

Second, both age-cohort differences and retest effects can potentially produce misfit to the expected outcome at a given age. Age-based retest models (such as that shown in Equation 1) assume that cross-sectional age differences and longitudinal age changes have equivalent effects on the outcome, or that the two effects of age show convergence after accounting for retest effects (Bell, 1953; McArdle & Bell, 2000; Miyazaki & Raudenbush, 2000). That is, in studies employing retest models, because age varies both between persons (i.e., persons begin the study at different ages) and within persons (i.e., aging occurs in the study), the time-varying predictor of age carries at least two potential effects corresponding to each source of variation. Whether or not the cross-sectional and longitudinal age effects are equivalent (i.e., show age convergence) can be tested empirically (see Sliwinski, Hoffman, & Hofer, 2010), as shown in Equation 2:

$$\begin{array}{cc}\hfill & \text{Level}1:{\mathrm{y}}_{\mathrm{t}\mathrm{i}}={\beta }_{0\mathrm{i}}+{\beta }_{1\mathrm{i}}\left({\text{Age}}_{\mathrm{t}\mathrm{i}}\right)+{\mathrm{e}}_{\mathrm{t}\mathrm{i}}\hfill \\ \hfill & \text{Level}2:{\beta }_{0\mathrm{i}}={\gamma }_{00}+{\gamma }_{01}\left({\text{AgeCohort}}_{\mathrm{i}}\right)+{\mathrm{U}}_{0\mathrm{i}}{\beta }_{1\mathrm{i}}={\gamma }_{10}+{\mathrm{U}}_{1\mathrm{i}}\hfill \end{array}$$ (2)

in which a variable for age-cohort (such as age at baseline or birth year) is included as a predictor of the intercept at level-2. If the cross-sectional and longitudinal effects of age are the same, then the fixed age-cohort slope γ₀₁ will be zero. In other words, if the outcome depends only on current age, then age-cohort will not contribute incrementally to the model. However, if it not only matters how old a given person is at each occasion, but also when that age was reached (i.e., an incremental age-cohort effect), then the fixed age-cohort slope γ₀₁ will be different than zero. Given a negative age slope (γ₁₀), a positive age-cohort slope γ₀₁ would indicate that the effect of cross-sectional age differences is smaller than the effect of longitudinal age changes, whereas a negative age-cohort slope γ₀₁ would indicate that the effect of cross-sectional age differences is larger than the effect of longitudinal age changes. Non-convergence of these two age effects can result from many other influences, including cohort effects and mortality-based selection (which can affect initial sample selection in age-heterogeneous samples as well as attrition in follow-up). Age-cohort effects may also be observed on the age slope, further complicating matters.

Testing for convergence of the cross-sectional and longitudinal effects of age (or of any accelerated time metric) relates directly to any model that attempts to control for retest effects statistically. Because age-cohort is almost never included in the retest model in addition to current age, the statistical separation of changes due to retest from changes due to aging is accomplished using between-person age differences to adjust the rate of observed within-person change, the same as in the group-based retest approaches (e.g., Thorvaldsson et al., 2006). Any observed non-convergence of the cross-sectional and longitudinal age effects then contributes directly to the observed retest effect. In general, age convergence is usually not tested formally as described in Equation 2. Instead, it is tested via less powerful group comparisons of “younger” and “older” cohorts (i.e., by performing a median split on cohort) after including retest effects, or is simply assumed (e.g., Ferrer et al., 2004, 2005; McArdle et al., 2002; Rabbitt et al., 2001, 2004, 2008, 2009; Salthouse et al., 2004). Thus, the extent to which the observed retest effects in these studies could be due to present but unmodeled age-cohort effects is generally unknown.

Purpose of the Current Study

In summary, significant recent attention has been given to the problem of retest effects in longitudinal studies of age-related change in cognition. Random effects models that attempt to control for retest effects statistically have become common-place, but empirical evidence as to their viability in this type of longitudinal data is still lacking. The current study aims to fill this gap by examining via simulation the extent to which effects of aging, age-cohort, and retest may be distinguished reliably given differing longitudinal design conditions and statistical model formulations. Critically, in our simulation generation models, retest effects were always specified as zero in order to permit a clear interpretation of any estimated retest effect as a Type I error. Of particular interest, then, is the extent to which ignoring existing age-cohort effects might create false estimates of retest, given how infrequently age-cohort effects (including mortality selection and other factors) are considered in practice. As detailed below, two kinds of retest effects were investigated: a single retest boost after the first occasion and per-occasion incremental retest gains. Study 1 examined the effect of an unmodeled age-cohort effect on the intercept in creating main effects of these two types of retest, and Study 2 examined the effect of an unmodeled age-cohort effect on the age slope in creating interactions of these two types of retest with age.

Study 1

Method

Simulation Design

The Study 1 simulation design included 500 replications of 500 hypothetical persons in a longitudinal study. The generation model is shown in Equation 3:

$$\begin{array}{cc}\hfill \text{Level}1:& {\mathrm{y}}_{\mathrm{t}\mathrm{i}}={\beta }_{0\mathrm{i}}+{\beta }_{1\mathrm{i}}\left({\text{Age}}_{\mathrm{t}\mathrm{i}}\right)+{\beta }_{2\mathrm{i}\dots 6\mathrm{i}}\left({\text{Retest}}_{\mathrm{t}\mathrm{i}}\right)+{\mathrm{e}}_{\mathrm{t}\mathrm{i}}\hfill \\ \hfill \text{Level}2:& {\beta }_{0\mathrm{i}}={\gamma }_{01}\left({\text{AgeCohort}}_{\mathrm{i}}\right)+{\mathrm{U}}_{0\mathrm{i}}\hfill \\ \hfill & {\beta }_{1\mathrm{i}}={\gamma }_{10}+{\mathrm{U}}_{1\mathrm{i}}{\beta }_{2\mathrm{i}\dots 6\mathrm{i}}={\gamma }_{20}\cdots {\gamma }_{60}\hfill \end{array}$$ (3)

in which y_ti is the outcome at time t for individual i. The level-1 model describes the change within persons over time as a function of an individual intercept and individual effects of age and retest, and the level-2 model describes how each of those individual effects is constructed. The data generation parameters and analysis models are described in Table 1. Complete data were simulated to mimic variable annual observations, such that 99% of the observations occurred within ± 2 weeks of the annual assessment (assuming a normal distribution for the variation).

Table 1.

Simulation Parameters and Data Analysis Models for Studies1 and 2

Study 1 Data Generation Parameter Values
50	Fixed Intercept (γ00)
−1	Fixed Per-Year Age Slope (γ10)
−0.25, 0, 0.25	Fixed Effect of Age-Cohort on Intercept (γ01)
0	Fixed Effect(s) for Single Boost Retest (γ20) or Incremental Retest (γ20…60)
75	Random Intercept Variance (${\tau }_{\mathrm{U}0}^2$)
0.25	Random Age Slope Variance (${\tau }_{\mathrm{U}1}^2$)
25	Residual Variance (${\sigma }_{\mathrm{e}}^2$)
Study 1 Data Analysis Models: Fixed Effects Included
1a	Age + Age-Cohort (Correct Model)
1b	Age + Single Boost Retest
1c	Age + Single Boost Retest + Age-Cohort
1d	Age + Incremental Retest
1e	Age + Incremental Retest + Age-Cohort
Study 2 Data Generation Parameter Values
50	Fixed Intercept (γ00)
−1	Fixed Per-Year Age Slope (γ10)
0	Fixed Effect of Age-Cohort on Intercept (γ01)
−0.05, 0, 0.05	Fixed Effect of Age-Cohort by Age Slope (γ11)
0	Fixed Effect(s) for Single Boost Retest (γ20) or Incremental Retest (γ20…60)
0	Fixed Effect(s) for Age by Single Boost Retest (γ70) or by Incremental Retest (γ70…110)
75	Random Intercept Variance (${\tau }_{\mathrm{U}0}^2$)
0.25	Random Age Slope Variance (${\tau }_{\mathrm{U}1}^2$)
25	Residual Variance (${\sigma }_{\mathrm{e}}^2$)
Study 2 Data Analysis Models: Fixed Effects Included
2a	Age + Age-Cohort + Age-Cohort*Age (Correct Model)
2b	Age + Single Boost Retest + Single Boost Retest*Age
2c	Age + Single Boost Retest + Single Boost Retest*Age + Age-Cohort + Age-Cohort*Age
2d	Age + Incremental Retest + Incremental Retest*Age
2e	Age + Incremental Retest + Incremental Retest*Age + Age-Cohort + Age-Cohort*Age

Sixteen simulation conditions were created by crossing 3 dimensions. First, the data included either 3 or 6 waves. Second, variation in age at baseline was manipulated to create age-cohorts, such that 99% of the baseline ages fell within either a 20-year or a 40-year range (given a normal distribution). These dimensions of waves and cohort age range will permit an examination of how the relative amount of cross-sectional versus longitudinal variation in age may influence estimation of the age and retest slopes. Third, an incremental linear effect of age-cohort (as baseline age) on the intercept of γ₀₁ = −0.25, 0, or 0.25 per year was included to examine the deleterious effects an unmodeled age-cohort effect on the estimated retest effects.

Analysis Models

The five analysis models estimated in Study 1 differed systematically in their fixed effects, as shown in Table 1. Model 1a was the generating model and included no fixed slopes for retest to serve as a baseline, while the other models included one of two kinds of retest slopes. First, a single boost retest slope (i.e., γ₂₀ only as a boost after baseline) was included in Models 1b and 1c to represent the most simplistic option (i.e., a single retest boost after the first testing). Second, a series of occasion-specific retest increments (i.e., γ₂₀ up to γ₆₀ using degrees of freedom equal to the number of occasions minus 1) was included in Models 1d and 1e to represent the most complex option (i.e., retest effects that persist throughout the study). These two types of retest effects can logically be viewed as the extremes between which many other specifications of retest effects (e.g., linear or quadratic occasion slopes, latent basis slopes) will fall. Critically, because the generation model never included any retest effects, any obtained non-zero estimate of a retest effect must result from the influence of the missing age-cohort effect on the intercept, as seen by comparing Models 1c and 1e, which included an effect of age-cohort, to Models 1b and 1d, which did not include an effect of age-cohort.

Outcome Variables

Two outcome variables were analyzed. The first was mean bias, calculated per replication as: mean bias = slope estimate – generation value. Second, to assess the quality of the standard errors, power rates were examined for each slope as the proportion of simulation replications in which the null hypothesis of no effect would have been rejected at the .05 level. For retest effects, power rates are actually Type I error rates, given that retest effects were never included in the generation model. Separate 3-way analyses of variance were then conducted for each slope (age, age-cohort, and retest) within each of the five analysis models for each outcome. Table 2 provides the mean bias and power/Type I error rates for the estimated slopes for age, age-cohort, and retest across simulation conditions and analysis models. Because of the large number of replications per condition (N = 500), partial η² effect size estimates were used to assess practical significance, and only effects from simulation variables of partial η² ≥ .05 (as calculated from SS_effect / [SS_effect + SS_error] from the full model) are presented below.

Table 2.

Mean Bias and Power/Type I Error Rates in Study 1

Model Parameter	No Retest		Single Boost Retest				Incremental Retest per Occasion
	Model 1a		Model 1b		Model 1c		Model 1d		Model 1e
	Bias	Power	Bias	Power	Bias	Power	Bias	Power	Bias	Power
Age Slope
c = −0.25, w = 3, r = 20	0.00	1.00	−0.22	1.00	−0.01	0.89	−0.25	1.00	0.19	0.05
c = −0.25, w = 3, r = 40	−0.01	1.00	−0.24	1.00	−0.01	0.88	−0.25	1.00	0.11	0.05
c = −0.25, w = 6, r = 20	0.00	1.00	−0.07	1.00	0.00	1.00	−0.25	1.00	0.09	0.06
c = −0.25, w = 6, r = 40	0.00	1.00	−0.15	1.00	0.00	1.00	−0.25	1.00	−0.23	0.07
c =  0, w = 3, r = 20	0.00	1.00	0.00	1.00	0.02	0.85	0.00	1.00	0.16	0.04
c =  0, w = 3, r = 40	0.01	1.00	0.00	1.00	0.01	0.88	0.00	1.00	0.21	0.06
c =  0, w = 6, r = 20	0.00	1.00	0.00	1.00	0.00	1.00	0.00	1.00	0.07	0.07
c =  0, w = 6, r = 40	0.00	1.00	0.00	1.00	0.00	1.00	0.00	1.00	0.13	0.06
c = 0.25, w = 3, r = 20	0.00	1.00	0.22	1.00	0.00	0.88	0.24	1.00	0.08	0.05
c = 0.25, w = 3, r = 40	0.00	1.00	0.25	1.00	0.00	0.87	0.25	1.00	0.62	0.04
c = 0.25, w = 6, r = 20	0.00	1.00	0.08	1.00	0.00	1.00	0.25	1.00	0.13	0.06
c = 0.25, w = 6, r = 40	0.00	1.00	0.15	1.00	0.00	1.00	0.25	1.00	0.37	0.05
Cohort Slope
c = −0.25, w = 3, r = 20	0.00	0.25			0.01	0.12			−0.19	0.05
c = −0.25, w = 3, r = 40	0.01	0.31			0.01	0.14			−0.10	0.05
c = −0.25, w = 6, r = 20	0.00	0.55			0.00	0.49			−0.08	0.05
c = −0.25, w = 6, r = 40	0.00	0.89			0.00	0.78			0.23	0.05
c =  0, w = 3, r = 20	0.00	0.03			−0.02	0.05			−0.17	0.03
c =  0, w = 3, r = 40	−0.01	0.07			−0.01	0.05			−0.21	0.05
c =  0, w = 6, r = 20	0.00	0.05			0.00	0.07			−0.06	0.06
c =  0, w = 6, r = 40	0.00	0.05			0.00	0.03			−0.14	0.05
c = 0.25, w = 3, r = 20	0.00	0.26			−0.01	0.13			−0.08	0.04
c = 0.25, w = 3, r = 40	0.01	0.34			0.00	0.11			−0.62	0.05
c = 0.25, w = 6, r = 20	0.00	0.53			0.00	0.46			−0.13	0.05
c = 0.25, w = 6, r = 40	0.00	0.92			0.00	0.81			−0.37	0.05
Retest Slope
c = −0.25, w = 3, r = 20			0.34	0.20	0.01	0.05	0.26	0.13	−0.18	0.05
c = −0.25, w = 3, r = 40			0.34	0.22	0.00	0.05	0.24	0.12	−0.11	0.05
c = −0.25, w = 6, r = 20			0.20	0.11	−0.03	0.04	0.23	0.12	−0.10	0.05
c = −0.25, w = 6, r = 40			0.46	0.38	0.01	0.05	0.25	0.12	0.23	0.05
c =  0, w = 3, r = 20			−0.01	0.06	−0.04	0.05	−0.02	0.06	−0.18	0.04
c =  0, w = 3, r = 40			0.02	0.06	0.01	0.05	0.02	0.05	−0.19	0.05
c =  0, w = 6, r = 20			−0.01	0.03	−0.01	0.03	−0.01	0.04	−0.07	0.06
c =  0, w = 6, r = 40			0.01	0.04	0.00	0.05	−0.01	0.04	−0.15	0.05
c = 0.25, w = 3, r = 20			−0.34	0.19	−0.01	0.06	−0.25	0.13	−0.08	0.05
c = 0.25, w = 3, r = 40			−0.37	0.27	−0.01	0.06	−0.26	0.14	−0.62	0.05
c = 0.25, w = 6, r = 20			−0.25	0.14	−0.03	0.07	−0.27	0.11	−0.15	0.04
c = 0.25, w = 6, r = 40			−0.46	0.40	−0.01	0.02	−0.25	0.12	−0.38	0.05

Table 2 Note: c = age-cohort effect, w = waves, and r = cohort age range. Power rates for all retest slopes actually reflect Type I error rates given their omission from the generation model. The incremental retest slope estimates reported in Models 1d and 1e reflect those from the first incremental retest effect (at the second occasion).

Results and Discussion

Estimation of Age Slopes

As shown in the top of Table 2, no problems with the age slopes were found in the correct Model 1a (age + age-cohort only). In Model 1b (age + single boost retest), bias in the age slopes differed by the missing age-cohort effect (η² = 0.78), age-cohort by waves (η² = 0.30), and age-cohort by age range (η² = 0.07), such that, as expected, the age slopes were biased towards the missing age-cohort effect, more so for 3 than 6 waves and for a 40-year than 20-year age range. In Model 1d (age + incremental retest), the age slopes were also biased towards the missing age-cohort effect (η² = 0.83), but uniformly so. Power to detect the age slopes was uniformly 100% in Models 1b and 1d (as in the correct Model 1a).

However, when slopes for both age-cohort and an extraneous single retest effect were included (Model 1c), although no problems with bias were observed, power rates for the age slopes differed by number of waves (η² = 0.07), such that power was ≈ 88% for conditions with 3 waves (instead of 100% for all conditions as in Model 1a). Finally, when slopes for both age-cohort and extraneous incremental retest effects at each occasion were included (Model 1e), although no simulation design effects were found for bias or power, this was due to the overall poor quality of the age slope estimates. The age slopes were positively biased in all conditions but one, and power to detect the age slope across conditions was actually near the Type I error rate (4-7%), rather than 100% as it had been in Model 1a. In sum, although including an extraneous single boost retest effect after the first occasion had very little impact on the recovery of the age slopes (i.e., no bias and only small reductions in power given 3 waves in Model 1c), including extraneous incremental retest effects at each occasion had a much more deleterious impact, creating bias in the age slope estimates and much higher standard errors (as indicated by the abysmal power rates to detect the age slopes in Model 1e relative to Model 1a).

Estimation of Age-Cohort Slopes

As shown in the middle of Table 2, no simulation design effects or problems with bias were observed in Model 1a, in which the age and age-cohort slopes were specified correctly without extraneous retest slopes. As expected, in Model 1a power rates to detect the age-cohort slopes differed by the size of the age-cohort effect (η² = 0.25), waves (η² = 0.13), and age-cohort by waves (η² = 0.07), such if an age-cohort effect was present, power rates to detect it ranged from 25% to 92% across conditions (with greater power for 6 than 3 waves). The power rates observed in Model 1a serve as a baseline with which to evaluate the power to detect age-cohort slopes when including extraneous retest effects (Models 1c and 1e).

First, when including slopes for both age-cohort and an extraneous single retest effect (Model 1c), although no problems with bias were observed, power to detect the age-cohort slopes differed significantly by waves (η² = 0.19), the age-cohort effect (η² = 0.17), and age-cohort by waves (η² = 0.11), such that power was greater for 6 than 3 waves, but was lower overall (12-81% relative to 25-92% across conditions in Model 1a without retest effects). Second, when including slopes for both age-cohort and extraneous incremental retest at each occasion (Model 1e), although no simulation design effects were found for bias or power, this was due to the poor quality of the age-cohort slope estimates (as was found for the age slopes in Model 1e as well). The age-cohort slopes in Model 1e were negatively biased in all conditions but one, almost perfectly off-setting the positive average bias found for the age slopes in the same conditions in Model 1e. Power to detect the age-cohort slopes was also near Type I error rate (4-7%) across conditions rather than 25-92% across conditions, as in the correct Model 1a.

Thus, to summarize, the same pattern of results was found for recovery of the age-cohort slopes as was found for recovery of the age slopes: whereas including an extraneous single boost retest effect has very little effect on the recovery of the age or age-cohort slopes (no bias and small reductions in power in Model 1c relative to Model 1a), including extraneous incremental retest effects at each occasion (Model 1e) had a much more deleterious impact on the recovery of the age and age-cohort slopes, creating bias in the estimates and inflated standard errors (as indicated by the abysmal power rates to detect the age and age-cohort slopes relative to Model 1a). However, the bias observed in the age and age-cohort slopes appeared to be compensatory within each condition, such that the same model predictions would be made in Model 1e as in Model 1a, although the inferences about the significance of each effect would be very different (i.e., it would appear that neither age nor age-cohort contributed in Model 1e, resulting from the additional collinearity created by including extraneous retest effects at each occasion).

Estimation of Single Boost Retest Slopes

We now turn to the estimated retest slopes themselves, which were always zero in the generation models. When a single retest effect was included without controlling for age-cohort (Model 1b), effects of the missing age-cohort effect were found for bias (η² = 0.47) and for Type I error rate (η² = 0.06). As shown in the bottom of Table 2, the single retest slope was biased away from any missing age-cohort effect, with Type I error rates ranging from 11-40% across conditions. Thus, if a negative age-cohort effect was missing, a positive retest effect was observed, and if a positive age-cohort effect was missing, a negative retest effect was observed instead (even thought negative retest effects are logically impossible in cognitive tests in which higher scores indicate better performance). After including a slope for the age-cohort effect, however (Model 1c), the single retest slopes were estimated near zero (bias ≤ .04 in absolute value) with acceptable Type I error rates (ranging from 2-7%).

Estimation of Incremental Retest Slopes

Models 1d and 1e included incremental retest effects at each occasion. Because the results for the estimated retest effects were nearly identical at the 2nd or 3rd occasions given 3 waves, and at the 4th, 5th, or 6th occasions given 6 waves, results for the incremental retest effect at the 2nd occasion only are presented in the bottom of Table 2. When incremental retest slopes were included without age-cohort (Model 1d), effects of the missing age-cohort effect were found for bias (η² = 0.28), such that the incremental retest slope was biased away from any missing age-cohort effect (i.e., a positive retest slope given a negative missing age-cohort effect; a negative retest slope given a positive missing age-cohort effect). Type I error rates ranged from 11-13% in those conditions. After controlling for age-cohort (Model 1e), the bias in the estimated incremental retest slopes almost perfectly matched the bias in the age-cohort slopes, but with acceptable Type I error rates (ranging from 4-6%).

Study 1: Summary

Study 1 examined the effects of longitudinal design characteristics (number of waves, baseline age range, and age-cohort effects on the intercept) on estimation of the slopes for age, age-cohort, and retest (a single effect or incremental effects at each occasion), with three primary findings. First, correct inferences about retest can only be obtained once the total effect of age is considered, including additive differential effects of cross-sectional age differences. When an age-cohort effect was present but not modeled (Models 1b and 1d), it was absorbed by the retest slopes, such that a negative missing age-cohort slope became a positive retest slope, and vice-versa, with considerable Type I error rates for the retest slopes. Only when the age-cohort slope was included were the Type I error rates for the retest slopes acceptable.

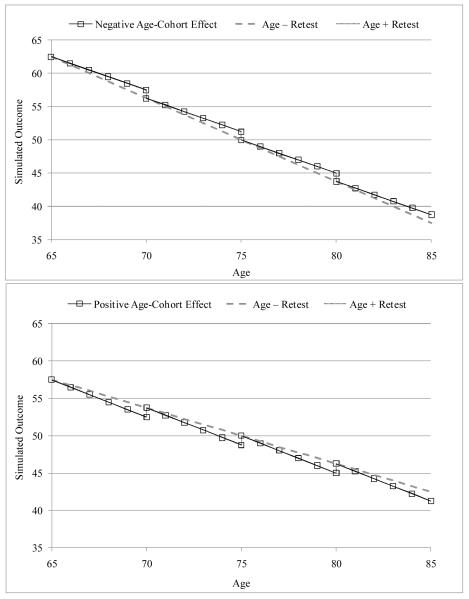
The tradeoff between age-cohort and retest is illustrated in Figure 1, which plots the predicted outcomes given 6 waves and a 20-year baseline age range with an age-cohort effect of −0.25 (top) or 0.25 (bottom). The lines with squares represent 6-year predicted trajectories for 4 age cohorts based on the correct Model 1a (age and age-cohort effects). The dashed line is the “true” age slope predicted from Model 1d (omitting age-cohort but with incremental retest). As shown in the top of Figure 1, the non-convergence of trajectories due to the negative age-cohort effect is exactly compensated for by positive retest effects. Consider the overlap between the 65- and 70-year-old cohorts at age 70. Because the predicted outcome at age 70 is higher for persons who have been in the study longer (but who come from younger cohorts), either a single negative age-cohort effect (that holds across occasions) or positive incremental retest effects at each occasion will cover this discrepancy. The bottom of Figure 1 shows the opposite, in which non-convergence of the age trajectories can be described by either a single positive age-cohort effect or a set of negative incremental retest effects (although negative retest effects should be impossible in cognitive tests in which higher scores indicate better performance).

Figure 1.

Predicted trajectories from Study 1 for the simulation condition of 6 waves and a 20-year baseline age range. The predicted outcomes are shown when including the correct effects of age and age-cohort (separate lines with squares) or for the effect of age controlled for retest (dashed line), given a negative age-cohort effect (top panel) or a positive age-cohort effect (bottom panel).

The second finding from Study 1 is that including unnecessary retest effects compromises the model’s ability to recover other related effects – those of age and age-cohort. Because the predictor variables for age, age-cohort, and retest will usually be highly correlated, the collinearity that arises from adding retest obliterates the power to detect each effect down to Type I error rate levels (whether it actually exists or not). Finally, the third finding from Study 1 is that not all retest effects are created equal: the problems for recovery of the age and age-cohort effects arising from the inclusion of extraneous incremental retest effects appeared much more severe than when including a single boost retest effect instead. This is likely because the single boost retest variable has less collinearity with the age and age-cohort variables, whereas the incremental retest variables have free reign to represent other effects at each occasion (perhaps including retest, but more likely including other unmodeled sources of variance as well). In sum, Study 1 illustrates that age-based retest models will result in biased retest effects in the presence of unmodeled age-cohort influences, given that both age-cohort and retest effects are created by the same non-convergence of the age trajectory.

Study 2

Study 1 examined how the accurate estimation of retest effects is diminished by the presence of an unmodeled age-cohort effect on the intercept. In addition to postulating retest effects as main effects, however, several studies have investigated moderation of retest effects by other variables, such as age. Study 2 thus expanded on Study 1 to demonstrate how interactions of retest effects with age can result solely from unmodeled age-cohort by age interactions.

Method

Simulation Design

The simulation design for Study 2 included 500 replications of 500 hypothetical persons as in Study 1. The model used to simulate data is shown in Equation 4:

$$\begin{array}{cc}\hfill \text{Level}1:& {\mathrm{y}}_{\mathrm{t}\mathrm{i}}={\beta }_{0\mathrm{i}}+{\beta }_{1\mathrm{i}}\left({\text{Age}}_{\mathrm{t}\mathrm{i}}\right)+{\beta }_{2\mathrm{i}\dots 6\mathrm{i}}\left({\text{Retest}}_{\mathrm{t}\mathrm{i}}\right)+{\beta }_{7\mathrm{i}\dots 11\mathrm{i}}\left({\text{Age}}_{\mathrm{t}\mathrm{i}}\right)\left({\text{Retest}}_{\mathrm{t}\mathrm{i}}\right)+{\mathrm{e}}_{\mathrm{t}\mathrm{i}}\hfill \\ \hfill \text{Level}2:& {\beta }_{0\mathrm{i}}={\gamma }_{00}+{\gamma }_{01}\left({\text{AgeCohort}}_{\mathrm{i}}\right)+{\mathrm{U}}_{0\mathrm{i}}{\beta }_{1\mathrm{i}}={\gamma }_{10}+{\gamma }_{11}\left({\text{AgeCohort}}_{\mathrm{i}}\right)+{\mathrm{U}}_{1\mathrm{i}}\hfill \\ \hfill & {\beta }_{2\mathrm{i}\dots 6\mathrm{i}}={\gamma }_{20}\cdots {\gamma }_{60}{\beta }_{7\mathrm{i}\dots 11\mathrm{i}}={\gamma }_{70}\cdots {\gamma }_{110}\hfill \end{array}$$ (4)

in which y_ti is the outcome at time t for individual i. The level-1 model now describes the change within persons over time as a function of an individual intercept, time-varying age slope, retest slope(s), and interaction(s) of age with retest. The level-2 model then describes how each of those individual effects is constructed. The data generation parameters and analysis models are described in Table 1. In all generating models, the main effects and age interactions for retest (either as a single effect or incremental effects at each occasion, as in Study 1) were set to zero. Data were simulated to mimic annual observations ± 2 weeks. Simulation conditions again included 3 or 6 waves and either 20 or 40 years of cohort age range at baseline. The fixed effect of age-cohort on the age slope (age-cohort*age interaction) was varied as γ₁₁ = −0.05, 0, or 0.05 per year (rather than an age-cohort effect on the intercept only as in Study 1) in order to examine the effect of unmodeled age-cohort*age interactions on estimation of the retest*age interactions.

Analysis Models and Outcomes

The five analysis models estimated in Study 2 are shown in the bottom of Table 1. Model 2a was the generating model and contained no retest main effects or retest*age interactions to serve as a baseline. Models 2b and 2c included a single boost effect of retest after the first occasion as well as its interaction with age. Models 2d and 2e instead included incremental effects of retest at each occasion as well as their interactions with age. Models 2c and 2e also included effects of age-cohort on the intercept and age slope, whereas Models 2b and 2d did not. The outcomes were again mean bias and power rates (or Type I error rates for retest effects) per condition (with 16 total conditions), and partial η² effect size estimates were again used to assess practical significance.

Results and Discussion

Estimation of Age Slopes

The top of Table 3 lists the mean bias and power rates for the age slopes per condition across models. No problems with bias or power rates were found in the correct Model 2a (age, age-cohort, and age-cohort*age only). When a single retest and retest*age effects were included instead of age-cohort and age-cohort*age effects (Model 2b), although no problems with power were found, bias in the age slopes differed by the missing age-cohort*age effect (η² = 0.08) and age-cohort by waves (η² = 0.07), such that the age slopes were slightly biased away from the missing age-cohort*age effect, with greater bias for 6 than 3 waves.

Table 3.

Mean Bias and Power/Type I Error Rates for Age and Cohort Effects in Study 2

Model Parameter	No Retest		Single Boost Retest				Incremental Retest per Occasion
	Model 2a		Model 2b		Model 2c		Model 2d		Model 2e
	Bias	Power	Bias	Power	Bias	Power	Bias	Power	Bias	Power
Age Slope
c*a = −0.05, w = 3, r = 20	0.00	1.00	0.00	1.00	−0.01	0.87	−0.01	1.00	−0.55	0.05
c*a = −0.05, w = 3, r = 40	0.01	1.00	0.01	1.00	0.01	0.89	0.01	1.00	0.35	0.05
c*a = −0.05, w = 6, r = 20	0.00	1.00	0.08	1.00	0.00	1.00	0.01	1.00	0.23	0.06
c*a = −0.05, w = 6, r = 40	0.00	1.00	0.04	1.00	0.00	1.00	0.00	1.00	−0.11	0.06
c*a =  0, w = 3, r = 20	0.00	1.00	0.01	1.00	0.00	0.88	0.01	1.00	−0.09	0.07
c*a =  0, w = 3, r = 40	−0.01	1.00	0.00	1.00	0.00	0.87	0.00	1.00	−0.08	0.05
c*a =  0, w = 6, r = 20	0.00	1.00	0.00	1.00	0.00	1.00	0.00	1.00	0.20	0.05
c*a =  0, w = 6, r = 40	0.00	1.00	0.00	1.00	0.00	1.00	0.00	1.00	0.00	0.06
c*a = 0.05, w = 3, r = 20	0.00	1.00	−0.01	1.00	−0.01	0.89	0.00	1.00	0.19	0.04
c*a = 0.05, w = 3, r = 40	0.02	1.00	0.00	1.00	0.02	0.86	0.00	1.00	−0.08	0.05
c*a = 0.05, w = 6, r = 20	0.00	1.00	−0.09	1.00	0.00	1.00	−0.01	1.00	−0.01	0.05
c*a = 0.05, w = 6, r = 40	0.00	1.00	−0.04	1.00	0.00	1.00	0.00	1.00	0.07	0.05
Cohort Slope
c*a = −0.05, w = 3, r = 20	−0.01	0.06			0.00	0.05			0.54	0.05
c*a = −0.05, w = 3, r = 40	0.00	0.06			0.00	0.04			−0.35	0.04
c*a = −0.05, w = 6, r = 20	0.00	0.04			0.00	0.03			−0.23	0.05
c*a = −0.05, w = 6, r = 40	0.00	0.07			0.00	0.03			0.11	0.05
c*a =  0, w = 3, r = 20	0.01	0.04			0.01	0.04			0.10	0.06
c*a =  0, w = 3, r = 40	0.01	0.06			0.00	0.05			0.08	0.05
c*a =  0, w = 6, r = 20	0.00	0.05			0.00	0.05			−0.19	0.06
c*a =  0, w = 6, r = 40	0.00	0.04			0.01	0.04			0.01	0.06
c*a = 0.05, w = 3, r = 20	0.00	0.04			0.02	0.04			−0.19	0.04
c*a = 0.05, w = 3, r = 40	−0.01	0.03			−0.02	0.05			0.08	0.04
c*a = 0.05, w = 6, r = 20	−0.01	0.05			0.00	0.05			0.01	0.04
c*a = 0.05, w = 6, r = 40	0.00	0.03			0.00	0.04			−0.07	0.04
Cohort*Age Slope
c*a = −0.05, w = 3, r = 20	0.00	0.66			0.00	0.60			0.00	0.59
c*a = −0.05, w = 3, r = 40	0.00	1.00			0.00	1.00			0.00	1.00
c*a = −0.05, w = 6, r = 20	0.00	0.99			0.00	0.94			0.00	0.69
c*a = −0.05, w = 6, r = 40	0.00	1.00			0.00	1.00			0.00	1.00
c*a =  0, w = 3, r = 20	0.00	0.05			0.00	0.05			0.00	0.06
c*a =  0, w = 3, r = 40	0.00	0.07			0.00	0.07			0.00	0.06
c*a =  0, w = 6, r = 20	0.00	0.05			0.00	0.04			0.00	0.04
c*a =  0, w = 6, r = 40	0.00	0.05			0.00	0.03			0.00	0.05
c*a = 0.05, w = 3, r = 20	0.00	0.72			0.00	0.67			0.00	0.65
c*a = 0.05, w = 3, r = 40	0.00	1.00			0.00	1.00			0.00	1.00
c*a = 0.05, w = 6, r = 20	0.00	0.97			0.00	0.92			0.00	0.65
c*a = 0.05, w = 6, r = 40	0.00	1.00			0.00	1.00			0.00	1.00

Table 3 Note: c*a = age-cohort by age effect, w = waves, and r = cohort age range. Power rates for all retest slopes actually reflect Type I error rates given their omission from the generation model. The incremental retest slope estimates reported in Models 2d and 2e reflect those from the first incremental retest effect (at the second occasion).

After slopes for the age-cohort, age-cohort*age, single boost retest, and retest*age effects were all included (Model 2c), no problems with bias were found, although power to detect the age slopes was higher for 6 than 3 waves (η² = 0.07; for which ≈ 88% power was observed, in contrast to 100% across conditions in Model 2a). When incremental retest and retest*age effects were included instead of age-cohort and age-cohort*age effects (Model 2d), no problems with bias or power for the age slopes were found. Finally, after slopes for age-cohort, age-cohort*age, incremental retest, and retest*age effects were all included (Model 2e), although no simulation design effects were significant, considerable but idiosyncratic bias in the age slopes were observed, coupled with power rates that approximated Type I error rates instead (4-7%). Thus, as in Study 1, the extraneous incremental retest and retest*age effects at each occasion severely compromised the power to detect the age slopes that were actually present.

Estimation of Age-Cohort and Age-Cohort*Age Slopes

Table 3 also provides the mean bias and power/Type I error rates for the age-cohort and age-cohort*age slopes per condition across models. Age-cohort effects on the intercept were never included in the generation model, and so power rates approximated Type I error rates in all models as expected. Although significant bias in the age-cohort effects was observed in Model 2e (with incremental retest effects), the bias appeared to off-set that for the age slopes in the same conditions.

With regard to the age-cohort*age interaction, no problems with bias were found in the correct Model 2a. As expected, in Model 2a power rates to detect the age-cohort*age slopes differed by the size of the age-cohort*age effect (η² = 0.75) and age range (η² = 0.15), such that power rates ranged from 66% to 100% when present (with greater power for 40 than 20 years cohort age range). No problems with bias were observed given extraneous single retest and retest*age effects (Model 2c), although power again differed by the size of the age-cohort*age effect (η² = 0.71) and age range (η² = 0.08), such that power rates to detect the age-cohort*age slopes were lower by ≈ 5% in the 20-year conditions in Model 2c relative to Model 2a. Finally, no problems with bias were observed when adding extraneous incremental retest and retest*age effects at each occasion (Model 2e), although power to detect the age-cohort*age slopes differed by age-cohort (η² = 0.59), cohort age range (η² = 0.13), and age-cohort by age range (η² = 0.07), such that power rates were noticeably lower for the 6 waves, 20 year conditions in Model 2e than in Model 2a. Thus, extraneous incremental retest*age parameters appear particularly problematic for detecting existing cohort*age interactions when less of the age variance was cross-sectional.

Estimation of Single Boost Retest and Retest*Age Slopes

Table 4 provides the mean bias and Type I error rates for the single retest and retest*age slopes per condition across models. When not controlling for age-cohort and age-cohort*age (Model 2b), effects for the missing age-cohort*age effect were found for bias in both the retest slopes (η² = 0.07) and the retest*age slopes (η² = 0.59) as well as for age-cohort*waves in the retest*age slopes (η² = 0.12). As shown in Table 4, if a negative age-cohort*age effect was missing, the retest slope was positively biased and the retest*age slope was negatively biased, more so for 6 than 3 waves (with the opposite pattern for a positive missing age-cohort*age effect). Although no simulation design effects were found for Type I error in the retest slopes, significant design effects were found for Type I error in the retest*age slopes for age-cohort (η² = 0.17), waves (η² = 0.12), and age-cohort*waves (η² = 0.06), such that Type I error rates for the retest*age slopes (if an age-cohort*age effect was missing) were greater for 6 than 3 waves, with Type I error rates of 14-78% in those conditions. After controlling for age-cohort and age-cohort*age, however (Model 2c), the single retest and retest*age effects were estimated near zero with acceptable Type I error rates (3-6%) instead.

Table 4.

Mean Bias and Power/Type I Error Rates for Single Retest Effects in Study 2

Simulation Condition	Single Boost Retest Slope				Single Boost Retest*Age Slope
	Model 2b		Model 2c		Model 2b		Model 2c
	Bias	Power	Bias	Power	Bias	Power	Bias	Power
c*a = −0.05, w = 3, r = 20	0.09	0.06	0.00	0.04	−0.06	0.14	0.00	0.04
c*a = −0.05, w = 3, r = 40	0.08	0.07	0.00	0.05	−0.05	0.27	0.00	0.05
c*a = −0.05, w = 6, r = 20	0.12	0.08	0.01	0.06	−0.12	0.43	0.00	0.04
c*a = −0.05, w = 6, r = 40	0.17	0.09	0.01	0.04	−0.09	0.77	0.00	0.04
c*a =  0, w = 3, r = 20	−0.01	0.05	0.01	0.05	0.00	0.05	0.00	0.05
c*a =  0, w = 3, r = 40	−0.02	0.08	−0.02	0.06	0.00	0.04	0.00	0.04
c*a =  0, w = 6, r = 20	−0.02	0.06	−0.02	0.06	0.00	0.06	0.00	0.05
c*a =  0, w = 6, r = 40	0.00	0.04	0.01	0.04	0.00	0.04	0.00	0.04
c*a = 0.05, w = 3, r = 20	−0.08	0.07	0.03	0.05	0.06	0.15	0.00	0.03
c*a = 0.05, w = 3, r = 40	−0.06	0.05	−0.01	0.06	0.05	0.26	0.00	0.06
c*a = 0.05, w = 6, r = 20	−0.07	0.06	0.03	0.06	0.12	0.45	0.00	0.06
c*a = 0.05, w = 6, r = 40	−0.14	0.08	0.01	0.04	0.09	0.78	0.00	0.04

Table 4 Note: c*a = age-cohort*age effect, w = waves, and r = cohort age range. Power rates for the single boost retest and retest*age slopes actually reflect Type I error rates given their omission from the generation model.

Estimation of Incremental Retest and Retest*Age Slopes

Table 5 provides the mean bias and Type I error rates for the incremental retest and retest*age slopes per wave and per condition across models. When not controlling for age-cohort and age-cohort*age (Model 2d), design effects on the bias due to the missing age-cohort*age effect were found in the incremental retest slopes per wave, such that the size of the effect on the bias increased across waves (η² = .01, .07, .17, .23, and .32 for the incremental retest slopes in waves 2-6, respectively). As seen in the left columns of Table 5, the retest slopes were biased in the opposite direction as the missing age-cohort*age effect, with the size of this bias increasing across waves, and with higher than acceptable Type I error rates that also increased across waves, ranging up to 16% in those conditions. For the incremental retest*age slopes from the same Model 2d (without age-cohort), significant design effects of the missing age-cohort*age effect were found for bias (η² = 0.20, equivalent across the retest*age slopes from each wave), such that the retest*age slope was biased towards from the missing age-cohort*age effect. Type I error rates for the retest*age slopes were higher than acceptable (up to 15%) but constant across waves. Finally, after controlling for age-cohort and age-cohort*age (Model 2e), the retest slopes were estimated with considerable yet idiosyncratic bias across conditions but with acceptable Type I error rates, while the retest*age slopes were estimated with no bias and with acceptable Type I error rates.

Table 5.

Mean Bias and Power/Type I Error Rates for Incremental Retest Effects in Study 2

Model Parameter	Incremental Retest Slope				Incremental Retest*Age Slope
	Model 2d		Model 2e		Model 2d		Model 2e
	Bias	Power	Bias	Power	Bias	Power	Bias	Power
Retest at Wave 2
c*a = −0.05, w = 3, r = 20	0.05	0.05	0.55	0.04	−0.04	0.08	0.00	0.04
c*a = −0.05, w = 3, r = 40	0.04	0.06	−0.34	0.05	−0.03	0.11	0.00	0.04
c*a = −0.05, w = 6, r = 20	0.06	0.06	−0.20	0.05	−0.05	0.08	0.00	0.03
c*a = −0.05, w = 6, r = 40	0.04	0.05	0.12	0.05	−0.04	0.15	0.00	0.05
c*a =  0, w = 3, r = 20	−0.01	0.05	0.09	0.06	0.00	0.04	0.00	0.04
c*a =  0, w = 3, r = 40	−0.02	0.08	0.05	0.05	0.00	0.05	0.00	0.05
c*a =  0, w = 6, r = 20	−0.03	0.06	−0.22	0.06	0.00	0.05	0.00	0.05
c*a =  0, w = 6, r = 40	0.00	0.04	0.00	0.06	0.00	0.05	0.00	0.05
c*a = 0.05, w = 3, r = 20	−0.03	0.06	−0.17	0.04	0.04	0.07	0.00	0.02
c*a = 0.05, w = 3, r = 40	−0.02	0.06	0.09	0.04	0.03	0.12	0.00	0.05
c*a = 0.05, w = 6, r = 20	0.00	0.07	0.04	0.04	0.05	0.11	0.00	0.06
c*a = 0.05, w = 6, r = 40	−0.01	0.04	−0.05	0.04	0.04	0.13	0.00	0.05
Retest at Wave 3
c*a = −0.05, w = 3, r = 20	0.14	0.06	0.55	0.05	−0.04	0.08	0.00	0.05
c*a = −0.05, w = 3, r = 40	0.10	0.06	−0.34	0.04	−0.04	0.14	0.00	0.05
c*a = −0.05, w = 6, r = 20	0.09	0.06	−0.27	0.05	−0.04	0.07	0.01	0.04
c*a = −0.05, w = 6, r = 40	0.10	0.06	0.10	0.05	−0.03	0.14	0.00	0.04
c*a =  0, w = 3, r = 20	−0.01	0.04	0.09	0.06	0.00	0.03	0.00	0.04
c*a =  0, w = 3, r = 40	0.00	0.05	0.08	0.05	0.00	0.05	0.00	0.05
c*a =  0, w = 6, r = 20	0.02	0.05	−0.18	0.06	0.00	0.04	0.00	0.04
c*a =  0, w = 6, r = 40	0.01	0.04	0.01	0.06	0.00	0.04	0.00	0.03
c*a = 0.05, w = 3, r = 20	−0.15	0.07	−0.20	0.03	0.04	0.09	0.00	0.06
c*a = 0.05, w = 3, r = 40	−0.08	0.06	0.10	0.04	0.04	0.14	0.00	0.05
c*a = 0.05, w = 6, r = 20	−0.13	0.08	0.01	0.04	0.05	0.10	0.00	0.07
c*a = 0.05, w = 6, r = 40	−0.12	0.07	−0.09	0.04	0.04	0.14	0.00	0.05
Retest at Wave 4
c*a = −0.05, w = 6, r = 20	0.25	0.11	−0.20	0.05	−0.05	0.10	0.00	0.06
c*a = −0.05, w = 6, r = 40	0.19	0.11	0.12	0.05	−0.04	0.16	0.00	0.06
c*a =  0, w = 6, r = 20	−0.02	0.06	−0.21	0.06	0.00	0.06	0.00	0.06
c*a =  0, w = 6, r = 40	−0.01	0.04	−0.01	0.06	0.00	0.03	0.00	0.03
c*a = 0.05, w = 6, r = 20	−0.20	0.09	0.03	0.05	0.05	0.09	0.00	0.04
c*a = 0.05, w = 6, r = 40	−0.18	0.09	−0.08	0.04	0.04	0.15	0.00	0.07
Retest at Wave 5
c*a = −0.05, w = 6, r = 20	0.31	0.11	−0.23	0.04	−0.04	0.08	0.00	0.04
c*a = −0.05, w = 6, r = 40	0.23	0.11	0.08	0.04	−0.03	0.14	0.00	0.05
c*a =  0, w = 6, r = 20	0.01	0.05	−0.19	0.06	0.00	0.06	0.00	0.05
c*a =  0, w = 6, r = 40	−0.01	0.07	0.00	0.05	0.00	0.05	0.00	0.05
c*a = 0.05, w = 6, r = 20	−0.33	0.12	0.00	0.03	0.04	0.07	0.00	0.05
c*a = 0.05, w = 6, r = 40	−0.23	0.12	−0.06	0.03	0.04	0.16	0.00	0.05
Retest at Wave 6
c*a = −0.05, w = 6, r = 20	0.40	0.10	−0.24	0.05	−0.05	0.08	0.00	0.04
c*a = −0.05, w = 6, r = 40	0.34	0.16	0.12	0.05	−0.04	0.15	0.00	0.05
c*a =  0, w = 6, r = 20	−0.01	0.06	−0.20	0.06	0.00	0.04	0.00	0.05
c*a =  0, w = 6, r = 40	−0.01	0.06	−0.01	0.06	0.00	0.05	0.00	0.04
c*a = 0.05, w = 6, r = 20	−0.41	0.12	0.00	0.04	0.05	0.08	0.00	0.04
c*a = 0.05, w = 6, r = 40	−0.32	0.16	−0.08	0.04	0.04	0.14	0.00	0.06

Table 5 Note: c*a = age-cohort*age effect, w = waves, and r = cohort age range. Power rates for the incremental retest and retest*age slopes actually reflect Type I error rates given their omission from the generation model.

Study 2: Summary

Study 2 examined the effects of longitudinal design characteristics (number of waves, baseline age range, and age-cohort effect on the age slope) on estimation of the slopes for age, age-cohort, age-cohort*age, retest (single or incremental at each occasion), and retest*age, with two primary findings. First, correct inferences about retest effects can only be obtained once the total effect of age is considered, this time including potential effects of age-cohort on the age slope rather than on the intercept (i.e., an effect of age-cohort that changes over time). When an effect of age-cohort*age was present but not modeled (Models 2b and 2d), it was absorbed by the retest and retest*age slopes, such that a negative missing age-cohort*age effect became a positive retest slope paired with a negative retest*age slope, while a positive missing age-cohort*age effect became a negative retest slope paired with a positive age-cohort*age slope, with Type I error rates for both that were higher than acceptable (particularly the single retest*age slopes). Only when the age-cohort and age-cohort*age effects were included were the Type I error rates acceptable for the retest and retest*age slopes (single and incremental).

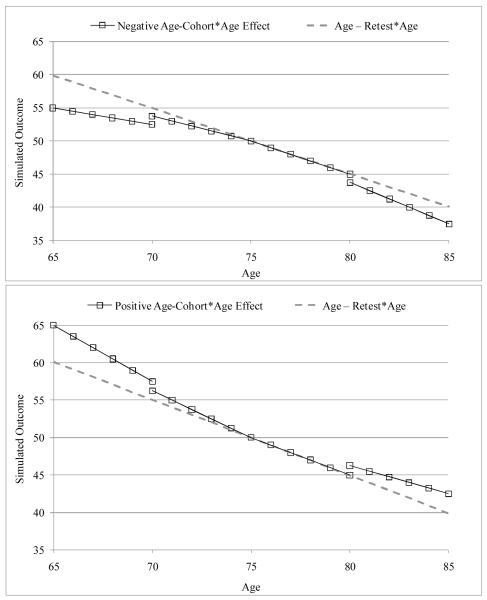
This tradeoff between age-cohort*age and retest*age is illustrated in Figure 2, which plots the predicted outcomes given 6 waves and a 20-year age range with an effect of age-cohort*age of −0.05 (top) or 0.05 (bottom). The lines with squares represent 6-year predicted trajectories for 4 age cohorts based on the correct model without retest (Model 2a). The dashed line is the “true” age slope predicted from Model 2d (omitting age-cohort and age-cohort*age but including incremental retest and retest*age at each occasion). As shown in the top of Figure 2, the non-convergence of the trajectories due to the negative age-cohort*age effect can be closely compensated for by positive incremental retest effects that increase across waves paired with negative retest*age effects that are constant across waves. That is, the widening distance between the cohorts as age increases can be explained by an age-cohort effect that becomes more negative as age increases (the generation model) or by increasingly positive incremental retest effects at each occasion that are dampened by negative retest*age interactions (of equal magnitude across occasions). The opposite is seen in the bottom of Figure 2, in which an age-cohort effect that becomes more positive as age increases can be represented by increasingly negative incremental retest effects at each occasion that are dampened by positive retest*age interactions of equal magnitude across occasions (even though negative retest effects should still be impossible in cognitive tests in which higher scores indicate better performance).

Figure 2.

Predicted trajectories from Study 2 for the simulation condition of 6 waves and a 20-year baseline age range. The predicted outcomes are shown when including the correct effects of age and age-cohort*age (separate lines with squares) or for the effect of age controlled for retest and retest*age (dashed line), given a negative age-cohort*age effect (top panel) or a positive age-cohort*age effect (bottom panel).

The second finding from Study 2 is that including unnecessary retest*age effects also compromises the model’s ability to recover other related effects, but the extent to which this occurs depends on the kind of retest effect. In Study 2, the two kinds of retest*age effects (single versus incremental) were comparable in the small power problems they caused in detecting the age-cohort*age interaction, but the incremental retest and retest*age effects were again much more problematic for detecting the age slope (which was estimated with significant bias and power rates that approximated Type I error rates instead). Thus, it appears that retest effects that change over time can be distinguished from age-cohort effects that change over time given a enough age-cohort variability, although not without also causing problems for the age slopes.

General Discussion

In longitudinal studies with widely-spaced occasions, although effects of retest are confounded with other sources of within-person change, the aim of age-based retest models is to estimate aging-related change as if individuals had not been repeatedly tested. The current study explored the viability of these models by examining estimation of slopes for age, age-cohort, age-cohort by age, retest, and retest by age for two kinds of retest effects varying in parsimony (either a single boost after the first occasion or incremental improvements at each subsequent occasion). In these simulations, retest effects were always zero in the generation models so that any estimated retest effect could be readily interpreted as a Type I error. Although likely an over-simplification given that retest effects likely do exist to some degree, this simple model allowed a clear examination of how model misspecification (i.e., omission of age-cohort effects) can result in non-zero estimates of retest effects even when retest effects do not exist in the data.

The primary result of these simulation studies is that between-person age differences that do not align with within-person age change will masquerade as retest effects, even if there are no retest effects to be found. In these models, estimation of age-cohort differences and retest gains is based on the same lack of age convergence information, which is insufficient to independently identify these different effects. That is, a missing age-cohort effect will create a retest effect in the opposite direction for both single boost and incremental per-occasion retest effects. The fact that significant negative retest effects were nevertheless found in a context in which they were created simply by positive missing age-cohort effects is further evidence that what one might interpret as “retest” cannot be distinguished from “cohort” or other reasonable possibilities. As such, unmodeled age-cohort effects may be responsible (at least in part) for reported anomalies such as retest effects that were maximal at the third occasion (Ferrer et al., 2004), that did not depend on the size of the test-retest interval (Rabbitt et al., 2004; Salthouse, 2009; Salthouse & Tucker-Drob, 2008), or that were significantly negative – a decline due to test exposure (Rabbitt et al., 2004; Rabbit, Lunn, & Wong, 2008).

The fact that significant retest effects can be observed when they do not exist is only part of the problem – incremental retest effects at each occasion in particular will also greatly limit or destroy the power to detect existing, related effects of aging or age-cohort. Practically speaking, this implies that if one adds age-cohort to a model that already includes age and incremental retest, then age-cohort is not likely to have a significant addition, and thus those reasons for age non-convergence would be attributed to retest effects rather than age-cohort effects. While age-cohort effects and retest effects may be equally plausible explanations for a negative age-cohort effect (and thus a positive retest effect), it is harder to argue that a positive age-cohort effect is actually a negative retest effect (at least in cognitive tests in which higher scores indicate better outcomes; negative retest effects may be expected when they occur for other reasons, such as perceived experimenter demand characteristics in self-reported ratings of stress, health, etc.).

The intractable problem of distinguishing age, cohort, and time is certainly not new (e.g., Schaie, 1965), but the analog to this problem does not appear to have been recognized as it applies in distinguishing the effects of age, cohort, and retest via statistical models (in which retest can be thought of as “time”). When aging and retest effects are observed simultaneously within-persons, one can only estimate two out of the three effects (age, cohort, and retest); the third must be assumed absent or to be controlled by some other means. For instance, if one believes that retest effects are negligible after the second occasion, a reasonable (but unpopular) solution may be to remove the first occasion from the analysis, under the assumption that the effect of retest after the second occasion should be minimized. Alternatively, one could provide a pre-test occasion in which more extensive practice is given prior to the baseline observation, although this approach would be less useful for tests that do not require learning a new procedure (e.g., vocabulary tests, for which alternative forms may be more useful to reduce retest instead).

In the current study, including a single boost retest effect was less problematic than including incremental retest effects at each occasion, and we would expect similar results for other kinds of retest effects (e.g., retest posited as a linear slope or latent basis across waves) to the extent that the retest variables are less correlated with the age variable. However, we do not feel that the fundamental confound of the retest and aging processes occurring simultaneously within persons can be solved by the boost retest model. One reason is that the boost retest effect can account for any unexplained deviation between time 1 and 2, assuming a particular model for change (e.g., linear change here). Practically speaking, any unmodeled nonlinearity in the rate of change can create a boost that would be interpreted as retest. Although careful data exploration and model testing would reveal any systematic misfit of the model of change, to the extent that the selected model doesn’t fit perfectly, a boost retest parameter can capture these non-retest deviations. Further, after inclusion of the boost, the estimated rate of change reflects only the change after time 2 – functionally the same result as removing the first occasion.

A related issue is to what extent controlling for age-cohort effects can also be seen as a solution. Although age-cohort was represented by baseline age in our simulation data, in reality cohort effects are likely to be multifaceted and reflective of many sources that can result in different expectations for the outcome at a given age. Thus, such cohort effects may not be sufficiently captured simply by baseline age or birth year. One should also consider other relevant sources of individual differences (e.g., education, computer use, greater exposure to taking tests) resulting from generational experiences that may be related to cohort effects (i.e., aspects of cohort that are not defined exclusively by a linear effect of baseline age), as well as the likely inferential problems created by the influence of cohort and other related forces on the process of selective attrition. Thus, controlling for age-cohort may not be a panacea, either.

An example of this can be found in the work of Wilson and colleagues (Wilson et al., 2002; Wilson, Li, Bienias, & Bennett, 2006). The models examined in the current simulations included the most common retest model specification in which age is used as the basis of time in the level-1 model (i.e., as in grand-mean-centering), such that the effect of age-cohort in the level-2 model is specified as incremental to the effect of age (i.e., age-cohort as a contextual effect). In contrast, Wilson et al. (2002, 2006) used an alternative model using time instead of age at level 1 (i.e., as in group- or person-mean-centering), and in which the total effects (rather than the incremental effects) of age-cohort are specified at level 2. Without some minimal variability in the timing of the assessments, this model would not estimable. But Wilson et al. (2006) were able to estimate fixed and random effects of retest in their models, thus effectively modeling effects of aging, age-cohort (as indicated by baseline age), and retest at the same time.

Although significant retest effects were reported for several of their cognitive tests even after controlling for age-cohort effects, inspection of Wilson et al.’s (2006) results suggests some of the same problems observed in the current study – namely, highly inflated standard errors for the effects of age in their models with retest parameters (relative to their models without retest). Further, the pattern of the estimated retest effects was unpredictable, with improvements due to retest found for semantic memory but not for episodic memory, for word knowledge but not for word generation, for word retention but not for story retention, and for visuospatial ability but not for perceptual speed. In addition, in constructing 95% random effects confidence intervals (Snijders & Bosker, 1999, p.48-50) using their reported estimates, their results suggest that the individual retest effects observed were actually predicted to range from negative to positive (although positive on average in most outcomes), which complicates the interpretation of these parameters as simply retest effects. Finally, given the large amount of individual data (up to nine occasions per person), the retest effects at each occasion could also reflect simple misfit of the time trajectory, which they modeled using a quadratic trend. Thus, while the approach utilized by Wilson et al. could be informative for distinguishing aging effects from retest effects after controlling for age-cohort, alternative explanations for their estimated retest effects remain.

In conclusion, although this study strongly suggests that caution should be employed in attempting to statistical control for retest effects in long-term studies of aging, it also highlights an inferential issue regarding the interpretation of the retest-controlled age slopes per se. That is, although the use of retest models is often motivated by the need to estimate the “test naive” age trajectory that would have been observed without the influence of repeated test exposure, all these models can do is estimate the age trajectory that would have been obtained holding retest constant instead. But because retest occasion cannot be held constant across time within a given person, such a “naïve” aging effect could never be directly observed.

An approach that is more likely to be more useful is to measure retest explicitly instead. For example, it may be useful to quantify a person’s tendency to improve from repeated testing or one’s maximal practiced performance by using external data, such as through alternative longitudinal designs in which the effects of age and retest are observed over different time scales (i.e., measurement burst designs, Nesselroade, 1991; Sliwinski, 2008). In the same way that within-person aging effects can only be measured directly via long-term longitudinal designs in which aging has time to occur, within-person retest gains can only be measured directly in short-term longitudinal designs in which retest effects can occur but in which aging effects cannot. Only through careful consideration of such alternative longitudinal designs can the effects of aging, age-cohort, and retest be distinguished informatively.