Linear or Nonlinear? Automatic Structure Discovery for Partially Linear Models

Abstract

Partially linear models provide a useful class of tools for modeling complex data by naturally incorporating a combination of linear and nonlinear effects within one framework. One key question in partially linear models is the choice of model structure, that is, how to decide which covariates are linear and which are nonlinear. This is a fundamental, yet largely unsolved problem for partially linear models. In practice, one often assumes that the model structure is given or known and then makes estimation and inference based on that structure. Alternatively, there are two methods in common use for tackling the problem: hypotheses testing and visual screening based on the marginal fits. Both methods are quite useful in practice but have their drawbacks. First, it is difficult to construct a powerful procedure for testing multiple hypotheses of linear against nonlinear fits. Second, the screening procedure based on the scatterplots of individual covariate fits may provide an educated guess on the regression function form, but the procedure is ad hoc and lacks theoretical justifications. In this article, we propose a new approach to structure selection for partially linear models, called the LAND (Linear And Nonlinear Discoverer). The procedure is developed in an elegant mathematical framework and possesses desired theoretical and computational properties. Under certain regularity conditions, we show that the LAND estimator is able to identify the underlying true model structure correctly and at the same time estimate the multivariate regression function consistently. The convergence rate of the new estimator is established as well. We further propose an iterative algorithm to implement the procedure and illustrate its performance by simulated and real examples. Supplementary materials for this article are available online.

1. INTRODUCTION

Linear and nonparametric models are two important classes of modeling tools for statistical data analysis and both have their unique advantages. Linear models are simple, easy to interpret, and the estimates are most efficient if the linear assumption is valid. Nonparametric models are less dependent on the model assumption and hence able to uncover nonlinear effects hidden in data. Partially linear models, a class of models between linear and nonparametric models, inherit advantages from both sides by allowing some covariates to be linear and others to be nonlinear. Partially linear models have wide applications in practice due to their flexibility.

Given the observations (y_i, x_i, t_i), i = 1, …, n, where y_i is the response, x_i = (x_i1, …, x_ip)^T and t_i = (t_i1, …, t_iq)^T are vectors of covariates, the partially linear model assumes that

$$y_i=b+{\mathbf{x}}_i^{\text{T}}\mathit{\beta }+f({\mathbf{t}}_i)+{\epsilon }_i,$$ (1.1)

where b is the intercept, β is a vector of unknown parameters for linear terms, f is an unknown function from R^q to R, and ε_i’s are iid random errors with mean zero and variance σ². In practice, the most used model for (1.1) is the following special case when q = 1:

$$y_i=b+{\mathbf{x}}_i^{\text{T}}\mathit{\beta }+f(t_i)+{\epsilon }_i.$$ (1.2)

For example, in longitudinal data analysis, the time covariate T is often treated as the only nonlinear effect. Model estimation and inference for (1.2) have been actively studied under various smooth regression settings, including smoothing splines (Wahba 1984; Engle et al. 1986; Heckman 1986; Rice 1986; Chen 1988; Hong 1991; Green and Silverman 1994; Liang, Hardle, and Carroll 1999), penalized regression splines (Ruppert, Wand, and Carroll 2003; Liang 2006; Wang, Li, and Huang 2008), kernel smoothing (Speckman 1988), and local polynomial regression (Fan and Gijbels 1996; Fan and Li 2004; Li and Liang 2008). Interesting applications include the analysis of city electricity (Engle et al. 1986), household gasoline consumption in the United States (Schmalensee and Stoker 1999), a marketing price-volume study in the petroleum distribution industry (Green and Silverman 1994), the logistic analysis of bioassay data (Dinse and Lagakos 1983), the mouthwash experiment (Speckman 1988), and so on. A recent monograph by Hardle, Liang, and Gao (2000) gave an excellent overview on partially linear models, and a more comprehensive list of references can be found there.

One natural question about the model (1.1) is, given a set of covariates, how one decides which covariates have linear effects and which covariates have nonlinear effects. For example, in the Boston housing data analyzed in the article, the main goals are to identify important covariates, study how each covariate is associated with the house value, and build a highly interpretable model to predict the median house values. The structure selection problem is fundamentally important, as the validity of the fitted model and its inference heavily depends on whether the model structure is specified correctly. Compared to the linear model selection, the structure selection for partially linear models is much more challenging because the models involve multiple linear and nonlinear functions and a model search needs to be conducted within some infinite-dimensional function space.

Furthermore, the difficulty level of model search increases dramatically as the data dimension grows due to the curse of dimensionality. This may explain why the problem of structure selection for partially linear models is less studied in the literature. Most works we mentioned above assume that the model structure (1.1) is given or known. In practice, data analysts oftentimes have to rely on their experience, historical data, or some screening tools to make an educated guess on the function forms for individual covariates. Two methods in common use are the screening and hypothesis testing procedures. The screening method first conducts univariate nonparametric regression for each covariate or unstructured additive models and then determines linearity or nonlinearity for each term by visualizing the fitted function. This method is useful in practice but lacks theoretical justifications. The second method is to test linear null hypotheses against nonlinear alternatives, sequentially or simultaneously, for each covariate. However, proper test statistics are often hard to construct and the tests may have low power when the number of covariates is large. In addition, these methods handle the structure selection problem and the model estimation separately, making it difficult to study inferential properties of the final estimator. To our knowledge, none of the existing methods can distinguish linear and nonlinear terms for partially linear models automatically and consistently. The main purpose of this article is to fill this gap.

Motivated by the need of an effective and theoretically justified procedure for structure selection in partially linear models, we propose a new approach, called the LAND (Linear And Nonlinear Discoverer), to identify model structure and estimate the regression function simultaneously. By solving a regularization problem in the frame of smoothing spline ANOVA, the LAND is able to distinguish linear and nonlinear terms, remove uninformative covariates from the model, and provide a consistent function estimate. Specifically, we show that the LAND estimator is consistent and establish its convergence rate. Furthermore, under the tensor product design, we show that the LAND is consistent in recovering the correct model structure and estimating both linear and nonlinear function components. An iterative computational algorithm is developed to implement the procedure. The rest of the article is organized as follows. In Section 2 we introduce the LAND estimator. Statistical properties of the new estimator, including its convergence rate and selection consistency, are established in Section 3. We discuss the idea of two-step LAND in Section 4. The computational algorithm and the tuning issue are discussed in Section 5. Section 6 contains simulated and real examples to illustrate finite sampling performance of the LAND. All the proofs are relegated to the Appendix. Due to the space restriction, Appendix 4 is given in online supplementary materials.

2. METHODOLOGY

2.1 Model Setup

From now on, we use x_i R^d instead of (x_i, t_i) to represent the entire covariate vector, as we do not assume the knowledge of linear or nonlinear form for each covariate. Without loss of generality, all covariates are scaled to [0, 1]. Let {x_i, y_i}, i = 1, …, n, be an independent and identically distributed sample. The underlying true regression model has the form

$$y_i=b+\sum _{j\in I_L}{x}_{ij}{\beta }_j+\sum _{j\in I_N}{f}_j(x_{ij})+\sum _{j\in I_O}0(x_{ij})+{\epsilon }_i,$$ (2.1)

where b is an intercept, I_L, I_N, I_O are the index sets for nonzero linear effects, nonzero nonlinear effects, and null effects, respectively. Let the total index set be I = {1, …, d}; then I = I_L ∪ I_N ∪ I_O and the three subgroups are mutually exclusive. The model (2.1) can be regarded as a hypothetical model, since I_L, I_N, I_O are generally unknown in practice. Since nonlinear functions embrace linear functions as special cases, we need to impose some restrictions on f’s to assure the identifiability of terms in (2.1). This issue will be carefully treated later.

The model (2.1) is a special case of the additive model

$$y_i=b+g_1(x_{i1})+\cdots +g_d(x_{id})+{\epsilon }_i.$$ (2.2)

Without loss of generality, we assume that the function components in (2.2) satisfy some smoothness conditions, say, differentiable up to a certain order. In particular, we let g_j ∈ , the second-order Sobolev space on χ_j = [0, 1], that is, = {g: g, g′ are absolutely continuous, g″ ∈ L²[0, 1]}. Using the standard theory in functional analysis, one can show that is a reproducing kernel Hilbert space (RKHS), when equipped with the following norm:

$${\left|\right|g_j\left|\right|}_{{\mathcal{H}}_j}^2={\left\{{\int }_0^1{g}_j(x)dx\right\}}^2+{\left\{{\int }_0^1{g}_j^{\prime }(x)dx\right\}}^2+{\int }_0^1{\{g_j^{″}(x)\}}^{2}dx.$$

The reproducing kernel (RK) associated with is R(x, z) = R₀(x, z) + R₁(x, z) with R₀(x, z) = k₁(x)k₁(z) and R₁(x, z) = k₂ (x)k₂(z) − k₄(x − z), where $k_1(x)=x-\frac{1}{2},k_2(x)=\frac{1}{2}\{k_1^2(x)-\frac{1}{12}\}$, and $k_4(x)=\frac{1}{24}\{k_1^4(x)-\frac{1}{2}{k}_1^2(x)+\frac{7}{240}\}$. See the works of Wahba (1990) and Gu (2002) for more details. Furthermore, the space has the following orthogonal decomposition:

$${\mathcal{H}}_j=\{1\}\oplus {\mathcal{H}}_{0j}\oplus {\mathcal{H}}_{1j},$$ (2.3)

where {1} is the mean space, ${\mathcal{H}}_{0j}=\{g_j:g_j^{″}(x)\equiv 0\}$ is the linear contrast subspace, and ${\mathcal{H}}_{1j}=\{g_j:{\int }_0^1{g}_j(x)dx=0,{\int }_0^1{g}_j^{\prime }(x)dx=0,g_j^{″}\in {\mathcal{L}}_2[0,1]\}$ is the nonlinear contrast space. Both 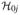and , as subspaces of , are also RKHS and respectively associated with the reproducing kernels R₀ and R₁. Based on the space decomposition (2.3), any function g_j ∈ can be correspondingly decomposed into the linear part and nonlinear part

$$g_j(x_j)=b_{0j}+{\beta }_j\left(x_j-\frac{1}{2}\right)+g_{1j}(x_j),$$ (2.4)

where the term $k_1(x_j)={\beta }_j(x_j-\frac{1}{2})\in {\mathcal{H}}_{0j}$ is the “linear” component and g_1j(x_j) ∈ is the “nonlinear” component. The fact that 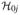and are orthogonal to each other assures the uniqueness of this decomposition.

The function g(x) = b + g₁(x_i1) + … + g_d(x_id) is then estimated in the tensor sum of ’s, that is, $\mathcal{H}={\oplus }_{j=1}^d{\mathcal{H}}_j$. The decomposition in (2.3) leads to an orthogonal decomposition of :

$$\begin{array}{l}\mathcal{H}=\underset{j=1}{\overset{d}{\oplus }}{\mathcal{H}}_j=\{1\}\oplus \underset{j=1}{\overset{d}{\oplus }}{\mathcal{H}}_{0j}\oplus \underset{j=1}{\overset{d}{\oplus }}{\mathcal{H}}_{1j}\\ =\{1\}\oplus {\mathcal{H}}_0\oplus {\mathcal{H}}_1,\end{array}$$ (2.5)

where ${\mathcal{H}}_0={\oplus }_{j=1}^d{\mathcal{H}}_{0j}$ and ${\mathcal{H}}_1={\oplus }_{j=1}^d{\mathcal{H}}_{1j}$. In the next section, we propose a new regularization problem to estimate g ∈ by imposing some penalty on function components, which facilitates the structure selection for the fitted function.

2.2 New Regularization Method: LAND

Throughout the article, we regard a function g(x) as a zero function, that is, g ≡ 0, if and only if g(x) = 0, ∀x ∈ χ. With the above setup, we say X_j is a linear covariate if β_j ≠ 0 and g_1j ≡ 0, and X_j is a nonlinear covariate if g_1j(x_j) is not zero. In other words, we can describe the three index sets in the model (2.1) in a more explicit manner:

$$\begin{array}{l}\text{Linear}\text{index}\text{set}:I_L=\{j=1,\dots ,d:{\beta }_j\ne 0,g_{1j}\equiv 0\},\\ \text{Nonlinear}\text{index}\text{set}:I_N=\{j=1,\dots ,d:g_{1j}\ne 0\},\\ \text{Null}\text{index}\text{set}:I_O=\{j=1,\dots ,d:{\beta }_j=0,g_{1j}\equiv 0\}.\end{array}$$

Note that the nonlinear index set I_N can be further decomposed as I_N = I_PN ∪ I_LN, where I_PN = {β_j = 0, g_1j ≠ 0} is the index for purely nonlinear terms and I_LN = {β_j ≠ 0, g_1j ≠ 0} is the index for covariates whose linear and nonlinear terms are both nonzero.

The model selection problem for (2.2) is therefore equivalent to the problem of identifying I_L, I_N, I_O. To achieve this, we propose to solve the following regularization problem:

$$\underset{g\in \mathcal{H}}{min}\frac{1}{n}\sum _{i=1}^n{[y_i-g({\mathbf{x}}_i)]}^2+{\lambda }_1\sum _{j=1}^d{w}_{0j}{\left|\right|{\mathcal{P}}_{0j}g\left|\right|}_{{\mathcal{H}}_0}+{\lambda }_2\sum _{j=1}^d{w}_{1j}{\left|\right|{\mathcal{P}}_{1j}g\left|\right|}_{{\mathcal{H}}_1},$$ (2.6)

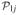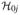where and are the projection operators respectively from to and . The regularization term in (2.6) consists of two parts: = |β_j| is equivalent to L₁ penalty on linear coefficients (Tibshirani 1996), and is the RKHS norm of g_j in . In the context of second-order Sobolev space, we have ${\left|\right|{\mathcal{P}}_{1j}g\left|\right|}_{{\mathcal{H}}_1}={\{{\int }_0^1{[g_{1j}^{″}(x)]}^{2}dx\}}^{1/2}$. Our theoretical results show that this penalty combination enables the proposed procedure to distinguish linear and nonlinear components automatically. Two tuning parameters (λ₁, λ₂) are used to control overall shrinkage imposed on linear and nonlinear terms. As shown in Section 3, when (λ₁, λ₂) are chosen properly, the resulting estimator is consistent in both structure selection and model estimation. The choices of weights w_0j and w_1j in (2.6) are discussed in the end of this subsection. We call the new procedure linear and nonlinear discoverer (LAND) and denote the solution to (2.6) by ĝ. The model structure selected by the LAND is defined as

$$\begin{array}{l}{\widehat{I}}_L=\{j:{\widehat{\beta }}_j\ne 0,{\widehat{g}}_{ij}\equiv 0\},{\widehat{I}}_N=\{j:{\widehat{g}}_{1j}\ne 0\},\\ {\widehat{I}}_O=I\backslash \{{\widehat{I}}_L\cup {\widehat{I}}_N\}.\end{array}$$

We note that the penalty proposed in (2.6) is related to the COSSO penalty for nonparametric model selection proposed by Lin and Zhang (2006) and Zhang and Lin (2006). The following remark reveals the link and difference between the new penalty and the COSSO penalty.

Remark 1

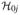Denote $J_l(g)={\sum }_{j=1}^d{\left|\right|P_{0j}g\left|\right|}_{{\mathcal{H}}_0}$ and $J_n(g)={\sum }_{j=1}^d{\left|\right|{\mathcal{P}}_{1j}g\left|\right|}_{{\mathcal{H}}_1}$. We also denote the COSSO penalty term as $J_c(g)={\sum }_{j=1}^d{\left|\right|{\mathcal{P}}_{j}g\left|\right|}_{\mathcal{H}}$, where is the projection operator from to = ⊕ and is the previously defined RKHS norm. Based on ${\left|\right|{\mathcal{P}}_{j}g\left|\right|}_{\mathcal{H}}=\sqrt{{\left|\right|{\mathcal{P}}_{0j}g\left|\right|}_{{\mathcal{H}}_0}^2+{\left|\right|{\mathcal{P}}_{1j}g\left|\right|}_{{\mathcal{H}}_1}^2}$, the Cauchy–Schwarz inequality implies that

$$\frac{J_l(g)+J_n(g)}{\sqrt{2}}\le J_c(g)\le J_l(g)+J_n(g)$$

for any g ∈ .

The above remark implies that the penalty term in (2.6) includes the COSSO penalty as a special case when equal weights and smoothing parameters are used for regularization. The LAND is much more flexible than the COSSO by employing different weights and smoothing parameters, which makes it possible to distinguish linear and nonlinear components effectively.

The weights w_0j and w_1j are not tuning parameters as they need to be prespecified by data. We propose to choose the weights adaptively such that unimportant components are assigned with large penalties and important components are given small penalties. In this way, nonzero function components are protectively preserved in the selection process, while insignificant components are shrunk more toward zero. This adaptive selection idea has been employed for linear models in various contexts (Zou 2006; Wang, Li, and Jiang 2007; Zhang and Lu 2007) and SS-ANOVA models (Storlie et al. 2011), and it was found to be able to greatly improve performance of nonadaptive shrinkage methods if the weights are chosen properly. Assume g̃ is a consistent estimator of g in . We propose to construct the weights as follows:

$$w_{0j}=\frac{1}{{\mid {\stackrel{\sim }{\beta }}_j\mid }^{\alpha }},w_{1j}=\frac{1}{{\left|\right|{\stackrel{\sim }{g}}_{1j}\left|\right|}_2^{\gamma }}\text{for}j=1,\dots ,d,$$ (2.7)

where β̃_j, g̃_1j are the decomposition of g̃ according to (2.4), || · ||₂ represents the L₂ norm, and α > 0 and γ > 0 are some positive constants. We will discuss how to decide α and γ in Section 3. A natural choice of g̃ is the standard SS-ANOVA solution, which minimizes the least squares in (2.6) subject to the roughness penalty. Other consistent initial estimators should also work.

Remark 2

The implementation of the LAND procedure requires an initial weight estimation. We point out this two-step process has a different nature from that of classical stepwise selection procedures. In forward or backward selection, variable selection is done sequentially and involves multiple decisions. At each step, the decision is made on whether a covariate should be included or not. These decisions are generally myopic, so the selection errors at previous steps may accumulate and affect later decisions. This explains instability and inconsistency of these stepwise procedures in general. By contrast, the model selection of the LAND is not a sequential decision. It conducts model selection by solving (2.6) once, where all the terms are penalized and shrunken toward zero simultaneously. The initial weights are used to assure the selection consistency of the LAND, which is similar to the adaptive LASSO in linear models.

3. THEORETICAL PROPERTIES

In this section, we first establish the convergence rates of the LAND estimator. Then under the tensor product design, we show that the LAND can identify the correct model structure asymptotically, that is, Î_L → I_L, Î_N → I_N, Î_O → I_O with probability tending to 1.

To facilitate the presentation, we now define some notations and state the technical assumptions used in our theorems. First, we assume the true partially linear regression is

$$\begin{array}{l}{y}_i=g_0({\mathbf{x}}_i)+{\epsilon }_i,\\ g_0({\mathbf{x}}_i)=b_0+\sum _{j\in I_L}{x}_{ij}{\beta }_{0j}+\sum _{j\in I_N}{f}_{0j}(x_{ij})+\sum _{j\in I_O}0(x_{ij}),\end{array}$$ (3.1)

where b₀ is the true intercept, β_0j’s are the true coefficients for nonzero linear effects and f_0j’s are the true nonzero functions for nonlinear effects. For any g ∈ , we decompose g(·) in the framework of function ANOVA:

$$g(\mathbf{x})=b+\sum _{j=1}^d{\beta }_j{k}_1(x_j)+\sum _{j=1}^d{g}_{1j}(x_j),$$

where g_1j ∈ . For the purpose of identifiability, we assume that each component has mean zero, that is, ${\sum }_{i=1}^n{\beta }_j{k}_1(x_{ij})+{\sum }_{i=1}^n{g}_{1j}(x_{ij})=0$ for each j = 1, …, d. For the final estimator ĝ, the initial estimator g̃, and the true function g₀, their ANOVA decomposition can also be expressed in terms of the projection operators. For example, $g_{1j}^0={\mathcal{P}}_{1j}{g}_0$ for j = 1, …, d.

Given data (x_i, y_i), i = 1, …, n, for any function g ∈ , we denote its function values evaluated at the data points by the n-vector g = (g(x₁), …, g(x_n)). Similarly, we define g₀ and g̃. Also, define the empirical L₂ norm || · ||_n and inner product 〈·, ·〉_n in Rⁿ as

$${\left|\right|g\left|\right|}_n^2=\frac{1}{n}\sum _{i=1}^n{g}^2({\mathbf{x}}_i),{\langle g,h\rangle }_n=\frac{1}{n}\sum _{i=1}^{n}g({\mathbf{x}}_i)h({\mathbf{x}}_i);$$

and thus ${\left|\right|y-g\left|\right|}_n^2=(1/n){\sum }_{i=1}^n{\{y_i-g({\mathbf{x}}_i)\}}^2$. For any sequence r_n → 0, we denote λ ~ r_n when there exists an M > 0 so that M⁻¹r_n ≤ λ ≤ Mr_n.

We will establish our theorems for fixed d under the following regularity conditions:

• (C1)ε is assumed to be independent of X, and has the sub-exponential tail, that is, E[exp(|ε|/C₀)] ≤ C₀ for some 0 < C₀ < ∞
• (C2) ${\sum }_{i=1}^n({\mathbf{x}}_i-1/2){({\mathbf{x}}_i-1/2)}^{\prime }/n$ converges to some non-singular matrix
• (C3)the density for X is bounded away from zero and infinity.

3.1 Asymptotic Properties of the LAND

The choices of weights w_0j’s and w_1j’s are essential to the LAND procedure. In Section 2, we suggest using the weights constructed from the SS-ANOVA solution g̃: w_0j = |β̃_j|^−α and $w_{1j}={\left|\right|{\stackrel{\sim }{g}}_{1j}\left|\right|}_2^{-\gamma }$ for j = 1, …, d. The standard smoothing ANOVA g̃ is obtained by solving

$$\underset{g\in \mathcal{H}}{min}\frac{1}{n}\sum _{i=1}^n{[y_i-g({\mathbf{x}}_i)]}^2+\lambda \sum _{j=1}^d{\left|\right|{\mathcal{P}}_{1j}g\left|\right|}_{{\mathcal{H}}_1}^2.$$ (3.2)

In the following theorem, we show that the LAND estimator has a rate of convergence n^−2/5 if the tuning parameters are chosen appropriately.

Theorem 1

Under the regularity conditions (C1) and (C2) and the weights stated in (2.7) and (3.2), if λ₁, λ₂ ~ n^−4/5 and α ≥ 3/2, γ ≥ 3/2, then the LAND estimator in (2.6) satisfies:

$${\left|\right|\widehat{g}-g_0\left|\right|}_n=O_P(n^{-2/5})\text{if}{g}_0\text{is}\text{not}\text{a}\text{constant}\text{function}$$

and

$${\left|\right|\widehat{g}-g_0\left|\right|}_n=O_P(n^{-1/2})\text{if}{g}_0\text{is}\text{a}\text{constant}\text{function}.$$

Remark 3

Theorem 1 is consistent with corollary 1 in the COSSO article (Lin and Zhang 2006) since we assume the same order of two smoothing parameters λ₁ and λ₂. It is worth pointing out that we do not have the optimal parametric rate when the nonparametric component of g is zero. This is not surprising because we still apply the standard nonparametric estimation method, which yields n^−2/5-rate, even when the true function g is purely linear.

3.2 Selection Consistency

To illustrate the selection consistency of our LAND procedure, we give an instructive analysis in the special case of a tensor product design with a smoothing spline ANOVA model built from the second-order Sobolev spaces of periodic functions. For simplicity, we assume that the error ε’s in the regression model are independent with the distribution N(0, σ²) here. The space of periodic functions on [0, 1] is denoted by ${\mathcal{H}}_{\mathit{per}}=\{1\}\oplus {\oplus }_{j=1}^d{\mathcal{H}}_{0j}\oplus {\oplus }_{j=1}^d{\mathcal{S}}_{\mathit{per},j}$, where 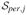is the functional space on x_j, and

$${\mathcal{S}}_{\mathit{per}}=\left\{f:f(t)=\sum _{v=1}^{\infty }{a}_v\sqrt{2}cos(2\pi vt)+\sum _{v=1}^{\infty }{b}_v\sqrt{2}sin(2\pi vt),\text{with}\sum _{v=1}^{\infty }(a_v^2+b_v^2){(2\pi vt)}^4<\infty \right\}.$$

We also assume that the observations come from a tensor product design, that is,

$$\{{\mathbf{x}}_1,{\mathbf{x}}_2,\dots ,{\mathbf{x}}_d\},$$

where x_j = (x_1,j, …, x_njj)′ and x_i,j = i/n_j, for i = 1, …, n_j n_j, and j = 1, …, d. Without loss of generality, we assume that n_j equals some number m for any j = 1, …, d.

Theorem 2

Assume a tensor product design and g₀ ∈ . Under the regularity conditions (C1) to (C3), assume that (i) n^1/5λ₁w_0j → ∞ for j ∈ I\I_L; (ii) $n^{3/20}{\lambda }_2^2{w}_{1j}^2\to \infty$ for j ∈ I\I_N, we have Î_L = I_L, Î_N = I_N, Î_O = I_O with probability tending to 1 as n → ∞.

Remark 4

To achieve the structure selection consistency and convergence rate in Theorem 1 simultaneously, we require that λ₁, λ₂ ~n^−4/5, α > 3, γ > 29/8, by considering the assumptions in Theorems 1 and 2 and Lemma A.1 in the Appendix if we use the weight of the form (2.7).

Remark 5

The proof of the selection consistency requires detailed investigation on eigen-properties of the reproducing kernel, which is generally intractable. In Theorem 2, we assume that the function belongs to the class of periodic functions and x has a tensor product design. This makes our derivation more tractable, since the eigenfunctions and eigenvalues of the RK for H_per have particularly simple forms. Results for this specific design are often instructive for general designs, as suggested by Wahba (1990). We conjecture that the LAND is still selection consistent in general cases. This is also supported by numerical results in Section 5, where neither the tensor product design nor the periodic function is assumed in the examples. Note that the special design condition is not required for the convergence rate results in Theorem 1.

4. TWO–STEP LAND ESTIMATOR

As shown in Section 3, the LAND estimator can consistently identify the true structure of partially linear models. In other words, the selected model would be correct as the sample size goes to infinity. In finite sample situations, if the selected model is correct or approximately correct, it is natural to ask whether refitting data based on the selected model would improve model estimation. This leads to the two-step LAND procedure: at step I, we identify the model structure using the LAND, and at step II we refit data by using the selected model from step I. In particular, we fit the following model at the second step:

$$y_i=b+\sum _{j\in {\widehat{I}}_L}{\beta }_j{k}_1(x_{ij})+\sum _{j\in {\widehat{I}}_N}{g}_{1j}(x_{ij})+\sum _{j\in {\widehat{I}}_o}0(x_{ij})+{\epsilon }_i,$$ (4.1)

where (Î_L, Î_N, Î_O) are the index sets identified by ĝ. Denote the two-step LAND solution by ĝ^*. The rationale behind the two-step LAND is: if the selection in step I is very accurate, then the estimation of ĝ^* can be thought of as being based on a (approximately) correct model. This two-step procedure thus will yield better estimation accuracy as shown in the next paragraph.

Let Ω_n = {I_L = Î_L and I_N = Î_N}. In the first step, we estimate I_L and I_N consistently, that is, P(Ω_n) → 1, according to Theorem 2. In the second step, we fit a partial smoothing spline in (4.1). Denote the solution as β̂^* and ${\widehat{g}}_{1j}^{\ast }$. Within the event Ω_n that is, Î_L = I_L and Î_N = I_N, we know that, by the standard partial smoothing spline theory (Mammen and van de Geer 1997),

$$\left|\right|{\widehat{\mathit{\beta }}}^{\ast }-{\mathit{\beta }}_0\left|\right|=O_P(n^{-1/2}),$$ (4.2)

$${\left|\right|{\widehat{g}}_{1j}^{\ast }-g_{1j}^0\left|\right|}_2=O_P(n^{-2/5}),$$ (4.3)

under regularity conditions. In addition, we know that β̂^* is also asymptotically normal within the event Ω_n. Since Ω_n is shown to have probability tending to 1, we can conclude that (4.2) and (4.3) hold asymptotically. Moreover, comparing (4.2)–(4.3) with Theorem 1, we conclude that the convergence rates of both linear and nonlinear components can be further improved to their optimal rates by implementing the above two-step procedure.

In Section 6, we find that the LAND and two-step LAND perform similarly in many cases. If the LAND does a good job in recovering the true model structure correctly, say in strong signal cases, then the additional refitting step can improve the model estimation accuracy. However, if the selection result is not good, say, in weak signal cases, the refitting result is not necessarily better.

5. COMPUTATION ALGORITHMS

5.1 Equivalent Formulation

We first show that the solution to (2.6) lies in a finite-dimensional space. This is an important result for nonparametric modeling, since the LAND estimator involves solving an optimization problem in an infinite-dimensional space . The finite representer property is known to hold for standard SS-ANOVA models (Kimeldorf and Wahba 1971) and partial splines (Gu 2002).

Lemma 1

Let $\widehat{g}(\mathbf{x})=\widehat{b}+{\sum }_{j=1}^d{\widehat{\beta }}_j{k}_1(x_j)+{\sum }_{j=1}^d{\widehat{g}}_{1j}(x_j)$ be a minimizer of (2.6) in , with ĝ_1j ∈ for j = 1, …, d. Then ĝ_1j ∈ span{R_1j(x_i, ·), i = 1, …, n}, where R_1j(·, ·) is the reproducing kernel of the space .

To facilitate the LAND implementation, we give an equivalent but more convenient formulation to (2.6). Define θ = (θ₁, …, θ_d)^T. Consider the optimization problem:

$$\begin{array}{c}\underset{\mathit{\theta }\ge \mathbf{0},g\in \mathcal{H}}{min}\frac{1}{n}\sum _{i=1}^n{[y_i-g({\mathbf{x}}_i)]}^2+{\lambda }_1\sum _{j=1}^d{w}_{0j}\left|\right|{\mathcal{P}}_{0j}g\left|\right|\\ +{\tau }_0\sum _{j=1}^d{\theta }_j^{-1}{w}_{1j}{\left|\right|{\mathcal{P}}_{1j}g\left|\right|}_{{\mathcal{H}}_1}^2+{\tau }_1\sum _{j=1}^d{w}_{1j}{\theta }_j,\\ \text{subject}\text{to}{\theta }_j\ge 0,j=1,\dots ,d,\end{array}$$ (5.1)

where τ₀ is a constant that can be fixed at any positive value, and (λ₁, τ₁) are tuning parameters. The following lemma shows that there is a one-to-one correspondence between the solutions to (2.6) [for all possible pairs (λ₁, λ₂)] and those to (5.1) [for all (λ₁, τ₁) pairs].

Lemma 2

Set ${\tau }_1={\lambda }_2^2/(4{\tau }_0)$. (i) If ĝ minimizes (2.6), set ${\widehat{\theta }}_j={\tau }_0^{1/2}{\tau }_1^{-1/2}\left|\right|{\mathcal{P}}_{1j}\widehat{g}\left|\right|$; then the pair (θ̂, ĝ) minimizes (5.1). (ii) If (θ̂, ĝ) minimizes (5.1), then ĝ minimizes (2.6).

In practice, we choose to solve (5.1) since its objective function can be easily handled by standard quadratic programming (QP) and linear programming (LP) techniques. The nonnegative θ_j’s can be regarded as scaling parameters and they are interpretable for the purpose of model selection. If θ_j = 0, the minimizer of (5.1) is taken to satisfy || 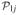g|| = 0, which implies that the nonlinear component of g_j vanishes.

With θ fixed, solving (5.1) is equivalent to fitting a partial spline model in some RKHS space. By the representer theorem, the solution to (5.1) has the following form:

$$\widehat{g}(\mathbf{x})=\widehat{b}+\sum _{j=1}^d{\widehat{\beta }}_j{k}_1(x_j)+\sum _{j=1}^d{\widehat{\theta }}_j{w}_{1j}^{-1}\sum _{i=1}^n{\widehat{c}}_i{R}_{1j}(x_{ij},x_j).$$ (5.2)

The expression (5.2) suggests that the linearity or nonlinearity of g_j is determined by the fact whether β̂_j = 0 or θ̂_j = 0 or not. Therefore, we can define the three index sets as:

$$\begin{array}{l}{\widehat{I}}_L=\{j:{\widehat{\beta }}_j\ne 0,{\widehat{\theta }}_j=0\},{\widehat{I}}_N=\{j:{\widehat{\theta }}_j\ne 0\},\\ {\widehat{I}}_O=\{j:{\widehat{\beta }}_j=0,{\widehat{\theta }}_j=0\}.\end{array}$$

5.2 Algorithms

In the following, we propose an iterative algorithm to solve (5.1). Define the vectors y = (y₁, …, y_n)^T, g = (g(x₁), …, g(x_n))^T, β = (b, β₁, …, β_d)^T, and c = (c₁, …, c_n)^T ∈ Rⁿ. With some abuse of notations, let R_1j also stand for the n × n matrix {R_1j(x_ij, x_i′j)}, for i, i′ = 1, …, n; j = 1, …, d, and ${\mathbf{R}}_{{\mathbf{w}}_1,\mathit{\theta }}={\sum }_{j=1}^d{\theta }_j{w}_{1j}^{-1}{\mathbf{R}}_{1j}$ be the Gram matrix associated with the weighted kernel. Let T be the n × (1 + d) matrix with t_i1 = 1 and t_ij = k₁(x_ij) for i = 1, …, n and j = 1, …, d. Then g = Tβ + R_w1θc, and (5.1) can be expressed as

$$\begin{array}{l}\underset{\mathit{\beta },\mathit{\theta },\mathbf{c}}{min}\frac{1}{n}{(\mathbf{y}-\mathbf{T}\mathit{\beta }-{\mathbf{R}}_{{\mathbf{w}}_1,\mathit{\theta }}\mathbf{c})}^{\text{T}}(\mathbf{y}-\mathbf{T}\mathit{\beta }-{\mathbf{R}}_{{\mathbf{w}}_1,\mathit{\theta }}\mathbf{c})\\ +{\lambda }_1\sum _{j=1}^d{w}_{0j}\mid {\beta }_j\mid +{\tau }_0{\mathbf{c}}^{\text{T}}{\mathbf{R}}_{{\mathbf{w}}_1,\mathit{\theta }}\mathbf{c}+{\tau }_1\sum _{j=1}^d{w}_{1j}{\theta }_j,\\ \text{s}.\text{t}.{\theta }_j\ge 0,j=1,\dots ,d.\end{array}$$ (5.3)

To solve (5.3), we suggest an iterative algorithm to alternatively update (β, θ) and c.

On one hand, with (β̂, θ̂) fixed at their current values, we update c by the following ridge-type problem: define z = y − Tβ̂ and solve

$$\underset{\mathbf{c}}{min}\frac{1}{n}{(\mathbf{z}-{\mathbf{R}}_{{\mathbf{w}}_1,\widehat{\mathit{\theta }}}\mathbf{c})}^{\text{T}}(\mathbf{z}-{\mathbf{R}}_{{\mathbf{w}}_1,\widehat{\mathit{\theta }}}\mathbf{c})+{\tau }_0{\mathbf{c}}^{\text{T}}{\mathbf{R}}_{{\mathbf{w}}_1,\widehat{\mathit{\theta }}}\mathbf{c}.$$ (5.4)

On the other hand, when ĉ is fixed at their current values, we can update (β, θ) by solving a quadratic programming (QP) problem. Define ${\mathbf{v}}_j=w_{1j}^{-1}{\mathbf{R}}_{1j}\widehat{\mathbf{c}}$ for j = 1, …, d and let V be the n × d matrix with the jth column being v_j. Then we obtain the following problem:

$$\underset{\mathit{\theta }\ge \mathbf{0},\mathit{\beta }}{min}\frac{1}{n}{(\mathbf{y}-\mathbf{T}\mathit{\beta }-\mathbf{V}\mathit{\theta })}^{\text{T}}(\mathbf{y}-\mathbf{T}\mathit{\beta }-\mathbf{V}\mathit{\theta })+{\lambda }_1\sum _{j=1}^d{w}_{0j}\mid {\beta }_j\mid +{\tau }_0{\widehat{\mathbf{c}}}^{\text{T}}\mathbf{V}\mathit{\theta }+{\tau }_1\sum _{j=1}^d{w}_{1j}{\theta }_j.$$ (5.5)

Further, we can write $\mid {\beta }_j\mid ={\beta }_j^{+}+{\beta }_j^{-}$ and ${\beta }_j={\beta }_j^{+}-{\beta }_j^{-}$ for each j, where ${\beta }_j^{+}$ and ${\beta }_j^{-}$ are respectively the positive and negative part of β_j. Define w₀ = (w₀₁, …, w_0d)^T. Then (5.5) can be equivalently expressed as

$$\begin{array}{l}\underset{\mathit{\theta },{\mathit{\beta }}^{+},{\mathit{\beta }}^{-}}{min}\frac{1}{n}{(\mathbf{y}-T{\mathit{\beta }}^{+}+T{\mathit{\beta }}^{-}-\mathbf{V}\mathit{\theta })}^{\text{T}}(\mathbf{y}-T{\mathit{\beta }}^{+}+T{\mathit{\beta }}^{-}-\mathbf{V}\mathit{\theta })\\ +{\lambda }_1{\mathbf{w}}_0^{\text{T}}({\mathit{\beta }}^{+}+{\mathit{\beta }}^{-})+{\tau }_0{\widehat{\mathbf{c}}}^{\text{T}}\mathbf{V}\mathit{\theta },\\ \text{subject}\text{to}\sum _{j=1}^d{w}_{1j}{\theta }_j\le M,\mathit{\theta }\ge \mathbf{0},{\mathit{\beta }}^{+}\ge \mathbf{0},{\mathit{\beta }}^{-}\ge \mathbf{0}\end{array}$$ (5.6)

for some M > 0. Given any (λ₁, M), the following is a complete algorithm to compute ĝ.

Algorithm

• Step 0Obtain the initial estimator g̃ by fitting a standard SS-ANOVA model. Derive β̃_j, g̃_1j, j = 1, …, d, and compute the weights w_0j, w_1j, j = 1, …, d, using (2.7).
• Step 1Initialize θ̂ = 1_d and β̂_j = β̃_j, j = 1, …, d.
• Step 2Fixing (θ̂, β̂) at their current values, update c by solving (5.4).
• Step 3Fixing ĉ at their current values, update (θ, β) by solving (5.6).
• Step 4Go to step 2 until the convergence criterion meets.

6. NUMERICAL STUDIES

In this section, we demonstrate the empirical performance of the LAND estimators in terms of their estimation accuracy and model selection. We compare the LAND with GAM, SS-ANOVA, COSSO, and the two-step LAND (2LAND). Note that LAND and 2LAND procedures give identical performance for model selection. The GAM and COSSO fits were obtained using the R packages “gam” and “cosso,” respectively. The builtin tuning procedures in R packages are used to tune the associated tuning parameters.

The following functions on [0, 1] are used as building blocks of functions in simulations:

$$\begin{array}{l}{h}_1(x)=x,h_2(x)=cos(2\pi x),\\ h_3(x)=sin(2\pi x)/(2-sin(2\pi x)),\\ h_4(x)=0.1sin(2\pi x)+0.2cos(2\pi x)+0.3{(sin(2\pi x))}^2+0.4{(cos(2\pi x))}^3+0.5{(sin(2\pi x))}^3,\\ h_5(x)={(3x-1)}^2.\end{array}$$

For each function, we can examine whether it is a pure linear, pure nonlinear, or both linear and nonlinear function based on its functional ANOVA decomposition in (2.4). Simple calculation shows that h₁ is a pure linear function, h₂, h₃, and h₄ are pure nonlinear functions, and h₅ contains both nonzero linear and nonlinear terms.

For the simulation design, we consider four different values of theoretical R² as R² = 0.95, 0.75, 0.55, 0.35, providing varying signal-to-noise ratio (SNR) settings. For the input x, we consider both uncorrelated and correlated situations, corresponding to ρ = corr(X_i, X_j) = 0, 0.5, 0.8 for all i ≠ j. The combination of four levels of R² and three levels of produces twelve unique SNR settings.

To evaluate the model estimation performance of the estimator ĝ, we report its integrated squared error ISE = E_X{g(X) − ĝ(X)}². The ISE is calculated via a Monte Carlo integration with 1000 points. For each procedure, we report the average ISEs over 100 realizations and the corresponding standard errors (in parentheses). To evaluate performance of the LAND in structure selection, we summarize the frequency of getting the correct model structure (power) and an incorrect model structure (Type I error) over 100 Monte Carlo simulations. In particular, the power related measures include:

1. the number of correct linear effects identified (denoted as “corrL”)

2. the number of correct nonlinear effects identified (denoted as “corrN”)

3. the number of correct linear and nonlinear effects identified (denoted as “corrLN”)

4. the number of correct zero coefficients identified (denoted as “corr0”).

The Type I error related measures include:

1. the number of linear effects incorrectly identified as nonlinear effects (denoted as “LtoN”)

2. the number of nonlinear effects incorrectly identified as linear effects (denoted as “NtoL”)

3. the number of linear or nonzero effects incorrectly identified as zero (denoted as “LNto0”).

The selection of tuning parameters is an important issue. Our empirical experience suggests that the performance of the LAND procedures is not sensitive to γ and α. We recommend to use γ = α = 4 based on Remark 4 and they work well in our examples. The choices of (λ₁, λ₂) [or (λ₁, M), equivalently] are important, as their magnitude directly controls the amount of penalty and the model sparsity. The numerical results are quite sensitive to λ’s. Therefore, we recommend to select the optimal parameters using cross-validation or some information criteria. In our simulation, we generate a validation set of size n from the same distribution of the training set. For each pair of tuning parameters, we implement the procedure and evaluate its prediction error on the validation set. We select the pair of λ₁ and λ₂ (or M) which corresponds to the minimum validation error.

6.1 Example 1

We generate Y from the model

$$Y=3h_1(X_1)+2h_2(X_2)+2h_5(X_3)+\epsilon ,$$

where ε ~ N(0, σ²). The pairwise correlation corr(X_j, X_k) = ρ for any j ≠ k. We consider three cases: ρ = 0, 0.5, 0.8. In this model, there are one purely linear effect, one purely nonlinear effect, one linear-nonlinear effect, and d – 3 noise variables. We consider d = 10 and d = 20, and the number of noise variables increases as d increases.

Table 1 summarizes the ISEs of all the procedures in twelve settings. To set a baseline for comparison, we also include the oracle model which fits the data using the true model structure. The 2LAND consistently produces smaller ISEs than GAM and SS-ANOVA in all the settings. The LAND is better than GAM and SS-ANOVA in most settings. We also note that the LAND and 2LAND perform similarly in the independent case. When the covariates are correlated at some degree, 2LAND tends to give better ISEs than the LAND as long as the signal is not too weak. The comparison between the LAND methods and COSSO is quite interesting. When R² is moderately large, say 0.75 and 0.95, the 2LAND overall gives smaller or comparable ISEs; if R² is small, say 0.55 and 0.35, the COSSO gives smaller errors. This pattern is actually not surprising, as the COSSO and LAND aim to tackle different problems. The COSSO can distinguish zero and nonzero components, while the LAND can distinguish zero, linear, and nonlinear components. Since the LAND methods are designed to discover a more detailed model structure than the COSSO, they generally estimate the function better if they can correctly separate different terms, which often require relatively stronger signals in data. The main advantage of the LAND methods is to produce more interpretable models by automatically separating linear and nonlinear terms, while other methods can not achieve this.

Table 1.

Average ISEs (and standard errors in parentheses) for 100 runs in Example 1

ρ	d	R2	GAM	SS-ANOVA	COSSO	LAND	2LAND	Oracle
0	10	0.95	0.17 (0.01)	0.11 (0.01)	0.11 (0.01)	0.05 (0.01)	0.06 (0.00)	0.06 (0.00)
		0.75	0.91 (0.05)	0.56 (0.03)	0.48 (0.03)	0.35 (0.03)	0.39 (0.02)	0.27 (0.02)
		0.55	2.17 (0.12)	1.31 (0.07)	1.07 (0.07)	1.28 (0.10)	1.12 (0.08)	0.61 (0.05)
		0.35	4.73 (0.28)	2.95 (0.17)	2.44 (0.15)	3.28 (0.18)	2.94 (0.18)	1.34 (0.11)
	20	0.95	0.50 (0.01)	0.19 (0.01)	0.18 (0.01)	0.05 (0.01)	0.07 (0.01)	0.06 (0.00)
		0.75	2.48 (0.07)	1.04 (0.04)	0.82 (0.04)	0.46 (0.03)	0.60 (0.03)	0.25 (0.02)
		0.55	5.92 (0.17)	2.46 (0.09)	2.01 (0.11)	1.81 (0.11)	1.89 (0.10)	0.55 (0.05)
		0.35	13.29 (0.39)	5.60 (0.22)	4.18 (0.17)	5.18 (0.22)	5.10 (0.22)	1.17 (0.11)
0.5	10	0.95	0.16 (0.01)	0.11 (0.01)	0.10 (0.01)	0.09 (0.01)	0.06 (0.01)	0.06 (0.00)
		0.75	0.87 (0.05)	0.57 (0.03)	0.45 (0.03)	1.06 (0.06)	0.48 (0.03)	0.27 (0.02)
		0.55	2.08 (0.11)	1.35 (0.06)	1.07 (0.07)	1.94 (0.09)	1.33 (0.08)	0.61 (0.04)
		0.35	4.68 (0.27)	2.97 (0.14)	2.44 (0.15)	3.32 (0.14)	2.99 (0.15)	1.37 (0.09)
	20	0.95	0.41 (0.01)	0.19 (0.01)	0.16 (0.01)	0.24 (0.03)	0.07 (0.01)	0.06 (0.00)
		0.75	2.27 (0.05)	1.02 (0.04)	0.74 (0.04)	1.06 (0.07)	0.67 (0.04)	0.24 (0.02)
		0.55	5.48 (0.13)	2.46 (0.09)	1.86 (0.09)	2.42 (0.10)	2.08 (0.08)	0.55 (0.02)
		0.35	12.36 (0.28)	5.46 (0.20)	3.60 (0.15)	4.97 (0.20)	5.11 (0.20)	1.21 (0.12)
0.8	10	0.95	0.16 (0.01)	0.11 (0.01)	0.10 (0.01)	0.28 (0.01)	0.07 (0.01)	0.06 (0.00)
		0.75	0.89 (0.05)	0.56 (0.03)	0.47 (0.03)	1.07 (0.05)	0.52 (0.03)	0.27 (0.02)
		0.55	2.15 (0.11)	1.35 (0.06)	1.06 (0.07)	1.87 (0.10)	1.35 (0.07)	0.61 (0.04)
		0.35	4.74 (0.25)	2.98 (0.14)	2.29 (0.13)	3.33 (0.14)	2.94 (0.14)	1.36 (0.09)
	20	0.95	0.42 (0.01)	0.19 (0.01)	0.16 (0.01)	0.22 (0.03)	0.07 (0.05)	0.06 (0.01)
		0.75	2.24 (0.05)	1.04 (0.04)	0.76 (0.04)	1.11 (0.07)	0.76 (0.05)	0.24 (0.02)
		0.55	5.40 (0.12)	2.50 (0.10)	1.88 (0.09)	2.61 (0.11)	2.25 (0.11)	0.55 (0.05)
		0.35	12.17 (0.27)	5.59 (0.22)	3.47 (0.14)	5.31 (0.19)	5.49 (0.22)	1.20 (0.12)

Figure 1 plots the estimated function components by the SS-ANOVA and the 2LAND in one typical realization of Example 1. For illustration, we plot the first four function components. In each panel, the solid, dashed, dotted lines respectively represent the true function, the fit by SS-ANOVA, and the fit by 2LAND. We observe that both SS-ANOVA and 2LAND perform well in the first three panels, and 2LAND shows better accuracy in estimation than SS-ANOVA by producing a sparse model. In the last panel where the true function is zero, the 2LAND successfully removes it from the final model while the SS-ANOVA provides a nonzero fit.

Figure 1.

True and estimated function components for Example 1: True function (solid line), SS-ANOVA estimator (dashed line), and 2LAND estimator (dotted line). The online version of this figure is in color.

Table 2 reports the selection performance of the LAND under different settings. Note that the 2LAND is identical to the LAND for model selection. We observe that the LAND shows effective performance in terms of both power and Type-I error measures in all the settings. When the signal is moderately strong, the LAND is able to identify the correct model with high frequency since the “corrL,” “corrN,” “corrLN,” and “corr0” are all close to their true values and the incorrectly selected terms are close to zero. Except in weak signal cases, the frequency of missing any important variable or treating linear terms as nonlinear is low. In more challenging cases, with a small R² or a large number of noise variables, the LAND selection gets worse as expected but still performs reasonably well, considering that the sample size n = 100 is small.

Table 2.

Average selection results (standard errors in parentheses) for 100 runs in Example 1

ρ	d	R2	corrlin	corrnon	corrlnn	corr0	LNto0	LtoN	NtoL
		oracle:	1	1	1	d – 3	0	0	0
0	10	0.95	0.99 (0.01)	0.90 (0.03)	1.00 (0.00)	6.34 (0.18)	0.00 (0.00)	0.01 (0.01)	0.00 (0.00)
		0.75	0.99 (0.01)	0.71 (0.05)	1.00 (0.00)	5.23 (0.20)	0.00 (0.00)	0.01 (0.01)	0.00 (0.00)
		0.55	0.99 (0.01)	0.51 (0.05)	0.97 (0.02)	3.97 (0.19)	0.02 (0.01)	0.01 (0.01)	0.05 (0.02)
		0.35	0.92 (0.03)	0.33 (0.05)	0.74 (0.04)	2.33 (0.17)	0.10 (0.03)	0.05 (0.02)	0.43 (0.06)
	20	0.95	1.00 (0.00)	0.94 (0.02)	1.00 (0.00)	16.24 (0.27)	0.00 (0.00)	0.00 (0.00)	0.00 (0.00)
		0.75	1.00 (0.00)	0.71 (0.05)	1.00 (0.00)	13.38 (0.29)	0.00 (0.00)	0.00 (0.00)	0.00 (0.00)
		0.55	0.97 (0.02)	0.53 (0.05)	0.94 (0.02)	9.30 (0.03)	0.04 (0.02)	0.01 (0.01)	0.07 (0.03)
		0.35	0.92 (0.03)	0.31 (0.05)	0.67 (0.05)	5.80 (0.31)	0.10 (0.03)	0.02 (0.01)	0.49 (0.06)
0.5	10	0.95	1.00 (0.00)	0.92 (0.03)	0.95 (0.02)	6.49 (0.14)	0.00 (0.00)	0.00 (0.00)	0.05 (0.02)
		0.75	1.00 (0.00)	0.67 (0.05)	0.64 (0.05)	4.78 (0.18)	0.03 (0.02)	0.00 (0.00)	0.37 (0.05)
		0.55	0.95 (0.02)	0.43 (0.05)	0.48 (0.05)	3.23 (0.17)	0.13 (0.04)	0.01 (0.01)	0.61 (0.05)
		0.35	0.88 (0.03)	0.19 (0.04)	0.39 (0.05)	2.24 (0.15)	0.20 (0.04)	0.06 (0.02)	0.82 (0.06)
	20	0.95	1.00 (0.00)	0.91 (0.03)	0.97 (0.02)	16.23 (0.23)	0.00 (0.00)	0.00 (0.00)	0.03 (0.02)
		0.75	0.99 (0.01)	0.66 (0.05)	0.66 (0.05)	12.32 (0.29)	0.03 (0.02)	0.00 (0.00)	0.36 (0.05)
		0.55	0.90 (0.03)	0.48 (0.05)	0.46 (0.05)	8.14 (0.34)	0.12 (0.03)	0.02 (0.01)	0.65 (0.06)
		0.35	0.85 (0.04)	0.16 (0.04)	0.30 (0.05)	5.40 (0.28)	0.25 (0.04)	0.03 (0.02)	0.96 (0.07)
0.8	10	0.95	1.00 (0.00)	0.88 (0.03)	0.94 (0.02)	6.41 (0.13)	0.00 (0.00)	0.00 (0.00)	0.06 (0.02)
		0.75	1.00 (0.00)	0.61 (0.05)	0.66 (0.05)	4.44 (0.20)	0.05 (0.02)	0.00 (0.00)	0.35 (0.05)
		0.55	0.92 (0.03)	0.36 (0.05)	0.48 (0.05)	3.08 (0.17)	0.18 (0.04)	0.00 (0.00)	0.62 (0.05)
		0.35	0.91 (0.03)	0.16 (0.04)	0.42 (0.05)	1.88 (0.14)	0.15 (0.04)	0.03 (0.02)	0.88 (0.06)
	20	0.95	1.00 (0.00)	0.94 (0.02)	0.97 (0.02)	16.15 (0.23)	0.00 (0.00)	0.00 (0.00)	0.03 (0.02)
		0.75	0.95 (0.02)	0.64 (0.05)	0.72 (0.05)	11.20 (0.29)	0.07 (0.03)	0.00 (0.00)	0.31 (0.05)
		0.55	0.88 (0.03)	0.41 (0.05)	0.43 (0.05)	7.22 (0.31)	0.17 (0.04)	0.02 (0.01)	0.67 (0.06)
		0.35	0.81 (0.04)	0.17 (0.04)	0.26 (0.04)	4.78 (0.26)	0.29 (0.06)	0.04 (0.02)	1.05 (0.07)

6.2 Example 2

We modify Example 1 into a more challenging example, which contains a larger number of input variables and a more complex structure for the underlying model. In particular, let d = 20. Similarly to Example 1, we consider uncorrelated covariates, correlated covariates with pairwise correlations ρ = 0, 0.5, 0.8 respectively. The response Y is generated from the following model:

$$Y=3h_1(X_1)-4h_1(X_2)+2h_1(X_3)+2h_2(X_4)+3h_3(X_5)+(5h_4(X_6)+2h_1(X_6))+2h_5(X_7)+\epsilon ,$$

where ε ~ N(0, σ²). In this case, the first three covariates X₁, X₂, and X₃ have purely linear effects, the covariates X₄ and X₅ have purely nonlinear effects, and the covariates X₆ and X₇ have nonzero linear and nonlinear terms. There are d – 7 noise variables, and let n = 250.

Table 3 summarizes the prediction errors of various estimators under different settings. We consider four different values of theoretical R² as R² = 0.95, 0.75, 0.55, 0.35, which provide different signal-to-noise ratio (SNR) values and hence varying signal strength. We have similar observations as in Example 1. The LAND and 2LAND give similar performance, and both of them consistently produce smaller ISEs than GAM and SS-ANOVA in all the settings. The ISEs of the LAND and 2LAND are significantly better than that of the COSSO in all the cases except R² = 0.35, where the signal is very weak. In Table 4, we report the structure selection performance of the LAND under different settings. Overall, the LAND gives an effective performance as long as the signal is not too weak.

Table 3.

Average ISEs (and standard errors in parentheses) for 100 runs in Example 2

ρ	R2	GAM	SS-ANOVA	COSSO	LAND	2LAND	Oracle
0	0.95	1.07 (0.01)	0.16 (0.01)	0.25 (0.01)	0.07 (0.00)	0.08 (0.00)	0.07 (0.00)
	0.75	2.16 (0.05)	0.87 (0.03)	1.10 (0.05)	0.43 (0.03)	0.46 (0.03)	0.33 (0.02)
	0.55	4.14 (0.10)	2.07 (0.08)	2.19 (0.09)	1.51 (0.09)	1.54 (0.10)	0.72 (0.05)
	0.35	8.47 (0.22)	4.54 (0.17)	4.13 (0.17)	3.90 (0.17)	3.83 (0.18)	1.58 (0.10)
0.5	0.95	0.91 (0.01)	0.18 (0.01)	0.22 (0.01)	0.09 (0.01)	0.10 (0.00)	0.10 (0.00)
	0.75	1.95 (0.04)	0.93 (0.04)	1.07 (0.04)	0.81 (0.05)	0.71 (0.04)	0.42 (0.02)
	0.55	3.83 (0.09)	2.13 (0.07)	2.10 (0.07)	2.02 (0.09)	1.99 (0.02)	0.89 (0.05)
	0.35	7.92 (0.20)	4.31 (0.15)	3.74 (0.13)	4.16 (0.15)	4.12 (0.15)	1.66 (0.10)
0.8	0.95	0.93 (0.01)	0.19 (0.01)	0.24 (0.01)	0.10 (0.00)	0.11 (0.01)	0.10 (0.00)
	0.75	2.02 (0.04)	0.98 (0.03)	1.18 (0.04)	0.85 (0.04)	0.80 (0.04)	0.47 (0.02)
	0.55	3.96 (0.10)	2.29 (0.07)	2.26 (0.07)	2.15 (0.09)	2.16 (0.14)	0.99 (0.05)
	0.35	8.16 (0.21)	4.61 (0.15)	3.82 (0.13)	4.19 (0.15)	4.38 (0.17)	1.85 (0.10)

Table 4.

Average selection results (standard errors in parentheses) for 100 runs in Example 2

ρ	R2	corrlin	corrnon	corrlnn	corr0	LNto0	LtoN	NtoL
	oracle:	3	2	2	13	0	0	0
0	0.95	3.00 (0.00)	1.85 (0.04)	1.99 (0.01)	12.79 (0.09)	0.00 (0.00)	0.00 (0.00)	0.00 (0.00)
	0.75	2.95 (0.02)	1.66 (0.06)	1.91 (0.03)	11.98 (0.11)	0.05 (0.02)	0.00 (0.00)	0.01 (0.01)
	0.55	2.77 (0.05)	1.31 (0.07)	1.73 (0.05)	10.60 (0.23)	0.24 (0.05)	0.01 (0.01)	0.26 (0.05)
	0.35	2.31 (0.09)	0.90 (0.07)	1.39 (0.07)	9.29 (0.27)	0.88 (0.12)	0.06 (0.02)	0.55 (0.06)
0.5	0.95	2.97 (0.02)	1.81 (0.04)	1.98 (0.01)	12.55 (0.12)	0.00 (0.00)	0.03 (0.02)	0.00 (0.00)
	0.75	2.82 (0.04)	1.29 (0.07)	1.58 (0.05)	11.33 (0.18)	0.17 (0.04)	0.01 (0.01)	0.31 (0.05)
	0.55	2.50 (0.07)	0.98 (0.07)	1.07 (0.08)	9.66 (0.24)	0.57 (0.08)	0.02 (0.01)	0.90 (0.08)
	0.35	1.72 (0.11)	0.51 (0.06)	0.65 (0.07)	9.47 (0.31)	1.80 (0.17)	0.03 (0.02)	1.35 (0.09)
0.8	0.95	2.99 (0.01)	1.78 (0.05)	1.95 (0.02)	12.48 (0.18)	0.00 (0.00)	0.01 (0.01)	0.00 (0.00)
	0.75	2.62 (0.06)	1.30 (0.07)	1.50 (0.06)	11.07 (0.22)	0.38 (0.06)	0.00 (0.00)	0.34 (0.05)
	0.55	2.29 (0.08)	0.94 (0.06)	1.12 (0.07)	9.14 (0.27)	0.76 (0.09)	0.04 (0.02)	0.94 (0.07)
	0.35	1.46 (0.11)	0.53 (0.06)	0.63 (0.07)	9.70 (0.35)	2.34 (0.19)	0.06 (0.02)	1.05 (0.09)

In Figure 2, we plot the estimated functions given by SS-ANOVA and 2LAND for one typical realization of Example 2. Again, with the feature of automatic selection, 2LAND delivers overall better estimation than SS-ANOVA. In the last panel, the SS-ANOVA provides a nonzero fit to a zero component function, while the 2LAND successfully detects the variable as unimportant.

Figure 2.

True and estimated function components for Example 1: True function (solid line), SS-ANOVA estimator (dashed line), and 2LAND estimator (dotted line). The online version of this figure is in color.

In Table 4, we report the structure selection performance of the LAND under different settings. Similarly to Example 1, we observe that the LAND overall gives effective performance in all the settings. When the signal is moderately strong, the LAND procedure is able to identify the correct model with a high frequency and the incorrectly selected terms are close to zero. When the signal becomes quite weak, the LAND performance gets worse but is still reasonable.

6.3 Real Example

We apply the LAND to analyze the Boston housing data, which are available at the UCI Data Repository and can be loaded in R. The data are for 506 census tracts of Boston from the 1970 census, containing twelve continuous covariates and one binary covariate. These covariates are per capita crime rate by town (crime), proportion of residential land zoned for lots over 25,000 sq.ft (zn), proportion of non-retail business acres per town (indus), Charles River dummy variable (chas), nitric oxides concentration (nox), average number of rooms per dwelling (rm), proportion of owner-occupied units built prior to 1940 (age), weighted distances to five Boston employment centers (dis), index of accessibility to radial highways (rad), full-value property-tax rate per USD 10,000 (tax), pupil-teacher ratio by town (ptratio), 1000(B – 0.63)² where B is the proportion of blacks by town (b), and percentage of lower status of the population (lstat). The response variable is the median value of owner-occupied homes in USD 1000’s (medv).

We scale all the covariates to [0, 1] and fit the 2LAND procedure. The parameters are tuned using 5-fold cross-validation. From the thirteen covariates, the 2LAND identifies two linear effects: rad and ptratio, and six nonlinear effects: crime, nox, rm.dis, tax, and lstat. The remaining five covariates: zn, indus, chas, age, b, are removed from the final model as unimportant covariates. For comparison, we also fit the additive model in R with the function gam, which identify four covariates as in-significant at level α = 0.05: zn, chas, age, and b. Figure 3 plots the fitted function components provided by the 2LAND estimator. The first six panels are for nonlinear terms and the last two are for linear terms.

Figure 3.

The selected components and their fits by 2LAND for Boston Housing data.

7. DISCUSSION

Partially linear models are widely used in practice, but none of the existing methods can consistently distinguish linear and nonlinear terms for the models. This work aims to fill this gap with a new regularization framework in the context of smoothing spline ANOVA models. Rates of convergence of the proposed estimator were established. With a proper choice of tuning parameters, we have shown that the proposed estimator is consistent in both structure selection and model estimation. The methods were shown to be effective through numerical examples. An iterative algorithm was proposed for solving the optimization problem. Compared with existing approaches, the LAND procedure is developed in a unified mathematical framework and well-justified in theory.

In this article, we consider classical settings where d is fixed. It would be interesting to extend the LAND to high-dimensional data, with a diverging d or d ≫ n. For ultrahigh-dimensional data, we suggest to combine the LAND procedures with dimension reduction techniques such as Sure Independence Screening (Fan and Jinchi 2008; Fan, Feng, and Song 2011). Alternatively, we can first implement the variable selection procedures for high-dimensional additive models, using SpAM (Ravikumar et al. 2009) or the adaptive group LASSO (Huang, Horowitz, and Wei 2010). These procedures are consistent in variable selection for high-dimensional data, but they cannot distinguish linear and nonlinear terms. After variable screening is performed in the first step, the LAND can be applied to discover the more subtle structure of the reduced model.

Additive models are a rich class of models and provide greater flexibility than linear models. The possible model mis-specification associated with additive models is to overlook the potential interactions between variables. The LAND can be naturally extended to two-way functional SS-ANOVA models and conduct selection for both main effects and interactions. Interestingly, this extension makes it possible to detect subtle structures for interaction terms, such as linear-linear, linear-nonlinear, and nonlinear-nonlinear interactions between two variables.

Supplementary Material

supplementary data. Appendix.

The proof of Theorem 2 is given in Appendix 4, which is provided as online supplementary materials for this article. (Supplement.pdf)

APPENDIXES

Some Notations

Recall that the ANOVA decomposition of any g ∈ is $g(\mathbf{x})=b+{\sum }_{j=1}^d{\beta }_j{k}_1(x_j)+{\sum }_{j=1}^d{g}_{1j}(x_j)$. Then we define h_j(x_j) = β_jk₁(x_j) + g_1j(x_j), $H_0(\mathbf{x})={\sum }_{j=1}^d{\beta }_j{k}_1(x_j),H_1(\mathbf{x})={\sum }_{j=1}^d{g}_{1j}(x_j)$, and $H(\mathbf{x})={\sum }_{j=1}^d{h}_j(x_j)$. The same notational rule also applies to ĝ, g̃, and g₀.

Appendix 1. Important Lemmas: Convergence Rates of g̃

We derive the convergence rate of g̃ in Lemma A.1.

Lemma A.1

Suppose Conditions (C1)–(C3) hold. If we set λ ~ n^−4/5, then the initial solution (3.2) is proved to have the following convergence rates, for any 1 ≤ j ≤ d:

$$\begin{array}{r}{\left|\right|{\stackrel{\sim }{g}}_{1j}-g_{1j}^0\left|\right|}_2=O_P(n^{-1/5}),\\ \left|\right|\stackrel{\sim }{\mathbf{\beta }}-{\mathit{\beta }}_0\left|\right|=O_P(n^{-1/5}),\end{array}$$

where || · || is the Euclidean norm.

Proof

We first prove that ||H̃−H₀||₂ = O_P(n^−2/5). Denote $J_i(H)={\sum }_{j=1}^d{\left|\right|{\mathcal{P}}_{1j}H\left|\right|}_{{\mathcal{H}}_1}^2$. Since H̃ minimizes $H\mapsto {\left|\right|H_0+\epsilon -H\left|\right|}_n^2+\lambda J_i(H)$, we have the following inequality:

$$\begin{array}{l}{\left|\right|\stackrel{\sim }{H}-H_0\left|\right|}_n^2+\lambda J_i(\stackrel{\sim }{H})\le 2{\langle \stackrel{\sim }{H}-H_0,\epsilon \rangle }_n+\lambda J_i(H_0),\\ {\left|\right|\stackrel{\sim }{H}-H_0\left|\right|}_n^2\le 2{\left|\right|\epsilon \left|\right|}_n{\left|\right|\stackrel{\sim }{H}-H_0\left|\right|}_n+\lambda J_i(H_0)\\ \le O_P(1){\left|\right|\stackrel{\sim }{H}-H_0\left|\right|}_n+o_P(1)\end{array}$$ (A.1)

by the Cauchy–Schwarz inequality and the subexponential tail assumption of ε. The above inequality implies that ||H̃−H₀||_n = O_P(1) so that ||H̃||_n = O_P(1). By the Sobolev embedding theorem, we can decompose H(x) as H₀(x) + H₁(x), where ${\sum }_{j=1}^d{\left|\right|g_{1j}\left|\right|}_{\infty }\le J_n(H)$. Similarly, we can write H̃ = H̃₀ + H̃₁, where ${\stackrel{\sim }{H}}_0(\mathbf{x})={\sum }_{j=1}^d{\stackrel{\sim }{\beta }}_j{k}_1(x_j)$ and ||H̃₁||_∞ ≤ J_n(H̃). We shall now show that ||H̃||_∞/(1 + J_n(H̃)) = O_P(1) as follows. First, we have

$$\frac{{\left|\right|{\stackrel{\sim }{H}}_0\left|\right|}_n}{1+J_n(\stackrel{\sim }{H})}\le \frac{{\left|\right|\stackrel{\sim }{H}\left|\right|}_n}{1+J_n(\stackrel{\sim }{H})}+\frac{{\left|\right|{\stackrel{\sim }{H}}_1\left|\right|}_n}{1+J_n(\stackrel{\sim }{H})}=O_P(1).$$ (A.2)

Combining with Condition (C2), (A.2) implies that ||β||/(1+J_n(H̃)) = O_P(1). Since x ∈ [0, 1]^d, ||H̃₀||_∞/(1 + J_n(H̃)) = O_P(1). So we have proved that ||H̃||_∞/(1 + J_n(H∞)) = O_P(1) by the triangular inequality and the Sobolev embedding theorem. Thus, according to Birman and Solomjak (1967), we know the entropy number for the below constructed class of functions:

$$H\left(\delta ,\{\frac{H-H_0}{1+J_n(H)}:\frac{{\left|\right|H\left|\right|}_{\infty }}{1+J_n(H)}\le C\},{\left|\right|·\left|\right|}_{\infty }\right)\le M_1{\delta }^{-1/2},$$

where M₁ is some positive constant. Based on theorem 2.2 in the article by Mammen and van de Geer (1997) about the continuity modulus of the empirical processes { ${\sum }_{i=1}^n{\epsilon }_i(H-H_0)({\mathbf{x}}_i)$} indexed by H and (A.1), we can establish the following set of inequalities:

$$\lambda J_i(\stackrel{\sim }{H})\le [{\left|\right|\stackrel{\sim }{H}-H_0\left|\right|}_n^{3/4}{(1+J_n(\stackrel{\sim }{H}))}^{1/4}\vee (1+J_n(\stackrel{\sim }{H}))n^{-3/10}]\times O_P(n^{-1/2})+\lambda J_i(H_0),$$

and

$${\left|\right|\stackrel{\sim }{H}-H_0\left|\right|}_n^2\le [{\left|\right|\stackrel{\sim }{H}-H_0\left|\right|}_n^{3/4}{(1+J_n(\stackrel{\sim }{H}))}^{1/4}\vee (1+J_n(\stackrel{\sim }{H}))n^{-3/10}]\times O_P(n^{-1/2})+\lambda J_i(H_0).$$

Considering $J_n^2/d\le J_i\le J_n^2$, we can solve the above two inequalities to obtain ||H̃−H₀||_n = O_P(n^−2/5) and J_i(H̃) = O_P(1) given λ ~ n^4/5. Theorem 2.3 in the article by Mammen and van de Geer (1997) further implies that

$${\left|\right|\stackrel{\sim }{H}-H_0\left|\right|}_2=O_P(n^{-2/5}).$$ (A.3)

Recall that $\stackrel{\sim }{H}(\mathbf{x})={\sum }_{j=1}^d{\stackrel{\sim }{h}}_j(x_j)={\sum }_{j=1}^d{\stackrel{\sim }{\beta }}_j{k}_1(x_j)+{\stackrel{\sim }{g}}_{1j}(x_j)$ and ( $g_{1j}^0(·)$) is the true value of (β, g_1j(·)). We next prove ||β̂ − β₀|| = O_P(n^−1/5) and ${\left|\right|{\stackrel{\sim }{g}}_{1j}-g_{1j}^0\left|\right|}_2=O_P(n^{-1/5})$ for any j = 1, …, d based on (A.3). We first take a differentiation approach to get the convergence rate for β̃_j. Since the density for X is bounded away from zero and ${\int }_0^1{h}_j(u)du=0$, (A.3) implies

$$\underset{1\le j\le d}{max}{\int }_0^1{({\stackrel{\sim }{h}}_j(u)-h_j^0(u))}^{2}du=O_P(n^{-4/5}).$$ (A.4)

Agmon (1965) showed that there exists a constant C > 0 such that for all 0 ≤ k ≤ 2, 0 < ρ < 1 and for all functions γ: ℝ ↦ ℝ:

$${\int }_0^1{({\gamma }^{(k)}(x))}^{2}dx\le C{\rho }^{-2k}{\int }_0^1({\gamma }^2(x)dx+C^{4-2k}{\int }_0^1{({\gamma }^{(2)}(x))}^{2}dx.$$ (A.5)

Having proved that J_i(H̃) = O_P(1), we can apply the above interpolation inequality (A.5) to (A.4) with k = 1, ρ = λ^1/4, and $\gamma (x)={\stackrel{\sim }{h}}_j(x)-h_j^0(x)$. Thus we conclude that

$$\underset{1\le j\le d}{max}\int {((\partial /\partial u){\stackrel{\sim }{h}}_j(u)-(\partial /\partial u)h_j^0(u))}^{2}du=O_P(n^{-2/5}).$$ (A.6)

Note that we can write (∂/∂u)h̃_j(u) = β̃_j + (∂/∂u)g̃_1j(u) and $(\partial /\partial u)h_j^0(u)={\beta }_j^0+(\partial /\partial u)g_{1j}^0(u)$, respectively. Thus (A.6) becomes

$$\begin{array}{l}{O}_P(n^{-2/5})={({\stackrel{\sim }{\beta }}_j-{\beta }_j^0)}^2+2({\stackrel{\sim }{\beta }}_j-{\beta }_j^0){\int }_0^1\left(\frac{\partial }{\partial u}{\stackrel{\sim }{g}}_{1j}(u)-\frac{\partial }{\partial u}{g}_{1j}^0(u)\right)du+{\int }_0^1{\left(\frac{\partial }{\partial u}{\stackrel{\sim }{g}}_{1j}(u)-\frac{\partial }{\partial u}{g}_{1j}^0(u)\right)}^{2}du\\ ={({\stackrel{\sim }{\beta }}_j-{\beta }_j^0)}^2+{\int }_0^1{\left(\frac{\partial }{\partial u}{\stackrel{\sim }{g}}_{1j}(u)-\frac{\partial }{\partial u}{g}_{1j}^0(u)\right)}^{2}du\end{array}$$ (A.7)

for any 1 ≤ j ≤ d, where the second equality follows from the definition of in RKHS. Obviously, (A.7) implies that ${\stackrel{\sim }{\beta }}_j-{\beta }_j^0=O_P(n^{-1/5})$.

We next prove the convergence rate for g̃_1j by decomposing the function g_j(x_j) in another form; see example 9.3.2 in the book by van de Geer (2000). We can write g_j(x_j) = (b/d) + β_j(x_j − 1/2) + g_1j(x_j) = g_0j(x_j) + g_1j(x_j), where $g_{1j}(x_j)={\int }_0^1{g}_j^{(2)}(u){\psi }_u(x_j)du$ and ψ_u(x_j) = (x_j − ψ_u)1{u ≤ x_j}. Let ${\overline{\psi }}_u(x_j)={\alpha }_{0,u}^j+{\alpha }_{1,u}^j{x}_j$ be the projection in terms of empirical L₂-norm of ψ_u(x_j) on the linear space spanned by {1, x_j}. Let ψ̃_u(x_j) = ψ_u(x_j) − ψ̄_u(x_j). Then, we can further decompose

$$\begin{array}{l}{g}_j(x_j)=[(b/d)+{\beta }_j(x_j-1/2)]+\left[{\int }_0^1{g}_j^{(2)}(u){\alpha }_{0,u}^{j}du+x_j+{\int }_0^1{g}_j^{(2)}(u){\alpha }_{1,u}^{j}du\right]+{\int }_0^1{g}_j^{(2)}(u){\stackrel{\sim }{\psi }}_u(x_j)du\\ =g_{0j}(x_j)+g_{1j,\text{l}}(x_j)+g_{0j,\text{nl}}(x_j),\end{array}$$

where g_1j,l and g_1j,nl are the (orthogonal) linear and nonlinear components of g_1j, respectively. We define (g̃_0j, g̃_1j,l, g̃_1j,nl) and ( $g_{0j}^0,g_{1j,\text{l}}^0,g_{1j,\text{nl}}^0$) as the initial estimators and true values of (g_0j, g_1j,l, g_1j,nl), respectively. By corollary 10.4 in the work by van de Geer (2000), we have

$$\begin{array}{c}{\left|\right|{\stackrel{\sim }{g}}_{0j}+{\stackrel{\sim }{g}}_{1j,\text{l}}-g_{0j}^0-g_{1j,\text{l}}^0\left|\right|}_n=O_P(n^{-1/2})\text{and}\\ {\left|\right|{\stackrel{\sim }{g}}_{1j,\text{nl}}-g_{1j,\text{nl}}^0\left|\right|}_n=O_P(n^{-2/5}).\end{array}$$

By the triangle inequality and the result obtained previously, that is, ${\stackrel{\sim }{\beta }}_j-{\beta }_j^0=O_P(n^{-1/5})$, we have ${\left|\right|{\stackrel{\sim }{g}}_{1j,\text{l}}-g_{1j,\text{l}}^0\left|\right|}_n=O_P(n^{-1/5})$. Then combining the fact that g_1j = g_1j,l + g_1j,nl, we have shown ${\left|\right|{\stackrel{\sim }{g}}_{1j}-g_{1j}^0\left|\right|}_n=O_P(n^{-1/5})$ by applying the triangle inequality again. We further obtain the L₂-rate for g̃_1j, that is, ${\left|\right|{\stackrel{\sim }{g}}_{1j}-g_{1j}^0\left|\right|}_2=O_P(n^{-1/5})$, by applying theorem 2.3 from the book by Mammen and van de Geer (1997). This completes the whole proof.

Appendix 2. Proof of Theorem 1

Denote $J_l^w(H)={\sum }_{j=1}^d{\omega }_{0j}\mid {\beta }_j\mid$ and $J_n^w(H)={\sum }_{j=1}^d{\omega }_{1j}{\left|\right|{\mathcal{P}}_{1j}H\left|\right|}_{{\mathcal{H}}_1}$. We first rewrite (2.6) as

$$\frac{1}{n}\sum _{i=1}^n{(b_0+H_0({\mathbf{x}}_i)+{\epsilon }_i-b-H({\mathbf{x}}_i))}^2+{\lambda }_1{J}_l^w(H)+{\lambda }_2{J}_n^w(H).$$

Since we assume that $\sum _{i=1}^n{h}_j(x_{ij})=0$, the terms involving b in the above equation are ${(b_0-b)}^2+2(b_0-b){\sum }_{i=1}^n{\epsilon }_i/n$. Therefore, we obtain that $\widehat{b}=b_0+{\sum }_{i=1}^n{\epsilon }_i/n$ which implies that

$$\widehat{b}-b_0=O_P(n^{-1/2}).$$ (A.8)

Recall that $J(H)\equiv {\sum }_{j=1}^d\mid {\beta }_j\mid +{\sum }_{j=1}^d{\left|\right|{\mathcal{P}}_{1j}H\left|\right|}_{{\mathcal{H}}_1}$. It remains to prove that ||Ĥ − H₀||_n = O_P(n^−2/5) when J(H₀) > 0 and ||Ĥ − H₀||_n = O_P(n^−1/2) when J(H₀) = 0 as follows.

The definition of Ĥ implies the following inequality:

$$\begin{array}{l}{\left|\right|\widehat{H}-H_0\left|\right|}_n^2+{\lambda }_1{J}_l^w(\widehat{H})+{\lambda }_2{J}_n^w(\widehat{H})\le 2{\langle \epsilon ,\stackrel{\sim }{H}-H_0\rangle }_n+{\lambda }_1{J}_l^w(H_0)+{\lambda }_2{J}_n^w(H_0),\\ {\left|\right|\widehat{H}-H_0\left|\right|}_n^2\le 2{\left|\right|\epsilon \left|\right|}_n{\left|\right|\widehat{H}-H_0\left|\right|}_n+{\lambda }_1{J}_l^w(H_0)+{\lambda }_2{J}_n^w(H_0)\\ \le O_P(1){\left|\right|\widehat{H}-H_0\left|\right|}_n+o_P(1),\end{array}$$ (A.9)

where the second inequality follows from the Cauchy–Schwarz inequality, and the third one follows from the subexponential tail of ε. Hence, we can prove ||Ĥ − H₀||_n = O_P(1) so that ||Ĥ||_n = O_P(1). Now we consider two different cases that J(H₀) > 0 and J(H₀) = 0.

Case I

J(H₀) > 0.

We first prove

$$\frac{{\left|\right|\widehat{H}\left|\right|}_{\infty }}{J(H_0)+J(\widehat{H})}=O_P(1)$$ (A.10)

by the Sobolev embedding theorem. The Sobolev embedding theorem implies that ||g_1j(x_j)||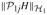_∞ ≤ , and thus we can establish that

$$\begin{array}{l}\frac{{\left|\right|{\widehat{H}}_0\left|\right|}_n}{J(H_0)+J(\widehat{H})}\le \frac{{\left|\right|\widehat{H}\left|\right|}_n}{J(H_0)+J(\widehat{H})}+\frac{\left|\right|{\widehat{H}}_1{\left|\right|}_n}{J(H_0)+J(\widehat{H})}\\ \le O_P(1)+\frac{{\sum }_{j=1}^d{\mid {\mathcal{P}}_{1j}\widehat{H}\left|\right|}_{{\mathcal{H}}_1}}{J(H_0)+J(\widehat{H})}\le O_P(1).\end{array}$$

Combining the above result with Condition (C2), we have ||β̂||/(J(H₀) + J(Ĥ)) = O_P(1) which further implies that ||Ĥ₀||_∞/(J(H₀) + J(Ĥ)) = O_P(1) by the assumption that x ∈ [0, 1]^d. Again, by the Sobolev embedding theorem, we have proved (A.10). By theorem 2.4 in the book by van de Geer (2000), we know the bracket-entropy number for the below class of constructed functions is

$$H_B\left(\delta ,\left\{\frac{H-H_0}{J(H_0)+J(H)}:H\equiv \sum _{j=1}^d{h}_j,\text{where}{h}_j\in \mathcal{G}\right\},{\left|\right|·\left|\right|}_{\infty }\right)\le M_2{\delta }^{-1/2},$$

where 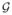= {h_j(x) = (x − 1/2)β_j + g_1j(x): 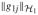< ∞} and M₂ is some positive constant. Based on lemma 8.4 from the work of van de Geer (2000) about the continuity modulus of the empirical processes 〈H − H₀, ε〉_n indexed by H in (A.9), we can establish the following set of inequalities:

$${\left|\right|\widehat{H}-H_0\left|\right|}_n^2+{\lambda }_1{J}_l^w(\widehat{H})+{\lambda }_2{J}_n^w(\widehat{H})\le [{\left|\right|\widehat{H}-H_0\left|\right|}_n^{3/4}{(J(H_0)+J(\widehat{H}))}^{1/4}]O_P(n^{-1/2})+{\lambda }_1{J}_l^w(H_0)+{\lambda }_2{J}_n^w(H_0).$$ (A.11)

Note that the sub-Gaussian tail condition in lemma 8.4 of the book by van de Geer (2000) can be relaxed to the assumed subexponential tail condition; see discussions on page 168 of that book. In the following, we will analyze (A.11) for the cases J(Ĥ) ≤ J(H₀) and J(Ĥ) > J(H₀). If J(Ĥ) ≤ J(H₀), then J(Ĥ) = O_P(1). Thus, (A.11) implies that

$${\left|\right|\widehat{H}-H_0\left|\right|}_n^2\le {\left|\right|\widehat{H}-H_0\left|\right|}_n^{3/4}J{(H_0)}^{1/4}{O}_P(n^{-1/2})+{\lambda }_1{J}_l^w(H_0)+{\lambda }_2{J}_n^w(H_0).$$ (A.12)

Since λ₁, λ₂ ~ n^−4/5, we have ||Ĥ − H₀||_n = O_P(n^−2/5) based on (A.12). We next consider the case that J(Ĥ) > J(H₀) > 0. In this case, (A.11) becomes

$${\left|\right|\widehat{H}-H_0\left|\right|}_n^2+{\lambda }_1{J}_l^w(\widehat{H})+{\lambda }_2{J}_n^w(\widehat{H})\le {\left|\right|\widehat{H}-H_0\left|\right|}_n^{3/4}J{(\widehat{H})}^{1/4}{O}_P(n^{-1/2})+{\lambda }_1{J}_l^w(H_0)+{\lambda }_2{J}_n^w(H_0),$$

which implies either

$${\left|\right|\widehat{H}-H_0\left|\right|}_n^2+{\lambda }_1{J}_l^w(\widehat{H})+{\lambda }_2{J}_n^w(\widehat{H})\le {\left|\right|\widehat{H}-H_0\left|\right|}_n^{3/4}J{(\widehat{H})}^{1/4}{O}_P(n^{-1/2})$$ (A.13)

or

$${\left|\right|\widehat{H}-H_0\left|\right|}_n^2+{\lambda }_1{J}_l^w(\widehat{H})+{\lambda }_2{J}_n^w(\widehat{H})\le {\lambda }_1{J}_l^w(H_0)+{\lambda }_2{J}_n^w(H_0).$$ (A.14)

Note that

$$\begin{array}{l}{\lambda }_1{J}_l^w(\widehat{H})+{\lambda }_2{J}_n^w(\widehat{H})\ge {\lambda }_1{w}_0^{\ast }\sum _{j=1}^d{\left|\right|P_{0j}\widehat{H}\left|\right|}_{{\mathcal{H}}_0}+{\lambda }_2{w}_1^{\ast }\sum _{j=1}^d{\left|\right|P_{1j}\widehat{H}\left|\right|}_{{\mathcal{H}}_1}\\ \ge r_{n}J(\widehat{H}),\end{array}$$ (A.15)

where $r_n={\lambda }_1{w}_0^{\ast }\wedge {\lambda }_2{w}_1^{\ast },w_0^{\ast }=min\{w_{01},\dots ,w_{0d}\}$ and $w_1^{\ast }=min\{w_{11},\dots ,w_{1d}\}$. Thus solving (A.13) gives

$${\left|\right|\widehat{H}-H_0\left|\right|}_n\le r_n^{-1/3}{O}_P(n^{-2/3}),$$ (A.16)

$$J(\widehat{H})\le r_n^{-5/3}{O}_P(n^{-4/3}).$$ (A.17)

Because of the conditions on λ₁, λ₂, w_0j, and w_1j, we know $r_n^{-1}=O_P(n^{4/5})$. Hence (A.16) and (A.17) imply that J(Ĥ) = O_P(1) and ||Ĥ − H₀||_n = O_P(n^−2/5). By similar logic, we can show that (A.14) also implies J(Ĥ) = O_P(1) and ||Ĥ − H₀||_n = O_P(n^−2/5).

So far, we have proved ||Ĥ − H₀||_n = O_P(n^−2/5) and J(Ĥ) = O_P(1) given that J(H₀) > 0. Next we consider the trivial case that J(H₀) = 0.

Case II

J(H₀) = 0.

Based on (2.7) and Lemma A.1, we know that $w_{0j}^{-1}=O_P(n^{-\alpha /5})$ and $w_{1j}^{-1}=O_P(n^{-\gamma /5})$ given that J(H₀) = 0. Thus we have $w_{0j}^{-1},w_{1j}^{-1}=O_P(n^{-3/10})$ based on the assumption that α ≥ 3/2, γ ≥ 3/2. Then we know that $r_n^{-1}=O_P(n^{1/2})$. From (A.16) and (A.17), we can get ||Ĥ − H₀||_n = O_P(n^−1/2) and J(Ĥ) = O_P(n^−1/2) = o_P(1).

Appendix 3. Proof of Lemmas 1 and 2

The proof of Lemma 1 is similar to those of lemmas 1 and 4 in COSSO, and the proof of lemma 2 is similar to that of lemma 2 in the COSSO article.