An Integrative Method for Identifying the Over-Annotated Protein-Coding Genes in Microbial Genomes

Abstract

The falsely annotated protein-coding genes have been deemed one of the major causes accounting for the annotating errors in public databases. Although many filtering approaches have been designed for the over-annotated protein-coding genes, some are questionable due to the resultant increase in false negative. Furthermore, there is no webserver or software specifically devised for the problem of over-annotation. In this study, we propose an integrative algorithm for detecting the over-annotated protein-coding genes in microorganisms. Overall, an average accuracy of 99.94% is achieved over 61 microbial genomes. The extremely high accuracy indicates that the presented algorithm is efficient to differentiate the protein-coding genes from the non-coding open reading frames. Abundant analyses show that the predicting results are reliable and the integrative algorithm is robust and convenient. Our analysis also indicates that the over-annotated protein-coding genes can cause the false positive of horizontal gene transfers detection. The webserver of the proposed algorithm can be freely accessible from www.cbi.seu.edu.cn/RPGM.

1. Introduction

Up to now, thousands of microbial genomes have been published in public databases. The explosive growth number of available genomic sequences presents unprecedented opportunities for probing the secret of life and extract biological information on genetics, which is highly dependent on the annotation quality of each genome. In most cases, many people think that gene finding in prokaryotic genomes is relatively easy due to lack of introns, and they usually deem the genes deposited in public databases such as GenBank or EMBL are correctly annotated. However, more and more researches indicate that the issue of gene finding in microbial genomes is far from thoroughly resolved; the annotation quality of microbial genomes has been questioned continuously in the past several years.^1–29 Many studies implied that some annotated protein-coding genes in most completely sequenced microbial genomes do not encode any proteins actually, but random open reading frames (ORFs) occurring by chance.^{1–9,11–26} In current public databases, the careful annotators have marked those questionable ORFs as hypothetical, then which of them encode protein, and which do not? As many users may take it for granted that all the annotated genes are true protein coding, this can easily lead to wrong conclusions. Then the researchers need to be aware of the existing errors in the annotation of even well-studied genomes and consider additional quality control for their results. Although many groups have performed re-annotation on different microbial genomes, some filtering strategies for the over-annotated ORFs seemed to be questionable due to the resultant increase in false negative, and then there is still much room for improvement. Moreover, it is regretful that there is no webserver or software reported for addressing the problem of over-annotated genes in public databases. Then the update speed of current databases based on the one-by-one re-annotating strategy is far from practical applications and the increasing rate of novel sequenced genomes, which will decrease greatly the value of public databases. Therefore, the problem is still open for protein-coding genes identification in microbial genomes.

Recent researches show that development of techniques by combination of multiple programs may produce a higher performance in prediction problems.^30–32 In this paper, we put forward a meta-approach for identifying the falsely annotated protein-coding genes in microbial genomes. The algorithm is evaluated by 61 microbial genomes and an average accuracy of 99.94% is obtained. The extremely high accuracy shows that the integrated method can grasp universal information of protein-coding genes. Subsequent analysis indicates that the predicting results are much reliable. In order to facilitate the potential users, we exploited an interface-friendly webserver aiming to NCBI's RefSeq resources. This platform only needs to input the accession number of the queried microbial genome, and then it is much convenient and easy to operate.

2. Methods

2.1. Numerical descriptors

The walking model method is such a kind of graphical representation that can transform biological sequences into visual patterns based on different encoding strategies. Since the first walking model was proposed by Hamori and Ruskin,³³ many graphical approaches have been reported for DNA sequences, which can provide intuitive pictures or useful insights for helping analysing complicated relations in biological systems.³⁴ The methodology proposed in this work is based on the TN curve and Z curve, from which we derive 75 numerical parameters to exhibit the intrinsic properties of protein-coding genes.

The TN curve is a recently proposed walking model by us, with which one can inspect information of trinucleotides both qualitatively and quantitatively.³⁵ Consideration of trinucleotides instead of individual and dual nucleotides has superior advantages for protein-coding genes. In this paper, we derive 54 parameters based on the encoding strategy of the TN curve to exhibit the specific structures of protein genes numerically, which are briefly introduced below.

(i) According to the encoding strategy of the TN curve, each kind of trinucleotide can be represented by a 2D Cartesian coordinates (x, y). Here, we determine the signs of x and y by the base at the first position ({+, +}→A, {−, +}→G, {−, −}→C, {+, −}→T) and decide the absolute values of x and y by the bases at the second and third positions (1→A, 2→G, 3→C, 4→T), respectively. Taking GCG as an example, the base ‘G’ at the first position denotes that the signs of x and y are negative and positive, respectively; the base ‘C’ at the second position and the base ‘G’ at the third position imply that the absolute values of x and y are 3 and 2, respectively. Therefore, GCG is represented by (−3, 2). In this way, other kinds of trinucleotides can also be denoted numerically. According to the definition, x> 0 or x< 0 mean that the base at the first position is an element of (A, T) or (G, C), which corresponds to week-H bond (A, T)/strong-H bond (G, C) groups, y> 0 or y< 0 mean that the first base is (A, G) or (C, T), which corresponds to purine (A, G)/pyrimidine (C, T) groups. Letting z= x× y, it is noted that when z> 0, x and y are positive or negative simultaneously, the second base must be A or C, which corresponds to the amino group, when z< 0, the sign of x is opposite to y, the first base must be G or T, which corresponds to the keto group. Thus, the 64 kinds of trinucleotides can be classified into two groups in three ways based on x, y and z, respectively. On the other hand, x links the first and second bases of a trinucleotide, and this can be used as an approximate descriptor of dual nucleotide. Similar results can be obtained for y which links the first and third bases of a nucleotide triplet. Then, we can obtain more information from these parameters.³⁵

In a protein-coding sequence, there are three forward and three reverse reading frames, of which usually only one can encode protein sequence. Supposing S= s₁s₂s₃s₄s₅s₆s₇s_8,… _, s_N−5s_N−4s_N−3s_N−2s_N−1s_N is a protein-coding sequence, the three forward frames {s₁s₂s₃, s₄s₅s₆, s₇s₈…}, {s₂s₃s₄, s₅s₆s₇, s₈…} and {s₃s₄s₅, s₆s₇s₈, …} are denoted by +0, +1 and +2, respectively. For frame +0, we can map it into a plot set ϕ(S₊₀) = {ϕ(s₁s₂s₃) ϕ(s₄s₅s₆)_, … _, ϕ(s_ns_n+1s_n+2) …}, where ϕ(s_ns_n+1s_n+2) = (x_n, y_n, z_n), x_n, y_n and z_n are the initial assignment introduced above, n= 1,4,7, …. Letting

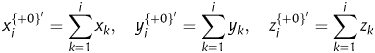to represent the cumulative effects of x_n, y_n and z_n in frame +0, respectively, where i ∈ [1, 2, 3, … , N⁺⁰], N⁺⁰ is the total number of trinucleotides in frame +0. We can transform frame +0 into six sets of 2D curves by {x_i, y_i, z_i, x′, y′, z′} vs. i, respectively. Then, six numerical descriptors corresponding to the six geometric centre of each 2D curve can be derived to describe the corresponding reading frame. In this way, we have a 3 × 6 = 18D vector V₁= [v₁, v₂, v₃, … , v₁₈] as a quantitative descriptor for a complete protein-coding sequence, which corresponds to the geometric centre of each 2D curve of frames +0, +1 and +2, i.e.

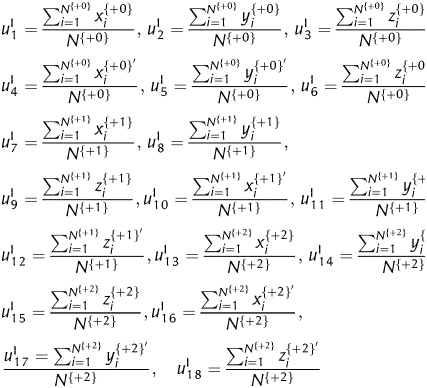Where, N^{+0}, N^{+1} and N^{+2} denotes the total number of trinucleotides in the three forward reading frames, respectively. To differentiate the present encoding strategy from the subsequent encoding strategies, an ‘I’ is marked at the top right corner.

(ii) Following the similar encoding strategy abovementioned, we can also determine the signs of x and y according to the base at the second codon position, and determine the absolute values of x and y by the bases at the first and third positions, respectively. Still taking GCG as an example, the base ‘C’ at the second position implies that the signs of x and y are both negative. The bases ‘G’ at the first and third positions imply that the absolute values of x and y are 2, respectively. Therefore, GCG is numerically represented by (−2, −2). Following the same steps introduced in (i), we can also derive an 18D vector, which corresponds to the geometric centres of the corresponding 2D curves of the three forward reading frames,

 where, l= 19, 20, 21, … , 36, Ω ∈ {x, y, z, x′, y′, z′}, j= +0, +1, +2 represents the three forward reading frames, N^{j} is the total number of trinucleotides in each reading frame.

(iii) In the third encoding strategy, the signs of x and y are determined by the category of the base at the third codon position, while the absolute values of x and y are decided by the bases at the first and second positions, respectively. Therefore, the trinucleotide GCG can be numerically represented by (−2, 3). Following the similar way in (i) and (ii), we have another 18D vector as numerical descriptors, i.e.

 where m= 37, 38, 39, … , 54.

To explain the implications of the derived 54 numerical descriptors, we present three short sequences that have the same trinucleotide compositions but different trinucleotide order as examples in Table 1. In our previous work, we have demonstrated that one can obtain intuitive information of trinucleotides both compositions and distributions based on x_i, y_i, z_i and their derivants x′, y′, z′, respectively.³⁵ As can be seen from Table 1, u₁, u₂ and u₃ have equal values, while the values of u₄, u₅ and u₆ differ greatly. This indicates that u₁, u₂ and u₃ reflect the information of trinucleotide compositions and u₄, u₅ and u₆ are sensitive to the trinucleotides orders along the corresponding sequences. For other numerical descriptors, the same results can also be observed. Then, we can obtain sufficient information from the two groups numerical descriptors u₁, u₂, u₃, u₇, u₈, u₉, … and u₄, u₅, u₆, u₁₀, u₁₁, u₁₂, … . Recently, we have re-annotated the genome of Amsacta moorei entomopoxvirus using an 18D vector according to encoding strategy III.³⁶ In the present work, the number of numerical descriptors is extended to 54. As we discussed above, based on each kind of encoding strategy, the 64 kinds of trinucleotides can be divided into two groups in three ways. That is, we can provide sufficient information with the 54D vector based on the three encoding strategies, which can reveal more universal properties for protein-coding genes than the 18D vector.

Table 1.

Numerical descriptors for two short sequence (a) ATG CAT TTA, (b) CAT ATG TTA and (c) ATG TTA CAT

Numerical descriptors	Encoding strategy I			Numerical descriptors	Encoding strategy II			Numerical descriptors	Encoding strategy III
	Seq. a	Seq. b	Seq. c		Seq. a	Seq. b	Seq. c		Seq. a	Seq. b	Seq. c
u1	7/3	7/3	7/3	u19	8/3	8/3	8/3	u37	2	2	2
u2	−1	−1	−1	u20	1/3	1/3	1/3	u38	7/3	7/3	7/3
u3	8/3	8/3	8/3	u21	2	2	2	u39	3	3	3
u4	14/3	3	19/3	u22	13/3	5	14/3	u40	7/3	11/3	8/3
u5	−1	−3	0	u23	1/3	7/3	4/3	u41	14/3	3	19/3
u6	28/3	8	20/3	u24	14/3	28/3	−2/3	u42	−2/3	−1/3	17/3

The Z curve is another graphical representation proposed for displaying information of individual nucleotides,^37,38 which has been applied to some protein-coding genes re-annotation works.^15,19,21 In this work, the 21 statistical numerical descriptors derived from the Z curve method are adopted to perfect the presented algorithm, which is introduced briefly below, for details refer to the work by Gao and Zhang.³⁹

Supposing a₁, c₁, g₁, t₁; a₂, c₂, g₂, t₂; a₃, c₃, g₃, t₃ denote the occurring frequencies of A, C, G and T at different codon positions 1, 4, 7, …; 2, 5, 8, …; 3, 6, 9, … , respectively, then, a_i, c_i, g_i, t_i (i = 1, 2, 3) can be mapped onto a point P_i in a 3D space, the coordinates of which are calculated by Z-transform

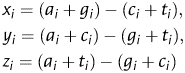Obviously, x_i, y_i and z_i display the statistical features of the base compositions at different codon positions, then nine numerical descriptors can be obtained,

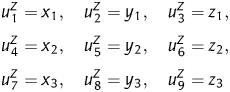In addition to the nine codon position-dependent parameters, 12 phase-specific dinucleotides were also considered. Let the occurring frequencies of the 16 dinucleotides AA, AC, … , and TT be denoted by p(AA), p(AC), … , p(TT), respectively. Using the Z-transform,

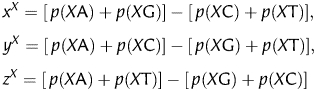where X = A, C, G and T. Then, an additional 12D vector can be obtained, which is written as follows,

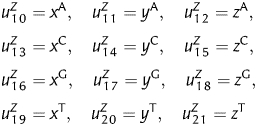Comparing with the 54D vector based on the TN curve, the 21 numerical descriptors provide statistical information of the base compositions at different codon positions and adjacent nucleotides. The critical differences between protein-coding genes and non-coding sequences exist, in that the former has regularly specific features such as asymmetric nucleotide distributions at the three codon positions and codon usage bias, while the latter does not. Then, how to propose sufficient numerical descriptors to exhibit the specific features of protein-coding genes is the core for gene prediction programs. Previous research showed that the first and second bases determine the category of translated amino acid, while the third base is associated with a synonymous codon.^40,41 Because of the uneven distribution of synonymous codons, protein-coding genes are different from non-coding sequences in gene structure, which can be used to find protein-coding sequences.⁴² In this paper, the outlined 75-component vector can be represented by the direct combinations of the subspaces, i.e. VÞ{V^I, V^II, V^III, V^Z}, the former three items reflect the compositions and distributions of trinucleotides along the DNA sequences and the latter item provides statistical significances of protein-coding genes. Therefore, the two groups of parameters can complement each other, which provide sufficient information for protein-coding genes from different angles.

2.2. The Fisher discriminant algorithm

The Fisher discriminant algorithm is a simple method that has been extensively used in gene prediction. For detail introductions, refer to the work by Zhang and Wang.¹³ To accomplish the presented algorithm, two sets of samples are required to train the discriminant coefficients, i.e. positive samples corresponding to true protein-coding genes and negative samples corresponding to non-coding ORFs. For each queried genome, its annotated known functional genes are used as the positive training set and the negative training set is composed of the shuffled complementary sequences of corresponding known functional genes, which has been initially introduced by Guo et al.³² It was found that the 75 parameters are sensitive to the specific gene structures. Then we shuffle the primary sequences only 50 times, hence the runtime can be shorten remarkably. The Fisher linear equation for discriminating the positive and negative samples in the 75D space V represents a super-plane, described by a vector C that has 75 components. To avoid loss of generality, the vector C was determined according to the criterion |C|²= 1. Besides, an appropriate threshold C₀ is obtained by strictly letting the false-negative rate and the false-positive rate to be identical. Once the vector C and the threshold C₀ are determined, each sequence is assigned a T_score= CV− C₀. Then the decision of coding/non-coding for each genes in the test set is simply performed by the criterion of T_score > 0 or T_score < 0, where C= (C₁, C₂, … , C₇₅) and V= (u₁, u₂ … , u₇₅).

2.3. Evaluation index

The accuracy (A_c), sensitivity (s_n) and specificity (s_p) proposed by Burset and Guigo⁴³ are used to evaluate the performance of the presented method

Where, TP and FN denote the number of coding ORFs that have been predicted as coding and non-coding sequences, respectively. Then, s_n is the proportion of the coding ORFs that have been predicted correctly as coding sequences. Similarly, TN and FP denote the number of non-coding sequences that have been predicted as non-coding and coding sequences, respectively. Then, s_p is the proportion of the non-coding sequences that have been correctly predicted as non-coding.

The Matthew's correlation coefficient (MCC) is also used to describe the agreement of predictions and annotation with a single value in the range of [−1, 1], where,

3. Results and discussions

3.1. Performance of the presented algorithm

According to the annotation files, the protein-coding genes in public databases can be classified into two groups, i.e. the genes with known function and those marked with different prefixes, such as ‘putative’, ‘probable’, ‘possible’, ‘possibly’, ‘similar’, ‘alternate’, ‘uncharacterized’, ‘unknown’, ‘predicted’, ‘conserved hypothetical’ and ‘hypothetical’ genes. In this study, we divide all the annotated protein-coding genes into four classes. The first class includes the known functional genes, while those marked ‘conserved hypothetical’ and ‘hypothetical’ genes are assigned to the third and fourth classes, respectively, the rest marked ‘putative’, ‘probable’, ‘possible’, ‘possibly’, ‘similar’, ‘alternate’, ‘uncharacterized’, ‘unknown’, and ‘predicted’ belong to the second class. It is noted that the genes in the first class are genuine protein-coding with validated functions, while some ORFs in other classes may be random sequences that are falsely predicted as protein-coding genes. In the presented re-annotating algorithm, the known functional genes in the first class and their corresponding shuffled sequences are used to train the Fisher coefficients and evaluate the predicting performance, this can also regarded as self-test. In addition, the 10-fold cross-validation is also employed to evaluate our algorithm. In the 10-fold cross-validation, the positive and negative samples composed of the known functional genes and their shuffled sequences are randomly divided into three groups averagely, one is used as the training set and the others are used as the testing set. Here, 61 bacterial and archaeal genomes (listed in Supplementary Table S1) are taken as examples to accomplish the algorithm. For convenience, the abbreviation names are used, for example, Candidatus Phytoplasma mali is abbreviated as C. Phytoplasma. The genome size of the 61 species ranges from 412 348 to 7 036 071 bp, and the G + C content ranges from 21 to 72%. In Supplementary Table S2, we present the sensitivity (s_n), specificity (s_p), accuracy (A_c) and the MCC of self-test and the 10-fold cross-validation. Since the proposed algorithm is a supervised learning strategy, which may be impacted by the shuffling negative samples, then the program is performed five times over each genome, and the mean evaluating indices are calculated. Because the threshold C₀ is strictly demined by the false-positive rate equal the false-negative rate, then, for self-test, s_n is identical to s_p, and A_c= s_n = s_p. In addition, some ORFs with lengths that cannot be divided by three integrally are excluded. For comparison, the results by 54- and 21-vectors are also presented in Supplementary Table S2. As can be seen, the overall average accuracies of self-test over the 61 microbial genomes are 99.62, 99.79 and 99.94% for the 54, 21 and 75D vectors, respectively. As for the 10-fold cross-validation, overall average accuracies of 99.55, 99.75 and 99.88% are obtained by 54, 21 and 75D vectors, respectively. The overall average MCCs over the 61 microbial genomes for the self-test are 0.9925, 0.9958 and 0.9989, for the 10-fold cross-validation, 0.9910, 0.9951 and 0.9977 obtained by 54, 21 and 75D vectors, respectively. Although the integrated algorithm achieves an extremely high performance, the parameters also increased. Then the main question remains open—why can this so-called combined methodology achieve such higher accuracy? Can we obtain more information about the specific protein-coding genes, in other words, can the integrated 75D vector grasp the universal features of protein-coding genes different from non-coding? To give explicit answer, we should perform sufficient analysis in the following sections.

3.2. Correlation between the G + C content and the Fisher coefficients

The ratio of G + C to the total bases appears to be constant in particular microbial genomes, but varies between species, which is found somehow related to phylogeny, as well as the genomic components, such as protein-coding genes, stable RNA genes and spacers including various signals.⁴⁴ Muto and Osawa's⁴⁵ researches indicated that the G + C content of each kind of genomic component positively but differentially correlate to the genomic G + C content for a given bacterium. When the genetic code was deciphered in the early 1960s, it was observed to be universal for most organisms, whereas there are no universal gene-finding parameters suitable for any organism, which can be reflected that the 61 sets of Fisher coefficients are dissimilar from each other. The 75 numerical descriptors in our algorithm are proposed to demonstrate the general features of protein-coding genes, and then it is interesting to explore the correlation between the genomic G + C content and the trained Fisher coefficients among different genomes.

To accomplish the analysis, the following steps are proposed. (i) Six species with different G + C contents, Buchnera (26%), Streptococcus uberis (36%), Yersinia pestis (47%), Brucella melitensis (57%), Pseudomonas aeruginosa (66%) and Clavibacter michiganensis (72%) are selected discretionarily. (ii) Based on the six genomes, six sets of the Fisher coefficients are obtained, each of which is trained by its known functional genes. (iii) Each set of the Fisher coefficients is singled out in turn to identify the known functional genes in other genomes. For convenience, we list the discriminating results in Table 2.

Table 2.

Accuracies of mutual validations for the genomes with different G + C content based on the 75D vector

Species	Buchnera (%)	S. uberis (%)	Y. pestis (%)	B. melitensis (%)	P. aeruginosa (%)	C. michiganensis (%)
Buchnera	100	88.79	50.25	9.01	0.97	0
S. uberis	99.79	99.87	87.11	60.66	12.84	2.15
Y. pestis	99.38	99.53	99.85	99.47	99.32	96.97
B. melitensis	91.99	96.86	96.59	100	99.46	99.24
P. aeruginosa	98.36	99.13	99.75	100	99.78	100
C. michiganensis	2.67	13.35	70.06	99.34	99.18	100

As can be seen from Table 2, 88.79% known functional genes of S. uberis genome can be correctly identified using the Fisher coefficients and threshold trained in Buchnera. With the increase in the G + C content, the discriminating accuracy obtained by the Fisher coefficients of Buchnera drops quickly. Observing the results obtained by the Fisher coefficients of C. michiganensis, it was found that 99.18% known functional genes of P. aeruginosa are correctly identified, with the decrease in the G + C content, the accuracy drops to an extremely low level (2.67% for Buchnera). As for the results obtained by S. uberis, it was found that 99.79 and 87.11% known functional genes of Buchnera and Y. pestis can be correctly identified, respectively, but the accuracy for genomes with significantly different G + C content is much lower. The similar phenomenon that high accuracies can be achieved among genomes with similar G + C contents can be observed in other species. To give an exhaustive interpretation, we also perform the similar steps based on the 54 and 21D vectors (Supplementary Tables S3 and S4), respectively. Meaningfully, the similar phenomenon to the above analysis can be found in both tables. In some sense, the genomic G + C content can reflect the phylogenetic relationship among bacteria and archaea,^45,46 and it was suggested that the divergence of genomic G + C content of various bacterial species in one genus is <10%.¹⁹ Therefore, we infer that genomes with similar G + C content may share similar gene-finding parameters.

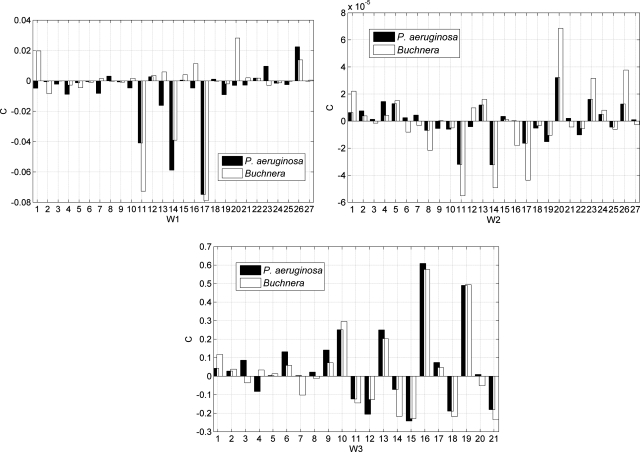
Among the six researched genomes, Y. pestis has a medium G + C content. Using the Fisher coefficients and threshold of Y. pestis, over 97% known functional genes of the other five genomes can be correctly identified. The similar results can also be observed in Supplementary Tables S3 and S4, which imply that the Fisher coefficients and thresholds trained by genomes with medium G + C content (∼50%) are much universal, this is consistent with previous works by Chen et al.¹⁹ In Table 2, the results obtained by P. aeruginosa are much conspicuous, for this genome has a high G + C content of 66%. As can be seen, much high accuracies over the other five tested genomes are achieved (≥98%) by this genome. By contrast, the results listed in Supplementary Tables S3 and S4 for P. aeruginosa is found to be much different in some cases. In Supplementary Table S3, only 21.36% known functional genes of Buchnera are correctly predicted by the coefficients of P. aeruginosa, while in Supplementary Table S4, the accuracy is 95.69%. Similarly, the accuracy on S. uberis based on the 54D vector is also lower than that of 21D vector. Then, we divide the 75 trained Fisher coefficients into three subcomponents, i.e. W₁= [C₁–C₃, C₇–C₉, C₁₃–C₁₅, C₁₉–C₂₁, C₂₅–C₂₇, C₃₁–C₃₃, C₃₇–C₃₉, C₄₃–C₄₅, C₄₉–C₅₁], W₂= [C₄–C₆, C₁₀–C₁₂, C₁₆–C₁₈, C₂₂–C₂₄, C₂₈–C₃₀, C₃₄–C₃₆, C₄₀–C₄₂, C₄₆–C₄₈, C₅₂–C₅₄], W₃= [C₅₅–C₇₅]. According to the definitions, W₁ and W₂ correspond to information of trinucleotides and their corresponding cumulative effects, and W₃ represents the information of base compositions and dinucleotides, respectively. For comparison, the three subcomponents for P. aeruginosa and Buchnera are intuitively plotted in Fig. 1. Observing the distribution of W₃, it seems that P. aeruginosa and Buchnera have similar patterns in the regions of 10–21, while in the regions of 1–9, the patterns of the two genomes seem to be much different. W₃ represents the Fisher coefficients that corresponding to the 21 statistical parameters, which reflect the statistical properties of base distributions in the three codon positions and phase-specific dinucleotides. The G + C content of P. aeruginosa is much different from that of Buchnera, which can account for the differences in regions 1–9 that correspond to base distributions at the three codon positions. While in regions 10–21, the similar tendency imply that there are some universal properties on the phase-specific dinucleotides in P. aeruginosa genome that accounts for the high accuracy on other genomes as shown in Supplementary Table S4, which needs further experimental validations. W₁ and W₂ represent the Fisher coefficients corresponding to the 54D vector that derived from the trinucleotide-based walking model, which reflects the distribution and compositions of trinucleotides along the DNA sequences. It was found that codon usages in protein-coding genes are highly dependent on the G + C content, then the remarkable differences in the G + C content between P. aeruginosa and Buchnera cause the low accuracy in Supplementary Table S3. From the bar graphs in Fig. 1, the accordant patterns of W₁ and W₂ can be observed, for both exhibit much different tendency between the two species. Then, the results of Fig. 1 indicate that the 75 integrative parameters in the presented re-annotating algorithm can demonstrate more underlying information of protein-coding genes.

Figure 1.

Comparing the Fisher coefficients (C) between P. aeruginosa and Buchnera.

3.3. Correlation between the genome size and the Fisher coefficients

Although it has been validated that the Fisher coefficients is much universal for genomes with medium G + C content, the high accuracy obtained by P. aeruginosa presented in Table 2 seems to be much unexpected, for its G + C content is up to 66%. On the other hand, the genome size of P. aeruginosa is 6 588 339 bp with 6286 annotated protein-coding genes. Then, another issue is questioned that whether the high accuracy is caused by its huge genomic contents. To explore the correlation between the genome size and the trained Fisher coefficients, four additional species with different genome size, Stenotrophomonas maltophilia (4 851 126 bp), Burkholderia cenocepacia (875 977 bp), Deinococcus radiodurans c2 (412 348 bp) and D. radiodurans c1 (2 648 638 bp) are selected, which have similar G + C content (66%) with P. aeruginosa (Supplementary Table S1). Whereupon we use the Fisher coefficients and threshold trained by P. aeruginosa, S. maltophilia, B. cenocepacia, D. radiodurans c2 and D. radiodurans c1 to identify the protein-coding genes in the genomes with different G + C content, where the other five species listed in Table 2 are employed, respectively. The predicting results are presented in Table 3. Among the four selected species, S. maltophilia has the biggest genome size, but it seems that its Fisher coefficients are not as universal as that of P. aeruginosa. Based on the coefficients and threshold trained by S. maltophilia, 98.99% known functional genes in C. michiganensis are correctly predicted, while the accuracy drops to 0.21% with the decrease in the G + C content. Deinococcus radiodurans c2 is the smaller chromosome of D. radiodurans R1, which has only 368 protein-coding genes, while its performance is comparable with that of P. aeruginosa. As for the other two species, the average accuracy of B. cenocepacia is higher than that of D. radiodurans c1, although the latter has a much bigger genome size.

Table 3.

Predicting results based on genomes with different sizes

Species	Buchnera (%)	S. uberis (%)	Y. pestis (%)	B. melitensis (%)	C. michiganensis (%)
P. aeruginosa	98.36	99.13	99.75	100	100
S. maltophilia	0.21	0.80	41.62	91.91	98.99
B. cenocepacia	71.46	81.58	93.68	99.47	99.12
D. radiodurans c2	98.15	99.53	99.80	100	100
D. radiodurans c1	7.60	71.09	95.64	99.54	99.87

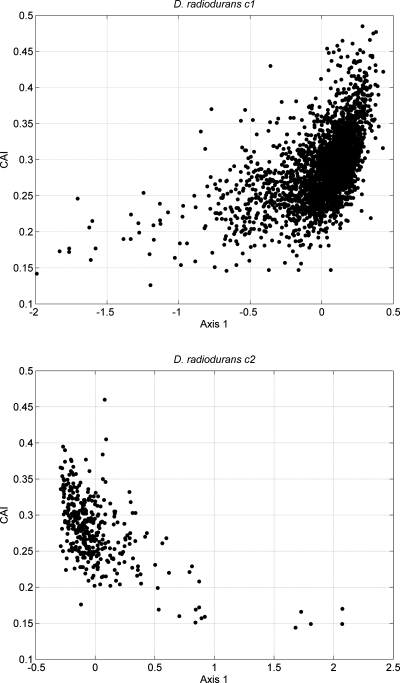
Deinococcus radiodurans c2 and D. radiodurans c1 are the smaller and larger chromosomes of D. radiodurans R1, respectively. In previous works, some authors deemed the bases distribution patterns in different chromosomes for one bacterium to be similar, then they do not have independent origins.¹⁵ While some other works conjectured that the smaller chromosome was originally a megaplasmid captured by an ancestral species.⁴⁷ Both the two chromosomes share similar G + C content. In the larger chromosome, the G + C contents of the annotated protein-coding genes range from 34.1 to 77.1%, with the average of 67.44%, the values of GC3 range from 28.2 to 96.3%, with the average of 83.54%. In the smaller chromosome, the G + C contents of the annotated protein-coding genes range from 37 to 76.1%, with the average of 67.14%, the values of GC3 range from 28.4 to 93.1%, with the average of 82.34%. Nevertheless, from Table 3, we note that there are much differences between the results obtained by D. radiodurans c2 and D. radiodurans c1, which indicates that their Fisher coefficients display discrepant properties. We speculate that the differences can be accounted by their intrinsic genes features. For protein-coding genes, the relative synonymous codon usage (RSCU) is an effective index used to examine synonymous codon usage without the confounding influence of amino acid composition of different gene samples.⁴⁸ Correspondence analysis (COA) can be used to investigate the major trend in codon usage variation among protein-coding genes. After performing COA on the RSCU values of the annotated protein-coding genes, it was found that axes 1 and 2 of COA account for 24.59 and 5.31% for D. radiodurans c2, and those for D. radiodurans c1 account for 15.6 and 5.69%, respectively. The prominent weight of the first principle suggests strong codon bias trend in both chromosomes. To assess the factors that affect the codon usage bias, we plotted axis 1 against their codon adaptation index (CAI) values in Fig. 2. CAI is used to measure the gene expression level,⁴³ highly expressed genes are presumed to have high CAI values. In Fig. 2, the scatter plot for D. radiodurans c1 indicates a significant positive correlation with the position of the genes on axis 1 and their corresponding CAI values (r = 0.5275, P < 0.01). Further analysis suggests that the coordinates of axis 1 also show a significant positive correlation with the GC3 (r = 0.9090, P < 0.01). On the contrary, from the scatter plot of D. radiodurans c2, a significant negative correlation between axis 1 and their CAI values (r = −0.5712, P < 0.01) can be observed. Further analysis shows that axis 1 is also significantly negatively correlate with the GC3 (r = −0.9267, P < 0.01). Furthermore, the CAI value shows positive correlation with GC3 in both D. radiodurans c1 (r = 0.3437, P < 0.01) and D. radiodurans c2 (r = 0.4726, P < 0.01). These results show that gene expression level and base compositions play an important role to shape the codon usage patterns in both chromosomes; the highly expressed genes prefer higher GC content at their synonymous third codon position. However, the opposite trends exhibit different evolutionary pressures on them, which seem to support the speculation that the smaller chromosome was originally a megaplasmid. Therefore, our analysis shows that there is no causality between the genome size and the Fisher coefficients, but the highly universal Fisher coefficients in some species imply that there may be general properties, which is worthy of further researching in the future. On the other hand, the present analysis implies that the integrated 75D vector is sensitive to the specific gene structures, which may provide novel clues for gene-finding algorithms.

Figure 2.

Scatter plot of axis 1 against CAI.

3.4. Why the filtered ORFs do not encode proteins

Using the presented re-annotating algorithm, we re-identified the protein-coding genes in the 61 genomes. For objectivity, the algorithm is performed five times on each genome, those ORFs with T_score <0 occurring equal or more than three times are recognized as non-coding. Consequently, an average of 99.94% over the 61 microbial genomes is achieved (Supplementary Table S2). From the predicting results listed in Supplementary Table S5, we can find that different numbers of ORFs are predicted as non-coding in most species. Taking the genomes of Pyrococcus horikoshii and Caulobacter crescentus as examples, 72 and 76 hypothetical genes are filtered as non-coding, respectively (Supplementary Table S6).

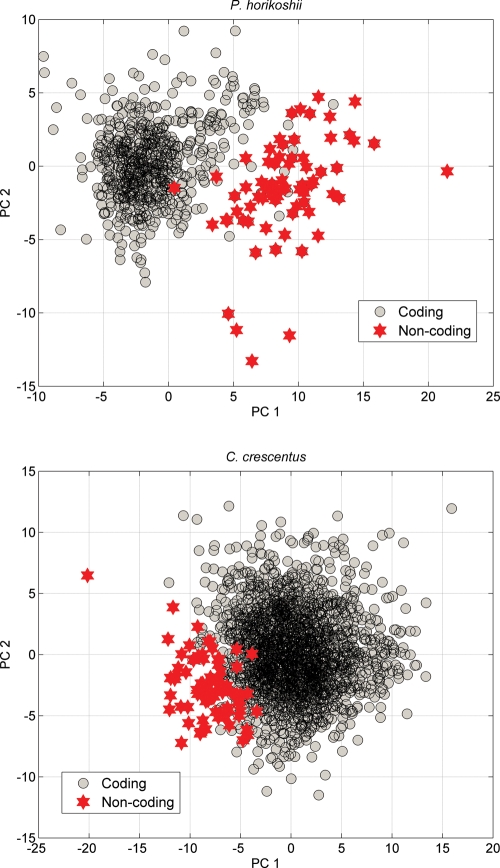
Previous analysis of protein-coding genes showed that there are severe restrictions on bases distributions at different codon positions because they are associated with different biological functions. It was found that the restrictions are universal that the first codon position prefers purine bases.⁴⁹ After calculating the purine–pyrimidine disparities at the first codon position, an average of −0.026 (−2.6%) is obtained for the 71 filtered hypothetical ORFs in P. horikoshii genome, while an average value of 0.3785 (37.85%) is obtained for the protein-coding genes. In C. crescentus genome, an average of 0.0425 (4.25%) for the 76 filtered hypothetical ORFs is obtained, while for those protein-coding genes, an average of 0.2131 (21.31%) is obtained. These results show that purine bases are dominant at the first codon position for the protein-coding genes, while the purine bases are equivalent to the pyrimidine bases for the recognized non-coding ORFs, which indicate that they are likely random sequences that are falsely predicted as protein-coding genes. The differences between coding and non-coding ORFs can also be displayed by the principal component analysis (PCA). PCA defines the correlation among the variables of given data. We have demonstrated that the integrative 75D vector carries sufficient information to exhibit the specific properties of protein-coding genes. After performing PCA, we project the 75 parameters of each ORF into a 2D coordinates by the first two principal components, which is shown in Fig. 3. It can be seen that the filtered non-coding ORFs are clustered far from the core of coding sequences. The different regions reflect that there are intrinsic differences between the recognized ORFs and coding sequences. Then, the results based on PCA also indicate that the filtered ORFs are unlikely to encode proteins.

Figure 3.

Projecting the annotated ORFs into 2D coordinates by PCA.

In the RefSeq database,⁵⁰ clusters of orthologous groups (COG)⁵¹ are used to shape the potential functions of proteins produced by the annotated ORFs. Each COG is a group of three or more proteins that have evolved from a common ancestor. Then, these ORFs assigned with a COG are highly likely to be true protein-coding genes. According to the annotation file of P. horikoshii, 98.69% (678 out of 687) known functional genes and 94.87% (37 out of 39) putative genes are marked COG, while among the 1229 hypothetical genes, only 740 (56.97%) are marked COG. In the annotation file of C. crescentus, the percentages of the marked COG of known functional genes, putative genes and hypothetical genes are 96.25% (2107 out of 2189), 100% (15 out of 15) and 51.21% (785 out of 1533), respectively. Among the recognized 71 + 76 = 147 non-coding ORFs in genomes of P. horikoshii and C. crescentus, none has been assigned with COG tags. According to the results in Supplementary Table S5, up to 925 hypothetical ORFs are recognized as non-coding, among which only 50 (5.41%) are marked with COG. Some previous works show that a significant fraction of annotated short ORFs may be not true genes, which is one of the major causes that account for the over-annotation of microbial genomes.^3,52 In P. horikoshii genome, the average length of the 71 annotated non-coding sequences is 391 bp, which is much shorter than that of these recognized protein-coding genes (858 bp). The similar result is also obtained in the genome of C. crescentus, in which the average length of the 76 annotated non-coding ORFs is 466 bp, while that of these protein-coding genes is 981 bp. In Table 4, we present the statistical results of the length distributions among all the 925 recognized non-coding ORFs. Then, from the above analysis, sufficient evidences suggest that most of these filtered ORFs are random sequences that are falsely predicted as protein-coding genes.

Table 4.

Distribution of sequence length among the 925 recognized non-coding ORFs

L ≤ 300 bp		300 bp < L < 500 bp		L > 500 bp		Average (bp)
Number	Percentage	Number	Percentage	Number	Percentage
367	39.68	335	36.22	223	24.11	411

3.5. Influence of horizontal gene transfer

Horizontal gene transfer (HGT) is one of the most important driving forces in prokaryotic evolution that can drift among bacteria not only from similar strains, but also from distantly related species.⁵³ In the cases of P. horikoshii and C. crescentus, 9 (PH0055, PH0216.1n, PH0221, PH0428, PH1184, PH1187, PH1741, PH1861, PHs009) and 16 (CC_0370, CC_0605, CC_0853, CC_1246, CC_1274, CC_1712, CC_2413, CC_2699, CC_2731, CC_2732, CC_2737, CC_3515, CC_3516, CC_3517, CC_3520, CC_3548) of the recognized non-coding ORFs listed in Supplementary Table S6 are detected as HGTs by the HGT database,⁵⁴ respectively. The predicting procedure employed in the HGT database is based on the parametric methods, which identify anomalous sequence signatures of all the genes and derived protein sequences for each organism. The parametric approaches are based on the hypothesis that sequence features are similar within a genome but differ significantly between genomes. However, just as the authors of the HGT database have pointed out, these predicting results should be used with caution, for other forces may be responsible for the codon usage or G + C content heterogeneity of a genome. A recent comparison of different HGT prediction programs showed that these sequence composition-based methods could predict very different classes of genes.⁵⁵ In addition, very recently acquired prophage elements tended to have sequence compositions that are more similar to the host genome, not representing amelioration but rather specialization and adaptation to their hosts.⁵⁶ A recent study of large viruses further supported that some genes with atypical sequence composition are not horizontally acquired but are likely related to certain functions and gene features.⁵⁷ This means that there are a considerable number of false negatives and false positives among the detecting results. Although very strict methodology has been outlined to improve the performance, recent researches show that the mean error of these HGT predicting methods is up to 39.96%, even for the most efficient programs.⁵⁸ In most cases, the false positives are attributed to pseudogenes, segments of fossilized DNA, and the compositional asymmetries between genes lying on the leading versus lagging strand, selection for translational efficiency, mutation biases and random drift.⁵⁹ In Section 3.4, we have verified that the filtered ORFs by our re-annotating algorithm are highly likely non-coding sequences that are over-annotated as protein-coding genes. On the other hand, our proposed algorithm is trained by the positive samples composed of those genuine protein-coding genes and the negative samples composed of the shuffled random sequences. Thereupon we infer that the 9 + 16 = 25 ORFs in P. horikoshii and C. crescentus that have been detected as HGTs by the HGT database are not laterally transferred in fact. That is, the falsely predicted protein-coding genes should also be taken into account for the false positives in HGT predictions in future studies.

3.6. Comparing the presented algorithm with other programs

In the past decade, many de novo gene-finding algorithms have been proposed for discriminating the protein-coding genes in prokaryotic genomes. Thereinto, the HMM-based methods such as Glimmer⁶⁰ and GeneMark⁶¹ are two most popular gene-finding programs that have been used in some re-annotating works.^17,25 Our re-annotating algorithm has been shown to enhance the predicting performance extremely. The initial annotations of the 61 genomes listed in Supplementary Table S1 did not use these HMM-based programs. Then it is interesting to compare the presented method with the two prevalent gene-finding programs. Glimmer 3.02 and GeneMark.hmm 2.4 are performed on the 61 species, and the performance is evaluated based on the known functional genes. In Supplementary Table S2, we present the predicting results. As a result, Glimmer 3.02 and GeneMark.hmm 2.4 achieve the average accuracies of 98.89 and 99.14%, respectively. It is noted that no records or appropriate reference species were found for S. maltophilia, Acidovorax citrulli and C. michiganensis genomes when performing the GeneMark.hmm program. Using the models trained by other species to annotate these genomes, the accuracies are much lower (<50% in most cases). By contrast, the presented integrative method achieves an average accuracy of 99.94%, which is ∼1% higher than the two other programs. Analysing the predicting results of Glimmer 3.02 and GeneMark.hmm 2.4, we found that although similar accuracy is obtained, the results differ greatly in most cases. Taking the genome of Escherichia coli CFT073 as an example, Glimmer 3.02, GeneMark.hmm 2.4 and our algorithm miss 21, 20 and 3 items of the 2580 annotated known functional protein-coding genes, respectively. Then highly similar accuracies are obtained by Glimmer 3.02 (99.19%) and GeneMark 2.4 (99.22%). Based on the two programs, 5155 (Glimmer) and 5015 (GeneMark) ORFs are predicted as protein-coding genes in E. coli CFT073 genome, respectively. Among the 5338 potential protein-coding genes annotated in the current RefSeq database, there are 4803 common items identified by Glimmer 3.02 and 4701 common items identified by GeneMark.hmm 2.4, which mean that 535 and 637 ORFs are excluded as non-coding by the two programs, respectively. Besides, there are only 4803 common items observed by Glimmer and GeneMark. These comparisons indicate that there are significant differences among the predicting results by Glimmer and GeneMark.hmm even they share similar accuracy. Then, it is difficult to determine which one is superior to another, and additional bioinformatics analysis is necessary to avoid the increase in both false positives and false negatives when using these programs. Recently, Luo et al.²⁵ excluded 608 annotated protein-coding genes in E. coli CFT073 genome from the RefSeq database. In their work, four gene-finding programs were adopted and the ORFs that are co-predicted less than three were deemed as non-coding. However, according to our analysis, this kind of filtering strategy is not rigorous enough, and some genuine genes can be lost, which results in the increase in false negatives. For comparison, we also re-annotated the protein-coding genes in E. coli CFT073 genome (Supplementary Table S5), and 77 hypothetical genes are recognized as non-coding. We have demonstrated that the presented integrative algorithm is reliable for the problem of over-annotation of protein-coding genes in microbial genomes, then we hope our work can provide an efficient platform for future re-annotation researches.

3.7. Stability of the re-annotating algorithm

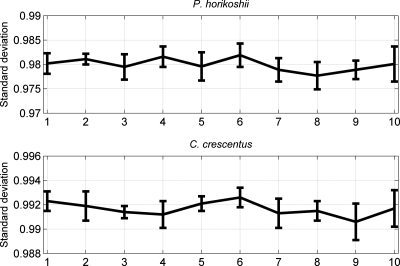
In the presented re-annotating algorithm, the negative samples used as the training set are generated by the randomly shuffled sequences. Then it is necessary to investigate the influence of the shuffled negative samples on the output of the re-annotating program. To accomplish the analysis, the known functional genes of P. horikoshii and C. crescentus genomes are employed following the subsequent steps. First, the re-annotating algorithm is performed on each genome 10 times, which correspond to 10 sets of negative samples. Then, for each genome, 10 vectors composed of the T_scores of these known functional genes are obtained. Finally, the correlations among the 10 vectors are calculated, and a 10 × 10 matrix can be obtained for each genome (Supplementary Tables S7 and S8). In the obtained 10 × 10 matrix, the elements listed in the diagonal equal to 1 (omitted in corresponding tables), which represent the self-correlation of each vector. The underlying assumption is that the more significantly correlated among the 10 vectors, the more stable the re-annnotating program is. The results can also be visualized in Fig. 4, in which we present the standard deviation and the average values of each column. The average correlation coefficients are bigger than 0.97 for both genomes. Then the correlations among the 10 vectors are overall significantly positively correlated (P < 0.01). This can be validated by normalizing the T_score vectors with the following equation, 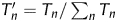, where T_n is the initial T_score of corresponding ORF. For convenience, we present the normalized results in Supplementary Table S9, from which one can find the results by the 10 running times are much consistent with each other. Therefore, our re-annotating algorithm is robust. Even so, the T_score of some individual ORFs may slightly fluctuate in some cases, hence we advise the users to perform the program more than one times (five in the present paper) and determine those ORFs with T_score <0 whose occurring times equal or more than a given threshold (three in the present paper) as non-coding.

Figure 4.

Correlations among the 10 vectors composed of each genome.

3.8. Conclusion

Genome annotation is a multi-level process and annotating errors can emerge at different stages.¹² As have been reported in many works, most of the over-annotated protein-coding genes are generated by the de novo gene-finding programs. However, it is difficult to validate these predicted genes by database searches or ‘wet’ experiments one by one, because the excessive computational and expensive cost. In addition, recent re-annotation works showed that only a limited proportion of hypothetical genes can be validated through database searches method.^24,25 Therefore, the deposit of experimental information cannot meet the update speed of explosively increased number of microbial genomes. In this work, we propose an integrative method for filtering the falsely predicted protein-coding genes in microbial genomes. After testing the re-annotating algorithm on 61 microbial genomes, we demonstrate that the re-annotating algorithm is efficient and robust based on sufficient bioinformatics analysis. Our study indicates that the phenomenon of over-annotated protein-coding genes exists in most microorganisms in different degree. Although many re-annotating works have been conducted on some functional microbial genomes in recent years, our research shows that precise analysis is necessary to avoid increasing the false-negative rate of protein-coding genes.

4. Availability

Based on our integrative re-annotating algorithm, webserver with a user-friendly interface was developed, which can be freely accessible from www.cbi.seu.edu.cn/RPGM. This web-based platform aims to the genomic sources in RefSeq databse, which is easy to operate. For convenience, we introduce the platform as follows.

1. Input

   The users are only required to input the accession number of their queried genome, for example, NC_000919.

2. Options

   The self-test is default in the program. To facilitate the users for evaluating the predicting results, the 10-fold cross-validation is also provided.

3. The Job ID

   When running the program every time, a Job ID will be assigned randomly, with which the users can retrieve the predicting results anytime within 3 days by input of the assigned ID.

4. Output

   In the output interface, the predicting results of the protein-coding genes in the four classes are listed and the trained Fisher coefficients can also be downloaded.

5. TN_curve Num 2.0: a generator for the 75-D vector

   We exploit a software package titled TN_curve Num 2.0 that can generate the 75D vector of a given DNA sequence, with which one can also generate the 75D vector of the corresponding shuffled sequence. TN_curve Num 2.0 can be downloaded from the webserver.

Supplementary data

Supplementary Data are available at www.dnaresearch.oxfordjournals.org.

Funding

This study is supported by National Natural Science Foundation of China (Projects No. 61073141, 30970561), Shandong Natural Science Foundation (Project No. ZR2010CQ041) and the Scientific Research Foundation of Graduate School of Southeast University (Project No. YBJJ1010).