TIP: A probabilistic method for identifying transcription factor target genes from ChIP-seq binding profiles

Abstract

Motivation: ChIP-seq and ChIP-chip experiments have been widely used to identify transcription factor (TF) binding sites and target genes. Conventionally, a fairly ‘simple’ approach is employed for target gene identification e.g. finding genes with binding sites within 2 kb of a transcription start site (TSS). However, this does not take into account the number of sites upstream of the TSS, their exact positioning or the fact that different TFs appear to act at different characteristic distances from the TSS.

Results: Here we propose a probabilistic model called target identification from profiles (TIP) that quantitatively measures the regulatory relationships between TFs and target genes. For each TF, our model builds a characteristic, averaged profile of binding around the TSS and then uses this to weight the sites associated with a given gene, providing a continuous-valued ‘regulatory’ score relating each TF and potential target. Moreover, the score can readily be turned into a ranked list of target genes and an estimate of significance, which is useful for case-dependent downstream analysis.

Conclusion: We show the advantages of TIP by comparing it to the ‘simple’ approach on several representative datasets, using motif occurrence and relationship to knock-out experiments as metrics of validation. Moreover, we show that the probabilistic model is not as sensitive to various experimental parameters (including sequencing depth and peak-calling method) as the simple approach; in fact, the lesser dependence on sequencing depth potentially utilizes the result of a ChIP-seq experiment in a more ‘cost-effective’ manner.

Contact: mark.gerstein@yale.edu

Supplementary Information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

Chromatin immunoprecipitation followed by microarray hybridization (ChIP-chip) and more recently by sequencing (ChIP-seq) have been widely used for genome-wide identification of transcription factor (TF) binding events (Harbison et al., 2004; Johnson et al., 2007; Park, 2009). To facilitate the processing and analysis of the resulting datasets, many methods and software packages have been developed. Most efforts have focused on identifying TF binding peaks that are regions of increased sequence read density or hybridization intensity relative to the background (Kharchenko et al., 2008; Nix et al., 2008; Pepke et al., 2009; Tuteja et al., 2009). In addition, methods have been proposed to combine genomic binding data with other biological information (e.g. histone modification, conservation, etc.) for predicting functional binding sites of TFs (Ernst et al., 2010; Kaplan et al., 2011; Ramsey et al., 2010; Ward and Bussemaker, 2008; Whitington et al., 2009; Won et al., 2010).

The genome-wide TF binding data provide useful biological insights for understanding transcriptional regulation. One of the important applications is to identify the target genes controlled by TFs and dissect the transcriptional regulatory networks underlying the relevant biological process as demonstrated in many studies (Boyer et al., 2005; Chen et al., 2008; Kim et al., 2008; Marson et al., 2008). In these studies, a simple peak-based method has been used to associate TF binding peaks with genes for determining the TF–target regulatory relationships. Specifically, the genes with promoters overlapping with one or more peaks were identified as the targets. This simple peak-based method is easy to implement, but it has several limitations. First, it treats all binding peaks equally without taking into account their relative positions to genes. Second, it does not provide confidence scores of the identified target genes, even though the significance of binding peaks is available. Third, the number of target genes identified is very sensitive to the number of binding peaks and the parameter setting such as the size of the DNA regions considered as promoters. Therefore, a more sophisticated method would be helpful for the utilization of genomic occupation data being produced increasingly.

In this work, we propose a probabilistic model (TIP) for identifying TF target genes based on ChIP-seq or ChIP-chip data (Fig. 1). The model calculates the regulatory potential of a TF to genes based on the TF's binding profile, i.e. its binding signals across the genome. The binding profiles for different TFs can be quite different—most are promoter associated, whereas a few are more distantly enhancer associated. Even for the promoter-associated TFs, their binding peaks can often be differentially distributed in the promoter regions. The probabilistic model we propose here integrates the binding signals within a broad DNA region surrounding a gene's transcription start site (TSS) and takes into account the binding characteristic profile of the TF. We apply the model to several datasets to demonstrate its efficiency, and benchmark it against the simple peak-based method. In particular, we show that it gives rise to a more biologically meaningful target gene set than the peak-based method. The model provides us with a powerful tool for better understanding the transcriptional regulatory relationships based on genome-wide TF binding data.

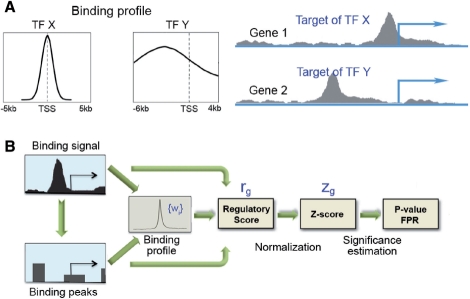
Fig. 1.

Schematic diagram of the probabilistic model for TF target gene identification. (A) Binding profiles for different TFs can be substantially different. If TF X and Y show the same signal pattern around the TSS of genes 1 and 2, gene 1 is more likely to be targeted by X and gene 2 by Y. (B) The regulatory potential of genes can be inferred based on TF binding signal (e.g. WIG file) or binding peaks.

2 METHODS

2.1 A ‘simple method’ for identifying TF target genes

ChIP-seq and ChIP-chip techniques have been widely used to identify the genome-wide localization of TFs. After mapping the sequenced reads to the reference genome (ChIP-seq) or normalizing the raw probe intensities (ChIP-chip), the binding signals of the TF at each nucleotide position of genome can be obtained, represented as continuous data in WIG, BedGraph or other format. Based on these files, a list of significant binding peaks can be identified by using the peak-calling methods (Wilbanks and Facciotti, 2010) such as MACS (Zhang et al., 2008), PeakSeq (Rozowsky et al., 2009), etc. In this section, we define the simple peak-based method for target identification to benchmark against.

With the processed data described above, it is often useful to associate the binding peaks of a TF with genes to identify potential regulatory targets. To do this, a simple method is to identify the genes that contain one or more binding peaks within their promoter region. Specifically, each gene containing the TF's binding peaks in the DNA region from n₁ base pairs upstream to n₂ base pairs downstream of its TSS are reported as the target gene, where n₁ and n₂ are user-specified parameters. In most cases, the numbers of target genes identified by this method are very sensitive to the total number of binding peaks as well as the definition of promoter region specified by n₁ and n₂.

2.2 TIP: a probabilistic model for identifying TF target genes

In this section, we propose a probabilistic model for the identification of TF target genes to overcome the limitations of the simple method. It is known that TF binding sites are not evenly distributed in the genome. As shown in previous studies, the majority of TFs show enriched binding peaks close to the TSS of genes (Birney et al., 2007; Zhang et al., 2007). Therefore, we treat binding peaks at different genomic locations differently, and design a probabilistic model for TF target gene identification that takes into account the total number, the position and the height of binding peaks.

Suppose that we have a set of genes (g) and a set of TFs (t), and given the binding profile of each TF t on each gene g, §(t, g), we want to calculate the posterior probability that each TF t targets each gene g, p(T(t, g) = 1|§(t, g)), where g∈{1,…, N}, t∈{1,…, M}, T is an indicator function, T(t, g)=1 if TF t targets gene g, and 0 otherwise, and N and M are, respectively, the total number of the genes and the TFs in consideration. Under some reasonable and mild assumptions, we can show that,

(1)

where C is a constant, w_i(t) is the prior probability that TF t targets any gene at position i, and s_i(t, g) is the binding signal of TF t at the i-th position of gene g. In simple words, Equation (1) states that, the posterior probability that TF t targets gene g is proportional to the weighted sum of the binding signals of TF t over all the positions on gene g.

Formally, we can briefly derive the above equation as follows:

(2)

(3)

(4)

(5)

(6)

(7)

where C₁ and C₂ are constants, w_i(t, g) is the prior probability that TF t targets position i of gene g, and we assume that all the genes share the same position-specific prior probabilities w_i(t) for each TF t, which is estimated by the proportion of the total amount of reads or peak heights covered at position i over all the genes and will be discussed in details later. In Equations (3) and (4), ~i denotes all the other positions except position i. In Equation (4), we assume that TF t can target any position i of gene g, and the binding signal at position i, s_i(t, g), is only determined by t's targeting at position i regardless of the targeting of t at other positions, and we assume that the data likelihood terms 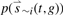for different positions are almost equal to each other in Equation (5). In Equation (6), we assume that the likelihood term p(s_i(t, g)|T_i(t, g)) is a function f of the position−specific binding signal s_i(t, g). In Equation (7), we assume that the function f is a linear function of the position-specific binding signal, and the last equation is used for calculating the regulatory potential score of TF t's targeting gene g.

To adopt a simpler notation, we drop the reference to TF t in the round brackets in subsequent descriptions, because all the calculations are performed independently for different TFs. First, we calculate the binding profile of the TF (the prior probabilities of the TF binding, (w_i) within a DNA region of size n centering at TSS (e.g. n = 10 kb). Second, we assign weight (w_i, the position-specific probability of TF binding) to each nucleotide position in this region based on the binding profile, and calculate the weighted sum of binding signals for genes, denoted as the regulatory scores. Third, we normalize these regulatory scores into z-scores and estimate their significance. Finally, we report a list of ranked target genes at a given significance level as well as the corresponding false positive rate. Note that the TF binding profile or the regulatory scores can be calculated based on binding peaks, or more efficiently, based on the mapped reads (ChIP-seq) or probe intensities (ChIP-chip), as we will elaborate in Sections 2.3 and 2.4.

2.3 Calculation of characteristic TF binding profiles around TSSs

For the ChIP-seq data, the binding profile of a TF surrounding the TSS can be calculated based on either mapped reads or binding peaks. Given a complete list of the mapped reads for a TF t, we calculate for each gene g the read coverage at each nucleotide i within a DNA region centering at the TSS [−n, n] (e.g. n = 10 kb), resulting in a binding signal vector of size 2n + 1, S(g)={s₁(g), s₂(g),…, s_2n+1(g)}. In this step, we extend all reads to their downstream by a number of base pairs (e.g. 200 bp), depending on the average length of DNA fragments in the ChIP-seq experiment. Then the vectors for all genes are averaged at each of the 2n+ 1 nucleotides to obtain the TF's binding profile, represented by the vector (w_i),

Alternatively, the vector (w_i) can also be calculated based on the binding peaks output from a peak-calling method, if the raw data or the mapped reads are not available. In this case, we first remap the peaks onto TSS regions around genes of length n on either side, and then calculate the average peak coverage at each position weighted by the heights of peaks. In general, the binding profiles calculated based on mapped reads and binding peaks are similar in shape.

Using the genomic occupation data obtained from the ChIP-chip experiments, the TF binding profile can be computed in the same way based on binding peaks. To calculate the binding profile based on hybridization intensities of probes, we use the same method as the one for ChIP-seq data, except that read coverage is replaced by probe intensity at each nucleotide position.

2.4 Calculation of the regulatory scores for genes

To calculate the regulatory score of a TF to a gene g mentioned in Section 2.2, we consider the DNA region [−n, n] centered at its TSS and calculate the binding signal at each position i [denoted as s_i(g)]. Given the binding profile (w_i) and the binding signal at each position, we calculate the regulatory score of the TF to the gene g as follows, based on the derived Equation (7) in Section 2.2:

The regulatory score summarizes the binding signals close to the TSS of a gene by weighing them using the characteristic profile of the TF. How the regulatory score is affected by the position and the intensity of binding signals can be found in Supplementary Figure S1. A higher score indicates higher regulatory potential. To normalize, we transform the regulatory scores for genes into z-scores:

where and σ(r) are the mean and the standard deviation of the regulator scores, respectively.

The significance for each gene is estimated based on its z-score, assuming a standard normal distribution. To correct for multiple testing, we calculate the corresponding Q-value (false positive rate) for each P-value using the method proposed in (Storey and Tibshirani, 2003). Alternatively, the false positive rate at a cut-off value z (z is positive) can also be calculated as follows:

The rationale behind this formula is that the distribution of z-scores should skew to the higher values if there exists a set of genuine target genes bound by the TF, whereas low z-scores mainly reflect ‘binding noise’ (Supplementary Fig. S2). Thus, the left side of the distribution for the z-scores can be treated as the null distribution, and the right side is a mixture of true positives and background binding.

The method we describe here can be applied to both the ChIP-seq and the ChIP-chip data. In this article, we use the DNA region [−10, 10] kb around the TSS for defining TF binding profiles (n=10 000) and other calculations. However, our results are very robust to the selection of n, because for most TFs the binding signals are enriched within a relatively narrow region around the TSS.

2.5 Motif analysis in promoter regions of genes

We download the promoter sequences (DNA regions 1 kb upstream to TSS) for all mouse RefSeq genes from the University of California at Santa Cruz (UCSC) Genome Browser at http://genome.ucsc.edu/ (Kent et al., 2002). The position weight matrix for STAT4 is downloaded from the TRANSFAC database (Wingener et al., 1996) at http://www.gene-regulation.com/. We search the promoter sequences for STAT4 binding motif by using the program FIMO in the MEME Suite (Bailey and Elkan, 1994).

All the datasets and gene annotation are based on mm9 (NCBI37) genome assembly for mouse and hg18 (NCBI36) for human. The annotation for human and mouse RefSeq genes is obtained from the UCSC Genome Browser (Kent et al., 2002). All the calculation and analysis are implemented in the R platform and the associated R code is available for download from http://archive.gersteinlab.org/proj/tftarget/.

3 RESULTS

Given the binding peaks of a TF in the genome, the simple method identifies genes with promoter regions overlapping with one or more peaks, and results in a target gene set without providing the confidence of each individual gene. In contrast, the probabilistic model provides a gene list ranked by a confidence score as well as the false positive rate of the list. In addition to the practical convenience, the target genes from the probabilistic model are of higher confidence as it considers more information than the simple method does, e.g. the distance of TF binding signal from the TSS. Although there is no gold-standard target set for a TF (i.e. a complete target gene list), we can use two criteria to compare the performance of the two methods.

First, we would expect that the expression levels of the target genes are more upregulated (or downregulated) when the TF is activated (or repressed) by cytokine or hormone stimulation or as a consequence of TF perturbation [overexpression, knockout (KO) or siRNA interference]. Second, we would expect overrepresentation of the binding motif for a TF in the promoters of its target genes. In this section, we first apply the probabilistic model to two datasets [STAT and estrogen receptor (ER)] containing both TF genomic occupation and gene expression profiles, and show that the target genes identified by the model are more differentially expressed in response to TF perturbation or activation than those identified by the simple method. Then we show the STAT4 binding motifs are more enriched in the target promoters identified by the probabilistic model. Finally, we apply our analysis to the TCF4 binding data containing two ChIP-seq replicates with substantial read depth difference, and show that the probabilistic model is not sensitive to the sequencing depth and it provides a confident target gene set for dataset with fairly low depth. Thus when applied to the ChIP-seq datasets, the probabilistic model provides a cost-efficient tool for identifying target genes (without requiring high read depth).

In our analysis, we utilized the datasets from the original publications, which provide mapped reads (STAT and TCF4) or signal track files (ER), as well as binding peak data. To identify the binding peaks, two-sample analysis from the CisGenome software package (Ji et al., 2008) was used for the STAT (Wei et al., 2010) and the TCF4 data (Mokry et al., 2010), while the sliding window method was used for the ER data (Stender et al., 2010). We apply the simple peak-based method to the binding peaks published with the original papers, assuming optimized parameter setting for peak-calling programs by the authors.

3.1 Reduced expression of STAT4 target genes in STAT4-deficient mice

STAT4 and STAT6 are two key TFs in the differentiation of the helper T cells. Wei et al. (2010) have profiled the genomic occupation of the two factors and have measured gene expression in T helper 1 or T helper 2 (Th2) cells from wild-type (WT) and STAT-deficient mice. We examine the binding preference of STAT4 and STAT6 across the whole genome, concentrating on the DNA regions surrounding the TSS of genes. We find that the ChIP-seq reads are more likely to be mapped to regions nearby TSSs as shown in Figure 2A for STAT4. This binding profile around the TSS enables us to more accurately evaluate the regulatory relationship of STAT4 to individual genes. For instance, if gene A contains a STAT4 binding peaks 100 bp upstream of its TSS and gene B contains a peak 900 bp upstream of its TSS, then it is reasonable to assume that A is more likely to be the regulatory target of STAT4. The probabilistic model is designed to take into account this binding profile information. We apply the model to identify the target genes of STAT4 and STAT6, and for each gene we calculate a regulatory score. We subsequently transform the regulatory scores into z-scores and estimate their P-values and Q-values (see Section 2 for details). In Figure 2B, we sorted genes in the increasing order of their z-scores for STAT4, that is, genes on the left side are more likely to be the regulatory targets of STAT4. Then we examine the differential expression of genes in WT versus STAT4-deficient mice [log2 (WT/KO)]. In principle, the expression of STAT4 target genes would be downregulated as a consequence of the STAT4 KO. As expected, the genes with higher z-scores (potential STAT4 target genes) tend to be more highly expressed in WT than in KO mice (Fig. 2B).

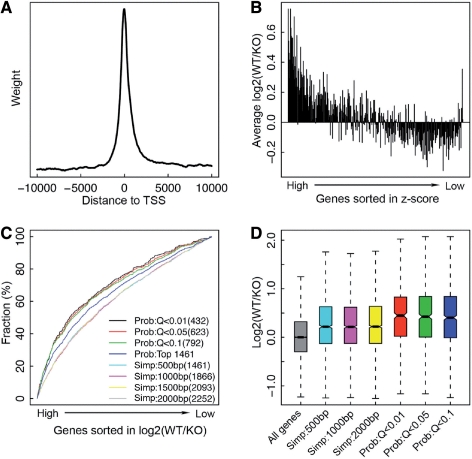
Fig. 2.

Reduced expression of STAT4 target genes in STAT4-deficient mice. (A) The binding profile of STAT4 around the TSS. (B) Reduced expression [high log2 (WT/KO)] of genes with high z-scores in STAT4-deficient mice. Genes are sorted in the decreasing order of z-scores and separated into bins of 50 genes. The average log2 (WT/KO) of the 50 genes in each bin is shown as the y-axis. (C) Cumulative distribution of genes in the gene list sorted by log2 (WT/KO) for target gene sets identified by different methods. (D) Distribution of log2 (WT/KO) for target genes identified by different methods.

Table 1 shows the target gene numbers of STAT4 and STAT6 in four ChIP-seq experiments. Signals from a negative control (using natural rabbit serum as antibody in Th2) have been used for identifying binding peaks. To take into account the non-specific binding in the probabilistic model, we excluded genes that are significant in the control. As shown, compared with the simple model the probabilistic model is more conservative, which gives rise to a relatively smaller target gene set even at a fairly relaxed cut-off value, e.g. at 10% false positive rate (Q < 0.1). The number of target genes identified by the simple method depends on the size of DNA region considered as promoter. Because STAT4 binding peaks tend to be located nearby the TSS of genes, we do not observe dramatic difference in target gene numbers when [−500, 500] and [−2000, 2000] are used as the cut-off. However, for other TFs with broader binding profile around the TSS, the target gene set size might strongly depend on the cut-off value, making it difficult to determine a confident set of target genes.

Table 1.

Number of STAT4 and STAT6 target genes identified by the simple method and the probabilistic model

	Cut-off	STAT4 WT	STAT4 KO	STAT6 WT	STAT6 KOa
Simple	[−500, 500] bp	1692	7	3084	927
method	[−1000, 1000] bp	2195	7	3407	1001
	[−1500, 1500] bp	2461	8	3657	1031
	[−2000, 2000] bp	2651	10	3806	1054
Probabilistic	Q<0.001	312	6	252	193
model	Q<0.01	466	9	400	279
	Q<0.05	661	24	602	367
	Q<0.1	848	45	757	469

Genes significant in the negative control (natural rabbit serum as antibody in Th2) are excluded.

^aOnly the SH2 domain of STAT6 is deleted.

It should be noted that STAT6 KO is not a KO that completely deletes the whole gene. Instead, only the DNA region encoding the SH2 domain of STAT6 protein is deleted. Thus, a large fraction of the STAT6 targets can still be identified in STAT6 KO (Table 1). Even in the clean knockout STAT4 KO, we still detect a few significantly bound genes as shown in Table 1. This is due to the fact that the sequencing signal for STAT4 KO ChIP-seq does not reflect a random background distribution. As shown previously, ChIP-seq using non-specific antibody or input DNA would exhibit enrichments of signal proximal to TSSs in a sample specific manner, leading to ‘artificial’ binding peaks or target genes (Rozowsky et al., 2009).

To evaluate the performance of the probabilistic model and the simple method, we sort genes in the decreasing order of log2 (WT/KO) and examine the distribution of target genes identified by the two methods. If a target gene set more accurately reflects a real regulatory relationship, we would expect a larger fraction of its genes present at the top of the ranked list (highly expressed in WT with respect to KO of STAT4). As shown in Figure 2C, the STAT4 target gene sets obtained from the probabilistic model demonstrate higher expression changes, log2 (WT/KO), than those identified by the simple method (Supplementary Fig. S3A). Moreover, the better performance of the probabilistic model is not due to its relatively smaller target gene set. When we choose the same number of target genes based on the probabilistic model output (top 1461), the probabilistic model still achieves better performance than the simple model (see blue curve in Fig. 2C). We also compared the expression difference of the target genes identified by the two methods in WT versus STAT4-deficient mice (Fig. 2D). As shown, both methods result in gene sets with higher log2 (WT/KO) than the ‘all genes’. In comparison to the simple method, the probabilistic model identifies target genes that show even higher log2 (WT/KO) values (P < 0.001). The reduced expression of STAT4 target genes identified by the probabilistic model in STAT4-deficient mice suggests that these bound targets captured by ChIP-seq reflect the actual regulatory relationships of STAT4 with genes. Similarly, we compared the expression changes of STAT6 targets in WT with respect to KO of STAT6, and achieved very consistent results (Supplementary Fig. S4). As we described, the probabilistic model can also take the binding peak data as input, and we identify target genes of STAT4 and examine their expression changes in WT versus KO of STAT4. These target genes show comparable magnitude of expression changes to those by the simple method but are significantly worse than those by the probabilistic model using the binding signal data (Supplementary Fig. S5). This suggests that improvement of the probabilistic method is mainly contributed by operating on signals instead of binding peaks. As such, if available we would strongly suggest applying the probabilistic model to the binding signal data rather than the binding peaks.

3.2 Induction of ER target genes in response to E2 treatment

Other than the mouse STAT4/6 data, we also performed a similar analysis on the human ER alpha (ERα) data (Stender et al., 2010). The data contain the genome-wide localization of human ERα and its mutant (mutERα) measured by the ChIP-seq experiment in MDA-MB-231 breast cancer cells. The mutERα harbors point mutations in the DNA binding domain that disable its ability to bind to its DNA response element. At the 1% false positive rate (Q < 0.01), the probabilistic model results in 312 target genes for the WT ERα and 41 for the mutant ERα (Supplementary Table S6). The number of target genes identified by the simple method, however, is strongly dependent on the parameter setting. If the DNA region (−500, 500) bp around the TSS is considered as promoter, it results in 349 target genes, whereas 1091 genes are identified when [−2000, 2000] window is used.

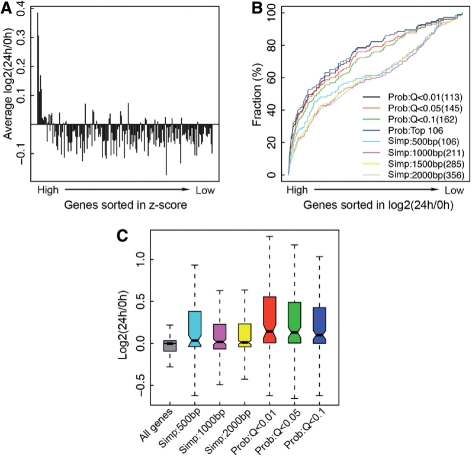
To validate these identified ERα -bound genes by ChIP-seq, Stender et al. (2010) have performed microarray experiments to examine their response to estradiol (E2), the hormone activating ERα. We therefore examined the correlation between ERα regulatory scores of genes and their expression levels. We found that genes with higher ERα regulatory scores are more responsive to E2 stimulation (Fig. 3A). Particularly, the genes with highest scores tend to be upregulated after 24 h treatment with E2. When sorted in the decreasing order of E2 responsiveness [log2 (24 h/0 h)], the target gene sets identified by the probabilistic model are more skewed to the higher responsive side than those gene sets by the simple method (Fig. 3B and Supplementary Fig. S3B), and they are more highly upregulated by E2 treatment (Fig. 3C).

Fig. 3.

Induction of ER α target genes by E2 treatment. (A) Enhanced expression of genes with high z-scores in response to E2 treatment. Genes are sorted and separated into bins as described in Figure 2. (B) Cumulative distribution of genes in the gene list sorted by log2 (24 h/0 h) for target gene sets identified by different methods. (C) Distribution of log2 (24 h/0 h) for target genes identified by different methods.

3.3 Enrichment of TF binding motif in the target promoters

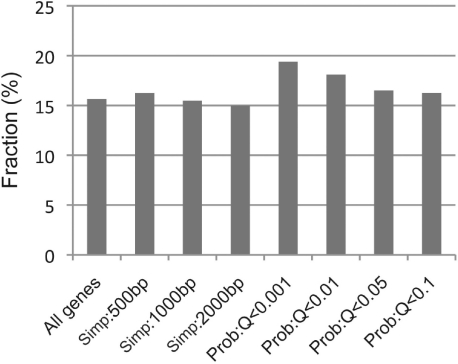
Another way to compare the performance of TF target gene identification methods is motif analysis. If the genomic occupation of a TF is mainly attributed to its direct binding to the DNA binding motif rather than mediated by any other DNA-binding proteins, we would expect to see the enrichment of its binding motifs in target gene promoters. Thus, we search the promoter region (1 kb upstream of TSS) of all mouse genes (23 573) for the occurrence of the STAT4 binding motif and compare the proportion of genes containing STAT4 binding motif from the target sets identified by the probabilistic model and the simple method. Overall, 3689 out of the 23 573 mouse genes (15.6%) contain at least one STAT4 binding motif in its promoter region (Fig. 4). As for the target gene sets identified by the simple method, the fractions of STAT4 motif-containing genes are at best slightly higher than the average. In contrast, the target gene sets identified by the probabilistic model include more STAT4 binding motif-containing genes. For example, the model results in 325 target genes at 0.1% false positive rate (Q < 0.001), of which 19.4% genes contain at least one STAT4 motif in their promoter (P=0.04). Thus, in comparison to the simple method, the probabilistic model identifies a target set of higher confidence.

Fig. 4.

Enrichment of the STAT4 binding motif in the promoter of its target genes. The y-axis indicates the percentage of genes that contain at least one STAT4 binding motif their promoters (DNA region within 1 kb upstream of TSS).

3.4 Consistency of target genes between replicates

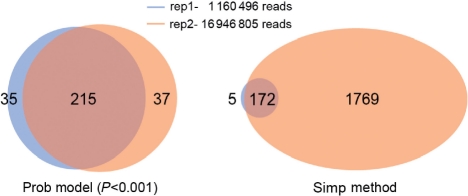
As described in Section 2, the simple method requires a predefined binding peaks from a peak-calling method, whereas the probabilistic model can calculate the regulatory scores of a TF to genes based on either the mapped reads or the binding peaks. In general, the number of binding peaks identified by peak-calling methods depends strongly on the sequencing depth of the ChIP-seq experiment. As a consequence, the target genes identified based on binding peaks is also sensitive to the sequencing depth. In contrast, based on the total mapped reads the probabilistic model results in very consistent target gene sets between replicate experiments with different sequence depths. Figure 5 shows the results for the TCF4 dataset, which contains two technical replicates with 1 160 496 and 16 946 805 mapped reads, respectively (Mokry et al., 2010). Due to a substantial difference in the sequencing depths, the two replicates result in quite different number of binding peaks—1128 for the former and 10 436 for the latter. Based on these binding peaks, the simple method identified 177 and 1941 target genes for the two replicates, respectively, with [−1000, 500] bp around the TSS as the promoter region (Fig. 5, the right panel). Based on the mapped reads, however, the probabilistic model ends up with 250 and 252 target genes for the two replicates at the significance level of 0.001 (P < 0.001). Despite the significant difference of the two replicates in their read depths, the target genes identified from them are highly consistent with 215 overlapping genes (Fig. 5, the left panel). This result is further confirmed by a simulation analysis. We generate 21 simulated sequencing datasets for TCF4 by sampling n reads (n = 5, 6,…, 25 M) from the pooled data of the two replicates (~ 18 M mapped reads). We then apply the probabilistic method to identify significant target genes for each dataset. Meanwhile, we call the peaks in these datasets using PeakSeq (Rozowsky et al., 2009) and subsequently determine the target genes using the simple method. The simulation results indicate that the probabilistic model provides consistent target genes, while the number of peaks called by PeakSeq (increase from 7716 for 5 M to 40 318 for 25 M) and target genes subsequently identified by the simple method (increase from 1458 for 5 M to 7923 for 25 M) are strongly dependent on the read depth (Supplementary Table S7).

Fig. 5.

Consistency of target genes in two experimental replicates of TCF4.

Thus, the probabilistic model based on the mapped reads provides a more cost-efficient tool for identifying the TF target genes. For many ChIP-seq experiments, it might not be necessary to perform such a high sequencing depth, if they are designed to identify target genes instead of specific binding peaks. In fact, with the increase of the read depth, the number of binding peaks from ChIP-seq data will keep growing (as more and more weak binding peaks are identified), while the number of target genes identified by our probabilistic model will not change substantially.

4 DISCUSSION

In this article, we propose a probabilistic model to identify TF target genes based on ChIP-seq or ChIP-chip data. We have shown that target genes identified by this model are more responsive to the stimulation or perturbation of the regulatory TF, and are more likely to contain its binding motif in their promoters, when compared with those identified by the simple method. Our model provides a gene list ranked by the regulatory potential by the TF and gives a confidence score, which allows the user to select a subset of genes for creation of testable hypothesis and further experimental investigation. With ever-increasing genomic occupation data, the model provides a powerful tool for understanding gene regulation.

As shown in Table 1, the genes identified by the model represent a very conservative set of regulatory targets by a TF due to the following reason. Our normalization of the regulatory scores is based on the mean of regulatory scores for all genes, including both targets and non-targets (Section 2.3). In the real data, the distribution of regulatory scores for all genes shows a normal like distribution from non-target genes on the left side and a very thick tail on the right side from target genes (Supplementary Fig. S8). We would expect to obtain more significant target genes, if only the regulatory scores for non-targets (which can be regarded as the background binding) are used for normalization. Obviously, the non-target genes are unknown in advance, but this issue can be circumvented by iteratively estimating significance and selecting non-targets for normalization. Alternatively, one can also normalize the regulatory scores based on the background binding estimated from a number of randomly selected DNA regions. It is also possible to further improve the method by taking into account the existence of TF binding motif, namely, assign higher weight to genes with motifs in DNA regions around their TSS. By combining with additional data such as expression data from TF perturbation experiments, the framework might also be adapted to predict functional binding sites. Although the ChIP-seq and ChIP-chip experiments have detected a large number of binding sites, many of them cannot be clearly connected with target gene regulation (Li et al., 2008; MacArthur et al., 2009). As such, a quantitative method introduced here or previously (Kaplan et al., 2011) would be useful for understanding functional binding.

It is interesting to see that the target genes identified by the probabilistic model are not sensitive to the sequencing depth as we have shown using the TCF4 data. When more reads are sequenced in a ChIP-seq experiment, more binding peaks, mostly weak ones, would be identified. These weak peaks are not quite discriminative from the background noise and their contribution to gene regulation might be limited. In this sense, the target genes identified by the simple method are not reliable, because it is only obvious to identify more targets with the increase in binding peaks. In contrast, the probabilistic model is not sensitive to these weak peaks, although it does result in new targets (when a gene is supported by multiple weak peaks). For many TFs, very high depth sequencing is not required if the cost-effective probabilistic model is used for target gene identification.

The ranked target gene list resulting from the probabilistic model for TFs has many potential applications. One immediate application is to construct the weighted regulatory network. Integrative regulatory networks have been constructed based on the target genes identified from ChIP-seq experiments for many TFs (Chen et al., 2008; Gerstein et al., 2010; Marson et al., 2008). Since the simple method was used for determining target genes, the regulatory relationships in these networks are binary with a high false positive rate. The binary representation of the regulatory relationships is not informative and in many cases does not reflect the nature of transcriptional regulation. The probabilistic model provides a method to construct weighted regulatory networks that reflect different regulatory strengths between TFs and their target genes. For example, we can simply weight the regulatory interactions by their significance estimated by the model. With more and more data coming out from the large-scale projects such as modENCODE (Gerstein et al., 2010; Roy et al., 2010) and ENCODE (Birney et al., 2007), we expect the probabilistic model to be very useful for a better understanding of the gene transcriptional regulation.