QM/MM Studies of Hairpin Ribozyme Self-Cleavage Suggest the Feasibility of Multiple Competing Reaction Mechanisms

Abstract

The hairpin ribozyme is a prominent member of small ribozymes since it does not require metal ions to achieve catalysis. Guanine 8 (G8) and adenine 38 (A38) have been identified as key participants in self-cleavage and -ligation. We have carried out hybrid quantum-mechanical/molecular mechanical (QM/MM) calculations to evaluate the energy along several putative reaction pathways. The error of our DFT description of the QM region was tested and shown to be ~1 kcal/mol. We find that self-cleavage of the hairpin ribozyme may follow several competing microscopic reaction mechanisms, all with calculated activation barriers in good agreement with those from experiment (20-21 kcal/mol). The initial nucleophilic attack of the A-1(2’-OH) group on the scissile phosphate is predicted to be rate-limiting in all these mechanisms. An unprotonated G8^- (together with A38H⁺) yields a feasible activation barrier (20.4 kcal/mol). Proton transfer to a non-bridging phosphate oxygen also leads to feasible reaction pathways. Finally, our calculations consider thio-substitutions of one or both non-bridging oxygens of the scissile phosphate and predict that they have only a negligible effect on the reaction barrier, as observed experimentally.

INTRODUCTION

The hairpin ribozyme is a self-cleaving and –ligating RNA motif found in the minus strand of the satellite RNA associated with the Tobacco ringspot virus, where it promotes double-rolling circle replication.^1-3 The hairpin ribozyme belongs to the class of small endonucleolytic ribozymes, whose members catalyze an internal transesterification reaction.⁴ That S_N2 type reaction starts with the nucleophilic attack of a specific 2’-hydroxyl group on its adjacent scissile phosphate moiety, proceeds through the pentacoordinated phosphorane transition state, and generates products with 2',3'-cyclic phosphate and 5'-hydroxyl termini.⁵ The hairpin ribozyme is a prominent small ribozyme because it achieves a rate acceleration similar to that of the other ribozymes without an obligatory presence of divalent metal ion.^4,6 This lack of a strict metal ion requirement for catalysis makes the hairpin ribozyme especially useful in probing for potential direct roles of nucleobases in RNA catalysis,⁷ where the major challenge is a detailed understanding of the contribution of specific functional groups to the reaction mechanism.⁸

A wide range of biochemical and structural studies has clearly identified guanine 8 (G8) and adenine 38 (A38) as main players in cleavage and ligation. Neither abasic substitution nor deletion of G8 does significantly perturb the ribozyme global structure, but the activity is reduced by three orders of magnitude.^9,10 However, the details of the catalytic mechanism of the hairpin ribozyme are not fully clear, with different pieces of evidence being not always mutually consistent.

In pre-catalytic crystal structures, N1 of G8 donates a hydrogen bond to the reactive 2’-oxygen of A-1, which is, however, catalytically inactivated by a 2’-O-methyl modification. Analogous hydrogen bonds between G8(N1) and the 2’-bridging oxygen were also identified in crystal structures of product and transition state mimics.^11-13 These findings, together with exogenous nucleobase rescue experiments, led to the proposal that G8 electrostatically stabilizes the transition state and/or acts as a general base (being deprotonated as G8^- before the reaction).^8,10,14-16 The former model, where G8 is involved dominantly in electrostatic stabilization of the transition state, was also supported by advanced hybrid semi-empirical/molecular mechanical (SE/MM) molecular simulations by York and coworkers. They showed that G8 could facilitate catalysis through stabilizing both the developing charge on the scissile phosphate and the strained backbone conformations adopted along the reaction pathway and concluded that the electrostatic stabilization might be the major factor in the catalysis.^17,18 As an energetically most favorable reaction profile was identified the mechanism, where the 2’-OH group is deprotonated by the non-bridging oxygen of the scissile phosphate before its nucleophilic attack. This mechanism, however, would likely not lead to any apparent pH dependence of the rate constant, inconsistent with experimental observations.^4,6,19-21 The pH-rate profile instead shows that the reaction rate increases with an apparent pK_a close to that expected from an adenine perturbed (toward more basic) by the nearby negatively charged RNA backbone.^4,6,19-21 This is best explained either by the A38 acting as a general base or by a model wherein the protonated adenine A38H⁺ acts as a general acid in cooperation with a general base of significantly higher pK_a than A38, such as a deprotonated G8^-. Thus, mechanisms involving proton transfer from the 2’-OH to one of the non-bridging oxygens together with electrostatic stabilization of the transition state by G8 alone are unlikely the main catalytic strategy of the hairpin ribozyme, although they still may contribute to cleavage, assuming that the observed pH dependence is due to an accompanying or competing catalytic strategy.

Classical molecular dynamics (MD) simulations with a canonical G8 show that the crystallographically observed hydrogen bond from G8(N1) to the 2’-oxygen of A-1 is readily lost when the inactivating 2’-O-methyl group is replaced with the native 2’-OH group, which leads to repuckering of the A-1 ribose ring.^22-24 Subsequently, G8(N1) establishes a new contact with the pro-S_P non-bridging oxygen of the scissile phosphate, thus forming a direct base-phosphate (BPh) interaction fluctuating between types 4BPh and 5BPh.²⁵ In contrast, simulations with a deprotonated G8^-, which is required for G8^- general base mechanism, show that G8^- shifts away from the active site due to electrostatic repulsion with the negatively charged scissile phosphate.²⁴ The most straightforward interpretation of these classical MD results is that G8^- is structurally not tolerated and must be negligibly populated in the crystal structure for G8 to reside proximal to the scissile phosphate. The G8 enol tautomer is, by contrast, well tolerated in the experimental geometry during MD simulation.²⁴

While such simulations can reveal the relative structural stability of catalytically relevant conformations, they cannot address their reactivity. It is thus possible that G8^- is still involved in catalysis. However, its chemical reactivity would have to be very high to compensate for the thermodynamic penalty associated with it representing only a minor equilibrium population. Recent experiments measuring the ionization state of 8-azaguanosine substituted for G8 also showed that the pK_a of the nucleobase is not perturbed by the active site so that only a negligible fraction of G8 will be deprotonated at a physiological pH of ~7, further underscoring that G8^- can act as a general base only if it is sufficiently reactive.²⁶ Thus, the possibility of general base catalysis by G8^- cannot be entirely ruled out, as also pointed out by Bevilacqua¹⁵ and most recently by Wilson and Lilley²⁷ upon careful analysis of all available experimental data.

Abasic substitution of A38 impairs catalysis by more than four orders of magnitude, while exogenous nucleobase rescue and fluorescence-monitored base titration experiments indicate that the protonation state of A38(N1) plays a direct role in catalysis as a general acid or base.^19,21,28 Similarly, recent NAIM experiments of ligation by the hairpin ribozyme and pH-rate profile measurement of cleavage using various adenine analogs showed that ionization of A38(N1) is required for catalysis.^21,29 Raman measurements show that the pK_a of A38 is shifted toward neutrality (5.5, up from 4.3³⁰) implicating that A38 to some extent is protonated in the pre-cleavage state at a physiological pH of ~7.^20,21 A direct participation of the A38H⁺ imino group in catalysis is also consistent with the available crystal structures (since crystals are typically grown at pH 6)^12,31-34 as underscored by recent MD simulations.²⁴ The role of A38 also has been studied by the SE/MM method, with the conclusion that mechanisms are plausible where either A38 stabilizes the transition state by hydrogen bonding or A38H⁺ acts as the general acid.^17,18 An alternative mechanism has been suggested from MD simulations where A38 acts as a proton shuttle, although this role requires some repositioning of the adenine during the reaction.²³ Earlier simulation studies also were used to suggest that a long-residency water molecule in the catalytic pocket may become activated to participate in catalysis as a proton shuttle.^16,22

In the current computational study, we employ a hybrid quantum mechanical/molecular mechanical (QM/MM) approach³⁵ based on a high-level DFT method for description of the active site (QM region) to further delineate the specific roles and protonation states of G8 and A38 in the active site of the hairpin ribozyme. The QM/MM method generally suffers from some limitations,³⁶ however, it can provide unique direct insights into the electronic structure, mechanism and energy changes involved in RNA catalysis. We have previously employed similar QM/MM in studies of halogenalkane dehalogenase³⁷ and the hepatitis δ-virus (HDV) ribozyme.³⁸ We here test a range of feasible reaction mechanisms including the proton shuttling mechanisms, where the 2’-OH nucleophile is activated by one of the non-bridging oxygens of the scissile phosphate as well as the general acid-base mechanism with deprotonated G8^- and protonated A38H⁺ acting as a general base and general acid, respectively. In addition, we considered thio-substitutions of one or both non-bridging oxygens of the scissile phosphate to find that they have only a negligible effect on the reaction barrier. The accuracy of the utilized QM method for uncatalyzed reaction is assessed to be ~1 kcal/mol using the benchmark MP2/CBS (complete basis set) ab initio calculations corrected to higher-order electron correlation effects by CCSD(T) method with small basis set of atomic orbitals. We suggest that the hairpin ribozyme may facilitate self-cleavage by several, essentially isoenergetic, microscopic reaction pathways, with the protonated A38H⁺ electrostatically stabilizing the transition state and/or directly participating in the reaction as a general acid.

METHODS

QM analysis of the uncatalyzed reaction

The uncatalyzed reaction modeling phosphodiester self-cleavage in water is considered as a reference reaction and the catalytic effects of the ribozyme are benchmarked to this reaction.³⁹ We performed several different QM investigations in order to: (i) assess the performance of the MPW1K functional used in our QM/MM calculations for the reference reaction on small model containing only 27 atoms and (ii) estimate the Gibbs energy corrections on larger models corresponding to the reactant, product and transition states of the different reaction mechanisms studied. A similar extrapolation of the Gibbs energy corrections from the uncatalyzed reaction was used in our recent QM/MM study of HDV ribozyme.³⁸

We used a model of the sugar-phosphate backbone comprising 3’-(1’-amino-4’-methylribose)-5’-methylphosphodiester (27 atoms in overall, Figure 1A). The starting geometries of reactant, transition states, intermediates and products of the uncatalyzed reaction were taken from our previous work.³⁸ They were further optimized by MPW1K/6-31+G(d,p) in water, represented by a polarizable conductor calculation model (CPCM) as implemented in Gaussian 09.⁴⁰ The recent implementation of continuum solvation models in Gaussian 09 is more robust and reliable because it incorporates a continuous surface charge formalism.⁴¹ Frequencies (under harmonic approximation) were calculated at the same level for each optimized structure to estimate corrections to the Gibbs energy at 300 K and 1 atm. The differences between the gas phase MPW1K/6-31+G(d,p) energies and the CPCM (ε_r = 78.4)/MPW1K/6-31+G(d,p) energies were used to estimate the solvation contributions to the energy profile of the reference reaction. Subsequently, single point calculations were performed at the MP2/cc-pVTZ and MP2/cc-pVQZ levels to estimate the MP2/complete basis set limit (CBS) energies.^42,43 The energy difference between the MP2/cc-pVDZ and CCSD(T)/cc-pVDZ calculations was used to estimate a CCSD(T) correction for higher-order correlation effects.⁴⁴ From these calculations the CBS(T) energies (MP2/CBS corrected to higher order correlation effects by CCSD(T)) were extrapolated using a previously described scheme.⁴⁵ The differences between the MPW1K/6-31+G(d,p) and CBS(T) single point gas phase energies were used to assess the mean unsigned error of the MPW1K functional used in the QM/MM studies.

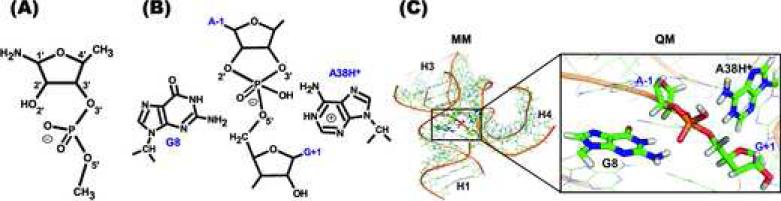
Figure 1.

(A) Scheme of the sugar-phosphate backbone model used in the reference reaction to assess the performance of MPW1K functional. (B) Scheme of the QM region (shown for the phosphorane intermediate state) containing the canonical G8 and protonated A38H⁺ species. (C) Initial snapshot (taken from MD simulations) of the pro-R_P/pro-R_P/G8/A38H⁺ path. The MM region and QM core are rendered as wires and thicker sticks, respectively. Water molecules and counter ions are not shown for simplicity. The model compound in panel A and structure in panel B are unconventionally drawn in the same orientation as the structure in panel C having 2’-OH on the left.

For the calculation of Gibbs energy corrections (involving zero point vibration energy, enthalpy correction to finite temperature, and entropy contribution derived by the standard harmonic oscillator approximation in the canonical ensemble), we extended the model of the sugar-phosphate backbone with N9-methylguanine and N9-methyladenine in the protonation states and conformations with respect to the phosphate of 3’-(1’-amino-4’-methylribose)-5’-methylphosphodiester that corresponded to the respective QM/MM paths in the hairpin ribozyme active site.

QM/MM calculations

A two-layer ONIOM method⁴⁶ with electronic embedding implemented in Gaussian03⁴⁷ was used for the QM/MM calculations. The MM region was treated by the AMBER (Cornell et al.) molecular mechanical force field parm99.⁴⁸ The QM region was described by DFT methods, namely by BLYP/6-31G(d) for geometry determinations and the more accurate MPW1K/6-31+G(d,p) for single-point energy calculations. The BLYP functional^49,50 with the density fitting approximation^51,52 was chosen as a compromise, providing sufficient geometrical accuracy at affordable computational cost.

The QM region (~64 atoms) comprises the N9-methyl-capped nucleobases G8 and A38, and the A-1/G+1 sugar-phosphate backbone (Figure 1B). Hydrogen atoms were added to the dangling bonds at the interface between the QM and MM regions. In all QM/MM calculations, the ribozyme was immersed in a water droplet with an ~10 Å thick layer of water molecules surrounding the RNA molecule. The initial positions of counter ions were taken from MD snapshot of the reaction intermediates from which the starting structures were prepared. An ~5 Å thick layer of waters on the surface of the droplet and counter ions outside the droplet were fixed during all QM/MM calculations to prevent any changes in energy due to a reorganization of the hydrogen bonding network at the water-vacuum interface. The entire system contained ~13,000 atoms, ~5,200 of which were fixed. The remaining atoms were allowed to geometrically relax during QM/MM optimization. We used phosphorane intermediate as a starting structure to avoid the technical problems with QM/MM scanning of the reaction path from reactant to product as was recently described in ref. 38. Instead we performed scan from intermediate to either reactant or product and used the microreversibility of the reaction to calculate the reaction profile.

The starting structures were prepared with the aid of classical explicit solvent simulations The experimental studies show that the protonated phosphorane is the dominant state at pH 7.⁵³ Thus to prepare the starting structures, we parameterized force field for the protonated phosphorane residue and performed two MD simulations with either a protonated pro-R_P or pro-S_P non-bridging phosphorane oxygen. A detailed description of the reaction intermediates MD simulations, which were used to prepare the starting structures of the QM/MM calculations, are available in the Supporting Information.

The reaction profiles were explored by flexible scans from the reaction intermediate by lengthening the distance between A-1(O2’) and G+1(P), or G+1(P) and G+1(O5’). Scans were performed with 0.1 Å steps, with all remaining degrees of freedom relaxed at each point (except for the atoms at the surface of droplet as indicated above). In addition, a two-dimensional scan on the potential energy surface (in the directions of the nucleophile attack of A-1(O2’) to scissile phosphate and the proton transfer from A-1(2’-OH) hydroxyl to G+1(pro-R_P/S_P) non-bridging oxygen) was performed to better localize the first (rate-determining) transition state for each mechanism studied.³⁸

In general, the energy barriers obtained at the BLYP level are underestimated, mainly due to the self-interaction error of the BLYP functional. The final single point energy values were therefore recalculated by the more accurate MPW1K DFT method,^54,55 using the 6-31+G(d,p) basis set. This method was shown to perform well for the phosphodiester cleavage reaction. The mean unsigned error of the MPW1K/6-31+G(d,p) method relative to the CBS(T) benchmark was 0.7 kcal/mol. The abbreviation CBS(T) refers to the MP2/CBS energy corrected for higher-order correlation effects by the CCSD(T) method with a smaller basis set,⁵⁶ as detailed above. Thus, the performance of MPW1K/6-31+G(d,p) was assessed in this study against the CBS(T) method, which was considered a reference method.

Since the QM/MM calculations only provide electronic energy changes along a chosen reaction pathway, ‘corrections’ (entailing zero-point energies, enthalpy correction to finite temperature and entropies) have to be introduced to obtain the Gibbs energies. The corrections for the Gibbs energies were extrapolated from the respective reference reactions (see previous paragraph), which shared the same reaction mechanisms as the corresponding QM/MM paths.³⁸

As the active site includes two titratable residues, G8 and A38 with pK_a's of 9.5²⁶ and 5.5,³⁴ respectively, the major protonation states under physiological conditions (pH ~7) have to be the canonical forms of the G8 and A38 nucleobases. Thus, if we consider the reactant state with different protonation states of these nucleobases, the calculated reactant Gibbs energy (and thus all energies calculated along the QM/MM pathway) must be corrected for the presence of only a minor equilibrium population of the potent ionization form of the catalytic species. The corrections for the protonated A38H⁺ and deprotonated G8^- are as follows:⁵⁷

$$\begin{array}{cc}\hfill \Delta G_{A38H^{+}}^{corr}& =RT\text{ln}10(\mathrm{pH}-\mathrm{p}{K}_a^{A38})\hfill \\ \hfill \Delta G_{G{8}^{-}}^{corr}& =RT\text{ln}10(\mathrm{p}{K}_a^{G8}-\mathrm{pH})\hfill \end{array}$$

which yield 2.1 and 3.4 kcal/mol (at 300 K and pH 7), respectively.

RESULTS

The Reference Reaction

The catalytic effect of enzymes is generally defined as the difference in reactivity between the enzyme catalyzed reaction and the corresponding uncatalyzed reaction in water. This catalytic effect consists of two terms: i) that related to the shift of the reaction mechanism from the uncatalyzed reference reaction in water to the reaction in the enzyme and ii) the difference in Gibbs energy barrier between enzymatic and uncatalyzed reference reaction in water involving the same mechanism as in the enzyme.³⁹ The first term is assumed to be trivial albeit important, while the second term is often called the true catalytic effect.³⁹

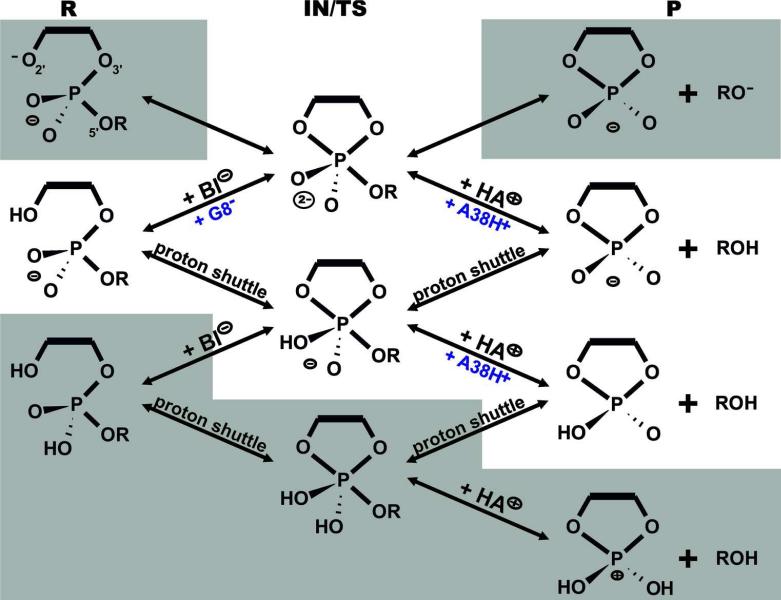
In our case, we defined the self-cleavage of endo/exo-3’-(1’-amino-4’-methylribose)-5’-methylphosphodiester (Figure 1A) in water as the reference uncatalyzed reaction. To our best knowledge, this model compound is a sufficiently representative model for RNA backbone and its self-cleavage, because it involves a large portion of the sugar-phosphate backbone.^38,58-63 In the self-cleavage reaction, the 2’-OH group attacks the negatively charged phosphate group (phosphodiester), forming a sp³d hybridized phosphorus, i.e. the phosphorane group, which splits to products (2’,3’-cyclo-phosphate and alcohol) in an exocyclic cleavage step.^38,60,64,65 The proton of 2’-OH group is either transferred via phosphate/phosphorane non-bridging oxygen toward the leaving 5’-alcoholate or is accepted by external general base while the O5’ leaving oxygen is in turn protonated by external general acid. Two intermediate states (represented by two local minima on the Gibbs energy reaction profile) were observed for proton shuttling mechanisms, where the proton is transferred via phosphate/phosphorane non-bridging oxygen. These intermediates corresponded to the single protonated phosphorane form. On the other hand, no intermediates were observed in case of general acid-base reaction including explicit participation of general acid and general base, where the only one transition state involved deprotonated (doubly charged) phosphorane group.

The Gibbs energy profile of the reaction path invoking the proton shuttle via the phosphate/phosphorane non-bridging oxygen was calculated for two reasons: i) to assess the quality of our MPW1K/6-31+G(d,p) method describing the QM region in QM/MM calculations against reference CBS(T) calculations, which is the QM method of highest affordable quality; and ii) to find the overall reaction barrier of the reference reaction in water.

The gas-phase energies (Table 1) show that the mean unsigned error (MUE) of the MPW1K/6-31+G(d,p) method with respect to CBS(T) is 0.7 kcal/mol, and the maximum unsigned error is 1.1 kcal/mol for the transition state (the last transition state of proton transfer from the non-bridging oxygen to the leaving O5’ alcoholate) and 1.8 kcal/mol for the products. Both MPW1K and CBS(T) gas phase energies were calculated based on the geometries optimized at the CPCM(ε_r = 78.4)//MPW1K/6-31+G(d,p) level. The MUE agrees well with the corresponding values estimated in our previous calculations, which were obtained for slightly different geometries optimized at the IEFPCM(ε_r = 78.4)//B3LYP/6-31G(d,p) level.³⁸ This finding indicates that the MPW1K/6-31+G(d,p) method provides reasonably accurate energies within thermochemical accuracy of ~1 kcal/mol for the sugar-phosphate self-cleavage reaction. This observation implies that the MPW1K/6-31+G(d,p) method should provide reasonably accurate electronic energies in QM/MM calculations and its inaccuracy is rather marginal compared to other source of errors within the QM/MM scheme.³⁶

Table 1.

The MPW1K functional errors obtained as a difference between MPW1K/6-31+G(d,p) and CBS(T) gas phase energies of the endo/exo-3’-(1’-amino-4’-methylribose)-5’-methylphosphodiester self-cleavage reaction (for Reference Reaction scheme see Figure S4 in Supporting Information).^a

endo (pro-RP)	TS1	IN1	TS2	IN2	TS3	P	P’
MPW1K/6-31+G(d,p)	29.4	26.7	36.2	30.1	36.4	2.3	17.2
CBS(T)	28.9	27.1	36.8	30.0	37.4	4.1	19.0
MPW1K error	-0.5	0.4	0.5	0.0	1.0	1.8	1.8

exo (pro-SP)	TS1	IN1	TS2	IN2	TS3	P	P’
MPW1K/6-31+G(d,p)	27.4	21.2	32.3	26.1	36.8	2.3	17.2
CBS(T)	27.1	21.7	32.4	26.6	37.9	4.1	19.0
MPW1K error	-0.4	0.4	0.1	0.5	1.1	1.8	1.8

^aEnergies are given in kcal/mol and related to the reactant state. Geometries were optimized at CPCM (ε_r= 78.4)/MPW1K/6-31+G(d,p) level (see Methods for details).

Considering the reference reaction in water (see the Supporting Information, Table S1), the estimated overall reaction barrier (the highest barrier along the reaction path) corresponds to the leaving of the 5’-alcoholate and its protonation by one of the non-bridging oxygens of the phosphorane intermediate with 34.6 kcal/mol in both the endo (proton transfer via pro-R_P oxygen) and exo (proton transfer via pro-S_P oxygen) paths. The profiles differ by ~0-5 kcal/mol from those published in our previous work,³⁸ due to variations in solvation energies calculated by continuum solvation models. In the previous work we used IEFPCM solvation model⁶⁶ implemented in Gaussian 03 while here we employed the very recent implementation of the CPCM model in Gaussian 09, which should provide significantly more reliable solvation energies as it incorporates a continuous surface charge formalism.⁴¹ It is worth noting that a reliable estimate of solvation energy of a large and conformationally variable anion by a continuum solvation model is not a trivial task. The present estimates of solvation energies, therefore, arguably represent (despite all effort) the weakest point in our estimation of Gibbs energies of the reference reaction in water.

Rationale for setting up our QM/MM calculations

We performed extensive QM/MM calculations to test possible specific roles and plausible protonation states of the catalytically essential residues G8 and A38 of the hairpin ribozyme. Several conformations of the ribozyme were tested as potential initial geometries for the calculations. To arrive at suitable starting structures, we first carried out two classical MD simulations of the possible monoanionic phosphorane intermediates, one with the protonated G+1(pro-R_P) oxygen of the phosphorane and the other with the G+1(pro-S_P) oxygen protonated instead, both featuring a canonical G8 and a protonated A38H⁺ in the active site (Figure 1C and see the Supporting Information for details). Starting geometries based on other combinations of G8 and A38 protonation states were not considered since they lead to distortions of the active site in MD simulations.²⁴ The phosphorane intermediates were used because direct QM/MM-based potential energy surface scans of the self-cleavage reaction starting from its reactant state caused an inaccurate localization of transition states and unreliably high activation barriers. Such problems were recently reported and analyzed in a QM/MM study of the HDV ribozyme.³⁸ Instead, we followed the reaction path from the intermediate backward to the reactant and forward to the product, assuming that the energy profile from reactant to intermediate is obtained by inversion of the former profile due to the expected microscopic reversibility of the reaction.

Initially, we selected four starting structures for our QM/MM calculations, two with a protonated G+1(pro-R_P) oxygen and two with a protonated G+1(pro-S_P) oxygen. These specific structures chosen corresponded to MD snapshots with A38H⁺ and G8 most tightly bound to the scissile phosphate (see the Supporting Information). After preliminary QM/MM scans along the reaction profile, only the two structures with the lowest activation barriers were selected for further calculations, one with protonated G+1(pro-R_P) oxygen, the other with protonated G+1(pro-S_P) oxygen (see the Supporting Information). These two geometries were then used to prepare starting structures with different protonation states of the active site to explore specific reaction paths. In addition to structures with canonical G8 and protonated A38H⁺, we considered combinations of canonical G8 with canonical A38, tautomeric N1,O6-enol form of G8 with protonated A38H⁺, and deprotonated G8^- with protonated A38H⁺ (Figure 2, see Table S2 for detail information about protonation state of all key groups in all states along the reaction paths). Finally, we also carried out three scans in which one or both non-bridging oxygens of the scissile phosphate were replaced by sulfur. Altogether, we considered 11 possible reaction pathways of the hairpin ribozyme self-cleavage (Table 2).

Figure 2.

Schematic of all reaction paths possible in hairpin ribozyme self-cleavage. Physically less meaningful pathways involving unlikely protonation states (at pH ~7) of the phosphate or 2’-OH nucleophilic group in precursor or product state (gray background) were not considered in this study.

Table 2.

List of the specific reaction mechanisms studied here (the mechanisms containing thio-substitutions formally correspond to the pro-R_P/pro-R_P/G8/A38H⁺ path and are summarized separately in Table 4).

Name	General base	General acid	G8 form	A38 form
G/A+/G8-/A38H+	G8-	A38H+	G8-	A38H+
pro-RP/pro-RP/G8/A38H+	G+1(pro-RP)	G+1(pro-RP)	G8	A38H+
pro-RP/pro-RP/G8t/A38H+	G+1(pro-RP)	G+1(pro-RP)	G8t	A38H+
pro-RP/pro-RP/G8/A38	G+1(pro-RP)	G+1(pro-RP)	G8	A38
pro-RP/A+/G8/A38H+	G+1(pro-RP)	A38H+	G8	A38H+
pro-SP/pro-SP/G8/A38H+	G+1(pro-SP)	G+1(pro-SP)	G8	A38H+
pro-SP/pro-SP/G8t/A38H+	G+1(pro-SP)	G+1(pro-SP)	G8t	A38H+
pro-SP/pro-SP/G8/A38	G+1(pro-SP)	G+1(pro-SP)	G8	A38

The identifying names of each QM/MM scan are composed of four indicators separated by “/”: i) the groups acting as general base, ii) general acid, iii) the protonation state of the G8 and iv) A38 in precursor state at the beginning of the cleavage reaction. Details of protonation states of G8, A38 and phosphate/phosphorane/cyclic phosphate in all R, IN/TS, and P states are listed in Table S2 in Supporting Information.

The QM/MM approach utilized here directly provides the electronic energy but does not include a Gibbs energy correction term. The correction terms for each reactant, transition, intermediate or product (R, TS, IN, or P) state along the reaction coordinate were derived from a reference reaction (see the Supporting Information, Tables S3a and S3b), which we modeled as just the sugar-phosphate backbone flanked by guanine and adenine (see Methods). For each reaction path, we used the Gibbs energy correction terms from the corresponding reference reaction mechanism with matching protonation states of guanine and adenine.

Mechanisms involving proton shuttling by the non-bridging scissile phosphate oxygens

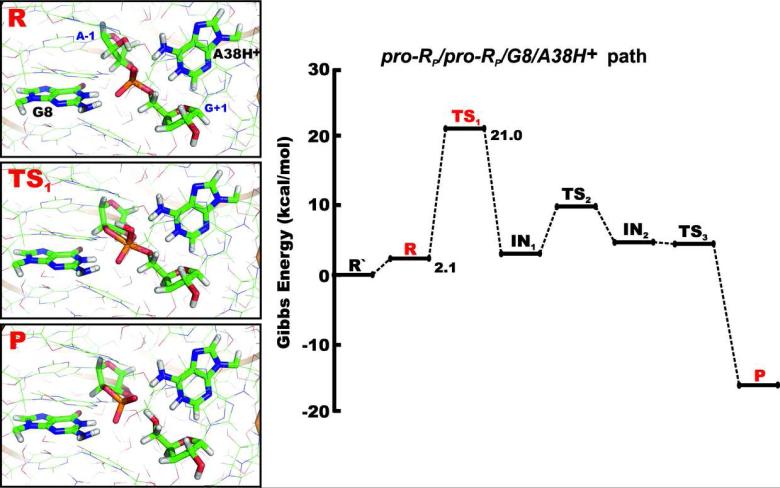
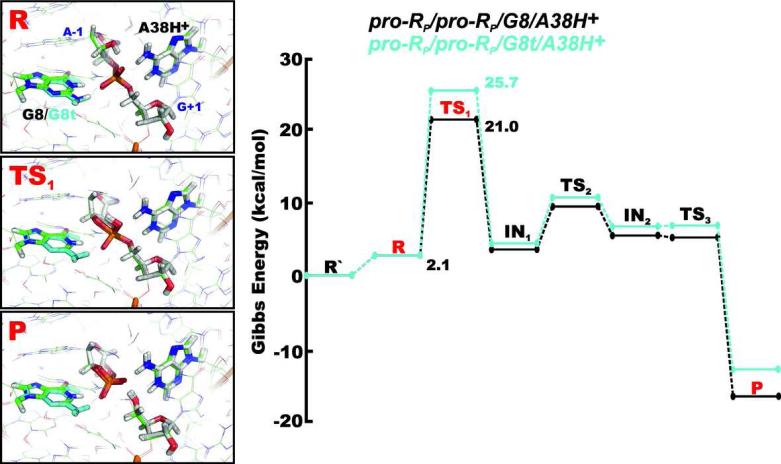
In the proton shuttle mechanisms (Figure 2), either the G+1(pro-R_P) or G+1(pro-S_P) non-bridging oxygen of the scissile phosphate activates the A-1(2’-OH) as a nucleophile by accepting its proton and further acts as a shuttle by transferring this proton to the leaving group G+1(O5’). In our QM/MM calculations, we observed two pentahedral single protonated phosphorane intermediates (IN₁ and IN₂) along the reaction paths, with the hydroxyl group of the protonated phosphorane non-bridging oxygen oriented toward the A-1(O2’) and G+1(O5’) oxygens, respectively. The reactions thus proceed through three transition states, TS₁, TS₂ and TS₃ (Figure 3). The first reaction step, corresponding to the inline attack of the A-1(2’-OH) hydroxyl group, has the highest energy barrier along the reaction coordinate in both the pro-R_P/pro-R_P/G8/A38H⁺ and pro-S_P/pro-S_P/G8/A38H⁺ reaction paths (Table 3) and is thus rate-limiting. The proton transfer from A-1(2’-OH) hydroxyl group to one of the non-bridging oxygens is simultaneous with the nucleophilic attack. The proton of the 2’-OH group is then shuttled via the G+1(pro-R_P) and G+1(pro-S_P) non-bridging oxygens in the pro-R_P/pro-R_P/G8/A38H⁺ and pro-S_P/pro-S_P/G8/A38H⁺ mechanisms, respectively. The Gibbs energy barriers calculated for the rate-limiting first transition state TS₁ (and thus also the overall barrier) of these reaction paths are 21.0 kcal/mol and 23.0 kcal/mol, respectively (Table 3).

Figure 3.

Schematic diagram for the relative Gibbs energy profile along the pro-R_P/pro-R_P/G8/A38H⁺ path. The structures in boxes show details of the active site (from the same angle as Figure 1C with the QM core highlighted as thicker sticks) in the reactant, transition and product states (R, TS₁ and P, respectively). All energies are relative to the R’ state that represents the reactant with the dominant protonation states of G8 and A38 at pH ~7, i.e. both nucleobases in canonical forms.

Table 3.

Computed reaction Gibbs energy barriers in kcal/mol of various paths representing the proton shuttling and G8^- general base reaction mechanisms (see Tables S4a, S4b in Supporting Information for the MPW1K/6-31+G(d,p) and BLYP/6-31G(d) reaction barriers without any corrections).^a

	Rb	TS1c	IN1	TS2	IN2	TS3	P
pro-RP/pro-RP/G8/A38H+	2.1	21.0	3.3	9.6	4.7	4.5	-16.9
pro-RP/A+/G8/A38H+	2.1	21.0	3.3	9.6	4.7	3.8	-7.4
pro-RP/pro-RP/G8t/A38H+	2.1	25.7	3.9	10.8	5.7	6.1	-13.2
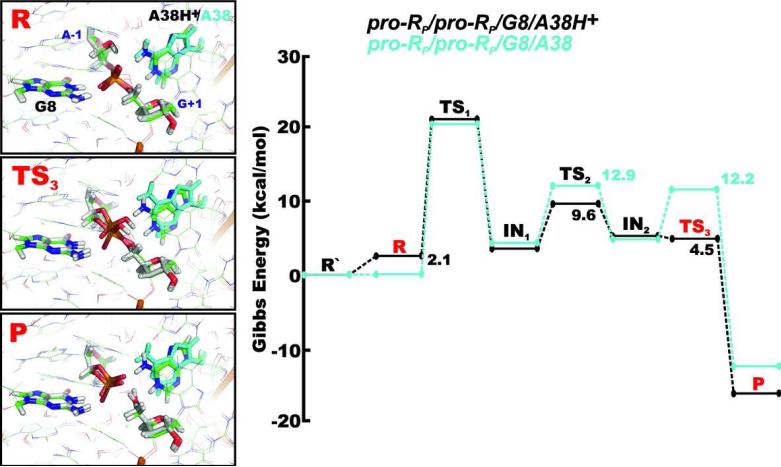
pro-RP/pro-RP/G8/A38	0.0	20.5	4.0	12.9	4.5	12.2	-12.8
pro-SP/pro-SP/G8/A38H+	2.1	23.0	11.3	14.9	5.6	6.3	-11.6
pro-SP/pro-SP/G8t/A38H+	2.1	30.3	14.4	16.5	8.2	5.3	-8.5
pro-SP/pro-SP/G8/A38	0.0	23.2	16.1	18.1	8.9	11.5	-8.1
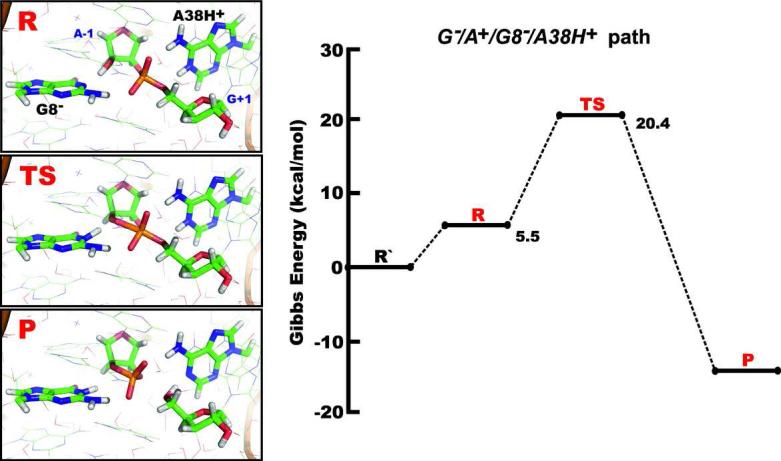
G-/A+/G8/A38H+d	5.5	20.4					-13.9

^aThe Gibbs energies are composed of QM/MM energy calculated at MPW1K/6-31+G(d,p):AMBER level, the Gibbs energy correction obtained from the reference reaction at MPW1K/6-31+G(d,p) level (see Methods) and the correction to respective protonation state of adenine A38 and guanine G8.

^bThe energies of reactants containing protonated adenine or deprotonated guanine are corrected by the Gibbs energy required to protonate A38 or deprotonated G8, considering recent estimated adenine A38 pK_a of 5.5³⁴ (2.1 kcal/mol at 300 K) and guanine G8 pK_a of 9.5²⁶ (3.4 kcal/mol at 300K).

^cThe highest Gibbs energy (corresponding to the rate-limiting step) is shown in bold.

^dThe G8^- general base reaction mechanism involves only one transition state and no intermediate.

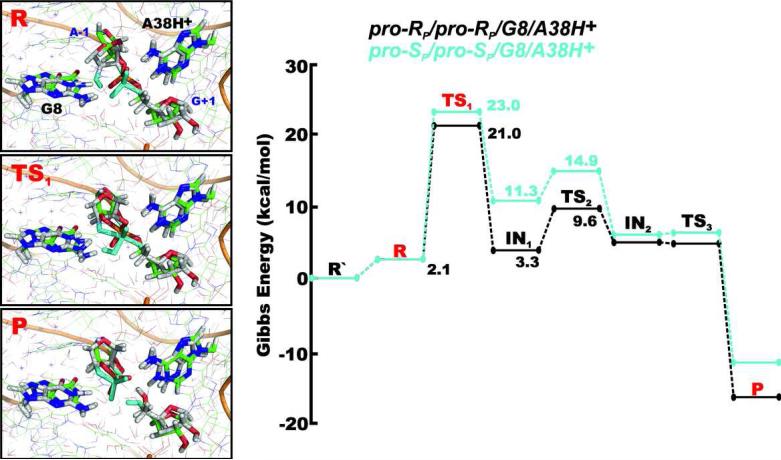
The reactant state of the pro-R_P/pro-R_P/G8/A38H⁺ mechanism populated primarily the C3’-endo conformation of the A-1 ribose ring with the A-1(2’-OH)...G+1(pro-R_P) oxygen hydrogen bond (Figure 3). The pro-S_P/pro-S_P/G8/A38H⁺ mechanism instead dominantly exhibited the C2’-endo (crystal-structure-like)¹³ pucker of the A-1 ribose. A 4BPh interaction between the protonated adenine A38H⁺ and the scissile phosphate comprising the A38H⁺(N1H)...G+1(O5’) and A38H⁺(N6H)...G+1(pro-R_P) oxygen hydrogen bonds was found in both mechanisms. The guanine G8 formed the 4BPh interaction with the scissile phosphate associated with the bifurcated G8(N1H/N2H)...G+1(pro-S_P) oxygen hydrogen bond in both mechanisms, with exception of the TS₁, IN₁ and TS₂ states of the pro-S_P/pro-S_P/G8/A38H⁺ mechanism, where it was weakened by the transient proton on the G+1(pro-S_P) group. In this case, the 4BPh interaction was replaced by a 5BPh-type G8(N1H)...A-1(O2’) hydrogen bond (Figure 4). This weakened BPh contact between G8 and the scissile phosphate most likely contributed to the increased Gibbs energy barrier of the pro-S_P/pro-S_P/G8/A38H⁺ mechanism (Figure 4).

Figure 4.

Comparison of geometries and Gibbs energy profiles of the pro-R_P/pro-R_P/G8/A38H⁺ (green structures) and pro-S_P/pro-S_P/G8/A38H⁺ (white and cyan structures) reaction mechanisms, differing in which non-bridging oxygen mediated the proton shuttle. All energies are relative to the R’ state that represents the reactant with the dominant protonation states of G8 and A38 at pH ~7, i.e. both nucleobases in canonical forms.

Our set of proton shuttling mechanisms was extended by the pro-R_P/A⁺/G8/A38H⁺ path, in which the initial reaction steps up to the second intermediate IN₂ are equivalent with the pro-R_P/pro-R_P/G8/A38H⁺ mechanism. Then, however, the G+1(O5’) leaving oxygen is protonated during the exocyclic cleavage step (IN₂→TS₃→P) by A38H⁺(N1H), which is thus acting as general acid (see the Supporting Information, Figure S5). Therefore, the pro-R_P/A⁺/G8/A38H⁺ mechanism shared both the rate-limiting step and the corresponding Gibbs energy barrier of 21.0 kcal/mol with the pro-R_P/pro-R_P/G8/A38H⁺ path. It showed a slightly lower barrier for exocyclic cleavage in comparison with the pro-R_P/pro-R_P/G8/A38H⁺ mechanism (TS₃ equals to 3.8 kcal/mol, Table 3), but the localized product state (P) is about 9.5 kcal/mol higher compared to the pro-R_P/pro-R_P/G8/A38H⁺ path, where the protonated G+1(pro-R_P) non-bridging oxygen of the scissile phosphate acts as the proton donor (see the Supporting Information, Figure S5). This energy difference between product states is a consequence of protonation of non-bridging oxygen of the cyclic phosphate in the pro-R_P/A⁺/G8/A38H⁺ path. The pK_a of the sp³ hybridized phosphate is ~1, but the pK_a of the sp³d hybridized phosphorane equals to 11-15.⁵³ Consequently, the protonation of the non-bridging oxygen is favored in the phosphorane intermediates and phosphorane-like transition states, but not tolerated in reactant and product states. We assume that the structure labeled here as the product state of the pro-R_P/A⁺/G8/A38H⁺ mechanism can further relax in energy by subsequent proton transfer from non-bridging oxygen of the cyclic phosphate to adenine A38 and thus it is most likely not the final state of pro-R_P/A⁺/G8/A38H⁺ path. Such proton transfer might be facilitated by a proton hopping mechanism via the G+1(O5’) oxygen (i.e., by a concerted proton transfer from the non-bridging oxygen to G+1(O5’) and proton transfer from G+1(O5’) back to A38) or via water molecules. In other words, we expect that proton transfer following the pro-R_P/A⁺/G8/A38H⁺ mechanism will result in the product state equivalent to e.g. the pro-R_P/ pro-R_P /G8/A38H⁺ path and thus both these paths are chemically equivalent.

Role of the G8 nucleobase

We investigated the possible direct participation and energetic contribution of G8 residue in the cleavage reaction by considering the N1,O6-enol tautomer of G8 (G8t) or deprotonated form of G8 (G8^-) in the active site of the hairpin ribozyme.

In comparison with the pro-R_P/pro-R_P/G8/A38H⁺ and pro-S_P/pro-S_P/G8/A38H⁺ paths, the incorporation of the G8 N1,O6-enol tautomer does not shift the rate-limiting step (which remains the nucleophile attack), but significantly increases the barrier height of this step to 25.7 kcal/mol and 30.0 kcal/mol for the pro-R_P/pro-R_P/G8t/A38H⁺ and pro-S_P/pro-S_P/G8t/A38H⁺ mechanisms, respectively (Table 3 and Figure 5). No direct participation of the G8t(N1) nitrogen in the cleavage reaction was observed. In addition, the Gibbs energy correction to a different protonation state of G8 in its tautomeric form which was not included in our computations would further and substantially increase the observed reaction barrier, as guanine tautomers are highly unfavorable in water.⁶⁷

Figure 5.

Comparison of geometries and Gibbs energy barriers of the pro-R_P/pro-R_P/G8/A38H⁺ and pro-R_P/pro-R_P/G8t/A38H⁺ reaction mechanisms in the presence of canonical G8 (green structures) and N1,O6-enol tautomer G8t (white and cyan structures), respectively. All energies are relative to the R’ state that represents the reactant with the dominant protonation states of G8 and A38 at pH ~7, i.e. both nucleobases in canonical forms.

Further, we calculated energies for the reaction path where the deprotonated G8^- form abstracts the proton from the A-1(2’-OH) group, thereby acting as general base (path G^-/A⁺/G8^-/A38H⁺, Figure 6). The reaction proceeds through the dianionic phosphorane transition state (TS) and we did not detect any phosphorane intermediate state. The cleavage reaction immediately generated a product (P) with the 2’,3’-cyclic phosphate and the G+1(5’-OH) termini. The proton transfer to the leaving G+1(O5’) group occurred from the protonated A38H⁺, thus acting as general acid (Figure 6). The estimated overall reaction barrier is 20.4 kcal/mol (Table 3). It is worth noting that we also calculated a profile with deprotonated nucleophile A-1(2’-O^-), canonical G8 and protonated A38H⁺ in the active site. However, during the initial optimization of the reactant state, the A-1(2’-O^-) group spontaneously (without energetic barrier) abstracted the proton from G8(N1) and then the reaction scan followed the G^-/A⁺/G8^-/A38H⁺ reaction pathway.

Figure 6.

Schematic diagram for the Gibbs energy profile of the G^-/A⁺/G8^-/A38H⁺ path, representing combined G8^- general base and A38H⁺ general acid mechanism. All energies are relative to the R’ state that represents the reactant with the dominant protonation states of G8 and A38 at pH ~7, i.e. both nucleobases in canonical forms.

Role of the A38 nucleobase

Besides the protonated A38H⁺, which was recently suggested to be structurally important within the active site of the hairpin ribozyme,²⁴ we also considered the canonical A38 species. The proton shuttling reaction paths with the canonical form of A38 were calculated in order to probe for a direct influence of the protonation state of A38 on the proton shuttling mechanisms and barrier heights of the TS states along the reaction pathway. Note that the active site structure with canonical A38 was derived from the starting structure with protonated A38H⁺, so the conformation of A38 is rather similar to the conformation of A38H⁺, placing it next to the scissile phosphate, i.e. the same conformation as observed in crystal structures. This assumption was necessary since MD simulations show that the canonical A38 degrades the adjacent S-turn motif, leading to its expulsion from the active site.²⁴

In comparison with the pro-R_P/pro-R_P/G8/A38H⁺ and pro-S_P/pro-S_P/G8/A38H⁺ paths, the incorporation of the canonical A38 neither changes the rate-limiting step, which remains the nucleophile attack, nor significantly affects the highest Gibbs energy barrier along the reaction path that equals to 20.5 kcal/mol and 23.2 kcal/mol for the pro-R_P/pro-R_P/G8/A38 and pro-S_P/pro-S_P/G8/A38 paths, respectively (Table 3). However, whereas the protonated adenine A38H⁺ is able to form a base-phosphate interaction classified as 4BPh contact,²⁵ which is rather typical for guanine and belongs to the strongest base-phosphate contact, the canonical adenine is not able to form a such 4BPh contact.^25,68 In other words, the lack of hydrogen at the A38(N1) position and the absence of the corresponding interaction between the A38(N1) and G+1(O5’) weakens the base-phosphate interaction between A38 and the scissile phosphate,²⁴ causing the A38 to slightly move away from the scissile phosphate in both the pro-R_P/pro-R_P/G8/A38 and pro-S_P/pro-S_P/G8/A38 paths (Figure 7). The presence of the canonical A38 species thus increases the barrier of the exocyclic cleavage (TS₃ transition state) by 7.7 kcal/mol and 5.2 kcal/mol in the pro-R_P/pro-R_P/G8/A38 and pro-S_P/pro-S_P/G8/A38 paths, respectively.

Figure 7.

Comparison of geometries and Gibbs energy profiles of the pro-R_P/pro-R_P/G8/A38H⁺ (green) and pro-R_P/pro-R_P/G8/A38 (white and cyan) reaction mechanisms, i.e., in presence of protonated A38H⁺ and canonical A38 form. All energies are relative to the R’ state that represents the reactant with the dominant protonation states of G8 and A38 at pH ~7, i.e. both nucleobases in canonical forms.

Thio-substitution on non-bridging oxygens of the scissile phosphate

We carried out a set of reaction profile calculations within the pro-R_P/pro-R_P/G8/A38H⁺ path, in which we replaced one or both non-bridging oxygens of the scissile phosphate by sulfur. The cleavage reaction of all three thio-analogs follows the same reaction profile as the pro-R_P/pro-R_P/G8/A38H⁺ path. The rate-limiting step is associated with the nucleophilic attack, accompanied by formation of the TS₁ state (Table 4). Generally, the observed thio-effects were very small and resulted in a negligible shift of the overall barrier in comparison with the pro-R_P/pro-R_P/G8/A38H⁺ mechanism. The difference is below the accuracy of our QM/MM method. Notably, the largest but still small shift (of ~0.9 kcal/mol) was observed for the pro-S_P thio-analog (Table 4). In addition, we did not observe any changes considering hydrogen bond interactions and positioning of key nucleobases within the active site of the hairpin ribozyme. The differences in barrier height for substitutions of the pro-R_P oxygen (pro-R_P thio-analog) and both non-bridging oxygens (pro-R_P/pro-S_P thio-analog) were within ~0.2 kcal/mol in comparison with the comparable pro-R_P/pro-R_P/G8/A38H⁺ path (Tables 3 and 4). The overall results agree with experimentally observed lack of thio-effects.⁶⁹ However, it should be noted that while our calculations do not reveal any thio-effect on the self-cleavage reaction, it is still possible that thio-substitution could influence the equilibrium population of the catalytically competent active site conformations. This would not be captured by our computations.

Table 4.

The Gibbs energy profiles in kcal/mol of the pro-R_P/pro-R_P/G8/A38H⁺ reaction mechanism with the thio-substitution on one or both non-bridging oxygens.^a

	Rb	TS1c	IN1	TS2	IN2	TS3	P
pro-RP thio-analog	2.1	21.1	8.5	13.0	8.3	7.4	-14.5
pro-SP thio-analog	2.1	21.9	7.8	12.3	11.3	9.0	-14.6
pro-RP/pro-SP thio-analog	2.1	20.8	10.3	13.2	6.6	7.5	-15.0

^aThe Gibbs energies are composed of QM/MM energy calculated at MPW1K/6-31+G(d,p):AMBER level, the Gibbs energy correction obtained from the reference reaction at MPW1K/6-31+G(d,p) level (see the Supporting Information, Tables S5a, S5b, S5c) and the correction to protonation state of adenine A38.

^bThe energies of reactants containing protonated adenine are corrected by the Gibbs energy required to protonate A38, considering recent estimated adenine A38 pK_a of 5.5³⁴ (2.1 kcal/mol at 300K).

^cThe highest Gibbs energy barrier is shown in bold.

DISCUSSION

We carried out QM/MM calculations to evaluate plausible reaction mechanisms of hairpin ribozyme self-cleavage and the associated roles of the active site nucleotides G8 and A38. An emphasis is placed on the quality of the description of the electronic structure, i.e., quality of the QM core of the QM/MM procedure. Our main suggestion is that several competing microscopic reaction pathways are energetically equivalent, at least within the approximations that are inherent to our approach.

Accuracy of the QM/MM method utilized

The accuracy of QM/MM calculations is generally limited by: (i) the accuracy of the MM method, (ii) the accuracy of the QM method, (iii) the coupling between the QM and MM regions, and (iv) the conformational sampling.³⁶

Accuracy of the MM method usually has only a small effect on the overall quality of the QM/MM Gibbs energy profiles obtained.^36,70,71 By contrast, the accuracy of the QM method rather significantly limits their quality. Therefore, we carefully tested the MPW1K density functional against the CBS(T) method for the reference reaction. The CBS(T) method is based on MP2/CBS energies corrected using CCSD(T) energies.^45,72-75 For our reference reaction, the MUE of MPW1K/6-31+G(d,p) against CBS(T) energies is 0.7 kcal/mol, indicating that the MPW1K method provides a reasonably accurate description of the studied reaction.

Another critical point of QM/MM schemes is the communication between the QM and MM regions. There are two approaches for the coupling between regions, namely, mechanical and electronic embedding.³⁶ We employed the more physically based electronic embedding scheme, which assures that the QM wave function (and thus the electron density of the QM region) is polarized by the MM atom-centered point charges (the surrounding ribozyme, water molecules and ions). The coupling still remains the least accurate part of the QM/MM scheme.⁷⁶ However, in many cases the accuracy of the QM method dominates over that of the coupling in determining the overall accuracy of a QM/MM scheme. Unfortunately, this likely is not the case of the G^-/A⁺/G8^-/A38H⁺ reaction path with deprotonated G8^- (cf. Table 2 for abbreviations). The reaction barrier of the corresponding uncatalyzed reference reaction with G8^- general base is determined almost completely by the solvation terms, while the gas phase electronic energy contribution is negligible (see Table S3b). Similarly, the barrier of the G-/A⁺/G8^-/A38H⁺ reaction mechanism in QM/MM is driven by the coupling between the QM and MM regions, i.e., the polarization effect and the electrostatic interactions between both regions that are included in a one-electron Hamiltonian. The QM energy almost does not contribute to the barrier height. Then the barrier strongly depends on the least accurate term of the QM/MM scheme, which potentially compromises the accuracy of its height estimation. In contrast, the accuracy of the barriers of the other mechanisms is determined by the accuracy of the QM method, which is estimated to be ~1 kcal/mol (see above).

Regarding sampling, we explored the potential energy surface by relaxed scans along the defined reaction coordinate from several starting structures generated by classical MD simulation. This approach may suffer from several drawbacks: i) localization of the proper transition state is challenging, due to the multidimensionality and complexity of the potential energy surface, ii) the method does not account for zero-point energies and entropy contributions directly, and iii) some quantum effects such as hydrogen atom tunneling are neglected.

To reduce the first uncertainty, we initiated the scans from intermediate towards reactant and product.³⁸ The rate-limiting transition states involving proton transfer from the 2’-OH group were ultimately localized by two-dimensional scans in the directions of nucleophilic attack and proton transfer (see the More O'Ferrall-Jencks plot showing 2D scan calculations in HDV ribozyme in ref. 38).

The corrections for the Gibbs energies were extrapolated from the reference reaction, assuming that the reaction has the same entropy contribution in the enzyme and in solution. The small values of Gibbs energy corrections suggest that this rather crude approximation can be justified. The only direct way to compute estimates of Gibbs energy profiles would be to perform QM/MM or SE/MM MD combined with one of the free energy perturbation methods. This strategy has been successfully applied by York and coworkers,^17,18 using the semiempirical (SE) AM1/d-PhoT method in combination with the potential of mean force. However, equivalent QM/MM simulations would be prohibitively demanding and could not be executed in combination with a high-quality QM core. Thus, we inevitably need to make a trade-off between accuracy and sampling. The applicability of the QM/MM MD would be restricted to less accurate GGA functionals that are not recommended for chemical reactions (due to their self-interaction error) or to even less accurate SE methods. For example, the mean unsigned error (MUE) of activation energies calculated by the AM1/d-PhoT method, which is a popular semiempirical method that was carefully parameterized for sugar-phosphate self-cleavage reactions, against the DFT (B3LYP/6-311++G(3df,2p)) reference is 8.3 kcal/mol.⁷⁷

In summary, the QM/MM scheme employed here, featuring a sufficiently accurate QM method and modest conformational sampling (see above) is a viable alternative to QM/MM simulations using a less accurate QM description or even SE/MM simulations. Comparison of these distinct approaches can provide additional insights into the convergence of the results and can help with their interpretation.

The reaction mechanisms considered here

Earlier classical MD simulations suggested that the canonical G8 (and to some extent also the G8-enol tautomer, G8t) and the protonated A38H⁺ species are most compatible with the crystal structures. The presence of unprotonated G8^- and canonical A38 led to large structural perturbations of the active site.²⁴ Here, we have analyzed reaction profiles of several plausible microscopic pathways of the self-cleavage reaction catalyzed by the ribozyme (Figure 2). Specifically, the roles of the canonical G8, deprotonated G8^-, G8-enol tautomer, canonical A38 and protonated A38H⁺ species were considered.

We identified four different microscopic reaction mechanisms (pro-R_P/pro-R_P/G8/A38H⁺, pro-R_P/A⁺/G8/A38H⁺, pro-R_P/pro-R_P/G8/A38 and G^-/A⁺/G8^-/A38H⁺) with Gibbs energy barriers of 20-21 kcal/mol, which agree with the experimentally estimated barrier of 20-21 kcal/mol.⁶ In all cases the nucleophilic attack of the 2’-OH group is predicted to be rate-limiting. The estimated overall barriers match the previously published results by York et al., who used a very different SE/MM with Gibbs energy perturbation method. However, the rate-limiting step in the SE/MM study was shifted to the exocyclic cleavage.^17,18 This difference may be caused by the limited accuracy of the semiempirical AM1/d-PhoT method with MUE of 5.3 kcal/mol for the reaction energy and 8.3 kcal/mol for the activation energy.⁷⁷ Our QM method has MUE below 1 kcal/mol. The SE/MM barriers were nevertheless corrected for the intrinsic inaccuracy of the AM1/d-PhoT method by using the differences of reactant and transition state energies between the AM1/d-PhoT and B3LYP methods on a small model system.¹⁷ However, it is possible that the energies of this model reaction and the SE/MM ribozyme model are not fully equivalent and thus the corrections are not transferable. Conversely, differences in sampling may contribute to the difference in the predicted rate-limiting step. As noted above, with contemporary computer resources all available QM/MM methods remain approximate.

Possible roles of the active site guanine G8

Previous studies suggested that G8 may be involved in the reaction mechanism either in its canonical form through electrostatic stabilization or in its deprotonated form as general base.^{8,10,14,16-18,22-24} We explicitly followed both reaction paths. Among the feasible microscopic reaction mechanisms identified, three of them involve the canonical G8 (pro-R_P/pro-R_P/G8/A38H⁺, pro-R_P/A⁺/G8/A38H⁺ and pro-R_P/pro-R_P/G8/A38) and one the deprotonated G8^- (G^-/A⁺/G8^-/A38H⁺). As discussed above, while the QM/MM method should perform well for the three mechanisms involving the canonical G8, the accuracy of the calculated barrier height for the G^-/A⁺/G8^-/A38H⁺ mechanism is less certain. Consequently, the real reactivity of G8^- may differ (in any direction) from the calculated data. However, reaction mechanism with G8^- as general base and a protonated A38H⁺ as general acid (G-/A⁺/G8^-/A38H⁺) is consistent with the experimental pH-rate profile.²⁶ The pK_a of 5.5 would correspond to A38 acting as general acid whereas the pK_a of 9.5 would correspond to G8 acting as general base. In contrast, the proton shuttle does not provide any obvious pH dependence of the reaction rate. This indirectly supports the G^-/A⁺/G8^-/A38H⁺ mechanism. However, it does not rule out contributions from other mechanisms. Even though we observed only transient hydrogen bonding between G8(N1) and A-1(2'-OH) in our prior MD studies^22-24, it is possible that this hydrogen bond may coincide with the deprotonation of G8^- and thus may become significantly populated during the short lifetime of a catalytically competent G8^- state that initiates cleavage. We carried out additional classical MD and preliminary ab initio MD (ADMP QM/MM level)^37,78,79 simulations to probe the stability of the active site containing G8^- (data not shown). We found that G8^- bound to the scissile phosphate is metastable and is tolerated in the active site only for time scales of approximately tens of ps.

The plausibility of proton shuttling mechanisms

In all chemically feasible proton shuttling mechanisms considered here, the 2’-OH nucleophile is activated by the G+1(pro-R_P) non-bridging oxygen. Such pro-R_P proton transfer requires reactant states (R) with A-1 C3’-endo sugar-pucker and a newly formed A-1(2’-OH)...G+1(pro-R_P) hydrogen bond. This is at first sight incompatible with the existing crystal structures of the pre-cleavage state of the hairpin ribozyme, many of which bear the inactivating A-1(2’-methoxy) group. However, MD studies starting from the crystal structures but utilizing the native A-1(2’-OH), have shown that the required conformation forms spontaneously in majority of simulations with A38H⁺.^23,24

The proton shuttling to the non-bridging oxygen is not widely considered because of the low pK_a (~1) of the phosphate group.⁸⁰ However, the pK_a of the phosphorane intermediate ranges from 11 to 15,^53,80 suggesting that the basicity of the non-bridging oxygen significantly increases during the nucleophilic attack. All calculations of the ribozymes and uncatalyzed reactions reveal that nucleophilic attack of 2’-oxygen and proton transfer of 2’-OH hydrogen are simultaneous. Thus the basicity of non-bridging oxygen at the time of proton transfer is significantly higher compared to the basicity of intact phosphate group. At first sight (due to much higher acidicity of sulfur compared to oxygen) one may assume that the proton shuttling mechanism should be associated with a significant thio-effect, which is not seen in experiments.⁶⁹ However, our calculations considering thio-substitutions predict only negligible thio-effect on the reaction barrier. If this prediction is correct, the proton shuttling mechanism would not be a priory inconsistent with the lack of observed thio-effects. The possibility of proton transfer to the non-bridging oxygen was suggested as a plausible mechanism in the glmS riboswitch⁸¹ and was also noted previously for the hairpin ribozyme albeit with consecutive proton transfer (from 2’-OH to phosphate group) followed by nucleophile attack of 2’-O^- nucleophile.^17,18 Thus, a proton transfer to the scissile phosphate group should be considered a plausible reaction pathway in small ribozyme catalysis. However, in case of the hairpin ribozyme it would have to be complemented by some additional mechanism or catalytic strategy to explain the experimentally observed pH-rate profiles.

We recently suggested also another mechanism where the proton is shuttled via the A38 base.²³ Although this is consistent with the pH-rate profile, it could not be investigated in the present study because of the necessary repositioning of A38 from the orientation where it uptakes the 2’-OH proton to the orientation where it protonates the leaving 5’-oxygen. It cannot be captured by our potential energy surface scans. Very extensive QM/MM MD runs would be required to describe this mechanism. However, taking into account our QM/MM and QM Gibbs energy profiles of the catalyzed and uncatalyzed reactions, respectively, we found a potential obstacle for this mechanism. We did not observe any intermediate state in any acid-base mechanism with explicit general acid and general base and an unprotonated phosphorane. One may assume that the mechanism with A38 acting as both general base and acid also would lack any intermediate. Without a metastable intermediate, A38H⁺ may simply not have enough time to rearrange into a position suitable for protonating the leaving G+1(O5’) oxygen.

Possible roles of the active site adenine A38

We found that the A38H⁺ may act as a general acid^12,31-34 together with G8^- acting as a general base. In addition, among three chemically feasible proton shuttling mechanism calculated here (pro-R_P/pro-R_P/G8/A38H⁺, pro-R_P/A⁺/G8/A38H⁺ and pro-R_P/pro-R_P/G8/A38), the reaction path with A38H⁺ acting as general acid shares the initial part of the reaction with the pro-R_P/pro-R_P/G8/A38H⁺ mechanism, but involves a product state that is 9.5 kcal/mol less stable due to protonation of the cyclic phosphate. However, subsequent deprotonation of the cyclic phosphate, which may be accompanied by protonation of A38, should lead to energy relaxation of the product. Thus, both mechanisms are chemically equivalent, underlining the versatility of the hairpin ribozyme whose active site A38 could act either by electrostatic stabilization of the transition state or by acting as general acid.

The pro-R_P/pro-R_P/G8/A38 path shares much of its mechanism with the pro-R_P/pro-R_P/G8/A38H⁺ path, and is also chemically feasible for the following reason. Although the pro-R_P/pro-R_P/G8/A38 path has a significantly higher barrier of the exocyclic cleavage step, the rate-limiting step remains the nucleophilic attack, which is not affected by the protonation state of A38. Thus we suggest that both protonated A38H⁺ and canonical A38 are able to electrostatically stabilize the transition state (provided they adopt proper reactant geometry) to such an extent that the exocyclic cleavage step has a lower barrier than the nucleophilic attack, which remains the rate-limiting step. The present QM/MM studies together with our previous MD simulations suggest that the important role of A38H⁺ (compared to A38) could be structural stabilization of the S-turn of the B domain and the catalytically competent active site conformation.²⁴ This agrees with recent crystallographic studies of different A38 substitutions, where a structural destabilization of the native S-turn and active site conformation were observed.³² We note, however, that S-turn destabilization was observed in a simulation with canonical A38, which corresponds to a pH significantly higher than the perturbed pK_a of A38. Still, it is possible that a minor but non-negligible population of protonated A38H⁺ at a pH slightly higher than the pK_a of A38 might suffice to stabilize the native S-turn topology. It also cannot be ruled out that the RNA force field is not fully perfect and over-destabilizes the S-turn.

CONCLUSIONS

We have calculated energy profiles along various meaningful mechanisms of the self-cleavage reaction of the hairpin ribozyme by the QM/MM method.³⁶

We used a QM/MM method with accurate description of the QM core at the expense of less robust conformational sampling. Our data complement the earlier SE/MM studies^17,18 utilizing the opposite strategy, namely, to use a semiempirical approximation (albeit corrected for B3LYP energies) in the description of the QM core but coupled with robust SE/MM MD simulations. Where comparable, the two diverse approaches provide rather consistent results and suggest that several reaction pathways may be competing. However, our approach in all cases predicts the nucleophilic attack of the 2’-OH group coupled with the proton transfer deprotonating the 2’-OH group as rate-limiting, while the SE/MM approach predicts the exocyclic cleavage step as rate-determining. The limitations of both methodologies are discussed above.

We found that the reaction mechanism may involve either a deprotonated G8^- and a protonated A38H⁺ acting as general base and general acid, respectively, or be facilitated by a proton shuttle mechanism via the pro-R_P non-bridging oxygen of the scissile phosphate (the pro-S_P oxygen does not seem to be competitive). We so far did not identify a suitable water molecule that alternatively could play such a proton shuttle role.

While the reaction profiles of the three proton shuttling mechanisms were likely estimated quite accurately, the G8^-/A38H⁺ general acid-base mechanism is prone to be affected by over-polarization of the QM region (a well-known QM/MM problem). Thus, we are not able to accurately determine whether the G8^-/A38H⁺ general acid-base mechanism can effectively compete with the proton shuttling mechanisms.

The experimentally observed pH-rate profiles cannot be straightforwardly explained by the proton shuttling mechanisms which should not lead to any detectable pH dependence. Thus, we propose that at least one other mechanism competes with the proton shuttling mechanisms to produce the experimentally observed pH-rate profile. The G8^-/A38H⁺ general acid-base mechanism is a plausible candidate since it may compete effectively, notwithstanding the discussed uncertainty of our barrier height estimate, with the proton shuttling paths. The main obstacle for this mechanism is the observation that so far classical MD simulations do not reveal a tendency of G8^- to easily establish a catalytically productive geometry. Therefore, we would have to assume either that the G8^- is considerably more reactive (which is rather consistent with our data) or that G8 has a high propensity of transiently forming the proper hydrogen bonding with A-1(2'OH) immediately after deprotonation.

Proton shuttling via the pro-R_P non-bridging oxygen of the scissile phosphate is not often considered a viable option due to the low pK_a of ~1 of the non-bridging oxygen of phosphate. The pK_a of the non-bridging oxygen of the phosphorane, however, is 11-15 and thus its basicity is substantially increased in comparison with the phosphate state.⁵³ The transition and intermediate states of sugar-phosphate backbone self-cleavage involve an sp³d hybridized phosphorus, which has an electronic structure closer to phosphorane than to phosphate so that the basicity of the non-bridging oxygen is rather high. Since we also predict that the deprotonation of the 2’-OH is simultaneous with the nucleophilic attack, the increased basicity of the non-bridging oxygen suggests that proton shuttling cannot be dismissed outright. The lack of experimentally observed thio-effect also does not rule out the proton shuttling mechanisms as any thio-effect was also not observed in our QM/MM calculations.

We found that the protonated A38H⁺ can either act as general acid or be involved in electrostatic stabilization of the transition state. Furthermore, we found that the reaction path involving a canonical A38 is also feasible, assuming a properly structured catalytic core as the starting point. The protonation state of A38 does not perturb or switch the rate-limiting step, which is the nucleophilic attack of the 2’-OH on the scissile phosphate. In addition or alternatively, the protonated A38H⁺ may play a key structural role due to stabilization of the S-turn and the overall active site architecture. Our observations thus suggest that several, energetically equivalent microscopic reaction mechanisms may be in competition during hairpin ribozyme catalysis. Their relative contributions may then be influenced by the specific reaction conditions.