Impact of epistasis and pleiotropy on evolutionary adaptation

Abstract

Evolutionary adaptation is often likened to climbing a hill or peak. While this process is simple for fitness landscapes where mutations are independent, the interaction between mutations (epistasis) as well as mutations at loci that affect more than one trait (pleiotropy) are crucial in complex and realistic fitness landscapes. We investigate the impact of epistasis and pleiotropy on adaptive evolution by studying the evolution of a population of asexual haploid organisms (haplotypes) in a model of N interacting loci, where each locus interacts with K other loci. We use a quantitative measure of the magnitude of epistatic interactions between substitutions, and find that it is an increasing function of K. When haplotypes adapt at high mutation rates, more epistatic pairs of substitutions are observed on the line of descent than expected. The highest fitness is attained in landscapes with an intermediate amount of ruggedness that balance the higher fitness potential of interacting genes with their concomitant decreased evolvability. Our findings imply that the synergism between loci that interact epistatically is crucial for evolving genetic modules with high fitness, while too much ruggedness stalls the adaptive process.

1. Introduction

As a population adapts to its environment, it accumulates mutations that increase the chance for the long-term success of the lineage (or lineages) it represents. The standard picture for this process is Fisher's geometric model [1] of evolution by small steps, i.e. the accumulation of many mutations with small benefit. The evidence supporting this concept, however, is scarce [2] and many open questions remain [3].

More modern treatments use stochastic substitution models [4–8] to understand the adaptation of DNA sequences. If the mutation rate is small and selection is strong, the adaptive process can explore at most a few mutational steps away from the wild-type, so that mutations are fixed sequentially and deleterious mutations play only a minor role (if any) [8]. However, if the rate of mutation is high (and/or selection is weak) mutations can interact significantly and adaptation does not proceed solely via the accumulation of only beneficial (and neutral) mutations. Instead, deleterious mutations play an important role as stepping stones of adaptive evolution that allow a population to traverse fitness valleys. Kimura [9], for example, showed that a deleterious mutation can drift to fixation if followed by a compensatory mutation that restores fitness. Recent work using computational simulations of evolution has shown that deleterious mutations are crucial for adaptation, and interact with subsequent mutations to create substantial beneficial effects [10–14]. Even though the potential of interacting mutations in adaptive evolution has been pointed out early by Zuckerkandl & Pauling [15], their importance in shaping adaptive paths through a fitness landscape has only recently come to the forefront [16–19], and is still a topic of much discussion [20–23]. In this respect, the impact of the sign (i.e. positive or negative) as well as the size of epistasis on adaptation, and how this impact is modulated by the mutation rate, has not received the attention it deserves [24–26].

If we move from the single gene level to networks of genes, the situation becomes even more complex. Gene networks that have been explored experimentally are strongly epistatic [27–30], and allelic changes at one locus significantly modulate the fitness effect of a mutation at another locus. To understand the evolution of such systems, we have to take into account the interaction between loci, and furthermore abandon the limit where mutations on different loci fix sequentially. Here, we quantify the impact of epistasis on evolutionary adaptation (and the dependence of this impact on mutation rate), by studying a computational model of a fitness landscape of N loci, whose ruggedness can be tuned: the NK landscape model of Kauffman [31–34]. The model (and versions of it known as the ‘blocks model’) has been used to study a variety of problems in evolution (e.g. [32,35–40]), but most concern the evolution of beneficial alleles at a single locus. Models that study interacting gene networks (e.g. transcriptional-regulatory networks) have focused mainly on the topology, robustness and modularity of the network [41–44]. Instead, we are interested in the evolution of the allelic states of the network as a population evolves from low fitness to high fitness: how interacting mutations allow the crossing of fitness valleys, and how the ruggedness of the landscape shapes the evolutionary path. The NK model can describe genetic interactions that are more complex than what can be described by analytical models, which generally handle no more than two loci (see [45,46]). Here we use N = 20 loci, while retaining the ability to carry out simulations with high statistics.

As opposed to most work studying adaptation in the NK fitness landscape, we do not focus on population observables such as mean fitness, but rather study the line of descent (LOD) in each population in order to characterize the sequence and distribution of mutations that have come to represent the evolutionary path (e.g. [10,13]). We consider this approach more valuable because it more closely mimics studies in nature where usually the information we gain about evolutionary history is from surviving lineages. The mutations that are found on the LOD are not independent of each other in general, and paint a complex picture of adaptation that involves deleterious and beneficial mutations that are conditional in the presence of each other: a picture of valley crossings, compensatory mutations and reversals. Further, we are specifically interested in evolution in landscapes of intermediate ruggedness, as fitness of neighbouring genotypes in maximally rugged landscapes of K = N − 1 are uncorrelated (see [47] for an analysis of evolution in maximally rugged landscapes).

(a). NK model

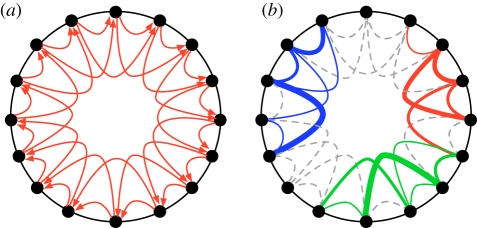
The NK model of genetic interactions [31–33] consists of circular, binary sequences encoding the alleles at N loci, where each locus contributes to the fitness of the haplotype via an interaction with K other loci. For each of the N loci, we create a lookup-table with random numbers between 0 and 1 (drawn from a uniform distribution) that represent the fitness component w_i of a binary sequence of length K + 1. For example, the case K = 1 (interaction with one other locus) is modelled by creating random numbers for the four possible binary pairs 00,01,10,11 for each of the N loci, that is, the fitness component at one locus is conditional on the allele at one other locus (usually adjacent). Because independent random numbers are drawn for the four different combinations, the fitness contribution of a locus to the overall fitness of the organism can change drastically depending on the allele of the interacting locus. The case K = 0 is the simplest, because loci do not interact, and therefore there is no epistasis, except in the case of consecutive mutations at the same locus (reversals), which give rise to ‘self-interaction’. This choice gives rise to a smooth landscape with only a single peak, which any search algorithm can locate in linear time. Increasing K makes the fitness of a locus dependent on a total of K + 1 loci, resulting in a rugged landscape with multiple local peaks. At the same time, the fitness of K + 1 loci is affected by a single mutation, giving rise to pervasive pleiotropy that amplifies the ruggedness of the landscape by increasing the effect of single mutations. Pleiotropy is one of the main assumptions behind Fisher's geometric model, and appears to be common in nature [48,49]. Increasing K increases ruggedness, i.e. it increases both the number of peaks (frequency) and the variation in genotype fitness (amplitude). In the NK model, the increased peak amplitude is caused by pleiotropy: when each fitness component is determined by K + 1 loci, then it is also true that each locus acts pleiotropically, affecting K + 1 fitness components. As the lookup-tables contain 2^K+1 random numbers, the likelihood of finding a haplotype of very high fitness increases with K. The average height of the global peak thus increases with K [50]. For this reason, we expect that adaptation will result in higher fitness when loci interact more, as long as the evolutionary dynamics allows the population to locate the higher peaks. We argue that this effect is not solely an artefact of this model, but that it is also an effect that should be observable empirically (see §3). However, we also provide control simulations where the height of the fitness peaks is normalized. In figure 1a, we show an example haplotype with N = 16 and K = 2, indicating the potential interactions. For high-fitness haplotypes, some interactions are stronger than others (figure 1b) and lead to the formation of clusters of strongly interacting loci (modules).

Figure 1.

NK model haplotypes for N = 16 and K = 2. For these parameters, the fitness contribution of each locus is determined by interacting with two loci (adjacent in the representation shown here), giving rise to blocks of 2K + 1 interacting genes. (a) Interactions between loci represented by lines, with arrows indicating which loci affect the fitness component of other loci. (b) Actual epistatic interactions on a particular high-fitness peak, where the width of the lines indicates the strength of epistatic interactions (thicker lines equal higher values of ɛ, defined in the main text). Three modules of interacting loci are coloured. The remaining interactions (dashed grey lines) are weak (arrowheads omitted for clarity).

While the NK model is an abstract model of a fitness landscape, the number of interacting genes that we consider (N = 20) is comparable with that of viruses (e.g. HIV has 15 proteins, see [51]), or else to modular pathways whose function directly affects the fitness of the organism. Genetic networks with modular structure are common in living organisms [52], and examples of modules with approximately 20 genes or proteins include fibrin blood clotting with 26 genes [53] and human mitochondria with 37 genes [54]. The modular composition of such structures ensures that selection can act on them without affecting other traits at the same time, and the breaking of pleiotropic constraints between modules coding for separate traits is thought to result in networks with a high level of modular partitioning [55].

In our implementation of the NK landscape, we choose the fitness of each haplotype to be the geometric mean of the values w_i found in the lookup-tables:

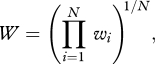1.1

rather than the average as is done traditionally [33]. This form is more realistic than its additive counterpart and has been suggested before [39,56]. In such a landscape, single mutations can potentially have a large effect on fitness, including lethality. The landscape defined by equation (1.1) gives rise to very few neutral mutations because each locus contributes to fitness in one way or the other, and we have not explicitly introduced alleles with zero fitness (lethals). We note that the results presented here do not depend on whether fitness is the arithmetic or the geometric mean (electronic supplementary material, figure S1).

(b). Quantifying epistasis

Two mutations (A and B) occurring on a haplotype with wild-type fitness W₀ are said to be independent if the fitness effect of the joint mutation equals the product of the fitness effect of each of the mutations alone. If the fitness effect of the double mutant is W_AB/W₀, while the fitness effect of each of the single mutations is W_A/W₀ and W_B/W₀, respectively, then mutational independence implies (see illustration in figure 2)

1.2

Figure 2.

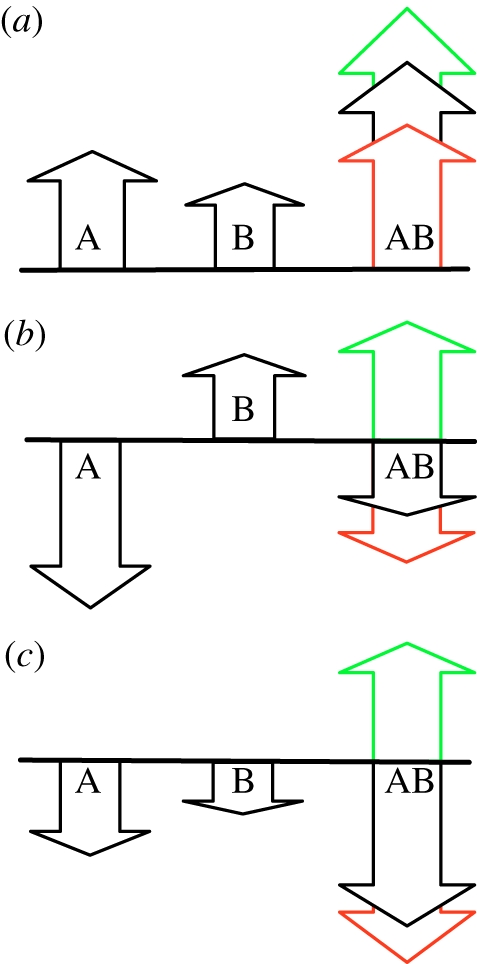
Schematic illustration of epistasis. Two mutations A and B can interact epistatically in different ways with varying effects on fitness. The fitness of the wild-type is represented by the black baselines, and the heights of arrows represent the fitness after one mutation (W_A or W_B) and after both mutations (W_AB). Green, positive epistasis, red, negative epistasis, black, no epistasis. In (a), two independently beneficial mutations may have their joint effect increased or diminished (W_AB larger or smaller), while in (b) the independent effect of the two mutations is deleterious and beneficial, respectively, and the combined expected effect on fitness is deleterious. In (c), each mutation by itself is deleterious, but when they interact, the result can be reciprocal sign epistasis (green arrow). These sketches illustrate an additive model, where the sum of W_A and W_B is equal to W_AB without epistasis. In our model, using the geometric mean this corresponds to taking the logarithms of the fitness.

We quantify epistasis as the deviation from this equality, such that:

1.3

is zero when the combined effect of the two mutations is the same as the product of the individual effects on fitness. This definition is equivalent to the usual quantitative definition of epistasis in a two-locus two-allele model (cf. [57], but see [17] for a different definition) and transforms to the well-known additive definition of epistasis when the individual fitness effects are replaced by their logarithms (e.g. [58]). Such a quantitative measure of epistasis was also used in assessing epistasis between mutations in experiments with Escherichia coli [59] and digital organisms [60]. For organisms on the LOD (see §4) of an evolutionary run, A and B refer to two substitutions that need not be adjacent either on the LOD or on the haplotype. We do see examples of non-consecutive mutations interacting, such as when a valley is crossed in more than one step (e.g. in figure 3, K = 4), but here we restrict ourselves to studying the interaction between adjacent mutations on the LOD only, so that if W_AB is the fitness of the haplotype that has both substitutions A and B, then the type preceding this sequence on the LOD has fitness W_A. W_B is found by reverting the first substitution (A), and measuring the fitness of the haplotype carrying only the second mutation (B).

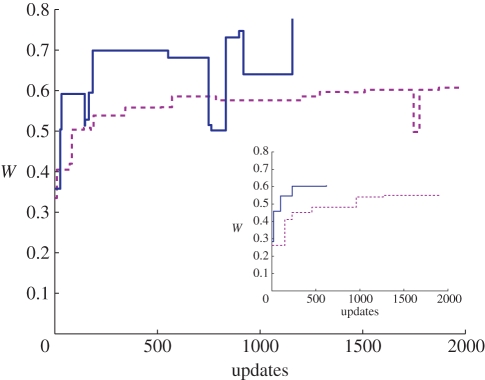
Figure 3.

Representative examples of adaptation in single lineages. Fitness on the LOD for a simulation lasting 2000 updates. The adaptive ascent is only shown until the lineage has attained the same fitness as it has after 2000 updates, for N = 20, K = 0 (dashed line) and K = 4 (solid line), at a high mutation rate μ = 10⁻². The inset shows an example LOD at μ = 10⁻⁴, which has only beneficial mutations on the LOD.

2. Results

We studied the impact of epistasis on adaptation by conducting evolutionary runs with different K (which changes landscape ruggedness) and a fixed number of loci (N = 20), for different per-locus mutation rates μ at a constant population size 𝒩 of 5000 individuals. In order to study only that part of evolutionary adaptation where a population climbs a local peak, each evolutionary run was initiated with a random selection of haplotypes of less than average fitness so that initially many beneficial mutations are available, akin to experiments with RNA viruses that are forced through bottlenecks [2,61], or are subject to environmental change [62]. The evolutionary dynamics of each run were similar in most cases: the population quickly adapts and situates itself near the top of a local peak, after which it enters a period of stasis when exploration of the adjacent parts of the landscape does not turn up any more beneficial mutations (figure 3). This protocol is different (in terms of adaptation) from experiments in which only deleterious effects of mutations are studied, and advantageous mutations are found to be rare [63]. Thus, in this work we study the transient period of adaptation as opposed to mutation–selection balance. Initiating populations with only a single genotype does not change the evolutionary dynamics we observe (electronic supplementary material, figure S1).

(a). Epistatic pairs on the line of descent

The mode of fixation of mutations, that is, whether they go to fixation one by one or whether multiple mutations can interact in the same individual before fixation, is determined by the mutation supply rate, i.e. the product of the mutation rate per genome per generation and the population size, μ_g𝒩. When this product is less than about 10, mutations usually go to fixation or are lost before the next mutation occurs [7,38,64,65]. This does not imply that mutations cannot interact, but instead that deleterious mutations are unlikely to be incorporated into the genome. When the mutation supply rate is significantly larger than 10, mutations occur frequently enough that they can interact with each other before the first goes to fixation (the concurrent mutations regime [66–68]). Given our population size of 5000 and 20 loci, at the smallest rate we investigate (μ = 10⁻⁴), the mutation supply rate is 10, and mutations largely go to fixation separately, with the result that the fraction of deleterious substitutions is less than 1 per cent. The mutation supply rates we investigate range from 10 to 1000, but are substantially smaller than the supply rate in the long-term evolution experiment with E. coli for example. In that case, an upper bound on the mutation rate per genome is μ_g ≈ 0.74 × 10⁻³ [69], while the effective population size is 𝒩 ≈ 3 × 10⁷ [70], for a μ_g𝒩 ≈ 22 000. While the per-locus mutation rate we use is higher than what we would expect in organisms that do not express a mutator phenotype [71], we expect that the results will not change significantly if we could decrease the mutation rate while at the same time increasing the population size commensurately. In fact, it was shown (at least for neutral evolution [64]) that evolutionary dynamics is essentially unchanged if the two factors μ_g and 𝒩 are varied independently, as long as the product is the same.

When the mutation supply rate is low, we do not expect that epistasis between mutations plays a significant role in the fixation of any individual mutation, simply because it is unlikely that any pair went to fixation in tandem. As a consequence, we expect that the number of interacting pairs on the LOD of populations evolving at low mutation rate equals the rate at which they were produced. In other words, selection cannot amplify or reduce the number of interacting pairs. It is easy to compute the naive expectation of how many pairs of mutations interact by chance in the NK model. If we ignore ‘self-interactions’ (a mutation can interact with itself when it is reversed by the next mutation on the LOD), the fitness of each locus is determined by K others, but also plays a role in the fitness determination of K other sites. As a consequence, 2K pairs out of the possible N − 1 pairs (each locus can potentially interact with N − 1 others in the absence of reversals) are interacting owing to chance alone, that is, simply because they were within K of each other. If we find more than 2K/(N − 1) mutational pairs on the LOD that interact epistatically, then we can conclude that these interactions contributed to why such pairs are on the LOD, in other words, that epistasis is selected for. However, in reality, mutational events can include more than two mutations per haplotype, leading to a fraction of interacting mutations that is elevated from the naive expectation 2K/(N − 1). To calculate the corrected fraction, we numerically obtain the fraction of all mutational pairs that will interact before the mutations are screened by selection by randomly mutating pairs of haplotypes and testing if any mutations are a distance of K loci or less away from each other (see electronic supplementary materials for details).

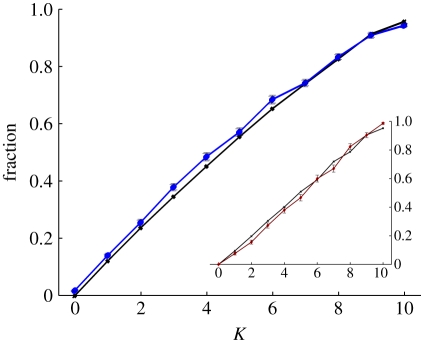
We found that the fraction of epistatic pairs on the LOD differs significantly from the fraction available (the pre-selection prediction) when the mutation rate is high (μ = 10⁻²; figure 4). We conclude that because deleterious mutations enable organisms to cross valleys between peaks, the LOD is enriched by epistatic pairs that include deleterious mutations. For smaller mutation rates this is not the case, as valleys cannot be crossed (see inset in figure 4 for μ = 10⁻⁴).

Figure 4.

Fraction of epistatic pairs on the LOD. The fraction of mutational pairs on the LOD that interact epistatically (circles) is larger than the numerical pre-selection prediction (crosses) for μ = 10⁻² (p = 0.013672, Wilcoxon signed-rank test). For smaller mutation rates (μ = 10⁻⁴ shown in inset), there is no significant difference from the expectation (p = 0.23242, Wilcoxon signed-rank test). Reversals have been excluded from this analysis. Lines are drawn to guide the eye.

(b). Mechanism of interaction between mutations

The majority of consecutive pairs of mutations on the LOD are pairs of beneficial mutations (BB pairs; see electronic supplementary material, figure S3a), followed by BD, DB and DD pairs (see table 1 for definitions). The relative fraction of these pairs depends on the mutation rate, but is roughly independent of K. How (and how often) these mutations interact, however, does depend on K. Let us first look at the second mutation of an interacting pair of substitutions, to which we can give the labels B⁺, B⁻, D⁺ and D⁻, depending on whether they were beneficial or deleterious on the background of the preceding substitution, and on whether they interacted positively or negatively with it.

Table 1.

Relationship between positive/negative and synergistic/antagonistic epistasis for different mutational pairs. (Positive (ɛ > 0) and negative (ɛ < 0) epistasis imply synergistic/antagonistic if the two mutations are both beneficial or both deleterious, but when the mutations are of opposite effect, the meaning of synergy or antagony is unclear (dashes). A substitution can be characterized by how it interacts with the mutation that precedes it on the LOD using the sign of ɛ. Beneficial substitutions are designated as B⁺ or B⁻, depending on whether they interacted epistatically with the preceding substitution to form positive or negative epistasis, respectively. D⁺ and D⁻ similarly indicate deleterious substitutions with positive and negative epistasis. Alternatively, writing BB⁺ indicates that both substitutions increased fitness (with the second B being on the background of the first), and that the second substitution had a larger beneficial effect on the background of the first than it would have had on the background of the wild-type. DB⁻ denotes a deleterious followed by a beneficial substitution that did not increase fitness as much as it would have if the deleterious substitution had not occurred.)

designation	epistasis	sign	effect	designation	epistasis	sign	effect
DD−	ɛ < 0	negative	synergistic	DB−	ɛ < 0	negative	—
DD+	ɛ > 0	positive	antagonistic	DB+	ɛ > 0	positive	—
BB−	ɛ < 0	negative	antagonistic	BD−	ɛ < 0	negative	—
BB+	ɛ > 0	positive	synergistic	BD+	ɛ > 0	positive	—

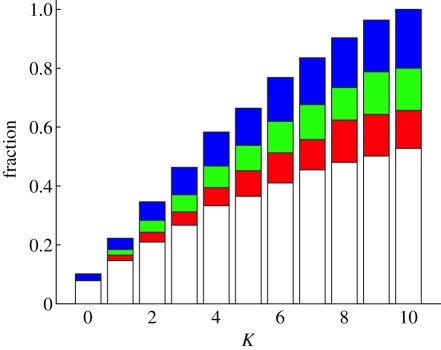
All four types of epistatic mutations increase in frequency at the expense of mutations that do not interact epistatically (figure 5). Overall, we observe that as K increases, the population uses deleterious mutations that interact epistatically to adapt more efficiently, as valleys are crossed to ascend higher fitness peaks. This effect is severely diminished when the mutation supply rate is low (μ_g𝒩 < 10), in which case mutations typically go to fixation before a second mutation occurs (electronic supplementary material, figure S2). Crossing fitness barriers is enabled mostly by pairs of the type DB⁺, that is, a deleterious mutation followed by a mutation whose benefit is enhanced by the presence of the preceding deleterious mutation (see electronic supplementary material, figure S3b). This synergy between deleterious and beneficial mutations can go as far as sign epistasis, i.e. a mutation that is beneficial only in the presence of the preceding deleterious mutation, but deleterious in its absence. At K = 0, most mutational pairs consist of two beneficial mutations that do not interact epistatically, except when the second mutation occurs at the same locus as the first, thereby reversing the first mutation (figure 5). Reversals mostly consist of deleterious–beneficial pairs exhibiting positive epistasis DB⁺, with a small minority of beneficial–deleterious pairs exhibiting negative epistasis (BD⁻). Once K = 5, most of the DB pairs show positive epistasis, showing that interacting mutations ease the traversal of fitness barriers (electronic supplementary material, figure S3).

Figure 5.

Fraction of types of the second substitution among all epistatic pairs. Blue, D⁻; green, B⁻; red, D⁺; white, B⁺. Height of bar shows the fraction of all epistatic mutations of a particular type on the LOD for μ = 10⁻². At this mutation rate, a considerable fraction of epistatic substitutions are D⁺ and D⁻, while those fractions are lower for μ = 10⁻³ and 10⁻⁴ (electronic supplementary material, figure S2).

(c). Correlation between epistasis and beneficial effect

We define the mean size of epistasis on the LOD as the mean ɛ between all consecutive pairs:

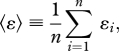2.1

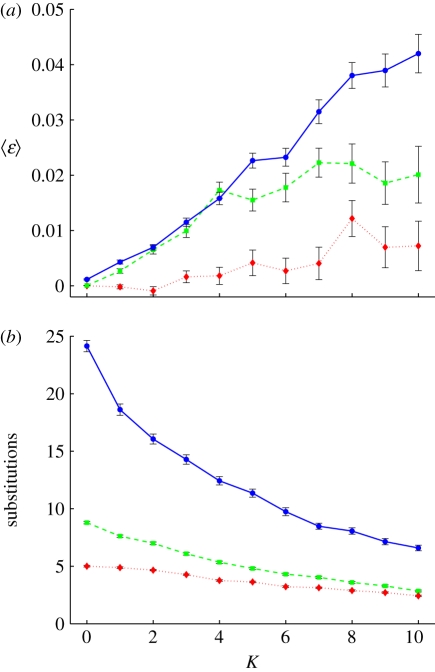
where the sum runs over all substitutions on the LOD, ɛ_i is the size of epistasis of the ith pair (between mutation i + 1 and i on the LOD, given by equation (1.3)), and n is the number of pairs (one less than the number of substitutions). This measure has an expectation value of zero if negatively and positively interacting pairs occur with equal likelihood, and with equal and opposite strength, on the LOD. We are studying the mean of ɛ in order to compare this measure across evolutionary runs that differ in the average number of mutations on the LOD. We find that 〈ɛ〉 increases with K for all three mutation rates (figure 6a). Higher mutation rates result in larger 〈ɛ〉 on the LOD, because the higher rate decreases the waiting time for new mutations, making it easier for a lineage to cross a valley in the fitness landscape via a deleterious mutation. If a mutation is deleterious, the lineage that carries this mutation needs another mutation that at least compensates for the fitness loss before the lineage goes extinct.

Figure 6.

Mean ɛ and substitutions on the LOD. (a) 〈ɛ〉 on the LOD as defined by equation (2.1). Each datum is the average of 200 LODs and error bars are s.e. Mutation rates are μ = 10⁻² (blue line), μ = 10⁻³ (green dashes) and μ = 10⁻⁴ (red dots). Population size is 5000, N = 20 and the replacement rate is 10%. Lines are drawn to guide the eye. (b) Total number of substitutions as a function of K, mutation rates and colours as in (a).

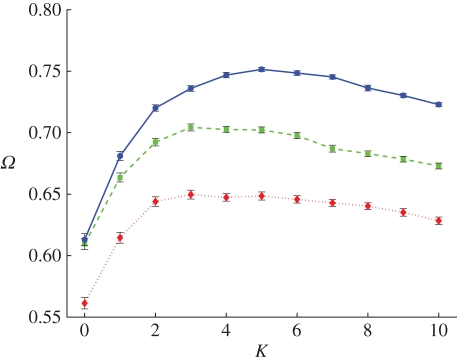
While 〈ɛ〉 increases with K, the number of substitutions during adaptation decreases (figure 6b), and the fraction of deleterious substitutions is mostly unchanged between low and intermediate K (electronic supplementary material, figure S4). The origin of the decrease in the number of substitutions is clear: for K = 0, mutations that increase fitness are not difficult to find because the landscape is smooth. More rugged landscapes risk confining the population to local peaks, and even though valleys can be crossed towards higher fitness peaks that are close, ultimately the ruggedness puts a stop to further adaptation [72]. Even though the number of substitutions decreases with K, higher fitness levels are achieved at intermediate K compared with lower K. Indeed, the attained fitness, Ω (the fitness of the best genotype at the end of a simulation run), increases with K up to intermediate values (figure 7), and the time to reach the attained fitness is shorter when K is higher (electronic supplementary material, figure S5). This also explains why the observed attained fitness for K = 0 and μ = 10⁻⁴ is not maximal in figure 7a as we would expect for a smooth landscape: the time to reach the peak is just too long given the length of the run. Increasing the simulation time to 100 000 updates does give the population enough time to reach the peak (data not shown). For K ≤ 5, the attained fitness is an increasing function of both 〈ɛ〉 and the mean selection coefficient (electronic supplementary material, figure S6), that is, higher 〈ɛ〉 goes hand in hand with higher achieved fitness.

Figure 7.

Attained fitness Ω as a function of K for three different mutation rates (colours and parameters as in figure 6a) on LOD. K_opt, the point at which Ω is maximal, is larger for higher mutation rates.

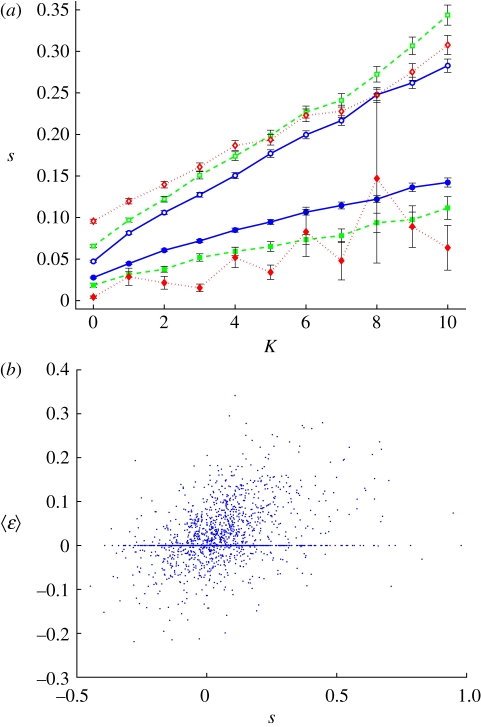
That higher fitness can be achieved with fewer substitutions seems counterintuitive (see [73]), yet is an effect achieved both by epistasis and pleiotropy. Pleiotropy can result in a single mutation increasing K + 1 fitness components at the same time, leading to the same fitness increase with fewer mutations. With luck, one mutation will increase fitness in all or most of the K + 1 components that it affects, amplifying the effect of the mutation. Pleiotropy is therefore directly responsible for the increase in potential selection coefficients as a function of K. Even though the chance that a mutation will have a positive effect on all K + 1 interacting loci becomes smaller as K increases, the relationship between fitness increase per substitution is an approximately linear function of K (figure 8a), indicating that each mutation on the LOD carries a ‘bigger punch’ as the number of interacting loci, K, increases. Both peak frequency and amplitude correlate with K, and together these two cause the increase in average selection coefficients for mutations by increasing the slope leading up to the peaks. Just such an interaction between traits to achieve higher fitness has also recently been observed in quantitative trait loci affecting skeletal characters in mice [49].

Figure 8.

Strength of selection coefficients and epistasis. (a) The effect on fitness of beneficial, s_b (open symbols), and deleterious substitutions, s_d (solid symbols), both increase approximately linearly as a function of K (colours and parameters as in figure 6). (b) Correlation between size of epistasis 〈ɛ〉 and effect of substitutions s, shown here for K = 5 and μ = 10⁻². Reversal substitutions are excluded because they do not contribute to adaptation. Including them would only strengthen the overall correlation. Pearson correlation coefficient r = 0.3549.

Besides changing the degree of pleiotropy, K also directly modulates epistasis. More epistasis causes the frequency of peaks and valleys to increase, which, in addition to pleiotropy, causes increased selection coefficients. The correlation between the benefit a mutation provides and the amount of epistasis ɛ between this and other mutations, as evidenced by figure 8b, mirrors the observation of a correlation between directional epistasis and the deleterious effects of mutations seen in other computational studies of evolution [43,74,75], as well as in protein evolution in vitro [76], bacterial evolution [77] and even viroids [78]. Because beneficial mutations are rare in most of these studies, a correlation between positive effects and epistasis has not been shown before. Varying the mutation rate does not qualitatively change these results.

As K increases, the mean height of peaks decreases beyond K = 1 (electronic supplementary material, figure S7) because many more shallow peaks appear than high ones. Yet, the global peak height continues to increase beyond K = 5 (but note that peaks can never exceed W = 1, no matter what the K is). Thus, part of the observed effect comes from the fact that landscapes with higher K contain higher peaks [50]. To test whether the observed increase in mean beneficial effect with K of single substitutions solely stems from the increase in peak height, we ran control simulations in which the fitness landscape is normalized such that the range in fitness is the same across all K. In this case, the global peak is fixed at the same height in all fitness landscapes, while the frequency of peaks remains unaffected. In this instance of the NK model, the attained fitness is never larger than what can be attained at K = 0, and decreases as K increases owing to the increased ruggedness of the landscape (see electronic supplementary material, figure S8a). Yet, the selection coefficients are still an increasing function of K even in the normalized landscape, but the slope is shallower than for the non-normalized model (electronic supplementary material, figure S8b). Thus, beneficial mutations still cooperate synergistically for a ‘bigger punch’ per mutation, even if the peak height is normalized.

3. Discussion

We studied how interacting mutations impact the evolutionary dynamics for populations evolving in an artificial fitness landscape in which the ruggedness is determined by a single parameter K, in the ‘strong mutation’ limit. We found that increasing the ruggedness of the landscape by increasing K has several consequences. First, the mean epistatic effect per substitution 〈ɛ〉 monotonically increases with K (figure 6). Second, the number of substitutions on the LOD decreases, while the fraction of those substitutions that are deleterious or beneficial remains largely unchanged (electronic supplementary material, figure S4). We might intuit that fewer beneficial substitutions will impair adaptation, but here we instead observe a third effect, namely that those higher peaks that appear as K is increased can be located faster and in fewer steps (figure 7), because the mean selection coefficient per mutation (figure 8) increases with K in an approximately linear fashion. This effect is robust even if we correct for the increasing height of fitness peaks with increasing K in this landscape, and reflects the proliferation of adaptive opportunities that come with synergistic interactions.

Ruggedness is normally viewed as an impediment to adaptation, because the presence of valleys means that a lineage has to suffer a decrease in fitness before it can gain a fitness advantage [14]. However, in the NK model, increased ruggedness not only translates into more peaks to ascend and more valleys to cross, but also increases both the fitness difference between the peaks and the valleys (amplitude) and the height of the global peak. The attained fitness is maximal at K = 3 to 5, from which we infer that an intermediate amount of epistasis and pleiotropy is most conducive to adaptation (figure 7). The population is able to take advantage of the presence of higher peaks that exist for higher K, particularly for the highest mutation rate. The observed decrease in the attained fitness at K > 5 is caused by longer waiting times to new mutations (as was shown in Clune et al. [14]), which is a consequence of the increasingly rugged structure of the NK landscape for high K. As we increase K, the increased average effect of single mutations (either beneficial or deleterious) is counterbalanced by the increasing ruggedness of the landscape, which makes it more likely that the population becomes stuck on a suboptimal fitness peak instead of locating the global peak. This lowers the average attained fitness of the population compared with lower K.

As the number of peaks increases with K (thus shortening the mutational distance between peaks), the fitness decrease that an organism must endure while traversing the valley in between the peaks becomes larger. As a consequence, successful lineages must have an increased benefit per substitution for higher K. Indeed, with increasing K, the distribution of single-substitution fitness effects becomes broader (electronic supplementary material, figure S9), allowing some mutations to increase the fitness of the haplotype by as much as a factor of K + 1 compared with the case of K = 0. This is an effect of pleiotropy, which is inseparable from epistasis in this implementation of the NK model, and has a direct counterpart in empirical fitness landscapes as well [49]. Further investigation into the different roles and impacts of epistasis and pleiotropy is important for the understanding of the dynamics of the NK model, as well as for the relative roles of epistasis and pleiotropy in adaptive evolution.

As discussed, the results presented here are a consequence of the increased frequency and amplitude of the peaks as well as the increase in global peak height (the height of the highest peak) of the landscape as K is increased. It could be argued that this increase in the size of the highest peaks (even as the mean peak height decreases) is an artefact of the NK model that has no counterpart in how biological fitness landscapes change when the number of interactions between genes changes. Instead, we believe that the increase in adaptive potential is germane, because interacting loci can work synergistically to produce higher fitness when compared with a set of non-interacting loci. In a sense, increasing K creates a more modular landscape of epistatically interacting genes. Indeed, searching for epistatically interacting genes is one method to search for modules in metabolic genes [79], and a clustering method has been used recently to find modules from epistatically interacting pairs of genes in yeast [30]. The authors of that study found a dependence of the fraction of pairs that are epistatic on the size of the deleterious effect of a mutation that mirrors the dependence we observe here (electronic supplementary material, figure S10), and thus strongly epistatic pairs of mutations have the largest fitness effect also in yeast.

For the NK model, we can understand why the global peak fitness increases as a direct consequence of the modularity of the fitness components: each fitness component w_i is controlled by K + 1 loci, giving 2^K+1 possible values. It is more likely to find higher fitness values in those larger samples. So, just as in the biological pathways with modular structure in yeast, the more loci that contribute to a fitness component, the better this component can be fine-tuned to optimize its contribution to fitness. Given these considerations, we contend that the NK fitness landscape, obtained from interacting loci that synergistically contribute to the function of traits, is a reasonable and appropriate model for describing interacting gene networks in biological organisms.

4. Methods

(a). Simulations

We simulate the evolutionary process by randomly removing 10 per cent of the population every update, and replacing them with copies of a subset of the remainders, selected with probabilities proportional to individual fitness. This is akin to the Wright–Fisher model for haploid asexuals [80], but with overlapping generations. In evolution experiments implemented in flow reactors (for example, continuous culture experiments, see [81]), the replacement rate is akin to the flow rate of the reactor. Varying the replacement rate does not change the conclusions we reach in this study. We define the period of adaptation as beginning at update zero, and ending when the lineage first reaches the same fitness that it acquired at the end of the simulation. In this manner, we exclude from the analysis reversal mutations (i.e. mutations undoing previous mutations at the same locus) that occasionally occur after a fitness peak has been ascended. If we included those reversals, both the number of deleterious substitutions and the amount of epistasis measured would be affected, even though they do not contribute to adaptation.

In order to study the part of the evolutionary trajectory that corresponds to climbing the nearest fitness peak, we choose as the ancestral population a sample of individuals with fitness in the lowest 50 per cent of a randomly generated population where the haplotypes of the individuals are uncorrelated. As a consequence, many beneficial mutations are possible, so individual lineages may climb different peaks (except for K = 0, in which case there is only one peak), and the lineage that happens to climb the fastest will be most likely to outcompete the other organisms in the population. This protocol is similar in spirit to that used in earlier studies [2,61], where a population of Φ 6 viruses was put through bottlenecks in order to study the dynamics of re-adaptation. For each mutation rate and for each K, we collected 200 independent evolutionary runs and extracted one LOD (see below) from each. In our results, we report the average values across these 200 samples, and provide standard errors.

The probability of each locus changing its binary value is set by a per-site mutation rate μ. While the average rate of mutation is fixed, the process itself is stochastic so that the distribution of the number of mutations per organism is Poisson-random with the given mean. We vary K from 0 (no interaction between neighbouring loci) to 10, where each locus interacts with 10 of its neighbouring loci. Because the haplotypes are circular, for K = 10 all mutational pairs interact (100% of mutational pairs are epistatic).

(b). Line of descent

We study the sequence of mutations that accumulates as populations adapt from an initial state of low fitness to the maximum fitness they can attain given their environment, by studying a single individual lineage from its inception to the end of the simulation run (typically 2000 updates of the population). We do this by picking the most fit organism after a set number of simulation updates, and then track this individual's ancestry all the way back to the beginning of the simulation. This sequence of haplotypes defines a sequence of mutations as the LOD, and we discard all other data from that simulation [10,13]. For asexual populations in a single niche (no frequency-dependent selection), the LOD accurately represents the population as each substitution that appears on the LOD between the origin and the most common recent ancestor is shared by the whole population.