Evidence for water structuring forces between surfaces

Abstract

Structured water on apposing surfaces can generate significant energies due to reorganization and displacement of water as the surfaces encounter each other. Force measurements on a multitude of biological structures using the osmotic stress technique have elucidated commonalities that point toward an underlying hydration force. In this review, the forces of two contrasting systems are considered in detail: highly charged DNA and nonpolar, uncharged hydroxypropyl cellulose. Conditions for both net repulsion and attraction, along with the measured exclusion of chemically different solutes from these macromolecular surfaces, are explored and demonstrate common features consistent with a hydration force origin. Specifically, the observed interaction forces can be reduced to the effects of perturbing structured surface water.

Introduction

Hydration energies of charges and polar molecules are large, and the displacement of water in the binding or folding reactions of macromolecules has significant energetic consequences [1]. Water organized by these groups generally has preferred orientations. Additionally, nonpolar surfaces seem to structure water [2] and their interaction with water is considered to underlie the hydrophobic force [1,3]. Since water forms hydrogen-bonded networks, the structuring of water by charges, polar, and nonpolar groups on a macromolecular surface will likely perturb adjacent water layers. What happens when two surfaces are brought into close proximity, such that the last few water layers on each surface are in contact? Can water still optimally hydrate each surface? As surfaces approach, the change in hydration energy defines a hydration force. There is significant experimental and theoretical evidence that water in tight spaces is far different from bulk water [4–7]. How much water is perturbed by surfaces is still a much debated question. The range of water perturbation seems dependent on technique. Estimates vary from indicating that only the first layer is different from bulk water [8,9] to a perturbation that extends several layers into solution [10–16]. Extended surfaces seem to order water better than small molecules [11,12]. Water structuring is additionally convoluted with electrostatics through nonlocal dielectrics [17,18] and dielectric saturation [19]. Enough uncertainty exists in modeling water that there is not a definitive expectation for hydration forces as for van der Waals interactions or electrostatics. An interaction of molecules acting through water structuring has been advocated by several others [20–25].

Our basic approach has been to look for commonalities among measured forces for many different classes of macromolecules. We measure forces using the osmotic stress technique [26,27]. Ordered arrays of macromolecules are equilibrated against a polymer solution, very typically PEG. The polymer chosen is excluded from the macromolecular array and applies an osmotic pressure on it. PEG is a particularly useful polymer since it is excluded from many macromolecules. Salts, water, and small solutes equilibrate between the polymer solution and condensed array. The average interaxial spacing between macromolecules, D_int, can be determined by x-ray scattering to good accuracy. The resulting osmotic pressure Π vs D_int curves are thermodynamic force measurements. Combined measurement of the osmotic pressure and volume V (obtained through D_int) gives a convenient entry into many thermodynamic expressions based on the Gibbs-Duhem equation [28–31].

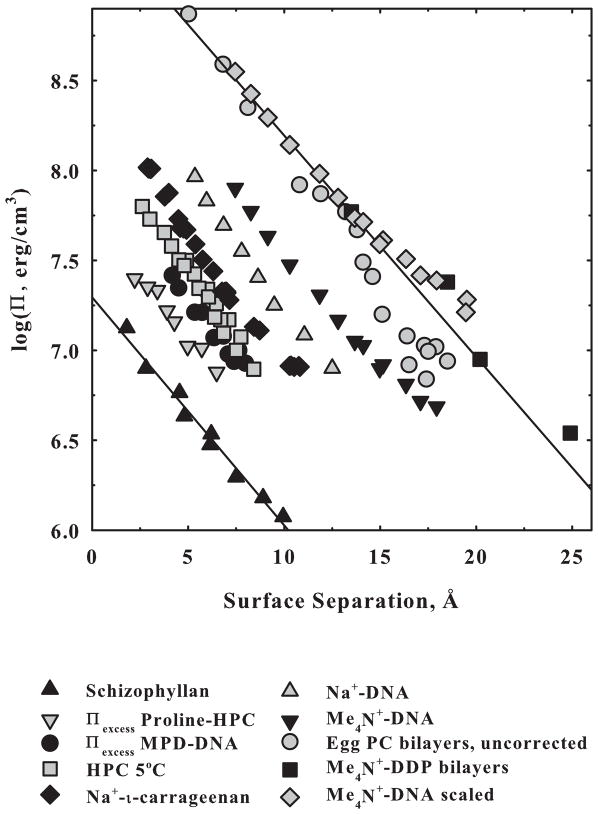
Figure 1 shows the dependence of osmotic pressure on surface to surface separations for a variety of biologically relevant macromolecules ranging from highly charged DNA and didodecylphosphate bilayers to net neutral, zwitterionic PC bilayers to completely uncharged carbohydrates schizophyllan and hydroxypropyl cellulose. The striking feature is the common exponential dependence of the force on distance with an apparent decay length of ~ 3–4 Å. This common force characteristic for these very different systems suggests a common origin that we have concluded is due to water structuring. The range of interaction is ~ 15–20 Å, which corresponds to about three to four water layers on each surface. The chemical potential change of a water molecule at Π = 10⁶ erg/cm³, the osmotic pressure at the large separations, is quite small, only ~10⁻³ kT. When summed over the many water molecules separating the surfaces, however, the integrated energies can be large. The pre-exponential factors or force amplitudes vary more than 100-fold for this set of macromolecules. These force curves smoothly change, not at all like the oscillatory forces seen experimentally and predicted theoretically between hard, fixed surfaces [22]. Biological surfaces are soft and compliant.

Figure 1.

A comparison of forces measured for several different systems in ordered arrays. Π is the osmotic pressure applied by the excluded polymer in the bulk solution acting on the condensed macromolecular phase. Distances are given as approximate surface-to-surface separations of macromolecules. Schizophyllan [55] and hydroxypropyl cellulose (HPC) [30] are completely uncharged. DNA in NaBr and TMABr, tetramethyl ammonium, (unpublished data) and ι-carrageenan in NaCl (unpublished data) are highly charged linear double helices. DDP (didodecyl phosphate) in TMA⁺ salt is a highly charged planar bilayer (data from [56]). Egg PC is a zwitterionic planar bilayer that has the phosphate and quaternary amine of the head group covalently linked (data from [57]). The TMA⁺-DNA force has also been corrected to planar packing and to the same surface area/phosphate as DDP. The close overlap of the corrected TMA⁺-DNA, egg PC (that has about the same surface area/molecule as DDP) and TMA⁺-DDP forces illustrates the striking similarity of these homologous systems. The salt concentrations for the charged surfaces are high enough that forces are insensitive to ionic strength. The excess pressures due to solute exclusion are also shown for the nonpolar alcohol methylpentane diol (MPD) at 1 molal interacting with DNA and for zwitterionic proline at 1 molal interacting with uncharged HPC. The straight lines show a decay length of ~4 Å. The force amplitudes span a range greater than 100-fold.

An order parameter theory was initially developed to account for the forces first seen between zwitterionic lipid bilayers [32,33]. It is based on a surface structuring of water on the macromolecular surface that propagates into solution characterized by a water-water correlation length, λ. Correlation lengths of 3 – 5 Å have been observed for density fluctuations in pure water [34,35]. Two exponential forces are expected from the order parameter theory [36]– one from the direct interaction of hydration structures on apposing macromolecular surfaces characterized by a decay length λ. This term can be either attractive or repulsive depending on the mutual structuring of water on the two surfaces; the hydrogen bonding of the intervening water can be either disrupted or reinforced as surfaces approach [29,36,37]. Attraction will occur when complementary water structures on apposing surfaces are correlated. A second order term that gives rise to an exponential force with a λ/2 decay length reflects a disruption of the stabilizing water structure extending out into solution from one surface simply due to the presence of another surface. This force is always repulsive and resembles in form electrostatic image charge repulsion. The magnitude of the force depends on the strength of water structuring on the surface. In spite of its simplicity, this formalism provides a good first order description of the forces between divergent macromolecular systems.

In the rest of this review, we will focus on two specific and divergent systems, highly charged DNA and nonpolar uncharged hydroxypropyl cellulose (HPC). The ~4 Å decay length force is prominent in both systems not only as a repulsion but also, under appropriate conditions, as an attraction that drives spontaneous assembly. Furthermore, the exclusions both of nonpolar alcohols from DNA and of salts and polar solutes from HPC are also characterized by this 4 Å decay length force. Hydration forces measured between lipid bilayers have been extensively reviewed [27,38–40].

DNA

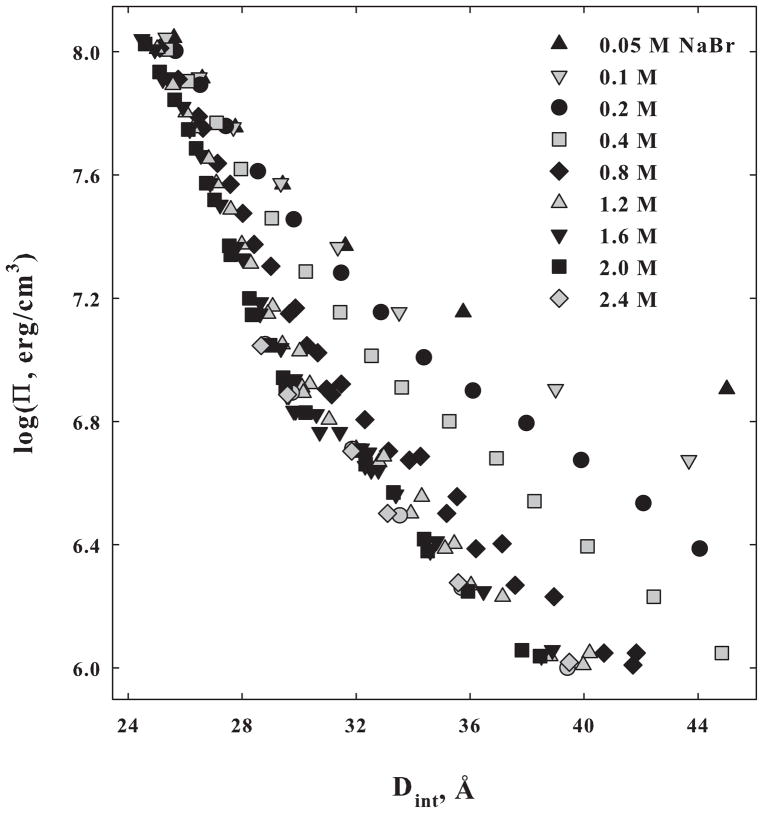
Figure 2 shows NaDNA force curves as dependent on NaBr concentration. Forces converge to a salt concentration insensitive interaction at high osmotic pressures. At low osmotic pressures, two force regimes are apparent. The force is salt concentration dependent for ionic strengths less than ~ 0.8 M as would be expected for an electrostatic interaction. The apparent decay length at low pressures is close to the expected Debye-Huckel shielding length for these ionic strengths. At salt concentrations higher than ~0.8 M, the forces at lower pressures converge to a single curve. The apparent decay length of the salt insensitive, low pressure force is ~4.2 Å. At these high ionic strengths, the presumed hydration force dominates the electrostatic interaction. After subtracting the low pressure forces, the high pressure force has a exponential decay length of ~2.0 Å that is independent of salt concentration over the entire range measured.

Figure 2.

The dependence of DNA-DNA forces on NaBr concentration is shown. The diameter of DNA is ~ 20 Å. Forces converge at high pressures for all salt concentrations. For ionic strengths less than ~ 0.8 M, an electrostatic interaction dominates at low pressures. The decay length of the apparent exponential in this regime is consistent with the Debye-Huckel shielding length. At higher ionic strengths, the forces at low pressures converge. The apparent exponential decay length is ~ 4.2 Å. The decay length of the high pressure force obtained after subtracting the low pressure forces is ~ 2 Å and has an amplitude independent of salt concentration.

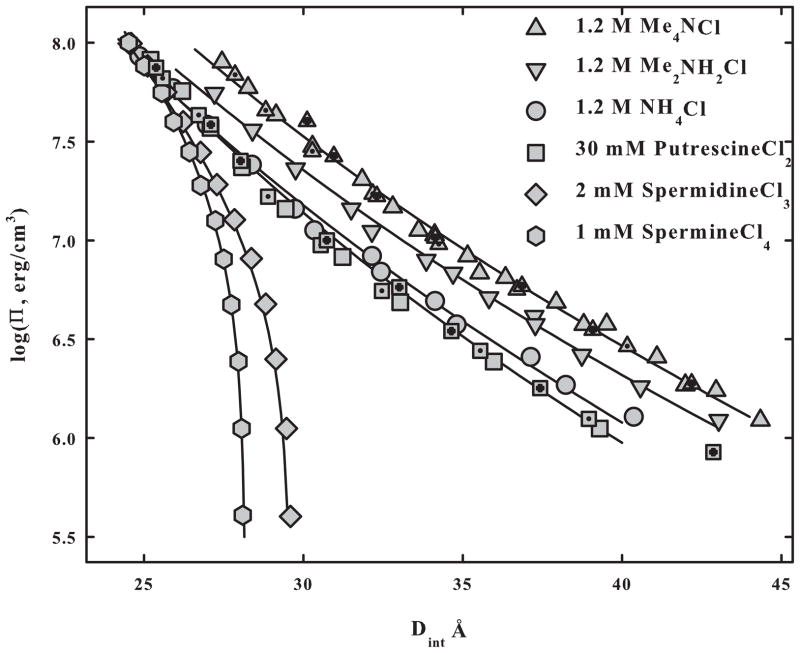
This double exponential fit with λ and λ/2 decay lengths is seen to describe many DNA systems. DNA force curves and fits are shown in Figure 3 for a set of amine cations that show repulsion at all distances, TMA⁺ (tetramethylammonium), DMA⁺ (dimethylammonium), NH₄⁺, and the divalent ion putrescine²⁺ (1,4-diaminobutane). The salt concentrations are high enough that forces are only weakly dependent on the ionic strength. The best fitting decay lengths λ vary between 4.2 and 4.8 Å. Unlike decay lengths, magnitudes of the ~4 Å decay length exponential force depend significantly on the particular ion bound to the DNA surface as might be expected from figure 1. Forces are remarkably insensitive to temperature (between 5° and 50° C) for all the cations in figure 3, as shown for TMA⁺ and putrescine²⁺.

Figure 3.

DNA force curves with different amine counterions are fit to double exponential functions with λ and λ/2 decay lengths. All counterion concentrations are large enough that forces depend only slightly on ionic strength. Spermidine³⁺ and spermine⁴⁺ spontaneously precipitate DNA. The amplitude of the λ decay length exponential changes from repulsive to attractive between putrescine²⁺ and spermidine³⁺. The best fitting decay length λ varies between 4.2 – 5.0 Å. The λ/2 decay length exponential is repulsive for all the charged amines shown. The amplitudes of the λ/2 decay length exponential for DNA interactions in NH₄⁺, putrescine²⁺, spermidine³⁺, and spermine⁴⁺ are closely comparable. A similar result for the λ/2 decay length force was found for DNA with an extended set of homologous arginine peptides ranging from +1 to +6 charges. The triangle symbols with dots and crosses are for DNA in 1.2 M TMA⁺ at 5° and 50° C, respectively. The square symbols with dots and crosses are for DNA in 30 mM putrescine²⁺ at 5° and 50° C. In spite of the ~25% decrease in the dielectric constant of water between 5° and 50° C, forces change negligibly.

DNA will spontaneously assemble with several metal cations such as Co(NH₃)₆³⁺, Mn²⁺, and Cd²⁺, alkyl amines of at least +3 charge such as spermidine and spermine, and oligoarginines and oligolysines also of at least +3 charge. Many transition metal cations will precipitate DNA but without x-ray order presumably by disrupting the double helix and coordinating with base nitrogens. The osmotic stress force curves of the spontaneously precipitated DNA assemblies show common characteristics. Without any applied osmotic pressure, DNA surfaces are not touching, but are rather separated by some 6–15 Å depending on the nature of the condensing ion. As the helices are pushed closer, a ~ 2 Å exponential decay length force is observed. Curve fitting of the Co(NH₃)₆³⁺-DNA data suggested that the attractive force had a 4.5 Å exponential decay length [29]. As with net repulsion seen with univalent cations, the decay lengths of the two force components differ by a factor of two. This was confirmed by combining the osmotic stress, pushing measurements of the repulsive free energy with single molecule, magnetic tweezer pulling experiments to measure the depth of the attractive energy well at the equilibrium spacing [41]. The force curves and fits for DNA condensed by spermidine³⁺ and spermine⁴⁺ are shown in figure 3. Force curves are insensitive to the concentration of these ions over a wide range [42], provided the DNA is condensed. In contrast to the wide range of amplitudes for the 4.5 Å exponential decay length force seen in figure 3, the curves for NH₄⁺, putrescine²⁺, spermidine³⁺, and spermine⁴⁺ converge to a common force curve at high osmotic pressures. Further work on a set of homologous (Arg)_1–6 peptides [43] showed that the amplitude of the λ/2 Å decay length force was relatively insensitive to the length or charge of the arginine peptide. The amplitude of the ~4.5 Å decay length force, however, varied substantially, changing from repulsion to attraction at about Arg₂. This is consistent with the importance of a correlation of arginine and DNA charges on apposing helices for the direct interaction ~4 Å decay length force but not for the ~2 Å decay length image force.

The precipitation of DNA by Mn²⁺ has the added feature that it is temperature dependent. Increasing temperature favors attraction. At critical pressures, force curves show abrupt transitions between a repulsive 3.5 – 4 Å decay length exponential force and ~2 Å decay length force [44]. Transition osmotic pressures are dependent on temperature and Mn²⁺ concentration. The distance dependence of the change in entropy and enthalpy can be calculated from the temperature-dependent force curves [28]. The ΔS and ΔH curves vary exponentially with distance with a decay length between 3.5–5 Å over the entire distance range. The abrupt transition in decay lengths is not seen in the data. The ΔH and TΔS are much larger than ΔG over the entire range. The temperature dependence is likely due to a shift in binding position of Mn²⁺ on DNA to sites that can better correlate complementary surface hydration structures on apposing surfaces. Intermolecular forces couple with Mn²⁺ binding modes to result in transitions.

HPC

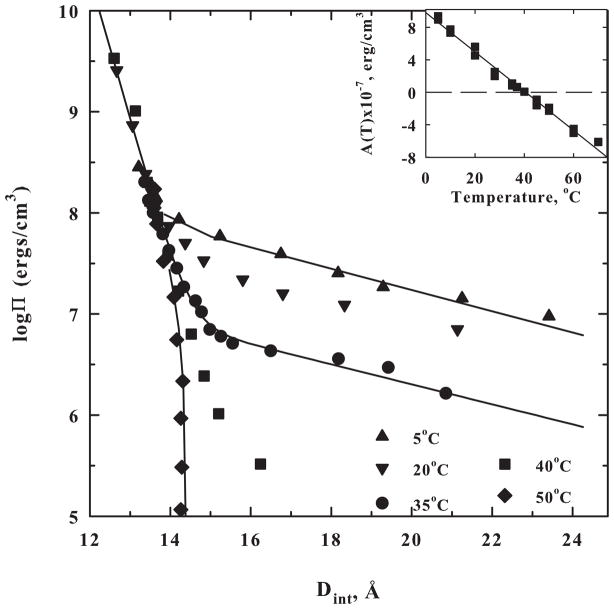
Hydroxypropyl cellulose, HPC, is cellulose modified with nonpolar i-propanol groups substituting the sugar hydroxyls. HPC will spontaneously precipitate from dilute solution at ~42°C. The temperature dependent force curves of HPC are shown in figure 4 [30]. Dry HPC has an interaxial spacing of ~ 12.5 Å. At close spacings, a very steeply rising force is seen that could be a combination of the 2 Å hydration force and a short ranged steric repulsion due to i-propanol groups extending into the space between polymer chains. A 2 Å decay length force, however, is not clearly seen in this case. At larger spacings, a 4–4.5 Å decay length (assuming hexagonal packing of HPC chains) exponential force is observed that has a temperature dependent amplitude. The longer ranged force smoothly changes from repulsion to attraction at ~40°C. The spacing between HPC chains at Π = 0 continues to decrease as the temperature is further increased. The pre-exponential factor of the ~4 Å decay length force in fact varies linearly with temperature (figure 4 inset). Not surprisingly, ΔS and ΔH extracted from the temperature dependence of the force also vary exponentially with spacing with the same ~4 Å decay length. As with Mn²⁺-DNA, ΔH and TΔS are much larger than ΔG. These nearly offsetting compensations of enthalpy and entropy have been suggested to be a feature of hydration changes [45–47].

Figure 4.

Hydroxypropyl cellulose forces are temperature dependent. The diameter of HPC is ~ 12.5 Å. The amplitude of the ~ 4 Å decay exponential is strongly temperature dependent, changing from repulsive to attractive at ~ 40 °C. At higher temperatures, the spacing between polymer chains continues to decrease with no applied osmotic pressure indicating that the attractive force continues to increase. At close spacings, the last 2 Å of separation, a very rapidly changing force is observed, probably due to the steric clash of i-propyl groups extending from the cellulose backbone. The solid lines are double exponential fits to the data. The low pressure force decay length is fixed at 4 Å. The decay length of the high pressure steric interaction is taken as 0.25 Å. The amplitude of this very short-ranged force shows negligible temperature dependence. The inset to the figure shows the linear dependence of the amplitude of the 4 Å decay length force at 12.5 Å, A(T), on temperature. Data taken from [30].

Within a hydration force framework, the temperature dependence of the force amplitudes would indicate a temperature dependent surface hydration structure. If we assume that HPC assembly is due to a favorable hydrophobic interaction of methyl groups, then either the water structure around these methyl groups is becoming stronger or the structuring due to the hydroxyl groups that presumably oppose precipitation is becoming weaker.

Solute and salt interactions with DNA and HPC

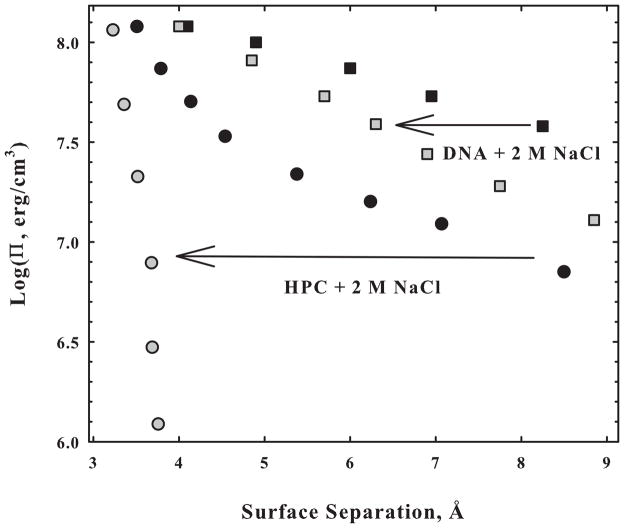
Comparing DNA and HPC illustrates the common force features shared by these charged and uncharged surfaces that seem likely due to water structuring. This same class of force also dominates the interaction of HPC and DNA with small molecules. Figure 5 shows the effect of adding 2 M NaCl on HPC and DNA osmotic stress forces. Contrary to conventional expectation, HPC interactions are much more sensitive to added salt than are forces between highly charged DNA helices. In fact HPC spontaneously precipitates from dilute solution in 2 M NaCl at 20°C. This is not because salt directly modulates the forces between HPC chains, but because salt is highly excluded from the vicinity of HPC chains and applies its own osmotic pressure on the condensed array [31]. Basic thermodynamics allows the extent of solute exclusion as dependent on the spacing between DNA helices or HPC chains to be extracted from the change in spacing with salt or solute concentration. This is tantamount to measuring the forces between solutes and macromolecular surfaces.

Figure 5.

The addition of 2 M NaCl has a much larger impact on neutral and nonpolar HPC-HPC forces than on DNA-DNA interactions. In both cases, the samples were initially in 10 mM TrisCl (pH 7.5), 1 mM EDTA. Salt is acting on HPC through exclusion. The difference in salt concentration between the HPC phase and the bulk solution results in an excess osmotic pressure acting on the condensed phase.

The concentration of preferentially excluded salt or solute in the macromolecular phase will be less than in bulk solution. A number of excess waters in the macromolecular phase can be defined as the number that must be removed to equalize the two concentrations. The dependence of the number of excess water molecules in the macromolecular phase with intermolecular spacing is defined by the relative changes in PEG and solute osmotic pressures necessary to keep a constant volume [31,48]. In essence, the difference in solute concentration between the bulk solution and macromolecular phase results in an excess osmotic pressure, Π_excess.

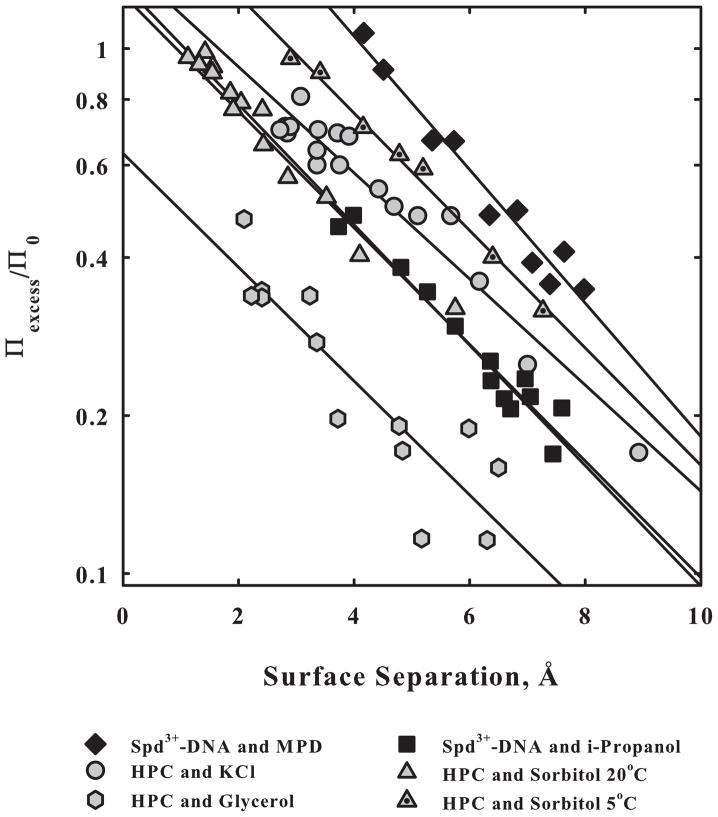
Figure 6 shows the distance dependence of Π_excess normalized by the maximal solute osmotic pressure, Π₀, for the exclusion of 2 nonpolar alcohols from spermidine condensed DNA and of two polyols and a salt, KCl, from HPC. Complete exclusion is given by Π_excess/Π₀ = 1 while Π_excess/Π₀ = 0 indicates no preferential interaction. The exponential decay lengths vary between 3.5 to 4.3 Å for the six curves. The same force acting on macromolecules also underlies the interaction of salts and solutes, both charged and uncharged, with macromolecules. Several different solute or salt concentrations were used to generate the curves. The insensitivity of Π_excess/Π₀ to solute concentration indicates that the number of excess waters at a fixed interaxial spacing of macromolecular surfaces is independent of the solute concentration.

Figure 6.

The exclusion of nonpolar alcohols from spermidine³⁺ condensed DNA and of salts and polar solutes from HPC mirrors the forces between macromolecules. Interaxial spacings have been adjusted for macromolecular diameters to give surface separations. The excess osmotic pressure due to exclusion is calculated from the dependence of the interhelical spacing between macromolecules on the salt or solute concentration; Π₀ is the maximal osmotic pressure that could be applied by the salt or solute if completely excluded from the macromolecular phase. For each curve, several different concentrations of salt or solute were used. The overlap indicates that the excess number of water molecules at a fixed spacing is constant, independent of solute concentration. The exponential decay lengths vary between 3.5 and 4.3 Å. Data taken from [31,48,51].

Integrating curves as shown in Figure 6 gives a total number of excess waters per length of macromolecule. The energy associated with exclusion can be calculated as the salt or solute osmotic pressure acting on the excess water or as the excess osmotic pressure acting on all the water.

A set of twelve alcohols was examined for DNA to determine the dependence of the exclusion amplitude on the chemical nature of the alcohol [49]. The apparent exponential decay lengths for all the alcohols are similar and vary between 3.4 to 4.4 Å. The integrated numbers of excess waters for each alcohol are in good agreement with their ability to decrease the critical spermidine concentration necessary to precipitate DNA from dilute solution [48,49]. Exclusion amplitudes vary by a factor of ~5 between methanol and methylpentanediol. To a good first order approximation, the exclusion amplitude for this set of alcohols depends linearly on the number of alkyl carbons in excess of hydroxyl groups, Δ(C-O). Overall solute size or steric exclusion affects exclusion negligibly in comparison to the chemical nature of these alcohols. The exclusion of nonpolar alcohols from DNA should likely be correlated with dielectric constant or polarity, but dielectric constant does not determine exclusion. Glycerol, Δ(C-O) = 0, is not excluded from DNA (as expected from the plot of exclusion amplitudes and Δ(C-O)), but has a dielectric constant of ~40, about half that of water. The linear dependence of exclusion on Δ(C-O) implies that the total exclusion can be represented as a simple sum of the exclusion amplitudes for the individual chemical moieties comprising the solute.

Uncharged HPC offers the chance to investigate preferential hydration effects of salts without complications from electrostatic interactions. The distance dependence of the exclusion of KCl from HPC is quite similar to that for the exclusion of alcohols from DNA. The amplitude of salt exclusion from HPC follows the Hofmeister series for anions, F⁻ > Cl⁻ > Br⁻ [31]. The identity of the cation has much less effect on exclusion. I⁻ is actually included in the HPC phase. The measured hydration interaction of these salts with HPC also correlates well with their ability to lower the precipitation temperature of HPC [31].

Unlike the interaction of alcohols with DNA, there is a more significant variation of decay lengths with the anion species; λ = 5.5, 4.2, and 3 Å for F⁻, Cl⁻, and Br⁻, respectively. A difference in exclusion between cations and anions from the HPC surface would lead to a charge separation that would contribute an additional electrostatic component to the total decay length. This variation could also result from the different polarizabilities of these anions and a contribution from dispersion forces between ions and HPC to the overall force.

This striking connection between Hofmeister effects and hydration forces underscores the important role of water in mediating these interactions at close distances. It has long been considered that perturbations in water structure underlie the Hofmeister series [50]. Hydration forces provide a natural connection.

The exclusions of nonpolar alcohols from charged DNA and of charged salts from nonpolar HPC would appear to be mirror image systems. The number of excess waters per salt per i-propyl group calculated from exclusion curves confirms this. The exclusions of a strong kosmotropic salt KF from HPC per isopropyl group along HPC and of isopropanol from DNA per strong kosmotropic phosphate group along the DNA are both characterized by ~9 excess water molecules.

The distance dependence of exclusion from HPC has also been investigated for a set of naturally occurring neutral osmolytes [51] that are commonly used to stabilize native protein conformations against denaturation, glycine betaine, glycerol, sorbitol, TMAO, and proline [52–54]. Figure 6 shows that the exclusion of the uncharged polyol sorbitol is about as strong as KCl. Charge itself is not defining the interaction. Once again, exclusion of these naturally occurring osmolytes from HPC is characterized by an apparent exponential distance dependence with a 3.5 – 4.3 Å decay length. Since sorbitol is simply two glycerols linked together, the two-fold greater force magnitude for sorbitol exclusion relative to glycerol can be rationalized as a sum of the forces over the individual groups as was seen for alcohols and DNA. This again reinforces the important role of chemical constituents of solutes and surfaces and how they drive solute exclusion.

The energy to transfer a hydroxypropyl group on HPC from water to 1 osmolal (~24 atm) glycine betaine is ~ about 100 cal/mole. This energy of exclusion is comparable to that estimated for the exclusion of glycine betaine from the peptide bond [52]. Hydration force exclusion of these polar solutes from hydrophobic amino acid side chains also will make a significant contribution to protein stability.

The exclusion of the neutral polar solutes from HPC is significantly temperature dependent, similar to HPC-HPC forces. This emphasizes that the solute-surface interaction is more than a simple steric exclusion but that actual physical forces underlie exclusion. Sorbitol exclusion (see figure 5), for example, is characterized by ~ 33 excess waters/saccharide unit at 5 °C compared to ~20 at 20 °C. The temperature dependence of the number of preferentially included waters indicates that water structuring about the macromolecular surface, solute, or both is temperature dependent. The apparent exponential decay length does not depend significantly on temperature.

The force amplitudes of alcohol-DNA and salt-HPC exclusions show very little temperature dependence suggesting that the hydrophobic and ionic hydration is comparatively insensitive to temperature over the range from 5° –50° C. The temperature dependence of the interaction of HPC with neutral hydrogen bonding solutes suggests that water structuring due to hydrogen bonding with solute is temperature sensitive. This is consistent with the temperature dependence of forces between HPC polymers.

Conclusions

The common force characteristics of the interactions between charged or uncharged macromolecular surfaces and of the exclusion interactions of neutral alcohols with charged DNA or of charged salts and neutral polar solutes with HPC argue for a common force origin that we have concluded is due to water structuring. The same forces seen between regular, repeating surfaces in macroscopic ordered arrays such as with DNA and HPC will also determine the strength and specificity of the binding reactions and conformational transitions of proteins, DNA, and carbohydrates in solution and in the cell.

Several challenges remain. Coupled measurements of water structural perturbations in a confined space and the energetics associated with creating the tight spacing, i.e., the force amplitude, need to be performed in order to directly connect the two. The additivity of alkyl carbon and hydroxyl oxygen contributions to alcohol interactions with DNA suggests hydration interaction amplitudes can be parsed to the level of individual chemical groups perhaps by defining equivalent ‘hydration charges’ analogous to electrostatic interactions.

There is variation in measured values of λ between 3 and 5 Å that is not well understood. It may reflect a coupling of hydration forces and macromolecular structure. Ions can bind or dissociate or shift binding locale with the additional contribution from hydration interactions. Malleable conformations can adapt to optimize hydration interaction energies.

Above all, more force measurement experiments at close spacings are necessary to stimulate theoretical advances.