Minimum Energy Path to Membrane Pore Formation and Rupture

Abstract

We combine dynamic self-consistent field theory with the string method to calculate the minimum energy path to membrane pore formation and rupture. In the regime where nucleation can occur on experimentally relevant time scales, the structure of the critical nucleus is between a solvophilic stalk and a locally thinned membrane. Classical nucleation theory fails to capture these molecular details and significantly overestimates the free energy barrier. Our results suggest that thermally nucleated rupture may be an important factor for the low rupture strains observed in lipid membranes.

Membrane bilayers define boundaries for cells and are directly involved in many cellular functions [1]. Understanding the natural processes of the cell therefore requires understanding the physical and mechanical properties of its membranes. The fusion of membranes and the controlled transport of materials across cells involve the formation of transient membrane pores, while the resistance against cell lysis (rupture) is determined by the stability of the membrane against the formation of pores, e.g., during osmotic swelling. In addition to these natural processes, pores can be formed by antimicrobial peptides [2] or electroporation [3]. The latter is a common method for introducing foreign material, such as drugs or genes, to the cell [4].

Several experimental methods have been developed to study pore formation under an applied tension [5–7]. A variety of computational methods have also been used to study the energetic and structural properties of membrane pores [8–14]. Conventional molecular dynamics simulations often require very high tensions, where pore formation is no longer a rare event. On the other hand, the potential of mean constraint force method can be applied to study pore formation as an activated process [12–14]. The method requires artificially selecting a reaction coordinate constraint that, in general, may not coincide with the true transition pathway involving local lipid rearrangements. Furthermore, computer simulations are limited by the number of amphiphiles and are usually performed under constant area. A pore opening under such conditions simultaneously relaxes the surface tension and can either expand, reseal, or stabilize, depending in a nontrivial manner on the system size [14]. In solvent-free models of lipids consisting of two or three beads, there is disagreement between density functional predictions [9] and Monte Carlo simulations [11] with regard to the existence of small metastable pores. The interpretation of structures comparable to the lipid molecular size is highly problematic for these overly simplified models.

In this Letter, we study the full minimum energy path (MEP) to pore formation and rupture by combining the string method [15] with dynamic self-consistent field (DSCF) theory [16]. As opposed to calculations that require physical insight to impose one or more constraints on the system [17], the string method automatically determines the reaction coordinate of the MEP connecting two stable states on a given free energy landscape, while DSCF theory provides a full description (at the mean-field level) of the lipid conformation changes. We begin with an arbitrary set of states between two free energy minima. The states are connected on the free energy landscape by a string and relax towards the MEP by an iterative procedure. First, all states are evolved independently for some time Δt according to $\frac{\partial {\varphi }_I}{\partial t}=-D\frac{\delta F}{\delta {\varphi }_I}$, where ϕ_I is the monomer volume fraction, D is the mobility coefficient, and F is the free energy functional of the system. Note that for a system not at equilibrium, the gradient cannot be computed using the usual SCF theory, but can be obtained by solving for a hypothetical external potential [18]. Then, to prevent the states from falling into one of the two end states, we make use of the connectivity imposed by the string. Precisely, we reparameterize the states equidistantly along the string. The procedure is repeated until the dynamics balance the reprameterization; i.e., the evolution of the string has reached a steady state. At this point the string coincides with the MEP [15] and the free energy and density profiles of all states along the MEP are immediately known without additional calculations. We note that a similar strategy was recently employed to study the nucleation of order-order transitions in diblock copolymer melts [19].

A starting point for discussing pore formation and rupture is often based on classical nucleation theory (CNT) [20,21]. For a membrane under tension γ > 0, CNT defines the free energy of a pore of radius r as

$$F=2\pi r\sigma -\pi r^2\gamma .$$ (1)

Here σ > 0 is the line energy. The first term is the cost of forming the rim of a pore and the second term is the relief in elastic energy. The above expression leads to a free energy barrier F^* = πσ²/γ at a critical radius r^* = σ/γ, beyond which the pore grows indefinitely (ruptures).

For membranes with different tensions γ, we obtain properties of the nucleation pathway, including the structure and activation energy F^* of the critical nucleus. Comparing the values of our calculated F^* with those predicted by CNT, we find that CNT is valid only for small γ, where the free energy barrier is nearly insurmountable on experimentally realistic time scales. For the physically relevant regime, where F^* ≲ 𝒪(10 kT), CNT significantly overestimates the barrier height. Furthermore, in this regime the critical nuclei are not well-defined pores, as assumed by CNT, but rather “stalks” of amphiphile head groups or, in the case of large γ, merely a local thinning of the membrane.

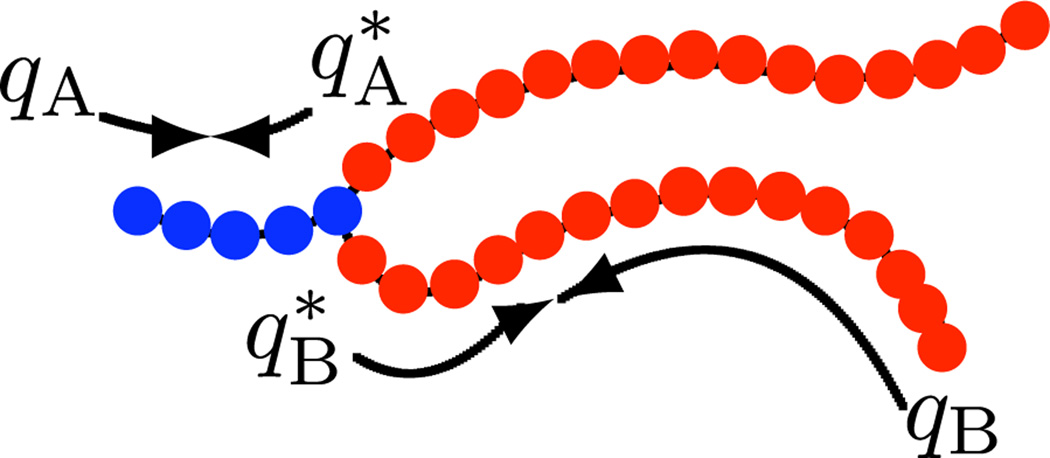
Our model consists of a bilayer assembled from double-tailed amphiphiles in explicit solvent. The amphiphiles are modeled as discrete Gaussian chains having a solvophilic block and two solvophobic tails (see Fig. 1). The solvents are represented as monomers. The different monomer species are assumed to interact with short-ranged, pairwise potentials, and the hard-core repulsion is accounted for by treating the system as incompressible. We work mostly in the grand canonical ensemble, where the numbers of amphiphile and solvent molecules are controlled by their chemical potentials. kT is used as the energy unit. The explicit form of the Hamiltonian and the derivation of the self-consistent field theory are given in the supplemental material [22]. Briefly, the interactions among particles are decoupled and replaced with interactions between particles and effective fields [23]. The resulting field-theoretic partition function can be generically written Ξ = ∫ Dω exp(−F[ω]). Here F is an effective, complex-valued free energy that depends on the field variable ω. The mean-field approximation amounts to assuming that a single field configuration ω^* dominates the functional integral so that Ξ ≈ exp(−F[ω^*]). In our model F[ω^*] is given by

$$F=-\frac{e^{{\mu }_P}}{{\upsilon }_P}{Z}_P({\xi }_A,{\xi }_B)-\frac{e^{{\mu }_S}}{{\upsilon }_S}{Z}_S({\xi }_S)+{\displaystyle \sum _{J\ne K}}{\displaystyle \int }d\mathbf{r}\left[{\chi }_{\mathit{\text{JK}}}{\varphi }_J{\varphi }_K-{\xi }_J{\varphi }_J+\frac{{\kappa }_J}{2}{(\nabla {\varphi }_J)}^2\right].$$ (2)

The Flory χ parameters and the square-gradient coefficients capture, respectively, the local and nonlocal part of the short-ranged interactions [24]. Their values are chosen to reproduce some known experimental properties of lipid membranes. The incompressibility condition ϕ_S + ϕ_A + ϕ_B = 1 is used to eliminate ϕ_S and we have used the imaginary nature of the potential field variables at the saddle point to redefine the conjugate potential fields iξ → ξ [23]. The partition functions that arise in Eq. (2) are for a single molecule in its respective field (s) and are given by Z_S = ∫ dre^−υ_Sξ_S for the solvents and $Z_P=\int d\mathbf{r}{q}_A(\mathbf{r};N_A)e^{2{\upsilon }_A{\xi }_A}{q}_B^2(\mathbf{r};N_B+1)$ for the amphiphiles. The chain propagators q_A and q_B account for the chain connectivity and the Boltzmann weight due to the self-consistent potential field. They begin at the free ends and are used to obtain the single-chain statistics for each arm of the amphiphile. The total partition function for the amphiphile follows naturally by joining the propagators at the branch point, where an extra exponential factor e^2υ_Aξ_Ais included to correct for overcounting the joined monomer; see [25] for details on the chain propagator calculation. We then apply DSCF theory, together with the string method, to the free energy functional given by Eq. (2). In what follows, we discuss the main results.

FIG. 1.

(color online). An amphiphile consisting of a solvophilic (A) segment of N_A = 5 monomers with volume υ_A = 0.05 nm³ (blue [dark gray]) and two solvophobic (B) segments, each with N_B = 15 monomers with volume υ_B = 0.05 nm³ (red [medium gray]). q_I and $q_I^{*}$, where I = A, B, are the chain propagator and complementary chain propagator, respectively. Additional parameters include the solvent (S) monomer volume: υ_S = 0.15 nm³, and interaction parameters: χ_AB, χ_BS, χ_AS = 75, 18, 0 and κ_A, κ_B, κ_S = 0, 8, 0.

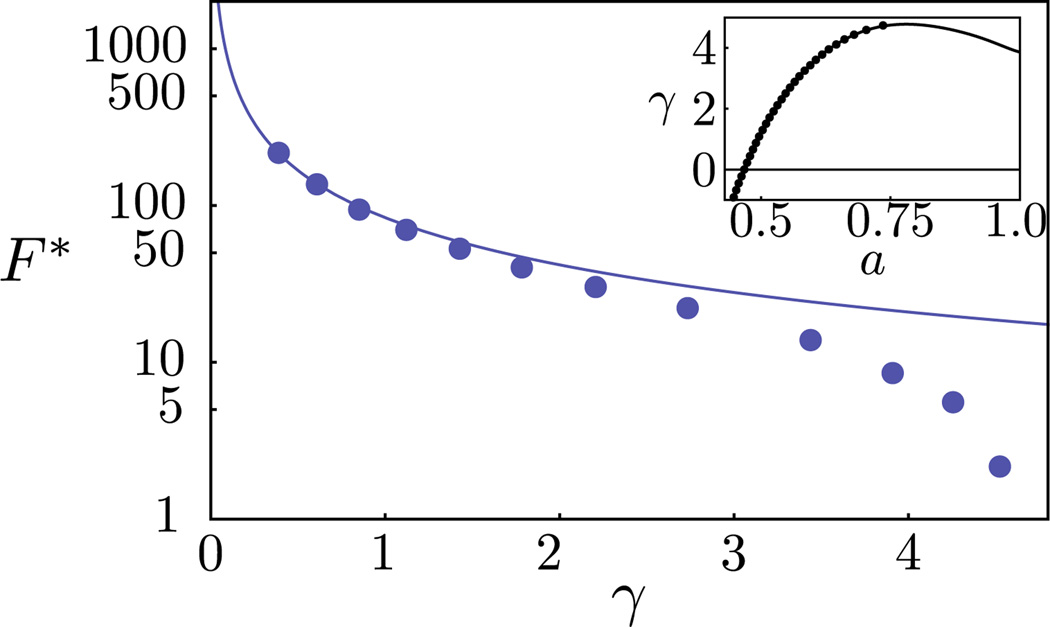
Consider a membrane under tension γ. If the membrane size is much larger than the size of the critical nucleus, we may regard pore formation and rupture as occurring at constant tension, which we implement as the boundary condition. In what follows, we work in the grand canonical ensemble, as it is most convenient for studying the MEP. In this open system, the excess grand potential [Eq. (2) relative the bulk solution] per unit area directly gives the tension up to the rupture value, identified as the point of vanishing slope in the Fig. 2 inset. This corresponds to a critical tension γ_c ~ 4.77 kT/nm² and an areal strain of ~0.6. The linear stretching modulus is found to be 170 mN/m, which falls within the range for lipid membranes, as determined from micropipette aspiration experiments [26]. Finally, to confirm that the results are independent of the ensemble choice, we repeat the same calculation in the canonical ensemble. In this closed system, the tension is evaluated according to $\gamma =f+a\frac{\partial f}{\partial a}{|}_n$. Here f is the Helmholtz free energy per unit area and a is the area per lipid. The results from these two ensembles are identical.

FIG. 2.

(color online). The free energy barrier as a function of the surface tension: DSCF-MEP (markers) and CNT (line). Inset: the surface tension as a function of the area per lipid: grand canonical (markers) and canonical (line) ensemble.

The rupture captured above corresponds to the limit of metastability for a uniform membrane. In reality, thermal fluctuations and lipid rearrangements can nucleate pore formation and rupture when the membrane is subjected to a positive tension γ. If the time scale for nucleation is sufficiently long relative to the time scale for molecular relaxation, then the nucleation rate is of the form ν = ν₀ exp(−F^* /kT), where ν₀ is some transition frequency associated with the molecular relaxation. Assuming a molecular relaxation time on the order of 10 µs [27], nucleation will take place on experimentally relevant time scales if F^* ≲ 𝒪(10 kT). For any given tension, the DSCF-MEP calculations provide an exact description (within the mean-field framework) of the nucleation pathway. In Fig. 2, we plot the free energy barrier F^* as a function of the membrane tension γ on a log-linear plot. Also shown is the result from CNT [Eq. (1)], where the line energy σ is a phenomenological parameter that is assumed constant and used to describe the excess free energy cost associated with forming the rim of a pore. An equilibrium line energy is only well defined for a pore with zero curvature in a tensionless membrane. Our SCF method determines this value (σ_eq = 5.16 kT/nm) as input into the CNT. For small γ, the predictions from CNT agree well with the DSCF-MEP calculations. Indeed, we expect CNT to become exact in the limit γ = 0. However, in this regime, the barrier is too high, and the rate vanishingly small, for nucleation to be a relevant mechanism. As γ increases, the free energy barrier decreases (reflecting the fact that the metastable intact membrane becomes less stable) and vanishes at the critical tension (γ_c), corresponding to the spinodal. From Fig. 2, CNT severely overpredicts the free energy barrier in the important regime where γ ~ 3–4 kT/nm², and completely fails to capture the spinodal. To understand the source of discrepancy between CNT and our results, we examine the MEP for three representative values of γ.

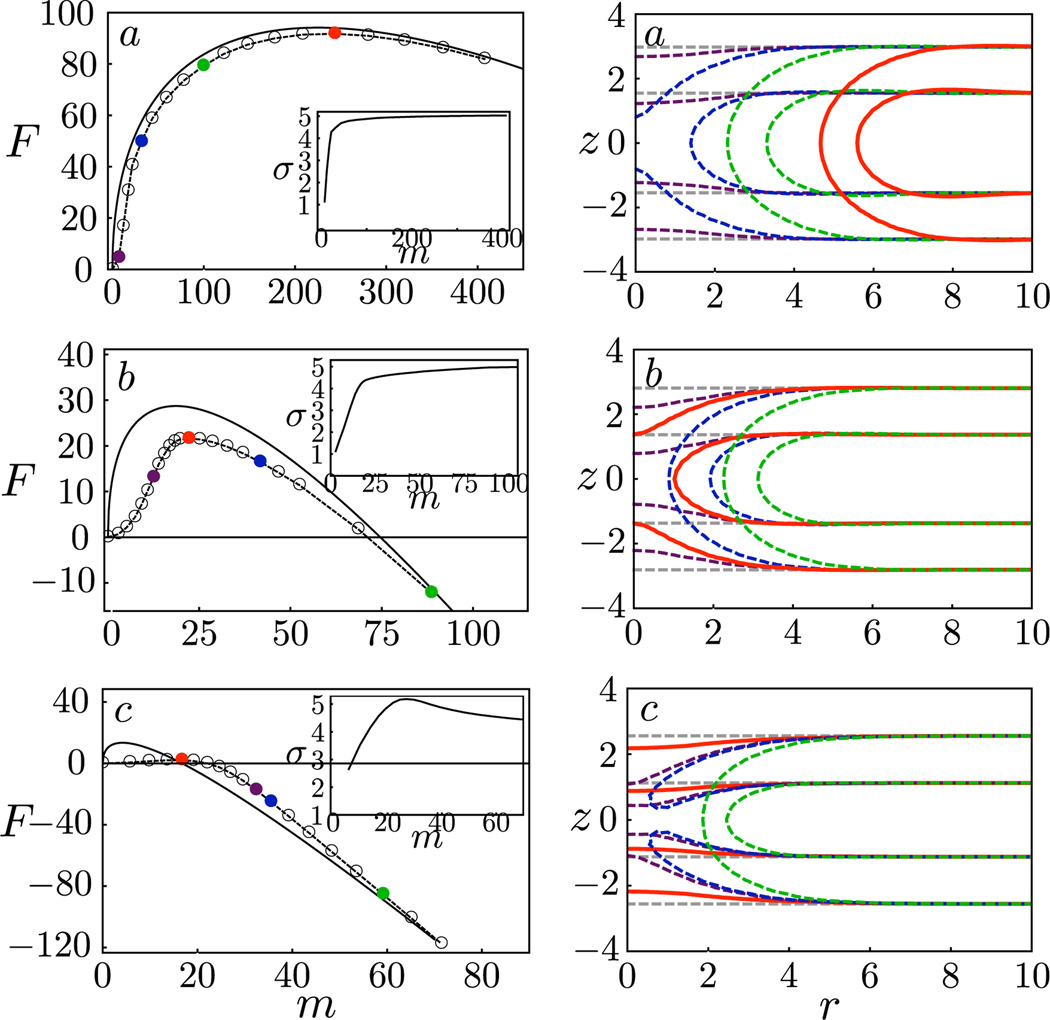
On the left panel of Fig. 3, we show the free energy profile and the line energy (inset) as a function of a reduced reaction coordinate, here taken to be the deficiency in the number of lipid molecules in the bilayer, m. We choose to use m rather than the radius r because the latter is only well-defined for macroscopic pores. The free energies of the states along the MEP are given by the markers and the prediction from CNT is given by the solid line. Here the line energy used for the CNT result is obtained from the respective membrane containing a pore with zero curvature. On the right panel, we plot the density profiles of the amphiphiles for selected states along the MEP.

FIG. 3.

(color online). Left: Free energy as a function of the deficiency in the number of lipids: MEP (dashed lines, states given by the colored markers) and CNT (solid lines). Right: density profiles for images along the respective MEPs. The contour lines correspond to 25% of the maximum solvophilic (A) density of the initial intact membrane. In all cases, the critical nucleus is shown in red [medium gray] and the intact membrane in light gray. From top to bottom: γ_a, γ_b, γ_c = 0.85, 2.73, 4.52.

For γ = 0.85 kT/nm² [Fig. 3(a)], except at the very initial stages, the MEP closely follows the prediction from CNT, with the nucleation process largely involving the expansion of a well-defined solvophilic pore with negligible penetration of solvents. The density profile is nearly invariant (but shifted in radial direction) once the pore forms. For this low γ, the free energy barrier is F^* = 92.18 kT, indicating that nucleation of a large pore leading to rupture is highly improbable. In fact, even smaller, transient pores are unlikely. The blue [dark gray] image where the membrane has not yet formed a pore already requires a substantial free energy cost. Next consider γ = 2.73 kT/nm² [Fig. 3(b)] and observe that CNT overpredicts the free energy barrier and underpredicts the size of the critical nucleus. From the density profiles obtained from the DSCF-MEP calculations, we see that the critical nucleus is not even a well-defined pore, but rather a “stalk” of solvophilic monomers that contains finer molecular structure than can be captured by CNT. Therefore, CNT is not a good model for the MEP in the intermediate regime where F^* = 21.59 kT. We note that a similar structure has been observed as a transition state [17] for the fusion of two bilayers. Finally, consider a membrane approaching the spinodal: γ = 4.52 kT/nm² [Fig. 3(c)]. Here CNT grossly overpredicts the nucleation barrier and underpredicts the size of the critical nucleus. In fact, the nucleation pathways predicted by the two methods qualitatively differ, with the CNT prediction crossing the MEP and approaching it from below at large pore sizes. From the density profiles [Fig. 3(c), right], we find, not surprisingly, that a small perturbation involving local membrane thinning is enough to nucleate pore formation and rupture. Interestingly, rupture occurs even before the membrane is able to fully prepare for pore formation and a solvophobic hole that is penetrated by solvents forms in the membrane. Only afterwards do the amphiphiles rearrange to line the pore with solvophilic monomers and seal off the hole. This can be seen from the contour lines given in blue [dark gray] and green [medium-light gray]. The free energy barrier in this case is only twice the thermal energy, and hence we do not expect the picture of nucleation as a rare event to hold. However, with longer-chain amphiphiles, such as in the case of polymersomes [5], we expect a higher barrier height for the same amount of strain. Thus the scenario presented in this near-spinodal case can still be relevant.

To gain further insight, we separate the free energy from our DSCF-MEP calculations into a piece involving the reduction in the elastic free energy, and other contributions. In analogy with CNT, we consider the reduction in the elastic energy to be given by the second term in Eq. (1), where we use the lipid number deficiency m and the area per lipid in a uniform membrane to define the pore size. For a macroscopic pore, m is related to the pore radius r as $r~\sqrt{m}$. The first term can then be considered an operational definition of the line energy σ, which now represents all the excess free energy to the elastic free energy. Figure 3 insets show the behavior of σ as a function of m. In all three cases, for sufficiently large pores, σ approaches a constant value less than the equilibrium value given earlier for the tensionless membrane (σ_eq = 5.16 kT/nm²). We also see that for small m, there is a strong size dependence in the line energy, including a nonmonotonic dependence for case (c) that captures the initial penalty for forming a solvophobic hole. Importantly, when the critical nucleus involves a pre-pore state with molecular features that cannot be captured by CNT, the size dependence of σ becomes important.

Finally, if we associate rupture as occurring when the nucleation barrier is surmountable on experimentally relevant time scales, our results indicate that the strain at which rupture occurs can be significantly lower than the strain at the limit of mechanical stability of the membrane. Thus, thermally nucleated rupture may be an important factor for the low rupture strains observed in lipid membranes [6].

In conclusion, we have combined the string method with DSCF theory to obtain the MEP to pore formation and rupture for a range of membrane tensions. For the experimentally relevant regime where F^* ≲ 𝒪(10 kT), the critical nucleus is somewhere between a stalklike structure [Fig. 3(b)] and a thinned membrane leading to a hole that is partially exposed to solvents [Fig. 3(c)]. In this regime, CNT fails to capture the important local rearrangements of the lipids and significantly overpredicts the nucleation barrier. Within the framework of mean-field theory for describing spatially localized fluctuation phenomena, the present work (and that by Cheng et al. [19]) represents the most advanced methodology in treating nucleation in soft condensed matter, including membranes. The combination of the string method and DSCF theory opens the way to studying a wide range of related membrane nucleation phenomena beyond pore formation and rupture, such as membrane fusion and fission [28,29], and particle insertion and penetration [30].