Electronic Structure of a Low-spin Heme/Cu Peroxide Complex: Spin-State and Spin-Topology Contributions to Reactivity

Abstract

This study details the electronic structure of the heme-peroxo-copper adduct {[(F₈)Fe(DCHIm)]-O₂-[Cu(AN)]}⁺ (LS^AN) in which ${\mathrm{O}}_2^{2-}$ bridges the metals in a μ-1,2 or “end-on” configuration. LS^AN is generated by addition of coordinating base to the parent complex {[(F₈)Fe]-O₂-[Cu(AN)]}⁺ (HS^AN) in which the ${\mathrm{O}}_2^{2-}$ bridges the metals in an μ-η²:η² or “side-on” mode. In addition to the structural change of the ${\mathrm{O}}_2^{2-}$ bridging geometry, coordination of the base changes the spin state of the heme fragment (from S = 5/2 in HS^AN to S = 1/2 in LS^AN) that results in an anti-ferromagnetically coupled diamagnetic ground state in LS^AN. The strong ligand field of the porphyrin modulates the high-spin to low-spin effect on Fe-peroxo bonding relative to non-heme complexes, which is important in the O—O bond cleavage process. Based on DFT calculations, the ground state of LS^AN is dependent on the Fe—O—O—Cu dihedral angle, wherein acute angles (< ~150°) yield an anti-ferromagnetically coupled electronic structure, while more obtuse angles yield a ferromagnetic ground state. LS^AN is diamagnetic, and thus has an antiferromagnetically coupled ground state with a calculated Fe—O—O—Cu dihedral angle of 137°. The nature of the bonding in LS^AN, and the frontier molecular orbitals which lead to this magneto-structural correlation, provide insight into possible spin topology contributions to O—O bond cleavage by cytochrome c oxidase.

1. Introduction

Cytochrome c oxidase (CcO) catalyzes the terminal enzymatic step of the electron transport chain, the reduction of dioxygen to water.^1,2 The source of the electrons is cytochrome c (cyt c), and the reaction is overall highly thermodynamically favorable. The excess free energy produced from the redox reaction is efficiently converted into a chemiosmotic potential by pumping protons from the mitochondrial matrix across the inner membrane into the intermembraneous space as follows:

$$4[(\text{cyt}\mathrm{c})]{\text{Fe}}^{2+}+8{\mathrm{H}}_{\text{ in}}^{+}+{\mathrm{O}}_2\to 4{[(\text{cyt}\mathrm{c})\text{Fe}]}^{3+}+2{\mathrm{H}}_2\mathrm{O}+4{\mathrm{H}}_{\text{ out}}^{+}$$

The proton gradient is used downstream by ATP synthase to generate ATP. Despite the fact that the overall reaction is thermodynamically favorable, the first, one-electron reduction of dioxygen is uphill, necessitating sophistication at the oxygen reaction site to overcome this facet of catalysis. Nature has selected a unique hetero-bimetallic active site, which features a copper ion strategically juxtaposed ~5 Å above a heme cofactor.^3,4 The copper is ligated by three histidine residues, one of which is covalently tethered to a nearby tyrosine residue, a crosslink that is thought to be functional.⁵

A simplified consensus mechanism for CcO is illustrated in Figure 1. Entry into catalysis begins from the reduced enzyme R with the binding of dioxygen to form intermediate A, which has been assigned as a formally ferric-superoxo species based on transient resonance Raman experiments.^6–8 The next intermediate, P_M, has been assigned as a ferryl-heme — cupric hydroxide — tyrosine radical based on a variety of spectral and chemical evidence. The existence of a high-valent Fe(IV)=O in P_M is based on mixed O₂ isotope resonance Raman spectral studies which unequivocally demonstrated that in P_M, the O—O bond is broken.⁹ Evidence for the involvement of the crosslinked tyrosine, specifically as a net H• donor, comes from ATR-FTIR,^10–12 EPR,¹³ and an iodination reaction followed by degradative mass spectrometry (MS).¹⁴

Figure 1.

Schematic of the catalytic cycle of oxygen reduction by CcO. Pink arrows indicate proton pumping steps. The axial base on heme has been omitted for clarity.

The conversion of state A to P_M is of significant interest from a fundamental standpoint as it contains the reductive cleavage of the O—O bond. Moreover, the proposed net H• abstraction from tyrosine provides impetus for study of the nature of the active oxidant. Collman and co-workers have recently synthesized a binucleating scaffold derived from the picket-fence porphyrin motif wherein a copper binding site was engineered into the pocket above the heme. This system was able to abstract H• from phenols both inter-¹⁵ and intra-¹⁶ molecularly (when a phenol was tethered to one of the copper ligand arms) and reduce O₂ to H₂O under rate-limiting electron flux.¹⁷ An Fe(III)-superoxo species was trapped and is proposed to function as the active oxidant. We and others have hypothesized involvement of an unobserved peroxo intermediate during the A to P_M conversion.^18–20 A synthetic example that demonstrates the structural feasibility of such an intermediate comes from Naruta and coworkers, who succeeded in the crystallographic characterization of a heme—peroxo—copper adduct that has a μ-η²:η¹ peroxo core.²¹ The synthetic strategies employed independently by Collman and Naruta involve a porphyrin ligand scaffold with a preorganized copper binding site in close proximity to the heme.^22,23 An alternative strategy using discrete heme and copper monomer components has also been successful as a result of favorable reaction kinetics.²⁴ In an early example,²⁵ the reaction of a mixture of [(F₈)Fe^II] and [(TMPA)Cu^I(CH₃CN)]⁺ with dioxygen at subambient temperatures resulted in the formation of {[(F₈)Fe]-O₂-[Cu(TMPA)]}⁺ that, based on spectroscopic studies, also contains a μ-η²:η¹ peroxo core.^26,27 Neither the crystallographically characterized complex nor {[(F₈)Fe]-O₂-[Cu(TMPA)]}⁺ perform the biomimetic O—O bond cleavage reaction with phenols.

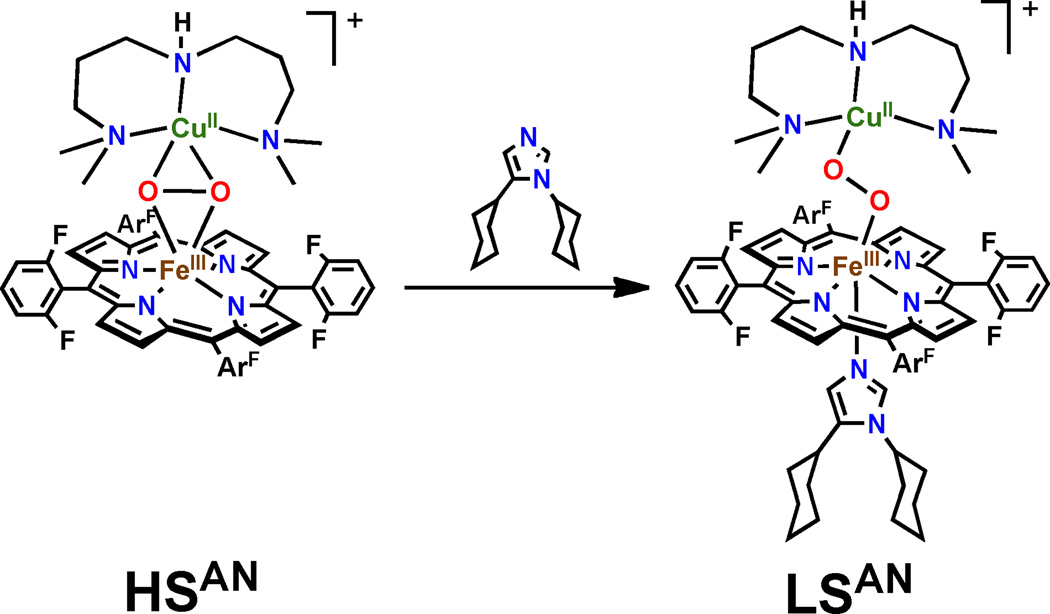
To test the ability of peroxo formulations for the net hydrogen atom abstraction from tyrosine, the systematic synthesis and spectroscopic definition of small molecule heme—peroxo—copper adducts with varying ligand scaffolds has been pursued. The studies have proven fruitful, including the recent preparation and spectroscopic elucidation of the heme-peroxo-copper adduct {[(F₈)Fe(DCHIm)]-O₂-[Cu(AN)]}⁺ (LS^AN, AN = bis[3-(dimethylamino)propyl]amine]), in which the peroxo moiety bridges in a μ-1,2 (η¹:η¹) or “end-on” geometry. The heme fragment of LS^AN is low-spin (S = 1/2) and is anti-ferromagnetically coupled to the Cu(II) (S = 1/2) to yield a diamagnetic ground state. LS^AN is generated from the reaction of {[(F₈)Fe]-O₂-[Cu(AN)]}⁺ (HS^AN)^28,29 with coordinating base (dicyclohexyl imidazole, DCHIm) (Figure 2).²⁹ HS^AN contains a μ-η²:η² or “side-on” peroxo structure type, with a high-spin (HS, S = 5/2) ferric heme antiferromagnetically coupled through the peroxo to the Cu(II) (S = 1/2) resulting in an S_T = 2 ground state. Based on initial low-temperature studies,²⁹ LS^AN (but not HS^AN) is reactive towards phenol, and thus provides a unique platform to survey the factors that contribute to reactivity in heme—peroxo—copper adducts. This manuscript details the electronic structure of LS^AN, based on the correlation of spectral features with density functional theory calculations (Figure 3, using the geometry optimized truncated model from reference 30), and compares the spin-state/reactivity correlations in heme-copper adducts with that previously detailed for non-heme iron-peroxo complexes.³¹ During the course of these studies, we developed a magneto-structural correlation deriving from the mechanism of magnetic superexchange in LS^AN, which has implications for spin topology contributions to O—O bond cleavage by CcO.

Figure 2.

Addition of coordinating base to HS^AN results in formation of a distinct intermediate LS^AN.

Figure 3.

Optimized geometric structures of LS^AN, HS^AN, and HS^TMPA. Models were optimized with the BP86 functional within the spin-unrestricted formalism on the respective BS spin surfaces.

2. Results and Analysis

2.1. Resonance Raman Excitation Profile

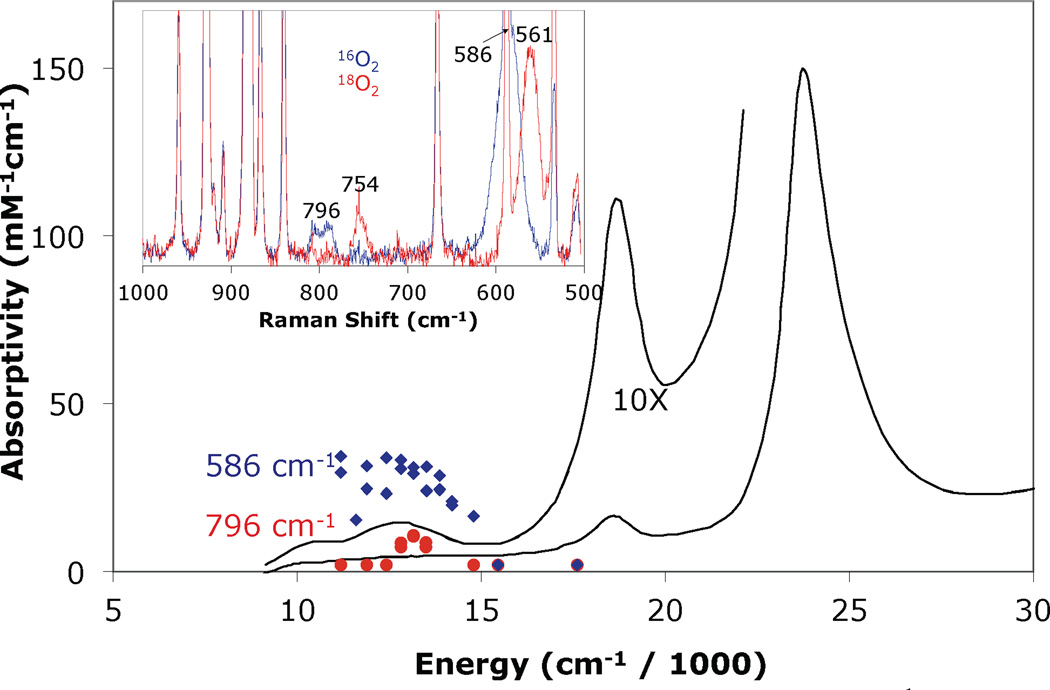
The absorption spectrum of LS^AN is shown in Figure 4 and is dominated by the heme spectral features at 421 nm (ε: 142.7 mM⁻¹cm⁻¹), 537 (ε: 11.5 mM⁻¹cm⁻¹), and two low energy features at 789 nm (ε: 1.5 mM⁻¹cm⁻¹) and 951 nm (ε: 0.9 mM⁻¹cm⁻¹). The resonance Raman spectrum of LS^AN displays three oxygen isotope modes at 796 cm⁻¹, 586 cm⁻¹, and 394 cm⁻¹. Previously, these bands were assigned as the ν_O—O (796 cm⁻¹), ν_Fe—O (586 cm⁻¹), and tentatively as the δ_N—Fe—O (394 cm⁻¹) modes.³⁰ The excitation dependence of the intensity of the ν_O—O and ν_Fe—O vibrational features (the δ_N—Fe—O feature was too weak to be profiled) correlate to the 789 nm absorption band in the UV-visible spectrum (Figure 4). The ν_Fe—O is significantly more intense than the ν_O—O, indicating the absorption band is a ${\mathrm{O}}_2^{2-}\to {\text{Fe}}^{\text{III}}$ CT transition. Such a low energy ${\mathrm{O}}_2^{2-}\to {\text{Fe}}^{\text{III}}$ CT transition is unusual, and is indicative of a highly covalent peroxo-iron interaction (vide infra).

Figure 4.

Resonance Raman excitation profiles of the 586 cm⁻¹ () and 796 cm⁻¹ () features of LS^AN at 77K in THF overlaid with the 193 K absorption spectrum (—). Inset: Resonance Raman spectrum of LS^AN prepared with ¹⁶O₂ () and ¹⁸O₂ ().³⁰

2.2 Electronic Structure Calculations: Correlations to Experimental Data

To further probe the spectral features of LS^AN, DFT calculations were performed on a truncated model of LS^AN (by changing the cyclohexyl rings of the bound imidazole to methyl groups). As detailed below, the computed properties of LS^AN reproduce the experimentally observed diamagnetic ground state, the isotope sensitive vibrational modes, the low-energy CT transitions observed optically, and the coupling of the Raman vibrational modes to the CT transition. Thus, the calculations are used to enhance the spectral assignments, and to understand the peroxo-Fe and peroxo-Cu bonding in LS^AN.

2.2.1. Analytical Frequencies

The normal modes derived from an analytical frequency calculation on the optimized geometric coordinates of LS^AN were used to correlate to the resonance Raman data and to verify the assignment of the isotope sensitive bands. The potential energy distributions (PED) of the normal modes are given in Table 1. Due to the large size of the molecule, the Fe—O—O—Cu core modes coincide in energy with ligand modes, and thus mix, leading to fractional components of the core modes distributed over several modes of the molecule which adds complexity to the analysis. Nonetheless, it is clear that the DFT calculation predicts oxygen isotope sensitive clusters of modes at 840 cm⁻¹ (ν166, ν167), ~594 cm⁻¹ (ν129, ν131), and ~487 cm⁻¹ (ν109, ν103) assigned as the ν_O—O, ν_Fe—O, and ν_Cu—O vibrations respectively. The PED of these modes support their assignment, as indicated by the high distribution of these respective internal coordinates in the corresponding normal modes. The DFT calculations also predict a low energy mode at 383 cm⁻¹ (ν88), which downshifts to 379 cm⁻¹ in the ¹⁸O₂ isotopologue. This mode, although mixed with a variety of other motion, is best described as the trans-axial δ_NIm—Fe—O bend, consistent with the assignment in reference 30. No other modes with significant oxygen isotope dependence were found in the calculations. The ν_Cu—O is not observed in the resonance Raman spectrum due to a lack of Cu—O excited state distortion upon excitation into the peroxo → Fe(III) CT transition (see Section 2.2.4.).

Table 1.

DFT derived vibrational modes and potential energy distribution.

		energy (cm−1)		potential energy distribution (%)
mode	k	16O2	18O2	νO—O	νFe—O	νCu—O	δFe—O—O	δCu—O—O	δN—Fe—O
υ88	0.80	383	379	0	6	7	6	0	8
υ103	0.43	460	452	0	−2	18	−1	0	0
υ109	0.75	487	477	−1	−8	35	0	0	0
υ129	1.84	589	562	0	26	4	−11	−2	−1
υ131	1.79	594		0	20	3	−10	−1	−2
υ166	4.07	839	795	37	−2	0	0	0	0
υ167	4.17	840		36	−2	0	0	0	0

2.2.2. Electronic Structure

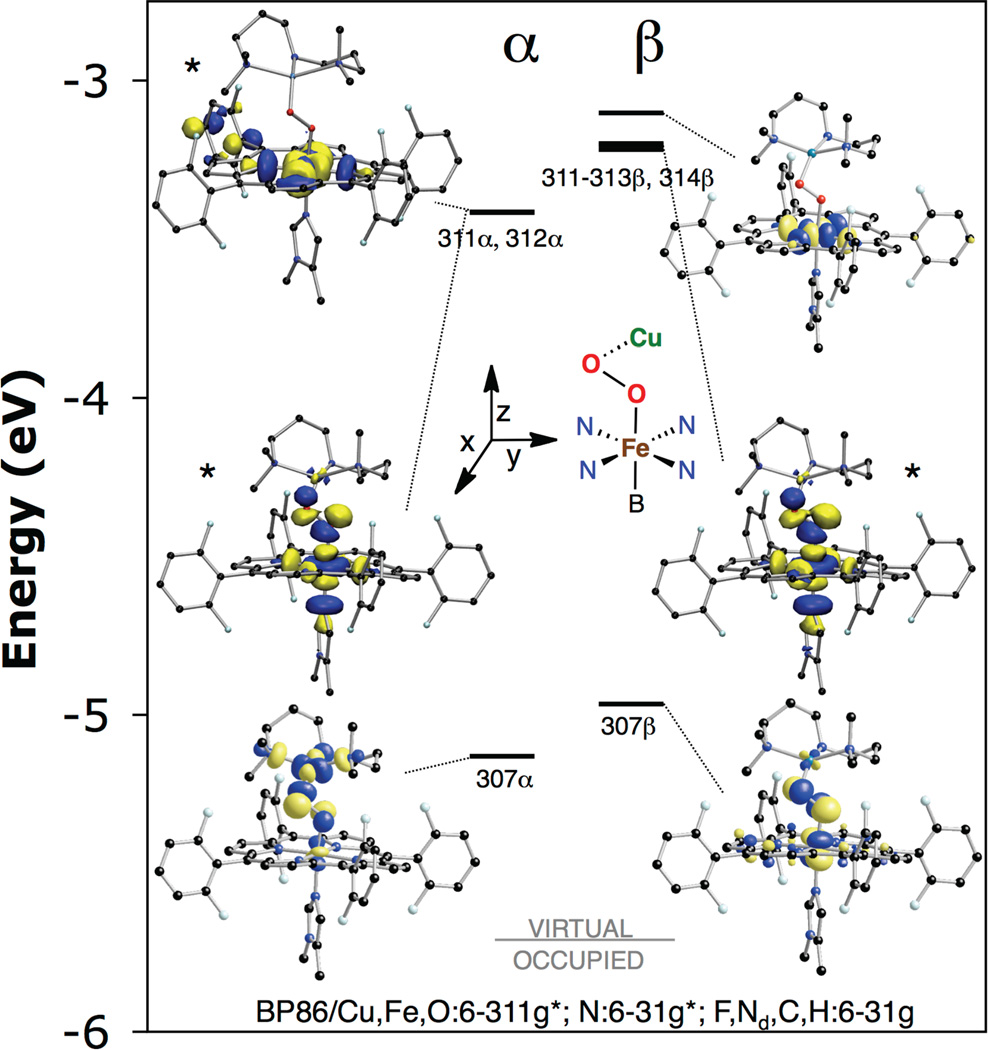
Consistent with the observed diamagnetism in the NMR spectrum,²⁹ LS^AN is well described as a broken-symmetry (BS) singlet (S_T = 0) that is calculated to be 2.2 kcal/mol lower in energy than the triplet. In this singlet, the low-spin Fe(III) and the Cu(II) are anti-ferromagnetically coupled. The low-spin electronic configuration of the heme is a consequence of the axial ligation of imidazole. The molecular orbital diagram and key unoccupied molecular orbitals are shown in Figure 5 and Table 2. The unoccupied opposite-spin partner of a half occupied natural orbital reflects the uncompensated spin of the occupied orbital, and thus the unoccupied orbital can be used for the analysis of the bonding. The Fe(III) has a single unpaired d electron of α-spin which results in a localized unoccupied β-spin Fe 3d_xz orbital (307β). Note that for these analyses the z-axis is along the Fe—O bond and the x-axis is perpendicular to the O—O bond. Two additional unoccupied α/β-spin orbital pairs exist at higher energy in the Fe 3d manifold (311α, 312α, mixture of 311–313β,³² 314β) which correspond to the 3d_x²−y² and 3d_z² of the LS Fe(III). The Cu(II) center has a single unpaired electron of β-spin, which results in an unoccupied α-spin Cu 3d_x²−y² orbital (307α). These Fe 3d_xz and Cu 3d_x²−y² are the magnetic orbitals, and productively overlap through the peroxo π^* orbital as described below to yield an overall diamagnetic ground state. The magnitude of the coupling between the Fe and Cu centers is calculated from the splitting between the S_T = 0 and 1 states using Equation 1.³³ Expressed in terms of the Heisenberg-Dirac-van Vleck Hamiltonian, −2JS₁•S₂, the magnitude of the antiferromagnetic exchange parameter was calculated to be J = −611 cm⁻¹.

$$-2J={}^{3}E-\frac{2^{\mathit{\text{BS}}}E-{\langle S^2\rangle }_{\mathit{\text{BS}}}{}^{3}E}{2-{\langle S^2\rangle }_{\mathit{\text{BS}}}}$$ (1)

Figure 5.

Molecular orbital diagram of LS^AN showing key unoccupied anti-bonding orbitals from a spin-unrestricted BP86 calculation (isovalue 0.05 a.u.). Isosurface for asterisked orbitals are linear combination of orbitals (top left: 311α − 312α, middle left: 311 + 312α, middle right: 311β − 312β + 313β).

Table 2.

Mulliken population analysis of unoccupied metal or peroxo based molecular orbitals from a spin-unrestricted BP86 calculation of LS^AN in the BS (S_T = 0) state.

orbital	level	occ	E(eV)	Fe	O2	Cu	rest
307α	Cu x2–y2 − O2	0	−5.131	6.1	29.3	42.7	21.8
311α	Fe z2 − O2	0	−3.418	59.4	11.6	0.7	28.3
312α	Fe x2–y2	0	−3.414	60.7	6.7	0.4	28.3
307β	$\text{Fe xz}-{\mathrm{O}}_2{\mathrm{\pi }}_{\mathrm{v}}^{*}$	0	−4.965	39.8	32.3	2.4	25.5
311β	$\text{Fe }{\mathrm{z}}^2-{\mathrm{O}}_2{\mathrm{\pi }}_{\mathrm{\sigma }}^{*}+\mathrm{L}$	0	−3.217	14.6	3.8	0.1	81.5
312β	$\text{Fe }{\mathrm{z}}^2-{\mathrm{O}}_2{\mathrm{\pi }}_{\mathrm{\sigma }}^{*}+\mathrm{L}$	0	−3.203	31.1	8.0	0.2	60.7
313β	$\text{Fe }{\mathrm{z}}^2-{\mathrm{O}}_2{\mathrm{\pi }}_{\mathrm{\sigma }}^{*}+\mathrm{L}$	0	−3.198	18.4	4.7	0.1	76.8
314β	Fe x2–y2	0	−3.102	65.1	0.0	0.0	34.9
		spin density		0.63	0.12, −0.10	−0.41

The magnitude of the antiferromagnetic exchange coupling constant in HS^AN between the high-spin Fe(III) and Cu(II) centers, calculated from the splitting between the S_T = 2 and 3 states (−6J), was previously determined to be J = −759 cm⁻¹.²⁹ In order to quantitatively compare the exchange interaction between LS^AN and HS^AN, J must be expressed in terms of a sum of the individual magnetic orbital pathway contributions (Equation 2) where n_A and n_B are the total number of unpaired electrons on the two metal centers, A and B, distributed over their respective 3d orbitals (i and j).³⁴ As reported previously for HS^AN,²⁹ a single efficient (out of five possible) superexchange pathway exists between the five 3d orbitals on the Fe(III) and the single 3d orbital on the Cu(II) (the Fe 3d_xz and the Cu 3d_x²−y² orbitals interact), and its contribution to the total J value is scaled by a factor of 1/5 (n_A = 5, n_B = 1, in Equation 2). A single pathway exists in LS^AN between the Cu 3d_x²−y² and the Fe 3d_xz and based on Equation 2 with n_A = n_B = 1, it is considerably less efficient relative to HS^AN. The difference in efficiency is a result of the difference in core geometries between LS^AN and HS^AN. In HS^AN, the side-on μ-η²:η² peroxo core geometry allows for much better overlap between the respective Fe/Cu magnetic orbitals compared to the end-on μ-1,2 geometry for LS^AN, the specific basis of which is explored below.

$$J=\frac{1}{n_A{n}_B}{\displaystyle \sum _{i,j=1}^{n_A{n}_B}}{J}_{A_i{B}_j}$$ (2)

2.2.3. Excited States

The absorption spectrum of LS^AN (Figure 4) is dominated by the heme spectral features. Nonetheless, a relatively weak band is observed at 789 nm which is profiled by the ν_Fe—O and the ν_O—O modes in the resonance Raman spectrum and thus assigned as a peroxo → Fe CT. To obtain quantitative insight into the origin of this feature, time-dependent (TD)-DFT calculations were performed on LS^AN within the unrestricted formalism using the B3LYP functional on the BP86 optimized model. The B3LYP functional was selected based on the best correlation to the data.³⁵ An absorption spectrum was simulated by assuming that each transition gives rise to a Gaussian band shape with a full-width at half maximum of 3000 cm⁻¹ (Figure 6).

Figure 6.

TD-DFT derived absorption spectrum () generated by the individual transitions (sticks) using 3000 cm⁻¹ half-width Gaussian functions. Overlaid is the experimental absorption spectrum (—). Electron density difference maps (green: positive (gain) phase; gray: negative (loss) phase; isovalue 0.005 a.u.) of the two low energy LMCT transitions (excited states 3 and 6).

TD-DFT predicts two low-energy transitions at 7637 cm⁻¹ (1309 nm) and 12894 cm⁻¹ (776 nm), along with several transitions at higher energy (Table S2). As is evident from inspection of the electron density difference maps (EDDMs) in Figure 6, and analysis of the donor and acceptor orbitals, both transitions are peroxo LMCT in nature. An EDDM is calculated by evaluating the electron density difference (EDD, Equation 3) over space, where the Ψ_a and Ψ_d are the acceptor and donor orbital transition components evaluated at a point in space and c is the transition component coefficient, summed over all transition components i. The lowest energy transition (Table 3 and Figure 7) is the ${\mathrm{O}}_2^{2-}{\mathrm{\pi }}_{\nu }^{*}\to \text{Cu }{\mathrm{d}}_{{\mathrm{x}}^2-{\mathrm{y}}^2}$ excitation based on the donor (306a) and acceptor (309a) orbitals (i.e. excitation of an electron from the peroxo-Cu σ-bonding MO to its σ-antibonding counterpart). This predicted transition is correlated to a low energy absorption feature experimentally observed at 951 nm (10515 cm⁻¹, Figure 4) suggestive of an assignment; however, the experimental feature is too low in energy to probe via resonance Raman spectroscopy. The higher energy transition has two orbital components (306β to 307β and 306β to 309β) in which the donor (306β) is the ${\mathrm{O}}_2^{2-}{\mathrm{\pi }}_{\nu }^{*}$ orbital (Table 3, Figure 7). The acceptors are formally assigned as a porphyrin and Fe 3d_xz MO, respectively, based on their populations. However, due to coincidental near degeneracy these orbitals are mixed. Specifically, the 307β MO contains 8.7 % Fe, 9.8 % ${\mathrm{O}}_2^{2-}$ , and 80.1% porphyrin character and the 309β MO is composed of 62.6 % Fe, 12.6 % ${\mathrm{O}}_2^{2-}$ , and 23.0 % porphyrin. Thus, the 12894 cm⁻¹ transition is assigned as the ${\mathrm{O}}_2^{2-}{\mathrm{\pi }}_{\nu }^{*}\to \text{Fe }3{\mathrm{d}}_{\text{xz}}$ transition (i.e. excitation of an electron from the peroxo-Fe π-bonding MO to its π-antibonding counterpart), which compares well with the experimentally determined peroxo → Fe CT at 789 nm (12674 cm⁻¹). This assignment is consistent with the lack of porphyrin vibrations and the lack of enhancement of a ν_Cu—O vibration in the resonance Raman spectrum upon excitation into this absorption envelope as described below.

$$\mathit{\text{EDD}}={\displaystyle \sum _{i=1}^n}{c}_i^2({\mathrm{\Psi }}_{\mathit{\text{ai}}}{(x,y,z)}^2-{\mathrm{\Psi }}_{\mathit{\text{di}}}{(x,y,z)}^2)$$ (3)

Table 3.

Mulliken population analysis of important donor and acceptor molecular orbitals from a TD-DFT calculation of LS^AN in the BS (S = 0) state using the B3LYP functional within the spin-unrestricted formalism.

orbital	level	occ	E(eV)	Fe	O2	Cu	rest
302α	$\text{Fe yz}-{\mathrm{O}}_2{\mathrm{\pi }}_{\mathrm{\sigma }}^{*}$	1	−7.807	14.8	18.0	4.9	62.3
303α	${\mathrm{O}}_2{\mathrm{\pi }}_{\mathrm{\sigma }}^{*}+\text{Fe yz}$	1	−7.584	25.3	39.6	9.8	25.4
306α	${\mathrm{O}}_2{\mathrm{\pi }}_{\mathrm{v}}^{*}$	1	−6.783	6.0	79.1	7.6	7.3
309α	$\text{Cu }{\mathrm{x}}^2-{\mathrm{y}}^2-{\mathrm{O}}_2{\mathrm{\pi }}_{\mathrm{v}}^{*}$	0	−3.974	4.2	23.8	48.9	23.0
317α	$\text{Fe }{\mathrm{z}}^2-{\mathrm{O}}_2{\mathrm{\pi }}_{\mathrm{\sigma }}^{*}$	0	−2.187	62.8	16.1	1.5	19.6
302β	$\text{Fe xz}+{\mathrm{O}}_2{\mathrm{\pi }}_{\mathrm{\sigma }}^{*}$	1	−7.427	45.9	10.5	5.3	38.3
303β	${\mathrm{O}}_2{\mathrm{\pi }}_{\mathrm{\sigma }}^{*}+\text{Fe yz}$	1	−7.207	18.5	47.2	11.9	22.5
306β	${\mathrm{O}}_2{\mathrm{\pi }}_{\mathrm{v}}^{*}-\text{Fe xz}$	1	−6.785	13.7	67.4	3.3	15.6
307β	Por	0	−4.265	8.7	9.8	0.3	81.3
309β	$\text{Fe xz}-{\mathrm{O}}_2{\mathrm{\pi }}_{\mathrm{v}}^{*}$	0	−3.306	62.6	12.6	0.2	24.6
319β	$\text{Fe }{\mathrm{z}}^2-{\mathrm{O}}_2{\mathrm{\pi }}_{\mathrm{\sigma }}^{*}$	0	−1.815	68.8	13.5	0.2	17.5
		spin density		0.83	0.10, −0.19	0.52

Figure 7.

Molecular orbital diagram of LS^AN derived from a B3LYP TD-DFT calculation. Vertical arrows indicate LMCT transitions (excited states 3 and 6) which are assigned as ${\mathrm{O}}_2^{2-}{\mathrm{\pi }}_{\nu }^{*}\to \text{Cu }3{\mathrm{d}}_{{\mathrm{x}}^2-{\mathrm{y}}^2}$ (left) and ${\mathrm{O}}_2^{2-}{\mathrm{\pi }}_{\nu }^{*}\to \text{Fe }3{\mathrm{d}}_{\text{xz}}$ (right), respectively, which are the only low energy transitions with significant intensity (see Figure 6).

2.2.4. Excited State Distortions

TD-DFT calculations were performed on LS^AN to predict the excited state distortions (and thus resonance enhancements in the Raman spectrum) of the normal modes ν167, ν131, ν109, and ν88 (ν_O—O, ν_Fe—O, ν_Cu—O, and δ_NIm—Fe—O respectively, see Table 4 and Section 2.2.1.) to evaluate the assignment of the trans-axial bend (δ_NIm—Fe—O) at 394 cm⁻¹ and to rationalize the lack of a copper-peroxo stretch (ν_Cu—O) upon excitation into the ${\mathrm{O}}_2^{2-}{\mathrm{\pi }}_{\nu }^{*}\to \text{Fe }3{\mathrm{d}}_{\text{xz}}$ charge transfer transition. The computational distortions were obtained by systematically varying the ground state geometry of LS^AN in the positive and negative directions along the respective normal mode, and performing a TD-DFT calculation to determine the resulting change in the ${\mathrm{O}}_2^{2-}{\mathrm{\pi }}_{\nu }^{*}\to \text{Fe }3{\mathrm{d}}_{\text{xz}}$ CT transition energy. The calculations provide a value for ${\left(\mathrm{\Delta }{E}_{O_2\to \mathit{\text{Fe}}}^{\mathit{\text{TD}}-\mathit{\text{DFT}}}/\mathrm{\Delta }{Q}_k\right)}_0$ , the excited state distorting force along mode Q_k, where ΔE is the change in the excitation energy and ΔQ_k is the dimensionless nuclear distortion parameter of the k^th normal mode. The value ${\left(\mathrm{\Delta }{E}_{O_2\to \mathit{\text{Fe}}}^{\mathit{\text{TD}}-\mathit{\text{DFT}}}/\mathrm{\Delta }{Q}_k\right)}_0$ is equivalent to a first order electron-nuclear coupling term when the distortion from the equilibrium geometry is small.

Table 4.

Summary of DFT derived excited state distortion parameters.

	ν88 (δNIm—Fe—O)		ν109 (νCu—O)		ν131 (νFe—O)		ν167 (νO—O)
	O2→Cu	O2→Fe	O2→Cu	O2→Fe	O2→Cu	O2→Fe	O2→Cu	O2→Fe
${\left(\mathrm{\Delta }{E}_{\mathit{\text{CT}}}^{\mathit{\text{calc}}}/\mathrm{\Delta }{Q}_k\right)}_0$ (erg•1012)	0.082	−1.184	−0.429	0.137	1.588	2.820	0.710	1.139
kcalc (mDyn/Å)	0.797		0.749		1.789		4.17

The energy of the calculated ${\mathrm{O}}_2^{2-}\to \text{Fe }3{\mathrm{d}}_{\text{xz}}$ CT transition (Table 4 and Figure 8) was significantly altered when the molecular geometry was stepped along the ν_O—O, ν_Fe—O, and δ_NIm—Fe—O modes, indicating large excited state distortions (1.139, 2.820, −1.184 erg × 10¹², respectively). In contrast, the CT energy perturbation by distortion along the ν_Cu—O mode is minimal indicating a very small excited state distortion along this mode (0.137 erg × 10¹²). Thus, excitation into the ${\mathrm{O}}_2^{2-}\to \text{Fe}(\text{III})$ CT transition is expected to produce little if any resonance Raman intensity for the ν_Cu—O mode, consistent with experiment. The excited state distortion forces were also calculated for the ${\mathrm{O}}_2^{2-}\to \text{Cu}(\text{II})$ CT transition predicted at 7627 cm⁻¹. Excitation into this band would lead to enhancement of the ν_Cu—O, ν_O—O, and ν_Fe—O modes, and little (if any) enhancement of the δ_NIm—Fe—O mode.

Figure 8.

Dependence of the ${\mathrm{O}}_2^{2-}{\mathrm{\pi }}_{\nu }^{*}\to \text{Fe }3{\mathrm{d}}_{\text{xz}}$ CT transition energy of LS^AN on the displacement of the metrical parameters along the normal modes ν167 (), ν131 (), ν109 (), and ν88 () determined by unrestricted B3LYP TD-DFT calculations with an S = 0 ground state.

2.3. Electronic Structure Calculations: Nature of Bonding

2.3.1. The Fe-peroxo bond

The composition and assignment of key unoccupied molecular orbitals are given in Table 2 and are graphically depicted in the diagram in Figure 5 (key occupied molecular orbitals are given in Table S1). Upon binding to Fe, the doubly degenerate fully occupied peroxo π^* orbitals split into ${\mathrm{\pi }}_{\mathrm{\sigma }}^{*}$ and the ${\mathrm{\pi }}_{\mathrm{v}}^{*}$ where the z-axis is along the Fe—O vector and the ${\mathrm{\pi }}_{\mathrm{\sigma }}^{*}$ is in the Fe—O—O plane. Both the ${\mathrm{\pi }}_{\mathrm{\sigma }}^{*}$ and the ${\mathrm{\pi }}_{\nu }^{*}$ contribute to the bond with the Fe in LS^AN. The dominant interaction is of σ-bonding character and consists of donation from the filled ${\mathrm{\pi }}_{\mathrm{\sigma }}^{*}$ of the peroxo (299α and 304β) into the unoccupied Fe d_z² (the unoccupied spin-up d_z² mixes into 311α–312α, and the unoccupied spin-down d_z² mixes into 311β–313β). The second significant interaction which is of π-bonding character is the donation of the filled ${\mathrm{\pi }}_{\nu }^{*}$ of the peroxo (303β) into the half-occupied Fe d_xz orbital (307β). These interactions between the ${\mathrm{O}}_2^{2-}$ and the Fe(III) lead to a net very covalent bond, as quantified by the mixing of ${\mathrm{O}}_2^{2-}$ character into the unoccupied Fe d orbitals. In the spin-up σ-antibonding orbital ( $\text{Fe }3{\mathrm{d}}_{{\mathrm{z}}^2}-{\mathrm{O}}_2^{2-}{\mathrm{\pi }}_{\mathrm{\sigma }}^{*}$ , 311α), the contributions are 59.4 % Fe and 11.6 % ${\mathrm{O}}_2^{2-}$ , and in the spin-down partner (mixture of 311β–313β), 64.1 % Fe and 16.5 % ${\mathrm{O}}_2^{2-}$ . The π-antibonding orbital ( $\text{Fe }3{\mathrm{d}}_{\text{xz}}-{\mathrm{O}}_2^{2-}{\mathrm{\pi }}_{\nu }^{*}$ , 307β) is composed of 32.3 % ${\mathrm{O}}_2^{2-}$ and 39.8 % Fe.

The Fe-peroxo interaction in LS^AN is significantly more covalent than that found for HS^AN. Quantitatively, the σ and π bonding in HS^AN consist of a single peroxo donor interaction with a half occupied Fe d orbital in which the anti-bonding ${\mathrm{O}}_2^{2-}$ orbital contributions are 18.5 % for σ and 13.4 % for π. As described above, the peroxo total σ and π donor contributions for LS^AN are 28.1 % and 32.3 % respectively. The increase in Fe-peroxo covalency of LS^AN results from: 1) the LS Fe(III) electronic structure that leads to a lack of repulsion in the σ-bonding framework because the Fe 3d_z² is unoccupied, and 2) a strong π donor bonding interaction between the peroxo π^* orbital and the Fe due to the shorter Fe-O distance (LS^AN = 1.82 Å; HS^AN = 2.06, 1.90). The increased Fe-peroxo covalency of LS^AN significantly impacts the O—O bond relative to HS^AN due to the nature of the peroxo donor orbitals that are π anti-bonding with respect to the O—O bond. A stronger Fe—O bond would be expected to strengthen the O—O bond. A strengthening of the O—O bond in LS^AN is reflected in the shorter O—O bond distance (1.40 Å) compared to that of HS^AN (1.47 Å). However, this correlation is complicated by differences in Cu bonding (side-on versus end-on) which dominates the O—O bond strength for HS^AN and is considered further below.

2.3.2. The Cu-peroxo bond

The composition and assignments of key unoccupied molecular orbitals are given in Table 2 and are graphically depicted in the diagram in Figure 5 (key occupied molecular orbitals are given in Table S1). The Cu—peroxo bonding in LS^AN is dominated by a single interaction of σ character. This interaction consists of donation from the filled ${\mathrm{O}}_2^{2-}{\mathrm{\pi }}^{*}$ into the singly occupied Cu 3d_x²−y² orbital (307α). The interaction is also very covalent, with 29.3 % of ${\mathrm{O}}_2^{2-}$ character mixed into the spin-up Cu based hole (307a). The ${\mathrm{O}}_2^{2-}{\mathrm{\pi }}^{*}$ contribution is a mixture of ${\mathrm{\pi }}_{\mathrm{\sigma }}^{*}\text{ and }{\mathrm{\pi }}_{\nu }^{*}$ orbital components (19.7 % and 9.4 % respectively),³⁶ as a result of maximizing overlap between the ${\mathrm{O}}_2^{2-}{\mathrm{\pi }}^{*}$ and the Cu 3d hole, which is dictated by the Fe—O—O—Cu dihedral angle competing against the sterics of the ligand scaffold (see below).

The magnitude of the Cu-peroxo donor interactions in LS^AN and HS^AN are similar. In HS^AN, in which the ${\mathrm{O}}_2^{2-}{\mathrm{\pi }}_{\mathrm{\sigma }}^{*}$ interacts with the Cu 3d_x²−y², the Cu based hole is composed of 41.4 % Cu and 29.6 % O₂ character.²⁹ Thus, despite the fact that in HS^AN the peroxo is bound η² rather than η¹ as in LS^AN, the Cu-peroxo covalencies are equivalent. While the σ-donor covalencies are similar in magnitude, the side-on geometry of HS^AN allows for a backbonding interaction between Cu and ${\mathrm{O}}_2^{2-}$ , in which a filled Cu d orbital contributes electron density into the antibonding ${\mathrm{O}}_2^{2-}{\mathrm{\sigma }}^{*}$ orbital (see reference²⁹ for details). This backbonding is not present in LS^AN due to the η¹ peroxo coordination to the Cu.

2.3.3. Dependence of the ground state on Fe—O—O—Cu dihedral angle

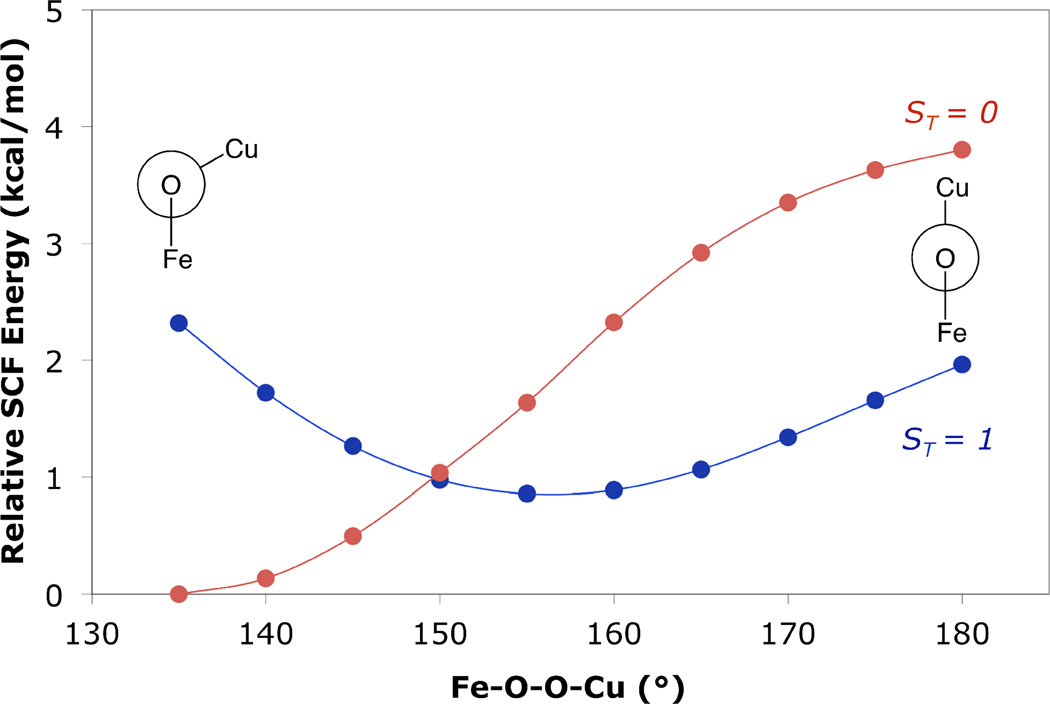
A relaxed potential energy scan was performed on LS^AN with the BP86 functional to assess the behavior of the singlet and triplet PES along the Fe—O—O—Cu coordinate. Calculations using the B3LYP functional and performed in an analogous manner qualitatively reproduce the results of the BP86 calculations. The Fe—O—O—Cu dihedral angle of LS^AN was distorted in 5° increments from 135° to 180°, and the remaining geometric parameters were allowed to relax on the triplet surface. Single point energies on the BS (S_T = 0) surface were performed at each point and spin projected (Figure 9) to allow comparison between the energies of the singlet and triplet surfaces. At Fe—O—O—Cu dihedral angles less than ~150°, the calculations predict the singlet to be lower in energy. In contrast, at dihedral angles above ~150°, the triplet state is predicted to be lowest in energy. Consequently, DFT calculations predict minima on the triplet and BS surface which vary in the Fe—O—O—Cu dihedral angle, with minimum energy values at ~155° and ~140° respectively.

Figure 9.

DFT (BP86) relaxed potential energy scan of the Fe—O—O—Cu dihedral angle of LS^AN on the triplet surface () and SP energy on the spin-purified singlet surface (). Newman projections are along the O—O vector.

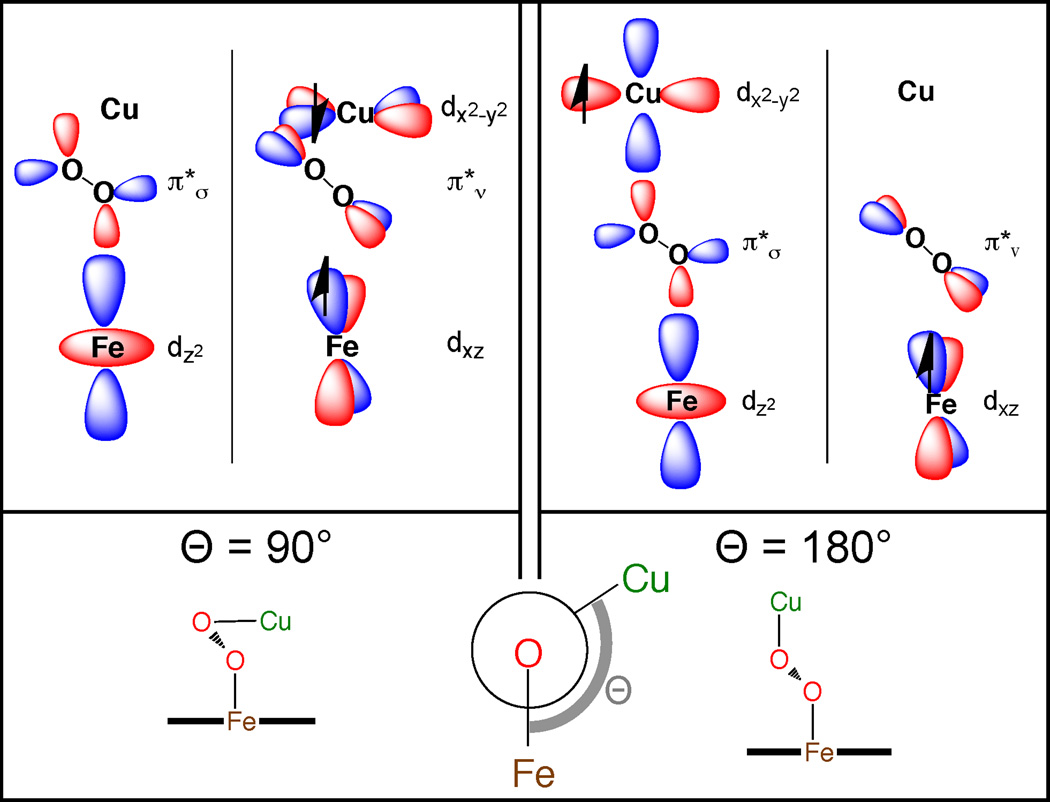
An angular overlap model can be used to describe the spin state dependence on the Fe—O—O—Cu dihedral angle. In the planar Fe—O—O—Cu dihedral limit (180°, Figure 10, right), the ${\mathrm{O}}_2^{2-}{\mathrm{\pi }}_{\mathrm{\sigma }}^{*}$ interacts with the singly occupied Cu d_x²−y² and the unoccupied Fe 3d_z² orbitals, and the orthogonal ${\mathrm{O}}_2^{2-}{\mathrm{\pi }}_{\nu }^{*}$ orbital interacts with the Fe 3d_xz. In this case, the magnetic orbitals (Fe 3d_xz and Cu 3d_x²−y²) are orthogonal, resulting in a ferromagnetically coupled electronic configuration. As the Fe—O—O—Cu dihedral angle distorts away from planar, the Cu 3d_x²−y² overlap with the ${\mathrm{O}}_2^{2-}{\mathrm{\pi }}_{\mathrm{\sigma }}^{*}$ decreases and overlap with the ${\mathrm{O}}_2^{2-}{\mathrm{\pi }}_{\nu }^{*}$ increases. In the 90° limit (not accessible in LS^AN due to sterics) the Cu 3d_x²−y² would interact exclusively with the ${\mathrm{O}}_2^{2-}{\mathrm{\pi }}_{\nu }^{*}$ (Figure 10 left). The ${\mathrm{O}}_2^{2-}{\mathrm{\pi }}_{\nu }^{*}$ also interacts with the singly occupied Fe 3d_xz orbital, and thus there is overlap of the magnetic orbitals that results in an antiferromagnetically coupled ground state for dihedral angles < ~150°. Note that the low efficiency of superexchange in LS^AN compared to HS^AN as quantified by a smaller J reflects the decreased overlap with the peroxo ${\mathrm{\pi }}_{\nu }^{*}$ as a result of the Fe—O—O—Cu dihedral angle of 137°, as the peroxo ${\mathrm{\pi }}_{\nu }^{*}$ is the only pathway in LS^AN that can allow for superexchange between the half-occupied Fe and Cu orbitals. In contrast, the Fe—O—O—Cu dihedral has minimal impact on the superexchange in HS^AN because both ${\mathrm{\pi }}_{\mathrm{\sigma }}^{*}\text{ and }{\mathrm{\pi }}_{\nu }^{*}$ overlap with magnetic orbitals on the Fe and thus are effective pathways.

Figure 10.

The orbital basis for the dependence of ground state spin of LS^AN on the Fe—O—O—Cu dihedral angle Θ in the limits of 90° (left) and 180° (right). The dihedral angle governs the interaction of the Cu hole with the two peroxo π^* orbitals.

3. Discussion

Impact of Heme Spin State on the O—O Bond and Correlation to Non-Heme Iron

To assess the impact of the spin state of the heme on the peroxo moiety in heme-peroxo-copper complexes, three species were compared (LS^AN, HS^AN, and {[(F₈)Fe]-O₂-[Cu(TMPA)]}⁺, (HS^TMPA)). These three complexes are spectroscopically well-characterized and DFT structures are available wherein the peroxo group bridges the metals in a μ-1,2, μ-η²: η², and μ-η²:η¹ fashion respectively (Figure 3). The DFT calculated O—O bond lengths are used as a probe of the bonding within the peroxo group. Previously, we described the affect of η² coordination of peroxo to copper in HS^AN. In this configuration, backbonding from the Cu d manifold into the ${\mathrm{O}}_2^{2-}{\mathrm{\sigma }}^{*}$ significantly weakens the O—O bond, and is reflected in a long (1.47 Å) O—O bond length. In both HS^TMPA and HS^AN the peroxo is coordinated η² to Fe, and the Fe—O bonds lengths are the same. However, HS^TMPA has η¹ coordination to Cu and thus no backbonding, which results in significantly shorter O—O bond length (1.43 Å) in HS^TMPA. LS^AN has the shortest calculated O—O bond length (1.40 Å), indicating LS^AN has a significantly stronger O—O bond than both HS^AN and HS^TMPA.

To achieve a stronger O—O bond in LS^AN, the peroxo group must be a better donor to the Fe, which is strongly modulated by the spin of the heme. Upon binding the axial base, the Fe e_g orbitals are destabilized as the Fe is pulled into the porphyrin plane. The Fe d_z² is destabilized by virtue of having an additional axial donor interaction, and the Fe d_x²−y² orbital is strongly destabilized by more efficient interaction with the porphyrin, which together result in a low-spin heme ground state in LS^AN. The low-spin ground state of the heme yields a significantly more covalent Fe-peroxo interaction in LS^AN due to lack of the electron-electron repulsion between the ${\mathrm{O}}_2^{2-}{\mathrm{\pi }}_{\mathrm{\sigma }}^{*}$ and Fe d_z². This stronger Fe—O interaction leads to a stronger O—O bond, due to nature of the peroxo donor orbital which is anti-bonding with respect to the O—O bond.

The correlation of a more covalent Fe—O interaction in the LS heme of LS^AN leading to a stronger O—O bond is opposite of the behavior observed in non-heme iron, in which a more covalent Fe—O in LS adducts results in a weaker O—O bond.^31,37 In HS and LS non-heme iron complexes, the π bonding contributions are of similar magnitude, and the bonding differences are found in the σ bonding framework. Specifically, in non-heme iron the valence orbitals of the Fe are of appropriate energy to potentially interact with the in-plane π^* or π orbitals of the peroxo. Upon going from HS to LS in non-heme Fe, the peroxo donor contribution to the Fe-O σ bonding shifts from π^* to π^b in character. In contrast, upon going from HS to LS in heme, where the ligand field of the porphyrin in the LS case strongly destabilizes the Fe e_g orbitals, a bonding interaction with the in-plane π^b of the peroxo is not available. The general result obtained here for HS to LS correlation in heme versus non-heme iron has important implications for reactivity of a putative peroxo level intermediate in CcO. Namely, the putative LS peroxo-heme intermediate would have a strong O—O bond that would disfavor O—O bond homolysis. A strong O—O bond in LS peroxo-heme indicates a less reduced peroxo moiety, which would suggest a more electrophilic reactivity behavior, consistent with the possibility of net H-atom abstraction from the active site tyrosine as is proposed to generate the consensus tyrosyl radical in CcO intermediate state P_M.

Magneto-Structural Correlation of LS^AN

The singly occupied orbital on the Fe in LS^AN is of 3d_xz character (where the O—O vector defines the y axis), as a result of the π donor interaction with the peroxo ${\mathrm{\pi }}_{\nu }^{*}$ orbital. To achieve an efficient superexchange pathway, the Fe—O—O—Cu dihedral angle is torsionally distorted to maximize the overlap between the magnetic orbitals on the metals, for which there is an energetic advantage (calculated to be 2.2 kcal/mol with BP86), consistent with the observed diamagnetism of LS^AN. Specifically, since the magnetic orbital on the Fe is 3d_xz and interacts with the peroxo ${\mathrm{\pi }}_{\mathrm{v}}^{*}$ , the singly occupied orbital on the Cu must also interact with the ${\mathrm{\pi }}_{\mathrm{v}}^{*}$ to participate in a magnetic exchange interaction. A planar core (Figure 10, right) would result in the magnetic orbital on the Cu interacting with the peroxo ${\mathrm{\pi }}_{\mathrm{\sigma }}^{*}$ , an orbital which donates into the unoccupied Fe 3d_z². Under this scenario, the magnetic orbitals on the Cu and Fe would be orthogonal, and thus ferromagnetically coupled. This possibility of ferromagnetic coupling can only exist when the Fe is LS, as any Fe—O—O—Cu angle in a HS heme (S = 5/2) would result in the overlap of magnetic orbitals, and an anti-ferromagnetic ground state. The fact that the 1/2 occupied Cu d orbital has 9.4 % ${\mathrm{\pi }}_{\mathrm{\sigma }}^{*}$ and only 19.7 % ${\mathrm{\pi }}_{\nu }^{*}$ explains its relatively low J value. The possibility of ferromagnetic coupling for a LS Fe(III)—peroxo—Cu(II) species is potentially important for O—O bond cleavage as described below.

Effect of magnetic coupling on the spin topology of O—O bond rupture

We and others have hypothesized the involvement of an unobserved, intermediate peroxo moiety during CcO catalysis. Due to the architecture of the CcO active site, namely the distance between the heme a₃ and the Cu_B that has been crystallographically determined as > 4.5 Å, a putative end-on bridging peroxo intermediate would be expected to adopt an Fe—O—O—Cu dihedral angle > 150° in order to span the metals. From Figure 9, this would be within the ferromagnetic regime developed for LS^AN. Ferromagnetic coupling in such a putative species could impart a significant functional role, namely, the ability to cleave the O—O bond without a spin surface crossing.

Cleavage of the peroxo O—O bond requires two electrons. A μ-1,2 peroxo bridged state could be either anti-ferromagnetic or ferromagnetic coupled (Figure 11 left), with S_T = 0 or 1 respectively, as a consequence of coupling between the LS ferric heme (S = ½) and the Cu(II) ion (S = ½). The final state, P_M, consists of an Fe(IV)=O (S = 1), a Cu(II)-OH (S = ½) and a Tyr244• (S = ½). The spectroscopic data of P_M suggests the Cu(II)-OH and Tyr244• are anti-ferromagnetically coupled.³⁸ Thus, the final two electrons required to cleave the peroxo O—O bond would come from the Fe(III) (to generate the Fe(IV)=O) and the Tyr244 (to generate a Tyr244• radical). These two electrons are accepted by the peroxo σ^* orbital, and hence must be of opposite spin. In order to generate an S = 1 Fe(IV)=O, wherein the singly occupied orbitals are of 3d_xz and 3d_yz character, the electron that originates from the Fe 3d_yz and is accepted by the peroxide σ^* is spin-down. The second electron that comes from the Tyr, therefore, must be spin-up. In a situation where the Cu and Fe in the putative peroxo intermediate are antiferromagnetically coupled, the removal of a spin-up electron from the Tyr would result in an electronic configuration where the unpaired electrons in both the Cu^II and Tyr• would be spin-down (Figure 11 top right) and would necessitate a spin-surface crossing to access the final anti-ferromagnetic state for Tyr• and Cu^II in P_M. In contrast, in a situation where the Cu and Fe in the putative peroxo intermediate are ferromagnetically coupled (Figure 11 bottom left), removal of a spin-up electron from Tyr would result in an unpaired spin-down electron on Tyr•, and thus the final anti-ferromagnetically coupled Cu(II)-Tyr• state would be reached without a surface crossing. The anti-ferromagnetic coupling of the Tyr• with the Cu(II) reflects an efficient superexchange pathway, which in turn means overlap of the redox active molecular orbitals. The overlap of these orbitals is a necessary condition for facile electron transfer of the fourth and final electron from the crosslinked Tyr through the copper to cleave the O—O bond. Current studies (both chemical and computational) are underway to develop further quantitative insight into the mechanism of O—O bond cleavage in LS^AN and its relation to O—O bond cleavage by CcO where the Tyr is covalently tethered to the Cu bound His ligand.

Figure 11.

Illustration of the spin topology of a hypothetical enzymatic peroxo (I_P)¹⁹ O—O bond cleavage reaction to yield P_M starting from an anti-ferromagnetic (top) or ferromagnetic (bottom) coupled ground state. Two electrons (an α,β pair) originating from Fe and Tyr244 (PhOH) fill the σ^* of the oxygen to break the O—O bond.

5. Experimental Methods

Resonance Raman

Samples were prepared by exposure of a 1 mM solution of [(F₈)Fe(II)] and [(AN)Cu(I)]B(C₆F₅)₄ in THF to dioxygen at subambient temperatures (−80°C) in 5 mm rubber septa capped NMR tubes. DCHIm (1eq) was added and the tube was flame sealed. Isotopically labelled (¹⁸O₂) samples were prepared with ¹⁸O₂ in an analogous manner. Samples were excited at a variety of wavelengths, using either a Coherent I90C-K Kr+ ion laser, a Coherent 25/7 Sabre Ar+ ion laser, or an Ar+ pumped Coherent Ti:Saph laser while the sample was immersed in a liquid nitrogen cooled (77 K) EPR finger dewar (Wilmad). The power was ~2 mW at the sample for the high energy lines and >200 mW at the low energy lines. Data were recorded while rotating the sample to minimize photodecomposition. The spectra were recorded using a Spex 1877 CP triple monochromator with either a 600, 1200, or 2400 groves/mm holographic spectrograph grating, and detected by an Andor Newton CCD cooled to −80° C (for high energy excitation) or an Andor IDus CCD cooled to −80°C (for the low energy excitation). Spectra were calibrated on the energy axis to toluene. Excitation profiles were intensity calibrated to the solvent (THF) by peak fitting in the program Origin.

Calculations

Density functional theory (DFT) calculations were performed using Gaussian03.³⁹ The optimized molecular structure of LS^AN, HS^AN, and HS^TMPA have been reported previously (with cyclohexyl rings truncated to methyl groups in the case of LS^AN), in which the molecular structures were optimized using the BP86 functional within the spin-unrestricted formalism.²⁶ The basis sets employed on Fe, Cu and O₂ were of triple-ζ quality with polarization (6–311g*). A double- ζ quality, split-valence basis was used on all other atoms (6–31g), and was augmented with polarization on the metal bound N atoms (6–31g*). An ultrafine integration grid was employed as was auto density fitting. Due to spin effects on the Fe—O—O—Cu dihedral angle (vide supra), a one dimensional relaxed potential energy surface (1D PES) scan was performed in 5° steps from 135 – 180° using both the BP86 and B3LYP functionals. The scans were performed on the HS surface, then single point energies were calculated on the BS surface. Molecular orbitals, transition densities, and simulated TD absorption spectra were visualized using Lumo.⁴⁰ Mulliken population analyses were performed using QMForge.⁴¹ Vibrational frequency analysis was performed using VEDA4 adapted for large molecules (XL version).⁴²