Abstract
The effects of demographic stochasticity on the long-term behaviour of endemic infectious diseases have been considered for long as a necessary addition to an underlying deterministic theory. The latter would explain the regular behaviour of recurrent epidemics and the former the superimposed noise of observed incidence patterns. Recently, a stochastic theory based on a mechanism of resonance with internal noise has shifted the role of stochasticity closer to the centre stage, by showing that the major dynamic patterns found in the incidence data can be explained as resonant fluctuations, whose behaviour is largely independent of the amplitude of seasonal forcing, and by contrast very sensitive to the basic epidemiological parameters. Here we elaborate on that approach, by adding an ingredient which is missing in standard epidemic models, the ‘mixing network’ through which infection may propagate. We find that spatial correlations have a major effect on the enhancement of the amplitude and the coherence of the resonant stochastic fluctuations, providing the ordered patterns of recurrent epidemics, whose period may differ significantly from that of the small oscillations around the deterministic equilibrium. We also show that the inclusion of a more realistic, time-correlated recovery profile instead of exponentially distributed infectious periods may, even in the random-mixing limit, contribute to the same effect.
Keywords: networks, childhood infections, stochastic fluctuations
1. Introduction
The incidence patterns of childhood diseases in the twentieth century have been a challenge and a preferred testing ground for epidemiological models. One of the simplest epidemiological models one can consider is based on dividing the whole population into three classes of individuals: the susceptible; the infectious; and the permanently recovered (Anderson & May 1991). It is suitable to study the infection dynamics of diseases that confer long-lasting immunity, like childhood infections, provided that we take into account in the long-term dynamics the replenishment of susceptibles in the population through births.
The deterministic description of the basic susceptible–infectious–recovered (SIR) model in a closed population where renewal of susceptibles occurs through births with a constant birth rate and death rate is given by the equations
| (1.1) |
where s and i are the densities of susceptible and infectious individuals, respectively; γ is the recovery rate of the disease and β is its transmissibility (Anderson & May 1991). A crucial parameter for the behaviour of this model is the so-called basic reproductive rate, . For R0<1 the disease dies out, while for R0>1, the disease is endemic in the population. In this case, system (1.1) has a non-trivial endemic equilibrium at , , and the small oscillations around this equilibrium have damping factor −μ/(2s*) and period . The susceptible–exposed–infectious–recovered (SEIR) model considers an additional class of infected, but not yet infectious, individuals.
During the last decade, more sophisticated approaches building on the traditional SIR and SEIR models have brought considerable advances in understanding and selecting some of the fundamental ingredients of the complex dynamics of infectious diseases (Hethcote 1997; Grenfell et al. 2001; Wang 2006). The interplay between the system's nonlinearity and the periodic perturbation in seasonally forced SIR and SEIR models was shown to be a source of complex dynamics compatible with the diversity of observed incidence records (Earn et al. 2000; Bausch & Earn 2003; Dushoff et al. 2004).
This body of work belongs to an essentially deterministic framework, where demographic stochasticity plays a secondary role, except when addressing stochastic extinction (Bartlett 1957; Nåsell 2005). In this framework, the role of stochasticity is that of sustaining small-amplitude oscillations around the deterministic system's equilibrium that follow the natural frequency given by the local linear approximation (Bailey 1975; Bausch & Earn 2003; Lloyd 2004), or else that of promoting the switching between different competing attractors of the underlying deterministic model (Keeling et al. 2001; Allen & van den Driessche 2006).
Recently, a stochastic theory developed for a predator–prey competition model (McKane & Newman 2005) and then applied to the well-mixed SIR model (Alonso et al. 2007) has shown that the fluctuation power spectrum of the incidence time series is essentially determined, in both the presence and the absence of seasonal forcing, by the resonance with internal noise of the system's natural frequency in the deterministic (infinite population size) limit. The cross-correlation structure of this internal noise can be computed analytically from the transition probabilities, and it may shift the resonance peak away from the system's natural frequency. Both the amplitude and the coherence of these resonant fluctuations are large for the parameter values that correspond to some childhood diseases, so that they may be comparable even in large systems to the oscillations induced by seasonal forcing.
Apart from stochasticity, another missing ingredient of the standard epidemic models that has been attracting increasing attention is the host population contact structure, or ‘mixing network’ (Keeling & Eames 2005; Edmunds et al. 2006). Most of the research connecting networks and epidemiology dates from the last 5 years, when many fundamental results of network theory became widely known while new ones have been derived (Albert & Barabási 2002; Dorogovtsev & Mendes 2003; Boccaletti et al. 2006). These ideas originated in the mathematics and physics communities and were applied in an epidemiological setting from the beginning (Watts & Strogatz 1998; Kuperman & Abramson 2001; Pastor-Satorras & Vespignani 2001), prompting the interest of epidemiologists and several theoretical (May & Lloyd 2001; Eames & Keeling 2002; Keeling 2005) and field epidemiology (Jolly & Wylie 2002; Riley et al. 2003; Meyers et al. 2005) results.
Here we address the effect of relaxing the random mixing assumption on the behaviour of the resonant fluctuations of a stochastic SIR model. We assume that the host population contact network may be represented by a ‘small-world’ network of the type introduced by Watts & Strogatz nearly a decade ago (Watts & Strogatz 1998). Analysis of real networks of social contacts (Eubank et al. 2004) indicates that this is a reasonable first assumption to model the contact structure relevant for the propagation of airborne infections. We find that spatial correlations have a major effect on the enhancement of the amplitude and the coherence of the resonant stochastic fluctuations, providing ordered patterns of recurrent epidemics. The shift of the resonance peak away from the system's natural frequency also increases significantly due to correlations. The enhanced amplitude and coherence of the fluctuations imply that, in populations where a disease spreads predominantly through local infectious contacts, large epidemic outbursts with well-defined recurrence times are generated by internal noise alone, without the presence of seasonal forcing. This effect is illustrated in §2.2 with a particular example and studied systematically in §3.2.
Another assumption of the SIR model, which has been challenged (Keeling & Grenfell 1997; Lloyd 2001a; Wearing et al. 2005), is that of considering a constant recovery probability during the infection period. We study the effect on the resonant fluctuations of switching from the (uncorrelated) exponentially distributed infection periods used in Alonso et al. (2007) to the opposite limit of (time correlated) constant infection periods. Again, we find that the spectrum of stochastic fluctuations found in Alonso et al. (2007) changes under more realistic assumptions on the recovery profile in such a way that the oscillations become larger and more sharply defined. In this case, the peak frequency shift with respect to the deterministic prediction is larger, and towards larger frequencies.
Qualitatively, the effects of spatial and time correlations on the fluctuation spectrum are similar: both the spatial correlations, introduced through the host population contact network, and the time correlations, introduced via constant infection periods, lead to enhanced, more sharply defined, dominant peaks. There are analogues of this behaviour in many systems studied in statistical physics. The peak frequency shift, however, is more pronounced and has a different sign for the model with constant infection period. As discussed in §§2.2 and 3.3, this qualitative difference can be understood on the basis of an effective deterministic description.
These results show that the classical understanding of the incidence time patterns of endemic infectious diseases, which is mainly based on a seasonally forced deterministic description, is clearly insufficient to have a correct description of such fluctuations. These may be purely stochastic, and the diversity of incidence patterns found in real data for the same disease in different populations can be understood in this framework as an effect of population size and contact structure.
Moreover, the approximate period of the recurrent epidemics driven by internal noise in the presence of spatial and/or time correlations differs significantly from the period computed in the usual deterministic approach. This is an important cautionary note with regard to the use, in the framework of the deterministic description, of the recurrence period to help assess estimates of epidemiological parameters. The breakdown of the assumptions of random mixing of the population and/or of constant recovery rate during the infectious period implies important corrections to the dominant frequency of the fluctuations.
2. Methods
2.1 Susceptible–infectious–recovered dynamics in a randomly mixed discrete population
In a randomly mixed discrete population of N individuals, SIR dynamics may be described as a continuous-time Markov process on a population divided into three classes: susceptible; infectious; and recovered. The state of the system is characterized by the numbers S, I and R=N−S−I, of individuals in each of the three classes, and the events of infection, death, birth and recovery correspond to the following transitions and transition rates
| (2.1) |
where denotes the transition from state (S, I) to state (S′, I′) and is the corresponding transition rate.
As detailed in Alonso et al. (2007), a good approximation for the power spectrum of the stochastic fluctuations around the stationary population numbers can be computed analytically from the linear Fokker–Planck equation obtained from the next to leading-order terms in van Kampen's expansion of the master equation associated to (1.1). The leading-order terms of the expansion yield the deterministic equations (2.1) that describe the behaviour of the system in the limit of infinite populations.
Following this approach, we have computed the power densities PS and PI of the fluctuations of susceptibles and infectious individuals for process (2.1), scaled by the square root of the system size , as a function of the angular frequency ω,
| (2.2) |
where and , denoting as before by R0 the basic reproductive rate of the disease. The parameters D and T are equal to the determinant and the trace, respectively, of the linear approximation of (1.1) at the endemic equilibrium and have a simple dynamical interpretation: D is the square of the frequency of the small oscillations around the equilibrium when the damping is small and T is twice the damping factor of these oscillations.
Equations (2.2) are independent of N because the dependence of the amplitude of the fluctuations on system size has been scaled out, and they describe exactly the stochastic process (2.1) in the limit of large N. These power spectra are resonant like, showing that the amplitude of the fluctuations as a function of their time scale is governed by a mechanism of resonance of internal noise with the system's natural frequency . The resonance peak will be shifted away from , depending on the values of T and on the terms in the numerator of (2.2), which are determined by the cross-correlation structure of the internal noise. However, when T is small, the shift in the resonance peak with respect to is also small.
The relevance and universality of this type of ‘endogenous’ stochastic resonance for ecological systems in general was first argued in McKane & Newman (2005). The complete analytic description of the phenomenon given in McKane & Newman (2005) and Alonso et al. (2007) relies on the random mixing assumption and on the constant recovery rate assumption. The effect of relaxing these assumptions, crucial in more realistic settings, must be tested through stochastic simulations.
2.2 The SIR model on dynamic small-world networks
Complex network theory (Albert & Barabási 2002; Dorogovtsev & Mendes 2003; Boccaletti et al. 2006) focuses on abstract network models such as small-world networks, which interpolate between regular lattices and random graphs, and scale-free networks, exhibiting a power law distribution of the connectivity. In most, if not all, of the theoretical work in contact network epidemiology, the host population contact network is represented by one of these models. The choice of the right idealized network type, which will be disease specific, depends on the availability of data on disease-causing contacts which are hard to get and difficult to interpret (Keeling & Eames 2005). At this point, an important concern of contact network epidemiology is to collect data and build appropriate network models for different transmission mechanisms (Eubank et al. 2004).
As a first step to understanding the role of network structure correlations on the spectrum of stochastic fluctuations, we have modelled the mixing network of the populations as a small-world network (Watts & Strogatz 1998) built over a square lattice with 12 nearest neighbours per node. In these models a fraction of the links of the lattice is randomized by connecting nodes, with probability p, with any other node. These non-local connections are chosen randomly for each event, instead of being fixed in a frozen, partially random link configuration. This version of the small-world network model, which has been dubbed ‘dynamic’ or ‘annealed’ in the literature (Zanette 2003; Szabo & Vukov 2004; Volz & Meyers 2007), is motivated by the nature of the occasional social contacts the model tries to represent. For p=0, each node interacts with only its nearest neighbours on the lattice, as in ordinary representation of spatial structure. For p=1, the network of interactions is a random graph, where every pair of nodes, independently of the distance on the lattice between the two nodes, has the same probability of being connected. Random graphs have the property that the average path length, or average number of connections of the shortest path between two nodes, is ‘small’, i.e. of the order of the logarithm of the total number of nodes. For a range of p between 0 and 1 the network exhibits small-world behaviour, where predominantly local interactions (as in lattices) coexist with a short average path length (as in random graphs). Analysis of real networks (Eubank et al. 2004) reveals the existence of small-world behaviour in many interaction networks, including networks of social contacts.
An important consequence of the spatial correlations introduced by predominantly local contacts is what is called infective screening, or infective clustering. If all the infected neighbours of an infected node have many neighbours in common, each of them will be connected to a number of susceptibles which is smaller than the average number of susceptible neighbours per node, and infection will be less likely than in a randomly mixed population with the same density of infectious and susceptibles.
The qualitative analysis of time series of SIR and SEIR stochastic simulations on dynamic small-world networks for different values of the small-world parameter p shows that indeed the infection process becomes less and less efficient as p decreases and infective screening becomes more pronounced (Verdasca et al. 2005; Telo da Gama & Nunes 2006). The global effect of infective clustering may be quantified in terms of the value of βeff, defined as the average number of new infections per time step and infective individual divided by the density of susceptibles. For p=1, βeff coincides with the transmissibility β, but as p decreases, βeff also decreases. Another qualitative effect of spatial correlations reported in Verdasca et al. (2005) and Telo da Gama & Nunes (2006) is that they have a major effect on the enhancement of the amplitude of stochastic fluctuations, which become more and more pronounced as p decreases.
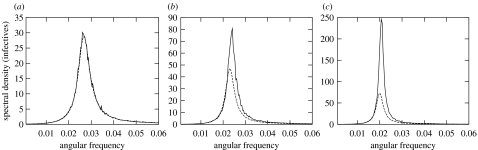
In order to quantify the effect of network structure on resonant stochastic fluctuations, we have computed the power spectrum of SIR time series on dynamic small-world networks for several values of p, and we have compared it with the analytic power spectrum given by (2.2) with βeff, the effective transmissibility, instead of β (see appendix A for the details of the simulations). The results are shown in figure 1. The solid lines are the averaged numerical power spectra of the stationary time series, and the dashed lines are the analytic power spectra given by (2.2) with the correction due to the effective transmissibility. We see that, as p decreases, the resonant fluctuations are larger and more coherent. Moreover, in the small-world regime, where local correlations become important, this effect is much more pronounced than in the predictions of an effective (corrected for infective screening) randomly mixed model, represented by the dashed lines in figure 1. However, this effective model does describe satisfactorily the shift to the left in the peak frequency, which means that this can be understood as a consequence of the reduced effective transmissibility.
Figure 1.
Fluctuation power spectra of infective time series for the SIR model on dynamic networks of nodes for small-world parameter p equal to (a) 1, (b) 0.4 and (c) 0.2 and βeff equal to (a) 1.32, (b) 1.01 and (c) 0.79; the networks are built over regular 1000×1000 lattices with 12 first neighbours and periodic boundary conditions. The solid lines are the averaged numerical power spectra of 400 stationary time series, each 32 768 time steps long. The dashed lines are the analytic power spectra given by (2.2), where for p smaller than 1 the value of the parameter β has been taken as βeff, defined as the actual number of new infections per time step and infective individual divided by the density of susceptibles. Parameter values: μ=6×10−4, β=1.32, τ=1/8.
The enhanced amplitude and coherence of the fluctuations imply that a typical time series will exhibit noisy but regular incidence oscillations, as shown in §3.2. These sustained oscillations are of a purely stochastic nature and they disappear in the infinite population limit.
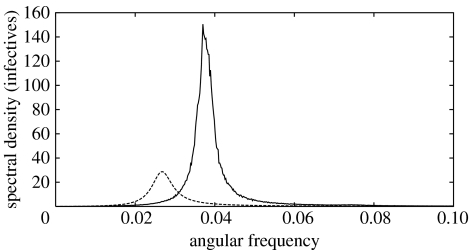
The influence of the recovery profile on the behaviour of the system has been discussed in Keeling & Grenfell (1997), Lloyd (2001b) and Wearing et al. (2005). In the standard SIR stochastic model, to which the analytic description (2.2) applies, the event of recovery occurs at a fixed rate during the infection, and the recovery time is exponentially distributed around the average infectious period τ=1/γ, or in other words uncorrelated. We have computed the power spectrum of the time series obtained from SIR simulations in randomly mixed populations where instead of uncorrelated infection periods the recovery profile was taken in the opposite limit of constant infection period τ or strongly time-correlated infections. The results are shown in figure 2. The solid line is the averaged numerical power spectra of the stationary time series, and the dashed line is the analytic power spectra given by (2.2) with γ=1/τ. We see that switching to more realistic (time correlated) recovery profiles leads to a similar effect of enhancing the amplitude and the coherence of the resonant stochastic fluctuations predicted by the theory developed in Alonso et al. (2007). In addition, there is a large shift to the right of the dominant frequency of the fluctuations, relative to the peak frequency predicted for the model with stochastic recovery (Alonso et al. 2007). Again, the shift in the peak frequency and its sign can be understood in terms of an effective deterministic description, as discussed in §3.3.
Figure 2.
Fluctuation power spectra of infective time series of stochastic SIR dynamics with deterministic and stochastic recovery on a randomly mixed population with N=106 individuals. Deterministic recovery occurs τ time steps after infection. The solid line is the averaged numerical power spectra of 400 stationary time series, each 32 768 time steps long. The dashed line is the analytic power spectra given by (2.2), with γ=1/τ. Parameter values: μ=6×10−4, β=1.32, τ=8.
Qualitatively, it is to be expected that correlations in the dynamics of the system's components should enhance the global density fluctuations. To assess quantitatively the effect of spatial and temporal correlations on the resonant fluctuation spectrum in the modelling of infectious childhood diseases, we have performed systematic simulations in a region of parameter space that includes the values for measles, chicken pox, rubella, pertussis and mumps according to published and estimated data for the pre-vaccination period (Bausch & Earn 2003). The amplitude and coherence of the stochastic fluctuations are measured by the overall amplification A, and by the coherence factor c, introduced in Alonso et al. (2007), where analytic results for a randomly mixed SIR stochastic model with external infection and constant recovery rate were presented for the same region of parameter space. The overall amplification A is the integral over all the frequencies of the power density of the scaled fluctuations, and it is equal to the mean square deviation of the time series from the equilibrium values, divided by the system size N. The coherence factor c is defined as the integral of the power density of the scaled fluctuations on the frequency interval that corresponds to periods within 10% of the peak period 2π/ωpeak, divided by A. It measures the relative contribution to the overall amplification of stochastic fluctuations that are distributed around the dominant period.
For the randomly mixed case p=1 with stochastic recovery, both A and c can be computed analytically from equations (2.2), which are exact in the limit of large N. In the remaining cases there is no analytic description, and the overall amplification A is computed as the ensemble average, over several runs, of the integral over all sampled frequencies of the power density of the stationary time series of the scaled fluctuations. The coherence factor c is computed in a similar way on the prescribed frequency interval. The details of the analytical and numerical computations are given in appendix A.
For the model with stochastic recovery, we have also computed, for several values of the small-world parameter p, the peak shift factor s, defined as the distance between the actual peak frequency and the natural frequency of the system in the deterministic description (1.1), , divided by . It measures the relative frequency shift of the dominant frequency due to the various ingredients that are missing in the deterministic description (resonance with correlated internal noise and contact network structure).
3. Results
3.1 Randomly mixed model: finite size effects
The randomly mixed model depends on the demographic and epidemiological parameters μ, β and γ. Following Alonso et al. (2007), we have taken μ fixed and equal to 5.5×10−5, and the reduced variables in the parameter plane (μ/γ, β/γ). These reduced parameters have an immediate epidemiological interpretation: μ/γ measures the acuteness, or relative time scale, of the disease and β/γ≈R0.
The values of the overall amplification
| (3.1) |
and of the coherence
| (3.2) |
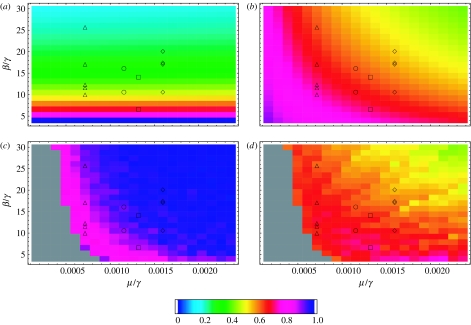
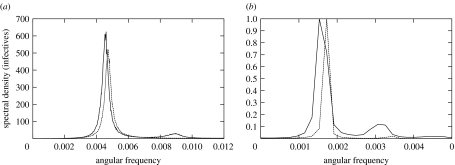
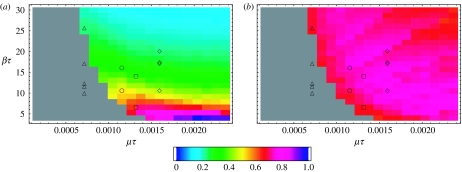
of the infectives power spectrum PI in (2.2) are shown in figure 3a,b for 441 points in parameter space. The values of A are normalized by the largest overall amplification 0.1902. We see that, for the basic SIR model, A is essentially determined by R0, and both the overall amplification and the coherence increase as R0 decreases with γ fixed. For each R0 the stochastic oscillations become more and more coherent as γ increases. The symbols mark the parameter values for measles, chicken pox, rubella and pertussis according to different data sources for the pre-vaccination period (Bausch & Earn 2003). The numerical results for the overall amplification and coherence obtained from simulations of the stochastic process (2.1) on a population of size N=106 are plotted in figure 3c,d. (see appendix A for the details of the simulations and numerical computations). Each datum point in figure 3c is the ratio of the corresponding analytic and numerical values of the overall amplification, while each datum point in figure 3d corresponds to the numerical value of the coherence as defined in (3.2). The datum points shown in grey correspond to parameter values where more than 60% of the 50 000-day long simulations ended up with zero infectives. It is clear that, for realistic population sizes, in a large region of parameter space, there are corrections to the analytic results of figure 3a,b, and that, the fluctuations for small β and large γ are larger than those predicted by the analytic approach. The numerical power spectra obtained from stochastic simulations for N=106 and 50×106 for values of (μ/γ, β/γ) for which these corrections are more significant are shown in figure 4a. The analytic power spectrum given by (2.2) overlaps the numerical curve for N=50×106 within the resolution of the figure. A breakdown of the analytic description for N=106 can be detected in the overall amplification and in the peak frequency shift, as well as in the loss of coherence due to the appearance of a small harmonic peak. This effect is more pronounced in the presence of spatial correlations, as shown in figure 4b and discussed in §3.2.
Figure 3.
Overall amplification and coherence of the randomly mixed model with stochastic recovery for 21×21 points in parameter space. The symbols mark the parameter values for measles (triangles), chicken pox (circles), rubella (squares) and pertussis (diamonds) according to different data sources for the pre-vaccination period. The analytic results for the amplification A are shown in (a), and the analytic results for the coherence c are shown in (b). The values of (a) are normalized by the largest overall amplification 0.1902. In (c,d) are plotted the numerical results for the overall amplification and coherence obtained from simulations of the stochastic process (2.1) on a population of size N=106. Shown in (c) are the values of the analytic plot (a) divided by the corresponding numerical values. Grey areas denote regions of parameter space for which less than 200 surviving runs 215 time steps long were obtained out of 500 trials.
Figure 4.
Numerical power spectra obtained from stochastic simulations for N=106 and 50×106 (solid and dotted lines, respectively) for values of (μ/γ, β/γ)=(0.00094, 7.9) with p=1. The spectra were taken from 218, instead of 215, time-step long simulations for increased resolution in frequency. The curve for N=106 shows a larger overall amplification and a peak frequency shift, as well as loss of coherence due to the appearance of a small harmonic peak. (b) Power spectra of stochastic simulations on a dynamic small-world network with p=0.2 and N=106 nodes (solid line) and N=50×106 (dotted line), for the parameter values (μ/γ, β/γ)=(0.00182, 4.0) chosen in the region where the amplitude of the harmonic peaks is larger. Both plots are scaled to the largest spectral power (3960 for N=106 and 71 000 for N=50×106). The ratio of the heights of the second peak to the first peak is approximately times smaller for the larger system, in line with the expected dependence.
The limitations of the analytic description (2.2) are due to the fact that a linear theory based on van Kampen's method is used to approximate the master equation up to next to leading-order terms, leaving out the contribution of terms of order and higher, whose influence on the dynamics becomes more important as the system size and/or the stability of the stationary state decreases.
3.2 Small-world network: effects of spatial correlations
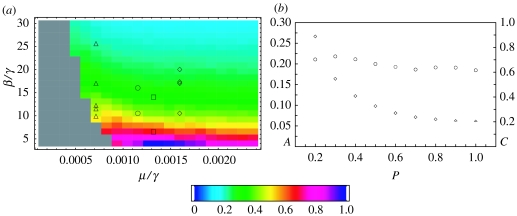
To assess the effect of spatial correlations on the resonant fluctuation spectrum, we have performed, for the same 441 points in parameter space, systematic simulations of SIR time series on dynamic small-world networks for several values of p (see appendix A for the details of the simulations). The results for the overall amplification A when p=0.6 are shown in figure 5a). The values of A are normalized by the largest value of the overall amplification, which is 0.2908. With respect to the analytic spectrum (2.2), the overall amplitude of the fluctuations increases by a factor of approximately 1.5, causing more occasional extinctions. As before, the grey region corresponds to parameter values where more than 60% of the 50 000-day long simulations ended up with zero infectives. The dependence of the amplitude of the fluctuations on the epidemiological parameters is qualitatively the same as for the randomly mixed (p=1) numerical results of figure 3c. It increases as R0 decreases, and, for fixed R0, it increases as γ increases. Close to the extinction boundary, especially for low R0, we find a departure from this general trend which can be due to a sampling bias, as we have had to select long time series without disease extinction from a large ensemble of trial runs.
Figure 5.
Overall amplification of the SIR model with stochastic recovery on a dynamic small-world network with N=106 individuals and p=0.6 (see appendix A for details of the simulations). The values of the overall amplification A are normalized in the plot by the largest amplitude (0.2908). Again, grey areas denote regions where only a small percentage of time series survive after 215 time steps (each sampled point requires the survival of at least 200 out of 500 runs). (b) Amplification A (diamonds) and coherence c (circles) for the point (μ/γ, β/γ)=(0.00116, 17.0) as a function of the small-world parameter p. The chosen point lies approximately at the centre of the region plotted in (a).
The most relevant effect of spatial correlations is the increase in the amplitude of the fluctuations as the small-world parameter p decreases. The plot of the overall amplification A as a function of p is shown in figure 5b (data points plotted with diamonds) for parameter values close to those of pertussis (for other disease parameter values the behaviour of the amplitude of the fluctuations as a function of p is similar). There is a fourfold increase in the amplitude of the fluctuations for p=0.2 with respect to the randomly mixed case p=1.
For the same parameter values, the plot of the coherence c as a function of p is also shown in figure 5b (data points plotted with circles). There is an increase in the coherence of the fluctuations as p decreases, which means that as the fluctuations get larger they also exhibit a more regular temporal pattern. For a fixed value of p, the coherence is uniformly very high in parameter space (results not shown), with changes of less than 10% in a region that includes all the parameter values considered for childhood infectious diseases. However, in a small region close to the β/γ=4 horizontal line and for p=0.2 there is loss of coherence, due to the appearance of harmonic peaks that are more pronounced than those found for p=1, and persist for larger values of N (figure 4b). Although the relative amplitude of the harmonic peaks seems to scale with , the fact that they are enhanced is due to the presence of spatial correlations, and could be related to the existence of an oscillatory phase for small values of μ/γ in deterministic SIR models that include, at the simplest level, the effect of these correlations (Benoit et al. 2006). Indeed, the breakdown of van Kampen's scaling is expected in the oscillatory phase of this model, where the ratio of the amplitudes of the harmonic peaks is constant, in the infinite size limit.
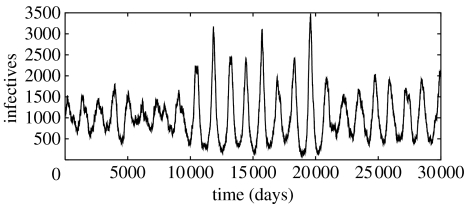
The combined effect of the spatial correlations on the amplitude and coherence of the fluctuations can be seen in figure 6, where a typical time series for the parameter values of figure 5b and p=0.2 is shown. The purely stochastic incidence peaks can be as high as 3500 individuals per day in a population of N=106, with troughs of one or two hundred infectious, and a period of recurrence of epidemics can be clearly identified. Indeed, the pattern of sustained oscillations shown in figure 6 is similar to that found in incidence data for measles in the pre-vaccination records of English cities of comparable population size (www.zoo.ufl.edu/bolker/measdata.htm), and it is more sharply defined than that of real time series for the most childhood disease incidence data (Olsen et al. 1988; Ferguson et al. 1996; Broutin et al. 2005; Trottier et al. 2006).
Figure 6.
Typical incidence time series for a population of N=106 and small-world parameter p=0.2. We have taken (μ/γ, β/γ)=(0.00116, 17.0) as in figure 5b.
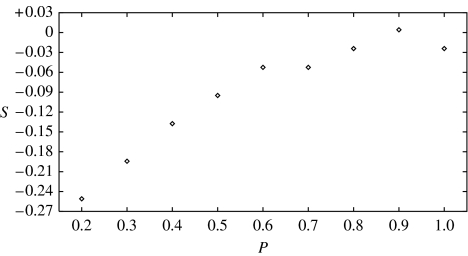
Another important effect of contact network structure is the shift in the dominant frequency of the power spectrum. In figure 7 we plot, as a function of p, the peak shift factor s, defined as the difference between the actual peak frequency and the natural frequency of the system in the deterministic description (1.1), , divided by . Again, we have chosen the same parameter values of figure 5b, (μ/γ, β/γ)=(0.00116, 17.0), but the results for other points in parameter space are similar. We found that, as p decreases, the dominant frequency of the time series is shifted increasingly to the left. As discussed in §2, this can be understood as a result of the reduced effective transmissibility due to clustering of infectives. Since both the overall amplification and the coherence increase as p decreases, the time series of long-term simulations will, as shown in figure 6, exhibit recurrent epidemics with approximate period close to that given by the dominant frequency of the resonant fluctuations. However, this value can be very different from the period that corresponds to the natural frequency of the system in the deterministic limit (1.1).
Figure 7.
The peak shift factor s as a function of the small-world parameter p. We have chosen (μ/γ, β/γ)=(0.00116, 17.0), the same parameter values as in figure 5b.
3.3 Recovery profile: effects of time correlations
The results for the overall amplification and coherence in the randomly mixed SIR model with deterministic recovery are shown in figure 8. The values of A in figure 8a are normalized by the largest value of the overall amplification 0.6901, which means that the overall amplitude of the fluctuations increases by a factor of approximately 3.5 with respect to the model with stochastic recovery. In agreement with the results of figure 2, the enhancement of the peak amplitude will in general be even larger, since, as shown in figure 8b, the coherence of the fluctuations for the case of deterministic recovery is larger for most parameter values. Realistic recovery profiles will therefore be associated with time series whose fluctuation power spectra will be larger and more sharply peaked than for constant recovery rate models. The peak frequency shift relative to this model is towards larger frequencies, and it may partially cancel the effect of internal noise correlations that shift the peak frequency to the left of , bringing the resulting dominant frequency closer to the natural frequency of the system in the deterministic description.
Figure 8.
Overall (a) amplification and (b) coherence for the randomly mixed SIR model with deterministic recovery over a population of N=106 individuals. The values of (a) are normalized by the largest overall amplification 0.6901. Again, grey areas denote regions of parameter space where fewer than 200 out of 500 runs survive 215 time steps.
In Lloyd (2001b), the basic SIR model (1.1) was modified to include a family, parametrized by an integer n, of infectious period distributions that interpolate between the exponential distribution (for n=0) and delta distribution associated with deterministic recovery (in the limit n→∞). Although there is no simple expression in closed form in this case for the period of the damped oscillations close to the system's equilibrium, it was shown that the period decreases as n increases. Our findings are in agreement with the expectation of an increase of the dominant frequency in the limit of fixed recovery time.
4. Discussion and conclusions
The relevance of the phenomenon of resonance with internal noise for the understanding of the long-term dynamics of childhood infections, with or without the presence of seasonal forcing, has been uncovered in Alonso et al. (2007). The power spectrum of the fluctuations of the stochastic process of infection in a population has been given a complete analytic description, under the following basic assumptions:
there is external infection at a small constant rate,
the population is randomly mixed and internal infection follows a law of mass action with constant transmissibility,
recovery from the disease occurs at a constant rate, and
the behaviour of the fluctuations is well described by the lowest order van Kampen expansion of the master equation.
The above basic assumptions correspond to a stochastic open SIR model and large population sizes.
We have extended the analytic results of Alonso et al. (2007) to a closed stochastic SIR model, with no external infection, which models an isolated population, and compared these with the results of extensive numerical simulations. Owing to stochastic extinctions, simulations of the long-term behaviour of this model require large population sizes, and we took N=106 as a typical value for the population size. We have found a good agreement between the analytic description and the results of the simulations for most values of the parameters. However, in a region of parameter space that includes in particular measles, we have found that there are significant finite size corrections to the analytic power spectrum of the fluctuations, which means that assumption (iv) is fulfilled only for much larger population sizes (indeed for population sizes of N=5×107 we have found good agreement between the analytic description and the results of the simulations, over the whole range of parameters).
We have then investigated the effects on the fluctuation power spectrum of relaxing (ii) or (iii) in order to account for more realistic contact networks of the population or disease recovery profiles. These are examples of spatial and temporal correlations that are always present in real interacting systems. In either case, the approximate analytic description is no longer valid and we must resort to systematic simulations. However, we have found fluctuation power spectra that are dominantly resonant like, which suggest that the basic mechanism at play is still resonance with demographic stochasticity.
Instead of assuming (ii), we have modelled the mixing network of the populations as a dynamic small-world network and considered several different values of the small-world parameter p that measures the degree of randomness of the contact network. We have found that, as p decreases, the resonant fluctuations become larger and more coherent over the whole range of parameters that are relevant for the description of childhood infections, and the dominant frequency of these fluctuations is shifted towards smaller frequencies.
Instead of (iii), we have considered the opposite (strongly correlated) limit of deterministic recovery at the end of the infectious period. Clearly, realistic recovery profiles will lie between these two extremes. We have found, again, resonant fluctuations that are much larger, and more coherent than when recovery occurs randomly at a constant rate, and that the dominant frequency is shifted to larger frequencies.
Then the main conclusion is that the importance of the phenomenon reported in Alonso et al. (2007) to the description of the long-term dynamics of childhood diseases is enhanced when the model is modified to include more realistic assumptions (correlations), either on the populations contact patterns (spatial correlations) or on the disease recovery profile (time correlations). Our results apply to a large region in the epidemiological and demographic parameter space, and in this sense they are applicable in general to the modelling of infectious disease dynamics. They show that stochasticity may play the leading role in determining the incidence temporal patterns, through resonance of internal noise with the dynamics that governs the system in the limit of an infinite population.
Our results also show that the analytic theory developed in Alonso et al. (2007) provides an overall good description for well-mixed populations and diseases with gradually decaying recovery profiles, and a useful guideline for the case of populations with non-trivial contact networks. When these contact networks include a large fraction, of 50% or more, of random connections, an effective theory based on the analytic treatment of the randomly mixed case with a correction of the transmissibility to account for infective screening gives a good description of the incidence fluctuations spectrum. In highly correlated contact networks, however, the overall amplitude of the fluctuations is much larger than was predicted by this effective theory.
The qualitative picture for the dependence of demographic stochasticity on the system parameters that emerges from our results is more subtle than one would expect from linear perturbation analysis, either of the deterministic model (1.1) or even of the full stochastic description (2.1). First, in the presence of correlations, the dominant frequency of these resonant organized fluctuations differs significantly from the natural frequency of the deterministic description. The fact that this naive expectation may seem to lead to a good description, as argued in Bausch & Earn (2003), must be attributed to the cancellation of several missing effects. Second, the amplitude of these fluctuations decreases with N, or more precisely with , but finite size effects will be important for realistic population sizes, of the order of 106, except for diseases with an epidemiological profile similar to that of pertussis. Third, the amplitude of the fluctuations increases when R0 decreases, and, for fixed R0, it decreases as γ decreases. This additional dependence of the amplitude of the fluctuations on the average infectious period is unaccounted for by the analytic description (2.2).
On more conceptual grounds, the finding that in finite, discrete populations internal noise together with correlations produces sustained incidence oscillations of significant amplitude all over the parameter region that includes childhood infectious diseases is of importance for the long-standing controversy in epidemiology and ecology as to the driving mechanisms of the pervasive noisy oscillations observed in these systems (Grenfell & Bjørnstad 2005). Whether these are mainly intrinsic or external seems to depend not only on the model's nonlinearities but also on the correlations between the systems' units, which most traditional approaches neglect.
As the need for spatial models of infectious disease transmission is increasingly acknowledged, there are different modelling strategies that try to reconcile explicit spatial representation with computational costs and the information available on the patterns of contact of the populations (see Riley 2007 and references therein). In the context of this discussion, it should be stressed that the kind of intrinsic stochastic effects highlighted in the present paper are specific of models that explicitly represent individuals (or small units such as households), and that computationally lighter, coarse-grained models will miss this phenomenology.
Acknowledgments
Financial support from the Foundation of the University of Lisbon and the Portuguese Foundation for Science and Technology (FCT) under contracts POCI/FIS/55592/2004 and POCTI/ISFL/2/618 is gratefully acknowledged.
Appendix A.
All simulations were carried out over a population of individuals arranged on a square lattice with periodic boundaries where each site connects to its 12 closest neighbours. A random fraction p of these local links is replaced at each step with random long-distance links. The population size was 106 individuals for all simulations, with the exception of the results of figure 4 where a population of 50×106 individuals was also considered.
The simulations implemented the stochastic process of the SIR model, or its modification to include deterministic, instead of stochastic, recovery on this network. For the case of stochastic recovery, we have used the efficient algorithm for stochastic processes in spatially structured systems described in Bortz et al. (1975). Local and long-range infections are dealt with separately, and a local (respective long range) infection event occurs with probability 1−p (respective p). For p=1, the presence of spatial structure is irrelevant, and the algorithm reduces to the application of the method of Gillespie (1976) to the stochastic process (2.1). When p<1 and local infections may occur, their probability depends on the number of infected neighbours of each susceptible node, and so susceptible nodes with k infected neighbours, k=0, …, 12, are treated as separate classes. For the case of deterministic recovery, this algorithm is extended with the inclusion of a linked list of infected nodes. Each entry in the list records the position of an infected node in the lattice, along with the time-step number (counting from 0 at the start of the run) at which this particular node should recover (in case it has not been removed previously by a stochastic death transition). The list is ordered by recovery time-step number; that is, it always contains the oldest nodes at the start. In this way, recovery is efficiently performed by checking, at the beginning of each time step, which nodes are due for recovery and replacing them in the lattice with recovered nodes.
The numerical results of figures 3, 5 and 8 were obtained through systematic simulations of the SIR model for a set of 21×21 evenly spaced points covering the (μ/γ, β/γ) plane, for the region depicted in the figures (and keeping μ=5.5×10−5 fixed). Four separate sets of simulations were carried out, one for each of the specific cases considered in the main text, namely the SIR model with stochastic recovery for p=1.0 and 0.6, the SIR model with stochastic recovery for (μ/γ, β/γ)=(0.00116, 17.0) and several values of p, and the SIR model with deterministic recovery and p=1.0.
For each sample point, 500 independent runs of the model were taken, each lasting for 50 000 time steps or days, of which only the last 215 are used; approximately 17 000 time steps are discarded at the beginning, to allow each run to ‘settle down’ to its steady state. If fewer than 200 of these 500 runs survive (i.e. finish with more than zero infectives), then this particular sample point is discarded (shown as grey in the plots); otherwise, the power spectral densities of the surviving runs are computed (using an FFT routine) and averaged together. The remaining power spectrum plots shown in the figures were obtained in the same way, except those of figure 4a, in which 218 time-steps long stationary time series were used, eight times longer than those used for other plots, to provide the increased frequency resolution necessary to check the perfect agreement with the analytical prediction (2.2) for 50×106 individuals.
From the final averaged spectrum, the quantities A, c and s are computed. The overall amplification, which is defined as , where PI(ω) is the power spectrum density of the scaled fluctuations, is numerically approximated by a sum over the squared moduli of the scaled coefficients of the discrete Fourier transform of the time series. Sincethe sampling interval is 1 day, the band width of the signal is ω∈[−π,π], and we have
where k is the integer index of the Fourier coefficient and L the sample length (here L=215). The coherence is defined as c=Ap/A, where Ap is the integral of the power spectrum density of the scaled fluctuations over the frequency range that corresponds to ±10% of the period of the dominant peak. The numerical value of Ap is obtained in the same manner as A from the squared moduli of the scaled coefficients , replacing the summation limits appropriately.
The position of the dominant peak ωpeak is found from the largest Fourier coefficient, and is also used to compute the shift factor shown in figure 7.
References
- Albert R, Barabási A.-L. Statistical mechanics of complex networks. Rev. Mod. Phys. 2002;74:47–97. doi: 10.1103/RevModPhys.74.47. [DOI] [Google Scholar]
- Allen L.J.S, van den Driessche P. Stochastic epidemic models with a backward bifurcation. Math. Biosci. Eng. 2006;3:445–458. doi: 10.3934/mbe.2006.3.445. [DOI] [PubMed] [Google Scholar]
- Alonso D, McKane A.J, Pascual M. Stochastic amplification in epidemics. J. R. Soc. Interface. 2007;4:575–582. doi: 10.1098/rsif.2006.0192. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anderson R.A, May R.M. Oxford University Press; Oxford, UK: 1991. Infectious diseases of humans. [Google Scholar]
- Bailey N.T.J. 2nd edn. Charles Griffin & Co; London, UK: 1975. The mathematical theory of infectious diseases. [Google Scholar]
- Bartlett M.S. Measles periodicity and community size. J. R. Stat. Soc. A. 1957;120:48–70. [Google Scholar]
- Bausch C.T, Earn D.J.D. Transients and attractors in epidemics. Proc. R. Soc. B. 2003;270:1573–1578. doi: 10.1098/rspb.2003.2410. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benoit J, Nunes A, Telo da Gama M.M. Pair approximation models for disease spread. Eur. Phys. J. B: Condensed Matter. 2006;50:177–181. doi: 10.1140/epjb/e2006-00096-x. [DOI] [Google Scholar]
- Boccaletti S, Latora V, Moreno Y, Chavez M, Hwang D.-U. Complex networks: structure and dynamics. Phys. Rep. 2006;424:175–308. doi: 10.1016/j.physrep.2005.10.009. [DOI] [Google Scholar]
- Bortz A.B, Kalos M.H, Lebowitz J.L. A new algorithm for Monte Carlo simulation of Ising spin systems. J. Comput. Phys. 1975;17:10–18. doi: 10.1016/0021-9991(75)90060-1. [DOI] [Google Scholar]
- Broutin H, Guégan J.-F, Elguero E, Simondon F, Cazelles B. Large-scale comparative analysis of Pertussis populations dynamics: periodicity, synchrony and impact of vaccination. Am. J. Epidemiol. 2005;161:1159–1167. doi: 10.1093/aje/kwi141. [DOI] [PubMed] [Google Scholar]
- Dorogovtsev S.N, Mendes J.F.F. Oxford University Press; Oxford, UK: 2003. Evolution of networks. [Google Scholar]
- Dushoff J, Plotkin J.B, Levin S.A, Earn D.J.D. Dynamical resonance can account for seasonality of influenza epidemics. Proc. Natl Acad. Sci. USA. 2004;101:16 915–16 916. doi: 10.1073/pnas.0407293101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eames K.T.D, Keeling M.J. Modelling dynamic and network heterogeneities in the spread of sexually transmitted diseases. Proc. Natl Acad. Sci. USA. 2002;99:13 330–13 335. doi: 10.1073/pnas.202244299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Earn D.J.D, Rohani P, Bolker B.M, Grenfell B.T. A simple model for complex dynamical transitions in epidemics. Science. 2000;287:667–670. doi: 10.1126/science.287.5453.667. [DOI] [PubMed] [Google Scholar]
- Edmunds W.J, Kafatos G, Wallinga J, Mossong J. Mixing patterns and the spread of close-contact infectious diseases. Emerg. Themes Epidemiol. 2006;3:10. doi: 10.1186/1742-7622-3-10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eubank S, Guclu H, Anil Kumar V.S, Marathe M.V, Srinivasan A, Torockzcai Z, Wang N. Modelling disease outbreak in realistic urban social networks. Nature. 2004;429:180. doi: 10.1038/nature02541. [DOI] [PubMed] [Google Scholar]
- Ferguson N.M, Anderson R.M, Garnett G.P. Mass vaccination to control chickenpox: the influence of zoster. Proc. Natl Acad. Sci. USA. 1996;93:7231–7235. doi: 10.1073/pnas.93.14.7231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gillespie D.T. A general method for numerically simulating the stochastic time evolution of coupled chemical reactions. J. Comput. Phys. 1976;22:403. doi: 10.1016/0021-9991(76)90041-3. [DOI] [Google Scholar]
- Grenfell B, Bjørnstad O. Epidemic cycling and immunity. Nature. 2005;433:366–367. doi: 10.1038/433366a. [DOI] [PubMed] [Google Scholar]
- Grenfell B.T, Bjørnstad O.N, Kappey J. Travelling waves and spatial hierarchies in measles epidemics. Nature. 2001;414:716–723. doi: 10.1038/414716a. [DOI] [PubMed] [Google Scholar]
- Hethcote H.W. An age-structured model for pertussis transmission. Math. Biosci. 1997;145:89–136. doi: 10.1016/S0025-5564(97)00014-X. [DOI] [PubMed] [Google Scholar]
- Jolly A.M, Wylie J.L. Gonorrhoea and Chlamydia core groups and sexual networks in Manitoba. Sex. Transm. Infect. 2002;78:145–151. doi: 10.1136/sti.78.suppl_1.i145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keeling M.J. Implications of network structure for epidemic dynamics. Theor. Popul. Biol. 2005;67:1–8. doi: 10.1016/j.tpb.2004.08.002. [DOI] [PubMed] [Google Scholar]
- Keeling M.J, Eames K.T.D. Networks and epidemic models. J. R. Soc. Interface. 2005;2:295–307. doi: 10.1098/rsif.2005.0051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keeling M.J, Grenfell B.T. Disease extinction and community size: modeling the persistence of measles. Science. 1997;275:65–67. doi: 10.1126/science.275.5296.65. [DOI] [PubMed] [Google Scholar]
- Keeling M.J, Rohani P, Grenfell B.T. Seasonally forced disease dynamics explored as a switching between attractors. Physica D. 2001;148:317–335. doi: 10.1016/S0167-2789(00)00187-1. [DOI] [Google Scholar]
- Kuperman M, Abramson G. Small world effect in an epidemiological model. Phys. Rev. Lett. 2001;86:2909–2912. doi: 10.1103/PhysRevLett.86.2909. [DOI] [PubMed] [Google Scholar]
- Lloyd A.L. Realistic distributions of infectious periods in epidemic models: changing patterns of persistence and dynamics. Theor. Popul. Biol. 2001a;60:59–71. doi: 10.1006/tpbi.2001.1525. [DOI] [PubMed] [Google Scholar]
- Lloyd A.L. Destabilization of epidemic models with the inclusion of realistic distributions of infectious periods. Proc. R. Soc. B. 2001b;268:985–993. doi: 10.1098/rspb.2001.1599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lloyd A.L. Estimating variability in models for recurrent epidemics: assessing the use of momentum closure techniques. Theor. Popul. Biol. 2004;65:49–65. doi: 10.1016/j.tpb.2003.07.002. [DOI] [PubMed] [Google Scholar]
- May R.M, Lloyd A. Infection dynamics on scale-free networks. Phys. Rev. E. 2001;64:066 112. doi: 10.1103/PhysRevE.64.066112. [DOI] [PubMed] [Google Scholar]
- McKane A.J, Newman T.J. Predator–prey cycles from resonant amplification of demographic stochasticity. Phys. Rev. Lett. 2005;94:218 102. doi: 10.1103/PhysRevLett.94.218102. [DOI] [PubMed] [Google Scholar]
- Meyers L.A, Pourbohloul B, Newman M.E.J, Skowronski D.M, Brunham R.C. Network theory and SARS: predicting outbreak diversity. J. Theor. Biol. 2005;232:71–81. doi: 10.1016/j.jtbi.2004.07.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nåsell I. A new look at the critical community size for childhood infections. Theor. Popul. Biol. 2005;67:203–216. doi: 10.1016/j.tpb.2005.01.002. [DOI] [PubMed] [Google Scholar]
- Olsen L.F, Truty G.L, Schaffer W.M. Oscillations and chaos in epidemics: a nonlinear study of six childhood diseases in Copenhagen, Denmark. Theor. Popul. Biol. 1988;33:344–370. doi: 10.1016/0040-5809(88)90019-6. [DOI] [PubMed] [Google Scholar]
- Pastor-Satorras R, Vespignani A. Epidemic spreading in scale-free networks. Phys. Rev. Lett. 2001;86:3200–3203. doi: 10.1103/PhysRevLett.86.3200. [DOI] [PubMed] [Google Scholar]
- Riley S. Large-scale spatial transmission models of infectious disease. Science. 2007;316:1298–1301. doi: 10.1126/science.1134695. [DOI] [PubMed] [Google Scholar]
- Riley S, et al. Transmission dynamics of the etiological agent of SARS in Hong-Kong: impact of public health interventions. Science. 2003;300:1961–1966. doi: 10.1126/science.1086478. [DOI] [PubMed] [Google Scholar]
- Szabo G, Vukov J. Cooperation for volunteering and partially random partnerships. Phys. Rev. E. 2004;69:036107. doi: 10.1103/PhysRevE.69.036107. [DOI] [PubMed] [Google Scholar]
- Telo da Gama M.M, Nunes A. Epidemics in small world networks. Eur. Phys. J. B: Condensed Matter. 2006;50:205–208. doi: 10.1140/epjb/e2006-00099-7. [DOI] [Google Scholar]
- Trottier H, Philippe P, Roy R. Stochastic modelling of empirical time series of childhood infectious disease data before and after mass vaccination. Emerg. Themes Epidemiol. 2006;3:9. doi: 10.1186/1742-7622-3-9. www.ete-online.com/content/3/1/9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Verdasca J, Telo da Gama M.M, Nunes A, Bernardino N.R, Pacheco J.M, Gomes M.C. Recurrent epidemics in small world networks. J. Theor. Biol. 2005;233:553–561. doi: 10.1016/j.jtbi.2004.10.031. [DOI] [PubMed] [Google Scholar]
- Volz, E. & Meyers, L. A. 2007 SIR epidemics in dynamic contact networks. (http://arxiv.org/abs/0705.2105) [DOI] [PMC free article] [PubMed]
- Wang W. Epidemic models with nonlinear infection forces. Math. Biosci. Eng. 2006;3:267–279. doi: 10.3934/mbe.2006.3.267. [DOI] [PubMed] [Google Scholar]
- Watts D.J, Strogatz S.H. Collective dynamics of small-world networks. Nature. 1998;393:440. doi: 10.1038/30918. [DOI] [PubMed] [Google Scholar]
- Wearing H.J, Rohani P, Keeling M.J. Appropriate models for the management of infectious diseases. PLoS Med. 2005;2:e174. doi: 10.1371/journal.pmed.0020174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zanette D. Dynamics of rumor propagation on small-world networks. Phys. Rev. E. 2003;65:041908. doi: 10.1103/PhysRevE.65.041908. [DOI] [PubMed] [Google Scholar]