Abstract
Even simple active systems can show a plethora of intriguing phenomena and often we find complexity where we would have expected simplicity. One striking example is the occurrence of a quiescent or absorbing state with frozen fluctuations that at first sight seems to be impossible for active matter driven by the incessant input of energy. While such states were reported for externally driven systems through macroscopic shear or agitation, the investigation of frozen active states in inherently active systems like cytoskeletal suspensions or active gels is still at large. Using high-density motility assay experiments, we demonstrate that frozen steady states can arise in active systems if active transport is coupled to growth processes. The experiments are complemented by agent-based simulations which identify the coupling between self-organization, growth, and mechanical properties to be responsible for the pattern formation process.
Keywords: active fluids, cytoskeleton, actin networks
How does a dynamic system approach its steady state and what is the nature of it? For a thermodynamic system Onsager’s regression hypothesis (1) asserts that the relaxation is governed by the same laws as the fluctuations in thermal equilibrium, and Boltzmann-Gibbs theory defines the nature of all steady states. For active systems like vibrated granules (2, 3), animal swarms (4–6), microorganisms (7–9), and cytoskeletal systems (10–13) there are no such general laws. Instead one finds a plethora of spatio-temporal patterns including swarming (5–8), density inhomogeneities (11, 13), and swirling patterns (9, 12). A common feature of these patterns is that they are all fluid-like (14–18). One might ask whether there is something like the analog of a solid-like or frozen state in active systems. At first sight such a frozen state seems to be impossible for active matter driven by the incessant input of energy which is expected to cause highly dynamic states through a perpetual balance between assembly and disassembly processes (13). Yet, there are examples where the constituents of active systems self-organize into nonequilibrium steady states with slowed dynamics or regular spatial patterns. Activity has been found to give rise to a diverging viscosity at the isotropic-nematic transition of active gels (19–21), and glassy behavior has recently been observed for confluent cell layers (22). Systems that are externally driven, like agitated granular media, exhibit a plethora of regular static patterns (23–25) and rotating assemblies (26). While in all these nonequilibrium systems degrees of freedom are slowed down or frozen-out, the very existence of a pattern or the anomalous rheological properties is only made possible by the activity in the system. Systems with frozen-out degrees of freedom have to be contrasted with nonequilibrium systems where the system ends up in a set of configurations from which it cannot escape. Once such an absorbing state is reached the dynamics ceases and the ensuing pattern is frozen-in (27, 28). Particularly illustrative examples are growing bacterial colonies showing natural selection (29) or periodically sheared colloidal suspensions which self-organize into an absorbing state where particles no longer collide but simply retrace their trajectories under the external drive (30).
Here we ask for the existence of steady states which carry the hallmarks of both an active system and a frozen absorbing state; i.e., where fluctuations are successively eliminated during a coarsening process while keeping the system in an active state. In driven systems frozen steady states can arise when particles are not only actively transported, but also integrated into new self-assembled higher-order structures where single particle fluctuations are arrested. A frozen active state combines the rapid self-organization characteristics of driven systems with the robustness, stability, and reproducibility of growth and self-assembly processes. Thus the combination of self-organization and growth that characterizes frozen active states may turn out to be important for many systems in biology and materials science. However, the complexity of most experimental systems defies the thorough identification and analysis of the intricate balance of the underlying principles that lead to a frozen active state.
To shed light on the mechanisms that govern the emergence of such states, we introduce a reconstituted system, where highly concentrated actin filaments are actively transported and crosslinked in the two-dimensional geometry of a motility assay. We show that the interplay of only three components, actin filaments, HMM motor proteins, and fascin crosslinkers is sufficient for the emergence of a frozen active steady state that consists of highly symmetric structures, rings, and elongated fibers that are actively assembled and propelled by the motor proteins. The reconstituted approach complemented by agent-based simulations allows us to correlate the formation of a frozen steady state with the mechanical properties of the emergent structures and enables us to identify the crosslinker mediated growth processes as driving mechanism for the emergence of frozen active steady states.
Results and Discussion
The system consists of actin filaments and fluorescently labeled reporter filaments that are propelled by nonprocessive motor proteins (HMM) immobilized on a glass cover slide (11, 12). Without crosslinkers and above a critical filament density the filaments self-organize to form coherently moving structures such as clusters and density waves (12). To investigate how the dynamic structure formation is affected by a defined growth process into higher-order structures, the crosslinker protein fascin is added and its concentration systematically varied. In this context fascin is ideally suited as it assembles polar filament structures and thus does not obstruct the material transport by the molecular motors.
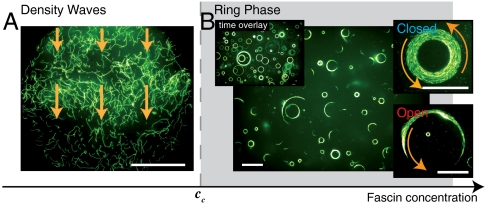
The addition of trace amounts of fascin does not suffice to change the pattern formation mechanisms in the system. Even at high filament densities the individual filaments display directional fluctuations that stem from the persistent random walk of single filaments in the motility assay. These fluctuations are responsible for the formation of density inhomogeneities that accumulate to form coherently moving structures such as clusters and density waves (Fig. 1A). Low fascin concentrations dampen these fluctuations by crosslinking events but are not sufficient to completely inhibit them. As a consequence structures like density waves are less pronounced (Fig. 1A).
Fig. 1.
Phase behavior as a function of the fascin concentration. Low fascin concentrations are not sufficient to fundamentally alter the pattern formation in the high-density motility assay and at an actin concentration of ρ = 10 μM the characteristic travelling density waves evolve (A). Compared to the case without crosslinkers the density waves are less pronounced as the crosslinker slightly hinders the formation of density inhomogeneities. Above a critical fascin concentration of cc = 0.075 ± 0.025 μM the pattern formation drastically changes as constantly rotating rings evolve (B) that are either closed or open Movie S1). In the steady state all actin filaments are incorporated in rotating rings and fluctuations on the single filament level are entirely absent. All scale bars are 50 μm.
This behavior drastically changes, if the added fascin concentration exceeds a critical concentration: Now the crosslinker leads to the emergence of rotating polar actin-fascin structures, which are effectively planar. The rotating speed of the rings is about 3 μm/ sec. While structure formation in the high-density motility assay relies on the balance between assembly and disassembly processes, the addition of crosslinker molecules promotes defined assembly processes and at the same time inhibits the disassembly of the emergent structures. This inhibition of the disassembly finally leads to a quiescent steady state where all filaments are firmly incorporated in constantly rotating rings (Fig. 1B, Movie S1); fluctuations on the single filament level are completely arrested. The absence of disassembly pathways renders the structure formation mechanism reminiscent to a coarsening process into an absorbing state (28) and the conditions during the pattern formation are directly reflected and “frozen-in” in the steady state.
In the frozen steady state constantly rotating rings are homogeneously distributed throughout the motility assay (Fig. 1B). No preferred direction of rotation is observable. Rings occur in two distinct conformations which are equally abundant: open and closed (Fig. 1B). Closed rings consist of self-contained and constantly rotating actin-fascin fibers. Open rings also move on a stable circular trajectory with uniform curvature radius, as can be seen in a time overlay (Fig. 1B). A characteristic distribution of ring curvature radii p(r) in the steady state is observed (Fig. 2A). The radii are broadly distributed with a decay towards large radii r. p(r) shows a pronounced maximum at 9.5 μm which is of the order of the persistence length of individual filaments. Towards small curvature radii, the distribution is characterized by a cut-off radius of rc ≈ 5 μm, below which no rings are found. The decay of the distribution for large radii is of double exponential shape (Fig. 2A). The double exponential nature of the curvature radii distribution is highly robust upon parameter variation and is conserved throughout variations of the fascin and actin concentrations (Fig. S1), making this to a generic feature of the system.
Fig. 2.
Ring curvature distributions and ring formation mechanisms. (A) shows the cumulative curvature radii distribution P(r) in the frozen steady state; the inset depicts the noncumulative distribution p(r). The distribution can be described by a double exponential decay according to P(r) ∝ A1 exp(r/l1) + A2 exp(r/l2) with decay lengths of l1 = 3.3 μm and l2 = 10.1 μm. This double exponential shape reflects the occurrence of two different ring morphologies: open and closed rings. These two different ring populations rely on distinct ring formation mechanisms that are related to the growth mechanisms in the system. While being transported, moving actin-fascin strings grow by merging with other strings of similar size. Merging events lead to elongated but still flexible strings that predominantly form closed ring if they cross their own tail (B). Open rings form upon a different mechanism (C): While moving, actin-fascin strings continuously pick up material—individual filaments or smaller actin-fascin strings. Thereby the strings grow predominately in width and get thicker and stiffer. If the strings are stiff enough the curvature freezes and the forces and fluctuations in the motility assay are not sufficient anymore to induce any change in curvature. While closed rings characteristically are small in size with radii of up to 30 μm, open rings are considerably broader and can have radii of up to 150 μm (A). The actin concentration was set to ρ = 3 μM and the fascin concentration was c = 0.2 μM. All scale bars are 50 μm. In (B) and (C) the investigated actin-fascin string is shown in red and its tip is marked by a yellow arrow.
The ring curvature distribution reflects the balance between aggregation processes and active transport (Fig. 2 B and C, Movie S2). Polar actin-fascin strings nucleate from individual actin filaments crosslinked by fascin. While being transported, the actin strings grow larger by two competing mechanisms, either by taking up individual filaments alongside the bundle, or by merging with adjacent structures, leading predominantly to an increased length. These growth processes in turn affect the mechanical properties of the structures. A growth in length results in long and thin strings with relatively low persistence lengths. The continuous growth alongside the strings yields shorter and thicker structures with a higher persistence length. It is the resulting increased stiffness of the individual strings which determines the susceptibility towards directional changes in the motility assay. Directional changes that alter a given curvature happen more seldom and have less effect for thicker and thus stiffer strings. This decline in the rate of directional changes can be seen in the trajectory of individual fibers that is composed of circular segments (Fig. S2).
The interplay between active transport and the mechanical properties of the emergent structures determines the actual ring formation processes, and leads to two generic ring formation mechanisms: Once strings have grown enough in length, they may close on themselves (Fig. 2B). Alternatively, lateral growth may increase the string’s stiffness to such an extent that their current curvature freezes-in without a ring closure and open rings result (Fig. 2C). While the ring closure leads to predominantly small ring diameters, the frozen-in curvature process naturally yields rings with larger curvature radii. This difference in the curvature radii of open and closed rings is reflected in cumulative curvature radii distributions P(r). Both distributions are of exponential shape, yet their decay lengths differ by a factor of 3 (Fig. 2A).
Thus the two growth processes competing for material in the active system not only lead to two ring populations—open and closed—but also directly affect the properties of the steady state by determining the size of the structures. Competition between continuous growth and merging processes of actively transported strings can readily be described using agent-based simulations (Fig. 3A, for details see Materials and Methods). These two competing aggregation processes already suffice to retrieve the coexistence of open and closed rings (Fig. 3B, Movie S3). Omission of one of these processes leads to the formation of either closed or open rings only. The cumulative radii distributions P(r) for open and closed rings decay exponentially in accordance with experimental observations (Fig. 3C). Moreover, the simulations allow for a backtracking of the steady state properties to the inherent noise in the active system which determines the stochasticity of each string’s trajectory: Lowering the amplitude or increasing the rate of curvature changes leads to an increase in the fraction of open to closed rings, Γ (Fig. 3D).
Fig. 3.
Cellular automaton simulations. The two experimentally observed aggregation processes—merging and growth stiffening are described using a continuous agent-based simulation. The actin-fascin strings are modeled as polar elongated strings that move with a velocity v on meandering trails (A). The tip is subjected to curvature changes of rate ω and a noise level α, resulting in a meandering trajectory (inset B). The strings stiffen due to growth processes of rate λ. Besides, merging events with adjacent objects occur if the relative angle |θ| between them is smaller than θc. These two aggregation processes lead to the emergence of rings in two configurations—open and closed (B). The occurrence of two ring configurations is reflected in the ring radii distribution p(r) and the corresponding cumulative distribution P(r) that can be separated in open and closed contributions (C). The distribution for open and closed rings decays approximately exponential. The ratio of open to closed rings Γ increases with the rate of the random turns ω, while it decreases with the noise level α (D and Fig. S5). If not indicated otherwise the parameters are ω = 0.1, λ = 0.4, α = 1.0, and θc = 100. All scale bars are one string length L0.
This relation can directly be tested in the experiment as the noise level in the system can be addressed by varying the motor density on the cover slip σm. A decreased number of motor proteins on the surface leads to more rugged trajectories of the strings and hence to smaller curvature radii (Fig. 4 A and B). In accordance with simulations a gradual decrease of the motor density shifts the fraction Γ from open to closed rings: Small motor densities favor the emergence of closed rings with a Γ of 0.5, while high motor densities lead to predominately open rings with Γ = 2 (Fig. 4C).
Fig. 4.
Dependence on the motor density. By varying the motor density σm on the surface, the feedback between growth, and the fluctuations that arise in the motility assay can be examined. In general high motor densities lead to less fluctuations and a more persistent movement as can be seen in the time overlay image in (B), σm = 700 nM, while low motor densities lead to a more fluctuations (A), σm = 30 nM. The higher the noise level (i.e., the lower σm) the higher is the chance for individual strings to cross their own tail and to form closed rings. The increased probability for ring closure events is directly reflected by the higher abundance of closed rings at low motor densities quantified by the ratio of open to closed rings Γ (C). The radial distribution of closed rings itself is unaffected as can be seen in the decay lengths ld of the exponentially decaying distributions (D). By contrast, the frozen-in curvature of the open rings directly reflects the fluctuations and the persistence of the movement in the motility assay: here ld monotonically increases with increasing motor concentration σm. The actin concentration was set to ρ = 3 μM and the fascin concentration was c = 0.2 μM. All scale bars are 50 μm.
Importantly, upon changing the motor density, the conformational statistics of closed rings remains invariant, while the distribution of open rings is shifted to smaller radii with smaller decay lengths (Fig. 4D). This observation can be attributed to the underlying coupling of growth and active transport through the mechanical properties of the emergent structures and the freezing mechanism that reflects the conditions during the assembly process. At low motor densities the less persistent movement (Fig. 4A) implies smaller frozen-in radii of the open rings. The ring closure process, on the other hand, is triggered by stochastic changes in a string’s trajectory, yet the radius is determined by the stiffness of each individual structure. As a consequence, closed rings get only more abundant but the ensuing distribution of curvature radii remains independent of the motor density σm.
Frozen-in structures directly document the conditions during the coarsening process, and thus are expected to strongly depend on the nucleation and growth mechanisms. In the present system the nucleation and growth mechanisms are governed by the filament and the crosslinker concentration. Increasing these concentrations not only leads to more nucleation seeds and thus actin-fascin strings but also to a more rapid growth process yielding stiffer strings. Above a critical material density at the surface, the strings are unable to pursue curved trajectories anymore and they are forced to align. Successively, the strings get increasingly interconnected and crosslinked to form frozen elongated and straight polar actin-fascin streaks with a thickness of up to 50 μm and a length in the order of centimeters (Fig. 5, Movie S4). The emergence of elongated structures following straight trajectories has severe consequences for the further growth process in the system. Compared to the rings the straight-moving streaks cover a large area leading to a more effective growth process. The effective growth process results in larger structures and gives way to coarsening and subsequent merging processes. While neighboring fibers initially tend to move in opposite directions, they gradually synchronize their directions of motions by merging (Fig. 5C). This synchronization is accompanied by a coarsening process, in the course of which fibers of the same polarity gradually merge to larger ones (Fig. 5B) which finally leads to large-scale symmetry breaking and a preferred direction of motion develops. After a time period of 10 min extended fiber structures uniformly move in the same direction, imposing a polarity in the entire flow chamber on the centimeter scale.
Fig. 5.
Collectively moving streaks. Above a certain material density, the ring formation processes are hindered and elongated actin-fascin streaks emerge that are aligned alongside the long axis of the flow chamber. Like in the ring phase, all individual filaments gradually get incorporated in large-scale polar structures and fluctuations on the single filament level cease. Initially the streaks move contrariwise. With time, a major direction of motion develops that is adopted by all streaks in the course of turning events (inset 2). The development of a major direction of motion is accompanied by a coarsening process, where polarly aligned fibers gradually merge to larger ones (inset 1). The actin concentration was set to ρ = 10 μM and the fascin concentration was c = 0.5 μM. All scale bars are 50 μm.
The phase boundary determining the transition from ring formation to fibers depends on both the actin and the fascin concentration (Fig. S3). Consequently, the critical material density is not related to the critical filament densities in the ordinary high-density motility assay without crosslinkers.
Conclusion
The minimal system presented here allows a systematic parameter control through the variation of motor, crosslinker, and actin concentrations. The good parameter control is mandatory for the robust and reproducible assembly of frozen steady states with structures of defined size and morphology and opens the door for various applications with the nanopattering of surfaces being a prime example, as suggested in motility assay experiments with microtubules (31, 32).
At the same time the high-density motility assay can serve as a versatile model system to explore the full breath of nonequilibrium steady states in active systems. In previous investigations it was shown that the interplay between assembly and disassembly of driven filament leads to dynamic patterns like swirls, clusters, and density waves (12). These nonequilibrium steady states are characterized by the perpetual built-up and destruction of structures driven by the incessant input of energy at the scale of an individual filament. Upon adding a single new ingredient, namely passive crosslinking molecules, we have found here that the nature of the nonequilibrium steady state changes fundamentally; the presence of crosslinking molecules facilitates permanent filament aggregation and thereby switches off the disassembly pathway. As a consequence, the system's dynamics drives the filament assembly into an absorbing state where the structure arrests while the filaments still move. The coarsening process towards this absorbing state combines active driving with filament aggregation. Once reached, this state is stable and independent of the activity of the system, yet it directly maps the assembly pathway. This “structural memory” relies on the intricate mechanical coupling between active transport and aggregation processes. This coupling and the ensuing aggregation mechanisms fully determine the statistical properties of the absorbing state.
From the experimental point of view, it remains a great challenge to unambiguously pinpoint the nature of the nonequilibrium phase transition. There exist only very few experimental systems that show clear evidence for an absorbing phase transition—with turbulent liquid crystals being probably the first example (33). The main difficulty lies in the quantitative measurement of the transition over long time and length scales in the absence of interfering long-range interactions or boundary effects (33). In this context the system introduced here could provide a versatile tool towards the investigation of absorbing transitions. Consisting of only a few purified components, the system allows for a precise investigation of the statistic properties of the phase transition. Future investigations might also want to explore analogies and differences between these active systems and externally driven systems showing shear-induced gelation (34) or aggregation (35). In general, the further investigation of active systems complemented by an assembly process that in turn affects the mechanical properties may set a new paradigm of frozen active states and seems to be an attractive route of explanation for many examples from cytoskeletal to colloidal systems.
Materials and Methods
Protein Preparation.
G-actin was obtained from rabbit skeletal muscle following a standardized protocol (36, 37). Actin polymerization was initiated by adding one-tenth of the sample volume of a tenfold concentrated F-buffer (20 mM Tris, 20 mM MgCl2, 2 mM CaCl2, 2 mM DTT and 1 M KCl). For fluorescence microscopy fluorescently labeled reporter filaments are used at a ratio of labeled to unlabeled filaments ranging from 1∶2 to 1∶50. Filaments were stabilized with Alexa-Fluor-488-phalloidin (Invitrogen) at a ratio of 1∶2. Unlabeled filaments are stabilized with phalloidin (Sigma) likewise at a ratio of 1∶2. Once polymerized, actin was used within 2 d. HMM is prepared from myosin II obtained from rabbit skeletal muscle following a standardized protocol (38). Recombinant human fascin is purified from Escherichia coli BL21-CodonPlus-RP and stored at -80 °C in 2 mM Tris/HCl (pH ∼ 7.4), 150 mM KCl at 64 μM, following ref. 39.
Sample Preparation.
Flow chambers were prepared with precleaned microscope slides (Carl Roth) and coverslips (Carl Roth, 20 × 20 mm, No. 1). Coverslips were coated with a 0.1% nitrocellulose solution diluted from a 2% solution (Electron Microscopy Sciences) in amyl acetate (Carl Roth). The coverslips were fixed to the microscope slides using parafilm, yielding an overall chamber volume of ∼30 μL. Prior to each experiment a 30 μL actin dilution (1–25 μM monomeric actin) was prepared by gently mixing labeled and unlabelled actin filaments with assay buffer (25 mM Imidazolhydrochlorid pH 7.4; 25 mM KCl; 4 mM MgCl2; 1 mM EGTA; 1 mM DTT). The flow chamber was incubated with HMM diluted in assay buffer. Prior to the insertion of the respective actin dilutions, surfaces are passified with a BSA solution [1 mg/mL BSA (Sigma) dissolved in assay buffer]. To start the experiment, 2 mM of ATP together with the respective fascin concentration dissolved in assay buffer (50 μM) is flushed into the flow chamber. Oxidation of the fluorophore was prevented by adding a standard antioxidant buffer supplement GOC (2 mg Glucose-Oxidase, Sigma; 0.5 mg Catalase, Fluka). To verify that the observed patterns are not affected by the use of GOC, control assays without the antioxidant supplement were performed. After addition of the motility buffer, flow chambers were sealed with vacuum grease (Bayer Silicones).
Actin and HMM Concentrations.
The numbers for the actin concentration denote the monomeric actin concentration inserted into the flow chamber. This concentration is slightly lowered by up to 10% by the subsequent rinse with the ATP-fascin dilution. The HMM concentrations σm given in the manuscript denote the concentration with which the flow chamber was incubated. The relation between σm and the motor density at the surface Ψ was determined to increase linearly in a wide concentration range with a ratio of: σm/Ψ = 0.04 nM μm2 (40). Above a HMM concentration of σm = 200 nM, the motor density at the surface saturates at a value of Ψ ∼ 6,000 μm-2 (41). If not indicated otherwise all experiments were performed at a HMM concentration of σm = 90 nM.
Image Acquisition and Preprocessing.
All data are acquired on a Leica DMI 2000 inverted microscope with a × 63 oil objective (numerical aperture: 1.4) or a × 40 oil objective (numerical aperture: 1.35). Images (resolution: 1,344 × 1,024 pixels) were captured with a charge-coupled device camera (C4880-80, Hamamatsu) attached via a 0.35 or 1.0 camera mount. Image acquisition and storage are carried out with the image processing software “OpenBox” (42).
Ring Curvature Statistics.
For each investigated parameter set the ring curvatures were recorded in up to 20 spots in different samples. To extract the ring curvatures for each spot 200 frames with a frame rate of 8.5 frames/s were recorded. After background subtraction (rolling ball radius of 50 pixels) we performed an average intensity projection of all 200 frames and converted the resulting picture into a binary image with a similar cut off for all samples. All these procedures were carried out with ImageJ. The subsequent ring recognition and the ellipsoid fit to the recognized structures were carried out with a custom written MATLAB routine. All signatures which are not of approximately circular shape (ratio of semiminor to semimajor axis < 0.7) are rejected.
Simulations.
The competition between continuous growth and merging processes is described using an agent-based simulation. Here the experimentally observed actin-fascin strings are modeled as elongated, polar strings that move with a velocity v on meandering trails (Fig. 3A). The heads of these strings pursue circular trajectories with stochastically varying curvatures and the tail strictly following the head’s trajectory. Further, the strings are subjected to aggregation processes which result in a continuous string thickening and merging processes between adjacent strings. In the following, these basic ingredients of the simulations—the computation of the random trajectories and the incorporation of the aggregation mechanisms—are described in detail.
Simulation of the String Trajectories.
In the absence of aggregation processes, the trajectory of the strings is determined by stochastic forces stemming from the HMM motor proteins at the surface. Similar to worm-like bundles (43, 44), it can be expected that the curvature distribution is of approximately Gaussian shape. Mathematically such a distribution can be generated by a stochastic process defined by the following update rule for the curvature κ
| [1] |
whereby n denotes the time step and η represents a random variable that is uniformly distributed over the interval [-α,α]. Stochastic changes of a given curvature occur with a rate ω, with equally spaced time intervals, tn+1 - tn = ω-1. The resulting distribution for the curvature is given in the Fig. S4.
Modelling of the Aggregation Mechanisms.
Aggregation of the strings into longer and thicker bundles affects the strings’ trajectories in a twofold way. While elongation of strings changes their probability to collide and form even longer strings or closed loops, thicker bundles that are the result of lateral aggregation, are less susceptible to curvature changes.
The elongation of strings is mainly based on merging events between adjacent strings, which occurs only for certain collision parameters: The colliding beads, say bead 1 and 2, have to be within a capture distance R1 + R2, where R1 and R2 denote the radii of the particular beads. The bead’s radius Ri mainly depends on the excluded volume of the strings and scales with the number of already merged strings M according to  , where
, where  denotes the initial radius and L the length of the structure. Further, strings only merge if the collision angles |θ| are smaller than a critical merging angle θc accounting for the binding properties of fascin, which is only able to link approximately parallel orientated filaments (45). The merging naturally includes ring closure events, when the head of a string interacts with its own tail.
denotes the initial radius and L the length of the structure. Further, strings only merge if the collision angles |θ| are smaller than a critical merging angle θc accounting for the binding properties of fascin, which is only able to link approximately parallel orientated filaments (45). The merging naturally includes ring closure events, when the head of a string interacts with its own tail.
The lateral aggregation is based on the continuous uptake of individual filaments and small strings, leading predominantly to a growth in thickness. The increase in thickness results in an increased stiffness of the strings that is modeled by a linear increase of what we call a tenacity parameter b(t)
| [2] |
with b0 being the initial tenacity b(τ = 0) and β determining the thickening speed. The time intervals are taken as equally spaced and τn+1 - τn = λ-1 defines the thickening rate λ. The linear tenacity increase modeled in Eq. 2 is motivated by a linear increase of the thickness of the strings implicitly implying an infinite filament reservoir. Because the experimentally observed ring formation is completed long before the filament reservoir is depleted, this is in good agreement with experimental observations. Thicker strings have a higher tenacity and are thus less susceptible to curvature changes. This reduced susceptibility to curvature changes can readily be modeled by modifying the update rule of Eq. 1 with a weight factor w[b(t)] that depends on the tenacity
| [3] |
The functional dependence of the weight factor w on the tenacity b is given by
| [4] |
The curvature distributions that result from the incorporation of Eqs. 2–4 are fundamentally different than the curvature distributions that result from the stochastic process defined by Eq. 1 (Fig. S4).
Parameters.
In all simulations, the initial bead radius was set to half of the unit length, and initially each string consisted of N = 10 beads, implying and initial string length of L0 = 10. The velocity was set to ν = 1.0; i.e., a string covers its own length in a simulation time of 10. All rates are measured in units of ν/L0. Thus a rate of 0.1 means that the corresponding stochastic process occurs on the time scale a string needs to cover its own length. For all simulations the thickening speed β was chosen to β = 0.2. For every simulation run, we started with 1,500 strings distributed randomly in space and orientation in a cubic simulation box of size Lbox = 50·L0 with periodic boundary conditions. The time discretization Δt is chosen to 0.1. The measured quantities are robust against changes in Δt and the size of the simulation box. In all simulations, the total simulation time was chosen to 5·104Δt, ensuring that all measured quantities are within a well saturated regime. The histograms and all values for Γ are averaged over 20 simulation runs of randomized initial configurations and curvature amplitudes. For visualization and image processing we used VMD and ImageJ.
Supplementary Material
Acknowledgments.
We thank K. Voigt and M. Rusp for assistance in the protein purification. We gratefully acknowledge funding from the European Research Council under the European Union's Seventh Framework Programme (FP7/2007-2013)/ERC CompNet (279476). Financial support from the Deutsche Forschungsgemeinschaft (DFG) in the framework of the Sonderforschungsbereich (SFB) 863 and the German Excellence Initiatives via the “Nano-Initiative Munich (NIM)” and the Technische Universität München—Institute for Advanced Study is gratefully acknowledged. V.S. and C.A.W. acknowledge support from the Elite Network of Bavaria by the graduate programmes CompInt and NanoBioTechnology and the International Graduate School of Science and Engineering (IGSSE).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission. D.P. is a guest editor invited by the Editorial Board.
See Commentary on page 19099.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1107540108/-/DCSupplemental.
References
- 1.Onsager L. Reciprocal relations in irreversible processes. I. Phys Rev. 1931;37:405–426. [Google Scholar]
- 2.Kudrolli A, Lumay G, Volfson D, Tsimring LS. Swarming and swirling in self-propelled polar granular rods. Phys Rev Lett. 2008;100:058001. doi: 10.1103/PhysRevLett.100.058001. [DOI] [PubMed] [Google Scholar]
- 3.Narayan V, Ramaswamy S, Menon N. Long-lived giant number fluctuations in a swarming granular nematic. Science. 2007;317:105–108. doi: 10.1126/science.1140414. [DOI] [PubMed] [Google Scholar]
- 4.Ward AJW, Sumpter DJT, Couzin LD, Hart PJB, Krause J. Quorum decision-making facilitates information transfer in fish shoals. Proc Natl Acad Sci USA. 2008;105:6948–6953. doi: 10.1073/pnas.0710344105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Couzin ID, Krause J, Franks NR, Levin SA. Effective leadership and decision-making in animal groups on the move. Nature. 2005;433:513–516. doi: 10.1038/nature03236. [DOI] [PubMed] [Google Scholar]
- 6.Ballerini M, et al. Interaction ruling animal collective behavior depends on topological rather than metric distance: Evidence from a field study. Proc Natl Acad Sci USA. 2008;105:1232–1237. doi: 10.1073/pnas.0711437105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Cisneros LH, Cortez R, Dombrowski C, Goldstein RE, Kessler JO. Fluid dynamics of self-propelled microorganisms, from individuals to concentrated populations. Exp Fluids. 2007;43:737–753. [Google Scholar]
- 8.Dombrowski C, Cisneros L, Chatkaew S, Goldstein RE, Kessler JO. Self-concentration and large-scale coherence in bacterial dynamics. Phys Rev Lett. 2004;93:098103. doi: 10.1103/PhysRevLett.93.098103. [DOI] [PubMed] [Google Scholar]
- 9.Riedel IH, Kruse K, Howard J. A self-organized vortex array of hydrodynamically entrained sperm cells. Science. 2005;309:300–303. doi: 10.1126/science.1110329. [DOI] [PubMed] [Google Scholar]
- 10.Nedelec FJ, Surrey T, Maggs AC, Leibler S. Self-organization of microtubules and motors. Nature. 1997;389:305–308. doi: 10.1038/38532. [DOI] [PubMed] [Google Scholar]
- 11.Butt T, et al. Myosin motors drive long range alignment of actin filaments. J Biol Chem. 2010;285:4964–4974. doi: 10.1074/jbc.M109.044792. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Schaller V, Weber C, Semmrich C, Frey E, Bausch AR. Polar patterns of driven filaments. Nature. 2010;467:73–77. doi: 10.1038/nature09312. [DOI] [PubMed] [Google Scholar]
- 13.Köhler S, Schaller V, Bausch AR. Structure formation in active networks. Nat Mater. 2011;10:462–468. doi: 10.1038/nmat3009. [DOI] [PubMed] [Google Scholar]
- 14.Simha RA, Ramaswamy S. Hydrodynamic fluctuations and instabilities in ordered suspensions of self-propelled particles. Phys Rev Lett. 2002;89:058101. doi: 10.1103/PhysRevLett.89.058101. [DOI] [PubMed] [Google Scholar]
- 15.Aranson IS, Tsimring LS. Pattern formation of microtubules and motors: inelastic interaction of polar rods. Phys Rev E. 2005;71:050901. doi: 10.1103/PhysRevE.71.050901. [DOI] [PubMed] [Google Scholar]
- 16.Aranson IS, Sokolov A, Kessler JO, Goldstein RE. Model for dynamical coherence in thin films of self-propelled microorganisms. Phys Rev E. 2007;75:040901. doi: 10.1103/PhysRevE.75.040901. [DOI] [PubMed] [Google Scholar]
- 17.Baskaran A, Marchetti MC. Hydrodynamics of self-propelled hard rods. Phys Rev E. 2008;77:011920. doi: 10.1103/PhysRevE.77.011920. [DOI] [PubMed] [Google Scholar]
- 18.Baskaran A, Marchetti MC. Statistical mechanics and hydrodynamics of bacterial suspensions. Proc Natl Acad Sci USA. 2009;106:15567–15572. doi: 10.1073/pnas.0906586106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Cates ME, Fielding SM, Marenduzzo D, Orlandini E, Yeomans JM. Shearing active gels close to the isotropic-nematic transition. Phys Rev Lett. 2008;101:068102. doi: 10.1103/PhysRevLett.101.068102. [DOI] [PubMed] [Google Scholar]
- 20.Liverpool TB, Marchetti MC. Rheology of active filament solutions. Phys Rev Lett. 2006;97:268101. doi: 10.1103/PhysRevLett.97.268101. [DOI] [PubMed] [Google Scholar]
- 21.Hatwalne Y, Ramaswamy S, Rao M, Simha RA. Rheology of active-particle suspensions. Phys Rev Lett. 2004;92:118101. doi: 10.1103/PhysRevLett.92.118101. [DOI] [PubMed] [Google Scholar]
- 22.Angelini TE, et al. Glass-like dynamics of collective cell migration. Proc Natl Acad Sci USA. 2011;108:4714–4719. doi: 10.1073/pnas.1010059108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Umbanhowar PB, Melo F, Swinney HL. Localized excitations in a vertically vibrated granular layer. Nature. 1996;382:793, 796. [Google Scholar]
- 24.Olafsen JS, Urbach JS. Clustering, order, and collapse in a driven granular monolayer. Phys Rev Lett. 1998;81:4369–4372. [Google Scholar]
- 25.Aranson IS, Tsimring LS. Patterns and collective behavior in granular media: theoretical concepts. Rev Mod Phys. 2006;78:641–692. [Google Scholar]
- 26.Tsai JC, Ye F, Rodriguez J, Gollub JP, Lubensky TC. A chiral granular gas. Phys Rev Lett. 2005;94:214301. doi: 10.1103/PhysRevLett.94.214301. [DOI] [PubMed] [Google Scholar]
- 27.Hinrichsen H. Non-equilibrium critical phenomena and phase transitions into absorbing states. Adv Phys. 2000;49:815–958. [Google Scholar]
- 28.Henkel M, Hinrichsen H, Lubeck S. Non-Equilibrium Phase Transitions: Volume 1: Absorbing Phase Transitions. The Netherlands: Springer; 2009. [Google Scholar]
- 29.Hallatschek O, Nelson DR. Life at the front of an expanding population. Evolution. 2010;64:193–206. doi: 10.1111/j.1558-5646.2009.00809.x. [DOI] [PubMed] [Google Scholar]
- 30.Corte L, Chaikin PM, Gollub JP, Pine DJ. Random organization in periodically driven systems. Nat Phys. 2008;4:420–424. [Google Scholar]
- 31.Hess H, et al. Molecular self-assembly of “nanowires” and “nanospools” using active transport. Nano Lett. 2005;5:629–633. doi: 10.1021/nl0478427. [DOI] [PubMed] [Google Scholar]
- 32.Liu HQ, et al. Biomolecular motor-powered self-assembly of dissipative nanocomposite rings. Adv Mater. 2008;20:4476–4481. [Google Scholar]
- 33.Takeuchi KA, et al. Directed percolation criticality in turbulent liquid crystals. Phys Rev Lett. 2007;99:234503. doi: 10.1103/PhysRevLett.99.234503. [DOI] [PubMed] [Google Scholar]
- 34.Liu C-H, Pine DJ. Shear-induced gelation and fracture in micellar solutions. Phys Rev Lett. 1996;77:2121–2124. doi: 10.1103/PhysRevLett.77.2121. [DOI] [PubMed] [Google Scholar]
- 35.Schmoller KM, Fernandez P, Arevalo RC, Blair DL, Bausch AR. Cyclic hardening in bundled actin networks. Nature Communications. 2010;1:134. doi: 10.1038/ncomms1134. [DOI] [PubMed] [Google Scholar]
- 36.Spudich JA, Watt S. Regulation of rabbit skeletal muscle contraction. 1. Biochemical studies of interaction of Tropomyosin-Troponin complex with Actin and proteolytic fragments of Myosin. J Biol Chem. 1971;246:4866–4871. [PubMed] [Google Scholar]
- 37.MacLean-Fletcher S, Pollard TD. Identification of a factor in conventional muscle Actin preparations which inhibits Actin filament self-association. Biochem Biophys Res Commun. 1980;96:18–27. doi: 10.1016/0006-291x(80)91175-4. [DOI] [PubMed] [Google Scholar]
- 38.Margossian SS, Lowey S. Preparation of Myosin and its subfragments from rabbit skeletal muscle. Methods Enzymol. 1982;85:55–71. doi: 10.1016/0076-6879(82)85009-x. [DOI] [PubMed] [Google Scholar]
- 39.Vignjevic D, et al. Formation of filopodia-like bundles in vitro from a dendritic network. J Cell Biol. 2003;160:951–962. doi: 10.1083/jcb.200208059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Toyoshima YY, Kron SJ, Spudich JA. The Myosin step-size—measurement of the unit displacement per ATP hydrolyzed in an invitro assay. Proc Natl Acad Sci USA. 1990;87:7130–7134. doi: 10.1073/pnas.87.18.7130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Sundberg M, et al. Selective spatial localization of actomyosin motor function by chemical surface patterning. Langmuir. 2006;22:7302–7312. doi: 10.1021/la060365i. [DOI] [PubMed] [Google Scholar]
- 42.Schilling J, Sackmann E, Bausch AR. Digital imaging processing for biophysical applications. Rev Sci Instrum. 2004;75:2822–2827. [Google Scholar]
- 43.Heussinger C, Bathe M, Frey E. Statistical mechanics of semiflexible bundles of wormlike polymer chains. Phys Rev Lett. 2007;99:048101. doi: 10.1103/PhysRevLett.99.048101. [DOI] [PubMed] [Google Scholar]
- 44.Bathe M, et al. Cytoskeletal bundle mechanics. Biophys J. 2008;94:2955–2964. doi: 10.1529/biophysj.107.119743. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Courson DS, Rock RS. Actin cross-link assembly and disassembly mechanics for alpha-Actinin and Fascin. J Biol Chem. 2010;285:26350–26357. doi: 10.1074/jbc.M110.123117. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.