On latent-variable model misspecification in structural measurement error models for binary response

Summary

We consider structural measurement error models for a binary response. We show that likelihood-based estimators obtained from fitting structural measurement error models with pooled binary responses can be far more robust to covariate measurement error in the presence of latent-variable model misspecification than the corresponding estimators from individual responses. Furthermore, despite the loss in information, pooling can provide improved parameter estimators in terms of mean-squared error. Based on these and other findings, we create a new diagnostic method to detect latent-variable model misspecification in structural measurement error models with individual binary response. We use simulation and data from the Framingham Heart Study to illustrate our methods.

1. Introduction

Covariate measurement error is a problem commonly encountered in epidemiological investigations (Carroll, 2005). One popular study, cited by numerous authors in the measurement error literature, is the Framingham Heart Study (Kannel et al., 1986), a study where one of the primary goals is to characterize the relationship between the risk of coronary heart disease and long-term systolic blood pressure. The true predictor in this application, long-term systolic blood pressure, can not be observed. Instead, systolic blood pressure readings are collected at periodic clinic visits for each subject and are viewed as error-contaminated versions of the true predictor.

In this paper, we consider structural measurement error models for a binary response Y, e.g., whether or not evidence of heart disease is detected. In a structural measurement error model, the true predictor can be viewed as a latent variable with its own distribution. Likelihood-based inference subsequently depends on this assumed latent-variable model, and its misspecification can adversely affect inference (Carroll et al. 2006, §5.6.3). This problem is exacerbated by the fact that diagnosing latent-variable model misspecification with the observed data directly is not possible. To address this issue, Huang, Stefanski, and Davidian (2006) developed simulation-based remeasurement methods to diagnose latent-variable model misspecification in structural measurement error models. Their methods provide a general framework to assess the adequacy of an assumed latent-variable model and the robustness of a target estimator to measurement error.

This research expands on the study presented in Huang et al. (2006) in the context of binary response. First, we extend the methods proposed in Huang et al. (2006) to investigate the effects of latent-variable model misspecification on likelihood-based estimators in structural measurement error models with pooled binary response. We show that using pooled binary response in place of individual binary response can result in better regression parameter estimates, and it lends to likelihood-based inference that is much less sensitive to covariate measurement error when the latent-variable model is misspecified. Second, using the pooled responses, we propose a new diagnostic method to detect latent-variable model misspecification with individual response data. This method possesses attractive properties and avoids the time-consuming remeasurement technique proposed by Huang et al. (2006).

2. Structural Measurement Error Models

We first define the structural measurement error model for individual response, as in Huang et al. (2006), and then extend its utility to pooled response.

2.1 Individual Response

For the ith individual, let Y_i, W_i, and X_i denote the binary response, the observed predictor value, and the true predictor value, respectively, for i = 1, 2,…, n. A structural measurement error model consists of three component models. The first component model is a generalized linear model for Y_i, conditional on X_i, given by Pr(Y_i = 1∣X_i) = h(β₀ + β₁X_i), where h(·) is a known inverse link function. Inference on the regression parameters θ = (β₀, β₁)^T is of central interest. The second component model is the classical measurement error model given by W_i = X_i + U_i, where U_i is the nondifferential measurement error (Carroll et al., 2006, § 2.5) and $U_i\sim N\left(\mathbf{0},{\sigma }_U^2\right)$. It follows that $W_i\mid X_i\sim N\left(X_i,{\sigma }_U^2\right)$. The nondifferentiality of the measurement error implies that given X_i, Y_i is independent of W_i. The third component model is the assumed model for X, with density denoted by $f_X^{\left(a\right)}\left(x;\mathit{\tau }\right)$, where τ is a parameter vector of length t. For individual i, the joint density of the observed datum, (Y_i, W_i), is given by

$$f_{Y,W}\left(Y_i,W_i;\mathit{\theta },\mathit{\tau },{\sigma }_U^2\right)=\int f_{Y\mid X}\left(Y_i\mid x;\mathit{\theta }\right)f_{W\mid X}\left(W_i\mid x;{\sigma }_U^2\right)f_X^{\left(a\right)}\left(x;\mathit{\tau }\right)dx,$$ (1)

where $f_{Y\mid X}\left(Y_i\mid x;\mathit{\theta }\right)=h{\left({\beta }_{\mathbf{0}}+{\beta }_{1}x\right)}^{Y_i}{\left\{1-h\left({\beta }_{\mathbf{0}}+{\beta }_{1}x\right)\right\}}^{1-Y_i},f_{W\mid X}\left(W_i\mid x;{\sigma }_U^2\right)={\sigma }_U^{-1}\phi \left\{{\sigma }_U^{-1}\left(W_i-x\right)\right\}$, and ϕ(·) denotes the N(0, 1) probability density function. We assume throughout that the n individuals are independent so that the loglikelihood of the observed data is

$$l\left(\mathit{\theta },\mathit{\tau },{\sigma }_U^2\right)=\sum _{i=1}^{n}log\left\{\int f_{Y\mid X}\left(Y_i\mid x;\mathit{\theta }\right)f_{W\mid X}\left(W_i\mid x;{\sigma }_U^2\right)f_X^{\left(a\right)}\left(x;\mathit{\tau }\right)dx\right\}.$$ (2)

The appearance of the primary regression model f_Y∣X(Y_i∣x; θ) and the assumed latent-variable model $f_X^{\left(a\right)}\left(x;\mathit{\tau }\right)$ within the integrand in (1) suggests that the choice of the assumed model for X can affect inference for θ based on (2).

2.2 Pooled Response

Suppose that G pools are formed from the n individuals, and let n_g denote the pool size for pool g, g = 1, 2, …, G, so that ${\sum }_{g=1}^G{n}_g=n$. Denote the individual binary responses in pool g by (Y_g1, Y_g2, …, Y_gng)^T and the corresponding pooled binary response by $Y_g^{\ast }=max\left\{Y_{g1},Y_{g2},\dots ;Y_{g{n}_g}\right\}$. Denote the observed and true predictor values in pool g by $W_g^{\ast }={\left(W_{g1},W_{g2},\dots ,W_{g{n}_g}\right)}^T$ and $X_g^{\ast }={\left(X_{g1},X_{g2},\dots ,X_{g{n}_g}\right)}^T$, respectively, and assume, as before, that W_gj = X_gj + U_gj, where $U_{gj}\sim N\left(\mathbf{0},{\sigma }_U^2\right)$ for all g and j. The major difference in the structural measurement error model for pooled response is in the first component model; i.e., the primary regression model. Here, the primary regression model relates the pooled response to the associated true predictors and is given by

$$Pr\left(Y_g^{\ast }=1\mid X_g^{\ast }\right)=1-\prod _{j=1}^{n_g}\left\{1-h\left({\beta }_{\mathbf{0}}+{\beta }_1{X}_{gj}\right)\right\}.$$ (3)

Our derivation shows that the joint density of the observed data for pool g, $\left(Y_g^{\ast },{\mathbf{\text{W}}}_g^{\ast }\right)$, can be written as

$$f_{Y^{\ast },{\mathbf{\text{W}}}^{\ast }}\left(Y_g^{\ast },{\mathbf{\text{W}}}_g^{\ast };\mathit{\theta },\mathit{\tau },{\sigma }_U^2\right)=Y_g^{\ast }\prod _{j=1}^{n_g}\int \frac{1}{{\sigma }_U}\phi \left(\frac{W_{gj}-x}{{\sigma }_U}\right)f_X^{\left(a\right)}\left(x;\mathit{\tau }\right)dx+\left(1-2Y_g^{\ast }\right)\times \prod _{j=1}^{n_g}\int \left\{1-h\left({\beta }_{\mathbf{0}}+{\beta }_{1}x\right)\right\}\frac{1}{{\sigma }_U}\phi \left(\frac{W_{gj}-x}{{\sigma }_U}\right)f_X^{\left(a\right)}\left(x;\mathit{\tau }\right)dx.$$

Assuming that the G pools are independent, the loglikelihood of the observed data based on the pooled responses is

$$l^{\ast }\left(\mathit{\theta },\mathit{\tau },{\sigma }_U^2\right)=\sum _{g=1}^{G}log\left\{f_{Y^{\ast },{\mathbf{\text{W}}}^{\ast }}\left(Y_g^{\ast },{\mathbf{\text{W}}}_g^{\ast };\mathit{\theta },\mathit{\tau },{\sigma }_U^2\right)\right\}.$$ (4)

Unless otherwise stated, we assume that ${\sigma }_U^2$ is known. In practice, ${\sigma }_U^2$ can be estimated when there are replicate surrogate measurements for each X, and it is straightforward to revise our approach (see Section 6). For either data structure, individual or pooled, it is worth emphasizing that if the first two component models in the structural measurement error model are correct, likelihood-based inference is consistent if the latent-variable model is correctly specified or if ${\sigma }_U^2=\mathbf{0}$. In the absence of measurement error, Vansteelandt, Goetghe-beur, and Verstraeten (2000) considered regression models of the form in (3) for modeling the prevalence of hiv using pooled responses from group testing. In such applications, forming pools is a natural and commonly-used technique to reduce testing costs. Our use of pooling in this paper is more general and is not restricted to applications in group testing.

3. Empirical Methods for Assessing Robustness

Huang et al. (2006) use remeasurement-based methods to assess the robustness of target estimators to measurement error in structural measurement error models. We summarize the salient aspects of this approach with models for individual binary response and then extend this technique to models for pooled response.

3.1 Individual Response

The remeasurement method involves further contaminating the observed covariate W. We call the further contaminated data the λ-remeasured data, where λ is a prespecified positive constant that controls the degree of further contamination. Specifically, for a chosen λ > 0, we first generate B sets of n independent random errors from a standard normal distribution, ${\left\{Z_{bi},i=1,2,\dots ,n\right\}}_{b=1}^B$, and form the λ-remeasured data defined by

$$W_{bi}\left(\mathrm{\lambda }\right)=W_i+\sqrt{\mathrm{\lambda }}{\sigma }_U{Z}_{bi},$$ (5)

for b = 1, 2,…, B and i = 1, 2,…, n. Note that, by this construction, the measurement error variance associated with W_bi(λ) is equal to $\left(1+\mathrm{\lambda }\right){\sigma }_U^2$ for all b and i.

Let Ω = (θ^T, τ^T)^T denote the r × 1 vector of unknown parameters, where r = 2+t, and suppose that Ω is to be estimated by solving the vector-valued estimating equation

$$\sum _{i=1}^n\mathit{\psi }\left(Y_i,W_i;\mathit{\theta },\mathit{\tau },{\sigma }_U^2\right)=\mathbf{0}$$ (6)

in the absence of further contamination. For example, if the maximum likelihood estimator (MLE) of Ω is desired, then ${\sum }_{i=1}^n\mathit{\psi }\left(Y_i,W_i;\mathit{\theta },\mathit{\tau },{\sigma }_U^2\right)=\left(\partial /\partial \mathrm{\Omega }\right)l\left(\mathit{\theta },\mathit{\tau },{\sigma }_U^2\right)$. In general, denote the estimator that solves (6) by Ω̂(0) = {θ̂(0)^T, τ̂(0)^T}^T. Based on (6), we construct the vector-valued estimating equation evaluated at the λ-remeasured data as

$$\sum _{i=1}^n{\mathit{\psi }}_B\left\{Y_i,{\stackrel{\sim }{W}}_i\left(\mathrm{\lambda }\right);\mathit{\theta },\mathit{\tau },\left(1+\mathrm{\lambda }\right){\sigma }_U^2\right\}=\mathbf{0},$$ (7)

Where ${\mathit{\psi }}_B\left\{Y_i,{\stackrel{\sim }{W}}_i\left(\mathrm{\lambda }\right);\mathit{\theta },\mathit{\tau },\left(1+\mathrm{\lambda }\right){\sigma }_U^2\right\}=B^{-1}{\sum }_{b=1}^B\mathit{\psi }\left\{Y_i,W_{bi}\left(\mathrm{\lambda }\right);\mathit{\theta },\mathit{\tau },\left(1+\mathrm{\lambda }\right){\sigma }_U^2\right\}$ and ${\stackrel{\sim }{W}}_i\left(\mathrm{\lambda }\right)={\left\{W_{bi}\left(\mathrm{\lambda }\right)\right\}}_{b=1}^B$. Solving (7) yields the same type of estimator as Ω̂(0) based on the λ-remeasured data; we denote this estimator by Ω̂(0) = {θ̂(0)^T, τ̂(0)^T}^T. Plotting one component of Ω̂(λ) versus λ, for λ ≥ 0, produces the simulation extrapolation, SIMEX, plot for that estimate (Cook and Stefanski, 1994; Stefanski and Cook, 1995). A constant or nearly constant SIMEX plot suggests that the considered estimator is robust to measurement error under the assumed model for X. A substantial deviation from constancy indicates that the estimator is sensitive to measurement error under the presumed model for X and that the estimator is biased, with the magnitude of bias depending on the size of measurement error variance.

In addition to the graphical SIMEX diagnostic, Huang et al. (2006) provide a quantitative assessment of robustness in the form of the test statistic

$$t_1^{\ast }\left(\mathrm{\lambda }\right)={\widehat{\nu }}_1^{-1}\left\{\widehat{\gamma }\left(\mathrm{\lambda }\right)-\widehat{\gamma }\left(0\right)\right\},$$

where γ is an element in Ω, γ̂(·) is the target estimator for γ, and ${\widehat{\nu }}_1^2$ is an estimator for var{γ̂(λ) − γ̂(0)}. The derivation of an estimator for var{γ̂(λ) − γ̂(0)} is provided in Web Appendix A. The statistic $t_1^{\ast }\left(\mathrm{\lambda }\right)$ evaluates the amount of change in the estimate as the measurement error variance increases from ${\sigma }_U^2$ to $\left(1+\mathrm{\lambda }\right){\sigma }_U^2$ after adjusting for background noise. If $t_1^{\ast }\left(\mathrm{\lambda }\right)$ deviates significantly from zero, one may conclude that the estimator is not robust to measurement error under the assumed latent-variable model. The operating characteristics of $t_1^{\ast }\left(\mathrm{\lambda }\right)$ are studied in Huang et al. (2006).

There is a delicate difference between the remeasurement method described above and the method described in Huang et al. (2006) in computing Ω̂(λ) at λ > 0. In Huang et al. (2006), when λ > 0, Ω is estimated B times, each time based on one set of λ-remeasured data of size n, and the final Ω̂(λ) is defined as the average of these B estimates. The modification here is to compute Ω̂(λ) only once based on all B sets of λ-remeasured data, which are combined in one vector-valued estimating equation (7). The solution to (7) is asymptotically equivalent to the older version of Ω̂(λ), but is far less cumbersome to compute.

3.2 Pooled Response

Generating the remeasured data in Section 3.1 does not involve the binary response Y. Therefore, the same data generation step applies when pooled responses are considered. Suppose that the target estimator for Ω, based on the data with pooled response, solves the vector-valued estimating equation

$$\sum _{g=1}^G{\mathit{\psi }}^{\ast }\left(Y_g^{\ast },{\mathbf{\text{W}}}_g^{\ast };\mathit{\theta },\mathit{\tau },{\sigma }_U^2\right)=\mathbf{0}.$$ (8)

Analogously to the construction of (7), the estimator for Ω of the same type, based on the λ-remeasured data with pooled response, is obtained by solving

$$\sum _{g=1}^G{\mathit{\psi }}_B^{\ast }\left\{Y_g^{\ast },{\stackrel{\sim }{\mathbf{\text{W}}}}_g^{\ast }\left(\mathrm{\lambda }\right);\mathit{\theta },\mathit{\tau },\left(1+\mathrm{\lambda }\right){\sigma }_U^2\right\}=\mathbf{0},$$ (9)

Where ${\mathit{\psi }}_B^{\ast }\left\{Y_g^{\ast },{\stackrel{\sim }{\mathbf{\text{W}}}}_g^{\ast }\left(\mathrm{\lambda }\right);\mathit{\theta },\mathit{\tau },\left(1+\mathrm{\lambda }\right){\sigma }_U^2\right\}=B^{-1}{\sum }_{b=1}^B\mathit{\psi }\ast \left\{Y_g^{\ast },{\mathbf{\text{W}}}_{bg}^{\ast }\left(\mathrm{\lambda }\right);\mathit{\theta },\mathit{\tau },\left(1+\mathrm{\lambda }\right){\sigma }_U^2\right\}$, ${\mathbf{\text{W}}}_{bg}^{\ast }\left(\mathrm{\lambda }\right)={\left\{{\mathbf{\text{W}}}_{\mathit{\text{bgj}}}^{\ast }\left(\mathrm{\lambda }\right)\right\}}_{j=1}^{n_g}$, for b = 1, 2,…, B, and ${\stackrel{\sim }{\mathbf{\text{W}}}}_{bg}^{\ast }\left(\mathrm{\lambda }\right)={\left\{{\mathbf{\text{W}}}_{bg}^{\ast }\left(\mathrm{\lambda }\right)\right\}}_{b=1}^B$, for g = 1, 2,…, G. Denote by g = 1, 2,…, G, Ω̂(0) = {θ̂(0)^T, τ̂(0)^T}^T. and Ω̂(0) = {θ̂(0)^T, τ̂(0)^T}^T the solutions to (8) and (9), respectively. As with individual response, the SIMEX plot of one component of Ω̂*(λ) can provide evidence of robustness or lack thereof. Furthermore, assuming independent pools, the construction of $t_1^{\ast }(\mathrm{\lambda })$ based on the solutions to (8) and (9) is identical to that based on individual response. As described in Web Appendix A, the variance estimator ${\widehat{\nu }}_1^2$ in this case is changed to reflect the fact that pools are the experimental units; not the individuals.

4. Robustness Findings

We now apply the previously outlined diagnostic methods to assess the robustness of target estimators resulting from data with different types of binary response.

4.1 Random versus Homogeneous Pooling

In studying the structural measurement error models with pooled responses, we consider two pooling strategies. The first strategy is to form the pools randomly, so that the composition of pools is independent of the individual covariate information. We henceforth refer to this as random pooling. The second pooling strategy we consider is motivated by Vansteelandt et al. (2000), who showed that, in the absence of covariate measurement error, a more precise estimator of $Pr(Y_g^{\ast }=1\mid {\mathbf{\text{X}}}_g^{\ast })$ results when one pools individuals with similarly observed covariates, that is, when X_g1, X_g2, …, X_gng are as homogeneous as possible. We refer to this as homogeneous pooling. In the presence of measurement error, the best homogeneous composition one can hope for is to pool individuals with similar W values. To implement this strategy, one can sort and partition the ordered W's into G pools, so that the datum for the first pool, say, is $\left(Y_1^{\ast },W_{11},W_{12},\dots ,W_{1n_1}\right)=\left(Y_1^{\ast },W_{\left(1\right)},W_{\left(2\right)},\dots ,W_{\left(n_1\right)}\right)$, where W₍₁₎, W₍₂₎, …, W_(n1) are the first n₁ order statistics of W₁, W₂, …, W_n. When generating λ-remeasured data, regardless of pool composition, we always contaminate the unsorted observed data W₁, W₂, …, W_n with the unsorted random noise ${\left\{Z_{bi},i=1,2,\dots ,n\right\}}_{b=1}^B$ to obtain ${\left\{W_{bi}\left(\mathrm{\lambda }\right),i=1,2,\dots ,n\right\}}_{b=1}^B$.

A complication with homogeneous pooling is that it renders a small amount of dependence among the pools due to the ordering of the observed covariates. Therefore, the MLE of Ω based on the homogeneous-pooling responses is not obtained by maximizing (4) as (4) is derived under the assumption of independent pools. In fact, we have found that maximizing the true loglikelihood from homogeneous pooling is practically infeasible. To estimate Ω in this situation, a sensible solution is to first estimate τ by maximizing the loglikelihood of W = (W₁, W₂, …, W_n)^T given by

$$l_W\left(\mathit{\tau },{\sigma }_U^2\right)=\sum _{i=1}^{n}log\left\{\int f_{W\mid X}\left(W_i\mid x;{\sigma }_U^2\right)f_X^{\left(a\right)}\left(x;\mathit{\tau }\right)dx\right\}.$$

This provides a consistent estimator for τ since the ordering does not enter at this level. We then estimate θ by maximizing (4) with τ fixed at its estimate. This simplifies the objective function to be optimized by assuming pools to be independent and yields a pseudo MLE for θ, which is biased, but much less so when compared to the estimator for θ resulting from maximizing (4) with respect to τ and θ simultaneously. The vector-valued estimating equation evaluated at the observed data corresponding to this two-stage approach is

$$\sum _{g=1}^G{\mathit{\psi }}^{\ast }\left(Y_g^{\ast },W_g^{\ast };\mathit{\theta },\mathit{\tau },{\sigma }_U^2\right)=\left(\begin{array}{c}\left(\partial /\partial \mathit{\tau }\right)l_W\left(\mathit{\tau },{\sigma }_U^2\right)\\ \left(\partial /\partial \mathit{\theta }\right)l^{\ast }\left(\mathit{\theta },\mathit{\tau },{\sigma }_U^2\right)\end{array}\right)=\mathbf{0}.$$

Another small complication with homogeneous pooling relates to the variance estimator for the pseudo MLE of Ω and the variance estimator ${\widehat{\nu }}_1^2$ in $t_1^{\ast }(\mathrm{\lambda })$. Both estimators are initially derived under the assumption of independent experimental units, which, in the case of pooled response, corresponds to independent pools. For the reasons previously outlined, these estimators are not appropriate for use with homogeneous pooling. To obviate this difficulty, we use the bootstrap to estimate these variances when homogeneous pooling is used.

4.2 Simulation Evidence

We conducted several simulations to evaluate the merit of pooling in structural measurement error models. For illustration, we take h(β₀ + β₁X) = Φ(β₀ + β₁X), where Φ(·) is the N(0, 1) distribution function, θ = (β₀, β₁)^T = (−2, 1)^T, and the true model for X to be the two-component mixture $f_X^{\left(a\right)}\left(x\right)=0.1f_1\left(x\right)+0.9f_2\left(x\right)$, where f₁(x) and f₂(x) denote the N(2.35, 0.41) and N(−0.26, 0.38) density functions, respectively. The two normal components are chosen to produce a bimodal distribution with mean 0, variance 1, skewness 1.3, and kurtosis 2. A random sample of size n = 2000 is generated from the structural measurement error model for individual data defined in § 2.1 with ${\sigma }_U^2=0.25$, so that the reliability ratio ${\sigma }_X^2/\left({\sigma }_X^2+{\sigma }_U^2\right)=0.8$ (Carroll et al. 2006, § 3.2.1). For both pooling protocols, we set n_g = 10, for g = 1, 2,…, G, yielding G = 200 pools. Thus, in the results which follow, the MLEs from the data with individual responses are based on 2000 responses while the estimates from the data with pooled response are based on only 200. The assumed models for X we consider are (a) a normal distribution, representing the situation wherein one misspecifies the latent-variable model and (b) a two-component mixture normal distribution, representing the situation in which one serendipitously chooses the correct parametric model. The estimators resulting from (b) serve as gold standards with which the estimators from (a) are compared. In the remeasurement method, we set B = 50 and take λ = 1.

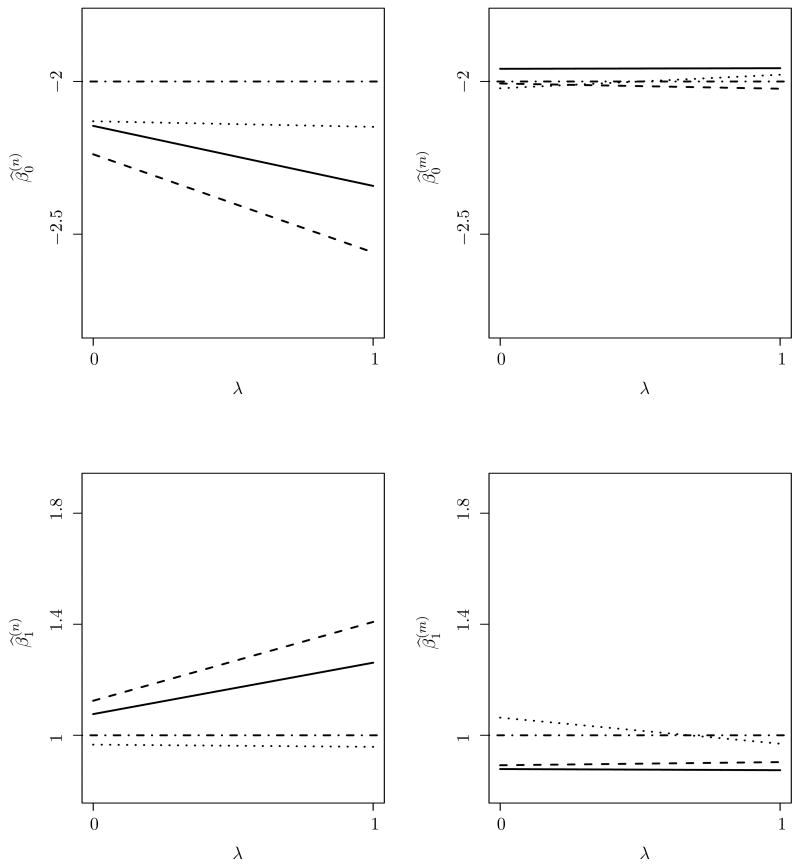
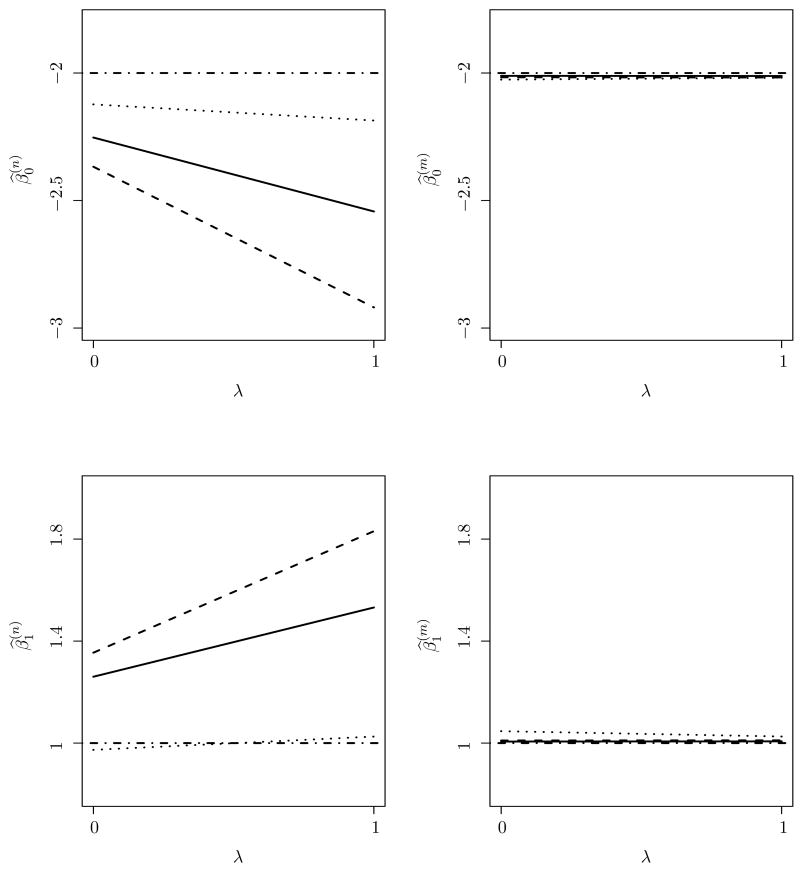
For λ ≥ 0, denote by ${\widehat{\mathit{\theta }}}_I^{\left(n\right)}\left(\mathrm{\lambda }\right)$, ${\widehat{\mathit{\theta }}}_R^{\left(n\right)}\left(\mathrm{\lambda }\right)$, and ${\widehat{\mathit{\theta }}}_H^{\left(n\right)}\left(\mathrm{\lambda }\right)$ the MLEs for θ from the data with individual response, the data with random-pooling response, and the pseudo MLE for θ from data with homogeneous-pooling response, respectively, when the assumed model for X is normal, and by ${\widehat{\mathit{\theta }}}_I^{\left(m\right)}\left(\mathrm{\lambda }\right)$, ${\widehat{\mathit{\theta }}}_R^{\left(m\right)}\left(\mathrm{\lambda }\right)$, and ${\widehat{\mathit{\theta }}}_H^{\left(m\right)}\left(\mathrm{\lambda }\right)$ the corresponding estimates when the assumed model for X is mixture normal. From the simex plots in Figure 1, it is evident that ${\widehat{\mathit{\theta }}}_H^{\left(n\right)}\left(\mathrm{\lambda }\right)$ is more robust to measurement error than either ${\widehat{\mathit{\theta }}}_I^{\left(n\right)}\left(\mathrm{\lambda }\right)$ or ${\widehat{\mathit{\theta }}}_R^{\left(n\right)}\left(\mathrm{\lambda }\right)$, despite the fact that the latent-variable model is misspecified and ${\widehat{\mathit{\theta }}}_H^{\left(n\right)}\left(\mathrm{\lambda }\right)$ is a pseudo MLE. For this simulation, all three estimates for θ under correct modeling do not appear to be sensitive to measurement error. To provide an overall assessment, we repeated the same simulation 300 times to observe the average pattern exhibited by the SIMEX plots in the setting described above. The averages of the 300 sets of ${\widehat{\mathit{\theta }}}_I^{\left(n\right)}\left(\mathrm{\lambda }\right)$, ${\widehat{\mathit{\theta }}}_R^{\left(n\right)}\left(\mathrm{\lambda }\right)$, and ${\widehat{\mathit{\theta }}}_H^{\left(n\right)}\left(\mathrm{\lambda }\right)$, as well as ${\widehat{\mathit{\theta }}}_I^{\left(m\right)}\left(\mathrm{\lambda }\right)$, ${\widehat{\mathit{\theta }}}_R^{\left(m\right)}\left(\mathrm{\lambda }\right)$, and ${\widehat{\mathit{\theta }}}_H^{\left(m\right)}\left(\mathrm{\lambda }\right)$, are plotted in Figure 2, and the values of these averages for λ = 0, 1 are given in Table 1. The observations from Figure 2 and Table 1 reconcile the patterns observed from the one Monte Carlo replicate depicted in Figure 1.

Figure 1.

simex plots for regression parameter estimates. The horizontal dot-dashed line is a reference line placed at the true parameter values. The left (right) panel depicts the estimates under a normal (mixture normal) assumption for X. The solid line, dashed line, and dotted line correspond to θ̂_I, θ̂_R, and θ̂_H, respectively.

Figure 2.

simex plots averaged over 300 Monte-Carlo replications. The horizontal dot-dashed line is a reference line placed at the true parameter values. The left (right) panel depicts the estimates under a normal (mixture normal) assumption for X. The solid line, dashed line, and dotted line correspond to θ̂_I, θ̂_R, and θ̂_H, respectively.

Table 1. Mean regression parameter estimates from 300 Monte-Carlo replications under the normal and mixture normal latent-variable assumption with β₀ = −2, β₁ = 1, and λ = 0, 1. Monte-Carlo mean-squared errors are in parentheses. IND, RP, and HP represent individual response, random-pooling response, and homogeneous-pooling response, respectively.

Normal	${\widehat{\beta }}_{\mathbf{0}}^{\left(n\right)}\left(\mathbf{0}\right)$	${\widehat{\beta }}_{\mathbf{0}}^{\left(n\right)}\left(1\right)$	${\widehat{\beta }}_1^{\left(n\right)}\left(\mathbf{0}\right)$	${\widehat{\beta }}_1^{\left(n\right)}\left(1\right)$
IND	−2.25 (0.064)	−2.54 (0.295)	1.26 (0.068)	1.53 (0.283)
RP	−2.37 (0.135)	−2.92 (0.846)	1.35 (0.126)	1.83 (0.691)
HP	−2.12 (0.015)	−2.19 (0.035)	0.97 (0.001)	1.03 (0.001)
Mixture normal	${\widehat{\beta }}_{\mathbf{0}}^{\left(m\right)}\left(\mathbf{0}\right)$	${\widehat{\beta }}_{\mathbf{0}}^{\left(m\right)}\left(1\right)$	${\widehat{\beta }}_1^{\left(m\right)}\left(\mathbf{0}\right)$	${\widehat{\beta }}_1^{\left(m\right)}\left(1\right)$
IND	−2.01 (< 0.001)	−2.01 (< 0.001)	1.01 (< 0.001)	1.01 (< 0.001)
RP	−2.02 (< 0.001)	−2.02 (< 0.001)	1.01 (< 0.001)	1.01 (< 0.001)
HP	−2.03 (0.001)	−2.02 (< 0.001)	1.05 (0.002)	1.03 (0.001)

4.3 Interpretation

Our overall simulation results indicate that, in the presence of latent-model misspecification, estimates computed from data with homogeneous-pooling response can be more robust to measurement error than those from data with individual response or with random-pooling response. An interesting related observation is given in Weinberg and Umbach (1999), who used pooled exposure assessments to improve the efficiency in case-control studies. Unlike our use of pooling, these authors pool the exposure covariates instead. When the exposure assessment is obtained from an error-prone assay, the authors show that the attenuation effect of measurement error on the naive MLEs (that is, estimators which ignore measurement error) can be magnified when the pooled exposure assessments are used in place of the individual exposure assessments. The authors reached this conclusion by showing that the reliability ratio of the pooled exposure data is lower than that of the individual exposure data.

Our use of pooling, which can lead to more robust estimators, involves the responses based on the sorted observed predictor values and is thus structurally different from the approach taken by Weinberg and Umbach (1999). However, the gains in robustness from homogeneous pooling can also be explained by the change in the reliability ratio. When we form pooled responses based on homogeneous covariates, the variation in the true predictor among the pools is usually larger than the variation in the true predictor based on the individuals. This is true so long as the reliability ratio of the individual data is not too small, that is, as long as the process of sorting the W data also approximately sorts the X's. Higher between-pool variance of the true predictor yields a higher reliability ratio for the pooled data. In this light, homogeneous pooling can alleviate the effect of measurement error.

Our findings are especially encouraging when group testing is used for cost concerns, because one may be able to realize large gains in robustness to measurement error in the presence of latent-model misspecification at a small fraction of the testing cost. One might naturally conjecture that using pooled responses in place of individual responses would cause a notable loss in precision when estimating θ. However, we have found that this may not be true. Inference based on the pooled responses can actually be more efficient than inference based on the individual responses when the between-pool variance of X is large and the pool sizes n_g are not so large that the pools conceal too much information. In fact, in our presented simulation study, with n_g = 10, we found that the mean-squared errors associated with ${\widehat{\mathit{\theta }}}_I^{\left(n\right)}\left(\mathrm{\lambda }\right)$ are generally much higher than the mean-squared errors associated with ${\widehat{\mathit{\theta }}}_H^{\left(n\right)}\left(\mathrm{\lambda }\right)$ (see Table 1). The reduction in bias due to measurement error in ${\widehat{\mathit{\theta }}}_H^{\left(n\right)}\left(\mathrm{\lambda }\right)$ can again be explained by the increase in the variance of the true predictor among the experimental units after forming homogeneous pools, which in turn increases the reliability ratio.

5. New Diagnostic Method

The statistic $t_1^{\ast }\left(\mathrm{\lambda }\right)$ proposed by Huang et al. (2006) is designed to test the hypothesis H₀₁: γ(0) = γ(λ), where γ is one of the elements in Ω, and where γ(0) and γ(λ) are the probability limits of the target estimators for γ based on the observed data and the λ-remeasured data, respectively. In the context herein, it is understood to mean that asymptotic results apply when the number of experimental units grows large without bound; that is, n for individual-response data and G for pooled-response data. Rejecting H₀₁ implies that the considered estimator for γ is not robust to measurement error. As nonrobustness can be a consequence of misspecifying the latent-variable model, rejection of H₀₁ can suggest latent-variable model misspecification. Because the model parameters are re-estimated based on the noisier data sets in the remeasurement method, computing $t_1^{\ast }\left(\mathrm{\lambda }\right)$ can be time-consuming. We propose a new test statistic for diagnosing model misspecification that does not require generating remeasured data or re-estimation based on noisier data.

The creation of our new statistic is motivated by the fact that when the latent-variable model is correctly specified, θ̂_I and θ̂_R are in close agreement, but that they can differ largely when the latent-variable model is misspecified (see Figures 1 and 2). This occurs because if the latent-variable model is correctly specified, so that the likelihood of the data with individual response and with random-pooling response are both correct, 0_I and 0_R are both consistent estimators of 0. However, close agreement between θ̂_I and θ̂_R is not guaranteed when the latent-variable model is misspecified.

5.1 Test statistic

For G > r, the new test statistic is defined by

$$t_2^{\ast }=\frac{G-r}{r\left(G-1\right)}\times {\left\{{\widehat{\mathrm{\Omega }}}_R\left(0\right)-{\widehat{\mathrm{\Omega }}}_I\left(0\right)\right\}}^T{\widehat{\sum }}^{-1}\left\{{\widehat{\mathrm{\Omega }}}_R\left(0\right)-{\widehat{\mathrm{\Omega }}}_I\left(0\right)\right\},$$

where Ω̂_(·)(0) is the MLE of Ω = (θ^T, τ^T)^T, subscripts I and R denote individual response and random-pooling response, respectively, and Σ̂ is an estimator of the variance-covariance matrix of Ω̂_R(0) − Ω̂_I(0), derived in Web Appendix B. Also shown in Web Appendix B, ${\left(G-r\right)}^{-1}r\left(G-1\right)t_2^{\ast }$ is a Hotelling's T²-type statistic; thus, $t_2^{\ast }$ follows an F(r, G−r) distribution under H₀₂. Structurally different from $t_1^{\ast }\left(\mathrm{\lambda }\right)$ the statistic $t_2^{\ast }$ tests the null hypothesis H₀₂ : Ω_R(0) = Ω_I(0), where Ω_R(0) and Ω_I(0) are the probability limits of Ω̂_R(0) and Ω̂_I(0), respectively. It is worth noting that $t_2^{\ast }$ does not depend on the remeasured data, so it is far easier to compute than $t_1^{\ast }\left(\mathrm{\lambda }\right)$.

5.2 Simulation Evidence

To examine the performance of the test statistics, we first computed $t_1^{\ast }\left(1\right)$ and $t_2^{\ast }$ using the simulated data from Figure 1 with n = 2000, G = 200 and n_g = 10. Table 2 displays the results. The variance estimate ${\widehat{\nu }}_1^2$, in the case of homogeneous pooling, is computed using 100 bootstrap resamples. Using 1.96 as a large-sample critical value, the values of $t_1^{\ast }\left(1\right)$ in Table 2 reinforce the visual findings revealed in Figure 1. That is, when the model for X is misspecified as normal, θ̂_H is more robust to measurement error than θ̂_I and θ̂_R. Furthermore, when the model for X is correctly specified, none of the three values of $t_1^{\ast }\left(1\right)$ provide sufficient evidence to conclude that the estimates are sensitive to measurement error or that the latent-variable model has been misspecified. Similarly, when the latent-variable model is misspecified as normal, the small probability values associated with $t_2^{\ast }$, computed with respect to the F(4, 196) reference distribution, provide strong evidence of model misspecification. When the latent-variable model is correct, $t_2^{\ast }$ does not indicate significant disagreement between Ω̂_R(0) and Ω̂_I(0), as seen through the large probability values, computed with respect to the F(7, 193) distribution.

Table 2. Values of $t_1^{\ast }\left(1\right)$ and $t_2^{\ast }$ associated with the regression parameter estimates from Figure 1 under the normal and mixture normal assumption. IND, RP, and HP represent individual response, random-pooling response, and homogeneous-pooling response, respectively. The numbers in parentheses in the rows for $t_2^{\ast }$ are the p-values associated with $t_2^{\ast }$.

	${\widehat{\beta }}_{\mathbf{0}}^{\left(n\right)}$			${\widehat{\beta }}_1^{\left(n\right)}$
Normal	IND	RP	HP	IND	RP	HP
$t_1^{\ast }\left(1\right)$	−4.18	−1.92	−0.34	4.91	2.27	−0.08
$t_2^{\ast }$	4.49 (0.002)	—	—	—	—	—
	${\widehat{\beta }}_{\mathbf{0}}^{\left(m\right)}$			${\widehat{\beta }}_1^{\left(m\right)}$
Mixture normal	IND	RP	HP	IND	RP	HP
$t_1^{\ast }\left(1\right)$	0.35	−0.72	1.11	−0.83	0.71	−0.68
$t_2^{\ast }$	0.37 (0.92)	—	—	—	—	—

To explore the power and size properties of the two statistics, we repeated the same simulation using 300 Monte Carlo replicates and recorded the proportion of times that H₀₁ and H₀₂ are rejected. Table 3 summarizes the results. Under correct modeling, our findings suggest that both test statistics have nearly-nominal size characteristics. In addition, the quantile-quantile plot of the 300 values of $t_2^{\ast }$ (not shown) strongly supports the limiting F distribution when the latent-variable model is correct. When the assumed latent-variable model is incorrect, the power of $t_1^{\ast }\left(1\right)$ under homogeneous pooling is low. This finding reinforces our robustness discovery.

Table 3. Rejection rates of $t_1^{\ast }\left(1\right)$ and $t_2^{\ast }$ based on 300 Monte-Carlo replications. Monte-Carlo standard errors are in parentheses. IND, RP, and HP represent individual response, random-pooling response, and homogeneous-pooling response, respectively.

	${\widehat{\beta }}_{\mathbf{0}}^{\left(n\right)}$			${\widehat{\beta }}_1^{\left(n\right)}$
Normal	IND	RP	HP	IND	RP	HP
$t_1^{\ast }\left(1\right)$	1 (0)	0.45 (0.03)	0.16 (0.02)	1 (0)	0.74 (0.03)	0.12 (0.02)
$t_2^{\ast }$	0.87 (0.02)	—	—	—	—	—
	${\widehat{\beta }}_{\mathbf{0}}^{\left(m\right)}$			${\widehat{\beta }}_1^{\left(m\right)}$
Mixture normal	IND	RP	HP	IND	RP	HP
$t_1^{\ast }\left(1\right)$	0.04 (0.01)	0.01 (0.01)	0.02 (0.01)	0.04 (0.01)	0.02 (0.01)	0.07 (0.01)
$t_2^{\ast }$	0.03 (0.01)	—	—	—	—	—

Under incorrect modeling, although high, the power of $t_2^{\ast }$ is slightly lower than that of $t_1^{\ast }\left(1\right)$ based on the individual responses. This is not totally unexpected, given the fact that $t_1^{\ast }\left(\mathrm{\lambda }\right)$ and $t_2^{\ast }$ detect latent-model misspecification in very different ways. When the latent-variable model is misspecified in a way that compromises likelihood-based inference, $t_1^{\ast }\left(\mathrm{\lambda }\right)$ reveals nonrobustness of a single target estimator γ̂ to measurement error as the noise level increases for the same data type, whereas $t_2^{\ast }$ detects the discrepancy between estimators of Ω resulting from different data types at a fixed level of noise. When the analyst has misspecified the true latent-variable model, Ω̂_R(0) and Ω̂_I(0) may be affected similarly, making misspecification difficult to detect (see Section 6). However, we have found that when n and G are large enough to produce reasonably precise estimates, the power of $t_2^{\ast }$ is often above 80% when the pool size n_g ≥ 4, making its use attractive because of computational ease. In practice, we recommend choosing G so that sê(β̂₀)/β̂₀ and sê(β̂₁)/β̂₁ are both small. Here, sê(·) denotes the estimated standard error, which we compute using the sandwich formula.

6. Application to Framingham Heart Study

We now apply the remeasurement method and the new testing procedure with data from the Framingham Heart Study. Our data set consists of 1615 male subjects who are followed for the development of coronary heart disease over six examination periods. At each of the second and third examination periods, each subject's systolic blood pressure is measured twice during two clinic visits. Additionally, the first evidence of coronary heart disease within the eight-year follow-up period from the second examination period is recorded for each subject. Define Y as the binary indicator of the first evidence of coronary heart disease within this follow-up period and the explanatory variable X as the long-term systolic blood pressure. The true predictor X is unobserved, and the two systolic blood pressure readings collected during the clinic visits can be viewed as error-contaminated versions of X.

In our analysis, we do not view X as time-dependent, and we take the average of the two systolic blood pressure readings measured in the second examination period as the value of the observed predictor, denoted by W. We use the average of the two systolic blood pressure readings measured in the third examination period as a replicate measurement of X so that we can estimate the measurement error variance ${\sigma }_U^2$, as in Carroll et al. (§5.4.2.1, 2006). Because ${\sigma }_U^2$ is estimated, we stack an additional estimating equation associated with ${\sigma }_U^2$ on top of the estimating equations in (6), (7), (8), and (9); in addition, σ_u in (5) is replaced with its estimate σ̂_u. To relate Y to X, we posit the probit model, Pr(Y = 1∣X) = Φ(β₀ + β₁X). For the assumed latent model for X, we choose a normal distribution and a two-component mixture normal distribution, assumptions under which we compute the statistics $t_1^{\ast }\left(1\right)$ and $t_2^{\ast }$. For illustration, we set n_g = 5, for g = 1, 2, …, 323. For the remeasurement method, we take B = 50 and λ = 1.

Values of $t_1^{\ast }\left(1\right)$ and $t_2^{\ast }$ for the Framingham data are listed in Table 4. Using these values, one can not find sufficient evidence of misspecification when the assumed latent-variable model is mixture normal. Under the normal model assumption, the statistic $t_1^{\ast }\left(1\right)$ based on individual response and $t_2^{\ast }$ suggest different conclusions, but this is not necessarily contradictory for the reasons noted in Section 5.2. At the current contamination level of the raw data (λ = 0), θ̂_R and θ̂_I are affected similarly by measurement error under the normal assumption. More importantly, our methods reveal a novel finding for these data; namely, if one prefers a simpler assumed latent-variable model, such as the normal, the pseudo MLE based on homogeneous-pooling responses is less sensitive to measurement error when compared to the MLE based on individual responses.

Table 4. Framingham data. Values of $t_1^{\ast }\left(1\right)$ and $t_2^{\ast }$ computed under the normal and mixture normal assumption. IND, RP, and HP represent individual response, random-pooling response, and homogeneous-pooling response, respectively. The numbers in parentheses in the rows for $t_2^{\ast }$ are the p-values associated with $t_2^{\ast }$.

	${\widehat{\beta }}_{\mathbf{0}}^{\left(n\right)}$			${\widehat{\beta }}_1^{\left(n\right)}$
Normal	IND	RP	HP	IND	RP	HP
$t_1^{\ast }\left(1\right)$	−2.87	−1.88	−1.67	2.92	1.93	1.51
$t_2^{\ast }$	0.21 (0.93)	—	—	—	—	—
	${\widehat{\beta }}_{\mathbf{0}}^{\left(m\right)}$			${\widehat{\beta }}_1^{\left(m\right)}$
Mixture normal	IND	RP	HP	IND	RP	HP
$t_1^{\ast }\left(1\right)$	0.46	0.80	−1.44	−0.45	−0.79	1.31
$t_2^{\ast }$	1.51 (0.16)	—	—	—	—	—

7. Discussion

When compared to individual binary response, we have shown that likelihood-based inference in structural measurement error models for pooled binary response can be more robust to covariate measurement error when the latent-variable model is misspecified. Moreover, pooling can improve efficiency in estimation. Pooled binary responses do arise naturally in group testing (Gastwirth and Johnson, 1994; Vansteelandt et al., 2000), and our findings suggest that latent-model misspecification may be less of a concern in this setting, so long as pools are composed homogeneously. However, as we have illustrated herein, our use of pooling is not restricted to group testing. Furthermore, including multiple covariates would not pose methodological challenges beyond those seen here. If, in addition to the mismeasured X, the analyst also uses V, measured without error, then the issue of model misspecification is only relevant to the model of X given V, and all of our techniques apply with $f_X^{\left(a\right)}\left(x;\mathit{\tau }\right)$ being replaced by an assumed conditional model. If the primary regression model depends on a multivariate error-prone covariate X, homogeneous pools can be formed by sorting the observed W data by the least noisiest covariate first. The rationale for this is to achieve the largest possible between-pool variance of X, noting that sorting the observed covariate associated with a heavily error-prone predictor may not change the between-pool variance of this predictor significantly.

We have also proposed a new test statistic $t_2^{\ast }$ for diagnosing model misspecification. The rationale for using $t_1^{\ast }\left(\mathrm{\lambda }\right)$ and $t_2^{\ast }$ as indicators of model misspecification are different, yet, they are united by a common, almost-counterintuitive theme. The construction of both statistics involves some form of information reduction, that is, one either adds more noise to the observed W to compute $t_1^{\ast }\left(\mathrm{\lambda }\right)$, or one conceals the individual responses to compute $t_2^{\ast }$. In the context of structural measurement error models for binary response, the fact that one can learn more from the data by reducing information is intriguing. In fact, we feel that this general idea could prove to be useful when examining model selection in a broader context.

It is important to remember that robustness does not guarantee consistency, yet, robustness is still a desirable property for an estimator to possess when measurement error exists. We do not suggest that estimates from pooled analyses should blindly replace those from the individual data. In fact, because the pseudo MLE is biased, we recommend using the MLE based on the original individual responses when there is insufficient evidence of latent-variable model misspecification. However, if there is a genuine uncertainty about the form of the true latent-variable model and one desires an estimator that is less sensitive to measurement error, the pseudo MLE based on homogeneous pooling is preferred.