Physics of Bacterial Morphogenesis

Abstract

Summary: Bacterial cells utilize three-dimensional (3D) protein assemblies to perform important cellular functions such as growth, division, chemoreception, and motility. These assemblies are composed of mechanoproteins that can mechanically deform and exert force. Sometimes, small-nucleotide hydrolysis is coupled to mechanical deformations. In this review, we describe the general principle for an understanding of the coupling of mechanics with chemistry in mechanochemical systems. We apply this principle to understand bacterial cell shape and morphogenesis and how mechanical forces can influence peptidoglycan cell wall growth. We review a model that can potentially reconcile the growth dynamics of the cell wall with the role of cytoskeletal proteins such as MreB and crescentin. We also review the application of mechanochemical principles to understand the assembly and constriction of the FtsZ ring. A number of potential mechanisms are proposed, and important questions are discussed.

INTRODUCTION

Physics, in a broad sense, is the study of matter interacting in space and time. Even for nonliving matter, there is much rich and complex behavior. For instance, a simple substance such as water can take on a range of physical forms. Under the right conditions, water can become spatially inhomogeneous and develop interfaces between a gaseous region and a liquid region, automatically partitioning space (130). When other molecules such as oily lipids and electrolytes are introduced into water, a further partitioning of space can occur from the formation of lipid bilayers and vesicles. The physics of a few component systems have been well studied. Many concepts such as free energies, phase behavior, cooperativity, stability, and nonequilibrium pattern formation have emerged from these studies (37, 71). Living systems are clearly quite a bit more complex, but bacteria appear to offer the best hope for a significant understanding. Mycoplasma, the smallest bacterium, has roughly 500 genes or a similar number of components. Escherichia coli has a bit more, about 4,000 genes. With these parts, bacteria are able to seek food, process information, communicate, and reproduce. The basic laws governing the interaction of protein components are rooted in physics, with the understanding that at the mesoscopic level of cells, complex and yet-undiscovered emergent physical phenomena are probably important (93). Indeed, it is quite likely that living systems take advantage of existing physical phenomena, adding regulatory components to increase precision and robustness necessary for life.

To understand the complex roles of genes, it is important to recognize that gene products often form spatial and temporal structures in the cell (Fig. 1). After DNA is transcribed and mRNA is converted to protein, the proteins themselves often self-assemble. These assembled structures are critical for protein function. In bacteria, a class of these structures is the bacterial cytoskeletal proteins that form filamentous structures. One of these genes is FtsZ, an essential cell division protein (17). FtsZ is recognized as a tubulin homologue (50, 101) and was shown to form a ringlike structure at the midcell (2, 54, 106, 114). Subsequently, a number of other bacterial cytoskeleton genes that form filamentous structures have been discovered. MreB is an actin homologue that forms filaments and is implicated in cell shape maintenance (46, 156, 158). RodZ colocalizes with MreB and serves a similar shape maintenance role (4, 12, 133, 157). Mbl, an MreB-like protein, is also associated with cell shape regulation in Bacillus subtilis (1). Crescentin is an intermediate filament homologue important for the curved shape of Caulobacter crescentus (7, 24). Because these structures are rodlike, they can deform and exert long-range mechanical forces. Forces, in turn, can significantly affect the assembly and functions of other structures in the cell. The mechanical properties of protein assemblies are discussed in “Secondary Structures and Their Interactions Determine the Protein Mechanical Response.”

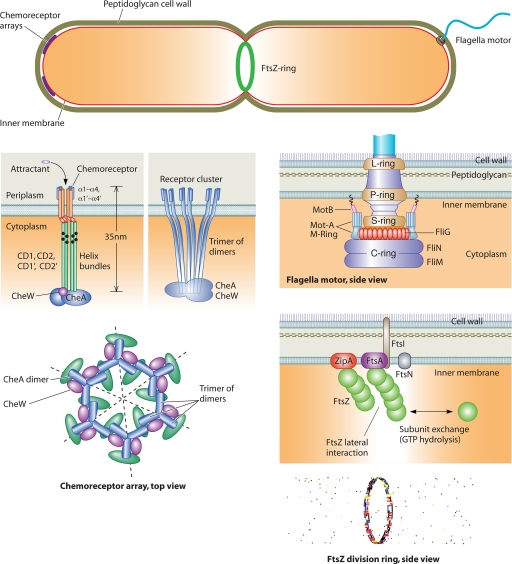
Fig. 1.

Microstructures in the bacterial cell. Structures such as the chemoreceptor array, the FtsZ ring, and the flagellar motor are made of multiple subunits operating in a coordinated fashion. Many of these assembled structures have been observed directly in electron microscopy images (23, 61, 95, 96). The properties of these structures are unique because the mechanics and chemistry in the subunits are coupled. Subunits are also mechanically coupled to each other, leading to cooperative effects.

Bacterial proteins also form temporally dynamic structures. MinCDE in E. coli is a system of 3 proteins that oscillate from pole to pole and regulate the positioning of the FtsZ ring (76, 104, 105, 108, 128, 129, 141). Remarkably, the Min assembly also oscillates and exhibits wavelike dynamics in vitro (98). Indeed, most of the assembled cytoskeletal structures in bacterial cells appear to be dynamic: FtsZ in the Z ring dynamically exchanges with monomers in the cytoplasm (139). MreB filaments connected with the membrane also exchange monomers with the cytoplasm (41, 136), although crescentin appears to be rather stable (28, 57). Indeed, MreB was thought to be a helical bundle (158), but recent evidence from B. subtilis suggests that MreB proteins are short filaments that are dynamically transported in a cell wall assembly complex (47, 64). Concepts in the dynamics of protein assemblies and their roles in the cell are discussed in Dynamics.

Interestingly, static mechanical properties and dynamic temporal properties of proteins are often coupled to perform cellular tasks. The basis of the coupling can be traced to the protein structure, which is generally flexible and deformable. As the protein deforms, the assembly kinetics and enzymatic activities of the protein often change. This complex interplay is the origin of the observed cooperativity in many biological systems and underlies the mechanism of bacterial propulsion by the flagellar motor (13, 14, 16, 18, 34, 109, 150, 173). It is also the basis of chemoreceptor performance and chemical gradient sensing (22, 48, 132, 137, 138, 154, 177). Indeed, it is likely that most cellular functions in eukaryotes and prokaryotes ultimately rely on this coupling between protein mechanics, enzymatic kinetics, and assembly dynamics.

After reviewing these physical concepts using bacterial examples, we will discuss the possible implication of these concepts in bacterial cell shape maintenance and bacterial cell division. These critical cell functions are achieved and regulated by an ensemble of bacterial genes. Our current understandings of these topics and some speculative mechanisms are discussed from a physical point of view.

MECHANICS OF PROTEIN ASSEMBLIES

Single-Protein Mechanics

When forces are applied to proteins, two kinds of deformations can occur. Type I deformation is a large deformation where the protein completely unfolds. This type of deformation has been studied with various techniques. However, unfolded proteins usually do not perform their intended biological functions. Therefore, we will not discuss examples of type I deformations here. Type II deformation is a smaller deformation where the protein remains folded, but the three-dimensional (3D) shape changes (allostery). These deformations power processes such as the movement of protein motors (75), the synthesis of ATP from ADP by ATP synthase (85, 174), and the gating of membrane channels (97, 140). These deformations require an input of energy, such as that from an externally applied force, or can be triggered by external energy sources, such as the binding of a small nucleotide to the catalytic site.

To understand the magnitude of type II deformation, it is useful to consider the energy scales and length scales in these deformations. A protein is around 3 to 10 nm in size. Typical allosteric movements are smaller. However, depending on the geometry of the protein, small allosteric movements can be levered. In myosin from eukaryotes, for example, the allosteric movement of the converter domain is less than a nanometer, but the movement is amplified by a long light-chain domain, generating a final movement, d, of ∼2 nm (75). Driving these movements are free energies derived from small nucleotides such as ATP and GTP. The chemical free energy storied in these nucleotides, ΔG, is on the order of 50 to 100 kJ/mol, or 80 to 160 pN nm. Usually, only a part of the available energy is converted to mechanical movement with an efficiency, ε, of ∼50%. The mechanical force expected from the energy conversion is then F = εΔG/d = 20 to 40 pN. Conversely, forces applied to proteins will also generate deformations of a similar magnitude. Because proteins are asymmetric 3D structures, the location and direction of the applied force are important. For example, 20 pN is often sufficient to unfold the protein if the force is applied to the C or N terminus (58). However, 20 pN is also sufficient to stall the rotational movement of E. coli ATP synthase under the right conditions (167). Thus, force can have a range of effects on proteins. Typically, 1 to 50 pN will have noticeable effects and can generate type II deformations.

Experimental measurements of protein deformations have been obtained from single-molecule experiments. Without applying any forces, because the energy scales of the allosteric movements, protein conformations will naturally fluctuate, and this fluctuation has been observed in single-molecule experiments (94, 175). It is also possible to probe conformational changes by directly applying forces to proteins using optical traps or magnetic tweezers. These experiments have been described in several reviews (69, 75, 110, 113). Protein deformations have also been studied by using all-atom computer simulations (89) and computational pattern recognition algorithms (59).

Examples of Bacterial Mechanoproteins

In bacteria, myosin-like contractile proteins that work on cytoskeletal filaments have not been discovered. However, there are several well-known rotary motors: the bacterial flagellar motor powers the swimming motion of E. coli by converting chemical energy stored in the electrochemical gradient in the inner membrane to rotational motion (13, 14, 16, 18, 34, 109, 150, 173). In this large motor assembly, 8 motor subunits (stators) operate together to turn a motor unit. Each stator makes small conformational changes as ions are passed across the membrane. The conformational change is geometrically converted to a rotation of the rotor through molecular-scale interactions at the interface between the rotor and stator. The ATP synthase of E. coli also makes a conformation change upon ATP hydrolysis to drive the rotation of a central shaft (85, 146, 165, 167, 174). ATP synthase has 3 ATP-hydrolyzing subunits, and the hydrolysis activity in these subunits is coupled to generate a coordinate rotation of the central shaft (146, 165, 167).

It is important to recognize that all proteins are mechanoproteins to some degree. While the flagellar motor and ATP synthase are spectacular examples, their principle of operation should apply to other proteins as well. Any protein that assembles in a quaternary structure will have some degree of coupling between subunits, which can lead to cooperative behavior.

Secondary Structures and Their Interactions Determine the Protein Mechanical Response

It turns out that common deformations in proteins can be further analyzed by considering the mechanical properties of common secondary structures such as α-helices and β-sheets (21, 32, 33, 143, 171, 178). Indeed, around 70% of all protein residues are in secondary structures; the rest are in random coils connecting these secondary structures. These structures are stabilized by hydrogen bonds and other nonspecific interactions (21). Large-scale allosteric movements are often transmitted by secondary structures. Without unfolding, α-helices can bend and twist and in the process can transmit significant forces (33, 171, 178). β-Sheets can also bend and store elastic energy (32, 143). These deformations can be geometrically levered into larger-scale motions.

Mechanical Properties of Extended Structures Can Lead to Novel Mechanisms

In cells, proteins rarely operate in isolation. Instead, proteins often self-assemble into extended structures such as filaments, sheets, and multidimensional arrays (Fig. 1). By assembling, the operations of individual units are mechanically coupled with other units, giving rise to collective behavior and cooperativity. New mechanisms can emerge with the assembled structures.

A number of bacterial proteins form filaments in the cells, in analogy to actin, microtubules, and intermediate filaments in eukaryotic cells. FtsZ is a homologue of eukaryotic tubulin (50, 101). MreB, Mbl, and ParM are homologues of eukaryotic actin (27, 55, 107). Crescentin is a homologue of the eukaryotic intermediate filament (25). Some of these bacterial filaments are implicated in shape maintenance in the cell. By forming extended filaments, these genes can take on conformations over much longer distance scales. Filaments can amplify small changes over long distances. If a monomer in the filament changes its shape by 1 nm, this movement can be levered over micrometers and turn into a change of hundreds of nanometers. Furthermore, since the monomers are physically linked, forces exerted by monomers are felt by other subunits over long distances. Mechanical forces can also alter chemical reaction rates (see Dynamics); therefore, the enzymatic activity of monomers in filaments will be coupled. This may have significant implications for the function of genes in the cell.

It should be noted that these filaments in bacteria are often not a single file of monomers. Protofilaments often bind together to form a bundle in a manner similar to that of microtubules, F-actin, and intermediate filaments. An interesting question is what controls the apparent size of the bundle. A clue may come from protein structure: in these bundles, monomers can bind to each other in a specific orientation. For example, the helically arranged binding interface between actin protofilaments gives rise to a double-stranded helical configuration similar to coiled coils (119). The asymmetrical shape of tubulin also contributes to the tube configuration of the microtubule bundle. Indeed, if the binding interaction depends on the spatial orientation of the monomers with respect to each other, competition between the mechanical deformation of the filaments and the binding interaction can give rise to bundles of different sizes (Fig. 2). By controlling the number of filaments in the bundle, the cell can further control the mechanical properties of the bundle (8, 83). The mechanical properties will influence the forces that can be exerted by these filaments (see “Forces Exerted by Extended Structures”).

Fig. 2.

Extended structures formed by proteins. (A) Protein filaments are 1D extended structures that can sustain mechanical forces. However, forces can affect the assembly of the filament and can induce filament breakage. (B) Two-dimensional extended structures are formed by proteins interacting laterally. When these 2D assemblies interact with another surface, such as the membrane, the curvature and rigidity of the assembly will determine the energies of the interaction. These interactions in turn will affect the dynamic exchange of subunits. (C) Filaments can form bundles by mechanically deforming the single filament to maximize the number of contacts between filaments. Thus, the geometry of the bonding interaction and mechanical properties of the protofilaments can regulate the bundle size.

Proteins can also form two-dimensional (2D) extended structures. By binding to other structures, such as the cell wall and the membrane, it is possible for the protein to sense curvature and localize in specific regions in the cell. In rodlike bacteria, the cell poles are roughly hemispherical, while the cell center is cylindrical. The radius of curvature, however, is quite large compared to typical protein sizes, ∼500 nm. This implies that individual proteins cannot easily discriminate between the pole and the cell center. However, if the protein forms a 2D sheet with a curvature that matches the membrane, the protein sheet does not have to bend in order to bind to the membrane and is thus energetically favorable to grow there (Fig. 2). If the 2D sheet is incompatible with the membrane curvature, mechanical strain must develop as the sheet grows larger. This competition between mechanical energy and chemical binding energy can lead to limits in the size of the 2D sheet. Thus, the mechanics of the assembled structure have a direct influence on where the structure can assemble. Such an example was recently described for Spo genes in B. subtilis (127, 159). The same mechanism is probably at work for the localization of chemoreceptor arrays to the E. coli cell pole.

In 2D extended structures, mechanical coupling between subunits can gain additional functional mechanisms that are quite different from those of one-dimensional (1D) filaments. In a 2D array, each subunit has more than 2 neighbors. In physics, this change in the number of neighbors leads to a change of the universality class, and new collective effects and phase transitions can emerge in 2D systems (19). This mechanism is significant for the chemoreceptor array, where mechanical coupling between receptor subunits allows the array to distinguish between subtle changes in attractant concentrations.

Forces Exerted by Extended Structures

We have seen that extended structures can exert forces by amplifying small local conformational changes. A simple model to estimate these forces is from the continuum theory of rods. Neglecting molecular details and assuming that the cytoskeletal bundle is a uniform rod, the mechanics of the bundle are characterized by its geometric curvature, its twist, and the amount of stretch (82, 99). The rod can have a preferred curvature or twist, which is the geometry of the rod in the absence of any external forces or constraints. In the preferred configuration, the rod does not exert forces, but if other objects exert external forces and torques, the rod will change curvature and twist to oppose the applied force. Thus, in a configuration away from its preferred curvature, the rod can exert forces. Indeed, the magnitude of the force is proportional to the curvature change squared, the length of the rod, and the stiffness of the rod (typically measured by bending modulus). For the same amount of change in curvature, a stiffer rod can exert a greater force.

A similar set of mechanical variables can describe forces exerted by 2D extended structures such as a sheet of protein aggregates, the cell wall, and the cell membrane. These structures can undergo large-scale bending and stretching deformations, change local curvature, and change local area, respectively. Again, the forces exerted by these geometrical changes are proportional to the mechanical modulus of bending and stretching (20). For 3D structures, deformations can occur in all directions and can result in the long-range coupling of proteins in the structure.

DYNAMICS

So far, we have discussed the mechanical responses of proteins and assembled protein structures. Many proteins also have enzymatic activity and perform chemical functions. For instance, ATP synthase binds small-nucleotide ATP and reversibly converts it to and from ADP and phosphate (85, 174). In a similar manner, FtsZ monomers catalyze the conversion of GTP to GDP (114). The speed of conversion is characterized by chemical rate constants. The free energy change of the reaction is characterized by equilibrium constants.

When protein mechanical deformation is considered, however, it becomes clear that mechanical deformation must influence protein enzymatic activity. To see this, we need to consider the total free energy of the protein, which includes a mechanical component that models the energy change as a function of its deformation and a chemical component that models the energy change as the enzymatic reaction goes to completion. Thus, these contributions suggest a modified understanding of protein function and an energy landscape description of the form

$$G=G\left(x,s\right)$$ (1)

where x is a mechanical deformation variable and s is the chemical state of the protein describing the state of the catalytic site. For instance, as the simplest mechanical deformation can be described as a linear spring, the total energy of the protein can be written as follows:

$$G\left(x,s\right)=\frac{1}{2}\kappa {\left[x-x_0\left(s\right)\right]}^2+c\left(s\right)$$ (2)

where x₀(s) is the mechanical equilibrium configuration of the protein, which can depend on the chemical state, s; κ is a mechanical spring constant; and c(s) describes the relative chemical energies of different chemical states at conformational equilibrium [x = x₀(s)]. A pictorial representation of this energy landscape is shown in Fig. 3. Note that in typical biochemical measurements of purified proteins, there are no constraints on x, and the protein is always relaxed to its mechanical equilibrium configuration. Thus, the first part of equation 2 is zero. In the cell, however, interactions between proteins in assemblies will exert forces on the protein, thus introducing changes in the mechanical variable. This in turn will affect the total free energy (G) and the reaction equilibrium constant. The result is a dramatic effect on enzymatic activity and kinetics.

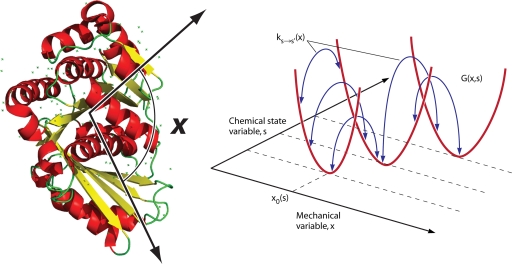
Fig. 3.

Mechanochemical description of protein energy landscape. For a protein such as the FtsZ monomer, which hydrolyzes GTP, the mechanical deformation of the protein, described by the variable x, can affect the chemical reaction rates, described by k_s→s′. The overall landscape is schematically shown on the right and is described by the function G(x,s).

Chemical Transition Rate Functions

To include the effect of mechanical deformations on enzymatic reaction rates, an extension of the rate constant concept is necessary. To see this, let us examine a couple of simple scenarios. Supposing that the protein P converts a substrate, A, to a product, B, the net free energy change of the reaction, ΔG, measures the energy difference of the system in the reactant state and the product state. In the absence of mechanical deformations, typically, this reduces to the chemical energy difference between A and B, c(s) in equation 2. However, if P is under mechanical strain, say x = x₁ in the reactant state and x = x₂ in the product state, then ΔG= Δc + (1/2)[κ(x₂ − x₀)² − κ(x₁ − x₀)²]. This is the new equilibrium constant for the reaction when there is mechanical strain present. Note that in this case, x₀ is the same for the reactant and the product.

Alternatively, the reaction could occur while the mechanical strain of the protein is fixed, say, at x₁, but the preferred configuration changes from reactant to product. In this case, the total free energy change is then ΔG = Δc + (1/2){κ[x₁ − x₀(B)]² − κ[x₁ − x₀(A)]²}. That is to say, the chemical equilibrium constant is now a function of the mechanical variable x₁.

The chemical equilibrium constant is related to the reaction rates of the conversion of A to B. To succinctly describe the overall reaction kinetics, it is easiest to define reaction rate functions instead of reaction rate constants, k_s′→s(x). From the condition of detailed balance, the transition rates must satisfy the energetic constraint as follows:

$$\frac{k_{s\to s\text{'}}\left(x\right)}{k_{s\text{'}\to s}\left(x\right)}=e^{-\left[G\left(x,s\right)-G\left(x,s\text{'}\right)\right]/k_{B}T}$$ (3)

where k_s′→s(x) is the backward reaction rate function and k_BT is the Boltzmann constant times the temperature. This constraint arises from our basic assumption that the underlying free energy landscape of the protein is a continuous single-valued function, as shown in Fig. 3. The transition rate functions describe energy changes along the reaction direction described by s. By specifying reaction rate functions, we are specifying a unique energy landscape for the protein, as shown in Fig. 3.

Biochemical measurements with purified protein represent the net rate of going from one mechanical equilibrium to another, x₀(s)→x₀(s′). In those experiments, the rate conformational relaxation should be much higher than chemical conversion in the binding pocket. Thus, those rates are approximately equivalent to k_s′→s(x₀) = k₀. For the process where the protein deformation goes from x₁ to x₂ when A converts to B, we can consider it a 2-step reaction, with the first reaction going from x₁ to x₁ and for A to B, and then in the B state, x₁ relaxes to x₂. Again, since mechanical conformational changes are typically fast, the overall rate constant is approximately k_A→B(x₁).

Forces Influence Protein Enzymatic Activity

With the energy landscape framework in mind, it is simple to consider the effect of forces on typical enzymatic reactions. Consider the simple situation where the AP complex is a mechanical spring, and when A is converted to B, the spring is broken. If a force, f, is applied to the AP complex, then the mechanical strain energy of the AP complex is f²/2κ, where κ is the spring constant. The mechanical energy of BP vanishes because the applied force no longer stretches the spring. Thus, ΔG becomes Δc − f²/2k according to equation 2. From equation 3, the forward and backward reaction rates are modified, although we cannot determine the full reaction rate function. A simple model for the forward and backward rates at this deformation is as follows:

$$k_{A\to B}=k_{A\to B}^0{e}^{-\left(\lambda f^2/2\kappa \right)/k_{B}T}{k}_{B\to A}=k_{B\to A}^0{e}^{-\left[\left(1-\lambda \right)f^2/2\kappa \right]/k_{B}T}$$ (4)

where $k_{A\to B}^0$ and $k_{B\to A}^0$are the reaction rates in the absence of forces:

$$\frac{k_{A\to B}^0}{k_{B\to A}^0}=e^{-\Delta c/k_{B}T}=e^{-\left[c\left(B\right)-c\left(A\right)\right]/k_{B}T}$$ (5)

λ is a phenomenological constant that approximately describes the location of the reaction transition state. Equation 4 is equivalent to Bell's model for force-dependent reaction rates (10). Here, we see that forces introduce mechanical strain in the protein and change the equilibrium constant of the reaction:

$$\frac{k_{A\to B}}{k_{B\to A}}=e^{-\left(\Delta c-f^2/2\kappa \right)/k_{B}T}$$ (6)

Thus, forces can have significant influences on the enzymatic activity of proteins. This influence partly explains the cooperativity between different proteins in an assembled structure: when one of the subunits undergoes enzymatic conversion and a conformational change, other units in contact will feel forces and alter their enzymatic rates. This cooperativity is the underlying mechanism that explains assembled structures ranging from the operation of molecular motors to the bacterial chemoreceptor array.

It is useful to keep in mind that models such as equation 2 and Fig. 3 are simplified approximations. It is possible to derive more sophisticated models of force-dependent kinetics. Depending on the complexity of the protein structures, catch-and-slip bond kinetics are sometimes seen for force-dependent bond ruptures (112, 151). It is also possible that more than one important mechanical variable are present for enzymes, which requires a higher-dimensional description. These aspects reflect the complexities in the protein energy landscape. Nevertheless, the mechanochemical concepts described here are a good simple approximation for most problems of interest.

Induced-Fit Model of Enzymatic Dynamics

Note that our specification of the protein energy in equation 2 has a connection with the induced-fit picture of enzyme allostery (147). Upon the binding of a small-molecule substrate and the release of enzymatic products, the enzyme changes shape. This is reflected by the fact that x₀(s) is a function of s. For each s, we postulate that there is a unique low-energy conformation. If there are forces and torques on the protein, then these forces will oppose conformational relaxation. When force balance is achieved, a new conformational equilibrium distinct from x₀(s) will occur. This picture is mechanically intuitive, yet it has a significant influence on our understanding of biochemistry because rates, k_s→s′(x), can sometimes be dramatically altered by forces.

Mechanochemical Processes

Given the energy landscape description of the protein, it is possible to quantitatively describe chemical changes under the application of forces. To combine mechanical deformations with chemical changes, one needs to consider dynamics on the energy surface in Fig. 3. The mathematical tools for describing these changes were summarized previously (144). Systems such as ATP synthase and the bacterial flagellar motor have been studied by using the mechanochemical approach (146, 165, 173, 174).

Assembly of Cytoskeletal Filament and Lessons from Microtubule Instability

The mechanochemical picture is also relevant for the assembly dynamics of bacterial cytoskeletal proteins. Detailed mechanical information on bacterial cytoskeletal proteins is currently sparse; however, since many of these proteins are homologues of eukaryotic actin and tubulin, analogous mechanisms are relevant. Later in this review, the mechanochemistry of FtsZ filaments is discussed in some detail. Here, we describe analogous dynamics in microtubules and the mechanochemical origins of microtubule instability. Some of the features of microtubule instability have implications for possible force generation mechanisms of FtsZ.

Microtubules are bundles of tubulin protofilaments, where there are approximately 11 protofilaments per tube (118). To form this bundle, there must be a favorable lateral interaction (negative binding energy per monomer) between the protofilaments. At the same time, tubulin monomers can hydrolyze GTP and change its conformation. In the GTP state, the assembled tubulin protofilaments appear to be straight; in the GDP state, the assembled protofilaments appear to be curved (118). Thus, if hydrolysis proceeds in the microtubule bundle, mechanical strain progressively increases (Fig. 4). At the same time, because of the lateral interaction that forces neighboring protofilaments to have the same curvature and because enzymatic reaction rates are determined by protein conformation, as described in “Chemical Transition Rate Functions,” GTP hydrolysis is inhibited unless both protofilaments become curved. These two competing effects conspire to determine the microtubule structure. When the lateral interactions win, the bundle grows, and an extension of the microtubule is observed. When curvature change and GTP hydrolysis win, the bundle destabilizes, and a shrinking of the microtubule occurs. These events lead to the observed microtubule instability (155).

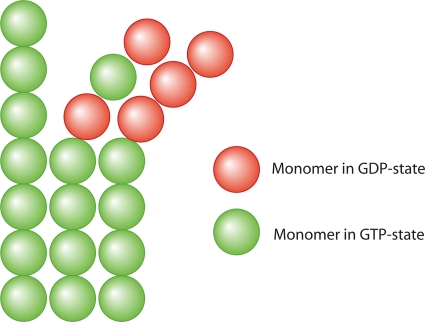
Fig. 4.

Mechanical coupling between protein subunits in a bundle can influence hydrolysis chemistry. Here protein monomers can convert from GTP to GDP. If there is an associated structural change in the protein filaments upon hydrolysis, and the protofilaments can bind laterally, strain energy can develop as monomers convert GTP to GDP. The strain energy can prevent hydrolysis from proceeding further, as described in “Forces Influence Protein Enzymatic Activity.” This mechanochemical coupling in a protein bundle can lead to cooperative effects and explains microtubule instability. A model that describes this coupling was reported previously (155).

Using the model in equation 2, it is possible to describe microtubule instability mathematically. We can use equation 2 to describe the energy of a tubulin monomer, where x is now the local curvature of the monomer. The lateral interaction energies between neighboring monomers would depend on the curvatures of the monomers:

$$G={\displaystyle \sum _n{\displaystyle \sum _i\frac{1}{2}\kappa \left(s_{n,i}\right){\left[x_{n,i}-x_0\left(s_{n,i}\right)\right]}^2+{\displaystyle \sum _{n,n+1}{\displaystyle \sum _i\Delta E\left(x_{n,i},x_{n+1,i}\right)}}}}$$ (7)

where x_n,i and s_n,i are the curvature and chemical state of the ith monomer in the nth protofilament, respectively. ΔE is the energy associated with the lateral interaction between monomers. Combined with the equation for energy are the chemical transition rates of monomers between different chemical states, k_{sn,i→s′n,i}, which is in turn influenced by the total energy of the microtubule complex. Using an approach like this, microtubule instability has been studied and explained quantitatively (155). Notice that an important parameter for this problem is the mechanical stiffness of the monomer, κ(s_n,i), which could depend on the chemical state of the monomer. The mechanical stiffness influences the overall energy and, therefore, the assembly and disassembly dynamics of the bundle.

In bacteria, FtsZ also forms filaments and bundles. Currently, the molecular organization of the FtsZ ring is not known. However, if FtsZ filaments are mechanically connected, then a similar coupling between GTP hydrolysis and mechanical curvature could be present. This mechanism could be involved in the triggering of bacterial cytokinesis. Note that this coupling results in catastrophic changes in the bundle configuration and is collective in nature. Forces from such catastrophes are likely to be impulse forces.

BACTERIAL CELL SHAPE AND MORPHOGENESIS

Cell Wall Synthesis and Turnover

After describing the general principles of mechanical influences in biology, we can apply these principles to understand a number of bacterial systems. A particular problem of interest is the apparent shape of the cell, which is determined by the geometry of the growing bacterial cell wall.

Extensive discussions about cell wall structure, architecture, and biosynthesis have been given by recent reviews (72, 163). A short outline is presented here. For Gram-negative bacteria, the cell wall is a single “living” molecule and is a network of peptidoglycan (PG) strands connected by peptide bonds. The cell wall also has mechanical rigidity and, along with mechanosensitive channels, protects the cell from osmotic shock. Glycan strands are made of alternating aminosugars, N-acetylglucosamine (GlcNAc) and N-acetylmuramic acid (MurNAc). The length of glycan strands indicates the degree of polymerization of GlcNAc and MurNAc. The length distribution is quite wide, but most glycan strands are much shorter than the circumference of the cell. The peptides are linked to the lactyl group of MurNAc. The muropeptide composition varies with the strain, the growth condition, and the growth phase (160, 161).

How the glycan strands are organized in the cell wall is a longstanding question in bacterial morphology and is still being debated. A classical model suggested that the glycan strands lie in the cell wall surface and are oriented along the circumferential direction of the cell (72, 87, 160, 161). This crystalline-layered model is challenged by the scaffold model (43–45, 111), which proposes that the glycan strands are normal at the cell surface. However, the average length of glycan strands is too long compared to the cell wall thickness, which suggests that the scaffold model is unlikely. More detailed discussions about the two structural models have been given by previous reviews (126, 162). A recent experimental study proposed the disordered layered model (63), which showed that the glycan strands are poorly ordered, although they lie in the cell wall surface, and they are mostly circumferential. This observation is nontrivial, since the architecture of the cell wall is a good indicator of its growth mode. A crystalline cell wall structure of a rodlike cell can maintain the cell radius and extend in the axial direction infinitely without any other guiding scaffold. For example, by using a “three-for-one” strategy (72, 163), i.e., replacing one existing glycan strand with three new strands, the bacterial cell can maintain a rod shape. However, increasing numbers of experiments have shown that bacterial cells require a bacterial cytoskeleton, such as the MreB filament, to maintain a cylindrical cell shape, which indicates that the disordered layered model might be more realistic.

The assembly of peptidoglycan precursor units occurs in the cytoplasm and the cytoplasmic membrane. Notably, several chemical steps are needed until the PG precursors are converted to the “activated” form. The activation of PG precursors requires energy derived from the hydrolysis of UDP. The activated PG subunits are then transported across the inner membrane to the periplasmic space, where they are inserted at growing points in the cell wall. The spatial pattern of insertion is important and can potentially affect the cell shape. A number of enzymes, penicillin binding proteins (PBPs), are involved in various stages of the synthesis process. At the final stages, the newly formed PG subunit is linked to the rest of the existing network by covalent bonds. Therefore, the energy stored during the activation of PG subunits is released during the final insertion and cross-linking process. An important aspect of PG synthesis is that the addition of PG subunits seems to be reversible; the existing PG strands are broken and replaced by new strands. Indeed, in Gram-positive bacteria, using radioactive pulse-labeling, one can detect PG turnover and the loss of PG units to the surrounding medium (125). In Gram-negative bacteria, the exchanged PG units are presumably recycled in the growth process (123, 124).

Models of Cell Growth and Cell Shape

Although the molecular mechanisms of PG synthesis in the bacterial cell wall have been studied, how these mechanisms translate to the observed geometrical shape of the cell is not understood. Some basic questions remain unsolved. How do rodlike bacteria maintain a specific radius but grow in the axial direction? How can enzymes insert PG strands in manners that maintain the global cell shape? Is there any size limit for bacteria? What factors determine the size limit, if it exists? Finally, how do cytoskeleton filaments affect the bacterial cell shape? Indeed, these questions about cell shape are fundamental to our understanding of organismal morphology. Thompson, who recognized the important role of mechanical forces in determining organismal shapes, was a pioneer in the study of growth and form (152). In the context of the bacterial cell wall, Koch developed the surface stress theory (86) to explain the morphology of bacteria. Cooper also proposed several models of PG synthesis and growth (35). These early models pointed out the essential role of mechanical forces in shaping the cell but lacked molecular mechanisms and connections to genetic components. There is also no mathematical demonstration of how these physical ideas can translate to the observed cell shape.

More recently, molecular-level models of the cell wall have been proposed. Holtje and Vollmer, based on biochemical studies in vitro and the fact that PG synthesis involves the turnover of existing PG material, proposed the 3-for-1 mechanism of cell wall growth (72, 163). This model assumes that an enzyme complex, possibly involving PBPs and hydrolases, inserts 3 PG strands while removing 1 existing strand. This model is appealing in several ways, but connections to the global shape of the cell are difficult to establish. Modern electron microscopy (EM) results (63) motivated Huang et al. to develop a static polymer model of the E. coli PG layer (77). The model was able to show that the cell shape is quite robust in response to cell wall damage and the appearance of network defects. The model argues that common bacterial cell shapes are the result of a simple spatial patterning of cell wall defects. Static-continuum models of the bacterial cell wall interacting with elastic cytoskeletal bundles have been considered as well (170). However, these models neglect the growth and remodeling of the PG layer, which have been shown to be an essential aspect of the PG life cycle.

Given the complexity of the cell wall molecular structure and the necessity of considering PG subunit turnover, it is useful to step back and consider a more coarse-grained view. For complex materials, continuum theories have been used extensively in many problems. These theories model the material with a constitutive law, usually specifying the microscale response of the material by a linear relationship between stress and strain. The material is characterized by several material constants, such as Young's modulus and Poisson's ratio. Indeed, this type of modeling of the cell wall was used previously, and the material constants have been measured for several bacterial cells (153, 166, 176). However, to fully explain the morphology of bacterial cells, these models have to be modified to include cell wall material growth and the dynamic turnover of PG material.

Such a model, which combines the mechanics of the cell wall with the chemistry of PG turnover, was recently considered by Jiang and Sun (80, 81). They argued that competition between mechanical strain energy from turgor pressure and the chemical energy of forming new PG bonds determines the growth of cell walls. The chemical bond energy per unit area is uniform if the PG layer is homogeneous. The mechanical energy depends on the local geometry of the cell wall. Thus, where new material can be added is controlled by mechanical stress. This automatically determines the favorable direction of the PG addition. Growth also changes the geometry of the cell wall and therefore changes the mechanical energy density. Such a feedback loop is used to regulate the growth and morphology of bacterial cells. The model provides a general framework for the study of common bacterial cell shapes. It explained why rodlike bacteria can maintain a constant radius but grow in the axial direction. The model can also explain the roles of the cytoskeleton, such as MreB, crescentin, and FtsZ, in cell shape determinations. Here we describe some essential elements of the model.

Mechanical Stresses in the Cell Wall

Mechanical stresses in the cell wall are the result mainly of turgor pressure, P, in the cell. The turgor pressure is about 2 to 5 atm in E. coli (Gram-negative bacterium) and is 15 atm in B. subtilis (Gram-positive bacterium) (153). Given that the cell wall thickness, h, is much smaller than the bacterium radius, R, the bacterial cell wall can be regarded as a thin shell. For a spherical cell with radius R, the stress field in the cell wall is isotropic and proportional to the radius; i.e., σ = PR/h. For a cylinder under pressure, σ₁₁ = PR/h and σ₂₂ = PR/h, where σ₁₁ and σ₂₂ are the stresses in the circumferential and axial directions, respectively. For cells with arbitrary shapes, the stress field can be solved from equilibrium equations for the theory of a thin shell (20, 80, 99). One notices that for a cylindrical cell, the stress from the turgor pressure in the circumferential direction is twice that in the axial direction.

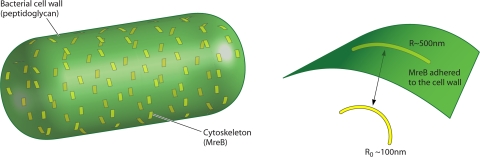
Other structures in bacteria can also affect stresses in the cell wall. For example, FtsZ monomers condense to form the Z ring and seem to apply a force on the cell wall to initiate cell division. MreB bundles can also potentially apply forces on the cell wall. Evidence of this comes from in vitro studies of Thermotoga maritima MreB, which forms bundles of curved polymers in an ATP-dependent manner (56). The curved bundle has a preferred radius of ∼100 nm, significantly smaller than the bacterial radius. Thus, if these bundles adhere to the cell wall, then upon ATP hydrolysis, MreB would exert a force. Assembly properties of purified T. maritima and B. subtilis MreB proteins have been studied (6, 9). A similar curvature change mechanism could be at work for MreB to exert forces in E. coli.

Previous experiments have shown that the MreB is essential for maintaining a rodlike shape. The disassembly of MreB leads to a reversible transformation from a short rod to a sphere. When A22, a small molecule that disrupts the assembly of MreB, is added to a medium, E. coli can transform from a rodlike shape to a spherical shape (5, 78). A22 causes similar morphological transformations in C. crescentus (67), where crescent-shaped cells transform into round lemon-shaped cells. Interestingly, the rodlike shape is recovered if MreB filaments are restored (79). Previous experiments also suggested that the MreB bundle contributes one-half of the stiffness of a whole cell (166). Similar to MreB, if crescentin in filamentous C. crescentus is deleted, cells lose their helical shapes and become straight rods (7, 24). Within the context of Jiang and Sun's model, they proposed that these filaments could exert mechanical forces on the cell wall and change the spatial pattern of PG addition and turnover, thus generating cells of different morphologies.

In addition to internal forces from the cytoskeleton, forces on the cell wall are also altered by external constraints. A good example is the growth of bacteria in a microchamber (24, 148). If cell division is inhibited, the cell becomes filamentous, and growth reaches the confinement of the microchamber. The chamber will apply a compression force at the ends of the cell. Beyond a critical force, the cell buckles, and a curved or even helical cell is seen. Data from these confinement experiments are also consistent with Jiang and Sun's model predictions.

Mechanochemical Model of Cell Wall Energy

The goal, therefore, is to develop a model that can mathematically compute the shape of the cell wall under the influence of cytoskeletal bundles and other forces. The model takes a coarse-grained view. Even though the PG synthesis process is complex, at the simplest level, it can be viewed as a reversible assembly reaction. Enzymes are involved in catalyzing the reaction, but the final PG synthesis steps do not require an input of other energy. Since the stored energy during PG subunit activation is released during PG insertion, the product is favored, and the overall free energy change is negative as more PG strands are added to the wall. However, because the cell wall is under constant tension from turgor pressure, the reaction is influenced by the mechanical stress in the network. The reaction of assembling new cell wall material can be thought of as a process where the area increases slightly, or A→A + dA (Fig. 5). The net free energy change of the reaction can be written as follows:

$$dG=G\left(A+dA\right)-G\left(A\right)=dU-\epsilon dA$$ (8)

where ε is the chemical bond energy per unit area and dU is the change in the mechanical energy of the formed PG network. Notice that as the cell grows larger, the mechanical strain energy change is positive, meaning that it makes the formed PG network unfavorable. Moreover, the mechanical energy depends on the shape and size of the cell wall and the internal turgor pressure. This simple consideration immediately points out that there could be a size and shape of the cell where the mechanical energy exactly balances the chemical bond energy, and dG = 0. When this configuration is reached, assembly and disassembly reactions exactly balance, and the cell wall stops growing.

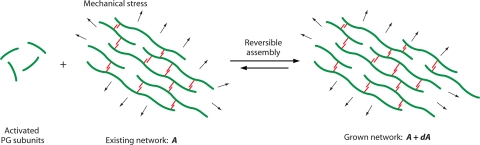
Fig. 5.

The PG cell wall grows by the addition of activated PG subunits to an existing cell wall under tension. Here the reaction depicts an existing network with area A, which can increase area by a small amount, dA. During the addition of PG, energy stored in the activated MurNAc and GlcNAc units drives the reaction. The assembly process is mediated by enzymes. One possibility is that since transpeptidases as well as hydrolyases are involved, the assembly reaction is reversible. Mechanical tension in the network shifts the reaction equilibrium and changes the net flux of materials to the right, thus affecting the size and shape of the cell.

The molecular mechanism of the PG addition supports the reversible-assembly idea. Both transpeptidases and hydrolases are needed to assemble and disassemble the PG network. In E. coli, the genome appears to code for up to 30 hydrolases. How these enzymes are coordinated is currently unknown, but it is clear that the growth of a new cell wall must break existing covalent bonds while forming new ones. The chemical steps of breaking existing PG bonds must depend on the stress in the network. The cell also maintains a high turgor pressure. Weak existing PG bonds can break spontaneously, resulting in a loss of PG material. The cell must continuously make new bonds to maintain a coherent structure.

By specifying the mechanical energy in this way, the model makes several assumptions. (i) The thickness of the cell wall is relatively small compared to the characteristic size of the cell so that the thin-shell theory can be used. (ii) The spontaneous curvature of the cell wall is zero, so the cell wall should be flat in the relaxed state. (iii) We also assume that the growth process is quite slow. Therefore, the cell wall is always in mechanical equilibrium. The mechanical energy G, is a combination of mechanical strain energy in the cell wall and the work done by turgor pressure at mechanical equilibrium. Using these assumptions, the total free energy of a cell wall can be written as a function of the current geometrical shape of the cell. The parameters of the model are the material constants of the cell wall, such as Young's modulus and the chemical energy per unit area. The chemical energy is determined by the density of chemical bonds in the PG network and the molecular geometry.

Cell Shape Is Determined by Growth Dynamics

Having defined the total cell wall energy, it is possible to estimate the growth dynamics by considering the net flux of the PG addition to the existing wall at different locations along the cell. For example, for a small increase in the radius of a spherical bacterium, there will be a corresponding change the mechanical energy and a change in the chemical energy. The net energy change is then given by equation 8. In the limit where the assembly is fully reversible, and not limited by the kinetics of assembly, the material flux should be proportional to the total energy change. In the case of the cell radius, R, it is as follows:

$$\frac{dR}{dt}=-M\frac{\partial G}{\partial R}$$ (9)

where M is a constant describing the kinetics of insertion. Note that M depends on the activity of PBP enzymes and could depend on their spatial location. Mutations of PBPs can potentially change the growth kinetics as well as the spatial distribution of growth. Indeed, mutants of PBPs show interesting changes in the cell shape (126), which will require further modeling studies. The model predicts that if the net energy change is zero, the cell stops growing. The dimension at which mechanical energy balances chemical energy can be considered the size limit of the bacterial cell.

Some Predictions of Jiang and Sun's Model

Spherical cells.

For growing spherical cells, the model makes particularly simple predictions. One can show that the total free energy of the cell wall is as follows (80, 81):

$$G=4\pi \left[\frac{P^2{R}^4}{8\left(\lambda +\mu \right)h-\frac{1}{3}{R}^{3}P}-\epsilon R^2\right]$$ (10)

where $\lambda =\frac{\nu E}{1-{\nu }^2}$ and $\mu =\frac{E}{2\left(1+\nu \right)}$, with E and ν being Young's modulus and Poisson's ratio, respectively. R is the radius of the current shape. When dG/dR = 0, we can derive a steady-state size for the cell:

$$R_s=\frac{\left(\lambda +\mu \right)h}{p}\left[1+\sqrt{1+\frac{4\epsilon }{\left(\lambda +\mu \right)h}}\right]$$ (11)

Rodlike cells.

For rodlike cells, a similar analysis is possible for 2 shape parameters, the cell radius, R, and the cell length, L. Under typical conditions where there are no external constraints, the growth equations predict that there is a steady radius but no steady-state length and that the cell should elongate indefinitely (81). This is in accord with observations of cells where division is inhibited. Another interpretation is that division is simply a way to separate a continuously elongating cell. We see that this result arises from the fact that the mechanical stress (and therefore contributions to the strain energy) in the axial direction is different from the stress in the circumferential direction. The flux of new material is therefore different for these two directions.

Cells with other shapes.

We can use a similar approach to study the growth of helical and curved torus-like cells. We have 3 parameters for curved cells and 4 parameters for helical cells. In these cases, it can be shown that the curved-cell shape cannot be maintained without other influences. One such influence could be cytoskeletal filaments such as crescentin. The maintenance of the curvature by crescentin will be discussed in the following section.

For cells with arbitrary shapes, this model allows us to write a set of equations that describes the growing shape of the cell. The detailed mathematics were described previously (see the supplemental material in reference 80). Therefore, given the mechanical model for cell wall energy, it is possible to compute the shape of the cell under different kinds of mechanical tension.

Forces from Cytoskeletal Proteins Can Explain Cell Shape Morphogenesis

Growth-induced instability in a cylindrical cell wall and suppression of instability by the MreB helix.

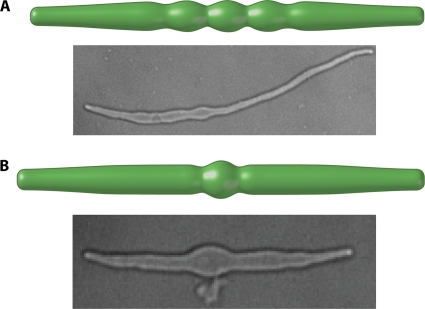
In the examples mentioned above, bacterial cells are considered a perfect sphere or a perfect cylinder. However, cells do not obey ideal geometries. Even for normal cells, there is a significant amount of deviation away from perfect cylindrical shapes. It is then natural to ask if the cylindrical cell shape is stable with respect to these shape imperfections. Within the framework of the model, one can show that a cylindrical cell is not stable with respect to these imperfections. A small deviation from the cylinder will eventually grow and become amplified. This is because in the presence of small imperfections, the stress along the cell wall is no longer uniform and tends to make cell wall growth more favorable in curved regions. This further amplifies the imperfection, leading to further growth. The growth of imperfections has a characteristic length somewhat larger than the natural length of E. coli. Therefore, the model predicts that a cell that starts as a rod will eventually develop wavelike shapes with a wavelength on the order of the characteristic length.

The question then becomes, if these shape imperfections are amplified, how does the cell maintain a rodlike shape? One possible explanation is that there are other forces on the cell wall that suppress this instability. MreB can potentially perform this role. Within the model, MreB filaments are described as filaments that change curvature and can exert an inward mechanical force (Fig. 6). The dynamic nature of MreB movement implies that this inward force should be modeled as a diffuse pressure field (80). The MreB filament reinforces the cell wall, and the total cell envelope can be regarded as a fiber-reinforced composite material. The result is that the steady-state shape of the cell is a cylinder if the MreB filaments are of sufficient stiffness (80). If MreB is deleted from the cell, only the turgor pressure term remains, and the model predicts a spherical cell. Previous experiments showed that the treatment of A22 in filamentous E. coli leads to an increase of cell width and that one or more bulges appear in the middle of the cells (80); the resulting cell shape appears to be wavelike and can indicate the onset of instability (Fig. 7). MreB can also affect cell division in an FtsZ-dependent manner (158). MreB bundles are disassembled around the septum at the beginning of cell division, and the overexpression of MreB inhibits cell division, and cells become filamentous (88, 164), which indicates that the disassembly of MreB is a prerequisite of cell division.

Fig. 6.

The bacterial cell wall is a composite material. Cytoskeletal filaments such as MreB adhere to the cell wall. If the intrinsic radius of curvature of MreB, R₀, is less than the cell radius, R, ∼500 nm, then the cell wall will experience a force. Due to the dynamic nature of MreB filaments, this force is best modeled as an inward pressure (80). This pressure, in turn, can regulate the growth dynamics of the cell wall. This mechanism can potentially explain the role of filaments such as MreB and crescentin in maintaining the cell shape.

Fig. 7.

Growth-induced instability in bacterial cells. Mathematically computed cell shapes are compared with E. coli cells grown in a standard culture. The instability exhibits a characteristic wavelength, which for E. coli is about 5 μm. The cells are grown from an FtsZ deletion strain that carries a plasmid expressing a thermosensitive FtsZ (courtesy of the Margolin laboratory). Upon a temperature upshift, cells become filamentous, and A22 was added to disrupt MreB. The model predictions are similar to the wavelike bulges seen in these cells with disrupted MreB.

Curvature maintenance by crescentin in curved rods and helices.

A similar mechanical role could be played by crescentin in C. crescentus. In the natural state, crescentin appears to form a left-handed helical bundle (4). When the helix is attached to the cell wall, its spontaneous curvature and twist will change the local stress in the cell wall to develop a helical cell (24, 84). Indeed, in C. crescentus, both MreB and crescentin may exert mechanical influences that affect the overall cell shape. Further evidence that mechanical forces can alter cell shape comes from the growth of cells in confined spaces. E. coli cells grown in microchambers become curved, clearly as a result of mechanical influences. The confinement comes from forces exerted by the chamber wall, which alter the growth dynamics of the cell wall in the same fashion as that of MreB and crescentin, generating curved cells. It should be noted that immediately after the removal of cells from confinement, the cells are still curved. However, the cells slowly remodel the cell wall until they reach a new steady-state shape according to the new forces on the cell wall, gradually becoming straight again (49, 148). E. coli cells do not naturally contain crescentin. The fact that cells without crescentin tend to become a straight rod again confirms that crescentin is needed to create a curved or helical shape.

Cell division and forces from the FtsZ ring.

Indeed, FtsZ ring contraction can be thought of as another mechanical influence on the cell wall. By exerting a contractile force, the Z ring can potentially influence the direction of new cell wall growth, resulting in an inward invagination (92). It is possible to use equation 4 to estimate the forces exerted by the Z ring. Computations show that the force exerted by the Z ring can be small, between a few pN in E. coli to tens of pN in B. subtilis. Moreover, the exact value of the Z ring force is no longer critical. Instead, the growth rate and its dependence on the stress in the cell wall become important. Thus, the Z ring has an effect similar to those of other bacterial cytoskeletal proteins, MreB and crescentin. What is not clear is what triggers the force generation process in the Z ring. The Z ring appears in the cell for a large part of the life cycle but seems to contract only during the division phase. One possibility is that the Z ring continuously exerts a small contractile force, but without significant cell wall remodeling, the cell shape does not change. Only when PBPs (FtsI and others) are recruited during division can the cell wall remodel significantly. These possibilities are consistent with Jiang and Sun's model.

Other proteins.

Several other bacterial proteins, such as PBPs (126), RodA (11, 70), and RodZ (12, 60, 65, 131, 133), can also significantly affect bacterial morphology. These proteins probably serve as molecular links that connect the cytoskeleton and peptidoglycan and form protein complexes that catalyze and regulate the insertion and modification of the PG network. The depletion of these proteins might affect the reaction rate or insertion pattern of new PG growth or break the linkage between the bacterial cytoskeleton and cell wall. Thus, these proteins can influence cell shape as well. In our model, their roles can be studied by examining how parameters of the model depend on the function of these proteins.

Model shortcomings and connections with molecular-level biochemistry.

The model discussed here seems to be consistent with the morphological dynamics of the bacterial cell and sets up the general framework that links mechanical influences with PG synthesis activity. However, the model is by no means molecularly detailed. Such details can occur through the parameter M in equation 9. This parameter describes the kinetics of the PG addition and can depend on the spatial location of PG synthesis. If PG synthesis occurs in a nonuniform manner, for instance, during cell division, the cell shape would also change accordingly.

The model also assumes a uniform and structurally constant PG network. The mechanical properties of the cell wall are assumed to be isotropic. The molecular arrangements of the cell wall of E. coli appear to be locally anisotropic (63). However, the wall of B. subtilis has additional structural complexity (65). In addition, the PG layer may not maintain constant network geometry under all conditions, especially when the cell is close to lysis. Within the context of the model, this implies that the total free energy of the cell wall is more complex than what is expressed in equation 8.

Finally, the model assumes that the cell shape is governed by the energetics of the PG addition, which is satisfied only when the rate of PG turnover is relatively high. Alternatively, for the opposite limit, when the rates of PG addition and subtraction are low, the cell shape may be the result solely of kinetic effects. Mechanical forces are still important but only modify the rate of cell wall addition and subtraction. This limit is interesting but currently unexplored.

BACTERIAL CELL DIVISION AND DYNAMICS OF THE Z RING

In the previous section, we showed that forces can influence the shape of the bacterial cell wall, and bacterial cell division seems to require a contractile force. The contractile force is hypothesized to originate from a unique organelle, the FtsZ ring (Fig. 1). FtsZ is the primary component of the Z ring. FtsZ is a cytoplasmic protein and must interact with membrane-bound FtsA and ZipA to form the Z ring. After the formation of the daughter cell and the completion of replication, FtsZ colocalizes with FtsA/ZipA at the midcell, although ZipA is not essential for division to succeed (131). FtsZ in the ring exists in a polymer form and continuously turns over even when division has not begun (139).

There are several unanswered questions regarding the role of FtsZ and other cytoskeletal proteins in cell division. Why do FtsZ filaments concentrate in a ring? What regulates the ring width and determines the internal molecular structure? If the Z ring exerts contractile forces, what is the molecular mechanism generating the force? These questions can be addressed only if the physical properties of FtsZ are understood.

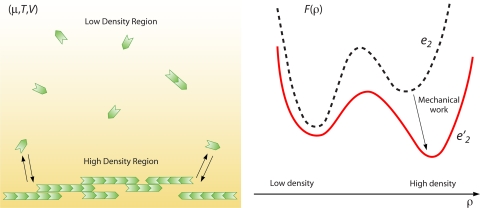
From a physical perspective, the spatial variation of protein assemblies suggests a phase transition between a disordered low-density phase to a more ordered high-density phase, in analogy with liquid gas transitions of everyday experience (130). A phase transition of the first order is the result of a competition between the entropic freedom of the low-density configuration and the enthalpic bonding of the high-density phase. In order to quantitatively understand the behavior of FtsZ in the cell, parameters such as the interaction free energy between FtsZ monomers, the interaction energy of FtsZ with other cellular proteins and the membrane, and the cytoplasmic concentration of FtsZ are needed.

Cooperative Assembly of FtsZ

Under typical cellular concentrations, FtsZ alone can form polymers and bundles. The length of the polymer and the number of filaments in the bundle are controlled by the free energies of forming longitudinal and lateral FtsZ-FtsZ bonds and the concentration of available monomers in the medium. Depending on the quantitative values of the longitudinal and lateral bond energies and the monomer concentration, FtsZ can take on diverse forms. The cell takes advantage of this rich behavior by manipulating all 3 variables. The cytoplasmic concentration of FtsZ seems to be around 2 to 5 μM (103, 131) and is set via an unknown mechanism. Several proteins are known to change the longitudinal and lateral bond energies of FtsZ: MinC is a negative regulator of FtsZ and decreases the favorable energies of both lateral and longitudinal bonds (39). Several other proteins seem to either enhance or diminish the propensity of FtsZ to form polymers and bundles, although these influences have not been quantified. Thus, to understand the bewildering forms of FtsZ, a quantitative polymerization model is necessary.

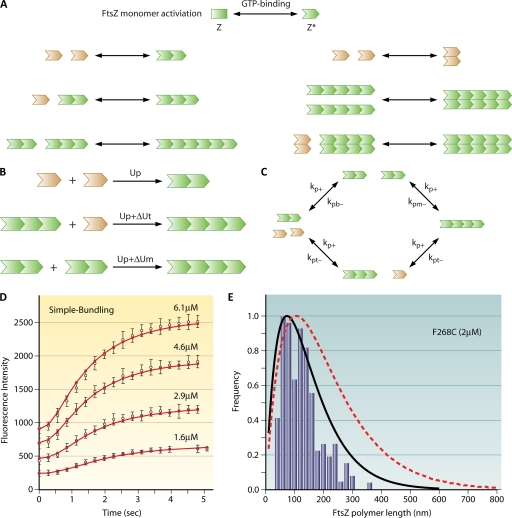
To decipher the polymerization mechanism of FtsZ, a series of investigations was carried out on FtsZ polymerization kinetics (26, 29–31, 53, 68, 115, 120). Using a fluorescence resonance energy transfer (FRET) assay, Gonzalez et al. and Oliva et al. measured FtsZ polymer formation in different buffers and at different concentrations (68, 120), and Chen et al. quantified the FtsZ filament length distribution (29). A puzzle in FtsZ assembly is that the polymer is initially assembled as a single strand (isodesmic), but the overall kinetics are cooperative. A critical concentration of the FtsZ monomer is needed to trigger polymer formation. To explain the observed cooperativity, Chen et al. proposed an actin-like 2-stranded model (30), which neglects the possibility of single filaments completely. Moreover, the model does not include filament bundles with more than 2 filaments, which are observed in abundance at higher concentrations. To model the kinetics of FtsZ polymerization and bundling more accurately, Lan et al. developed a more realistic set of kinetic models (90). The models are successful in explaining the cooperativity in FtsZ assembly, including lateral and longitudinal bond formation, and consider polymer fragmentation and annealing (Fig. 8). Due to the complexity of FtsZ polymerization mechanisms, Lan et al. introduced 3 related models, representing 3 limits of FtsZ kinetics. The essential features of these models are summarized in Fig. 8.

Fig. 8.

FtsZ assembly model. (Adapted from reference 90 with permission of Elsevier.) (A) FtsZ filaments are unstable. A kinetic model of FtsZ polymerization must consider filament breakage and annealing. The model described by Lan et al. (90) includes the formation of FtsZ bundles through favorable lateral bundling interactions as well as filament breakage. GTP hydrolysis is implicitly included in the breakage of filaments. (B) The model considers 3 types of polymer bonds with bond energies U_p, U_p + ΔU_t, and U_p + ΔU_m. (C) The rate constants for forming FtsZ polymer bonds are not independent (see reference 152 for details). (D) The model is able to explain the short-time polymerization data described by Chen et al. (30). (E) The model also explains the equilibrium FtsZ filament length distribution data (bars). The bundling interaction is important for the length distribution (black solid line). If the bundling interaction is neglected, the obtained length distribution disagrees with the experiment (red dashed line [31]).

Measurements of filament formation show that there is a noticeable lag time before FtsZ starts to polymerize, implying that FtsZ monomers go through several relatively slow activation steps before polymer formation. Before the addition of GTP, FtsZ is in the inactive monomer state, denoted as Z. After GTP is added (time zero), FtsZ binds GTP and becomes the activated monomer (Z*). Note that the activation step modeled effectively includes several steps and can include GTP turnover. To reduce complexity, these steps were modeled as a single step with an effective rate constant. After FtsZ monomers reach the activated Z* state, they can interact with each other longitudinally and laterally to form polymers and bundles. In order to quantitatively explain the kinetic data, Lan et al. postulated that the longitudinal interaction (polymer bond energy) varies depending on the position of the monomer in the filament (Fig. 8) (90). This implies that FtsZ can form three kinds of longitudinal bonds, depending on whether it has formed bonds at one or both longitudinal interfaces. Monomers forming a dimer bond have an energy, U_p; a monomer at the end of a filament has an energy, U_p + ΔU_t; and bonds in the middle of a filament have an energy, U_p + ΔU_m. This assumption implies that the equilibrium constants for the formation of these bonds are different. However, due to energy conservation, kinetic rate constants are not independent. Figure 8C shows two different pathways that form a filament with 4 subunits. Lan et al. were able to show that cooperativity could arise from continuous fragmentation and annealing of single filaments and is entropic in origin. The model estimates the bond energies between monomers and shows that a weak lateral bond exists, which stabilizes long filament bundles. The model can explain the available length distributions of filaments and compute the critical concentration. GTP hydrolysis is not explicitly contained in the model. However, immediately following GTP hydrolysis, FtsZ breaks its longitudinal bonds; thus, the obtained filament breakage rate implicitly describes the GTP hydrolysis activity. An interesting outcome of the model is that filament breakage also proceeds without GTP hydrolysis, although the rate of bond breakage is significantly lower.

Modeling of Z Ring Dynamics In Vivo

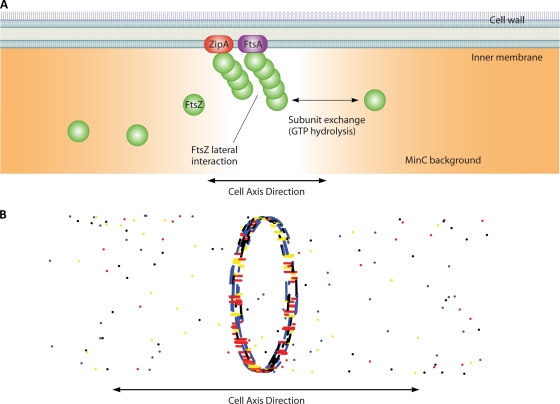
The predictions of the FtsZ polymerization model have important consequences for the Z ring in vivo. In the cell, FtsZ is at a concentration of roughly 5 μM, which implies that there are substantial amounts of short, single FtsZ filaments in the cytoplasm. On the inner membrane of the cell, FtsZ interacts with a number of proteins that seem to regulate the longitudinal and lateral bond energies of FtsZ. In E. coli, MinC forms a spatiotemporal gradient and seems to lower the longitudinal as well as the lateral bond energies (39). The result is that the formation of filaments with more than a few units is energetically favorable only near the midcell. The DNA binding proteins SlmA of E. coli (15) and Noc of B. subtilis (172) also regulate FtsZ ring formation, although cells lacking Min and SlmA/Noc also seem to form stable rings (90, 172). During Z ring formation, FtsZ binds membrane-bound FtsA, which anchors long filaments onto the membrane. Furthermore, long filaments are favored to bundle together. These factors drive the spontaneous colocalization of FtsZ-FtsA-ZipA at the midcell.

Modeling studies using realistic FtsZ interaction energies show that the nascent Z ring is made of short filaments in both the cell axis and the circumferential directions (Fig. 9) (91). The localization of FtsZ to the Z ring competes with the entropy of free FtsZ in the cytoplasm. To properly account for the entropic effect, the model must simultaneously compute the membrane domain and the cytoplasmic domain, allowing monomers to freely exchange between the domains. The procedure was outlined previously by Lan et al. (see the supplemental material in reference 91). All of the available FtsZ particles are simulated in two compartments. Compartment 1 represents the cellular cytoplasm, and compartment 2 represents the membrane surface near the site of the Z ring. The particles are free to exchange between compartments according to the change in the bond energies between FtsZ particles. Monomers are also free to diffuse in both compartments. The longitudinal bond energy, e₁, and the lateral bond energy, e₂, are interpreted as bond enthalpies. The entropic contribution to the free energy is accounted for by allowing FtsZ to diffuse in the cytoplasm.

Fig. 9.

Z ring formation. (A) The polymerization dynamics of FtsZ have direct implications for Z ring formation in vivo. The MinC background gradient (orange) and NOC lower the polymer bond energy of FtsZ and abolish lateral interactions completely. FtsZ also favorably interacts with membrane-bound ZipA and FtsA. Thus, long filaments are stable only in the midcell region. (B) Simulations show that the Z ring forms with a spontaneous colocalization of FtsZ and ZipA/FtsA. The nascent ring is disordered, with many short filaments in the cell axis direction instead of the circumferential direction. However, through exchange with the cytoplasm, the ring remodels to reach a configuration where most filaments are oriented in the circumferential direction.

Modeling and simulation studies show that the formed ring is disordered, and the density of FtsZ in the ring is governed by the lateral bundling energy between FtsZ particles and the binding energy between FtsZ and FtsA/ZipA. The effects of MinC and SlmA are accounted for by the introduction of a region near the midcell where the FtsZ interaction is the most favorable. Simulations show that under these assumptions, FtsZ spontaneously colocalizes with FtsA/ZipA, forming a relatively dense region at the midcell. Modeling also predicts that the turnover of FtsZ monomers is a natural outcome of fluctuations in the filament configuration: since the bonds are unstable, continuous breakage and reformation of FtsZ filaments are common. This turnover is sped up by GTP hydrolysis (see above). The turnover process also remodels the Z ring, making filaments more aligned in the circumferential direction, although the ring is generally not a continuous bundle wrapping around the cell circumference.

The model of Lan et al., however, did not include a number of potentially important factors in Z ring assembly. The mechanical deformation of FtsZ or the membrane was not considered. These deformations have small energies but can sum up to be significant (see the next section). Lan et al. also did not consider the kinetics of FtsZ turnover or GTP hydrolysis, although the rate of FtsZ turnover appears to be relatively high compared with the rate of division (139). The kinetics of Z ring assembly can be coupled to mechanics, as described in the introduction. There is potentially a rich set of phenomena that has not been explored.

Mechanical Properties of FtsZ

In addition to FtsZ formation kinetics, the polymer itself possesses material properties that are important for scaffolding and force generation in the Z ring. FtsZ polymers have bending rigidity, which is typically quantified as a persistence length, l_p. Furthermore, FtsZ filaments may be intrinsically curved, implying that the energetically favorable FtsZ conformation may be a bent conformation. The mechanical energy of a filament with a varying curvature, c(s), can be quantified by using the following expression:

$$E={\displaystyle {\int }_0^l\frac{1}{2}{k}_{B}T{l}_p{\left[c\left(s\right)-c_0\right]}^{2}ds}$$ (12)

where the integration is over the arc length, s, of the filament and k_BT is the Boltzmann constant times the room temperature; k_BTl_p is equivalent to the bending modulus of the filament (equal to YI in mechanical languages, where Y is Young's modulus of the filament and I is the moment of inertia) (20). c(s) is the curvature of the filament as a function of the arc length, and c₀ is the preferred or intrinsic curvature. When there are no external forces on the filament, mechanical equilibrium is obtained when c(s) = c₀. The mechanical energy expression in equation 9 can be derived by using an isotropic linear elastic model. The filament is modeled as a slender rod with a bending modulus, k_BTl_p. Only bending deformations are considered, and a twisting of the filament is ignored. Models such as equation 12 have been used to describe biofilaments such as DNA, actin, and microtubules.

For soft biofilaments at length scales of nanometers, thermal fluctuations are important, which can result in filament curvatures that are different from the preferred curvature. Indeed, the amplitude of curvature fluctuations depends on the filament bending modulus. Therefore, one can obtain an estimate of the bending modulus by examining a probability distribution of filament curvatures in an experiment. The curvature distributions can be compared to the Boltzmann distribution prediction, $P=\left[c\left(s\right)\right]\alpha e^{-E\left[c\left(s\right)\right]/k_{B}T}$, to obtain an estimate for the bending modulus.

The persistence length of FtsZ has been estimated in this way by examining electron microscopy images of FtsZ filaments at low-monomer concentrations (39). By assuming that the intrinsic curvature is zero, the estimate was an l_p of ∼180 nm. Other measurements using atomic force microscopy of FtsZ on surfaces have also been made (73, 74, 102, 117). However, all of these measurements can potentially have artifacts, especially if the preferred curvature of FtsZ, c₀ in equation 9, is perhaps nonzero. Alternatively, another estimate of the FtsZ persistence length is obtained if the filaments are treated as materially similar to microtubule protofilaments. The persistence length of the eukaryotic microtubule has been measured (169). By treating the microtubule as a hollow tube, Young's modulus of the microtubule can be computed. When Young's modulus is used to estimate the persistence length of protofilaments, one obtains an estimate of an l_p of ∼2 μm (3). The assumption made implicitly is that the microtubule is made of isotropic elastic material. It is an open question whether an isotropic mechanical estimate using Young's modulus is appropriate for complex protein filaments. Alternatively, a microtubule should be considered a bundle of protofilaments cross-linked by strong lateral bonds. The relationship between the persistence length of the protofilament and the persistence of the bundle is not straightforward and depends strongly on the number of protofilaments and the strength and geometry of cross-links (8). Therefore, the persistence length of FtsZ filaments is an open question and needs to be measured independently.

The mechanical property of FtsZ becomes important when considering that the geometry of FtsZ filaments is perhaps dynamic. It is possible that FtsZ filaments can change the preferred curvature, c₀, during GTP hydrolysis (3, 51, 52, 102). Filaments filled with GTP-FtsZ appear to be straight (no curvature) or at most have a slight curvature (radius of greater than a few hundred nanometers), implying that c₀ is ∼0 for GTP-FtsZ in equation 9. GDP-FtsZ filaments are perhaps more curved, although the evidence for this is currently still sparse. Possible curvature changes in FtsZ can lead to the generation of forces. This mechanism is discussed below in “Force generation through FtsZ curvature change.”

The geometry of FtsZ filaments has other consequences for Z ring organization, which are currently unexplored. For example, in order for the binding of FtsZ to the membrane through FtsA to occur, curvatures of the membrane and the FtsZ filament should approximately match. Otherwise, mechanical strains will result in the membrane and the FtsZ filaments. The favorable binding free energy can compensate for part of the mechanical strain. It is possible to estimate the relative probability of FtsZ orienting in the circumferential versus the cell axis directions. In the cell, the E. coli membrane has a radius of curvature of ∼500 nm in the circumferential direction and is approximately flat in the cell axis direction. FtsZ is also ∼10 to 100 nm in length. Thus, a curved FtsZ filament would prefer to align in the circumferential direction, whereas a straight FtsZ filament would align in the cell axis direction. The persistence length of the filament and bending rigidity of the membrane would determine the orientational probability. For 50-nm straight filaments, simple estimates show that the energy difference per filament between the cell axis direction and the circumferential direction is less than 0.1k_BT. However, for many filaments in bundles, a macroscopic order could emerge.

The cell membrane can also introduce long-range mechanical coupling between membrane proteins. If the FtsZ filaments were curved, then binding to the flexible membrane would introduce local curvature in the membrane. The characteristic size, R, of the curved region is governed by the bending constant, κ, and surface tension, γ, of the membrane: $R\sim \sqrt{\kappa /2\gamma }$. When two such curved regions are within distances of approximately R of each other, the curved membrane can mechanically interact, and it is favorable for the curved regions to merge (134). The merging of curved membrane regions can drive the colocalization of FtsZ filaments in the ring region. Indeed, the merging of FtsZ rings in vitro has been observed (121, 122). In the cell, the inner membrane properties are less clear. The anchoring of the membrane to the cell wall and the linkage between FtsZ and the membrane can also introduce additional mechanical influences. Combined with the uncertain geometry of the filament, a quantitative assessment of this mechanism is not currently available.

Additional factors also influence the alignment of FtsZ filaments. If the filaments interact laterally, then it is favorable to form long bundles of filaments. However, MinC lowers the longitudinal bond energies substantially and removes lateral interactions completely. The Z ring region is also likely to be quite narrow, ∼100 nm. Superresolution imaging of the FtsZ ring shows that the ring width is ∼120 nm before and during division (62). Thus, long FtsZ bundles can form only in the longitudinal direction. From modeling studies, it has been observed that the initially disordered ring has a large number of short filaments in the cell axis direction, but over time, it remodels to longer filaments in the circumferential direction. These predictions await experimental scrutiny.

There are still a number of physical properties of the Z ring that are still unexplained. The width of the Z ring is partially regulated by MinC, which lowers the FtsZ polymer bond energy. Nucleoid occlusion (NOC) also plays a role. ΔMinC cells do not have substantially wider rings (36, 142, 179). Instead, additional Z rings form at the cell poles. In cells overexpressing FtsZ, the rings do not become wider but appear to become unstable, developing spiral-like structures. The overexpression of FtsA also results in spirals. These structures could arise due to physical interactions between FtsZ/FtsA filaments and other cytoskeletal structures in the cell, and the exact origins are still mysterious.

Z Ring Force Generation Mechanisms

Force generation through FtsZ curvature change.

A number of physical mechanisms have been proposed for Z ring contraction. Early on, FtsZ was recognized as a tubulin homologue, and a tubulin-like mechanism was proposed for the Z ring, where GTP-FtsZ changes conformation (filament curvature) upon hydrolyzing GTP (53). Electron micrographs of GDP-FtsZ under certain conditions indeed show substantially curved filaments (73, 102, 117). As discussed in “Mechanical Properties of Extended Structures Can Lead to Novel Mechanisms,” a conformational change can exert a contractile force. A crude estimate can be obtained by using a mean field approximation where the curvature of the FtsZ bundle is proportional to the population of GDP-FtsZ in the ring (3, 91). The total energy of a bundle of n filaments attached to a substrate with a background curvature of R₀ is then as follows:

$$E=\frac{1}{2}n\langle L\rangle l_p{k}_{B}T{\left[\overline{c}-\frac{1}{R_0}\right]}^2$$ (13)

where 〈L〉 is the average length of the filament, k_BT equals 4.2 pN nm, and l_p is the persistence length of the FtsZ filament. c̄ is the average curvature of the bundle. The mean field approximation leads to $\overline{c}=x\cdot c\left(\text{GPT}\right)+\left(1-X\right)\cdot c\left(\text{GDP}\right)$, where c(GTP) and c(GDP) are the two possible preferred curvatures of the FtsZ filament and x is the fraction of GTP-FtsZ. From EM images, we estimate that c(GTP) is ∼0 and c(GDP) is ∼0.1 nm⁻¹. At the beginning of the Z ring contraction, R₀ equals 500 nm. From simulations, n is roughly 90, and 〈L〉 is ∼120 nm (91). Equation 13 is derived from equation 12 by assuming a constant curvature along the filament. From equation 13, the contractile force from the ring with radius R₀ is computed by taking the derivative of the energy with respect to the radius:

$$f=-\frac{\partial E}{\partial R_0}=n\langle L\rangle k_{B}T{l}_p\left[\frac{1}{R_0}-\overline{c}\right]\frac{1}{R_0^2}$$ (14)

From the parameter estimates, we see that the magnitude of the contractile force will depend critically on the stiffness of the FtsZ filaments or the value of l_p. A soft rope cannot exert significant contractile forces. An upper bound estimate of the force from a ring of FtsZ filaments was discussed previously, and it was shown that the force depends on the number of FtsZ filaments in the ring and the bending stiffness of the filaments (91). Using an estimated persistence length of ∼180 nm and the estimated physiological number of FtsZ filaments in the ring, the contraction force is less than 3 pN.

The mean field estimate of equation 13 is also unlikely to be correct when the cooperative aspects of FtsZ conformational changes are considered. For FtsZ, all the ingredients of a similar catastrophe are present. Thus, the conversion from a predominately straight GTP-FtsZ ring to a predominately GDP-FtsZ ring should be catastrophic, mediated by the lateral bundle interaction. A catastrophic conversion process would exert an impulse force over a short time interval. This is not favorable to Z ring contractions because the cell wall grows slowly. Only a persistent force exerted over long periods can significantly influence the growth dynamics of the wall (see Dynamics). It is possible that the mechanical resistance from the cell wall can prevent a rapid conversion of GTP-FtsZ. Thus, a mechanism based on FtsZ conformational changes is quite complex and requires a full-scale modeling approach where mechanics and the GTP conversion process are considered together.

Osawa et al. sought to reduce the complexity of the Z ring problem and developed an in vitro Z ring system (121, 122). They attached an amphiphilic helix to the C-terminal domain of FtsZ. This FtsZ isoform, after labeling with green fluorescent protein (GFP), was able to insert itself directly into the lipid bilayer. By mixing this mutant FtsZ with tubular lipid vesicles, Osawa et al. found that rings of FtsZ formed in the vesicles (122). The rings were narrow and appeared similar to the Z ring in vivo. Occasionally, the rings would coalesce, and a visible contraction of the tubular vesicles occurred. The contraction proceeds in a GTP-dependent manner, which demonstrates that the hydrolysis-driven conformational change can be a driving force for contraction. It is important to also recognize that peptides inserted into membranes can often change the membrane spontaneous curvature. The observation of membrane curvature changes upon a direct FtsZ insertion is not direct proof of FtsZ force generation. Also, from equation 13, we observe that the contraction force is proportional to the number of FtsZ filaments in the ring. This is supported by the observation that the rings did not begin to contract until several nascent rings had coalesced into a larger one. In vitro, the number of FtsZ filaments (or the concentration of FtsZ) in the lipid vesicle is not controlled and has not been measured. It is possible that the number of FtsZ filaments in the ring in vitro is much higher than that in vivo. When there is a sufficient number of FtsZ filaments, soft filaments can exert significant forces by bending. In vivo, there are approximately 2,500 FtsZ filaments in the ring. If the persistence length of FtsZ filaments is ∼180 nm, equation 13 suggests that the exerted force is quite small. Furthermore, mutants of FtsZ where GTP hydrolysis activity was abolished have been isolated (38, 116). These cells continued to divide using the Z ring. Alternative GTP-independent mechanisms of Z ring force generation must be considered to explain division in vivo.

Force generation through FtsZ condensation.

GTP-hydrolysis-driven conformational change cannot be the sole mechanism of contraction. As we mentioned above, mutants containing FtsZ that has no appreciable GTPase activity are viable, and cell division still proceeds (38, 116). It is possible that several mechanisms are contributing to the overall contractile process (66). In addition to a possible mechanical role of FtsZ in conformational changes, the collective behavior of an ensemble of FtsZ can also generate forces. As discussed in “Modeling of Z Ring Dynamics In Vivo,” Z ring formation and colocalization with FtsA/ZipA have strong connections with phase transition concepts in physics. Because FtsZ monomers interact with each other both longitudinally and laterally, it is enthalpically favorable for FtsZ to colocalize and form a high-density region. Entropy, however, opposes this process. It is entropically favorable to distribute FtsZ throughout the available space, giving a relatively uniform distribution. As the FtsZ concentration increases, the enthalpic component begins to dominate, and just as water vapor will become condensed liquid as the vapor pressure increases, FtsZ will condense and form high-density regions. The details of the phase behavior depend on parameters such as the magnitude of favorable binding interactions between FtsZ filaments, the concentration of cytoplasmic FtsZ, and the interaction energy between FtsZ and other proteins.

To illustrate the influence of these variables, let us consider the simpler problem of Lennard-Jones (LJ) fluid. The fluid particles have a physical size characterized by the length scale r₀. The particles also attract each other through van der Waals forces, characterized by the energy scale e₀. These two ingredients are sufficient to generate complex material behavior such as liquid and solid phases, interfaces, and critical phenomena. From statistical mechanics, the phase behavior of LJ fluid can be completely described by its free energy as a function of fixed parameters such as temperature, pressure, and chemical potential. An excellent model for LJ fluid is the van der Waals model, which is the basis for the van der Waals equation of state for all attractive fluids (130). The model writes the grand canonical free energy of the fluid at constant volume, V; temperature, T; and chemical potential, μ, as follows:

$$F\left(T,V,\mu \right)={\displaystyle \int \left[k_B{T}_{\rho \text{ln}}\frac{b\rho }{1-b\rho }-a{\rho }^2-\mu \rho \right]}dV$$ (15)

where ρ = N/V is the density of the fluid as a function of space. Notice that the spatial density does not have to be homogeneous; i.e., ρ(r) can be a function of space. (a,b) are parameters characterizing the attractive and repulsive interactions of the fluid; b is related to the molecular size r₀, and a is related to the energy scale e₀. The first term in the integral describes the entropic free energy of particles of volume b, which favors low densities. The second term describes the enthalpic contribution of particle attraction, which favors high densities. The last term is the chemical potential contribution that is set by the ambient particle density. From this free energy, it is possible to compute the pressure of the fluid and the equation of state, although it does not quantitatively reproduce spatial correlations between particles. In the form presented in equation 15, it also does not describe interfaces between difference phases. Nevertheless, the van der Waals model qualitatively reproduces the universal behavior of attractive fluids. Now, imagine that the volume of the fluid is allowed to vary, and the fluid particles are physically attached to the walls of the container. In this situation, the system will establish an equilibrium density that minimizes the free energy. If parameters such as a, b, and μ are changed, then the system will adjust and establish a new particle density. In the process of establishing the new density, the system can perform work by pulling on the walls of the container (Fig. 10). The energy source of this work derives from the energy of changing the parameters a, b, and μ.

Fig. 10.

The spatial distribution of FtsZ is a result of competition between entropic and enthalpic factors. Favorable interactions between FtsZ filaments contribute to the generation of high-density FtsZ regions. The cell can actively regulate FtsZ interactions using MinC and other division proteins. The spatial behavior of FtsZ can be understood by using a van der Waals picture (equation 15), where low-density and high-density FtsZ are both stable. The relative stability is regulated by the lateral interaction energy, e₂. Mechanical work can be generated by lowering e₂ and, in the process, developing contractile force.

To study this problem microscopically, simple computer simulations can be used to study LJ fluid. A textbook example is the lattice-gas model, which partitions space into boxes (Fig. 11). Each lattice position can be occupied or filled with a fluid particle. This model has all the essential behaviors of LJ fluid and can be readily explored on a personal computer. For the Z ring in the cell, due to the interaction of FtsZ with other proteins, the attractive interaction between FtsZ filaments varies with space. FtsZ is also not a structureless particle and forms longitudinal and lateral bonds. This implies that parameters such as a in equation 15 are related to bond energies e₁ and e₂ indirectly. Nevertheless, a lattice model is a powerful approach where these complexities can be explored fully. Lan et al. developed a lattice model to investigate the Z ring system using realistic bond parameters (91). The results show that in addition to the conformational change mechanism, lateral attraction between FtsZ polymers can also generate contractile forces. Effectively, the cell is actively regulating the parameters a and μ (b cannot be changed because the size of the FtsZ particle is fixed). By lowering the attractive parameter a, the Z ring generates mechanical work and a contractile force.

Fig. 11.

A lattice model of the FtsZ ring can be used to investigate Z ring phase behavior. The cellular space is partitioned into a membrane region (left) and a cytoplasmic region (not shown). The membrane region also includes FtsA and ZipA, which can bind to FtsZ. In the cytoplasmic region, FtsZ particles are allowed to interact with each other as well as to translate and rotate. The cytoplasmic simulation is necessary to properly account for FtsZ translational and rotational entropy. When the lateral interaction is lowered, FtsZ in the ring undergoes a condensation transition, and the ring contracts (right).

To form a ring, most of the FtsZ filaments must align and extend in the hoop direction at the division site. The lattice model of Lan et al. explains this from an energetic point of view (91). The longitudinal (polymer) bond energy, e₁ ∼ −17k_BT, is much larger than the lateral bond energy, e₂ ∼ −0.2k_BT. The system initially has many short filaments oriented randomly, but as the system evolves toward a steady state, 90% of the filaments eventually become oriented in the hoop direction. Simulations of the lattice model show that ∼2,500 FtsZ molecules and almost all FtsA plus ZipA molecules occupy ∼30% of the membrane area in the low-MinC region. In many places, there are empty voids, and the ring is not fully connected around the cell circumference. However, the ring is dynamic, and filaments constantly fluctuate. At steady state, there is a continuous exchange of FtsZ between the ring and the cytoplasm, in agreement with previous fluorescence recovery after photobleaching (FRAP) study results (139). There are ∼90 filaments in the ring, with lengths of between 15 and 450 nm. The average length is 127 nm.

If the lateral interaction is lowered even further from −0.2k_BT, the ring spontaneously undergoes a transition from the initial low-density state toward a high-density state. Now, attractions between FtsZ filaments are able to outcompete entropic effects, and the density in the ring increases. A priori, the FtsZ density could increase by either increasing the number of FtsZ monomers in the Z ring or decreasing the area where the ring resides by decreasing the ring radius. The ring radius can decrease via the action of PBP3 and peptidoglycan synthesis proteins that modify the cell wall. In a simulation, Lan et al. allowed the radius of the midcell to fluctuate and computed the acceptance of the radius change by using the Metropolis criterion (91). The results unambiguously showed that the FtsZ density increase is achieved by decreasing the cell radius, and the number of FtsZ monomers in the ring was nearly constant (91). The FtsZ density increases by Z ring contraction and not by recruiting more FtsZ monomers.

A number of mechanisms can regulate the lateral interaction energy between FtsZ particles. The binding of other division proteins can change the lateral interaction energy. ZapA is known to increase the bundling activity of FtsZ (40, 42, 100). By regulating the degree of lateral attraction between FtsZ particles using accessory proteins, perhaps the cell can regulate the timing of cell division.

It is possible to compute the contractile force and the free energy of the Z ring as a function of the ring radius and lateral contact energy by using the lattice model. From statistical mechanics, the contractile force is the derivative of the free energy with respect to the radius (37):

$$f=-\frac{\partial F}{\partial R_0}$$ (16)

Simulations show that the computed Z ring free energy decreases linearly from a cell radius of 500 nm to ∼250 nm. The percentage of FtsZ occupancy in the low-MinC midcell region increases from ∼30% to ∼60%. The contractile force, which is the slope of the free energy versus the radius, shows a proportional relationship with the lateral contact energy, increasing linearly from 5 pN at e₂ = −1.0k_BT to 20 pN at e₂ = −4k_BT. These forces are consistent with estimated values for accomplishing cytokinesis in E. coli. For B. subtilis, the cell wall is stiffer, and a larger contractile force is needed. Computation shows that 50 pN of force can be achieved by lowering e₂ further to −9k_BT, which is still significantly lower than e₁. To show that lateral interactions between FtsZ filaments drive contraction, the number of lateral bonds increases during contraction. The number of polymer bonds, however, is constant. The model results are in agreement with quantitative microscopy results. In essence, the cell can control the microscopic-phase behavior for the Z ring, and the condensation of FtsZ filaments can drive bacterial cytokinesis.

CONCLUSIONS AND PERSPECTIVES

Organisms take advantage of physical interactions between gene products to achieve biological function. In vivo, these interactions are typically complex and cannot be easily and quantitatively deciphered. For bacterial cell division and morphogenesis, progress is being made in developing a physical and quantitative understanding of these physical interactions. We have shown that mechanical forces can influence chemical reactions and, in particular, the molecular chemistry of the building of a new cell wall. The combined influences of forces and chemical assembly result in the observed shape of the cell. We also discussed the physical properties of FtsZ and how these properties can contribute to the scaffolding and force generation roles of the Z ring. We highlighted two possible force generation mechanisms: conformational-change-driven contraction and lateral-interaction-driven condensation. The viabilities of these mechanisms depend on the quantitative details of the cell and the molecular properties of FtsZ. These mechanisms also reveal the diversity of strategies which biological organisms can utilize to generate forces and accomplish cellular tasks. It is possible that conformational changes of FtsZ and the phase behavior of the Z ring are simultaneously contributing to the contractile force of the Z ring, giving rise to the robustness and redundancy necessary for successful division in a variety of environments.

The topics discussed in this paper have implications for other cells and organisms. For example, mechanical forces can have similar important roles in shaping yeast and plant cells, which all have growing cell walls. Mechanical forces are also implicated in the development of eukaryotic organs and tissues and the patterning of developing embryos (135). The role of lateral interactions between FtsZ particles also has corresponding implications for eukaryotic cells. Cytoskeletal filaments such as F-actin do not form bundles directly. However, there is a large group of bundling proteins that bind to actin filaments. These bundling proteins generate structures such as filopodia, lamellipodia, and actin stress fibers and are directly implicated in the mechanical properties of F-actin networks and cell motility. Thus, eukaryotic cells directly regulate the bundling and cross-linking activities of cytoskeletal filaments and indirectly regulate the phase behavior of the F-actin network. By varying the concentrations of bundling proteins, the cell generates regions of different actin densities. In the process, mechanical forces and work can be performed. In Dictyostelium discoidium, cell division does not require myosin to actively generate forces. Instead, actin cross-linking proteins are recruited to generate contraction (145, 168). Thus, similar mechanisms of force generation are at play during division in eukaryotic cells.

FtsZ is also a direct analogue of tubulin. Thus, a number of tubulin- and microtubule-related phenomena is possible in bacterial cells. We mentioned the possibility of a catastrophic conformation change in FtsZ bundles, similar to microtubule growth instability. Other microtubule-related functions, such as transport motors, could also exist in bacteria, although no ATP-driven transport motors have been identified in bacteria. FtsA is an FtsZ binding ATPase whose function is still currently mysterious.

The biological phenomena discussed in this paper also pose challenges for physicists to develop more precise and quantitative descriptions for complex biological materials such as the cell wall and the cytoskeleton network. For the cell wall, for example, the best estimate that we have for the constitutive relationship is that of a linear elastic material. From examining the molecular structure of the cell wall, it is clear that the linear elastic approximation is inadequate. More sophisticated models that relate molecular-level structure and dynamics to macroscopic shape changes are necessary. We sketched a simple theory for the cell wall, but quantitative comparisons with experiments will require better descriptions. For cytoskeleton filaments such as FtsZ, F-actin, and microtubules, the relationship among molecular-level events such as cross-linking, treadmilling, and cellular behavior still awaits further theoretical explanation.

Biographies

Sean X. Sun received his Ph.D. in theoretical chemistry from the University of California, Berkeley, where he studied chemical reaction dynamics and chemical physics of liquid systems. Dr. Sun is currently an associate professor in the department of Mechanical Engineering at the Johns Hopkins University, where he studies the fundamental role of mechanical forces in regulating biological function. He is interested in growth and morphology of cells, tissues, and organisms in eukaryotes as well as prokaryotes.

Hongyuan Jiang received his Ph.D. in Solid Mechanics from Brown University in 2009, where he studied lipid sorting in multicomponent membranes and the synchronization phenomenon in viscous fluid. Dr. Jiang is currently a postdoctoral research associate in the laboratory of Sean X. Sun in the department of Mechanical Engineering at Johns Hopkins University, where he studies the growth and morphology of bacterial cells and mechanochemical modeling in biology.