Atomic resolution dynamics on the surface of amyloid β protofibrils probed by solution NMR

Abstract

Exchange dynamics between molecules free in solution and bound to the surface of a large supramolecular structure, a polymer, a membrane or solid support are important in many phenomena in biology and material science. Here we present a novel and generally applicable solution NMR technique, known as Dark-state Exchange Saturation Transfer (DEST), to probe such exchange phenomena with atomic resolution. This is illustrated by the exchange reaction between amyloid β (Aβ) monomers and polydisperse, NMR invisible ('dark') protofibrils, a process of significant interest since the accumulation of toxic, aggregated forms of Aβ, from small oligomers to very large assemblies, have been implicated in the etiology of Alzheimer's disease^1–6. The ¹⁵N-DEST experiment imprints with single residue resolution dynamic information on the protofibril-bound species in the form of 15N transverse relaxation rates (¹⁵N-R₂) and exchange kinetics between monomers and protofibrils onto the easily observed two-dimensional ¹H-¹⁵N correlation spectrum of the monomer. The exchanging species on the protofibril surface comprise an ensemble of sparsely-populated states where each residue is either tethered to (via other residues) or in direct contact with the surface. The first eight residues exist predominantly in a mobile tethered state`, while the largely hydrophobic central region and part of the C-terminal hydrophobic region are in direct contact with the protofibril surface for a significant proportion of the time. The C-terminal residues of both Aβ40 and Aβ42 display lower affinity for the protofibril surface indicating that they are likely to be surface exposed rather than buried as in structures of Aβ fibrils^7–10, and may therefore comprise the critical nucleus for fibril formation^11,12. The ${}^{15}\mathrm{N}-R_{\mathit{2}}^{\mathit{\text{tethered}}}$ values, however, are significantly larger for the C-terminal residues of Aβ42 than Aβ40 which may explain the former’s higher propensity for rapid aggregation and fibril formation^13,14.

We recently reported the existence of a dynamic exchange process under pseudo-equilibrium conditions between monomeric and very high molecular weight, soluble species of Aβ40¹⁵. The latter form spontaneously in concentrated (150–300 µM) unstirred aqueous solution, and comprise polydisperse, non-fibrillar aggregates typical of worm-like protofibrils (Fig. S1a). Similar protofibrils are formed by Aβ42 under the same conditions (Fig. S1b). These protofibrils, which we have characterized extensively by atomic force and electron microscopy (Fig. S1), analytical ultracentrifugation (Fig. S3) and dynamic light scattering (Fig. S4) are far too large (1.8–85 MDa) to detect directly using solution NMR spectroscopy as their resonances are broadened beyond detection¹⁵, and their heterogeneous nature makes biophysical characterization challenging^5,16–19. Both the Aβ40 and Aβ42 protofibrils present in the equilibrated concentrated samples react strongly with the OC polyclonal antibody that recognizes so-called "fibrillar" oligomers and fibrils³ (Fig. S6b); the A11 polyclonal antibody recognizes so-called "pre-fibrillar" oligomers³ and reacts with both Aβ40 and Aβ42 protofibrils, albeit weakly with the former (Fig. S6a). The predominantly unstructured, intrinsically disordered, monomeric Aβ peptides^20,21, however, give rise to excellent solution NMR spectra¹⁵ (Fig. S7), and analytical ultracentrifugation indicates unambiguously that the NMR visible species is monomeric, and that there are no measurable quantities of low molecular weight oligomers present in either the dilute (Fig. S2) or concentrated (Fig. S5) samples. Indeed, in the concentrated samples containing monomer and protofibrils, there is no evidence by analytical ultracentrifugation of any species other than monomer and protofibrils with M_r in excess of 1.8 MDa (Figs. S4 and S5). In this work, we probe the protofibril-bound species at a residue-by-residue level using ¹⁵N-DEST, a novel two-dimensional transfer-of-saturation NMR experiment that exploits the exchange process between NMR invisible (‘dark state’) and easily observed monomeric states.

The essence of the 2D ¹⁵N-DEST experiment is based on the dramatic reduction in reorientational motions upon binding to the surface of the protofibrils resulting in transverse relaxation rates (¹⁵N-R₂) that are orders of magnitude larger than those of the free monomer. These large ¹⁵N-R₂ values preclude direct observation by solution NMR, but allow for efficient partial saturation of ¹⁵N longitudinal magnetization of the protofibril-bound form by a weak radiofrequency (RF) field, even at large offsets where the free monomer magnetization is completely unaffected. In the DEST experiment ¹⁵N longitudinal magnetization of the free monomer is prepared (refocused INEPT transfer), transferred by chemical exchange to the protofibril-bound form (binding), partially saturated (weak ¹⁵N saturation at a series of offsets), and transferred back to the free monomer (dissociation) where the partial saturation is recorded as an attenuation of the cross-peaks of the NMR observable free monomer relative to that in a reference spectrum obtained without saturation (see Full Methods and Fig. S8).

NMR measurements were made at 10°C, pH 6.8 using two concentrations of Aβ: a low concentration sample (50 µM) at which both Aβ40 and Aβ42 remain nearly entirely monomeric (>90%) for a long period of time (>2 months for Aβ40 and ~1 week for Aβ42) based on cross-peak intensities in a ¹H-¹⁵N heteronuclear single quantum coherence correlation (HSQC) spectrum; and a higher concentration sample in which the fraction of monomer decreases rapidly (over ~2 days for Aβ42 and ~1 week for Aβ40) after which a stable pseudo-equilibrium between monomer and protofibrils is maintained for more than a week¹⁵ (Fig. S9). The amount of protofibrils formed at a given initial concentration of Aβ is significantly higher for Aβ42 than Aβ40 (Fig. S9). Thus, for 270 µM Aβ40 and 160 µM Aβ42 samples, the concentration of monomer decreases to pseudo steady-state levels of ~110 and ~35 µM, respectively.

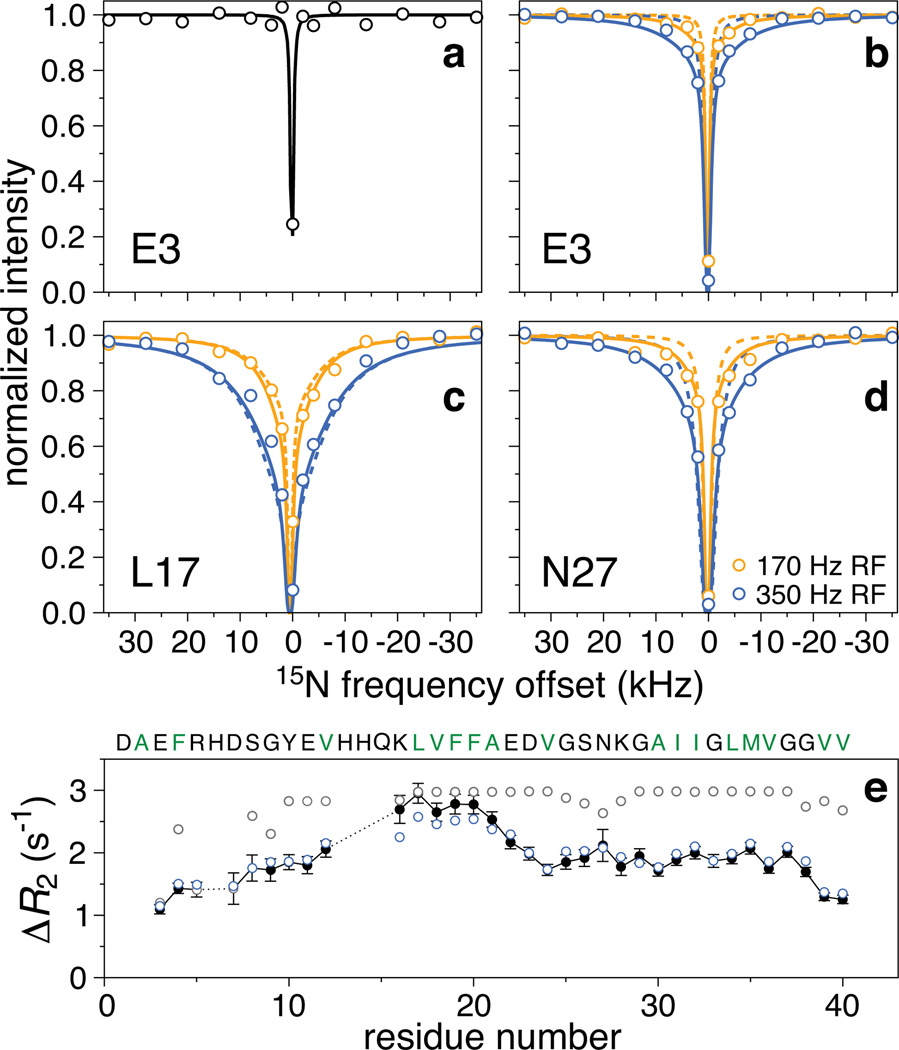
For the monomeric Aβ40 sample, the ¹H-¹⁵N cross-peaks in the DEST experiment display an extremely sharp saturation profile with no detectable attenuation for any residue until the saturation pulse is less than 2 kHz from the ¹⁵N resonance frequencies of the monomer (Fig. 1a, circles). This behavior, replicated for the monomeric Aβ42 sample, matches the predicted saturation profile for a ¹⁵N spin with relaxation parameters measured for the monomeric species (Fig. 1a, solid line). In contrast, the ¹H-¹⁵N cross-peaks in the 270 µM Aβ40 sample show significant partial saturation at offsets far from the monomer ¹⁵N resonances. Most importantly, the saturation profiles are clearly residue specific (Fig. 1b–d, circles). Relatively narrow profiles are observed for residues in the N-terminal region (Fig. 1b), very broad profiles for residues in the central (residues 17 to 21, e.g. Fig. 1c) and part of the C-terminal (residues 30 to 40) hydrophobic regions. Intermediate profiles are observed for residues in the hydrophilic region spanning residues 25 through 29 (Fig. 1d) as well as for the three C-terminal residues. Qualitatively similar behavior is observed for the 160 µM Aβ42 sample (Fig. S10a–d). The observed residue-specific saturation transfer profiles indicate that, when bound to the surface of the protofibrils, the average ¹⁵N-R₂ for each residue is highly sequence-position dependent.

Figure 1. ¹⁵N Dark-state exchange saturation transfer (DEST) and ΔR₂ for Aβ40.

Examples of normalized cross-peak intensities as a function of frequency offset from the ¹⁵N carrier (118.5 ppm): a, Glu-3 in the 50 µM Aβ40 sample (RF field strength of ¹⁵N saturation pulse = 170 Hz); b, c and d, Glu-3, Leu-17 and Asn-27, respectively, in the 270 µM Aβ40 sample with ¹⁵N saturation at RF field strengths of 170 (orange circles) and 350 (blue circles) Hz. The solid line in (a) is the calculated saturation profile for a ¹⁵N spin with the experimentally determined relaxation rates for monomeric Aβ40. The dashed and solid lines in (b)–(d) are the best-fits to an exchange model with a single protofibril-bound state (cf. Fig. 2a) and to a model incorporating residues tethered and in direct contact with the protofibril (cf. Fig. 2b), respectively. The s.d. of the DEST experimental data points is approximately equal to the size of the circles. e, Observed (black filled-in circles; error bars: 1 s.d.) versus calculated ΔR₂ values for the first (grey circles) and second (blue circles) models. The reduced χ² for the simultaneous best-fit to the DEST and ΔR₂ data is 9.0 for the first model and 1.8 for the second.

The ¹⁵N-DEST profiles can be quantitatively interpreted by incorporating a model of equilibrium chemical exchange within the framework of the McConnell equations^22,23. The simplest model describing the equilibrium between free monomer (M_monomer) and peptide transiently bound to the surface of the protofibril (M_oligomer) is a pseudo-first-order process characterized by global first order apparent association ($k_{\mathit{\text{on}}}^{\mathit{\text{app}}}$) and dissociation (k_off) rate constants (Fig. 2a) and residue-specific ¹⁵N-R₁ (longitudinal) and R₂ (transverse) values for the free monomer and protofibril-bound states. The value of the $k_{\mathit{\text{on}}}^{\mathit{\text{app}}}$ can be estimated from the difference, ΔR₂, in ¹⁵N-R₂ values between the samples with protofibrils present and the monomeric reference sample (50 µM)¹⁵. Since transverse magnetization for the protofibril-bound states decay extremely rapidly, the maximum observed ΔR₂ value, $\mathrm{\Delta }{R}_2^{\text{max}}$, is equal to $k_{\mathit{\text{on}}}^{\mathit{\text{app}}}$ under pseudo-equilibrium conditions (note that the observed ΔR₂ values are independent of nucleus and magnetic field¹⁵; see also Supplementary section 5 for a simple explanation of ΔR₂ and DEST experiments and their interpretation). The saturation profiles at two RF field strengths (170 and 350 Hz) and the ΔR₂ data for all residues (Fig. 1e for Aβ40 and Fig. S10e for Aβ42) were fit simultaneously optimizing the values of $k_{\mathit{\text{on}}}^{\mathit{\text{app}}}$ and k_off, and the residue specific ¹⁵N-R₂ values for the protofibril-bound species (see full Methods). The ¹⁵N-R₁ and R₂ values for the monomer were taken from relaxation data recorded on the low concentration (50 µM) sample. Although the ¹⁵N-R₁ values for the protofibril-bound state are unknown, these ¹⁵N-R₁ values have no effect on the fitted parameters within their uncertainties over the expected range (2 s⁻¹ ≥ ¹⁵N-R₁ ≥ 0.01 s⁻¹) due to the design of the experiment (see full Methods). The simple two-state model fails to account simultaneously for all the experimental data in the case of both Aβ40 (Fig 1b–e) and Aβ42 (Fig. S10), with systematic deviations for the DEST profiles (Figs. 1b–d, dashed lines) and failure to reproduce ΔR₂ as a function of sequence (Fig. 1e, grey open circles). Extension to a three-site exchange model that adds an intermediate species either on- or off-pathway, introducing additional unknown rate constants connecting monomer, intermediate and protofibril-bound states and residue-specific ¹⁵N-R₂ values for the intermediate state, also fails to fit the experimental data.

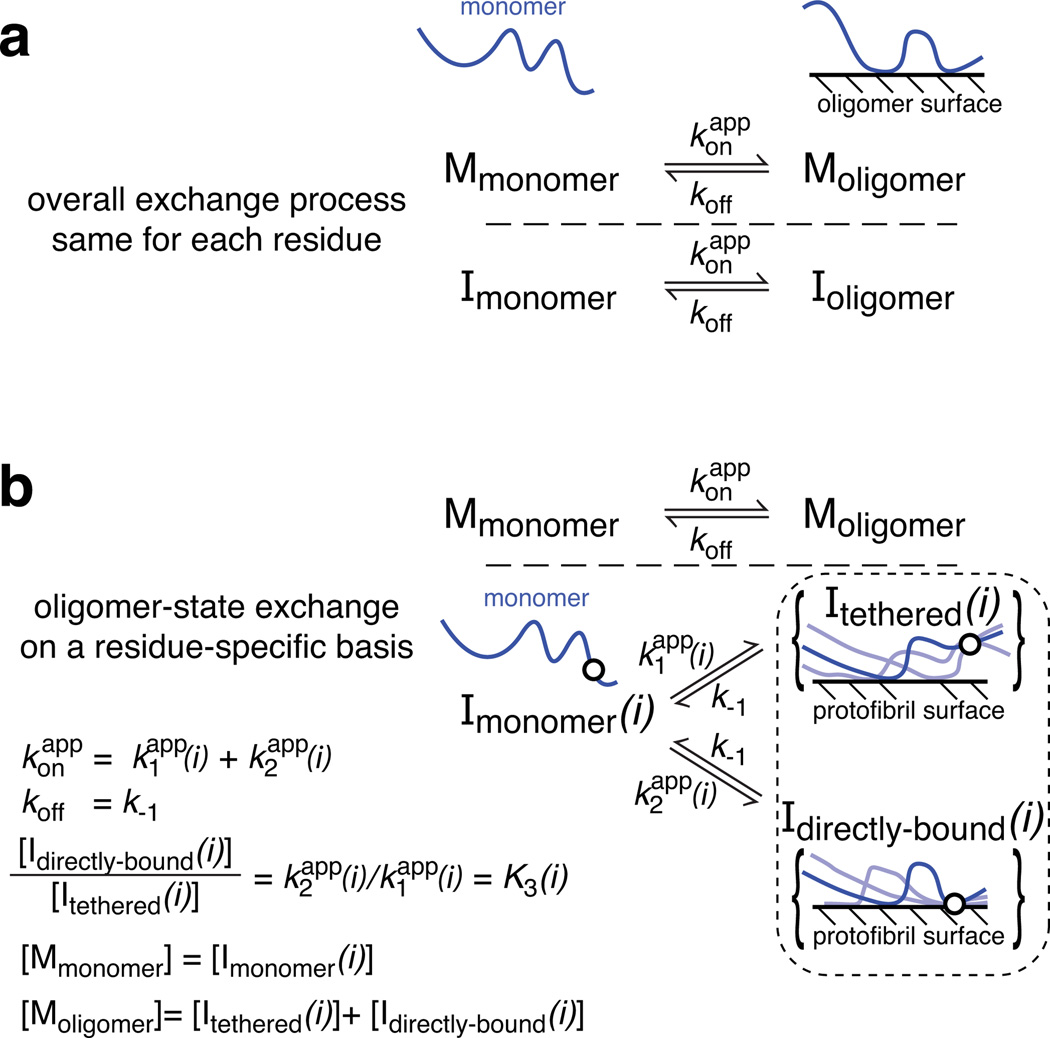
Figure 2. Kinetic schemes for monomer exchange on the surface of Aβ protofibrils.

a, The protofibril-bound peptide (M_oligomer) exists in only a single state. b, The protofibril-bound peptide exists as a large ensemble of states such that each residue can be either tethered or in direct contact with the surface of the oligomer with $K_3(i)=k_2^{\mathit{\text{app}}}(i)/k_1^{\mathit{\text{app}}}(i)$. The circle in the diagrammatic representation of the states represents a single residue that is either tethered or in direct contact and for which three possible chain configurations are shown.

The above results led us to investigate a simple modification of the two-state model in which the ensemble of protofibril-bound states is divided into two subsets where a given residue is either in direct contact with the protofibril surface (I_contact) or tethered (I_tethered) via residues in direct contact with the protofibril (Fig. 2b). The key to understanding this model lies in the observation that the variations in both ΔR₂ and ¹⁵N-DEST profiles are residue specific. This variation cannot be accounted for by postulating the existence of low molecular weight oligomers since, in that case, the ΔR₂ and DEST effects would be uniform throughout the peptide sequence (as each residue would be subject to the same events and the same average relaxation behavior when bound to the surface of the oligomers). Thus for each residue, i, there is a potentially different partitioning of the large number of conformational states into I_tethered(i) and I_contact(i). This partitioning is computed for a single residue at a time, the state of the other residues may be tethered, bound or interconverting between the two, and the correlation between states at different positions is not considered. Critical to the simplicity of the model is the retention of the overall two-state association/dissociation process; the global apparent association rate constant for the conversion of monomer to the protofibril-bound ensemble, $k_{\mathit{\text{on}}}^{\mathit{\text{app}}}$, is given by the sum of the pseudo-first order rate constants $k_1^{\mathit{\text{app}}}(i)\text{ and }{k}_2^{\mathit{\text{app}}}(i)$ for the conversion of a residue i from the monomeric state (I_monomer) to I_tethered(i) and I_contact(i), respectively; the global dissociation rate constant, k_off, from protofibril-bound states to monomer is the same for I_tethered(i) and I_contact(i) for all residues i (i.e. k_off = k₋₁ = k₋₂). Thus, the two-state equilibrium between monomer and protofibril-bound forms is preserved, and $k_{\mathit{\text{on}}}^{\mathit{\text{app}}}$ and k_off represent ensemble averaged rates. This model adds the fewest parameters to describe a system with a huge number of potential configurations (2⁴⁰ and 2⁴² for Aβ40 and Aβ42, respectively, where each residue is represented as either tethered or in direct contact) with differing behavior at each residue. Since there are so many combinations of states, the addition of further variation from the polydispersity of the protofibrils does not impact the interpretation of the data or its quantitative analysis in terms of the model in Fig. 2b.

A residue-specific equilibrium between the tethered and direct-contact states is described by the ratio of I_contact(i) to I_tethered(i), $K_3(i)=k_2^{\mathit{\text{app}}}(i)/k_1^{\mathit{\text{app}}}(i)$. Direct interconversion between I_contact(i) and I_tethered(i) is not necessary to fit the data and, hence, is not incorporated in the analysis presented in the main text (see Table S1 and Figure S11 for analysis including these kinetic paths). The ${}^{15}\mathrm{N}-R_2^{\mathit{\text{tethered}}}$ values for the I_tethered states are also residue-specific and describe the average dynamics of a given residue in the tethered state. In physical terms, this will depend upon the average length and flexibility of the segment separating residue i from other residues of the peptide in direct contact with the oligomer.

The model in Fig. 2b is a reduced, “model-free” representation of the actual system which clearly comprises a large ensemble of different states and interconversion networks. Although the model is phenomenological in that individual protofibril-bound states in the ensemble and the correlated behavior of residues are not explicitly considered, the smooth variation of the fitted parameters as a function of residue is indicative of correlated behavior at adjacent positions, as to be expected for a model that well describes physical behavior. Further, the model does not require that a single protofibril state be present or that the members of the protofibril ensemble even have the same interfaces with bound monomers. The ability to interpret the experimentally observed residue-by-residue differences between Aβ40 and Aβ42 demonstrates the success of the model.

Least-squares non-linear optimization of the scheme shown in Fig. 2b results in excellent fits to both the ¹⁵N-DEST saturation profiles (Fig. 1b–d and Fig. S10a–d) and the ΔR₂ data (Fig. 1e and Fig. S10e). For Aβ40 at 270µM, $k_{\mathit{\text{on}}}^{\mathit{\text{app}}}=3.0\pm 0.7{\mathrm{s}}^{-1}$, in agreement with the observed value of 3.0 s⁻¹ for $\mathrm{\Delta }{R}_2^{\text{max}}$ (Fig. 1e), and k_off = 51±12 s⁻¹, in good agreement with our previous estimate of ~73 s⁻¹ obtained from a one-dimensional ¹H saturation experiment¹⁵. The values of $k_{\mathit{\text{on}}}^{\mathit{\text{app}}}$ and k_off for Aβ42 at 160 µM are 2.4 s⁻¹ (in agreement with 2.3 s⁻¹ for $\mathrm{\Delta }{R}_2^{\text{max}}$) and 62 s⁻¹, respectively, although the standard deviations in these fitted parameters are higher due to lower experimental signal-to-noise (±1.8 s⁻¹ and ±46 s⁻¹). The values of ${}^{15}\mathrm{N}-R_2^{\mathit{\text{contact}}}$ are 18,800±700 s⁻¹ and 19,300±2000 s⁻¹ for Aβ40 and Aβ42, respectively, which are reasonable for the large, worm-like protofibrils seen in these samples by atomic force and electron microscopy (Fig. S1). From these rate constants one can deduce that the populations of transiently-bound Aβ40 and Aβ42 are ~6% and ~4%, respectively, that of free monomer.

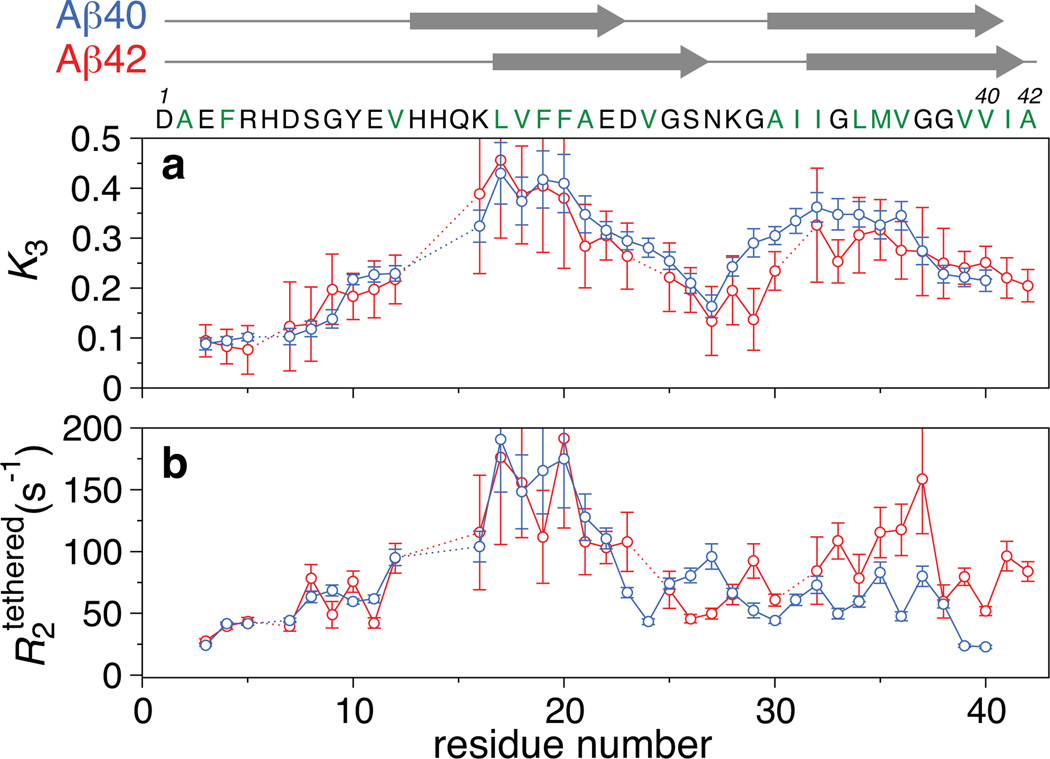
The residue-specific partitioning, K₃(i), between the direct-contact and tethered states (Fig. 3a) and the associated ${}^{15}\mathrm{N}-R_2^{\mathit{\text{tethered}}}$ relaxation values (Fig. 3b) provide the first characterization of the protofibril-bound forms of Aβ40 and Aβ42 at the single residue level. Qualitatively the K₃ and ${}^{15}\mathrm{N}-R_2^{\mathit{\text{tethered}}}$ profiles for Aβ40 and Aβ42 are similar, with the notable exception of the ${}^{15}\mathrm{N}-R_2^{\mathit{\text{tethered}}}$ values for the C-terminal residues. We also note that the values of K₃ and ${}^{15}\mathrm{N}-R_2^{\mathit{\text{tethered}}}$ are directly correlated with the observed widths of the saturation profiles and ΔR₂, respectively (Fig. S12), demonstrating that the model is consistent with a qualitative analysis of the data suggested directly from the observed residue-specific behavior.

Figure 3. Comparison of residue-specific fitted parameters describing the ensemble of protofibril-bound states.

a, Residue-specific equilibrium constant (K₃) for the relative partitioning of direct-contact and tethered states of the oligomer. b, ${}^{15}\mathrm{N}-R_2^{\mathit{\text{tethered}}}$ values for the tethered states. The values for Aβ40 and Aβ42 are displayed as blue and red circles, respectively. The proposed two β-strand regions in fibrils of Aβ40⁹ and Aβ42⁸ are indicated by arrows at the top of the figure. Error bars: 1 s.d.

For both Aβ40 and Aβ42 the first eight N-terminal residues have similar, small values of K₃ (0.08 to 0.14), indicating that these residues are predominantly tethered, spending only a small fraction (≤10%) of the time in actual direct contact with the protofibril surface. Correlated with this finding, these residues retain considerable flexibility as reflected by ${}^{15}\mathrm{N}-R_2^{\mathit{\text{tethered}}}$ values ranging from 20 to 80 s⁻¹. These observations are consistent with ¹³C linewidths in solid state NMR spectra of Aβ40 fibrils that are indicative of conformational disorder for the N-terminal segment¹⁰, although our data indicate a small but measurable population in direct contact with the protofibril surface.

The highest values of K₃ (>0.24) are seen for residues 16–25 and 28–37 of Aβ40 and residues 16–23 and 33–40 of Aβ42, corresponding roughly to the central and C-terminal hydrophobic regions that form intermolecular β-sheets at the core of amyloid fibrils^9,10. Although the ratio of direct-contact to tethered states in the Aβ40 protofibril-bound ensemble is very similar for the two regions (0.34±0.06 versus 0.32±0.04), the average ${}^{15}\mathrm{N}-R_2^{\mathit{\text{tethered}}}$ values are very different: 146±33 s⁻¹ for residues 16–22 falling to 61±16 s⁻¹ for residues 23–25, and 62±13 s⁻¹ for residues 28–37. This suggests that, in the tethered states, residues 28–37 of Aβ40 are considerably more flexible than residues 16–22. In terms of a physical picture this suggests that the C-terminal region of Aβ40 may be far from the protofibril surface when other residues (such as the 16–22 region) are bound, while the converse is true for the 16–22 region. For Aβ42, the average value of K₃ is slightly higher in the central hydrophobic region (0.35±0.06) compared to the 33–40 region (0.28±0.03), but in contrast to Aβ40, the corresponding ${}^{15}\mathrm{N}-R_2^{\mathit{\text{tethered}}}$ average values are quite similar (133±33 s⁻¹ and 99±35 s⁻¹, respectively), suggesting that the tethered states of the C-terminal hydrophobic region are on average less mobile and closer to the protofibril surface in Aβ42 than in Aβ40.

The most striking differences between protofibril-bound Aβ40 and Aβ42 are seen at the C-terminus. Intermediate K₃ values (0.21 to 0.23) associated with low ${}^{15}\mathrm{N}-R_2^{\mathit{\text{tethered}}}$ values (58, 24 and 23 s⁻¹ for residues 38, 39 and 40, respectively) are observed for the last three C-terminal residues of Aβ40 (Fig. 3). Thus, residues 38–40 in the ensemble of Aβ40 protofibril-bound states are more mobile and hence significantly less often buried than the central (residues 16–25) and C-terminal (residues 28–37) hydrophobic regions. This is in sharp contrast to Aβ40 fibrils where the C-terminal residues are located at the central core of the fiber, forming tight intermolecular contacts with both neighboring strands in the C-terminal cross-β sheet and adjacent subunits in the supramolecular structure⁹. Interestingly, the last two C-terminal residues of antibody-stabilized Aβ40 protofibrils also exhibit increased mobility as assessed by solid state NMR¹⁹, suggesting that enhanced dynamics of the C-terminal residues of Aβ40 are at least partially conserved when the protofibril-bound states are incorporated into the protofibril core. Although the population of direct-contact states for the C-terminal residues of Aβ42 is similar to that of Aβ40 (Fig. 3a), the corresponding ${}^{15}\mathrm{N}-R_2^{\mathit{\text{tethered}}}$ values are significantly higher for Aβ42 (76±16 s⁻¹ for residues 39–42 of Aβ42 versus 23.5±0.5 s⁻¹ for residues 39–40 of Aβ40; Fig. 3b). Thus, the mobility of the C-terminal residues in the tethered states of Aβ42 are hindered relative to that in Aβ40.

If dynamics of the C-terminal hydrophobic region and C-terminal residues in the protofibril-bound states, where Aβ40 and Aβ42 differ (Fig. 3), constitute the apparent free-energy barrier in the nucleation-dependent conformational change or polymerization separating disordered oligomers from fast-elongating amyloid fibrils²⁴, these observed differences may explain the higher rate of protofibril and fibril formation of Aβ42 relative to Aβ40^13,14.

Further, while the population of direct-contact states for the hydrophilic region between residues 27–29 is reduced for both Aβ40 and Aβ42, the K₃ values are higher for Aβ40 than Aβ42 (Fig. 3a). Since this region constitutes a hairpin turn in Aβ fibrils, the lower population of direct contact states for Aβ42 may facilitate hairpin and subsequent β-sheet formation, thereby enhancing the rate of incorporation of surface-bound monomers into the protofibril core.

In summary, ¹⁵N-DEST and ΔR₂ measurements probe exchange processes between monomer and protofibril-bound states of Aβ on times scale of 10–100 ms, and imprint the residue-by-residue footprint of the ‘dark’ protofibril-bound state on the easily observed monomer. These experiments are complementary to pulsed H/D exchange experiments that have been used to probe fibril formation and recycling on a million-fold slower time scale^25,26, as well as to spin-state selective methyl group relaxation dispersion experiments²⁷ that probe invisible state dynamics of supramolecular complexes on the intermediate chemical shift time scale of 50 µs to 10 ms²⁸. In contrast to relaxation dispersion which requires that the visible and invisible states have different chemical shifts, the DEST and ΔR₂ experiments rely entirely on large differences in transverse relaxation rates (R₂). For systems where a relatively small particle (i.e. a macromolecule whose resonances are directly observable by solution NMR) is in exchange with a state bound to a large particle (e.g. an aggregate, a fibril, a large supramolecular complex or a solid support), large differences in R₂ values will be present and consequently the R₂ values in the 'dark' state can be determined by DEST. The DEST experiment requires only that the exchange rate ($k_{\mathit{\text{on}}}^{\mathit{\text{app}}}+k_{\mathit{\text{off}}}$) be larger than the ¹⁵N-R₁ of the observed species. The Aβ monomer has a ¹⁵N-R₁ of ~1.5 s⁻¹, significantly faster and hence more limiting than for a larger protein. Since $k_{\mathit{\text{on}}}^{\mathit{\text{app}}}$ is a pseudo-first order rate constant, the use of higher concentrations can increase the apparent on-rate, thereby extending the range of applicability. The upper limit on the value of $k_{\mathit{\text{on}}}^{\mathit{\text{app}}}$ is ~100 s⁻¹, beyond which accurate determination of ΔR₂ is difficult. We anticipate that the DEST technique for examining dynamics at single residue resolution of otherwise invisible 'dark' states will be applicable to many areas of current interest both in biology (e.g. the interaction of unfolded proteins with the proteasome²⁹ and very large chaperones, the formation of low-affinity, large supramolecular complexes, the folding-upon-binding³⁰ of intrinsically disordered proteins) and material science (e.g. exchange reactions on surfaces).

METHODS SUMMARY

Solutions of uniformly ¹⁵N-labeled Aβ40 and Aβ42 were prepared from NaOH-treated stocks as described previously¹⁵. NMR samples, comprising 50 and 270 µM Aβ40 and 50 and 160 µM Aβ42 in 50 mM HEPES, pH 6.8, and 90% H₂O/10% D₂O, were prepared and maintained at 4 to 10 °C at all times. All NMR experiments were conducted at 10 °C on a Bruker 900 MHz spectrometer equipped with a triple resonance z-gradient cryoprobe. Fitting the DEST and ΔR₂ data to various kinetic schemes using the McConnell equations to determine the oligomer-bound R₂ values and kinetic parameters was carried out as described in the Full Methods.

Full Methods and any associated references are available in the online version of the paper at www.nature.com/nature.

METHODS

Description of the 2D ¹⁵N-DEST experiment and pulse sequence

Due to relatively small equilibrium magnetization of ¹⁵N nuclei, initial amide hydrogen (¹H_N) magnetization for the monomeric species is transferred to longitudinal ¹⁵N magnetization, after which a weak ¹⁵N saturation pulse is applied at a series of radio frequency (RF) offsets (ranging from +35 to −35 kHz) for a sufficient length of time (0.9 s) to allow the monomeric peptide to sample a protofibril-bound state where ¹⁵N-R₂ values are orders of magnitude larger than in the monomeric species and allow for efficient partial saturation by the weak RF field. Partial saturation is then transferred back to the monomeric state by chemical exchange, and recorded as a decrease in intensity of the ¹H-¹⁵N correlation cross-peaks for the NMR observable monomeric species relative to that in a reference spectrum obtained without saturation (see Methods and Fig. S8). Because initial ¹H_N to ¹⁵N magnetization INEPT transfer in the high molecular weight protofibrils is extremely inefficient owing to very fast ¹H and ¹⁵N transverse relaxation, the observed transfer-of-saturation only arises from peptides that begin the experiment as monomers, are incorporated into protofibrils, and subsequently released within the saturation time. The pulse sequence for the 2D HSQC-based ¹⁵N-DEST experiment is shown in Fig. S8. The pulse sequence is similar in spirit to that commonly used for measuring ¹⁵N-R₁ longitudinal relaxation except that the variable T₁ relaxation delay is replaced by a weak, continuous wave (CW) saturation pulse at variable radiofrequency (RF) offsets. The DEST experiment begins from the amide proton magnetization H_z of the monomeric peptide. Following the first INEPT transfer, longitudinal two spin order 2H_zN_z is obtained (Fig. S8, point a). The subsequent refocusing INEPT provides in phase N_z magnetization (Fig. S8, point b). The 90° ¹H pulse ϕ₂ not only flips the water signal back to the +z axis, but also purges any residual anti-phase magnetization 2N_yH_z prior to the ¹⁵N CW saturation pulse. The latter is applied for 0.9 s at a series of 15 different offsets (35, 28, 21, 14, 8, 4, 2, 0, −2, −4, −8, −14, −21, −28 and −35 kHz) from the ¹⁵N carrier frequency (set to 118.5 and 117.6 ppm and located at the center of the monomer spectrum of Aβ40 and Aβ42, respectively) and at two RF field strengths (170 and 350 Hz). In addition, two reference spectra were recorded at each concentration without saturation. During the CW ¹⁵N pulse, the magnetization (N_z) originating from the monomeric peptide is partially saturated when the peptide samples a protofibril--bound state. The latter cannot be directly observed due to extremely rapid transverse (R₂) relaxation. This partial saturation results in a reduction of the N_z magnetization by a multiplicative factor κ (relative to that in the reference spectrum with the saturation pulse turned off) which depends on the strength and frequency of the ¹⁵N saturation pulse as well as on the kinetics of the monomer-oligomer exchange process (see main text for more details), thereby providing valuable insight into the interconversion dynamics at atomic resolution. When the oligomer-bound peptide is released back into solution as a monomer, its reduced magnetization κN_z is detected via heteronuclear single quantum correlation. It is important to note that inversion of the phases of both the 90° ¹H pulse ϕ₁ and the receiver phase alternates the orientation of the N_z magnetization between the +z and −z axes. Summation of transients with these alternating phases removes non-exponential contributions to longitudinal relaxation (e.g. due to non-zero magnetization at Boltzman equilibrium) so that loss of magnetization due to R₁ relaxation at the end of the CW saturation pulse is a simple scaling factor e^−R₁t, and hence the R₁ dependence is effectively removed when cross-peak intensities are normalized to those in the spectrum without saturation³¹. Longitudinal cross-correlated relaxation interference between the ¹⁵N-¹H dipolar interaction and the ¹⁵N chemical shift anisotropy is eliminated by application of the 180° ¹H pulse train (with an interpulse delay of 100 ms) during the CW ¹⁵N pulse. With a cryogenic probe at a ¹H spectrometer frequency of 900 MHz, this interpulse delay is sufficient to return the water signal back to the +z axis through radiation damping. The dephasing INEPT following the saturation period results in an anti-phase term κ2N_xH_z (Fig. S8, point c). The antiphase ¹⁵N magnetization is then converted to amide proton anti-phase magnetization. The last refocusing INEPT, incorporating a WATERGATE scheme, not only rephases the anti-phase proton magnetization to in-phase κH_x, but also suppresses the residual water signal prior to direct detection of the monomeric peptide amide proton magnetization.

Data Acquisition and Analysis

All NMR experiments were recorded at 10 °C using a Bruker Avance-III spectrometer operating at ¹H frequency 900.27 MHz and equipped with a Bruker TCI z-axis gradient cryogenic probe. ¹⁵N-R₂ data on the 50 and 270 µM Aβ40 samples and 50 and 160 µM Aβ42 samples (prepared as described previously¹⁰) and ¹⁵N-R₁ data at 50 µM were measured using standard interleaved 2D ¹H-¹⁵N HSQC-based NMR experiments and analyzed as described previously¹⁵.

The 2D ¹⁵N-DEST spectra were acquired as 32 interleaved experiments (with the RF field strengths and frequencies for the CW ¹⁵N pulse given above). For Aβ40 each 2D experiment comprises 154* × 1900* complex data points in the indirect ¹⁵N and direct ¹H dimensions, respectively, with corresponding acquisition time of 77 and 175.6 ms. For Aβ42 78*×1900* complex points were acquired with acquisition times of 41 and 175.6 ms. 16 transients for Aβ40 and 32 for Aβ42 were collected per FID with a 1.7 s delay between scans. The total experimental times for Aβ40 and Aβ42 were each approximately 5 days.

The complete interleaved 2D data set was first split into 32 individual 2D data sets, one for each experiment at a particular ¹⁵N saturation pulse power level and frequency, using a C program written in house. Each experiment was then processed identically and analyzed using NMRPipe³². The time-domain data in each spectrum were apodized in the indirect ¹⁵N dimension with a 54°-shifted sine bell function. For the direct ¹H dimension, an exponential window function with a line broadening of 5 Hz for Aβ40 and 8 Hz for Aβ42 was applied, followed in the case of the Aβ40 data by a 72°-shifted squared sine bell. The additional line-broadening for the Aβ42 data was used to improve the signal-to-noise owing to the very low (~35 µM) concentration of free Aβ42 monomer. Time-domain data in the ¹⁵N and ¹H dimensions were then zero-filled to obtain a final complex 1024* × 4096* data matrix, with digital resolutions of 2.0 and 2.6 Hz, respectively. The residue-specific signal reduction factor κ as a function of frequency offset of the CW ¹⁵N saturation pulse was obtained from the ratio of peak heights in the saturation experiment versus the reference experiment with the saturation pulse turned off. (The Bruker pulse sequence and acquisition parameter files for the ¹⁵N-DEST experiment, as well as the processing scripts are available on request.)

Simultaneous fitting of the DEST and ΔR₂ data to kinetic models

A homogenous form of the McConnell equations²² describing a single spin in chemical exchange, as presented in Eq. 21 of Helgstrand et al.²³, was expanded to a three-state system. Due to the small gyromagnetic ratio of ¹⁵N nuclei and their sparse density in proteins, cross-relaxation between neighboring ¹⁵N nuclei in both monomer and protofibril-bound states is negligible, in marked contrast with the 1D ¹H transfer-of-saturation profiles reported previously¹⁵. Effects on the saturation due to cross-relaxation between ¹⁵N and directly-bonded ¹H nuclei, though predicted to be small, are removed with phase-cycling, placing the initial ¹⁵N magnetization during the saturation period on the +z and −z axes in alternating transients and measuring their intensity difference. The time dependence of the magnetization is given by:

$$\frac{\mathrm{d}}{\mathrm{d}t}\left[\begin{array}{l}E/2\\ I_x^A\\ I_y^A\\ I_z^A\\ I_x^B\\ I_y^B\\ I_z^B\\ I_x^C\\ I_y^C\\ I_z^C\end{array}\right]=-\left[\begin{array}{cccccccccc}0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& {\mathrm{\lambda }}^A+k_1+k_2& {\mathrm{\Omega }}^A& -{\mathrm{\omega }}_y& -k_{-1}& 0& 0& -k_{-2}& 0& 0\\ 0& -{\mathrm{\Omega }}^A& {\mathrm{\lambda }}^A+k_1+k_2& {\mathrm{\omega }}_x& 0& -k_{-1}& 0& 0& -k_{-2}& 0\\ -2{\mathrm{\Theta }}^A& {\mathrm{\omega }}_y& -{\mathrm{\omega }}_x& {\mathrm{\rho }}^A+k_1+k_2& 0& 0& -k_{-1}& 0& 0& -k_{-2}\\ 0& -k_1& 0& 0& {\mathrm{\lambda }}^B+k_{-1}+k_3& {\mathrm{\Omega }}^B& -{\mathrm{\omega }}_y& -k_{-3}& 0& 0\\ 0& 0& -k_1& 0& -{\mathrm{\Omega }}^B& {\mathrm{\lambda }}^B+k_{-1}+k_3& {\mathrm{\omega }}_x& 0& -k_{-3}& 0\\ -2{\mathrm{\Theta }}^B& 0& 0& -k_1& {\mathrm{\omega }}_y& -{\mathrm{\omega }}_x& {\mathrm{\rho }}^B+k_{-1}+k_3& 0& 0& -k_{-3}\\ 0& -k_2& 0& 0& -k_3& 0& 0& {\mathrm{\lambda }}^C+k_{-2}+k_{-3}& {\mathrm{\Omega }}^C& -{\mathrm{\omega }}_y\\ 0& 0& -k_2& 0& 0& -k_3& 0& -{\mathrm{\Omega }}^C& {\mathrm{\lambda }}^A+k_{-2}+k_{-3}& {\mathrm{\omega }}_x\\ -2{\mathrm{\Theta }}^C& 0& 0& -k_2& 0& 0& -k_3& {\mathrm{\omega }}_y& -{\mathrm{\omega }}_x& {\mathrm{\rho }}^C+k_{-2}+k_{-3}\end{array}\right]\times \left[\begin{array}{l}E/2\\ I_x^A\\ I_y^A\\ I_z^A\\ I_x^B\\ I_y^B\\ I_z^B\\ I_x^C\\ I_y^C\\ I_z^C\end{array}\right]$$ (1)

where I represents the magnetizations of the ¹⁵N spins in the rotating frame in the free monomer, and in the tethered and direct-contact protofibril-bound states (denoted by the superscripts A, B and C, respectively). The relaxation rates for transverse and longitudinal magnetization are λ and ρ, respectively; Ω is the resonance offset frequency calculated as the difference between the peak resonance frequency (accounting for peak folding in the case of Aβ42 Ala42) and the ¹⁵N carrier frequency + CW pulse offset, and ω the RF field strength of the CW saturation pulse applied along the appropriate axis; E is unity; and Θ is related to the equilibrium magnetization as described by Helgstrand et al²³. The rate constants are as follows (see Fig. 2b): k₁ and k₂ are the apparent first order rate constants for the forward reaction from the monomer to the tethered and direct-contact protofibril-bound states, respectively; k₋₁ and k₋₂ are the corresponding dissociation rate constants and in this instance k₋₁ = k₋₂ (see main text); k₃ and k₋₃ (not shown in Fig. 2b) are the rate constants for the conversion of tethered to direct-contact states, and vice versa, respectively. Detailed balance is ensured from the relationship k₋₃ = k₃k₁/k₂ (with k₋₁ = k₋₂). The numerical solution for $I_z^A$, the experimentally observed magnetization in the DEST experiment, after a given saturation time as a function of frequency offset was calculated using the matrix exponential function in the program Matlab. The solution is calculated for both initial ¹⁵N magnetization during the saturation period on the +z and −z axes, I_+z and I_−z, and the difference, I_+z − I_−z, is then computed at each frequency offset and RF field strength, normalized to the solution without saturation, and compared to the normalized experimentally observed intensity.

ΔR₂ values, for a given set of kinetic and relaxation rate constants, were calculated by subtracting the monomer ¹⁵N-R₂ values for each residue, measured experimentally on the monomeric 50 µM samples, from the calculated R₂ values. The calculated R₂ value for a system in equilibrium exchange is computed assuming a single exponential decay:

$$R_2^{\mathit{\text{calc}}}=-\text{ln}\left(\frac{I_x^A(\tau )}{I_x^A(0)}\right)/\tau$$ (2)

where the transverse magnetization, $I_x^A$, is computed at time τ = 0.2 s and time 0. The choice of 0.2 s for τ was chosen to match to one of the longer delays used in the experimental ¹⁵N-R₂ measurements. Simulated delays longer than ≈20 ms result in the same value of $R_2^{\mathit{\text{calc}}}$, validating the assumption of single exponential decay.

¹⁵N relaxation rates in the protofibril-bound states, and kinetic rate constants connecting monomer and protofibril-bound states in all schemes (cf. Fig. 2) were fit by simultaneous non-linear least squares minimization of the differences between the observed and calculated (Eq. 1) DEST profiles (at both applied RF field strengths for the CW ¹⁵N saturation pulse) and between the observed and calculated (Eq. 2) ΔR₂ values.