The Linear Interaction Energy Method for the Prediction of Protein Stability Changes Upon Mutation

Abstract

The coupling of protein energetics and sequence changes is a critical aspect of computational protein design, as well as for the understanding of protein evolution, human disease, and drug resistance. In order to study the molecular basis for this coupling, computational tools must be sufficiently accurate and computationally inexpensive enough to handle large amounts of sequence data. We have developed a computational approach based on the linear interaction energy (LIE) approximation to predict the changes in the free energy of the native state induced by a single mutation. This approach was applied to a set of 822 mutations in 10 proteins which resulted in an average unsigned error of 0.82 kcal/mol and a correlation coefficient of 0.72 between the calculated and experimental ΔΔG values. The method is able to accurately identify destabilizing hot spot mutations however it has difficulty in distinguishing between stabilizing and destabilizing mutations due to the distribution of stability changes for the set of mutations used to parameterize the model. In addition, the model also performs quite well in initial tests on a small set of double mutations. Based on these promising results, we can begin to examine the relationship between protein stability and fitness, correlated mutations, and drug resistance.

Introduction

Proteins are molecular machines whose thermodynamic stability and fitness are encoded in their amino acid sequence. Mutations can change the energetic landscape of a protein and thereby alter its structure and function. The coupling of sequence changes to protein energetics is a critical aspect of computational protein design, and is necessary for a complete understanding of protein evolution, human disease, and drug resistance. The computational protein design field employs sequence modifications to design novel protein folds, to modify thermostability and enzymatic activity, and to redesign protein-protein interfaces.^1–5 On the other hand, studies of sequence evolution have focused on examining the balance between stability and fitness of proteins found in nature⁶, for example, the role of the “stability/activity” tradeoff mechanism for residues located in protein active sites.^7–9. Furthermore, directed evolution experiments have designed proteins with novel functions through a series of functional but destabilizing replacements accompanied by a series of compensatory mutations highlighting the crucial role that stabilizing mutations play in the “evolvability” of a protein.^6,10,11 This compensatory stabilizing mechanism is also quite prevalent in the evolution of drug resistance.^12,13 The acquisition of drug resistance has been linked to primary mutations which cause the resistance at the cost of stability and are correlated with accessory mutations which restore activity and stability, as for example in HIV protease.¹⁴ Additional work by Ishikita and Warshel has shown how effective drug resistant mutations maintain catalytic efficiency and hence the local instability within the active site while weakening the binding affinity to a target drug.¹⁵ Therefore, it is important to understand how sequence changes can alter the thermodynamic stability and fitness of proteins to relate these effects to drug resistance and disease^6,16,17.

In order to tackle these problems, computational approaches must be sufficiently accurate to capture the underlying energetics and capable of handling large amounts of sequence data. Methods such as free energy perturbation and thermodynamic integration are in principle the most accurate of these approaches but are limited to a small number of mutations.^18–20 More efficient computational mutagenesis methods based on approximations to the free energy change, are used to predict protein stabilities for large databases of proteins. These methods are differentiated by their free energy function which can be categorized as knowledge-based/statistical²¹, empirical^22,23 or physics-based^24,25 potentials. These methods also vary in the extent of the conformational sampling used to model the structural changes induced by the mutation. Some approaches only model the mutated residue using a fixed backbone^22,23 while other methods include flexibility either through side chain repacking and backbone relaxation^26,27 or the generation of an ensemble of structures.²⁵ Lastly, the unfolded state is treated differently by these free energy methods; unfolded state effects have been included implicitly in the coefficients of the energy function²², explicitly represented by a specific term in the energy potential^23,26,28 or modeled as a short peptide of the original structure.^24,25

Many of these approximate methods, however, demonstrate limited accuracy according to a recent survey by Potapov et al.²⁹ In this report, they claim that these methods are “good on average and not in the details.” It is reported that the best method only achieved a correlation coefficient between experimental (ΔΔG_exp) and calculated (ΔΔG_calc) relative free energies of folding (compared to wild type) of 0.59 on a large set of single point mutations.¹ Since many of the most relevant biological problems involve multiple mutations, limitations with single point mutations may translate into large errors, especially since these methods are not typically tested with more than one mutation. Therefore, there is a need for further development of protein stability models with greater predictive accuracy.

A possible alternative to rigorous free energy methods on one hand and purely empirical approaches in the other are linear interaction energy models.^30,31 LIE approaches have a foundation in linear response theory^32–34 and the linear response approximation³⁵; physically motivated interaction energy estimators which only require the knowledge of the endpoints of a particular process are used to estimate the free energy change. This approach has been mainly applied to protein-ligand binding problems.^30,35–41 Typically, the LIE formulations use the following functional form to calculate the free energy of binding (ΔG_b), ^30,31

$$\mathrm{\Delta }{G}_b=\alpha (\mathrm{\Delta }{V}_{\mathit{vdw}})+\beta (\mathrm{\Delta }{V}_{\mathit{elec}})+\gamma (\mathrm{\Delta }A)+\delta$$ (1)

where ΔV_vdw, ΔV_elec and ΔA are differences between the quantities measured for the ligand complexed with the receptor and ligand free in solution. ΔV_vdw and ΔV_elec are the van der Waals and electrostatic interaction energies of the ligand with its environment. ΔA is the change in surface area between the receptor-ligand complex and the free ligand. Typically, these energies have been obtained from Molecular Dynamics or Monte Carlo simulations of the receptor-ligand complex and free ligand in explicit solvent. Recent studies in our lab and elsewhere have applied this formalism to studies in implicit solvent with approximate and more rigorous derivations.^39–41 α, β, γ, and δ are adjustable parameters which are obtained by fitting to experimental binding data.

Linear response has also been used to study protein stability and protein-protein interactions.^42–45 Previously, Warshel applied the linear response approximation to the calculation of absolute protein stabilities using an electrostatic energy function scaled with “focused” dielectric constants.^42,43 In addition, the LIE method has been used to calculate the absolute and relative binding affinities of protein-protein interfaces that contained different mutations to a crucial residue for binding (treating the mutated residue as a ligand).^44,45 Building on these ideas and our earlier work with LIE models, we have devised a LIE approach to calculate relative protein stabilities between wild type and single point mutations using the LIE method. For the protein stability problem, we consider the free energy change for replacing one protein residue with another in the folded and unfolded states (Figure 1). The difference between the corresponding wild-type and mutant energetic estimators can be used to construct a linear interaction energy model for the free energy of folding analogous to the LIE equation for the binding free energy.

Figure 1.

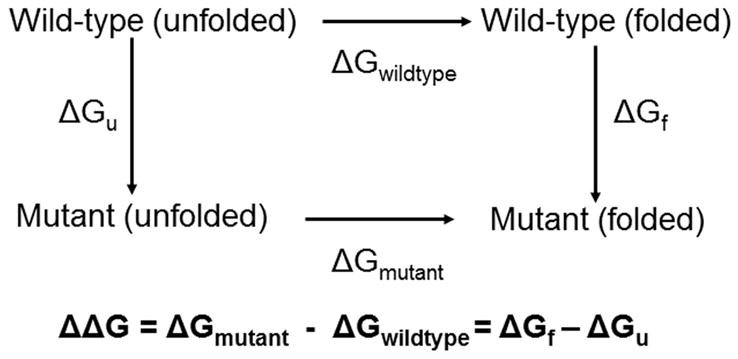
Thermodynamic cycle for calculating the relative changes in protein stability (ΔΔG). The ΔG_wild-type and ΔG_mutant are the free energy difference between the folded and unfolded state for the wild-type and mutant, respectively. The ΔG_f and ΔG_u is the free energy difference between mutant and wild-type in the folded and unfolded state, respectively. The relative free energy can be expressed as either the difference between ΔG_wild-type and ΔG_mutant or as the difference between ΔG_f and ΔG_u.

In this work, we have developed a computational approach based on the LIE method using the protein local optimization program⁴⁶ (PLOP) for conformational sampling, together with the Analytical Generalized Born plus Nonpolar (AGBNP) implicit solvent model⁴⁷ and OPLS force field^48,49 to predict the changes in the free energy of the native state induced by single point mutations. In the following section, we derive the LIE equations used to calculate protein stability. For the initial tests of this method, we performed side chain prediction for the structural models of the wild type and mutant structures and applied the LIE protein stability formulation on 822 mutations from 10 proteins. We found that a separate model based on mutation residue types (e.g. charged vs uncharged) showed improved results compared to a model which did not distinguish between residue types. All models were validated with jack-knife prediction tests. This approach has resulted in a correlation coefficient and an average unsigned error between the ΔΔG_exp and ΔΔG_calc of 0.72 and 0.82 kcal/mol respectively, which are among the best results reported to date for current protein stability prediction methods.

Materials and Methods

This section describes the methodology used to develop the LIE protein stability protocol. This involved the selection of single point mutations for our benchmark set, structure prediction for the wild-type and mutant structures, and derivation of the LIE equations for the calculation of relative protein stabilities. We also summarize in this section the analysis procedures used to evaluate the results of the LIE protein stability approach.

Selection of Mutations

A benchmark set of single point mutations was created from available ΔΔG_exp data in the Protherm database⁵⁰ and from Guerois et al.²² Mutations were selected if the wild type residue had a larger van der Waals volume than the mutant residue, the ΔΔG_exp measurement was performed between a pH of 5 and 9 and an X-ray structure existed for the wild-type protein; this was based on criteria applied by Guerois et al.²² Lastly, we required that the stability measurements were made within a relatively narrow temperature range (between 17°C and 37°C ) since we neglect effects of temperature variation in the LIE function.

From the filtered set, the 10 proteins with the largest number of mutations were selected for our current study (822 mutations) (Table 1). The proteins included in this study are: staphyloccal nuclease (PDB ID:1STN⁵¹), barnase (PDB ID:1BNI⁵²), FK506 binding protein (PDB ID:1FKJ⁵³), chymotrypsin inhibitor 2 (PDB ID:2CI2⁵⁴), protein L (PDB ID: 1HZ6⁵⁵), human tyrosine-protein kinase c-Src (PDB ID:1FMK⁵⁶), human lysozyme (PDB ID:1REX⁵⁷), bovine pancreatic inhibitor (PDB ID: 1BPI⁵⁸), fibronection (PDB ID: 1TEN⁵⁹) and T4-lysozyme (PDB ID:2LZM⁶⁰).

Table 1.

Proteins used for LIE protein stability calculations

Protein	%α	%β	Nmut
1stn	24	30	391
1bni	22	23	91
1fkj	14	37	31
2ci2	22	28	58
1hz6	35	48	57
1fmk	5	41	49
1rex	40	12	41
1bpi	21	26	40
1ten	0	51	39
2lzm	7	66	25

%α = percentage residues in an α-helical conformation in the whole protein; % β = percentage of residues in β-sheet conformation in the whole protein; N_mut= number of single point mutations;

Structure preparation

Structural models of the single point mutants were built using the torsional angle sampling implementation in the protein local optimization program (PLOP)⁴⁶. PLOP is typically used for its side chain and loop prediction capabilities in homology modeling problems^46,61,62, force field/implicit solvent evaluation studies ^63–66 and protein-ligand binding problems involving the modeling of receptor-induced fit effects⁶⁷. We have performed a side chain prediction test on a database of approximately 2190 polar side chains found in 30 proteins using the AGBNP implicit solvent model⁴⁷ with the OPLS-AA force field^48,49 and measured the accuracy of the predictions by calculating the heavy atom root mean squared deviation (RMSD) of the side chain of each predicted rotamer state relative to its corresponding minimized X-ray side chain rotamer. Using a RMSD cutoff of 1.5 Å, the side chain prediction accuracy was 79% and 75% with and without the crystal environment respectively. These results provide further evidence that the PLOP program can be employed with the OPLS-AA/AGBNP force field to predict the side chain rotamer geometries of the wild-type and mutant residue with good fidelity.

1) Minimization of structures

Minimizations were performed on all of the proteins using PLOP with the OPLS-AA/AGBNP force field. The Truncated Newton algorithm⁶⁸ was employed with a RMS tolerance of 0.5 kcal/mol Å using the default settings in PLOP.

2) Wild-type and mutant folded structure

The side chain conformations for both the wild-type and mutant forms were built using the side chain prediction algorithm in PLOP. Mutant structures were based on the wild-type structure and only differed at the mutated residue position. There are several steps involved in this algorithm incorporated into PLOP. The native backbone of the protein is held fixed while a conformational search is performed using a highly detailed rotamer library developed by Xiang and Honig⁶⁹. Rotamers are eliminated based on an adjustable overlap factor which is a measure of the extent of the “clash” of the rotamer with the residues of the protein which are held fixed. The remaining structures are scored based on a reduced non-bonded energy and clustered in torsional space using the K-means algorithm⁷⁰. The lowest energy rotamer is selected from the clustering procedure and the side chain rotamer is minimized using the TN algorithm⁶⁸. This procedure can be performed with or without the crystal packing environment. Side chain prediction was performed on the wild type and mutated residue of interest without crystal packing which should result in the preferred rotamer conformation in solution.

3) Unfolded state

The unfolded state was represented using a tetrapeptide model of the local environment of the residue of interest. This peptide contained the two neighboring residues on either side and was capped with an acetyl (ACE) and n-methyl amino group (NME). The peptide was modeled with the wild-type or mutated residues fixed in the folded state conformation. If the mutated residue was close to the N-terminus or C-terminus (1–2 residues away), the charge was maintained on the corresponding terminus of the unfolded state model.

Scoring

Energies were calculated using the OPLS AA/AGBNP force field. The AGBNP model contains the analytical pairwise descreening implementation of the Generalized Born (GB) model⁷¹ and a non-polar hydration term (G_np).⁴⁷

The polar solvation energy (G_el) is estimated using the GB equation

$$G_{el}\sim -\frac{1}{2}(\frac{1}{{\epsilon }_{in}}-\frac{1}{{\epsilon }_W})(\sum _i\frac{{q_i}^2}{B_i}+2\sum _{i<j}\frac{q_i{q}_j}{f_{ij}})$$ (2)

where ε_in is the dielectric constant of the interior of the solute, ε_w is the dielectric constant for water, q_i and q_j are the charges on atom i and j and

$$f_{ij}=\sqrt{r_{ij}^2+B_i{B}_{j}exp(-r_{ij}^2/4B_i{B}_j)}$$ (3)

where B_i and B_j are the Born radii of atoms i and j and r_ij is the distance between atoms i and j. The non-polar term contains two components: G_cav and G_vdw.^72,73

$$G_{np}=G_{\mathit{cav}}+G_{\mathit{vdw}}=\sum _i{\gamma }_i{A}_i+\sum _i{\alpha }_i\frac{a_i}{{(B_i+R_W)}^3}$$ (4)

G_cav accounts for the work required to make a cavity in solution and G_vdw accounts for the solute-solvent dispersive vdw forces. In Equation 5, the cavity component is a function of the surface area of atom i (A_i) and the surface tension parameter assigned to atom i (γ_i) while the van der Waals dispersionterm is expressed as a function of an adjustable van der Waals dispersion parameter (α_i)⁴⁷, the Born radii of atom i (B_i), the radius is of a water molecule (R_w) and

$$a_i=-\frac{16}{3}\pi {\rho }_W{\epsilon }_{iw}{\sigma }_{iw}^6$$ (5)

where ρ_w = 0.033428 ų is the number density of water at standard conditions and ε_iw and σ_iw are OPLSforce field Lennard Jones parameters for solute-solvent interactions with oxygen atom of TIP4P water.⁷⁴

LIE formulation for Protein Stability

The concepts behind the LIE protein stability model are derived from the ideas of linear response theory and the linear response approximation.^32–35 Protein stability is a measure of the free energy difference between the folded and the unfolded state (Figure 1). In this case, we are interested in determining the protein stability of the wild type (ΔG_wildtype) and the mutant (ΔG_mutant) in order to calculate the relative stability (ΔΔG). As illustrated in Figure 1, ΔΔG is equal to the differences of the alchemical free energies of transforming the wild-type residue into the mutated residue within the unfolded (ΔG_u) and folded (ΔG_f) states.

According to the LIE formalism, the free energy change at each step can be expressed as:

$$\mathrm{\Delta }G\propto (\mathrm{\Delta }<V>)$$ (6)

where Δ<V> is the change in the residue-environment average interaction energy in going from wild-type to mutant corresponding to the step of interest (for example, the electrostatic interaction energy for the transformation of the electrostatic interactions from those of the wild-type residue to those of the mutant).

We can write for the free energy of mutation in the folded state (ΔG_f) :

$$\mathrm{\Delta }{G}_f=\alpha (\mathrm{\Delta }<V_{LJ}>)+\beta (\mathrm{\Delta }<V_{el}>)+\gamma (\mathrm{\Delta }<G_{el}>)+\delta (\mathrm{\Delta }<G_{\mathit{cav}}>)+\epsilon (\mathrm{\Delta }<G_{\mathit{vdw}}>)$$ (7)

where Δ<V_LJ> is the change in the van der Waals interaction energy for intramolecular interactions within the protein, Δ<V_el> is the change in the electrostatic interaction energy, Δ<G_el> is the change in the polar solvation interaction energy, Δ<G_cav> is the change in the non-polar energetic component for cavity formation and Δ<G_vdw> is the change in the non-polar van der Waals dispersion energy between solvent and the solute. α, β, γ, δ, and ε are the corresponding LIE coefficients for the energetic estimators.

A similar equation applies to ΔG_u yielding the following expression for the change in folding energy:

$$\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathit{calc}}=\alpha (\mathrm{\Delta }\mathrm{\Delta }<V_{LJ}>)+\beta (\mathrm{\Delta }\mathrm{\Delta }<V_{el}>)+\gamma (\mathrm{\Delta }\mathrm{\Delta }<G_{el}>)+\delta (\mathrm{\Delta }\mathrm{\Delta }<G_{\mathit{cav}}>)+\epsilon (\mathrm{\Delta }\mathrm{\Delta }<G_{\mathit{vdw}}>)$$ (8)

where ΔΔG_calc is the free energy difference between the stability of the mutant and wild-type protein. ΔΔ<V_LJ> and ΔΔ<V_el> are the intramolecular interaction energy contributions to the stability change and ΔΔ<G_el>, ΔΔ<G_cav> and ΔΔ<G_vdw> are the solute-solvent interaction energy contributions to the stability change.

We define the interaction energy between a given residue and its environment as the difference between the total energy of the protein and the total energy of the protein without the residue of interest. This definition, which for pairwise decomposable potentials, reduces to the sum of pairwise interactions between the atoms of the residue and the other protein atoms, is a generalization of the interaction energy which is applicable for non-pairwise decomposable potentials such as the implicit solvent solvation free energy. The goal is to estimate the side chain’s contribution to the (free) energy of each (folded/unfolded) state. The energy of state-1 was first calculated for the structure with all of the solute-solute and solute-solvent interactions present. The second step was to eliminate interactions of the side chain for the second state in the calculation. The non-bonded and polar solvation energy terms were turned off by setting the partial charges and the well depth of the Lennard Jones’s equation to zero for side chain atoms (starting with C_β atom). The non-polar hydration was turned off by settng γ_i and α_i to zero. The difference between state-1 and state-2 represents the side chain’s interaction energy with the other residues of the protein and the solvent. Since the same structure is used for the state 1 and state 2, the covalent energy terms cancel out. This was done for both the folded and unfolded state model.

The LIE calculation for mutations involving glycine and proline is different since the partial charges of the backbone are different from the other residues. When the partial charges of the HA3 atom of the glycine or the side chain of the proline are set to zero, the backbone is left with an excess charge. For all other residues, the backbone remains neutral after the charges are turned off. For the second state corresponding to glycine and proline, we created a model where the partial charges of all the atoms in the residue were set to zero. Hence, the difference between state-1 and state-2 includes the electrostatic and reaction field interaction energy for the side chain and backbone of the residue in both the folded and unfolded state model. By taking the difference between the folded and unfolded state, the effect of turning off the charges on the backbone is eliminated.

The LIE equation requires five LIE coefficients for the energy terms. This fitting was performed using the multiple linear regression module in the statistical analysis program R. The whole set of 822 single point mutations was used for training and testing. Jack knife tests as described below were performed by iteratively training on 95 % of the data and testing on the remaining 5 % of the data set. We have developed two models for ΔΔG prediction (Table 2 and Table 3). For Model-1, five coefficients were obtained while for Model-2, five coefficients were obtained for each of the three mutation residue types (neutral, charged and glycine/proline). Coefficients were eliminated on the basis of p-values (p < 0.05 to reject the null hypothesis for a particular coefficient). If coefficients of terms with complimentary physical effects (e.g. electrostatic and reaction field interaction energies or intramolecular and solute-solvent van der Waals interaction energies) were of the same magnitude, their corresponding energy estimators were combined and refit. In this work, most of the models were fit to two coefficients except for the neutral residue model (Model-2).

Table 2.

Fitting results for Neutral, Charged, and Glycine/Proline mutations, Individually and Combined.

Residue Type	Model #	np	α	β	γ	δ	ε	< | error | >jack	rjack
All	1	2	0.32	0.07	0.07	0.00	0.00	0.95	0.60
Neutral	2	5	0.17	0.13	0.21	−0.19	−0.94	0.83	0.67
Charged	2	2	0.17	0.07	0.07	0.00	0.00	0.73	0.38
Glycine/Proline	2	2	0.53	0.08	0.08	0.00	0.53	0.94	0.75

np= number of LIE coefficients; α, β, γ, δ and ε are the LIE coefficients;

|error|_jack= average unsigned error for jack-knife validation; r_jack = pearson correlation coefficient for the jack knife validation;

The average unsigned error for the jack knife validation is in units of kcal/mol.

Models 1 and 2 were fit using the equation:

$$\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathit{calc}}=\alpha (\mathrm{\Delta }\mathrm{\Delta }<V_{LJ}>)+\beta (\mathrm{\Delta }\mathrm{\Delta }<V_{el}>)+\gamma (\mathrm{\Delta }\mathrm{\Delta }<G_{el}>)+\delta (\mathrm{\Delta }\mathrm{\Delta }<G_{\mathit{cav}}>)+\epsilon (\mathrm{\Delta }\mathrm{\Delta }<G_{\mathit{vdw}}>)$$

Table 3.

Comparison of the results for different mutation residue types using Model 1 and Model 2.

Residue-type	# of Mutations	Model-1	Model-2
All	822	0.61 (0.94)	0.72 (0.82)
Neutral	448	0.60 (0.88)	0.69 (0.80)
Charged	175	0.38 (0.84)	0.45 (0.72)
Glycine/Proline	199	0.72 (1.15)	0.77 (0.94)

The correlation coefficient is listed with the average absolute error in parenthesis (in units of kcal/mol).

We evaluated the predictive value of each of the models in this study (Table 2). We employed a jack knife approach where the corresponding jack knife Pearson correlation coefficient (r_jack) and average absolute error (<|error|_jack>) are reported. For Model-1 and Model-2, fitting resulted in r_jack and <|error|_jack> values that were very close to their values for the entire data set (Table 1) which suggests that these models are not biased by particular points in their training sets; this was not the case for Model-2(charged). For Model-2(charged), the corresponding r_jack and <|error|_jack > were slightly worse than the values reported for the entire data set which is indicative of some type of bias in our training set (Table 1). Nevertheless, Model-2 demonstrates more accuracy and precision than Model-1 even though Model-2 has more parameters (Model-1 has 2 parameters while Model-2 has 9 parameters).

Multiple Mutations

A small set of double mutations from serine protease inhibitor was taken from the Protherm database. These mutations were previously tested with the Eris program;²⁶ this approach uses a hybrid knowledge-based/physical energy function and allows for backbone flexibility. Our structural models for the wild-type and mutant state were built using the multiple side chain prediction module in PLOP. LIE calculations were performed using LIE equations and coefficients developed for Model-2. In 16 of the 17 cases, the double mutant was composed of two mutations of the same residue type so the coefficients for that specific residue type were selected for that ΔΔG calculation. For the double mutant with different mutations types (T58AE60A), we employed the coefficients developed for the charged residue model in the LIE equation for protein stability since electrostatic interactions are likely to dominate the effect of the double mutation.

Analysis

Both Pearson correlation coefficients and average absolute errors between the calculated and experimental ΔΔG were the statistical measures used to evaluate the different models and groups of mutations in this study. Nevertheless, we note that the Pearson correlation coefficient is the gold standard used to evaluate the quality of the stability change calculations since the absolute error is highly influenced by the relatively small range of the ΔΔG data.

In Table 3, we summarize the performance of the LIE algorithm at identifying two different types of mutations: stabilizing/destabilizing and hot-spot mutations similar to Potopov et al..²⁹ Stabilizing mutants had ΔΔG_exp < 0 kcal/mol while destabilizing mutants had ΔΔG_exp > 0 kcal/mol. Hot spot mutations had |ΔΔG_exp| > 2 kcal/mol while non-hot spot mutations had |ΔΔG_exp| < 2 kcal/mol. The stability ranges of the ΔΔG_calc and ΔΔG_exp values were compared using the following measures: accuracy, sensitivity and specificity, which were functions of the number of true positives (TP), true negatives (TN), false positives (FP) and false negatives (FN). Accuracy is calculated using the following expression:

$$\mathit{Accuracy}=\frac{TP+TF}{\mathit{Total}}$$ (9)

which evaluates the number of correct predictions relative to the total number of predictions. Sensitivity evaluates the number of correctly identified true positives relative to the total number of positives. Sensitivity is calculated with the following expression:

$$\mathit{Sensitivity}=\frac{TP}{TP+TN}$$ (10)

Specificity evaluates the number of correctly identified true negatives relative to the total number negatives. Specificity is calculated with the following expression:

$$\mathit{Specificity}=\frac{TN}{TN+FP}$$ (11)

In the analysis summarized in Table 4, hot spot residues are defined as positives while non-hot spot residues are defined as negatives.

Table 4.

Prediction of stabilizing/destabilizing and hot spot mutations

	Stabilizing/Destabilizing Mutations	Hot spot Mutations
Model	Accuracy (%)	Accuracy (%)	Sensitivity (%)	Specificity (%)
1	87	79	54	90
2	89	82	66	90

Stabilizing mutations had ΔΔGexp < 0 and destabilizing mutations had ΔΔGexp > 0.

Hot spot mutations had |ΔΔGexp|> 2 and non-hot spot mutations had |ΔΔGexp|< 2. Accuracy measures how many ΔΔGcalc have been predicted to be in the same direction of stability as the ΔΔGexp.

Sensitivity measures how many hot spot mutations were identified correctly relative to the total amount of hot spots. Specificity measures how many non-hot spots were correctly identified relative to the total number of non-hot spots. There are 727 destabilizing mutations, 71 stabilizing mutations and 255 hot spot mutations

$$\mathit{Accuracy}=\frac{TP+TN}{\mathit{Total}};\mathit{Sensitivity}=\frac{TP}{TP+FN};\mathit{Specificity}=\frac{TN}{TN+FP}$$

DSSP ⁷⁵ was used to classify the secondary structure of the wild type residues of each protein. Surface areas were calculated using the Shrake-Rupley algorithm⁷⁶. The fraction of the surface area exposed for each wild type residue (SA_res) was calculated with this expression

$$\%{SA}_{\mathit{res}}=\frac{{SA}_f}{{SA}_{exp}}\ast 100$$ (12)

where SA_f is the surface area of the wild-type residue and the SA_exp is the surface area of the completely solvent exposed residue. We approximated SA_exp by calculating the surface area of the wild-type residue in a tetrapeptide (GXG where the X represents the wild-type residue) capped with an acetyl (ACE) and n-methyl amino group (NME). Buried residues were defined as having less than 10% of their side chain exposed and exposed residues were characterized as having more than 50% of their side chain exposed.

Results

Calculation of Stability Changes Using Model-1 and Model-2

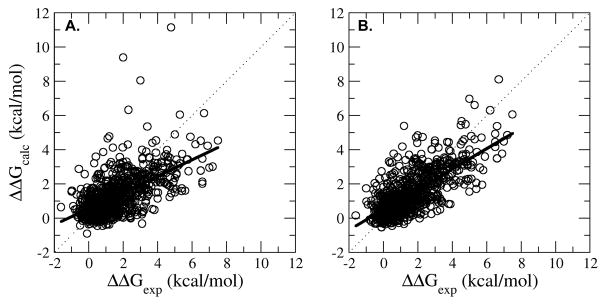
In this work, we tested the LIE protein stability approach on 822 single point mutations and compared the calculated results with corresponding experimental results. This set contained large to small mutations from 10 different proteins which contained varying secondary structural content. The first LIE protein stability model (Model-1) was parameterized using the data from all of the mutations (Table 1). The correlation coefficient and the average absolute error between the calculated and experimental ΔΔG were 0.61 and 0.94 kcal/mol, respectively (Table 3 and Figure 2a). These results are comparable with the best performing programs available today as reported by Potopov et al. ²⁹

Figure 2.

Calculated ΔΔG (ΔΔG_calc) versus experimental ΔΔG (ΔΔG_exp) for Model-1 (A) and Model-2 (B). Model-1 was trained on all mutation types and Model 2 was trained on separate mutation types (Model-2) (B). The dotted black line corresponds to the x=y line and the solid black line corresponds to the least squared fit line between ΔΔG_exp and ΔΔG_calc. The correlation coefficients were 0.61 and 0.72, for Model 1 and Model 2, respectively (See Table 1).

The second LIE protein stability model (Model-2) was parameterized to treat different types of mutations. We divided our mutations into three groups: neutral, charged and glycine/proline mutations. The neutral group training set contained mutations where the side chain of the wild-type and the mutant residue had a zero net charge. The charged group training set contained mutations involving ionizable residues (R,K,D,E) for the wild-type or mutant residue. The rationale behind separating the charged and neutral mutations is that the magnitude of the electrostatic and reaction field energies are much larger for charged groups and will dominate the fit of the electrostatic and polar solvation LIE coefficients. Secondly, for the Generalized Born type implicit solvent models the polarization of charged residues is underestimated within the protein compared to neutral residues resulting in the overstabilization of salt bridges. As a result, implicit solvent models have treated charged and neutral residues separately using different internal dielectric constants.^43,65 The remaining residue group contains mutations where the wild type residue is being mutated to a glycine or where proline is the wild type residue being mutated to a smaller residue. These mutations typically cause the largest changes to the structure and conformational entropy of the protein backbone and therefore should be treated differently than other mutations.

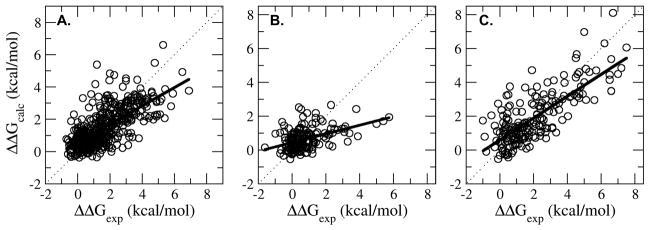
The three residue-type models exhibited correlation coefficients ranging from 0.45 to 0.77 and absolute errors ranging from 0.80 to 0.94 kcal/mol (Table 3 and Figure 3). The lowest correlation coefficient was from the prediction of mutations of or to charged groups (r = 0.45) however the absolute error of these mutants was quite low (0.72 kcal/mol). The largest absolute error was from predicting mutations to glycine (0.92 kcal/mol); it may be harder to reproduce the destabilizing effects of a glycine mutation since our sampling protocol is limited to side chain prediction in this work and the remainder of the protein is not allowed to relax. Nevertheless, these residue sub-types demonstrated an improvement in the correlation coefficient and absolute error between 7 and 18% with respect to an overall fit of LIE coefficients without respect to residue type (Table 3). With respect to predictions for the whole set of 822 mutations, the correlation coefficient and absolute error between the ΔΔG_calc and the ΔΔG_exp is 0.72 and 0.82 kcal/mol respectively, which is superior to Model-1 (0.61 and 0.94 kcal/mol) but the real advantage/improvement of Model-2 over Model-1 is the prediction of experimental outliers as described in the following section.

Figure 3.

Calculated ΔΔG (ΔΔG_calc) versus experimental ΔΔG (ΔΔG_exp) for Model-2. Model-2 involved separate fitting on mutations involving neutral (A), charged (B) and glycine/proline residues (C). The dotted black line corresponds to the x=y line and the solid black line corresponds to the least squared fit line between ΔΔG_exp and ΔΔG_calc. The correlation coefficients for the neutral, charged and glycine/proline residue models were 0.69, 0.45 and 0.77, respectively (See Table 1).

Why does Model-2 perform better than Model-1?

The main difference between the performance of Model-1 and Model-2 is the improvement in the predictions of hot spot mutations (|ΔΔG_exp| > 2 kcal/mol). The sensitivity measure quantifies how many hot spot mutations were correctly identified (true positive) compared to the total number of hot spot mutations predicted (true positive + false negative) and improved by 12% using Model-2 over Model-1 (Table 4). Furthermore, 80% of the calculated outliers in Model-1 are hot-spot mutations (an outlier is defined as having an absolute error larger than two standard deviations above the average absolute error of Model-1). Figure 4 shows the performance of Model-2 with the outliers of Model-1. By fitting individual mutation types (neutral, charged and Gly/Pro), 90% of these mutations demonstrate improved absolute errors relative to the results for Model-1. A notable example is E75V from Staph nuclease which had a predicted ΔΔG_calc of 6.33 and 2.70 kcal/mol with Model-1 and Model-2 respectively, relative to the ΔΔG_exp value of 2.30 kcal/mol. Model-2 is able to decrease the range of the ΔΔG_calc and the number of outliers which increases the correlation between ΔΔG_calc and ΔΔG_exp. The rest of the results section will focus on the analysis of results using Model-2.

Figure 4.

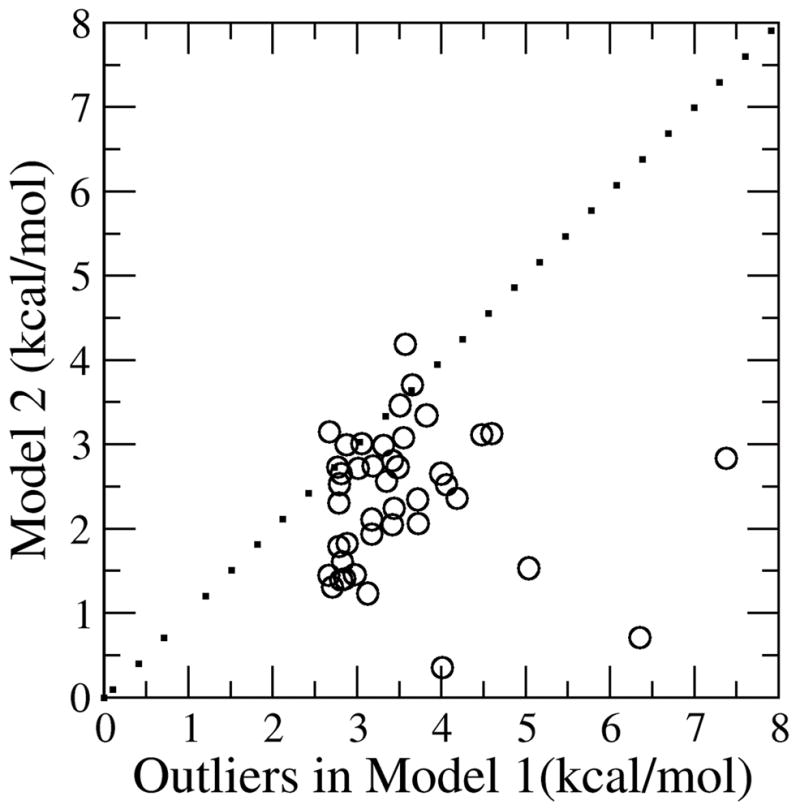
Absolute errors for Model 1 outliers using Model 2. All of the outliers had an absolute error higher than 2.5 kcal/mol using Model 1 (42 outliers). The dotted line is the x=y line. Any points below this line represent the outliers which had lower absolute errors for Model 2 compared to Model 1 (approximately 90 % in this case).

Performance of Model-2 with different types of mutations

Model-2 exhibits a very good correlation and a low average absolute error between experimental and calculated ΔΔG values (Table 3); values which are superior to those reported by Potapov et al..²⁹ In order to further understand the predictive abilities of Model-2, we evaluated the performance of mutations categorized by the surface area exposure and secondary structure of the wild-type residue and mutation type (alanine or non-alanine mutagenesis) (Table 5). Alanine (mutagenesis) and non-alanine mutations had similar correlation coefficients but non-alanine mutations had a higher average absolute error; this group contained all of the mutations involving glycine which demonstrated the highest absolute error of all three residue types in Model-2 (Table 3). Mutations categorized by secondary structure had correlation coefficients which ranged from 0.54 to 0.75. The turn population was the smallest population of mutations which appeared to affect the value of the correlation coefficient. The greatest variation in the results was seen amongst the groups divided up based on surface area exposure. Mutations involving highly exposed residues had the lowest correlation coefficient of all the different groups (r = 0.35). The poor performance of surface exposed mutations may be due to the ΔΔG range for mutations of this type; the ΔΔG range is very small which reflects the high dielectric solvent screening of these mostly polar and charged residues. Previous studies have also reported higher correlation coefficients for mutations involving buried residues compared to exposed residues.^22,25–27 In contrast, the mutations involving buried residues had the highest absolute error of all groups of mutations (average absolute error = 1.01 kcal/mol). Buried residues tend to be more sensitive to sequence changes. In this case, 57% of the buried mutations are destabilizing hot spot mutations (<|ΔΔG_exp|> = 2.52 kcal/mol, Table 6) with an average absolute error of 1.12 kcal/mol.

Table 5.

The Average Unsigned Error and Correlation Coefficient between the Calculated and Experimental ΔΔG values for the Different Structural Features

Type	NMUT	<|ΔΔGexp|>	<|ΔΔGcalc|>	< | error | >	r
Alanine mutagenesis	385	1.53	1.46	0.78	0.72
Non-Alanine	437	1.70	1.68	0.85	0.73
Beta	310	2.07	2.05	0.87	0.73
Helix	217	1.60	1.60	0.79	0.76
Turn	90	1.10	1.03	0.84	0.54
Coil	202	1.20	1.21	0.76	0.67
Exposed	257	0.69	0.62	0.60	0.35
Buried	277	2.52	2.18	1.01	0.69

N_MUT = number of residues;< |ΔΔGexp |>= average absolute experimental ΔΔG;< |ΔΔGcalc |>= average absolute calculated ΔΔG; <|error|>= average unsigned error (units of kcal/mol)

Table 6.

The Effect of Correct Structural Predictions on Energetic Predictions

Structural Predictions	Energetic Predictions	Count	Conditional probability
Correct	Correct	22	0.76
Correct	Incorrect	7	0.24
Incorrect	Correct	6	0.60
Incorrect	Incorrect	4	0.40

In the training set, there were 39 mutations which had corresponding structural information for the wild-type and mutant structures according to the Protherm database.

One of the apparent shortcomings of the LIE protein stability approach is distinguishing between stabilizing and destabilizing mutations. According to Table 4, Model-2 is quite successful at predicting whether a mutation is stabilizing or destabilizing (89% accuracy). Nevertheless, the sensitivity was quite different for the prediction of destabilizing and stabilizing mutations. Mutations with ΔΔG_exp values greater than 0 kcal/mol were predicted with a sensitivity of 95%, in contrast, mutations with ΔΔG_exp values less than 0 kcal/mol were predicted with a sensitivity of 23%. Hence, Model-2 performs poorly at correctly identifying stabilizing mutations. This is likely an effect of the distribution of ΔΔG_exp values in our benchmark set used to parameterize the LIE model. It is composed of mainly destabilizing mutations (91 %); and the range of ΔΔG values for stabilizing mutations which is very small.

What effect does structure prediction have on energy prediction?

We turn next to examine how the accuracy of the structure predictions affect stability change predictions. We evaluated the accuracy of the structural predictions using the criterion for a correct structure prediction that all χ dihedrals deviated from the X-ray rotamer geometry by less than +/− 30° and an energy criterion that the absolute error between the ΔΔG_calc and ΔΔG_exp was less than 1.5 kcal/mol (Table 6). Complete structural data, including both wild-type and mutant PDB structures, was available for 39 of the mutations. The distribution of mutation residue-types is different in this small set of mutations (67% neutral/18% charged/15% glycine/proline) with structural data compared to the larger benchmark set of 822 mutations (55% neutral/21% charged/24% glycine/proline). Correspondingly, the accuracy of the stability change calculations varies between these two sets; 72% of the stability changes were correctly predicted in the set where the structure of wild-type and mutant was known, in contrast, 86% of the stability changes were predicted correctly for the benchmark set of 822 mutations. Therefore, the small set includes a large percentage of mutations from the benchmark set that were challenging stability change predictions. For this set, the percentage of correct stability change predictions is reduced from 76% to 60% when the predicted side chain deviates by more than +/− 30° from the X-ray rotamer geometry (Table 6). In the cases of correct structure and incorrect stability change predictions (24%), all the mutations are from large residues (K,F, L, or Y) to alanine or glycine. Modeling additional structural reorganization and relaxation may be needed to capture the real effect of the mutation on the surrounding residues. Nevertheless, our results indicate that accurate structural models of wild-type and mutant enhance the ability to predict stability changes.

The accuracy of the stability change predictions is also affected by the range of possible energies that are sampled by a residue; this is highly dependent on the amino acid type, location of the residue and the energy function. For 60% of the incorrect structure predictions, ΔΔG_calc was predicted within +/− 1.5 kcal/mol. An explanation for this effect is that for these cases the X-ray and the incorrectly predicted rotamer state are approximately isoenergetic which results in very similar ΔΔG_calc values. For example, this effect is observed for the stability calculation of the S44A mutant in T4-Lysozyme (2LZM) where the wild-type rotamer was predicted incorrectly (Figure 5). In the X-ray structure, the hydroxyl group of the S44 side chain is solvent exposed and relatively close to a crystal water, in contrast, the S44 side chain is forming a hydrogen bond with backbone carbonyl group of N55 for the predicted rotamer (Figure 5). For the S44A mutant, the ΔΔG_calc values are 0.46 and −0.07 kcal/mol (relative to ΔΔG_exp = −0.34 kcal/mol) using the minimized wild type and the predicted rotamer as the wild-type model. In both cases, this method is robust enough to predict the correct stability changes despite the different side chain geometries. Nevertheless, stability change predictions are more sensitive to the side chain conformations of charged residues which are susceptible to forming salt bridges. For the stability calculation of the K116A mutant in staphylococcal nuclease (1STN), the wild type side chain geometry was predicted incorrectly and the absolute error of the stability change was greater than 1.5 kcal/mol. In the X-ray structure, the K116 side chain is solvent exposed and distant from most residues of the protein except from a crystal water (Figure 6). In contrast, the predicted rotamer state of K116 side chain forms an ion pair with the D122 side chain. If the correct wild type rotamer state is used, the ΔΔG_calc changes from 1.02 kcal/mol to 0.24 kcal/mol which is in better agreement with experimental measurements (ΔΔG_exp = −0.70 kcal/mol). The error in the ΔΔG_calc prediction of the K116G mutation appears to be a result of the erroneous salt bridge conformation formed by K116.

Figure 5.

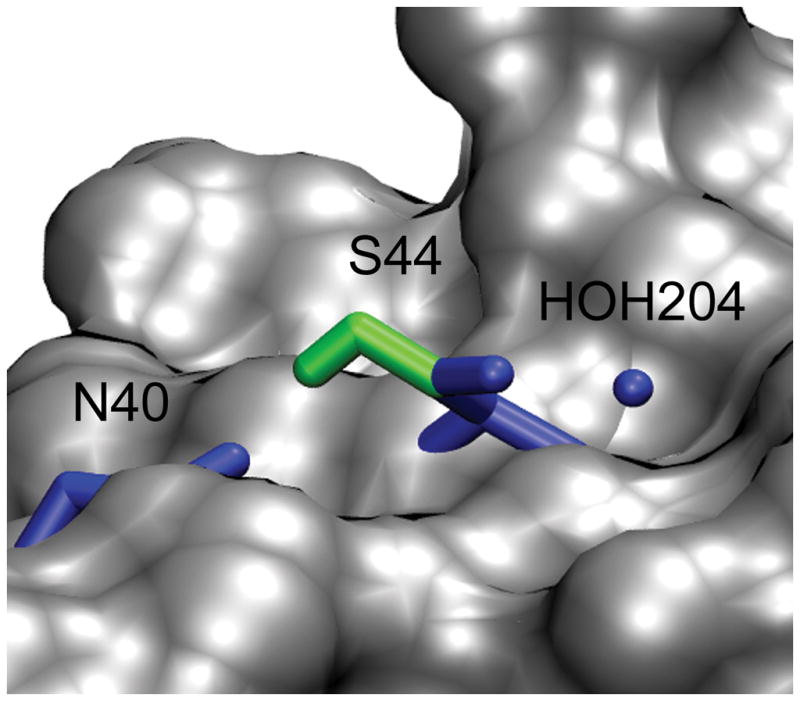
Incorrect structural predictions with accurate energy predictions. In each case, the wild-type rotamer geometry deviated from the crystal structure reference state by more than 30° for the ΔΔG_calc of the S44A mutant in T4-Lysozyme (2LZM). The X-ray model is shown in blue and the predicted models is shown in green. All of the atoms in licorice are heavy atoms except for the hydrogen of the hydroxyl group of S43.

Figure 6.

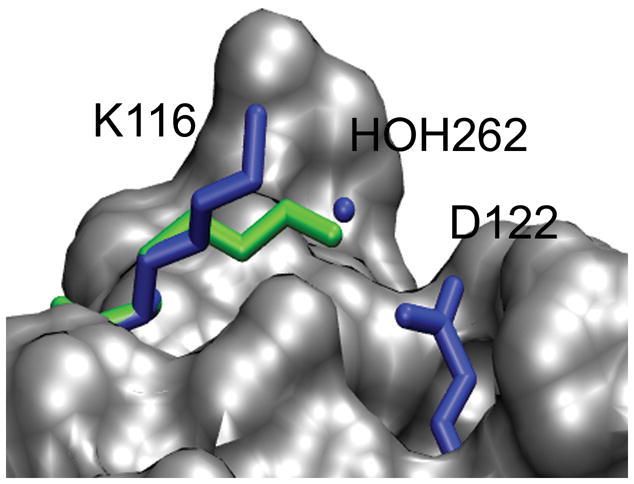
Incorrect structural predictions with incorrect energy predictions. In this case, the wild-type rotamer geometry deviated from the crystal structure reference state by more than 30° for the ΔΔG_calc of the K116A mutant (A) in staphylococcal nuclease (1STN). The X-ray model is shown in blue and the predicted model is shown in green.

Discussion

Physical interpretation of the LIE models

The LIE model approximates the free energy change with an empirical scoring function motivated by linear response theory which employs physically motivated energy estimators. In the protein stability LIE model, these estimators capture the differences between the energetic interactions of the mutant and the wild-type protein in the folded and unfolded state. For our calculations of the unfolded state, we use a local tetrapeptide model of the residue of interest with its two N- and C-termini neighboring residues. The role of this model is to capture possible residual structure in the unfolded state compared to a random coil model. By using the folded and unfolded state in our calculations, we see a significant increase in the accuracy of the stability calculations relative to only using the folded state (data not shown). Therefore, the unfolded state model does play a role in the stability calculation by screening the short range folded state interactions.

Based on Equation 6, the relative free energy change (ΔΔG) can be expressed as the difference between the residue-environment interaction energy in the folded (Δ <V_f>) and unfolded state (Δ <V_u>) in going from the wild-type to the mutant where i is one of the components of the energy.

$$\mathrm{\Delta }\mathrm{\Delta }{G}^i\propto (\mathrm{\Delta }<V_f^i>-\mathrm{\Delta }<V_u^i>)\propto (\mathrm{\Delta }\mathrm{\Delta }<V^i>)$$ (13)

The sign of ΔΔ<Vⁱ> determines whether a mutation is stabilizing or destabilizing relative to the wild-type protein. If the ΔΔ< Vⁱ > is positive, the wild-type is contributing more favorably to the folding free energy than the mutant (ΔΔGⁱ > 0), in contrast, if the ΔΔ<Vⁱ> is negative, the mutant is contributing more favorably to the folding free energy than the wild-type. The magnitude of ΔΔ<Vⁱ> indicates how important a particular energy estimator is to determining the relative free energy change of the mutant compared to the wild-type. In order to maintain the physical interpretation of the sign in Equation 13, the LIE coefficients should be positive. This is the case for all of the models except the neutral residue model (Model-2) (Supplemental Figure 1A). Here, the ΔΔV_LJ energies are shifted to more positive values since a large number of mutations in this group are buried hydrophobic residues that are mutated to smaller residues which results in an unfavorable loss of vdw contacts. ΔΔV_el and ΔΔG_el values are smaller but have more outliers because of the mutations involving surface exposed polar residues. All of the energies have positive coefficients except for the coefficients for the ΔΔG_vdw and ΔΔG_cav terms. The negative coefficient for the ΔΔG_vdw term is a result of fitting coefficients for the ΔΔV_LJ and ΔΔG_vdw energy estimators separately; these estimators are typically fit with the same coefficient which is positive.⁴¹ Separate fitting of each energy estimator improves the results relative to a model where the ΔΔV_LJ and ΔΔG_vdw energy estimators are combined however the physical meaning behind each of the coefficients is lost since both estimators are highly correlated. We hypothesize that the negative value for the coefficient of the ΔΔG_cav energy estimator reflects conformational reorganization effects which are not treated explicitly in our model. The corresponding coefficient absorbs the reorganization free energy difference between the wild-type and the single point mutant; this is always inversely correlated to the change in the side chain size during the mutation, as absorbed by its change in exposed surface area. In a previous protein-ligand binding study based on LIE models, negative coefficients were also observed for the surface area cavity free energy estimator⁴¹ and it was suggested that this energy term was statistically correlated with reorganization effects as well.

The model for mutations involving charged residues was originally fit using all five energetic descriptors but only required two coefficients after statistical refitting (Supplemental Figure 2). The driving force behind this model appears to be the electrostatic (ΔV_ele) and polar solvation (ΔG_el ) energies that span the broadest ranges of all the five energies. As a result, coefficients for these energetic descriptors are smaller than the corresponding values for the neutral residue model. The resulting energy distribution range decreases dramatically when these energies are combined. This effect is well known; it results from the fact that ΔG_el is a reaction field, which largely cancels the direct electrostatic energy term, ΔV_ele. The ΔΔG_cav and ΔΔG_vdw terms are less significant for fitting the charged residues since most of the charged residues are located on the surface (89%). These terms may become more significant as we add more mutation types to the model (small to large mutations).

The model for glycine/proline mutations was also originally fit with five coefficients but only required two coefficients during refitting (Supplemental Figure 3). ΔΔV_LJ makes the largest contribution to this model since the mutation involves the removal of the whole side chain and the loss of the most contacts. The coefficients for the ΔΔV_LJ and ΔΔG_vdw energy estimators are similar for this model; this is consistent with the previous LIE derivation for protein-ligand interactions in implicit solvent⁴¹ as well as previous derivations in explicit solvent where the vdw estimator includes solute-solute and solute-solvent vdw forces scaled by one coefficient.³⁰ Since the training set included charged residue to glycine mutations, the distributions and coefficients of the ΔΔV_el and ΔΔG_el energy estimators were similar to those observed for mutations involving charged residues.

Performance of Mutations involving Charged Residues

The mutations involving charged residues demonstrated the worst fit of the mutation residue-type models. Fitting was affected by the ΔΔG_exp range. The ΔΔG_exp range was the smallest for the mutations involving charged residues and largest for the mutations involving glycine/proline; this was similar to the trend in the corresponding correlation coefficients (Table 3 and Figure 3). The ΔΔG range (both experiment and calculation) is the largest for mutations involving glycine and proline since they typically involve large structural changes to the native state of the protein, in contrast, the smallest range is observed experimentally for mutations involving charged residues. Mutations involving charged residues are usually located in solvent exposed positions and because of solvent screening have a smaller effect on stability. Furthermore, the charged residue model training set constituted 40% of the stabilizing mutations in our data set which are the most difficult type of mutations to predict. ΔΔG predictions of stabilizing mutations were challenging because the LIE model was trained on a benchmark set containing mostly destabilizing mutations. Unfortunately, this bias is difficult to avoid since there are many more destabilizing than stabilizing mutations.^77,78

Comparison with previous methods

We compared the results for single point mutations from the LIE protein stability model (Model-2) to previous results from Potapov et al.²⁹ For the six different approaches, correlation coefficients ranged from 0.26 to 0.59 and the average absolute errors ranged from 1.00 to 1.69 kcal/mol. Based on these results, the LIE protein stability model is superior to these other approaches (r=0.72; <|error|> =0.82). Nevertheless, the original studies report significantly higher correlation coefficients for these methods, ranging from 0.62 to 0.75.^{22,24,25,27,79} The results from the protein survey were worse because the testing sets were larger and more diverse than in the original studies and unbiased through the removal of mutations used in the original training sets for each method. In addition, these programs may be optimized by the labs that developed them, and the comparison studies may not be using the programs in the optimum way.²⁷

Effects of Sampling for the Mutant Structural Model

The LIE protein stability approach appears to be among the best programs available to calculate stability changes despite the lack of structural relaxation in the current version of the LIE models. In our calculations, the protein-protein interactions are on average underestimated for the folded mutant because surrounding side chains do not repack to optimize the interactions with the smaller mutant residue. Nevertheless, the reorganizational cost for repacking the side chains around the mutated residue is also not accounted for and these two effects tend to cancel. Secondly, structural relaxation may only be beneficial for certain types of mutations. Yin et al.²⁶ and Kellogg et al²⁷ noted that using a flexible backbone sampling improved the correlation between the calculation and experiment for mutations where the wild-type residue was smaller than the mutant residue. Lastly, structural relaxation may also cause errors in the stability change calculation if the sampling approach introduces erroneous structural changes into the mutant structures. Kellogg et al. noted that using backbone relaxation actually degraded the results for the entire set of mutations.²⁷

Treatment of Conformational and Solvation Entropy

We note that the LIE protein stability equations are missing explicit terms for the treatment of entropy. Free energy changes produced by linear response models, such as the one employed here, implicitly include conformational entropy effects through the linear response expressions which relate potential energy differences to free energy differences. Moreover, the target of our calculations is relative stabilities resulting from the net contributions of the differences between the unfolded and folded states of the wild-type and mutant protein. The LIE models capture these relative entropic effects only in an average way. Solvent entropic effects are implicitly included in the solvation free energies modeled in this work by AGBNP effective potential, although important structural waters may not be correctly modeled under the continuum approximation on which the model is based.

Multiple mutations

Our broader interest is to apply this method to proteins with multiple mutations. We applied the LIE protein stability approach to a small group of double mutations from serine protease inhibitor using Model-2. This subset of 17 mutations is included in the Protherm database and has also been tested with the Eris approach.²⁶ Figure 7 shows a scatter plot of calculated vs experimental ΔΔG values for this subset of 17 mutations. Surprisingly, the correlation coefficient and average absolute error (r = 0.80 and <|error|> = 0.69 kcal/mol) improve compared to the single point mutation set. Using a fixed backbone approach, a correlation coefficient between experimental and calculated ΔΔG values of 0.69 (compared to 0.64 with single point mutations on a larger set) was reported for the Eris method, which is similar to the trend in our results. The improvement of double mutations over single point mutations is probably due to a cancellation of errors. In this test set, the positive cooperativity of the ΔΔG_exp for the double mutations compensates for the errors from the original model of single point mutations which underestimate ΔΔG_calc relative to ΔΔG_exp. Based on these results, it appears that the LIE protein stability approach is a potentially useful tool for calculating protein stability changes caused by multiple mutations that will be improved by incorporating structural relaxation in order to accurately capture the effects of cooperativity between mutated residues.

Figure 7.

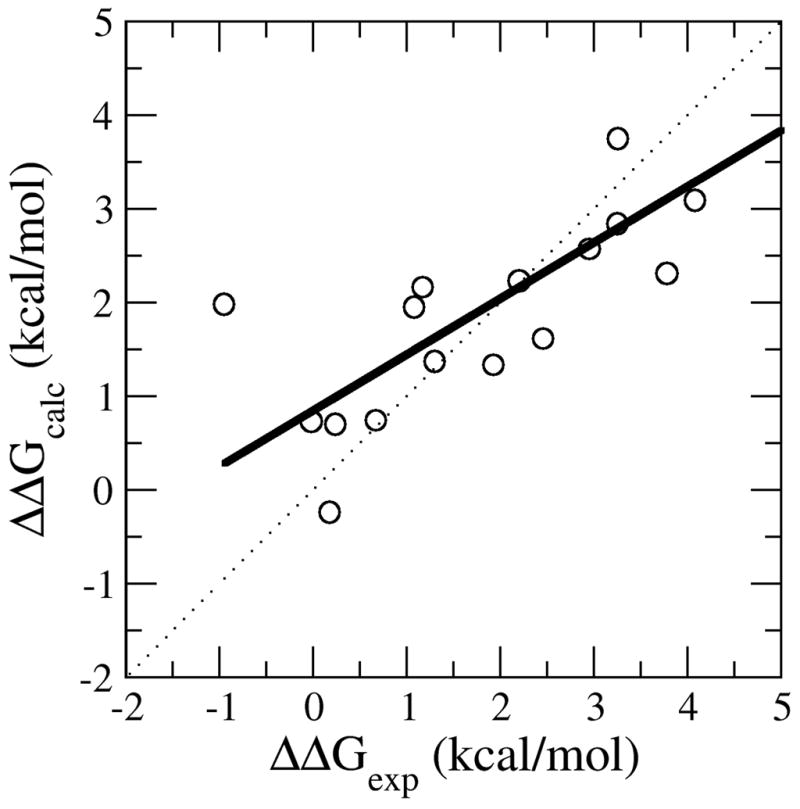
Calculated ΔΔG (ΔΔG_calc) versus experimental ΔΔG (ΔΔG_exp) for a set of serine protease inhibitor (2CI2) double mutants. The dotted black line corresponds to the x=y line and the solid black line corresponds to the least squared fit line between ΔΔG_exp and ΔΔG_calc. The correlation coefficient is 0.80 using Model 2.

Conclusions

In this work, we have presented an approach to calculate relative protein stabilities based on the Linear Interaction Energy model to estimate free energies and the protein local optimization program (PLOP) to sample side chain rotamer states. On a large set of single point mutations, this method leads to results that are comparable to or better than results reported for existing methods even without including structural relaxation in the calculations. Future work will focus on using a better sampling approach to allow for more extensive relaxation of the protein structure following mutations and a revised version of the AGBNP implicit solvent model⁸⁰ which includes a first shell solute-solvent term and an improved model for protein salt bridge formation. With further development of this approach to model multiple mutations, we can begin to integrate sequence data and energetic information to examine the relationship between protein stability, fitness and drug resistance.