Automated Prediction of Protein Association Rate Constants

SUMMARY

The association rate constants (k_a) of proteins with other proteins or other macromolecular targets are a fundamental biophysical property. Observed rate constants span over 10 orders of magnitude, from 1 to 10¹⁰ M⁻¹s⁻¹. Protein association can be rate-limited either by the diffusional approach of the subunits to form a transient complex, with near-native separation and orientation but without short-range native interactions, or by the subsequent conformational rearrangement to form the native complex. Our transient-complex theory showed promise in predicting k_a in the diffusion-limited regime. Here we develop it into a web server called TransComp (http://pipe.sc.fsu.edu/transcomp/) and report on the server’s accuracy and robustness based on applications to over 100 protein complexes. We expect this server to be a valuable tool for systems biology applications and for kinetic characterization of protein-protein and protein-nucleic acid association in general.

INTRODUCTION

The association between two proteins or between a protein and another macromolecular target is at the center of many biological processes. The association rate constants (k_a) often play essential functional roles (Schreiber et al., 2009). Observed k_a values span over 10 orders of magnitude, with high values reaching 10¹⁰ M⁻¹s⁻¹ and low values reaching 1 M⁻¹s⁻¹. The aim of this paper is to present a web server, TransComp, that accurately predicts association rate constants that fall in the high half of the k_a spectrum.

The association of two proteins, A and B, can be generally described by the kinetic scheme (Janin and Chothia, 1990; Alsallaq and Zhou, 2008):

$$\mathrm{A}+\mathrm{B}\underset{k_{-\mathrm{D}}}{\overset{k_{\mathrm{D}}}{\rightleftarrows }}\mathrm{A}*\mathrm{B}\stackrel{k_{\mathrm{c}}}{\to }\mathrm{C}$$

where A*B is a transient complex, in which the two proteins have near-native separation and orientation but have yet to form the short-range specific interactions of the native complex C. k_D denotes the diffusion-limited rate constant for forming the transient complex; k_–D is the rate constant for the reverse process; and k_c is the rate constant for the transition from the transient complex to the native complex via conformational rearrangement and inter-subunit tightening. The overall association rate constant is k_a = k_Dk_c / (k_−D + k_c). Both diffusion and conformational rearrangement can be rate-limiting. The diffusion-limited regime occurs when k_c ≫ k_–D; then k_a ≈ k_D. The conformational rearrangement-limited regime occurs when k_c ≪ k_–D, which leads to k_a = k_c k_D / k_−D.

The above mechanistic picture allows for a rationalization of the over 10 orders of magnitude span of observed k_a values (Alsallaq and Zhou, 2008). The rate constant for forming the transient complex via unbiased diffusion is ~10⁵ M⁻¹s⁻¹ (Northrup and Erickson, 1992; Zhou, 1997; Schlosshauer and Baker, 2004), which, due to the orientational restraints between the two subunits in the transient complex, is much lower than the often quoted Smoluchowski result of 10⁹ to 10¹⁰ M⁻¹s⁻¹. k_a values higher than this “basal” rate constant occur when proteins have long-range electrostatic attraction, which biases the diffusional approach toward the transient complex. Thus the high half of the k_a spectrum corresponds to the diffusion-limited regime. In contrast, in the low half of the k_a spectrum, conformational rearrangement plays a rate-determining role.

A widely used method for calculating k_a in the diffusion-limited regime is based on Brownian dynamics simulations (Northrup et al., 1988; Gabdoulline and Wade, 1997; Elcock et al., 1999; Gabdoulline and Wade, 2001, 2002; Frembgen-Kesner and Elcock, 2010). This approach has two practical limitations. The first is that it has no fixed way of determining the reaction criteria (i.e., the specification of when the transient complex is considered formed), which are often adjusted to achieve optimal agreement with experimental results, thus significantly compromising the predictive power. The second limitation is that, to account for electrostatic interactions between the associating proteins, the simulations take enormous computational times.

These two limitations were overcome by our recently developed transient-complex theory (Alsallaq and Zhou, 2008). The native complex is stabilized by numerous short-range specific interactions between the subunits, but relative translation and rotation are severely restricted. In contrast, the two subunits in the unbound state have few short-range interactions but complete translational and rotational freedom. The boundary between these two regimes naturally specifies the transient complex. Moreover, k_a was found to be accurately predicted as

$$k_{\mathrm{a}}=k_{\mathrm{a}0}\text{exp}(-\mathrm{\Delta }{G}_{\text{el}}^{*}/k_{\mathrm{B}}T)$$ (1)

where k_a0 is the “basal” rate constant for reaching the transient complex by random diffusion, and the Boltzmann factor captures the rate enhancement due to electrostatic attraction. Both k_a0 and $\mathrm{\Delta }{G}_{\text{el}}^{*}$ (the electrostatic interaction energy in the transient complex) can be efficiently calculated. The transient-complex theory, without adjusting any parameters, has been found to quantitatively rationalize experimental k_a results for a number of complexes, including that of a ribotoxin binding to an RNA loop on the ribosome (Alsallaq and Zhou, 2008; Qin and Zhou, 2008, 2009; Pang et al., 2011).

The transient-complex theory promises to solve half of the association rate constant problem, i.e., for the diffusion-limited regime where the association rate constants fall in the high half of the k_a spectrum. Here we show that this promise is indeed fulfilled by a web server implementation of this theory. The server predictions agree closely with experimental k_a results (ranging from 2.1 × 10⁴ to 1.3 × 10⁹ M⁻¹s⁻¹) for a sample of 49 protein complexes. Applications to over 100 complexes demonstrate the robustness of the TransComp server. These applications constitute the hitherto most extensive test of any computational method for predicting k_a. While TransComp does not directly deal with molecular flexibility during the association process, we illustrate here that, by judicially choosing the input structure of the protein complex, TransComp is able to treat three important classes of association processes that couple conformational changes. In doing so we not only predict the association rate constant but also provide mechanistic insight into the association process.

RESULTS AND DISCUSSION

Implementation of TransComp

The TransComp server can be accessed at http://pipe.sc.fsu.edu/transcomp/. The input is the structure of the native complex. The k_a calculation has three components: generation of the transient complex; calculation of the basal rate constant k_a0, and calculation of the electrostatic interaction energy $\mathrm{\Delta }{G}_{\text{el}}^{*}$ in the transient complex. While this overall procedure is the same as in the original version of the transient-complex theory (Alsallaq and Zhou, 2008; Qin and Zhou, 2008), a number of new features are introduced here to achieve full automation and significant improvement in robustness.

The transient complex is identified through mapping the interaction energy landscape in and around the bound-state energy well. Because we focus on the diffusion-limited regime, conformational rearrangement of the subunits is assumed to be fast and native conformations are assumed for the subunits. The resulting interaction energy function is a smooth surface in the six-dimensional space of relative translation and relative rotation. The three translational degrees of freedom are represented by the vector (r) from the center of the binding site on subunit A to the center of the binding site on subunit B. The three rotational degrees of freedom consist of a unit vector (e) fixed on subunit B and the rotation angle χ around e. In the native complex, the magnitude of r, denoted as r, is zero; e is perpendicular to the least-squares plane of the interface; and χ = 0. The six-dimensional translational/rotational space around the native complex is sampled randomly, with the sole restriction of r < r_cut, to find clash-free configurations. Instead of a fixed r_cut, here an automated procedure is used to determine r_cut so that the clash-free fraction of all configurations sampled passes a threshold.

The interaction energy is simply modeled by the number of contacts, N_c, between the two binding sites in any clash-free configuration. N_c is calculated on “interaction-locus” atoms across the interface, which are cross-interface “cognate” pairs of heavy atoms with < 5 Å intra-pair separations and > 3.5 Å inter-pair separations in the native complex. N_c is the sum of native contacts (formed between cognate pairs when distances are less than 3.5 Å plus the separations in the native complex) and nonnative contacts (formed between noncognate pairs when distances are less than 2.5 Å plus the separations in the native complex). As illustrated in Figure 1, the bound-state energy well is dominated by configurations with high N_c values but a very restricted range of accessible χ values. As the two subunits separate, there is a sudden expansion in the accessible χ. The range of accessible χ is represented by σ_χ, the standard deviation of χ for all configurations at a given N_c. Previously the transient complex was placed at the onset of the increase in σ_χ (Alsallaq and Zhou, 2008). Here we fit the dependence of σ_χ on N_c to a function used for modeling protein denaturation data as two-state transition, and identify the midpoint, where N_c is designated N_c*, of this fit with the transient complex (see Figure 1). That is, configurations with N_c = N_c* make up the transient-complex ensemble; and configurations with N_c > N_c* fall in the bound-state well. When either there is a significant gap in the sampled N_c values or the fitting of the dependence of σ_χ on N_c to the two-state function involves an excessive error, the k_a calculation is aborted. Either scenario indicates that the association is likely not a single-step process, and a direct application of TransComp would be inappropriate (see below for examples of adaptive use of TransComp in dealing with such exceptional cases).

Figure 1.

The output of a typical TransComp run. The table at the top lists the values of k_a0, $\mathrm{\Delta }{G}_{\text{el}}^{*}$, and k_a. The electrostatic surfaces of the two subunits are shown in the middle; each surface is accompanied by a ribbon representation of the other subunit in the native complex, to indicate the binding site. The graphs at the bottom show the N_c vs χ map and the N_c vs σ_χ curve, used for locating the transient complex. χ and σ_χ are in radians. The native complex and the transient complex are indicated by a green circle and a blue line, respectively.

The basal rate constant k_a0 is calculated from force-free Brownian dynamics simulations. Because no force (or torque) is calculated, these simulations are very efficient. Each Brownian trajectory starts from the bound-state well (i.e., from a configuration with N_c > N_c*) and is propagated in the translational/rotational space. At each time step where the criterion N_c > N_c* is satisfied, the protein pair is given a chance to form the native complex. If that happens, the trajectory is terminated. The survival fraction of the Brownian trajectories as a function of time allows k_a0 to be calculated.

The electrostatic interaction energy $\mathrm{\Delta }{G}_{\text{el}}^{*}$ in the transient complex is calculated by numerically solving the Poisson-Boltzmann equation, which is widely used for modeling biomolecular electrostatics. We randomly choose 100 configurations from the transient-complex ensemble, calculate the electrostatic interaction energy for each, and then average over the 100 of them to obtain $\mathrm{\Delta }{G}_{\text{el}}^{*}$. This calculation is also efficient because the solution of the Poisson-Boltzmann equation is done only for the 100 configurations. In comparison, in the approach of using Brownian dynamics simulations to directly obtain k_a, in principle one has to solve the Poisson-Boltzmann equation once at each time step, which amounts to prohibitive computational cost. The electrostatic rate enhancement predicted by the Boltzmann factor of $\mathrm{\Delta }{G}_{\text{el}}^{*}$ (Equation 1) tends to be overestimated when the magnitude of $\mathrm{\Delta }{G}_{\text{el}}^{*}$ is large (Zhou, 1997). Based on analytical results for the overestimate (Zhou, 1997), here we introduce a moderation factor, ${[1+{10}^{-4}\exp (-\mathrm{\Delta }{G}_{\text{el}}^{*}/k_{\mathrm{B}}T)]}^{-1}$.

TransComp accepts the input structure of the native complex in the pqr format, one file for each subunit, which includes coordinates, charge, and radius for each atom. The user can instead supply the Protein Data Bank (PDB) entry name and chain IDs for the two subunits or upload a PDB file for the complex; TransComp will take this input and generate the appropriate pqr files. Hydrogen atoms, typically missing in PDB files, are added. The coordinates in the pqr files are used to generate the transient complex; the charge and radius information is additionally needed for Poisson-Boltzmann calculations. The user specifies the ionic strength at which the Poisson-Boltzmann calculations are to be done. All TransComp computations are passed to the High Performance Computing facility at FSU. In a typical k_a calculation, the generation of the transient complex takes ~3 hours on 8 CPUs; the calculation of the basal rate constant takes ~2 hours on 8 CPUs; and the calculation of $\mathrm{\Delta }{G}_{\text{el}}^{*}$ takes ~0.5 hours on 100 CPUs.

Figure 1 presents the output of a typical TransComp run. In addition to the N_c vs χ map and the N_c vs σ_χ curve noted above for the purpose of locating the transient complex, the output contains the electrostatic surfaces of the two subunits, and the values of k_a0, $\mathrm{\Delta }{G}_{\text{el}}^{*}$, and k_a.

As stated, the input to TransComp is the structure of the native complex. In the absence of the native structure, one could model the structure of the native complex, e.g., by homology or by docking. Our previous study provides an example (Qin and Zhou, 2009). A potential problem with a modeled structure (or a low-resolution native structure) is the presence of steric clashes between the subunits, which could ruin the configurational sampling to determine the transient complex or the subsequent calculation of $\mathrm{\Delta }{G}_{\text{el}}^{*}$. We thus introduced a 1 Å threshold for any cross-interface atom pair in the input structure. If an atom pair with a distance below this threshold is present, the user is notified and the job is not submitted. An input structure in which no cross-interface atom pair has a < 5 Å separation is treated in the same way. Once a job is successfully submitted, the user is given a web link where the status of the job can be checked.

Proteins that associate with rate constants at the high end of the k_a spectrum inevitably experience electrostatic rate enhancement (Schreiber et al., 2009; Pang et al., 2011). In these cases the effects of charge mutation and ionic strength are usually of interest. Here TransComp provides a shortcut. Instead of calculating k_a for a mutant complex (or at a different ionic strength) from scratch, we can safely make the assumption that the transient complex is unaffected by the mutation (or change in ionic strength) (Alsallaq and Zhou, 2008). Then the only quantity that needs to be re-calculated is $\mathrm{\Delta }{G}_{\text{el}}^{*}$. That can then be combined with the k_a0 already calculated to obtain the k_a for the mutant complex (or at the new ionic strength). In the executable released at the TransComp website, we specifically built in a command for this shortcut.

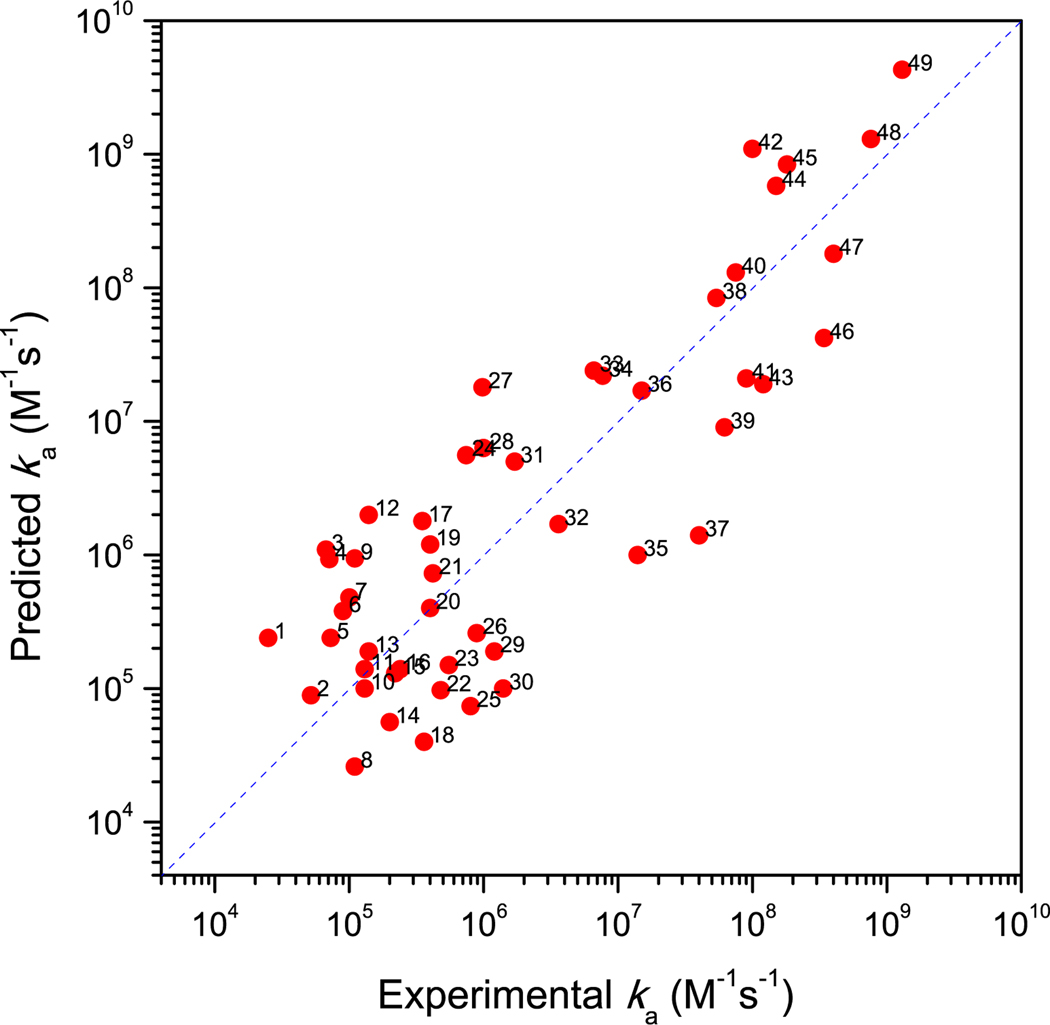
Validation on 49 Protein Complexes

We collected from the literature 49 complexes for which k_a measurements were reported (see Methods section for the sources of the collection). They are listed in Supplementary Information Table S1, and include enzyme-inhibitor, electron transfer, regulator-effector, and growth factor-cell receptor, and other types of complexes. The measured rate constants range from 2.1 × 10⁴ to 1.3 × 10⁹ M⁻¹s⁻¹. The TransComp predictions show good agreement with the measured values (Figure 2). The input structures were taken from the PDB, with entry names given in Table S1; for three complexes, the input structures underwent special treatment in order to treat conformational changes during association, as described below (Figure 3). The correlation between the predicted and experimental logk_a has an R² of 0.72, and the root-mean-square-deviation is 0.73, corresponding to a 5-fold error in k_a. There are no apparent systematic calculation errors with respect to the functional types of the protein complexes, the shapes or sizes of the structures of the complexes, or the magnitude of k_a (although it could be noted that the cases with high k_a values are dominated by enzyme-inhibitor and electron-transfer complexes). Overall the results in Figure 2 demonstrate the predictive power of TransComp for diverse protein complexes with k_a spanning a wide range.

Figure 2.

Comparison of predicted and experimental k_a results for 49 complexes. The numbers refer to entries in Table S1.

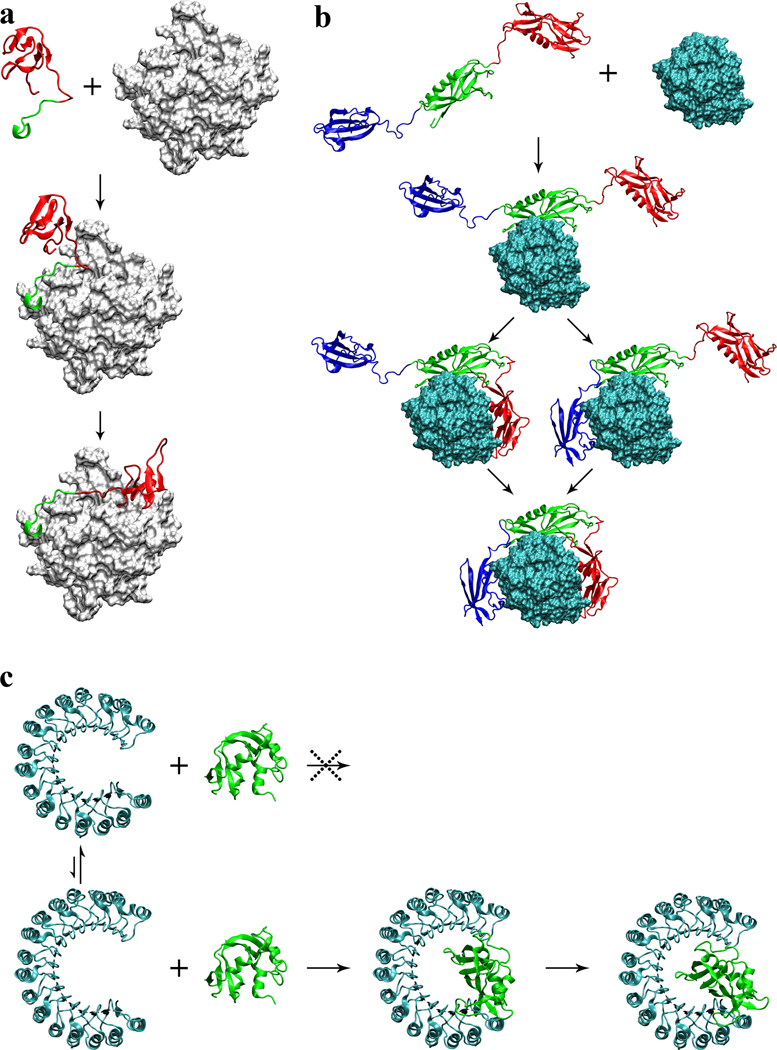
Figure 3.

Proposed association mechanisms of three complexes. (a) Hirudin/thrombin association. First the acidic C-terminal tail (in green) of hirudin docks to the fibrinogen recognition site on thrombin (gray surface); then the N-terminal domain (in red) coalesces around the active site. (b) Streptokinase/plasmin association. First the β domain (in green) of streptokinase docks to plasmin (cyan surface); subsequently the α and γ domains (in red and blue, respectively) coalesce around plasmin to form a tight complex. (c) Ribonuclease inhibitor/ribonuclease A association. Ribonuclease inhibitor (in cyan) undergoes conformational fluctuations, resulting in variations in the horseshoe opening. Small opening prevents the binding of ribonuclease A (in green); large opening allows deep insertion of the enzyme, and subsequently contraction leads to a tight complex.

The k_a values for several of the 49 complexes were computed in previous studies. For example, the association of barnase and barstar and of acetylcholinesterase and fasciculin was studied by brute-force Brownian dynamics simulations (Gabdoulline and Wade, 1997; Elcock et al., 1999; Gabdoulline and Wade, 2001; Frembgen-Kesner and Elcock, 2010). In three of these four studies, the reaction criteria were varied to reach agreement with experimental results, so strictly speaking k_a was not predicted. In the fourth study (Gabdoulline and Wade, 2001), the same criterion was applied to five complexes; good agreement with the experimental result was obtained for the association of barnase and barstar but k_a for the association of acetylcholinesterase and fasciculin was overestimated by 30-fold. We also studied the two complexes by using the transient-complex theory (Alsallaq and Zhou, 2008); the results produced here by TransComp are very similar to those reported in our previous study. Shaul and Schreiber (2005) introduced an empirical energy function that is similar in spirit to our $\mathrm{\Delta }{G}_{\text{el}}^{*}$ but is calculated on the native complex instead of our transient complex. They combined this empirical energy function with an adjustable basal rate constant to calculate k_a for barnase/barstar, acetylcholinesterase/fasciculin, and other complexes. We emphasize that no previous computational methods have been subjected to the kind of extensive tests shown in Figure 2 against experimental data.

In addition to the predictive power (afforded by the lack of adjustable parameters) and computational efficiency, TransComp has one more advantage over brute-force Brownian dynamics simulations. The contributions by random diffusion and long-range electrostatic interactions are teased out, so greater physical insight can be gained on the control of k_a. For example, the measured k_a values of the Gα_i1/RGS4 and elastase/elafin complexes are very close: 1.7 × 10⁶ M⁻¹s⁻¹ (Lan et al., 2000) and 3.6×10⁶ M⁻¹s⁻¹ (Ying and Simon, 1993). However, TransComp reveals that the two complexes have very different basal rate constants, 2.7 × 10⁴ M⁻¹s⁻¹ and 2.9 × 10⁶ M⁻¹s⁻¹, compensated by very different $\mathrm{\Delta }{G}_{\text{el}}^{*}$ values, –3.1 kcal/mol and 0.3 kcal/mol, leading to similar predicted k_a values, 5.0 × 10⁶ M⁻¹s⁻¹ and 1.7 × 10⁶ M⁻¹s⁻¹. We can thus conclude that the Gα_i1/RGS4 association is significantly enhanced by electrostatic attraction, but the elastase/elafin association is formed mostly via random diffusion. Consistent with the latter conclusion, the measured elastase/elafin k_a was little affected by an increase in ionic strength from 0.25 M to 1.1 M (Ying and Simon, 1993).

From Rate Constant to Association Mechanism

Among the 49 protein pairs, three (thrombin/hirudin, streptokinase/plasmin, and ribonuclease A/inhibitor) have unusually extended interfaces in the native complexes (Rydel et al., 1991; Wang et al., 1998; Kobe and Deisenhofer, 1995) (Figure 3), and our initial TransComp runs were aborted due to gaps in the sampled N_c values. The N_c gaps suggested to us that the formation of these three complexes was not a single-step process but involved extensive conformational changes. We show below that, by judicially choosing the input structures of the protein complexes, we can get around the limitation of TransComp in not explicitly incorporating molecular flexibility, and compute rate constants and mechanisms for three classes of association processes represented by the three systems displayed in Figure 3.

Hirudin is a potent thrombin inhibitor isolated from the bloodsucking leech Hirudo medicinalis. It consists of 65 residues and has a tadpole-like conformation with a compact N-terminal domain and a highly acidic, disordered C-terminal tail (Szyperski et al., 1992). The N-terminal domain binds to the active site of thrombin, while the C-terminal tail binds to a basic exosite, the fibrinogen recognition site (Rydel et al., 1991). Neutralization of the C-terminal acidic residues significantly reduces the binding affinity, primarily due to the decrease in k_a (Stone et al., 1989), whereas N-terminal charge mutations have little effect on k_a (Betz et al., 1992). In addition, k_a is strongly dependent on ionic strength, indicating significant electrostatic rate enhancement (Alsallaq and Zhou, 2008; Schreiber et al., 2009); at an ionic strength of 0.175 M k_a = 7.5 × 10⁷ M⁻¹s⁻¹. Stone and Hofsteenge (1986) proposed that the association of hirudin with thrombin involves two steps: binding of the C-terminal tail followed by the binding of the N-terminal domain, with the first step rate-limiting. Our TransComp calculation supports this proposal. Using just the C-terminal 12 residues in their native conformation (but with the diffusion constant scaled to that of full-length hirudin), TransComp predicts a k_a of 1.3 × 10⁸ M⁻¹s⁻¹ (with 320-fold electrostatic rate enhancement) at ionic strength = 0.175 M, in good agreement with the experimental k_a. The underlying assumption of this k_a calculation is that the transition to the native conformation of the C-terminal tail is rapid compared to the docking to the fibrinogen recognition site (Figure 3a), making the docking step diffusion-limited. The docking of the C-terminal tail then allows the N-terminal domain to rapidly coalesce around the active site to achieve an overall tight binding. Our k_a calculation based on this “dock-and-coalesce” mechanism can explain why the C-terminal charge neutralizations significantly reduce k_a whereas the N-terminal charge mutations have little effect on k_a. Hirudin is an example of intrinsically disordered proteins (IDPs) that undergo a disorder-to-order transition upon association, which often results in extended interfaces. Dock-and-coalesce seems to present an attractive mechanism for the association of these IDPs with their macromolecular targets. In particular, this mechanism allows an IDP to avoid the excessively low association rate that it would have if it were to associate as a rigid body. (Our initial TransComp run using the full structure of the native complex of hirudin with thrombin was based on the rigid-body scenario. Had we ignored the significant gaps in the sampled N_c values and carried on the calculation, we would have defined a “transient complex” that is distant, in terms of both relative separation and relative orientation, from the native complex. The calculated rate constant for forming even this distant intermediate via rigid-body diffusion was 20-fold lower than the observed k_a. The rigid-body scenario thus seems very unlikely for hirudin-thrombin association.)

Streptokinase is a thrombolytic drug that acts by binding to either plasminogen or plasmin to form a tight stoichiometric complex, which in turn cleaves substrate plasminogen to form plasmin. Streptokinase consists of three domains, α, β, and γ, connected by flexible linkers; in the complex with plasmin, the three domains embrace plasmin, leading to an extended, disjoint interface (Figure 3b). Studies with streptokinase fragments consisting of one or two domains suggest that the binding to plasminogen or plasmin is first established by the β domain and then reinforced by the α and γ domains (Conejero-Lara et al., 1998; Loy et al., 2001). This is akin to the dock-and-coalesce mechanism. The β domain is distinct from the α and γ domains by its strong charge complementarity with the binding site on plasmin. Our TransComp calculation with the isolated β domain (but with the diffusion constant scaled to that of full-length streptokinase) gives a k_a of 8.4 × 10⁷ M⁻¹s⁻¹, which compares well with the experimental value of 5.4 × 10⁷ M⁻¹s⁻¹ (Cederholm-Williams et al., 1979). Our results thus strongly support the association mechanism shown in Figure 3b, whereby the rate-limiting docking of the β domain of streptokinase is followed by fast coalescence of the α and γ domains around their respective binding sites on plasmin. It seems reasonable to suggest that, for any complex with an extended and disjointed interface, some form of the dock-and-coalescence mechanism may be operating.

Ribonuclease inhibitor is a leucine-rich repeat protein with a horseshoe shape; upon binding, ribonuclease A inserts deeply into the horseshoe (Kobe and Deisenhofer, 1995) (Figure 3c). The resulting snuggle fit is responsible for a very high binding affinity. The experimental k_a value (Lee et al., 1989), 3.4 × 10⁸ M⁻¹s⁻¹, is also high, consistent with the highly complementary electrostatic surfaces of the two proteins. Compared to the unbound structure (Kobe and Deisenhofer, 1996), the horseshoe opening (as measured by the closest distance, between His6 N_ε2 and Tyr430 O_η) in the ribonuclease A-bound structure increases from 12.0 Å to 14.4 Å. This opening is still too narrow for rigid insertion of ribonuclease A. We hypothesized that the horseshoe opening is flexible, and can widen further to allow for the insertion of ribonuclease A. A normal mode analysis based on the elastic network model by the EINemo program (Suhre and Sanejouand, 2004) identified the lowest-frequency mode as the oscillation of the horseshoe opening. Contraction along this mode resulted in a conformation that is very close to the unbound structure (C_α root-mean-square-deviation at 0.87 Å). Upon expansion to a horseshoe opening of 17.7 Å, the native-complex configuration can be easily generated by rigid-body insertion; TransComp then predicts a k_a of 4.2 × 10⁷ M⁻¹s⁻¹, which is comparable to the experimental value. Our calculations thus suggest that the conformational fluctuations of ribonuclease inhibitor occasionally allow the horseshoe opening to be wide enough for the insertion of ribonuclease A (Figure 3c). This mechanism is reminiscent of the gated substrate access to the buried active site of acetylcholinesterase (Zhou et al., 1998).

The three systems illustrate three important classes of association processes that couple conformational changes. In the first, an IDP undergoes a disorder-to-order transition and forms an extended interaction surface with the target protein. In the second, a multi-domain protein binds to a target, with each domain occupying a separate binding site. In both cases the association mechanism is likely to be stepwise and we specifically proposed the dock-and-coalesce mechanism. To calculate the association rate constants of the two systems we further assumed that the docking step is rate-limiting and the coalescing step is rapid. The third class of association processes involves the breathing motion of the target, which we captured by normal mode analysis. In calculating the rate constant, we further assumed that the breathing motion is fast and the subsequent association step is rate-limiting. In all these cases, it would be possible to remove the further approximations on the putative non-rate-limiting steps and calculate the overall association rate constants more rigorously.

Predictions on a Diverse Set of 132 Complexes

To test the robustness of TransComp, we applied it to a set of protein-protein complexes originally collected as a benchmark for protein-protein docking (Hwang et al., 2010). Out of the 176 enzyme-inhibitor, antibody-antigen, and other types of complexes, direct application of TransComp was successful in 132 cases; among these we could find experimental k_a values for 40 cases, which are part of the 49 complexes presented above. TransComp runs were aborted in the other 44 cases; they likely involve multi-step association processes and were not further pursued here. Depending on the extent of conformational change upon association, Hwang et al. (2010) grouped the docking benchmark set into a “rigid-body” category (with 121 complexes), a “medium-difficulty” category (with 30 complexes), and a “difficult” category (with 25 complexes). Not surprisingly, the success rate of TransComp runs for the rigid-body category (98/121 = 81%) was significantly higher than that of the medium-difficulty and difficult categories (34/55 = 62%).

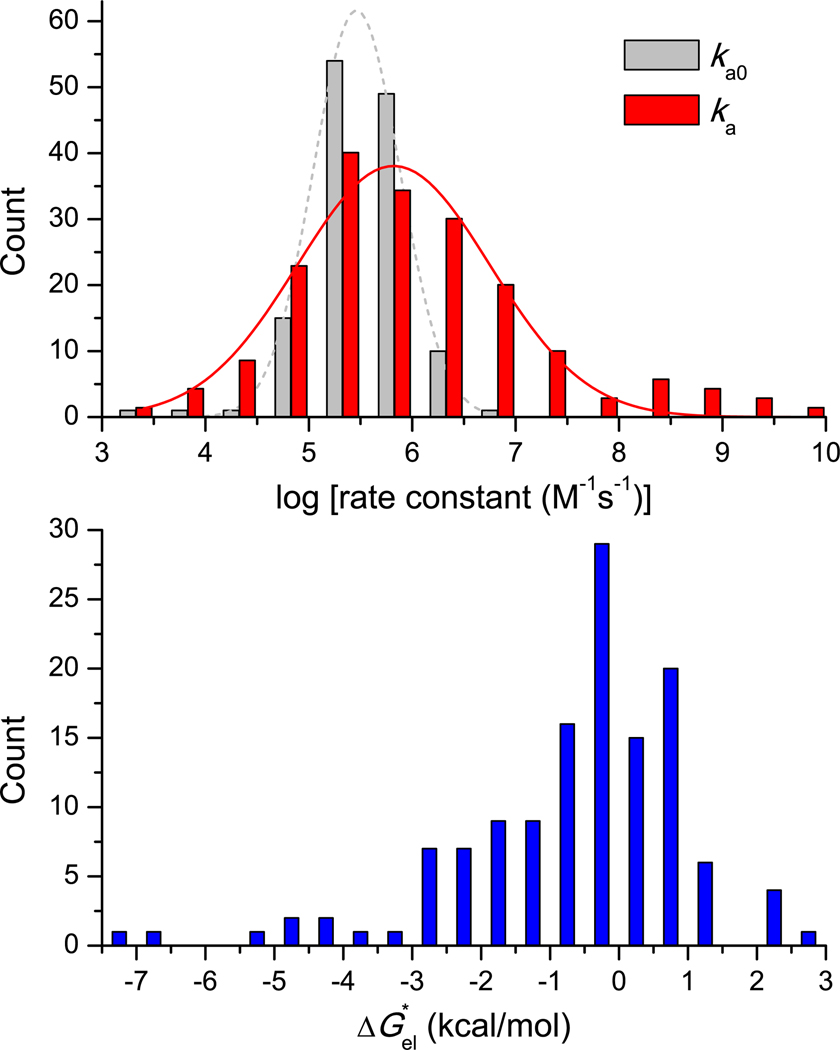
The calculated values of the basal rate constant k_a0, electrostatic interaction energy $\mathrm{\Delta }{G}_{\text{el}}^{*}$ at a common ionic strength of 0.15 M, and association rate constant k_a for the 132 complexes are listed in Table S2. Given the large number of cases studied, these values should constitute a good sample of the results to be expected in the diffusion-limited regime. The distribution of k_a0, k_a, and $\mathrm{\Delta }{G}_{\text{el}}^{*}$ are shown in Figure 4. k_a0 ranges from 3 × 10³ to 4 × 10⁶ M⁻¹s⁻¹, with the distribution peaking at 2.9 × 10⁵ M⁻¹s⁻¹ and spreading nearly one order of magnitude in both directions. This range of exactly calculated k_a0 values is consistent with previous estimates (Northrup and Erickson, 1992; Zhou, 1997; Schlosshauer and Baker, 2004). On the other hand, k_a ranges from 2.6 × 10³ to 4.2 × 10⁹ M⁻¹s⁻¹, with the distribution peaking at 4.6 × 10⁵ M⁻¹s⁻¹ and spreading nearly two orders of magnitude in both directions. The wider range of k_a can be attributed to the wide range in $\mathrm{\Delta }{G}_{\text{el}}^{*}$, from –7.2 to 2.6 kcal/mol, corresponding respectively to 10⁴-fold rate enhancement and 80-fold rate retardation. The distribution of $\mathrm{\Delta }{G}_{\text{el}}^{*}$ peaks at –0.5 kcal/mol, indicating that the association rates of the majority of the protein-protein complexes involve only modest electrostatic enhancement. Interestingly, $\mathrm{\Delta }{G}_{\text{el}}^{*}$ shows good correlation with the empirical function of Shaul and Schreiber (Shaul and Schreiber, 2005) calculated on the native complex, especially for the 98 cases in the rigid-body category (Figure S1).

Figure 4.

Distribution of k_a0, k_a, and $\mathrm{\Delta }{G}_{\text{el}}^{*}$ results for 132 complexes. (a) Histograms of k_a0 and k_a. Gaussian fits are shown as dashed and solid curves. (b) Histogram of $\mathrm{\Delta }{G}_{\text{el}}^{*}$. The data are listed in Table S2.

The modest electrostatic contributions to k_a for the majority of the protein-protein complexes leave ample room for improving electrostatic rate enhancement. This room is illustrated by comparing the complexes of barstar with barnase (1BRS; Table S1) and with ribonuclease Sa (1AY7; Table S2). The two nucleases are structurally similar (with a C_α root-mean-square-deviation of 0.4 Å for 35 core residues), and their complexes with barstar are also similar (Sevcik et al., 1998). Correspondingly the basal rate constants, 9.2 × 10⁴ to 7.9 × 10⁴ M⁻¹s⁻¹, of the two complexes are also very similar. However, the values of $\mathrm{\Delta }{G}_{\text{el}}^{*}$ are very different: –2.9 and –0.8 kcal/mol at ionic strength = 0.15 M. Across the binding interface, positively charged barnase strongly complements negatively charged barstar; in general such charge segregation and complementation are required for significant electrostatic rate enhancement (Pang et al., 2011). In contrast, the barstar-facing side of ribonuclease Sa has a mixed charge distribution. It can be expected that, by making this protein more positively charged, its association rate with barstar can be significantly increased.

CONCLUSION

We have developed the TransComp web server for automated prediction of protein association rate constants. Application to over 100 protein complexes has demonstrated the accuracy and robustness of the k_a calculations in the diffusion-limited regime. We have further shown that, with judicious adaptation, TransComp can also be used to study cases where conformational change is an integral part of the association process, yielding both k_a and the association mechanism. While the applications here focused on protein-protein association, previous studies have demonstrated the success of the underlying transient-complex theory on protein-RNA association (Qin and Zhou, 2008, 2009), indicating that TransComp is applicable to such systems as well.

TransComp will be useful for kinetic characterization of protein-protein and protein-nucleic acid association in general. Particularly noteworthy is its usage in systems biology, where association rate constants provide critical information but are missing in many cases. TransComp can also be used to design proteins with designer k_a values, through manipulating protein charges.

Recent years have seen significant progress in the theory and calculation of protein folding rates (Onuchic and Wolynes, 2004; Dill et al., 2008). In comparison, theoretical work on protein association rates is lagging. With the predictive power demonstrated here for the diffusion-limited regime, TransComp now provides a solution for half of the association problem.

METHODS

TransComp Implementation Details

The implementation of the transient-complex theory in TransComp, outlined in the main text, is basically as described previously (Alsallaq and Zhou, 2008; Qin and Zhou, 2008), but a number of new features are introduced here for automation and robustness. First, the r_cut value for sampling around the native complex to generate the transient complex is determined in an automated procedure. 10⁵ trial configurations are randomly generated around the native complex with the restriction r < r_cut; r_cut is successively increased from 6 Å with an increment of 1 Å. The minimum r_cut at which the clash-free fraction of the trial configurations reaches 10⁻³ is chosen. If this condition is not satisfied at r_cut = 10 Å, the threshold for the clash-free fraction is then lowered to 10⁻⁴. Second, after generating 10⁷ clash-free configurations, the value of N_c* defining the transient complex is determined by fitting the dependence of σ_χ on N_c to

$${\sigma }_{\chi }=\frac{a_1+(a_2+b_2{N}_{\mathrm{c}})\text{exp}[c(N_{\mathrm{c}}-{N_{\mathrm{c}}}^{*})]}{1+\text{exp}[c(N_{\mathrm{c}}-{N_{\mathrm{c}}}^{*})]}$$ [2]

which has the form used for modeling protein denaturation data as two-state transition. Configurations with N_c at the integer closest to N_c* and |χ| ≤ 90° make up the transient-complex ensemble. Third, we abort the k_a calculation when either there is a significant gap (≥ 8) in the sampled N_c values or the fitting of the dependence of σ_χ on N_c to the two-state function involves an excessive error (root-mean-square of residuals > 0.1). Otherwise the k_a calculation continues, with k_a0 obtained from 4000 force-free Brownian dynamics trajectories started from configurations with N_c ≥ N_c*, and $\mathrm{\Delta }{G}_{\text{el}}^{*}$ obtained from solving the nonlinear Poisson-Boltzmann equation by the APBS program (version 1.2) (Baker et al., 2001) according to a protocol described previously (Pang et al., 2011).

Collection of Protein Complexes with Experimental k_a Results

These 49 complexes came from two sources. The Shaul and Schreiber paper (Shaul and Schreiber, 2005) listed 18 complexes with experimental k_a values. We found structures for the native complexes in 16 of these cases, and three of these resulted in aborted TransComp runs and were not further studied. The second source was the docking benchmark (Hwang et al., 2010); among these 176 complexes, we found experimental k_a values from the literature for 40 cases. Combining the two sources, which have four overlapping cases, we obtained a total of 49 complexes with experimental k_a values. Among the 49 cases, initial TransComp runs were aborted for three, but we modified the input structures in these three cases to allow for the use of TransComp.

It should be noted that different experimental techniques can give different k_a values. A case in point is the association of CheY and CheA (1FFW; Table S1). Stopped-flow fluorescence measurements reported k_a = 6.2 × 10⁷ M⁻¹s⁻¹ (Stewart and Van Bruggen, 2004), but surface plasmon resonance (SPR) measurements reported k_a = 3.68 × 10² M⁻¹s⁻¹ (Schuster et al., 1993). Compared to solution-based methods, SPR may suffer from a number of technical limitations (Schreiber et al., 2009). Whenever possible, we avoided using k_a results measured by SPR.

HIGHLIGHTS.

• A method is presented for automated prediction of protein association rates.

• The prediction method is both accurate and robust, and has wide applications.

• With this method, half of the protein association problem is now solved.