REDUCED-DIMENSIONALITY MATCHING FOR 3-D RECONSTRUCTION OF PROSTATE BRACHYTHERAPY IMPLANTS FROM INCOMPLETE DATA

Abstract

X-ray fluoroscopy is widely used for intra-operative dosimetry in prostate brachytherapy. Three-dimensional locations of the implanted radioactive seeds can be calculated from multiple X-ray images upon resolving the correspondence of seeds. This is usually modeled as an assignment problem that is NP-hard. We propose an algorithm that allows us to derive an equivalent problem of reduced dimensionality based on practical observation that the optimal solution has almost zero cost if the C-arm pose is known. The reduced problem is efficiently solved by linear programming in polynomial time. Additionally, our method solves the hidden seeds problem. Simulation results demonstrate that the implanted seeds can be localized with a matching rate of ≥ 98.8 % and reconstruction error of ≤ 0.37 mm using three images with hidden seeds in a few seconds when the pose of the C-arm is known.

1. INTRODUCTION

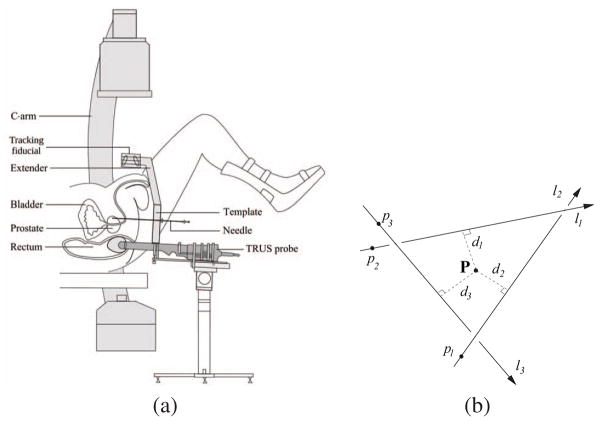
Prostate cancer is one of the most prevalent cancers in men, with 186,320 new cases and 28,660 deaths annually in the United States alone [1]. Low dose permanent brachytherapy is one of the most common treatment methods for low risk prostate cancer [2]. Its success mainly depends on the ability to treat the target gland with a therapeutic dose by implanting a sufficient number of radioactive seeds. Typically, a pre-operative implantation plan is made based on an ultrasound volume study. However, even though the implant procedure will be guided by ultrasound as shown in Fig. 1(a), the seeds are not always positioned accurately for various reasons including patient motion and edema. X-ray imaging has been previously proposed for imaging and reconstructing seed positions [3–8], thereby permitting intra-operative dosimetry modifications leading to improved outcomes.

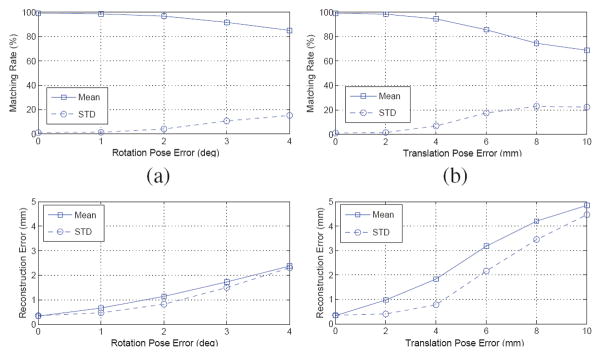
Fig. 1.

(a) A schemetic describing prostate brachytherapy procedure. (b) A symbolic intersection is calculated by finding the point with minimum sum of square distances from the lines.

The most common approach to the reconstruction of brachytherapy seeds from X-ray images is to 1) acquire a small number of images from several angles, 2) segment the seeds within each image, 3) determine which segmented seeds in each image correspond to the same physical seed, and 4) “triangulate” the positions of each physical seed from the corresponding seeds. At least three images are necessary to eliminate ambiguities and the optimization problem that is required to determine seed correspondence is NP-hard [6]. An underlying assumption is that all the seeds are segmented and their image coordinates are known. Since overlapping seeds are common [9], however, it is practically impossible to reliably identify and localize every seed in every image. Hidden seeds are usually recovered manually, and it is sometimes impossible to recover them when one seed completely hides another. The problem of overlapping seeds represents a significant impediment to the routine application of seed reconstruction in the clinic.

There has been some research on solving this so-called hidden seed problem where seeds cannot be reliably identified and localized on the projection images. Su et al. [9] extended Fast-CARS [4] to incorporate hidden seeds, but the new algorithm reconstructed a greater number of seeds than were actually present. Narayanan et al. [10] proposed a method which ordered the seeds using the epipolar constraints. However, it required co-planar images (co-linear X-ray sources) and could not reconstruct undetected seeds if they existed in the same search restriction band. Su et al. [11] proposed an adaptive grouping technique which divides the seed images into groups for efficient seed reconstruction and is capable of handling hidden seed problem. However, it may fail to detect overlapping seeds when the projection with the largest number of seed images among the divided groups is incomplete. Also, incorrect division of triplets, referred to as “overdividing” may cause false positive seeds. Intensity-based methods using tomosynthesis [12] and Hough trajectory [13] have also been proposed. However, these methods require unfeasibly large number of images to guarantee stable reconstruction.

We have previously proposed an optimal matching algorithm using dimensionality reduction [8]. In the present paper, we extend the previous method in order to address the hidden seed problem. This new algorithm also uses dimensionality reduction and it also introduces a pruning algorithm for efficient cost computation which allows us to significantly reduce the total computation time.

2. METHODS

When at least three images are used and all the 2-D seed locations are identified in every X-ray image, the correspondence problem can be formulated as a 3-D assignment problem (3DAP) [6, 8]. Given these matched seed locations, a reconstruction of the seed locations in 3-D can be achieved provided there are no ambiguities. It is more likely that such ambiguities are avoided when there are more X-ray images, but this in turn increases the complexity of the problem. The 3DAP is usually solved under the assumption that all the seeds are segmented and their image coordinates are known. However, in reality, there are significant amount of overlapping seeds, resulting in varying number of segmented seeds in each image. Here, we describe a new extension of the 3DAP to reconstructing overlapping seeds that are occluded in one or more X-ray images. The extended method uses three images, which is often sufficient in practice, and is extendable to more images.

2.1. 3-D Reconstruction as a matching problem: extension to hidden seed problem

In contrast to the 3DAP where exactly N implanted seeds are identified in every image, we consider a different number N_i of identified seeds in each image i with N_i ≤ N. We also consider I (≥ 3) X-ray images. Then the 3DAP can be extended to an extended assignment problem (EAP) in order to handle hidden seed problem in the following way.

$$\underset{x_{i_1{i}_2{i}_3\dots i_I}}{min}\sum _{i_1=1}^{N_1}\sum _{i_2=1}^{N_2}\sum _{i_3=1}^{N_3}\cdots \sum _{i_I=1}^{N_I}{c}_{i_1{i}_2{i}_3\dots i_I}{x}_{i_1{i}_2{i}_3\dots i_I},$$ (1)

where

$$\{\begin{array}{l}{x}_{i_1{i}_2{i}_3\dots i_I}\in \{0,1\}\hfill \\ {\sum }_{i_2=1}^{N_2}{\sum }_{i_3=1}^{N_3}\cdots {\sum }_{i_I=1}^{N_I}{x}_{i_1{i}_2{i}_3\dots i_I}\ge 1,\forall i_1\hfill \\ {\sum }_{i_1=1}^{N_2}{\sum }_{i_3=1}^{N_3}\cdots {\sum }_{i_I=1}^{N_I}{x}_{i_1{i}_2{i}_3\dots i_I}\ge 1,\forall i_2\hfill \\ ⋮\hfill \\ {\sum }_{i_1=1}^{N_2}{\sum }_{i_2=1}^{N_3}\cdots {\sum }_{i_{I-1}=1}^{N_{I-1}}{x}_{i_1{i}_2{i}_3\dots i_I}\ge 1,\forall i_I\hfill \\ {\sum }_{i_1=1}^{N_1}{\sum }_{i_2=1}^{N_2}{\sum }_{i_3=1}^{N_3}\cdots {\sum }_{i_I=1}^{N_I}{x}_{i_1{i}_2{i}_3\dots i_I}=N.\hfill \end{array}$$ (2)

c_i1i2i3…iI is the cost of matching point $p_{i_1}^1$ to points { $p_{i_2}^2,p_{i_3}^3,\dots ,p_{i_I}^I$} and x_i1i2i3…iI is a binary variable deciding the correctness of the match 〈i₁, i₂, i₃, …, i_I〉. Note that inequalities are used in the constraints (2) to handle the occurrence of hidden seeds. In this problem, a point can be chosen more than once in an image. The last equality forces the total number of seeds to be N which does not appear in the constraints set of the 3DAP.

2.2. Solving EAP with dimensionality reduction

2.2.1. Principle of the dimensionality reduction

A feasible solution of a 3DAP with I projection images, without hidden seeds, has (n!)^I−1 feasible solutions. Since the number of implanted seeds N in prostate brachytherapy is not small (~ 100), it is hard to solve (1) within clinically adequate time. However, both 3DAP and EAP have a salient feature that we can exploit: the optimal solution has a near-zero cost when the pose error is low (it is actually zero when the pose is known without error). We utilize this feature to reduce the number of variables in the problem, thus permitting us to get the optimal solution at a reasonable computational cost.

Let N′ = N₁N₂ … N_I. We rewrite the variables x_i1i2…iI and the costs c_i1i2…iI in vectorial forms such that x, c ∈ ℝ^N′. In the sequel we also make use of the notation u_ℓ to denote u_i1i2…iI. The EAP (1)–(2) reads as the following integer linear program

$$P:\underset{\mathit{x}\in \mathcal{C}}{min}{\mathit{c}}^{\text{t}}\mathit{x},$$ (3)

with the constraint set 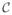= {x: Mx ≥ [1, …, 1]^t, x^t[1, …, 1] = N, x_ℓ ∈ {0, 1}}, where M is a matrix form of (2), except the last equation.

Since the value of x is either 0 or 1 and there must be N 1’s, an optimal solution of the problem P can be thought of as the selection of N cost coefficients such that the resulting cost is minimum while constraints are satisfied. Given a feasible solution, Lemma 1 in [8] states that all cost coefficients that are greater than the cost associated with this solution cannot be selected in the optimal solution. Since those coefficients can never be selected, the dimension of the problem can be reduced by removing those coefficients from further consideration. This yields a following equivalent problem of reduced dimensionality (for proof, see [8, Sec.2.2]):

$$\stackrel{\sim }{P}:\underset{\stackrel{\sim }{\mathit{x}}\in \stackrel{\sim }{\mathcal{C}}}{min}{\stackrel{\sim }{\mathit{c}}}^{\text{t}}\stackrel{\sim }{\mathit{x}},$$ (4)

where x̃, c̃ ∈ ℝ^K (K ≤ N′) and with the constraint set 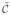= {x̃: M̃x̃ ≥ [1, …, 1]^t, x˜^t[1, …, 1] = N, x̃_ℓ ∈ {0, 1}} with M̃ = MR and where R is the dimensionality reduction matrix of size N′ × K such that ${\left[\begin{array}{cccccc}{x}_{i1}& 0& x_{i2}& 0& \dots & x_{iK}\end{array}\right]}^{\text{t}}=\mathbf{R}{\left[\begin{array}{cccc}{\stackrel{\sim }{x}}_1& {\stackrel{\sim }{x}}_2& \dots & {\stackrel{\sim }{x}}_K\end{array}\right]}^{\text{t}}$.

Once the reduced problem P̃ is solved, the optimal solution to the original problem P is simply given by x^* = Rx̃^*. If the dimensionality reduction is sufficiently large, then the new problem can be solved exactly in reasonable time even though the original problem is far too costly to solve.

2.2.2. Reconstruction accuracy and seed reconstruction

To compute 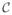, we need to compute 3-D intersection of the corresponding straight lines in space. Due to various errors, these straight lines never intersect, forcing us to compute a symbolic 3-D intersection point. The symbolic intersection is typically defined as the global minimum of an error function. Here we use reconstruction accuracy (RA²) based on L₂ norm of Euclidean distance from the intersection point to the lines as a cost function and propose a simple and quick method to minimize it.

Let I be the total number of 3-D straight lines, with line i defined as having unit direction l_i (a_i, b_i, c_i) and a point p_i on it, as shown in Fig. 1(b). Let P_I (x, y, z) be the representative intersection of these I lines. Let d_i be the Euclidean distance of P_I from line i. Thus, by definition, P_I achieves the minimum L₂ norm for the vector (d₁, d₂, …, d_I). In other words, we need to find a P_I such that it minimizes a function :

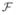$$\begin{array}{l}\mathcal{F}=I\times {RA}^2=\sum _{i=1}^I{d}_i^2=\sum _{i=1}^I{\left|\right|(P_1-p_i)\times l_i\left|\right|}^2\\ =\sum _{i=1}^I{(P_I-p_i)}^T\left[\begin{array}{ccc}{b}_i^2+c_i^2& -a_i{b}_i& -a_i{c}_i\\ -a_i{b}_i& a_i^2+c_i^2& -b_i{c}_i\\ -a_i{c}_i& -b_i{c}_i& a_i^2+b_i^2\end{array}\right](P_I-p_i)\\ =\sum _{i=1}^I{(P_I-p_i)}^T{A}_i(P_I-p_i).\end{array}$$ (5)

Then P_I can be analytically computed by solving $\nabla ℱ=0:P_I={\left[{\sum }_{i=1}^I{A}_i\right]}^{-1}\times \left[{\sum }_{i=1}^I{A}_i{p}_i\right]$.

This is the final seed coordinate. It can be computed very quickly by a few summations followed by a 3 × 3 matrix inversion. Note that P_I is chosen so as to minimize RA².

Once the EAP (1)–(2) is solved with RA² costs, the estimation of the 3-D location of the N implanted seeds can be determined by the symbolic 3-D intersection points P used to compute the N chosen RA² costs in the solution (those that corresponds to 1 in x).

2.2.3. Efficient computation of cost coefficients

Number of the cost coefficients increases exponentially as a function of the number of images. For N seeds and I images, there are N^I cost coefficients, when there is no hidden seeds. For three images, the computation of all the 100³ RA² cost coefficients with 100 implanted seeds requires only about 10 s using MATLAB on a Pentium4 PC. For six images, however, the computation of all the 100⁶ RA² cost coefficients would require an astonishing 116 days (100⁶ × 10 s) and thus is utterly impractical. An alternative to the exhaustive cost coefficients computation is required.

The dimensionality reduction approach described in Section 2.2.1 requires only to compute the K cost coefficients lower than a threshold. This implies that the exact value of most of the cost coefficients is not required. An efficient way to tell if a cost coefficient is actually higher than the dimensionality reduction threshold would allow to skip its exact computation. This unnecessary cost computation can be avoided by utilizing the following Lemma.

Lemma 2.1

Every RA² cost coefficient has the following lower bound:

$$2I(I-1)R{A}^2\ge \sum _{i_1,i_2\in \{1,2,\dots ,I\},i_2>i_1}d{(l_{i_1},l_{i_2})}^2$$ (6)

where d(l_i1, l_i2) is the Euclidean distance of line i₁ to line i₂ and with I images.

Proof

The midpoint P_I from I images is defined by $P_I=arg{min}_P{\sum }_{i=1}^I{\left|\right|(P-p_i)\times l_i\left|\right|}^2$.

Let then P_{i1,i2} = arg min_P Σ_i={i1,i2}||(P − p_i) × l_i||², then Σ_i={i1,i2}||(P_I − P_i) × l_i||² ≥ Σ_i={i1,i2||(P_{i1,i2 − p_i) × l_i||² = d(l_i1, l_i2)²/2. Combine this and $(I-1){\sum }_{i=1}^I{\left|\right|(P_I-p_i)\times l_i\left|\right|}^2={\sum }_{i_1,i_2\in \{1,2,\dots ,I\},i_2>i_1}{\sum }_{i=\{i_1,i_2\}}{\left|\right|(P_I-p_i)\times l_i\left|\right|}^2$ to get $(I-1){\sum }_{i=1}^I{\left|\right|(P_I-p_i)\times l_i\left|\right|}^2\ge {\sum }_{i_1,i_2\in \{1,2,\dots ,I\},i_2>i_1}d{(l_{i_1},l_{i_2})}^2/2$. Finally, this and (5) give us (6).

Based on Lemma 2.1, we propose a pruning algorithm for efficient RA² cost computation.

Pruning algorithm for efficient computation of RA² costs lower than a threshold

1. Compute every possible d(l_i1, l_i2)² for I images.

2. Compute c̃_1,2,…,I (i₁, i₂, …, i_I) = Σ_{i1,i2∈{1,2,…,I}, i2i1} d(l_i1, l_i2)² lower than the dimensionality reduction threshold η by pruning.

   For the first i images, we have ${\stackrel{\sim }{c}}_{1,2,\dots ,i}(i_1,i_2,\dots ,i_i)={\sum }_{i_1,i_2\in \{1,2,\dots ,i\},i_2>i_1}d{(l_{i_1},l_{i_2})}^2={\stackrel{\sim }{c}}_{1,\dots ,i-1}(i_i,\dots ,i_{i-1})+{\sum }_{i_1=1}^{i-1}d{(l_{i_1},l_i)}^2$. Thus, c̃ _1,2,…,i (i₁, i₂, …, i_i) increases as a function of the number of image i. When c̃_1,2,…,i (i₁, i₂, …, i_i) > η, the computation of c̃_1,2,…,I (i₁, i₂, …, i_I) is not required. Actually, a huge family of cost coefficients can be pruned in this case. This family is the following N ^I−i coefficients {c̃_1,2,…,I(i₁, i₂, …, i_i, 1: N, …, 1: N)}, assuming no hidden seed. This nice property allows a recursive algorithm where images are virtually added one at a time and where a list of coefficients lower than η is updated.

3. Compute the RA²cost coefficients whose indexes (i₁, i₂, …, i_I) are the same as those of the list of coefficients c̃_1,2,…,I (i₁, i₂, …, i_I) lower than.

More RA² costs coefficients are actually computed from the indexes of coefficients c̃_1,2,…,I lower than the dimensionality reduction threshold η, than strictly required because (6) is only an inequality. The performance of the pruning algorithm directly depends on the ratio of the number of RA²costs coefficients computed and the number of those actually lower than η. In practice, we observed that this ratio is in the range of 3 to 15, which is very compelling.

2.3. Optimization strategy: Linear programming

Integer Program (IP) such as 3DAP can be directly solved with standard techniques such as branch and bound. However, IP problems are NP-hard and may take an exponential amount of computation time. It has been shown that the linear program corresponding to the 2-D assignment problem (2DAP) has an integer solution even without integer constraints [14]. As well, this linear program can be solved efficiently in polynomial time using interior point methods [15]. To our knowledge, however, there is no analogous result for the 3DAP or EAP. We have implemented the linear program for the EAP followed by a test to see if its solution is binary (up to numerical errors) using MATLAB command linprog.

3. NUMERICAL RESULTS

The EAP algorithm was implemented using MATLAB 7.1 and tested on a Linux PC (Pentium4 2.92 GHz, 3.8GB RAM). We performed simulation studies using synthetic projection images. We considered seed density of 2 and 2.5 seeds/cc and prostate size of 35 and 45 cc, resulting in four cases with N = {72, 84, 96, 112} implanted seeds. For each case, three different data sets were generated. We assumed that the C-arm is calibrated and the pose of the C-arm is known without error. We also assumed that the image acquisition angle was 10° and generated six projection images on a 10° cone along the AP-axis in each data set. In each image, there were up to 5.6% hidden seeds. A total of 240 reconstructions were computed ( $4\text{case}\times 3\text{data}\text{sets}\times C_3^6$) using three images, and Table 1 shows the results. The results imply that implanted seeds can be localized with detection rate of ≥ 98.8% and reconstruction error of ≤ 0.37 mm up to 112 seeds when the pose is known. And average computation time for the seed matching was only 2 s or less.

Table 1.

Simulation results. Pose of the C-arm is assumed to be known without error. Up to 5.6% of seeds are hidden in each projection image.

Number of seeds	Mean match rate (%)	Mean ± STD recon. error (mm)	Computation time (s)
72	99.3	0.33 ± 0.06	1.01
84	99.0	0.30 ± 0.06	1.28
96	99.1	0.37 ± 0.06	1.58
112	98.8	0.35 ± 0.07	2.07

In order to evaluate the robustness of the algorithm to pose error, we added random error which is uniformly distributed on [−h, h] (we report this as h error) to the known pose. For rotation, random errors from 1° to 4° with 1° steps were added to the known rotation at each pose around random rotation axes. Translation errors varied from 2 mm to 10 mm with 2 mm steps. When we generated translation errors, we incorporated the fact that translation errors in depth are always significantly greater than those parallel to the plane [6]. Shown in Figure 2, our results imply that the EAP algorithm reliably finds the correct match and reconstruct the seeds with > 95% accuracy with up to 2° rotation error and 4 mm translation error. Contemporary tracking systems can easily achieve this tracking accuracy [16].

Fig. 2.

Matching rates and reconstruction errors as a function of (a, c) rotation and (b, d) translation pose errors.

4. CONCLUSION

This paper presents a computationally tractable and clinically feasible seed correspondence approach for brachytherapy seed reconstruction. The approach solves the problem of hidden seeds without the use of manual intervention while still maintaining low computation times using a new pruning algorithm for efficient computation of the RA² cost. In simulations, it matched over 98.8% of the seeds with a reconstruction error of less than 0.37 mm using three images. Simulation results also show that the algorithm is robust to realistic C-arm pose errors. Although the algorithm is formulated for any number of images, our testing herein was limited to just three images. Future work will explore the tradeoffs in computation time and performance when using more than three images and validations will be performed using both phantom and clinical data.