Predicting flexible loop regions that interact with ligands: The challenge of accurate scoring

Abstract

Flexible loop regions play a critical role in the biological function of many proteins and have been shown to be involved in ligand binding. In the context of structure-based drug design, using or predicting an incorrect loop configuration can be detrimental to the study if the loop is capable of interacting with the ligand. Three protein systems, each with at least one flexible loop region in close proximity to the known binding site, were selected for loop prediction using the CorLps program; a six residue loop region from phosphoribosylglycinamide formyltransferase (GART), two nine residue loop regions from cytochrome P450 (CYP) 119, and an eleven residue loop region from enolase were selected for loop prediction. The results of this study indicate that the statistically-based DFIRE scoring function implemented in the CorLps program did not accurately rank native-like predicted loop configurations in any protein system. In an attempt to improve the ranking of the native-like predicted loop configurations, the MM/GBSA and the Optimized MM/GBSA-dsr scoring functions were used to re-rank the predicted loops with and without bound ligand. In general, single snapshot MM/GBSA scoring provided the best ranking of native-like loop configurations. Based on the scoring function analyses presented, the optimal ranking of native-like loop configurations is still a difficult challenge and the choice of the “best” scoring function appears to be system dependent.

Introduction

In order to analyze and exploit the structure-function relationship of proteins a three dimensional protein structure is needed. Despite advances in nuclear magnetic resonance (NMR) and protein crystallographic techniques, the number of structurally characterized proteins is low compared to the number of known protein sequences. Currently, the Brookhaven Protein Database (PDB)¹ contains approximately 30,000 (95% sequence identity filter applied to approximately 70,000 total structures deposited) unique structurally characterized proteins compared to approximately 14 million protein sequences contained in the UniProtKB/TrEMBL database². To reduce the “structural knowledge gap”, homology or comparative modeling is often used to predict three dimensional protein structures. When sequence identity is relatively high (> 50%) between the target and template sequences, homology models are capable of accurately predicting the protein structure (<3 Å root mean square deviation (RMSD) of C_α atoms).³ Whereas the overall protein structure may be well predicted, sequence and structural variability between the target and template sequences is often found in loop regions. This variability often causes homology models of such regions to be less accurate compared to the core of the structure. In order to accurately model loop regions, additional loop prediction may be needed to refine the homology model.

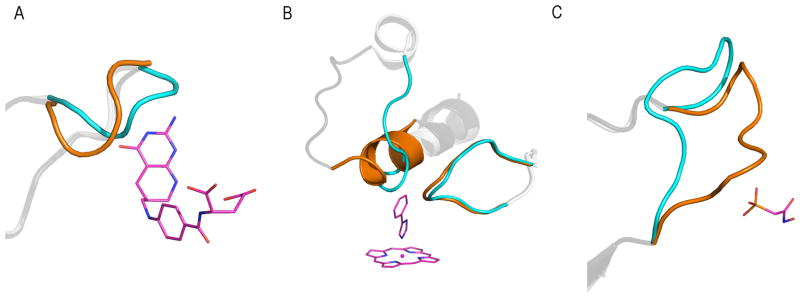
Although the configuration of loop regions is frequently incorrect in homology models, these structural elements are often critical to the biological function of many proteins.^4–25 Loop regions have been shown to be involved in processes ranging from protein-protein interactions to ligand binding. Despite their biological significance, loop regions are often missing from experimentally solved protein structures due to their inherent flexibility. In addition, flexible loop regions can adapt alternative configurations upon ligand binding (Figure 1).

Figure 1.

Examples of flexible loop regions in close proximity to the known binding site. (A) GART’s 6 residue loop region (apo: PDB-code 1GRC⁵⁵, blue cartoon; holo: PDB-code 1CDE⁵⁶, orange cartoon) near the ligand 5-deazafolic acid (shown in pink sticks). (B) CYP119’s 9-residue loop regions (apo: PDB-code 1IO7⁵⁷, blue cartoon; holo: PDB-code 1F4T⁵⁸, orange cartoon) near the ligand 4-phenylimidazole (shown in pink sticks along with porphyrin ring of the heme group). (C) Enolase’s 11-residue loop region (apo: PDB-code 1EBH⁵⁹, blue cartoon; holo: PDB-code 1EBG⁶⁰, orange cartoon) near the ligand phosphonoacetohydroxamic acid (shown in pink sticks).

In the context of structure-based drug design, using or predicting an incorrect loop configuration can be detrimental to the study if the loop is capable of interacting with the ligand. To overcome such problems in structure-based drug design, several concepts have been developed that model loop-ligand interactions that range from a mean field approach that represents the average physico-chemical profile of a loop²⁶ to attempts that use an ensemble of low energy loop conformations in docking⁴. The latter method aims to mimic conformational changes that occur in the protein or loop region upon ligand binding based on the conformational selection mechanism of ligand binding²⁷.

The conformational selection model assumes that the apo form of the protein samples higher energy conformations and the ligand selectively binds to a holo-like conformation and stabilizes this state of the protein. Extending the conformational selection model, the encoding hypothesis^28–32 assumes that the potential function of the ligand-free form of the protein encodes the direction of the protein fluctuations necessary to sample holo-like protein conformations that are critical for ligand binding to occur. Cavasotto and coworkers³³ used this hypothesis to derive collective variables, based on normal mode analysis of the apo form of cAMP-dependent kinase, to simulate loop flexibility coupled to ligand binding.

In this study, it is also assumed that holo-like protein conformations can be generated from the apo form of the protein with the ligand selectively binding to such a conformation. However, further local relaxation of the protein that is induced by ligand binding is allowed.³⁴ Assuming that the conformational selection model is valid, determining how much energy is required to transition the protein from an apo to holo conformation is critical in the context of loop regions that are known to undergo conformational changes upon ligand binding. This issue is important as the free energy associated with the protein conformational change upon ligand binding must be considered in the overall prediction of the free energy of binding ΔG_binding:

$$\mathrm{\Delta }{G}_{\mathit{binding}}=\mathrm{\Delta }{E}_{P-L}+\mathrm{\Delta }{G}_{\mathit{conformation}-P}$$ (1)

where ΔE_P-L represents the direct interaction between protein and ligand (including solvation effects) and ΔG_{conformation-P} is the free energy difference between the apo and holo protein conformations when the ligand is not bound. In the context of loop prediction, a related question is whether we can predict the lowest energy protein conformation under the influence of ligand binding,

$$\mathrm{\Delta }{E}_k=\mathrm{\Delta }{E}_{P-L,k}+\mathrm{\Delta }{E}_{\mathit{conformation}-P,k}$$ (2)

where k numerates the different loop conformations, and ΔE_{conformation-P,k} is the energy of loop conformation k without protein-ligand interactions. It should be noted that any vibrational entropy is neglected in this consideration. This article aims to address if ΔE_{conformation-P} can be reliably predicted with existing scoring procedures.

Loop prediction was carried out using the CorLps program³⁵ for each protein system shown in Figure 1. In an attempt to estimate ΔE_{conformation-P}, three different scoring concepts were tested: the statistically-based DFIRE scoring function^{36, 37} originally used in protein structural prediction, the all-atom physics-based MM/GBSA scoring function³⁸ frequently used to predict protein-ligand binding affinities, and the optimized all-atom physics-based MM/GBSA scoring function³⁹ designed to refine protein decoy structures (referred to as Optimized MM/GBSA-dsr, dsr being short for decoy structure refinement, throughout the remainder of this publication). The ability of the three scoring functions to select holo-like loop configurations from an ensemble of predicted loop regions was explored. In addition, the effect of the ligand on re-ranking native-like loop configurations was also evaluated.

Materials and Methods

Protein systems

Three protein systems, each with at least one flexible loop region in close proximity to the known binding site, were selected for loop prediction. A six residue loop region from phosphoribosylglycinamide formyltransferase (GART), two nine residue loop regions from CYP119, and an eleven residue loop region from enolase were selected for loop prediction. Summarized in Table 1, the X-ray structure of each protein system was obtained from the PDB database. All co-factors, water molecules, and co-crystallized ligands were removed prior to loop prediction. Only protein subunit A was present during the loop prediction process of CYP119 and GART.

Table 1.

Summary of protein systems used in loop prediction.

Protein System	PDB-code	Resolution	Substrate	Loop Length	Loop Residues
GART	1CDE, chain A	2.50 Å	DFZ: 5-deazafolic acid	6 residues	141–146
CYP119	1F4T, chain A	1.93 Å	PIM: 4-phenylimidazole	9 residues, 9 residues	150–158 348–356
Enolase	1EBG	2.10 Å	PAH: phosphonoacetohydroxamic acid	11 residues	35–45

Loop prediction

Loop prediction of all systems was performed using the CorLps program. CorLps employs the ab initio loop prediction grogram loopyMod⁴⁰ to generate an initial ensemble of energetically favorable loop conformations of each predicted loop region. Single loop prediction in GART and enolase was performed with 10,000 loop conformations initialized in loopyMod (with the CHARMM force field used to assign the van der Waal parameters) and the top-500 energetically favorable loop conformations were outputted. The ensemble of predicted loop conformations was then reduced using quality threshold (QT) clustering⁴¹ to remove conformations with low RMSD among each other. The maximum diameter of the clusters was set at 2 Å for enolase and 1 Å for GART to produce 300 unique predicted loop conformations. Following QT clustering, the side chains of residues within a 6 Å zone around the predicted loop region were optimized using SCAP⁴² and the top-100 predicted loop configurations were identified and ranked according to the DFIRE scoring function. The top-100 predicted loop configurations ranked by DFIRE is referred to as the DFIRE ensemble throughout the remainder of this publication.

Simultaneous prediction of two loop regions was performed in CYP119. Initially, each individual loop region was treated independently with the other loop temporarily removed from the protein structure. For each independent loop region, an ensemble of 500 energetically favorable loop conformations was generated using loopyMod. Described in the previous paragraph, identical loopyMod settings were used during simultaneous loop prediction. A 2 Å threshold was used to cluster each independent loop ensemble to produce a unique ensemble of 300 loop configurations for each loop region. To limit the computational time required to generate and optimize 300 * 300 possible combinations of the unique loop regions, a maximum number of 5,000 combined loop configurations were generated by initially combining the top-75 ranked single loop conformations of each clustered loop region. This number was increased in steps of 25 additional unique loop conformations until 5,000 possible loop configurations were generated that passed a steric clash filter. The steric clash filter removed any combined loop configuration with a predicted backbone or Cβ atom within 0.8 times the sum of their van der Waals radii. After passing the steric clash filter, the side chains of residues within a 6 A zone around the predicted loop regions were re-packed to allow the combined protein structure to adopt a lower energy configuration. The top-100 predicted loop configurations (DFIRE ensemble) were then selected according to the DFIRE scoring function.

RMSD analysis

To analyze the loop prediction quality of CorLps, the RMSD to the experimental X-ray protein structure was determined for each member of the DFIRE ensemble. An in-house C-program that uses the super function implemented in PyMOL⁴³ was used to align all predicted protein structures onto the X-ray structure. All backbone atoms, excluding those in the predicted loop region, were used in the alignment step. The RMSD value of each member of the DFIRE ensemble was determined using the PyMOL plug-in script rms_current.

Minimization of the predicted loop configurations

For each member of the DFIRE ensemble, the hydrogen bond network of the protein was optimized using the program Reduce⁴⁴ to assign histidine protonation and tautomer states and flip asparagine and glutamine side chains if needed. The tleap module of AMBER 9^{45, 46} was used to add missing hydrogens and to generate a topology and structure file for minimization using the AMBER ff03 force field. 50 steps of minimization with a 12 Å nonbonded cutoff and a distance-dependent dielectric solvation model was used to eliminate any close contacts between protein residues. Subsequently, 500 steps of steepest decent minimization with a 12 Å nonbonded cutoff and the Mongan, Simmerling, McCammon, Case, and Onufriev implicit solvation model⁴⁷ (igb=7) was performed to further minimize the system.

Re-scoring the predicted loop configurations

The ability of three scoring functions to optimally rank low RMSD predicted loop configurations was explored. Optimum ranking is defined as the ability to select the lowest RMSD predicted loop configuration (most native-like) as the top-predicted loop configuration. In the CorLps program, the statistically-based scoring function DFIRE is used to score and rank the predicted loop configurations and select the DFIRE ensemble. Two all-atom physics-based scoring functions, MM/GBSA and the Optimized MM/GBSA-dsr, were subsequently used to re-score the DFIRE ensemble to determine their ability to optimally rank low RMSD loop configurations within the DFIRE ensemble. The ability of the MM/GBSA and the Optimized MM/GBSA-dsr scoring functions to optimally rank low RMSD configurations was studied with and without the ligand present in each protein system.

Single snapshot MM/GBSA re-scoring

Rastelli and coworkers showed that MM/GBSA scoring of a single protein-ligand minimized structure produced results similar to averaging over multiple protein-ligand snapshots obtained from a molecular dynamics (MD) simulation when estimating ligand binding affinities in dihydrofolate reductase.⁴⁸ Although that study focused on the prediction of binding free energies and thus differs from our effort to rank predicted loop conformations, it provided motivation to utilize a similar approach in our problem of interest. Each member of the DFIRE ensemble was minimized using the protocol described in “Minimization of the predicted loop configurations” and the MM/GBSA protein energy was calculated using the mmpbsa.pl scripts included in AMBER9. This value was then used to re-rank the DFIRE ensemble of each protein system. Due to the high computational cost and variability associated with calculating the vibrational entropy of different loop conformation, only the force field energy, including implicit solvation effects, was computed for each predicted loop conformation.^{49, 50}

Trajectory MM/GBSA re-scoring

To determine if MM/GBSA scoring with an ensemble of snapshots obtained from an MD simulation optimally re-ranks the predicted loop configurations, each member of the DFIRE ensemble from GART, CYP119, and enolase was prepared for a MD simulation using the AMBER9 package. The tleap module was used to add missing hydrogen atoms to each protein structure and it was solvated in a 30 Å explicit water cap centered on the position of the co-crystallized ligand (ligand not present during MD simulations). To eliminate any close contacts present in the predicted protein structure, 800 steps of steepest decent followed by 200 steps of conjugate gradient minimization was performed. After minimization, the water molecules were allowed to equilibrate during 250 ps of MD simulation with the protein restrained by a force constant of 5 kcal/mol per Ų and all water molecules were contained within the initial 30 Å cap region by a 5 kcal/mol per Ų cap restraint. 5 ns of subsequent production MD was performed with all protein residues beyond 25 Å from the center of the water cap and all residues of the predicted loop regions restrained by a force constant of 1 kcal/mol per Ų. The simulations were performed with a 2 fs time step using the SHAKE⁵¹ algorithm to constrain bonds between any heavy and hydrogen atoms and a temperature of 300 K.

Upon completion of the production MD, the trajectory was stripped of explicit water molecules using the ptraj module. The mmpbsa.pl scripts were subsequently used to extract 20 snapshots from the trajectory and perform MM/GBSA calculations. The average MM/GBSA protein energy was then used to re-rank the DFIRE ensemble of each system.

Optimized MM/GBSA-dsr re-scoring

The Optimized MM/GBSA-dsr all-atom potential derived by Skolnick and coworkers was designed to refine protein decoy structures to a more native-like protein conformation (reduce the RMSD between the experimentally known protein structure and the protein decoy). To accomplish this task, each component of the Optimized MM/GBSA-dsr scoring function was optimally weighted to create a scoring function that ranked the native protein structure as the global minimum. The individual weights of the Optimized MM/GBSA-dsr scoring function used in this study are shown in Table 2. To determine if the Optimized MM/GBSA-dsr scoring function optimally re-ranks predicted loop configurations, the DFIRE ensemble from each protein system was scored and re-ranked following minimization with implicit solvation (protocol described in “Minimization of the predicted loop configurations”).

Table 2.

Weights of each component of the Optimized MM/GBSA-dsr scoring function derived by Skolnick and coworkers³⁹.

Component	BONDa	ANGb	DIHc	VDWd	VDW1–4e	ELEf	ELE1–4g	GBh	SAi
Weight	0.00	0.00	−1.25	1.00	1.04	−0.27	−0.16	−0.22	−0.51

^abond energy

^bangle energy

^cdihedral angle energy

^dvan der Waals energy

^eshort distance van der Waals energy of atom pairs separated by three bonds

^felectrostatic energy

^gshort range electrostatic energy of atom pairs separated by three bonds

^hgeneralized Born solvation energy

ⁱsurface area dependent solvation energy

The effect of the ligand: re-scoring loop configurations with the co-crystallized ligand

Co-crystallized ligand coordinates

To determine if loop-ligand interactions are necessary to stabilize native-like loop configurations, and thus critical to the loop ranking process, the co-crystallized ligand was added to each member of the DFIRE ensemble, using the experimentally determined position and conformation of the ligand.

Side chain optimization

In order to eliminate steric clashes between the predicted loop configuration and the added co-crystallized ligand, each member of the DFIRE ensemble was subjected to a side chain optimization step. To incorporate the interaction of the side chains with the bound ligand, the side chains of all residues within the predicted loop regions were optimized using an in-house algorithm similar to the published SCAP side chain prediction program. For each predicted loop configuration in the DFIRE ensemble, eight alternative low energy protein structures with optimized side chains were outputted and prepared for energy minimization. To refine each side chain optimized structure, a 25 Šexplicit water cap was constructed around the center of the ligand and 800 steps of steepest decent followed by 200 steps of conjugate gradient minimization were performed with the ligand and all protein residues beyond 20 Šfrom the center of the water cap restrained by a force constant of 5 kcal/mol per Ų. Minimizations that produced unrealistic protein structures, e.g. structures with broken bonds, were removed from subsequent MM/GBSA and Optimized MM/GBSA-dsr scoring calculations. In the case that all protein structures, generated by optimization of the side chains, possessed steric overlap with the ligand, the initial predicted loop configuration was used in the subsequent minimization.

Single snapshot MM/GBSA re-scoring

For each protein system, all structures with optimized side chains produced from each member of the DFIRE ensemble were minimized in implicit solvent with identical parameters as described in “Minimization of the predicted loop configurations”. This additional minimization step was needed to compare MM/GBSA scores of the predicted loop configurations with and without the ligand present. MM/GBSA calculations were carried out using the same procedure described in “Single snapshot MM/GBSA re-scoring without ligand”. The side chain optimized structure with the lowest (most favorable) MM/GBSA value was chosen as the energetically favorable protein conformation and subsequently used in Optimized MM/GBSA-dsr and trajectory MM/GBSA re-scoring.

Trajectory MM/GBSA re-scoring

Each predicted loop configuration in the DFIRE ensemble (following side chain optimization) of GART, CYP119, and enolase was prepared for a MD simulation and MM/GBSA re-scored using the same procedure described in “Trajectory MM/GBSA re-scoring without ligand”. The only change to this protocol was that the ligand was present during the MD simulation and MM/GBSA calculation.

Optimized MM/GBSA-dsr re-scoring

For all three protein systems, all DFIRE ensemble structures (following side chain optimization) were rescored with the Optimized MM/GBSA-dsr scoring function. The protocol described in “Optimized MM/GBSA-dsr re-scoring without ligand” was followed with the exception that the ligand was included during the implicit minimization and energy evaluation.

Results

Re-scoring the predicted loop configurations

Initial CorLps DFIRE scoring

To test the ability of CorLps to generate native-like loop configurations of loop regions with differing lengths, loop prediction was performed for each protein system shown in Table 1. Loop prediction accuracy was measured by comparing the RMSD of each member of the DFIRE ensemble to the experimentally known X-ray loop configuration. Listed in the “Backbone RMSD” column of Table 3, low RMSD (< 2 Å) loop configurations were produced for all protein systems, thereby suggesting that CorLps adequately sampled the conformational space accessible to the loop regions. The lowest backbone RMSD between a predicted loop configuration and the experimentally known X-ray loop configuration for GART (6-residue loop region), CYP119 (9-residue loop regions), and enolase (11-residue loop region) was 0.57 Å, 1.61 Å, and 1.43 Å. Similar RMSD values have been previously reported for loop regions of these lenghts in different protein systems.^{35, 40} It should be noted that recent novel loop prediction methods^{52, 53} were devised that demonstrate an ability to predict <1 Å loop conformations for many protein systems. These studies, however, did not focus on loop regions that interact with or are potentially stabilized by bound ligands.

Table 3.

The most native-like (three lowest RMSD) predicted loop configurations of GART, CYP119, and enolase. The ranked position of each loop configuration is shown after scoring with the DFIRE, single snapshot MM/GBSA, trajectory MM/GBSA, and the Optimized MM/GBSA-dsr scoring functions.

			Without co-crystallized ligand
Protein System	Backbone RMSDa	Heavy Atom RMSDa	DFIREb	Snapshot MM/GBSAc	Traj MM/GBSAd	Optimized MM/GBSA-dsre
GART	0.57	1.15	31	3	9	87
	0.74	1.30	19	46	74	68
	1.02	1.55	45	91	69	18
CYP119	1.61	2.92	50	6	37	87
	1.79	2.76	54	9	10	64
	1.80	2.99	81	50	87	96
Enolase	1.43	1.71	81	6	18	97
	1.70	2.31	12	9	38	83
	1.75	2.96	39	25	77	29

^aRMSD in Å to known X-ray loop configuration

^bDFIRE scoring function was used to rank predicted loop configurations

^ca single minimized structure was used to calculate a MM/GBSA score and rank loop configurations

^d20 snapshots from an MD trajectory were used to calculate a MM/GBSA score and rank loop configurations

^eOptimized MM/GBSA-dsr scoring function used to score and rank loop configurations

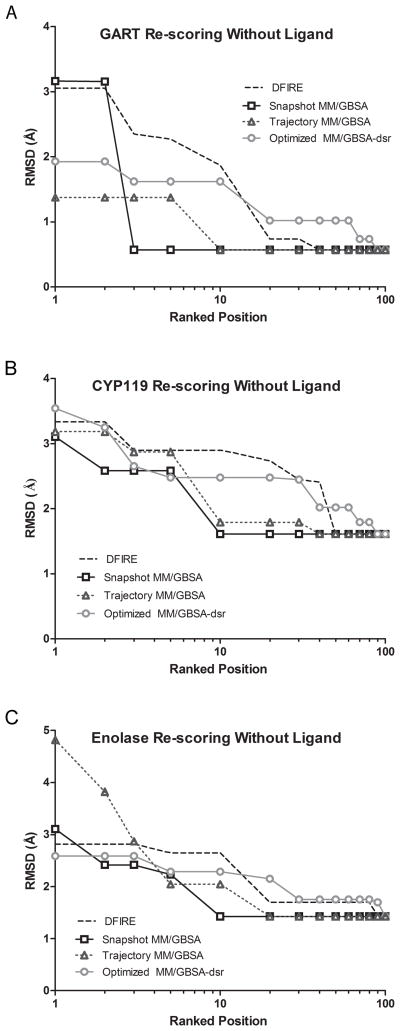
Although low RMSD (< 2 Å) loop configurations were produced for all protein systems used in this study, optimally ranking such loop configurations was a challenge. Listed in the column “Without ligand::DFIRE” in Table 3 and evident in Figure 2, the DFIRE scoring function implemented in CorLps did not rank the three lowest RMSD (most native-like) predicted loop configurations within the top-10 positions in any protein system. While the statistically-based scoring function was previously shown to identify the native loop conformation among the energetically lowest conformations within a set of decoy loop structures⁴⁰, DFIRE did not accurately rank low RMSD predicted loop configurations as the top-predicted loop configuration. A similar finding was reported in a previous publication.³⁵

Figure 2.

Lowest predicted RMSD identified within the top-100 ranked positions. DFIRE, MM/GBSA, and Optimized MM/GBSA-dsr scoring is shown for (A) GART, (B) CYP119, and (C) enolase.

Single snapshot MM/GBSA re-scoring

In an attempt to improve the ranking of low RMSD predicted loop configurations, the DFIRE ensemble of each protein system was re-ranked using the all-atom physics-based MM/GBSA scoring function. Shown in Figure 2, re-scoring with single snapshot MM/GBSA improved the ranking of low RMSD predicted loop configurations in all three systems compared to the initial DFIRE ranking. Furthermore, the column “Without co-crystallized ligand::Snapshot MM/GBSA” in Table 3 shows that re-scoring with single snapshot MM/GBSA improved the ranking of the most native-like loop configurations in GART, CYP119, and enolase. Of the three most native-like predicted loop configurations, one, two, and two were identified within the top-10 positions in the GART, CYP119, and enolase systems compared to none being identified by the DFIRE scoring function. In the GART system, the lowest RMSD predicted loop configuration was ranked in the top-3 positions using single snapshot MM/GBSA re-scoring without the ligand.

Trajectory MM/GBSA re-scoring

To determine if calculating the MM/GBSA score using an ensemble of snapshots from an MD simulation produced a more accurate ranking of native-like loop configurations, each member of the DFIRE ensemble from GART, CYP119, and enolase was subjected to a molecular dynamics simulation. An ensemble of 20 snapshots from the MD simulation was used to calculate the MM/GBSA energy of each predicted loop configuration. Shown in Figure 2, re-scoring using a trajectory calculated MM/GBSA value improved the identification of low RMSD predicted loop configurations compared to the initial DFIRE ranking in all three protein systems. However, summarized in the column “Without co-crystallized ligand::Traj MM/GBSA” of Table 3, the ranking of the most native-like predicted loop configurations did not improve compared to single snapshot MM/GBSA re-scoring. The ranking deteriorated in all protein systems as the lowest RMSD predicted loop configuration was no longer ranked within the top-10 positions.

Considering the ten lowest predicted RMSD loop configurations, there was not a clear indication that trajectory MM/GBSA re-scoring without the ligand produced a more accurate ranking. In the GART protein system, the ranking of low RMSD predicted loop configuration improved. Single snapshot MM/GBSA re-scoring identified one of the ten lowest RMSD predicted loop configurations within the top-10 positions and trajectory MM/GBSA re-scoring without the ligand identified two within the top-10 positions (Table S1). However, no improvement in the ranking was seen in the CYP119 system when using trajectory MM/GBSA re-scoring. Both single snapshot and trajectory MM/GBSA re-scoring identified two of the ten lowest RMSD predicted loop configurations within the top-10 positions (Table S1). Furthermore, the ranking deteriorated in the enolase protein system as trajectory MM/GBSA rescoring without the ligand identified one of the ten lowest RMSD predicted loop configurations within the top-10 positions while single snapshot MM/GBSA re-scoring without the ligand identified four (Table S1). Based on the above information, it is suggested that single snapshot MM/GBSA scoring re-ranks the predicted loop configurations with similar and even slightly improved quality compared to using a trajectory calculated MM/GBSA value.

Optimized MM/GBSA-dsr re-scoring

In the context of protein structure refinement, Skolnick and coworkers optimized an all-atom physics-based scoring function that uses the AMBER ff03 force field with a GBSA solvation model to rank native-like protein conformations with most favorable energy among an ensemble of decoy structures (Optimized MM/GBSA-dsr scoring function). To determine if the Optimized MM/GBSA-dsr scoring function outperforms MM/GBSA ranking of predicted loop regions, each member of the DFIRE ensemble was minimized with an implicit solvation model and subsequently re-ranked using this scoring function.

Shown in Figure 2, re-scoring using the Optimized MM/GBSA-dsr scoring function moderately improved the ranking of low RMSD predicted loop configurations compared to the initial DFIRE ranking in all three protein systems. However, evident from the column “Without ligand::Optimized MM/GBSA-dsr” in Table 3, the Optimized MM/GBSA-dsr scoring function did not re-rank the most native-like predicted loop configurations within the top-10 positions for any protein system. Furthermore, none of the ten lowest RMSD predicted loop configurations from each system were ranked in the top-10 positions using this scoring function (Table S1). In addition, Figure 2 illustrates that the Optimized MM/GBSA-dsr scoring function performs worse than single snapshot MM/GBSA re-scoring without the ligand. While shown to accurately score native-like protein conformations in a pool of decoy structures, the Optimized MM/GBSA-dsr scoring function did not accurately rank low RMSD predicted loop configurations.

The effect of the ligand: re-scoring loop configurations with the co-crystallized ligand

During the loop prediction process, the co-crystallized ligand is not present and therefore is assumed to be a non-integral part of the protein system. While this assumption may hold for some protein loop regions, it may be invalid in cases where the loop region interacts with a ligand. The three protein systems selected in this study each contain at least one loop region that is in close proximity to the binding site of the protein and potentially interacts with known ligands. Disregarding the ligand during the ranking of a predicted loop configuration neglects any interaction between it and the loop region that could stabilize a native-like or destabilize a non-native-like predicted loop configuration. Thus, including ligand-loop interactions may improve the ranking of native-like loop configurations. To begin to account for the effect of the ligand on the loop prediction process, the co-crystallized ligand was added to each member of the DFIRE ensemble of each protein system and the loop configurations were re-ranked using the single snapshot MM/GBSA, MM/GBSA trajectory, and the Optimized MM/GBSA-dsr scoring functions.

Single snapshot MM/GBSA re-scoring

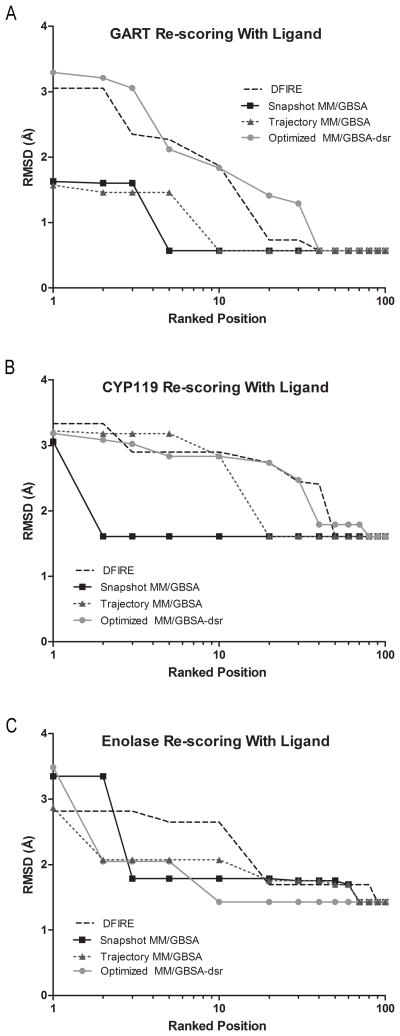
For loop configurations lacking steric overlap with the added co-crystallized ligand, single snapshot MM/GBSA scoring and re-ranking was applied to the DFIRE ensemble of each protein system. Shown in Figure 3, re-scoring with single snapshot MM/GBSA with the ligand improved the ranking of low RMSD predicted loop configurations in all three protein systems compared to the initial DFIRE ranking. In the GART system, the ranking of the most native-like predicted loop configurations was more accurate than using the DFIRE scoring function (Table 4, column “With co-crystallized ligand::Snapshot MM/GBSA”). Similar to the results of single snapshot MM/GBSA re-scoring without the ligand, the lowest RMSD predicted loop was identified within the top-10 positions (Figure 4A).

Figure 3.

Lowest predicted RMSD identified within the top-100 ranked positions after the addition of the co-crystallized ligand. DFIRE, MM/GBSA, and Optimized MM/GBSA-dsr scoring is shown for (A) GART, (B) CYP119, and (C) enolase.

Table 4.

The most native-like (three lowest RMSD) predicted loop configurations of GART, CYP119, and enolase. The ranked position of each loop configuration is shown after scoring with the DFIRE, single snapshot MM/GBSA, trajectory MM/GBSA, and the Optimized MM/GBSA-dsr scoring functions (co-crystallized ligand added).

				With co-crystallized ligand
Protein System	Backbone RMSDa	Heavy Atom RMSDa	DFIRE Rankingb	Snapshot MM/GBSAc	Traj MM/GBSAd	Optimized MM/GBSA-dsre
GART	0.57	1.15	31	5	10	40
	0.74	1.30	19	26	30	44
	1.02	1.55	45	36	23	47
CYP119	1.61	2.92	50	2	12	74
	1.79	2.76	54	8	14	39
	1.80	2.99	81	29	25	62
Enolase	1.43	1.71	81	62	66	10
	1.70	2.31	12	59	41	32
	1.75	2.96	39	29	19	12

^aRMSD in Å to known X-ray loop configuration

^bDFIRE scoring function was used to rank predicted loop configurations

^ca single minimized structure was used to calculate a MM/GBSA score and rank loop configurations

^d20 snapshots from an MD trajectory were used to calculate a MM/GBSA score and rank loop configurations

^eOptimized MM/GBSA-dsr scoring function used to score and rank loop configurations

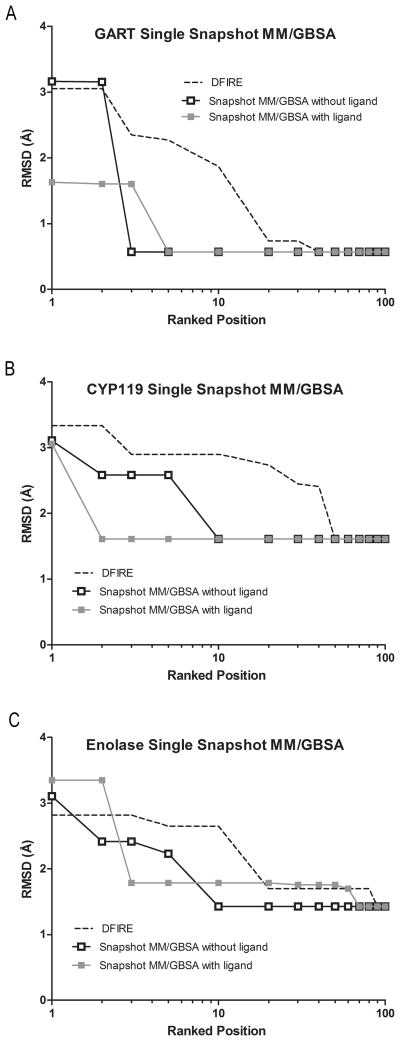
Figure 4.

Comparison of single snapshot MM/GBSA scoring with and without the ligand. The Lowest predicted RMSD identified within the top-100 ranked positions is shown for (A) GART, (B) CYP119, and (C) enolase.

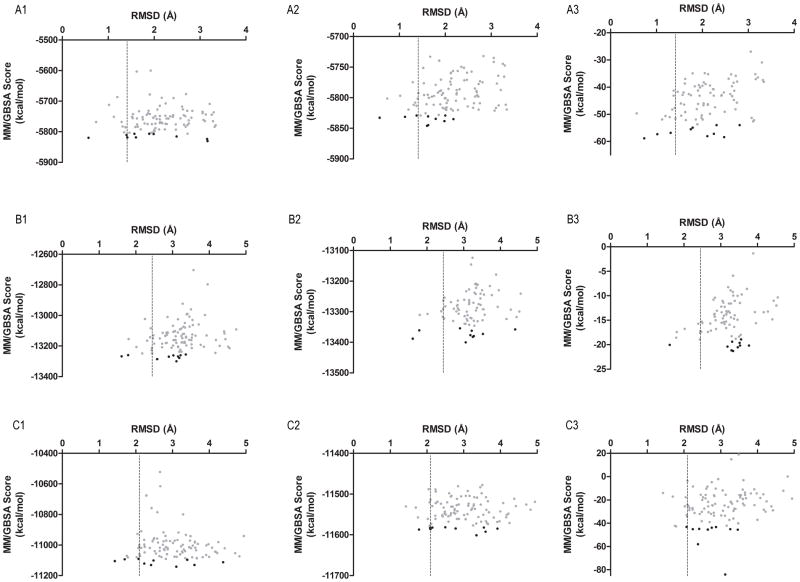
Evident from Figure 3A, a low-RMSD predicted loop configurations (RMSD < 2 Å) was identified in the top-ranked position, however, the lowest RMSD predicted loop configuration was ranked better in single snapshot MM/GBSA re-scoring without the ligand compared to MM/GBSA re-scoring with the ligand (Top-3 versus Top-5, Figure 4A). Although the ranking of the most native-like loop configurations slightly deteriorated, if the ten lowest RMSD predicted loop configurations are considered the ranking improves compared to using single snapshot MM/GBSA re-scoring without the ligand. Three of the ten lowest RMSD predicted loop configurations are ranked within the top-10 positions using this method compared to only one with single snapshot MM/GBSA re-scoring without the ligand (Table S1, Figure 5A1 and Figure 5A2).

Figure 5.

RMSD versus MM/GBSA graphs of the top-100 predicted loop configurations (shown as grey dots) from GART (row A), CYP119 (row B), and enolase (row C). The single snapshot MM/GBSA score of the protein without bound ligand, the single snapshot MM/GBSA score of the protein with bound ligand, and the direct interaction between the protein and ligand (ΔG_P-L) is shown in column 1, 2, and 3. The top-10 ranked predicted loop configurations are shown as black dots. The horizontal dashed line indicates the cutoff for the ten lowest RMSD predicted loop configurations. This figure caption will be rotated by 90 degrees to correspond to the above figure in order for the figure to fit on a single page.

Shown in the column “With co-crystallized ligand::Snapshot MM/GBSA” of Table 4, single snapshot MM/GBSA re-scoring with the ligand improved the ranking of the most native-like predicted loop configurations in CYP119. Similar to the results of single snapshot MM/GBSA scoring without the ligand, the two lowest RMSD predicted loop configurations were ranked within the top-10 positions. Using this scoring method, the lowest RMSD predicted loop configuration was ranked in the top-2 positions compared to being ranked within the top-6 in single snapshot MM/GBSA re-scoring without the ligand (Figure 4B). Although adding the co-crystallized ligand positively affected the ranking of the most native-like predicted loop configurations, no improvement occurred if the ten lowest RMSD predicted loop configurations are considered. Single snapshot MM/GBSA re-scoring with and without the ligand identified two of the ten lowest RMSD predicted loop configurations within the top-10 positions (Table S1, Figure 5B2 and Figure 5B1).

As in the GART and CYP119 systems, Figure 3C shows that the ranking of low RMSD predicted loop configurations improved compared to using the DFIRE scoring function in the enolase system. However, the ranking of the most native-like configurations deteriorated compared to single snapshot MM/GBSA re-scoring without the ligand. Single snapshot MM/GBSA scoring with the ligand did not identify any of the three most native-like loop configurations within the top-10 positions compared to two correctly identified when re-ranking using single snapshot MM/GBSA re-scoring without the ligand (Table 4, column “With co-crystallized ligand::Snapshot MM/GBSA”). Although single snapshot MM/GBSA rescoring with the ligand did not improve the ranking of the most native-like predicted loop configurations, if the ten lowest RMSD predict loop configurations are considered the ranking is similar between single snapshot MM/GBSA with and without the ligand. Both scoring methods identified three of the ten lowest RMSD predicted loop configurations within the top-10 positions (Table S1, Figure 5C1 and Figure 5C2).

Trajectory MM/GBSA re-scoring

To determine if trajectory MM/GBSA re-scoring with the ligand improved upon the ability of single snapshot MM/GBSA re-scoring to rank native-like loop configurations, each member of the DFIRE ensemble from GART, CYP119, and enolase was subjected to a MD simulation. An ensemble of 20 snapshots from the MD simulations was used to calculate the trajectory MM/GBSA energy of each predicted loop configurations. Using a trajectory calculated MM/GBSA value improved upon the initial DFIRE ranking in each protein system (Figure 3).. Following the same trend as seen in trajectory MM/GBSA re-scoring without the ligand, the column “With co-crystallized ligand::Traj MM/GBSA” of Table 4 shows that the ranking of the most native-like predicted loop configurations did not improve compared using single snapshot MM/GBSA re-scoring with the ligand. In the GART system, the lowest predicted RMSD loop configuration was identified within the top-10 positions, but this was not an improvement in the ranking compared to using single snapshot MM/GBSA re-scoring where the same loop configuration was ranked within the top-5 positions (Table 4). No improvement was found when considering the ten lowest RMSD predicted loop configurations, one was identified using trajectory MM/GBSA re-scoring versus three identified using single snapshot MM/GBSA re-scoring with the ligand present.

In CYP119, trajectory MM/GBSA re-scoring with the ligand identified none of the three most native-like predicted loop configurations in the top-10 positions compared to two correctly identified using a single snapshot MM/GBSA with the ligand (Table 4). Considering the ten lowest RMSD predicted loop structures, none were ranked within the top-10 ranked positions compared to two identified using single snapshot MM/GBSA re-scoring with and without the ligand (Table S1).

Similar to the results found for GART and CYP119 trajectory MM/GBSA re-scoring with the ligand present, no improvement in ranking the most native-like predicted loop configurations (Table 4). None of the ten lowest RMSD predicted loop configurations were identified within the top-10 positions compared to two correctly identified in single snapshot MM/GBSA re-scoring. Based on these results, trajectory MM/GBSA re-ranking with the bound ligand incorporated did not improve the identification of native-like loop configurations compared to single snapshot MM/GBSA.

Optimized MM/GBSA-dsr re-scoring

The DFIRE ensemble of each protein system was also re-scored using the Optimized MM/GBSA-dsr scoring function with the ligand included to determine if it outperforms standard MM/GBSA ranking of the predicted loop regions. Shown in Figure 3A and 3B, re-scoring with the Optimized MM/GBSA-dsr scoring function did not significantly improve upon the initial DFIRE ranking in GART and CYP119. Furthermore, the column “with ligand::Optimized MM/GBSA-dsr” in Table 4 shows that the Optimized MM/GBSA-dsr scoring function did not rank the most native-like predicted loop configurations (or any of the ten lowest RMSD predicted loop configurations, Table S1) within the top-10 positions in GART or CYP119. In addition, Figure 3A and 3B illustrates that the Optimized MM/GBSA-dsr scoring function with the ligand did not outperform single snapshot MM/GBSA re-scoring with the ligand.

While unsuccessful in the GART and CYP119 systems, Figure 3C illustrates that re-scoring the enolase DFIRE ensemble with the Optimized MM/GBSA-dsr scoring function improved upon the initial DFIRE ranking. The column “With ligand::Optimized MM/GBSA-dsr” in Table 4 shows that this method was able to identify one of the most native-like predicted loop configurations within the top-10 ranked positions. Furthermore, if the ten lowest RMSD predicted loop configurations are considered, Optimized MM/GBSA-dsr re-scoring with the ligand identified the same number of low RMSD predicted loop configurations when using single snapshot MM/GBSA re-scoring with and without the ligand. Each scoring function identified three of the ten lowest RMSD predicted loop configurations within the top-10 ranked positions (Table S1).

Comparison with experimental loop-ligand interactions

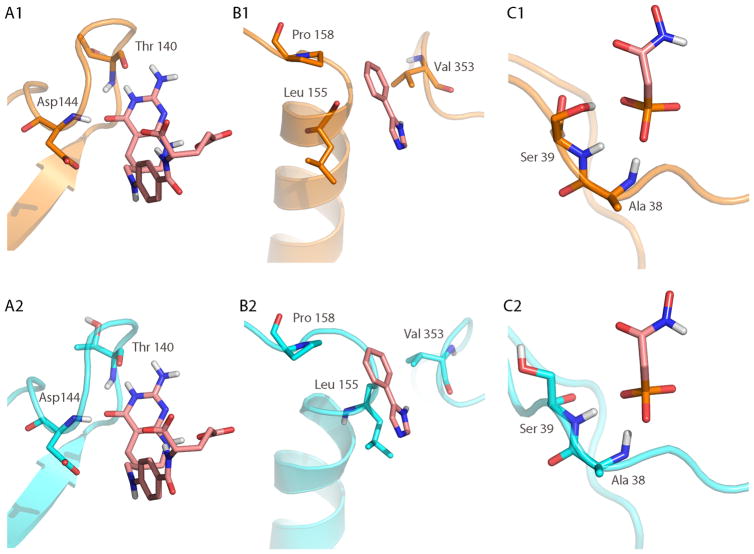
The use of backbone only RMSD as a measure of predictive accuracy is a common criterion in protein loop prediction in the context of homology modeling or structure prediction studies. However, when modeling protein-ligand complexes the side chains often interact with the bound ligand and should be considered as well.. In Tables 3 and 4, the all heavy atom RMSD values are reported in addition to the backbone only RMSD values for the three lowest RMSD predicted loop conformations in GART, CYP119, and enolase. As expected, the all heavy atom RMSD values display an increase in RMSD compared to the backbone only values in all protein systems. The question that needs to be investigated is whether the observed deviation from the experimentally known loop conformation prevents the formation of important protein-ligand contacts in the predicted loop configuration. As shown in Figure 6, important loop-ligand contacts are formed in all three systems that are similar to contacts seen in the experimental X-ray structure, also some differences in the steric interactions between CYP119 and the bound ligand was observed.

Figure 6.

Comparison of loop-ligand interactions between the X-ray structure (top row, shown in orange) and the lowest RMSD predicted structure (bottom row, shown in cyan). The co-crystallized ligand is shown in pink sticks in all panels. (A2) In the predicted loop structure of GART, the ligand forms the same two hydrogen bonds (Thr 140 and Asp 144) with the backbone of the loop as seen in the X-ray structure (A2). In CYP119, hydrophobic contacts dominate the interaction with the ligand. The contacts to Val 353 and Pro 158 are well conserved between the X-ray (B1) and predicted structure (B2). The hydrophobic contact with Leu 155, although present, has sterically changed in the predicted structure compared to the X-ray structure. (C) In the enolase system, the phosphate atom of the ligand interacts with two backbone amides (Ala 38 and Ser 39), but loses a hydrogen bond contact to the side chain of Ser 39 in the predicted structure.

Protein-ligand interaction energies (ΔG_P-L)

In general, no significant improvement in ranking native-like loop configurations upon inclusion of the bound ligand was observed. This finding was not surprising considering that the variation in the predicted energies of the different loop configurations, ΔE_{conformation-P,} varied more than the differences in the protein-ligand interaction energies (Figure 5, columns 2 minus the energy of the apo form compared to column 3). Using single snapshot MM/GBSA values to estimate ΔE_k and ΔE_P-L,k, the total variation within the DFIRE ensembles without the ligand bound was approximately 150 kcal/mol, 300 kcal/mol, and 130 kcal/mol for ΔE_{conformation-P} compared to the variation in the predicted protein-ligand interaction energy ΔE_P-L,k (approximately 30 kcal/mole, 20 kcal/mol, and 80 kcal/mol) for GART, CYP119, and enolase. Thus, ΔE_P-L,k had as smaller contribution to the overall variation in the predicted energy of the protein-ligand complex (ΔE_k) and did not significantly alter the ranking. The variation in ΔE_P-L,k and ΔE_{conformation-P} is likely overestimated by inherent errors in the scoring function. Such errors contribute more to the variation in ΔE_{conformation-P,k} as the calculation of this quantity involves a larger number of atom-atom interactions compared to the direct protein-ligand interaction, ΔE_P-L,k.⁵⁴ A weak correlation was identified between the ΔE_k and the RMSD of the loop configuration (raw data not shown). The Pearson correlation coefficient (r) for GART, CYP119, and enolase was 0.4, 0.3, and −0.1. The difference in correlation was consistent with the difficulty of identifying high-ranked low RMSD loop configurations in enolase and the generation of low RMSD loop conformations for GART (RMSD < 1Å).

We finally addressed the question if focusing on ΔE_P-L,k provides a more accurate measure to separate low RMSD loop conformation that have stronger interactions with the bound ligand from high RMSD loop conformations that lack important protein-ligand interactions. However, extracting the ΔE_P-L,k using single snapshot MM/GBSA did not display a strong correlation between the RMSD of the loop configuration and the predicted protein-ligand interactions (raw data not shown). The Pearson correlation coeeficient (r) for GART, CYP119, and enolase was 0.4, 0.2, and 0.0.

Discussion and Conclusions

Loop prediction for three protein systems, each with a differing length flexible loop region in close proximity to the known active site, was performed with the CorLps program. For each protein system, the DFIRE scoring function implemented in CorLps was used to determine the top-100 predicted loop configurations (DFIRE ensemble). The DFIRE scoring function was able to identify native-like predicted loop configurations (RMSD < 2 Å) for all protein systems, but such configurations were not accurately ranked.

In an attempt to accurately rank native-like loop configurations, each member of the DFIRE ensemble was re-ranked using three different methods: single snapshot MM/GBSA re-scoring, trajectory MM/GBSA re-scoring, and Optimized MM/GBSA-dsr re-scoring. In general, MM/GBSA re-scoring (with and without the ligand) improved upon the initial DFIRE ranking in all protein systems. Re-ranking the DFIRE ensemble of CYP119 with trajectory MM/GBSA scoring (with and without the ligand) did not provide an improvement in ranking native-like predicted loop configurations in comparison to using single snapshot MM/GBSA re-scoring. This suggests that the computational time required to score loop configurations using a trajectory MM/GBSA scheme is not beneficial to accurately rank native-like loop configurations.

The result that native-like loop configurations were ranked within the top-10 positions seems to be consistent with the conformational selection model of protein flexibility coupled to ligand binding. According to this model, incorporating ligand-loop interactions should stabilize and thus rank the most native-like predicted loop configuration in the top position. However, this study shows that existing scoring schemes are insufficient and no significant improvement in ranking the predicted loop configurations was observed when the protein-ligand interaction energy was included. The difference in predicted free energies between the loop configurations (ΔE_{conformation-P,k}) outweighed the ligand-loop interaction (ΔE_P-L,k).

One could argue that the predicted loop conformations deviate too much from the experimentally known loop conformation and that sampling of lower RMSD loop structures is necessary to utilize the strength of force-field based scoring methods such as MM/GBSA. Evaluation of the X-ray loop conformations using MM/GBSA revealed that for the CYP and enolase system the X-ray conformation of the loop is higher ranked (more favorable score) than any predicted loop conformation. For GART the X-ray conformation is ranked at 72^nd position with many loop conformations with RMSD > 2 Å ranked higher than the X-ray conformations.. Thus, sampling of low RMSD conformations (< 1 Å) may be necessary in all protein systems to accurately rank native-like loop conformations using methods such as MM/GBSA.

In summary, the ability of four different scoring schemes to accurately rank native-like predicted loop configurations was explored. The statistically-based DFIRE scoring function used in the loop prediction program CorLps did not accurately rank native-like configurations. Re-scoring using the physics-based single snapshot MM/GBSA method improved the initial DFIRE ranking in all protein systems. While unsuccessful in two protein systems, the Optimized MM/GBSA-dsr scoring function identified native-like loop configurations in the enolase system. Based on the scoring function analyses presented, the optimal ranking of native-like loop configurations is still a difficult challenge and the choice of the “best” scoring function appears to be system dependent. Novel scoring functions, or optimized versions of previously described scoring functions, are still needed to routinely rank native-like loop regions as the top-predicted loop configuration in diverse protein systems. Furthermore, although the effect of the ligand on the loop prediction process should not be neglected in theory, this study did not reveal if including the ligand during the re-scoring process aided in ranking native-like predicted loop configurations.