Protein Dynamics and Enzymatic Chemical Barrier Passage

Abstract

After many decades of investigation, the manner in which enzymes increase the rate of chemical reactions, at times by a factor of 10¹⁷ compared to the rate of the corresponding solution phase reaction, is still opaque. A topic of significant discussion in the literature of the past 5–10 years has been the importance of protein dynamics in this process. This feature article will discuss the authors' work on this still controversial topic with focus on both methodology and application to real systems. The end conclusion of this work has been that for specific enzymes under study, protein dynamics on both rapid timescales of barrier crossing (termed promoting vibrations by the authors) and of conformational fluctuations are central to the function of biological catalysts. In another enzyme we will discuss, the results are far less clear. The manner of the coupling of chemistry to protein dynamics has deep implications for protein architecture, both natural and created; and recent results reinforce the complexity of the protein form that has evolved to support these functions.

INTRODUCTION

Perhaps no question in physical enzymology to arise in the last 15 years has generated such heat as the importance of protein dynamics to the catalytic function of enzymes. At first glance, it is hard to understand why this issue should create such consternation. It has been an acknowledged, experimentally verified fact that protein motion has a profound effect on the barriers to binding and release of ligands in heme proteins. Functionally important motions have been known for decades¹. It has also been an acknowledged fact that mutations remote from active sites can cause significant changes in the competency of enzymatic catalysis². In fact, there are cases extant in the literature in which remote mutations change rates, but make no change in active site structure as seen in x-ray diffraction³. Given what seems to be an overwhelming surfeit of evidence that proteins move, and such motion is in some fashion directly coupled to the “business end” of enzymes – catalytic chemistry, one might ask where all the controversy lies.

Some of the controversy results from terminology, but the disagreements are real, as any attendee at a physical biochemistry conference will find. The point of view that will be adopted in this Feature Article is that motions that range from the femtosecond to millisecond all are potential contributors to catalysis. We make no assumptions regarding the importance of any specific type of motion. We employ unbiased computational methods (Transition Path Sampling coupled with reaction coordinate analysis) to investigate the question. We will now highlight cases in which we have shown very fast motions to contribute to chemical barrier passage in enzymes, and how these motions fit with slower motions on the timescale of enzymatic turnover. We will also show a case in which there is no significant coupling of an organized fast vibrational characteristic to barrier passage.

The structure of this Feature Article is as follows: First we show how our involvement in this problem developed. Aside from a history of our research effort in this area, the progression shows the relation of the properties found in reactions in non-biological condensed phases to those in enzymes. Second, we discuss our calculations in enzymes that show that rapid protein vibrations are directly part of the reaction coordinate, and so central to passage over the transition state. We also highlight a case in which such a vibration does not seem to exist. In this section we also highlight work from other groups that shows related results for very different enzymatic systems. Third, we discuss extended reaction coordinates, in other words motions on a far slower timescale, and how these motions relate to the fast ones already identified. Fourth, we discuss the relation of the results we have found to rate theories. Finally we close with work currently under way as relates to the issue of protein dynamics and enzymatic chemistry.

A BRIEF HISTORY

As a prelude to discussing our particular efforts, we will briefly sketch the history of how we became interested in this problem. This is in no way intended as a complete review of the field, and of a necessity, many important contributions will be absent from our description as this is a fairly personal resumé. The development of theories to predict rates of chemical reactions in condensed phases has been one of the great successes of theoretical chemistry in the past few decades. The towering achievement in this field is far older – Kramers' theory⁴. Our involvement in what was by then a fairly crowded field was the development of ways to handle this problem quantum mechanically. The method, following Zwanzig⁵ cast the Langevin equation in a Hamiltonian form where a reaction coordinate was bi-linearly coupled to a bath of oscillators. The quantum dynamics of this system was then solved with operator resummation methods we had developed⁶. This was applied with success assuming the properties of the bath can be represented as a spectral density⁷. Further application of the methodology to proton tunneling in benzoic acid crystals⁸ was not successful. We realized that what was missing was a specific motion in the system that symmetrically moved the proton donor and acceptor closer to each other. Mathematically, we showed that a symmetric coupling to an environmental bath mode, rather than an antisymmetric coupling as in the Zwanzig picture characterized this motion⁹. The fact that this symmetric coupling gave essentially different physics was not a surprise – Marcus had discussed just such an effect in gas phase dynamics many years earlier¹⁰. One interesting fact explained in these computations was that even though the transfer of the proton was completely quantum mechanical, kinetic isotope effects on the transferring particle were in fact suppressed. We also note that Hynes and co-workers¹¹ in pioneering work on liquid phase chemistry noted just such promoting vibrations, and drawn a parallel to enzymatic reactions¹².

The similarity of the experimental results described above to certain enzymatic reactions, coupled with the extraordinary results from the Klinman group showing what seemed to be decreased tunneling at lower temperatures¹³ led us to speculate that such a symmetrically coupled vibration, or as we came to call it, promoting vibration, could exist in certain enzymatic catalysts¹⁴.

What was not available was a rigorous way to identify such a coupling. Our initial attempts at this showed that a mathematical characteristic of the promoting vibration, if present, was significant change in the spectral density for the environment as reaction is traversed from reactants through the transition state to products,¹⁵ with the frequency of the peak which disappears at the transition state very close to that of the symmetrically coupled promoting vibration. We then applied this methodology to the reaction catalyzed by horse liver alcohol dehydrogenase¹⁶. We found exactly the mathematical evidence we predicted for such a promoting vibration with the frequency of the motion about 150 cm⁻¹. We were also able to show that a specific mutation at the active site in HLADH, known to decrease chemical rates and signs of tunneling also showed a decreased coupling of the promoting vibration to the transferred hydride¹⁷. We also note that soon after these initial publications, Cui and Karplus located such motions in triosephosphate isomerase¹⁸.

What was missing at this point was a rigorous way to both identify the promoting vibration (the above mentioned method only identified motion of a specific frequency – not the physical motion itself,) and critically to prove causality. There was no proof that the motion was necessary for reaction to happen, it could simply be a concomitant of the catalytic process. At this time, the Chandler group was developing the major ideas behind Transition Path Sampling¹⁹. The critical idea behind this advance was to find “reactive” trajectories for complex phenomena via a Monte Carlo walk in trajectory space. (The word reactive is in quotes because it certainly can be applied to situations in which chemical reaction is not involved²⁰.) Gathering a large number of these trajectories allows further calculation of an object known as the stochastic separatrix²¹. As we will discuss below, analysis of the separatrix allows the identification of all motions that are necessary for reaction to happen. In normal parlance, this is termed the reaction coordinate. This is the crucial step that allows our identification of rapid dynamics as part of chemistry in certain enzymes.

RAPID MOTIONS AND ENZYMATIC CATALYSIS

The first enzyme to which we applied the TPS methodology was human heart lactate dehydrogenase²². A large number of reactive trajectories were gathered and they were tested for decorrelation. Examination of the trajectories made it immediately clear that as we suspected for the related enzyme HLADH, human heart LDH has as part of each reactive trajectory a compressive motion that extends across the body of the protein to cause the donor and acceptor to approach closely. This motion is shown graphically in Figure 1. The timescale of this motion is roughly 150 femtoseconds. Analysis of the trajectories is suggestive, but not conclusive because causality is not established. In other words, seeing the compressive motion in the protein tells one solely that in the reactive trajectories we examine, compressive motion accompanies reaction. It does not prove that the motion is necessary for reaction. For example it could be that the protein simply follows motion of the donor and acceptor as they oscillate and this motion is not causative of reaction. In order to show causality, we employ the committor distribution analysis first suggested by Onsager²¹ and later expanded upon by Chandler and co-workers¹⁹. The stochastic separatrix is that hypersurface in configuration space from which trajectories initiated with random momenta chosen from a Boltzmann distribution have a 50% chance of proceeding to products or returning to reactants. It is certainly the most reasonable statistical definition of the transition state surface. Motion along the separatrix is the one type of motion that does not change the progress of reaction (it by definition stays at 50%) and so motion along the separatrix is determined by restriction of the reaction coordinate degrees of freedom. Thus an effective, but time consuming method for identification of the physical reaction coordinate is to guess at the degrees of freedom that must be held fixed (those belonging to the reaction coordinate,) hold them fixed and perform a constrained molecular dynamics simulation starting from a known point on the separatrix. If after this constrained motion, unconstrained dynamics with momenta again drawn randomly from a Boltzmann distribution yields a reaction probability of 50%, then one can say with confidence that the degrees of freedom chosen are in fact part of the reaction coordinate and are in fact causative of reaction, not simply a concomitant of reaction. It should be apparent how consuming of both human and computer time this approach is – many hundreds of QM/MM trajectories need to be run to perform the test. This exhaustive examination showed that in fact the protein promoting vibration involving the residues shown in Figure 1 was in fact part of the reaction coordinate, and so central to reaction not simply a concomitant of it²³. In contradistinction, when these tests were performed assuming the transferring hydride and proton alone formed the reaction coordinate, as might be guessed from biochemical intuition; committor distributions were not found to be peaked about .5, demonstrating that these degrees of freedom alone were not a good reaction coordinate. So to recap – this calculation shows that within the accuracy of the method (the CHARMM²⁴ potential with semi-empirical QM/MM for reaction,) rapid protein motion is part of the reaction coordinate.

Figure 1.

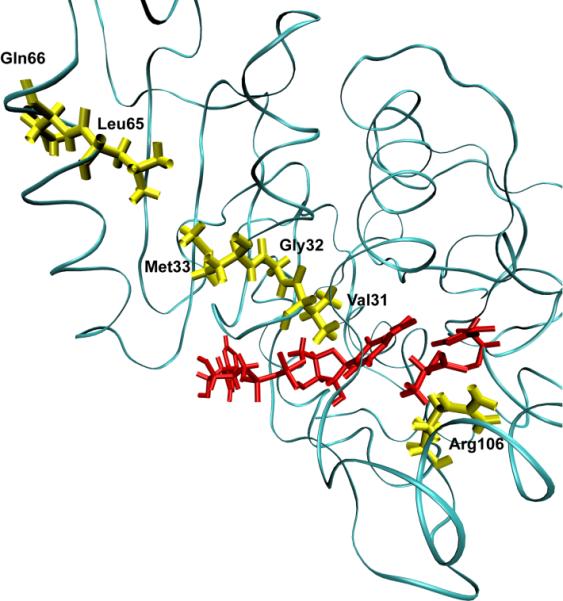
A ribbon diagram of a monomer of human heart lactate dehydrogenase. The donor and acceptor: the nicotinamide ring, and lactate are colored red. The promoting vibration residues, Val31, Gly32, Met33, Leu65, Gln66 (yellow) are compressed towards the active site bringing the NC4 of the nicotinamide ring and substrate carbon closer together while Arg106 (yellow) relaxes away locking the substrate in product formation. These residues span the entire length of the monomer to the edge of the protein.

The calculation of the necessary committor distributions for reaction coordinate confirmation is quite computationally demanding, as has been described. An important area of work in our group has been the development of methods that predict the components of the reaction coordinate based on the structure of the separatrix itself²⁵. These methods are highly successful and extremely efficient; yielding a good representation of the reaction coordinate “for free” when the separatrix is calculated. These methods are distinct from the committor distribution fitting methods that have been developed²⁶ for the determination of reaction coordinates. The fitting methods are really best applied to diffusive barrier passage, whereas our methods are best applied to direct barrier passage; the kind most often encountered in enzymatic chemical reactions. The idea behind the method is quite simple. The separatrix is the set of points in the configuration hypersurface that uniquely identifies geometries in which the reaction coordinate is unchanged in progress. At the separatrix, you are on the transition state surface because it is formed from the set of points with .5 probability committor values. Our definition of the components of the reaction coordinate is simply those degrees of freedom that do not change on the separatrix. In this sense then, the separatrix must be narrow in these degrees of freedom. The problem is that we do not have a mathematical description of the separatrix, only points in space. The separatrix is likely “narrow” in these special degrees of freedom in some non-Cartesian coordinate system. Thus what is needed is a method that identifies the correct parameterization of the separatrix and in doing so finds the coordinates for which there is minimal change. Finding the correct coordinate system in which to describe the separatrix is a non-linear fitting problem, and we use methods from machine learning known as kernel PCA²⁷. A usable representation of the topology of the separatrix is obtained when a single non-linear component is shown to accurately reproduce the entire separatrix. The members of the reaction coordinate are then identified as those that make minimal contribution to this single non-linear principle component. We have shown²⁵, that the components involved for the lactate dehydrogenase reaction closely align with those we “guessed and checked” in the past. The identification of reaction coordinates will likely continue to be one of the most challenging areas in rare event simulation.

At this point we know that there is motion in the body of the protein that brings the donor and acceptor sites in LDH closer together. This promoting vibration, however, need not be any specially selected motion in the vibrations of the protein matrix. It could simply be the case that there are all types of diffusive heat transfer in the protein, and it just so happens that this specific mode is effective in contributing to catalysis. In some sense, this is not important to understanding how the chemistry works, but it is critically important to developing an understanding of how the enzyme is constructed. It also suggests that if one wishes to construct an artificial enzyme with, the inclusion of such promoting vibrations is in fact a critical design feature.

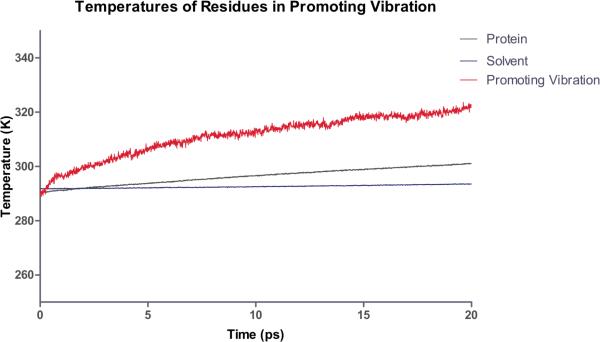
Recent unpublished work in our group has addressed exactly this question. In order to investigate this question we performed a numerical experiment much like that which Straub has implemented for myoglobin²⁸. We pumped heat into the active site and monitored the temperature at residues in the promoting vibration. Figure 2 shows a preliminary result of the temperature of the solvent, the protein as a whole, and that of the promoting vibration. It is clear from these data that not only is the promoting vibration unique in terms of chemistry, it is also unique in terms of protein architecture. Thermal energy transferred from the active site is preferentially channeled through the promoting vibration. These computations also provide a further check on the accuracy of our non-linear kernel methods for reaction coordinate identification. The amino acids identified via this reaction coordinate computation are in fact the dominant residues for heat transfer. In addition, it is worth mentioning that these calculations provide a perfect experimental test for the existence of a promoting vibration. Laser spectroscopic methods are able to monitor such temperature differences²⁹. Details of these calculations will follow in a subsequent publication³⁰.

Figure 2.

Preliminary results of a computational heating experiment. The nicotinamide ring is heated as described and the temperature of the solvent, protein and residues along the promoting vibration are monitored. The promoting vibration is clearly hotter than the rest of the protein indicating a preferred direction of thermal energy transfer.

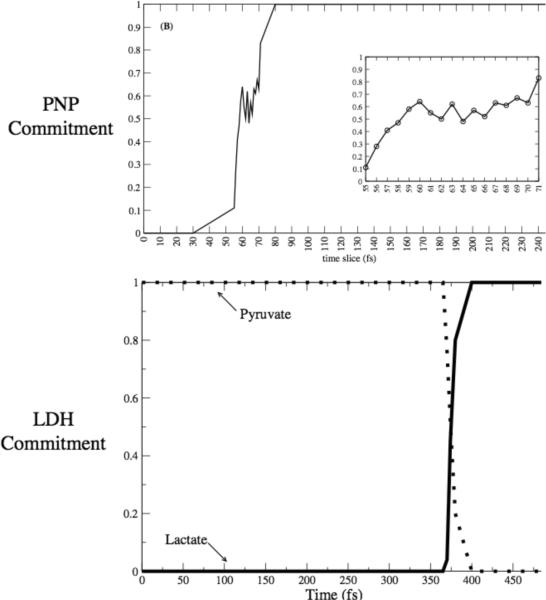
Though the dehydrogenases/reductases are central to metabolism, we must ask whether the hydrogen transfer reactions are unique in the involvement of protein dynamics in chemical barrier passage. First, they may well involve tunneling, and in this case through barrier transfer is exponentially enhanced by width reduction (tunneling is not part of the TPS framework, but this issue will be addressed in the future work section later in this Feature Article.) Second, in any simple atom transfer reaction, even if the transfer is completely over the barrier, it is easy to see from simple quantum chemistry arguments that moving the donor and acceptor closer together will significantly lower the barrier to reaction. We thus became interested in seeing if a promoting vibration was present in a very different class of enzymatic chemistry. We studied the reaction catalyzed by purine nucleoside phosphorylase: scission of the ribosidic bond in nucleosides. From a variety of experimental evidence we had reason to believe that this may well be the case. First, mutation on the surface of this protein that had absolutely no effect on the structure of the active site of the enzyme, increases the rate of on enzyme chemistry³. Second, crystal structures of transition state inhibitors showed a unique stacking of electronegative oxygen atoms directly adjacent to the scissile ribosidic bond. Our hypothesis was that compression of this bond could sufficiently polarize the electron density as to make the base a better leaving group. A variety of computations³¹ confirmed this hypothesis. The reaction mechanism from an atomistic point of view was also seen to be more complex than that of the hydride transfer of LDH. Figure 3 shows the difference between a committor distribution for a complex reaction like PNP (in the top panel) and one for a direct mechanism like that for LDH (bottom panel.). It is clear that more time is spent in the transition region for PNP. It should, however be emphasized that this “long” residence time is still measured in femtoseconds! The PNP reaction is actually a 2 step process, with the first rise in committor coming from a promoting vibration compression and initial breaking of the ribosidic bond; and the second rise coming from motion of the ribose ring towards the phosphate to form the ribose-1-phosphate product.

Figure 3.

Commitment probability values were calculated for both PNP (top panel) and LDH (lower panel) along sample trajectories from the reactive path ensembles for the respective enzymes. It is clear that the transition region for LDH is far shorter in time duration than for PNP, but even for PNP, the residence time is on the order of 10–20 fsecs.

While no attempt is made to be exhaustive in cataloguing work in this area, we do note that evidence for promoting vibrations has now been found both experimentally and theoretically in other enzymatic reactions. Sutcliffe and Scrutton have found such cases³², and interestingly, they find a case in aromatic amine dehydrogenase where a vibration of almost exactly the same frequency of that we have found in LDH is important to reaction³³. The fact that the timescale is almost the same speaks to the importance of matching this timescale to that of barrier passage. There remains controversy in the field as to whether promoting vibrations on this timescale are important in what might be termed the “hydrogen atom” of hydride transfer: dihydrofolate reductase. There is a suggestion in work of Hammes-Schiffer and colleagues³⁴ that in fact faster motions accompany reaction. We have recently begun TPS calculations on this enzyme, and have performed our non-linear kernel analysis on the separatrix generated. Our results also show that aspects of this motion are a necessary part of reaction, and that they are part of the reaction coordinate. Examination of the structure of the enzyme, along with the nature of the movement of the identified residues finds that the architecture of the enzyme does not permit the type of compressional vibration across the body of the enzyme through the active site to allow shortening of donor acceptor distance. The motions are subtler – those needed to positions of reactants in a final assault on the free energy barrier to reaction. In this case a purely statistical view is likely warranted. The nature of the fast timescale motion we find in DHFR is shown graphically in Figure 4.

Figure 4.

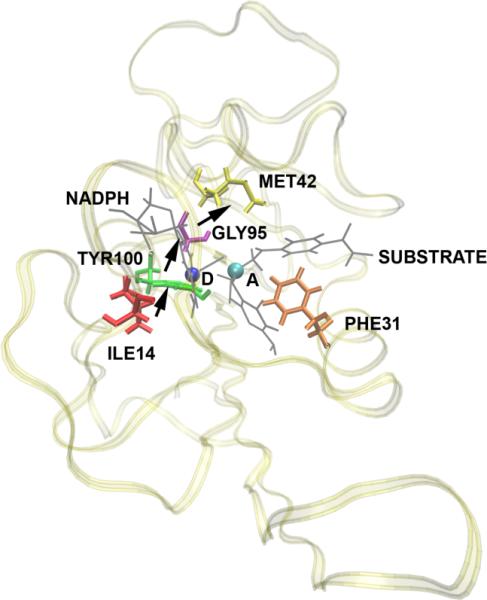
A diagram showing the residues that move and the direction of movement as a reaction crosses the separatrix in the DHFR reaction. Donor and acceptor are shown as a blue and green ball respectively. There is clearly no well-defined promoting vibration, and as yet we are able to show no rapid motions as parts of the reaction coordinate. It is also clear from the protein that the limited protein scaffold prevents the formation of the type of compressive promoting vibration seen in LDH.

It is has been accepted that dynamics plays a role on longer timescales in this enzyme², and Hammes-Schiffer and colleagues have suggested that millisecond timescale motions in a “coupled network” are critical to barrier passage. Recent experimental work from Allemann's group³⁵ questions this particular result and suggests that it is likely that the motions are faster and shorter range. (Note: these types of motion are certainly in harmony with the results we have from DHFR – short range and highly local.) Recent results from this group actually question the importance of conformational fluctuations in DHFR catalysis³⁶, and theoretical analysis of Warshel also questions the importance of millisecond conformational fluctuations³⁷. Thus it was of special interest for us to study the effect of conformational fluctuations in LDH as we have already seen this enzyme exhibits very different properties to DHFR. We will thus now being to address the question of how longer timescale motions relate to promoting vibrations and barrier passage in particular in the LDH system.

LONGER TIMESCALE MOTIONS AS EXTENDED REACTION COORDINATES

Our results that protein motions on the femtosecond to picosecond timescale are central to barrier passage in an enzyme may appear confusing to some enzymologists. Virtually all enzymes have a statistical turnover rate of roughly a millisecond – certainly not much faster. There is of course no contradiction in this fact – the rate-limiting step for many enzymes is in fact product release or substrate binding. What this implies is that the enzyme spends the vast majority of the time from its initial encounter with substrate until product release “engaged in activities” other than barrier passage. The question then becomes what are these “activities”? The “activities” are conformational changes from slow loop movements to relatively fast local rearrangements that allow the enzyme to function. Another way of stating this is the portion of the reaction coordinate we have described is that central piece that tracks chemical barrier passage. It would be of great value to extend this reaction coordinate in some fashion closer to the binding event.

The first technical difficulty presented by this endeavor is the timescales are simply too long for convention molecular dynamics. Obviously, one cannot simply take the reactive trajectories we have generated and extend them back in time long enough to view the earlier processes that occur in the catalytic process. In some fashion, then a method is needed to search the highly complex free energy surface of the protein. This then highlights the second technical difficulty, which is that this free energy surface is almost assuredly quite complex with a great many local minima. If one simply performed say a Monte Carlo walk on the surface with annealing to local minima, one would find only a tiny fraction of the possible minima, and those may well not all be functionally relevant. The goal is to search the surface in such a fashion that the chemically distinct basins³⁸ are in at least a reasonable fashion explored.

Our method to accomplish this grew out of the recognition that in the reaction catalyzed by LDH, the distance of the donor and acceptor is central to reactivity. Thus, if one wishes to locate the functionally important conformations, they must all have this donor acceptor distance within a range that allows reaction as assisted by the promoting vibration³⁹. The specific computational tool we choose was to restrain this distance to that found in the crystal structure, and allow the rest of the protein to explore conformational space via Langevin dynamics and minimization⁴⁰. Once a set of candidate conformations were obtained in this fashion, they were further minimized with gradual release of the donor acceptor constraints.

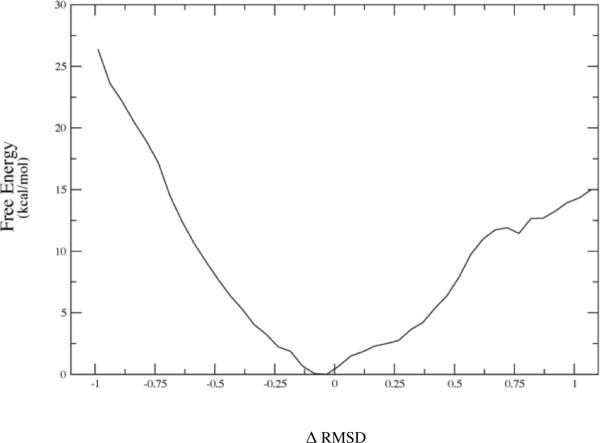
The first data that we reported was that in the vast majority of cases, release of the constraints allows the donor and acceptor to move far beyond the selected range and so to fall into conformations that are not catalytically competent. In fact, the number was far less than 10%. We then wanted to understand the energetics of conformational motion in the enzyme. To do this we found the minimum free energy path between all sets of basins that had low donor acceptor distance. The minimum average potential energy path and the associated free energies we discovered on a selected path are shown in Figure 5. These basins have relatively small but detectable differences in geometry of the active site, and this is shown graphically in Figure 6. The central difference between the different low donor acceptor distance conformations was in the positioning of the active site loop over the reactive center. It is known that reaction cannot occur in LDH if this loop is not closed, and this result shows how critical positioning of this loop is to catalysis. In fact, analysis of the paths between the short donor acceptor conformations both always involve a significant widening of the donor acceptor distance, and partial opening of the loop conformation. The effective free energy barrier to these motions from the free energy minimum (that is not reactive) was always in the 10-kcal/mol range. In retrospect, not surprisingly, these conformations that were stable in potential energy became free energy maxima when the free energy along the path between the low donor acceptor conformations was calculated. This is simply a statement of the rarity of these catalytically competent conformations. Finally, Figure 7 shows a calculation of the chemical barrier to reaction in a variety of the conformations. As expected, the free energy maxima, short donor acceptor distance has the lowest chemical barrier to reaction – almost zero.

Figure 6.

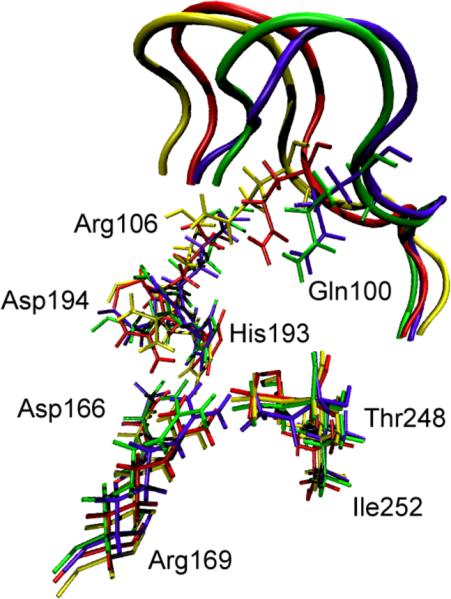
Overlay of the active site residues of 4 representative potential energy stable conformations (three of which are part of Figure 5a.) Residues belonging to the same conformation are shown with the same color. At the top of the picture, the active site loop is shown (residues 96–106, its residues 100 and 106 are shown explicitly) The 4 residues at the bottom of the figure are related to each other by a simple translation. However, the important residues His193, Arg106, Gln100 and Asp194 are being pushed by the active site loop (which has a different closed position in each of the 4 conformations), and their geometric arrangement is different in a non-trivial way among the 4 conformations. Transitions between these conformations were seen to always involve partial loop opening.

Figure 7.

The chemical barrier to reaction along the free energy path of the conformational transformation in Figure 6b. The reaction proceeds from right (Lactate) to left (Pyruvate). The lowest chemical barrier is obtained at the end point high free energy (rare) conformations. The highest barrier to reaction occurs at the lowest free energy conformation – the minimum in Figure 5b.

Thus to summarize, we have found the nature of motions and conformations that bring the system to the catalytically competent state that have short donor-acceptor distance. These conformations are very rare and, there is a free energy barrier of entropic origin toward these competent conformations. This last finding suggests that perhaps an appropriate description of catalysis in this enzyme is a search for these rare competent conformations, followed by the reactive event that is assisted by fast sub-picosecond protein motions. More artfully put, one may describe the function of the enzyme as a conformational filter that performs a stochastic, but efficient search through conformation space that allows chemical reaction to happen in an almost barrierless fashion. The tradeoff in free energy is simply the wait for the enzyme to locate a catalytically competent conformation in which there is essentially no barrier to reaction. This focuses the view of enzymatic catalysis on the probabilistic rather than energetic component.

At this point, it is appropriate to discuss the claim that has been made by some that enzymes make no use of dynamics at all in their catalytic process. There are two principal arguments that have been invoked to state that dynamics plays no role in enzymatic catalysis. The first is that catalysis by anything means accelerating a chemical reaction rate over some reference – invariably a solution rate. The argument then goes that if the mechanism of dynamic contribution is the same in the solvent as in the catalyst (enzyme,) then it is not fair to claim that dynamics is important in catalysis. This is in fact true, but quite legalistic. The question of scientific interest is “how does an enzyme work?” The answer may well partially be that it works in the case of hydride transfer by squeezing the donor and acceptor close together. You can consider an analogous reaction in solution. Here it is well known that a cage in the solvent will constrain donor and acceptor and a non-equilibrium fluctuation in the cage will drive them close together. This is exactly when reaction happens. The enzyme does exactly this, but it does it many, many times more efficiently. In some cases it is possible that the underlying mechanism of reaction in a solvent is exactly the same as an enzyme, but the extraordinary efficiency with which the enzyme accomplishes this is still a question of abiding interest.

The second argument is a statistical argument. It is often presented as relating to deviations from Boltzmann statistics or pre-exponential factors as corrections to transition state theory. We find these arguments to be confusing at best, so we will try to reframe them in language more common to statistical mechanics. This is an issue of timescale separation. If we imagine that the only thing that effects rates of chemistry in an enzyme are very slow motions, then the transitions between the conformations are decoupled from chemistry, and each conformation will have a rate which can be assigned to it. Then the overall rate is simply the average of the rates from each conformation weighted by the probability of finding that conformation. This is likely what is referred to as a “Boltzmann probability.” It is still of interest, however to know if the motion of the protein create an ensemble of barriers that are significantly different; does protein motion create an ensemble of barriers that differ from the gas or solution phase, etc.

The next possibility is that the motion is actually faster than the average time for passage over the barrier. For example bond vibrations are on the order of a femtosecond, but barrier passage in the case of say purine nucleoside phosphorylase takes multiple tens of femtoseconds. In this case the bond vibrations are simply averaged over to obtain a free energy, more accurately a potential of mean force (equilibrium solvation,) or the exponential part of a TST expression.

The crucial point is that for the promoting vibrations we have found, the dominant timescale of vibration is the same timescale as the barrier passage. In fact the promoting vibration is a central component of the reaction coordinate, and so of necessity the correct free energy calculation. Another way we have described this is to identify the effect of the promoting vibration as a position dependent friction¹⁴. More will be said about this in our discussion of rate theories below.

RATE COMPUTATION

While we emphasize that none of the computations we have described from our work are currently aimed at rate calculation, an important question is how our results might inform on methods of doing so. Clearly, one of the most popular methods of rate calculation is transition state theory. Given the inherent complexity of a reaction in any condensed phase, especially that of an enzyme, it seems almost incredible that it can provide reasonable accuracy. We now address how out TPS calculations might inform on this issue.

The original transition state theory or “Absolute Rate Theory” as proposed by Eyring⁴¹ was based on the claim that there is an equilibrium established between the reactants and the transition state. Our TPS calculations clearly show that the transition state is far too ephemeral for such equilibrium to occur. This of course in no way invalidates the potential accuracy of TST, as it is well known that no equilibrium is needed to derive the approach^42,43

Truhlar has developed a comprehensive suite of methods that allow correction to the simplest transition state formulae⁴⁴. There are two issues that on first glance would leave a skeptical critic thinking that TST had no chance of working. The first is simply that in a complex system the topology of the free energy surface is such that there should be many, many saddles, and so it is likely that there should be many, many transition states. In fact our calculations show convincingly that this is simply not what nature has arranged, at least as far as donor and acceptor pairs are concerned. In our calculations in LDH we have shown that though the reactive trajectories that are members of the transition path ensemble arrive at the transition state (the separatrix) in many ways, when there, they are highly similar in characteristics, and the separatrix seems to be fairly low dimensional²³. The concern may be raised that the search we performed for TPS in the LDH case was simply not broad enough. We have reinitiated these calculations with a far larger perturbation in the “shooting” move. Figure 8 below shows that even the most separated members of the transition path ensemble for LDH are in fact quite similar as they pass the separatrix. In addition, we have been applying transition path sampling to the reaction catalyzed by DHFR. We have attempted in these calculations to force as large a search of trajectory space as we possibly can. Again, in this enzyme we find a true bottleneck at the separatrix. Figure 9 shows the overlay of two of the members of the separatrix in this enzyme. Given the floppy nature of DHFR one might have supposed that this enzyme would exhibit a less restricted transition state region than LDH, but this seems to not be the case. It should be emphasized that this was not a required outcome. There could have been multiple highly divergent paths through the separatrix.

Figure 8.

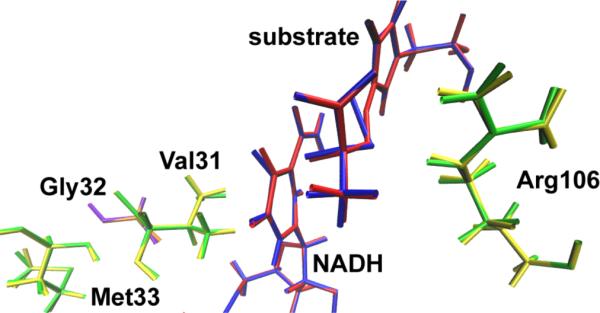
Shown above are snapshots of two members of the separatrix found from the largest Monte Carlo step TPS simulation we have accomplished on LDH. Green and yellow, and red and blue show the 2 structures of the promoting vibration and the NADH/lactate respectively. These 2 members are the most separated in trajectory space, and it is clear that at the separatrix, they almost perfectly overlay. It is shown that common motions guide each path over the transition surface are evident in the complete overlap of the configurations at the transition state.

Figure 9.

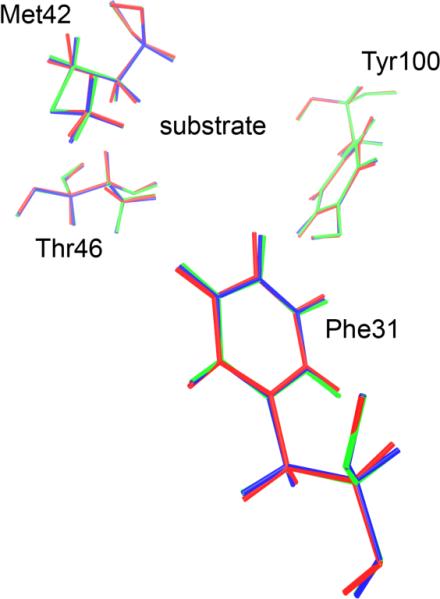
2 DHFR configurations are presented as the chemistry passes the separatrix, as in Figure 8 above for LDH. These configurations show a bit more variability than those of LDH in Figure 8, as expected given the far more flexible protein structure, but even in this case; there is very strong overlap of the 2 configurations.

The second question one may pose is if there is a promoting vibration, and a multidimensional reaction coordinate, how does one identify a transition state in low dimension. There still is a bottleneck; it simply is embedded in a higher dimensional space. The crucial point here is that the promoting vibrations we have found are motions on a similar timescale to that of barrier passage. They are not so fast that they can be simply averaged over to obtain a single free energy barrier in their environment, and they are not so slow that they can be assumed fixed for the purposes of rate calculation. In the language of transition state theory, these dynamics effect both the location of the TS and the height of the free energy barrier. We have discussed these issues and the relation to Grote-Hynes theory previously¹⁴. In the Generalized Langevin Equation (GLE) formulation we presented in Reference 14, the promoting vibration creates a GLE with a fluctuating reaction coordinate potential (i.e. the simple reaction coordinate has a free energy barrier modulated by another degree of freedom on a similar timescale to its own dynamics.) The best analogy to these models in TST would be found in the ensemble averaged variational transition state methods Truhlar and co-workers have devised⁴⁵. Barriers in which the promoting vibration had strongly compressed the donor acceptor would be lower in the ensemble of rates and have a greater contribution to the rate. In this view of TST, one cannot locate a singe TS that accurately dominates the rate.

One argument that has been made against the importance of dynamics in enzymatic chemistry is that since the TST recrossing statistic (κ) for enzymatic reactions is always close to 1, there can be no dynamic effects. Dynamical effects such as promoting vibrations raise the rate of reaction. Their presence or absence could never be detected by the value of κ - as stated above, they are part of the free energy. For example we have extended our barrier crossing calculations for many nanoseconds, and have never seen a recrossing event – we are in total agreement that κ is 1.

One question often asked is how much of an effect a fast motion such as the promoting vibration may have on the free energy barrier. Some years ago, a rough calculation on HLADH suggested that the promoting vibration lowers the barrier by 30% over the static case¹⁴. Clearly this will be significantly different from system to system. There is no clear way to test this number – there is not a simple mutation that breaks the promoting vibration, but we are investigating this possibility with experimental collaborators. The results described here in no way invalidate the possible overriding importance of such well-described effects as dipolar stabilization. On the other hand, we did try to initiate reactive trajectories in LDH with the promoting vibration restrained. This resulted in no reactive trajectories. This was not published because the restrained unsuccessful trajectories do not form a recognizable ensemble distribution.

A final rate theory we would be remiss to not mention is the forward flux formulation of Chandler⁴⁶. This is of course an exact formulation of the rate, much like the flux correlation formulation⁴⁷ is a formally exact method to compute the quantum rate. In these correlation function theories, TST like result are recovered from a t→0 limit. The usefulness of the result depends on the choice of the dividing surface, as in TST. To obtain an accurate result in the enzymatic case, this dividing surface would have to be found for the full reaction coordinate, not simply reactive particle transfer. So if there were a promoting vibration as part of the reaction coordinate, it would be included in the dividing surface search. It should be emphasized that such an approach does not guarantee accuracy – obviously the short time limit of the correlation functions involved is a drastic approximation.

CURRENT DIRECTIONS

We are currently involved with a number of further investigations, both basic and applied, which deserve mention. First, we are investigating rapid motions in DHFR. As we discussed, there has been brief mention of rapid motions near the barrier to reaction, but there is as yet no proof as to whether these are in fact promoting vibrations and coupled to reaction or simply motions that appear when reaction happens. One can imagine arguments both for and against the importance of promoting vibrations in DHFR. On the pro side, this reaction does exactly the same chemistry at ADH and LDH, and so one could imagine a similar effect. On the con side, the protein itself is drastically different. It is a small protein that supports far less dense structure than LDH, and so potentially less organized vibrational fluctuations. Previous studies of the enzyme have argued both for and against the possibility of a promoting vibration. Figure 4 demonstrates that the types of vibrational motion coupled to chemistry near the top of the free energy barrier cannot be a simple compressional motion. The question is: are the motions near the top of the barrier coincident with or causative of chemistry. As we have described, preliminary results showing motion coupled to reaction via separatrix analysis, but in a far less obvious fashion than LDH (and likely less importantly so.) Another question relates to slower motions and catalysis. A large and superbly argued body of experimental literature shows that remote mutations have significant effects on kinetics of the enzyme, and the changes are seen to correlate with dynamic changes observable by NMR². This has been supplemented by Benkovic and Hammes-Schiffer's description of networks of coupled motions. However, a recent experimental result calls the existence of large-scale vibrational motion as it effects enzymatic catalysis into question³⁵. It is clear that close approach of donor and acceptor are critical for hydride transfer in this enzyme as it was for LDH. Given that fact, the approach we have taken to discovering important conformational transitions in LDH can be applied to DHFR.

It is worth mentioning that protein dynamics is not absolutely necessary to biological catalysis. Inhibition of DHFR by such drugs as methotrexate is a wide-ranging medical therapy for such illnesses as cancer, autoimmune disease and pathogenic infection. In response to such treatment, a resistant strain has been discovered that produces a brand new highly impaired, but active DHFR⁴⁸. Structurally, this DHFR is little more than a box that is able to bind substrates at an active site. Given the rigidity of the architecture it seems likely that there is little dynamics possible, though we have not performed TPS calculations or conformational hunting on the free energy surface for this enzyme. Such work may be useful to validate these theoretical hypotheses. This enzyme also seems to speak to a constant question that is raised when rapid motions are implicated in chemistry. That is how is it possible that natural selection could act on such effects, when they are never to our knowledge rate limiting. This enzyme seems to point to the fact that primordial enzymes were little more than active sites. Evolutionary modification of these initial active site geometries and simple dynamics likely came first, followed by the creation of our now recognized complex protein architecture. We may speculate that this was done for both regulatory purposes and for catalytic efficiency. Thus the order of evolutionary development may well be crude active site (as in the DHFR mentioned above) followed by protein dynamics, finally followed by regulatory mechanism. We do not know if it is possible to investigate such hypotheses with the modern arsenal of bioinformatics, but it seems an intriguing proposition for research.

The next area of work is really an extension of the calculations we have reported previously and here. That is an investigation of the sampling in a TPS simulation. Like any Monte Carlo algorithm, it is possible that the TPS methodology can get trapped in local minima. There has been significant work in conformational sampling to find ways around this, but it is less clear how this might relate to reactive trajectories. The problem is further complicated by the fact that generation of the first seed trajectory for TPS is often the hardest part of the entire endeavor. This makes it unlikely that a way around this problem is to generate multiple different starting “seeds.” The best approach would thus seem to be to execute shooting moves with as large a perturbation as possible. This will of course significantly lower the acceptance probability of each move, but should maximize the probability of escape from a trap. We are currently attempting this for both LDH and DHFR. In the case of LDH while we are able to see distinct areas of trajectory space, the variability of structures on the stochastic separatrix still seems quite low. DHFR presents an interesting difficulty. Because, as mentioned, the protein is significantly more flexible than LDH large perturbation of the system via large shooting moves rapidly generates trajectories that are unstable as manifest by atomic clashes. Further experimentation will tell if this can be avoided, but it seems at present that this protein is simply barely stable in the reactive conformation.

Another area of work is to add quantum dynamics to the TPS methodology. TPS is inherently a classical simulation tool. As such, the only clear way to add quantum mechanics is to do so as an approximate add-on to classical mechanics. We⁴⁹ and Reichman⁵⁰ have suggested that centroid MD⁵¹ is a possible way around this problem. Because centroid MD is a fully classical methodology on a modified “quantumized” potential, all the standard features of TPS can be maintained. We are currently implementing this method for hydride transfer to test how the conclusions of previous work may vary if quantum tunneling is allowed for the transferring particles. Because tunneling is maximized by shortening the barrier, and this is consonant with barrier lowering when donor and acceptor are moved closer together, there is no reason to expect any significant changes in conclusion, but for completeness, the calculation will be done. There is in fact a fascinating question that can be addressed once this technology is developed – that is the “use” of tunneling by evolution. In other words, addressing the question of whether the structures of enzymes have evolved to maximize tunneling. There have been arguments both for and against this. At first glance this question seems foolish – evolution should not be anthropomorphized and it does not “know” about quantum mechanics. If the goal is to make the chemical step happen at a certain rate, then all chemistry will be explored to make that happen. Having said that, there has been published data (though not unquestioned) that purported to show that amounts of tunneling in enzymatic systems were exactly the same as in solution reactions⁵². The question can be far more directly addressed with classical and quantum TPS simulations. If there are significant deviations between classical and quantum reaction coordinates, then it is shown that quantum mechanics plays a significant role. Enzymes at different stages of evolution can then be compared in this fashion.

CONCLUSIONS

The work we have described in this feature article describes current and past work on the importance of enzyme motion on the chemical event of barrier crossing. As we have described, to the extent that one believes that such basic methodologies as molecular mechanics and QM/MM simulations are valid, then it is clear that the generation of an ensemble of reactive trajectories and their subsequent analysis via committor distributions or the methods we have developed based on the topology of the separatrix show unequivocally that in a few specific enzyme cases (LDH and PNP) hundreds of femtosecond motion are part of the reaction process and hence part of the reaction coordinate. In addition, in the case of LDH, the motion is directly identifiable as a compression motion, and this motion forms a preferred channel for heat conduction. It equally well seems that such motions are not part of the barrier passage mechanism of DHFR.

It is worth returning to the argument that such fast motions could simply not be part of the catalytic mechanism because they are so many orders of magnitude faster than turnover. It must be noted, the rate of turnover of an enzyme is rarely governed by chemistry. This certainly does not imply that chemical mechanism is not important, and that enzymes have not developed catalytic mechanism to allow barrier passage many orders of magnitude faster than enzymatic turnover. The question of how these designs were crafted through evolution is a deep one, and not part of the current discussion. We suggest, however, that consideration of such protein motions (dynamics) should be made a part of artificial protein design, though such inclusion makes the design problem even more complex. It may be hypothesized that lack of attention to this concept in such otherwise completely reasonable approaches such as catalytic antibodies⁵³ is one of the reasons that catalysts created this way are still so far from proficiency of even fairly mediocre enzymes. The final comment to make is that the accuracy of a statistical theory (finding the right free energy barrier) while incredibly useful does not answer the types of mechanistic question we have here posed.

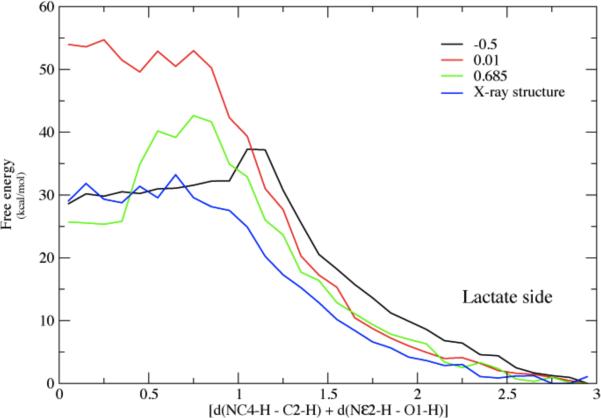
Figure 5a.

Converged average potential energies between stable, low-distance donor acceptor conformations. The energies are computed using finite temperature string methods. Numerical labels are arbitrary names given to clusters of conformations that structural analysis showed to be identical. The x-axis, which denotes conformational variation, is the string image number.

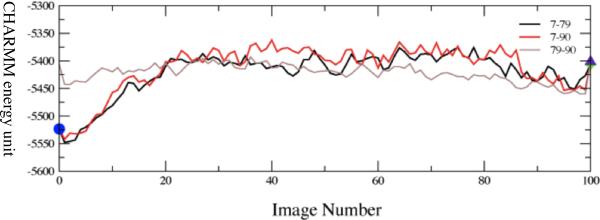
Figure 5b.

The converged free energy corresponding to one of the potential energy curves above (red curve labeled 7–90.) Note that the minima in average potential energy are on the edges of a rising free energy. The minima on Figure 5a given in string images correspond to −.50 and + .69 angstroms in Δ-RMSD units along the string coordinate on 5b.

Biographies

Steven Schwartz received the B.A. from Columbia College in New York in 1980, majoring in Chemistry and Mathematics. He studied for the Ph.D. with Bill Miller at UC Berkeley, graduating in 1984. After a postdoc with Phil Pechukas, he joined AT&T Bell Laboratories as a Member of Technical Staff. He joined the faculty of the Albert Einstein College of Medicine in 1994, where he is currently Professor of Biophysics and Biochemistry. In July 2012 he will join the chemistry department of the University of Arizona. His research interests revolve around theoretical investigations of enzymatic reactions, condensed phase chemistry, and mixed quantum classical methodologies.

Dimitri Antoniou received his B.Sc. in Physics from the University of Athens, Greece, in 1985, and his Ph.D. in Theoretical Condensed Matter Physics from Indiana University in 1991. He joined the Department of Biophysics at the Albert Einstein College of Medicine in 1994 as a postdoctoral associate, and since 2001 he has been employed there as Research Faculty. His research interests include applications of methods of nonequilibrium statistical physics to chemical and biological systems